Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique
Abstract
1. Introduction
2. Methodology
2.1. Description of Uncertainty Sources
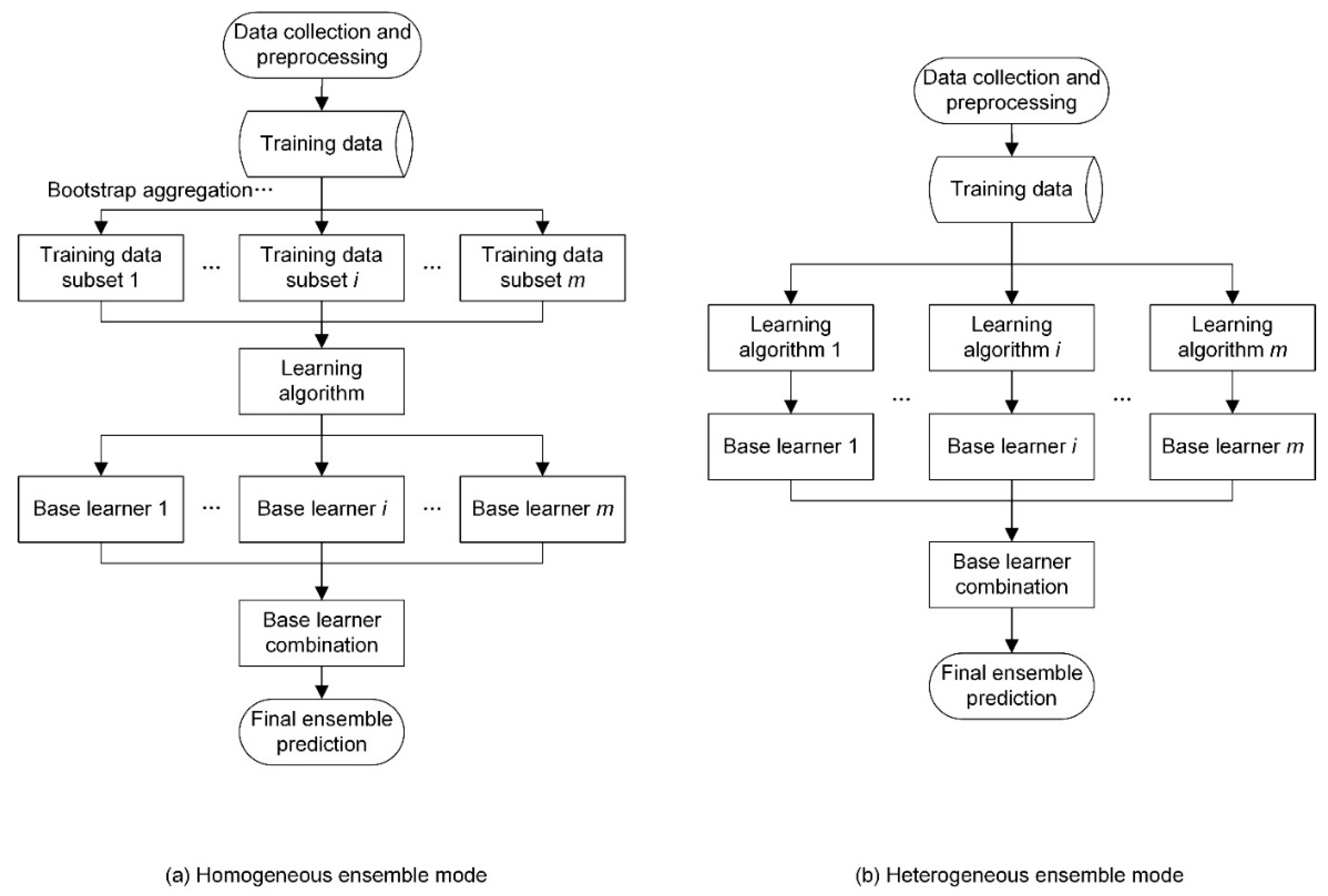
2.2. Ensemble Prediction
2.3. Quantile Regression Neural Network
2.3.1. Quantile Regression
2.3.2. Quantile Regression Neural Network
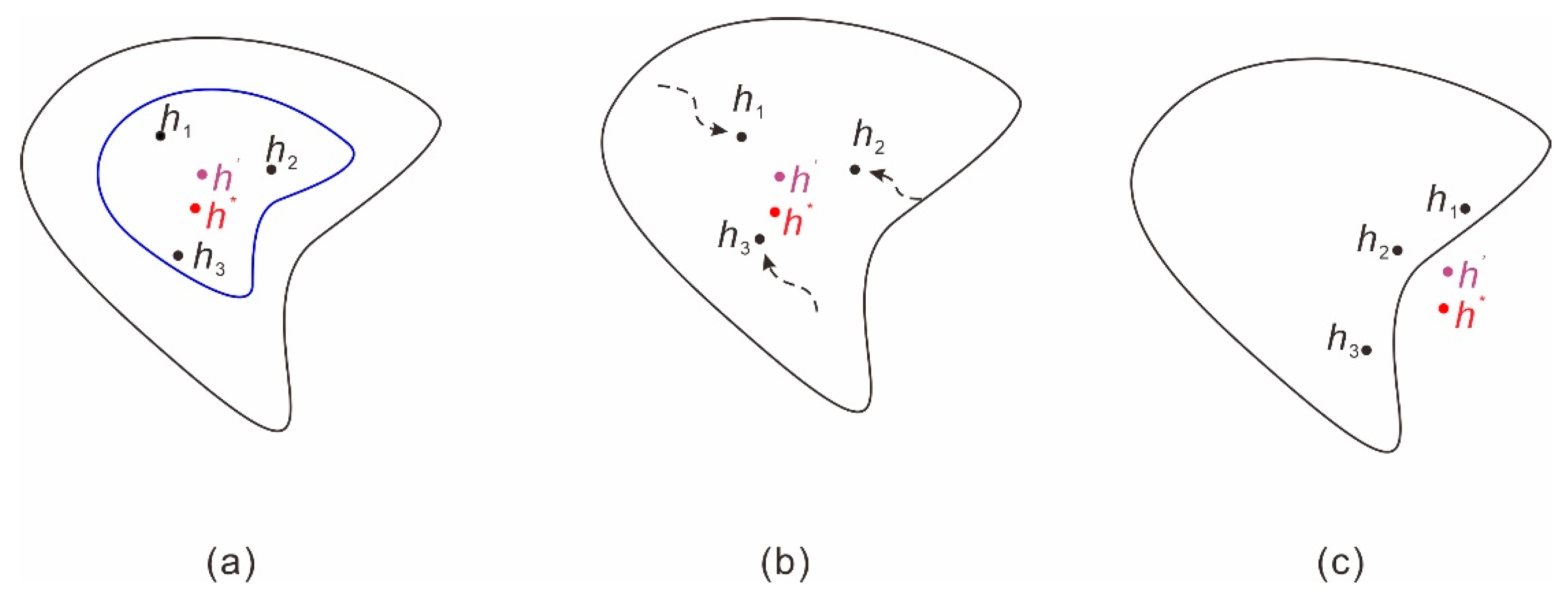
2.4. Kernel Density Estimation (KDE)
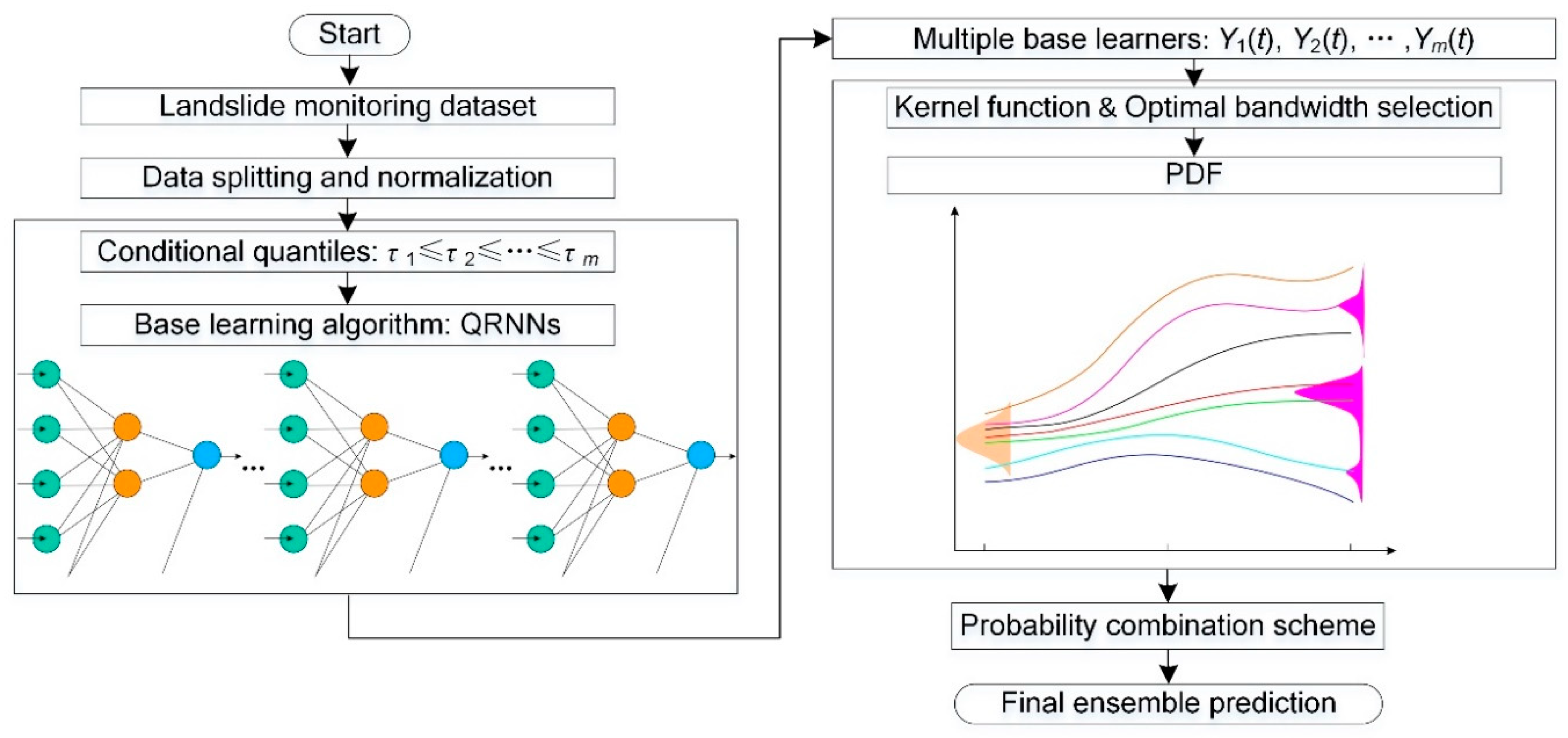
2.5. Ensemble Prediction Employing QRNNs and KDE
2.6. Evaluation Metrics and Uncertainty Quantification
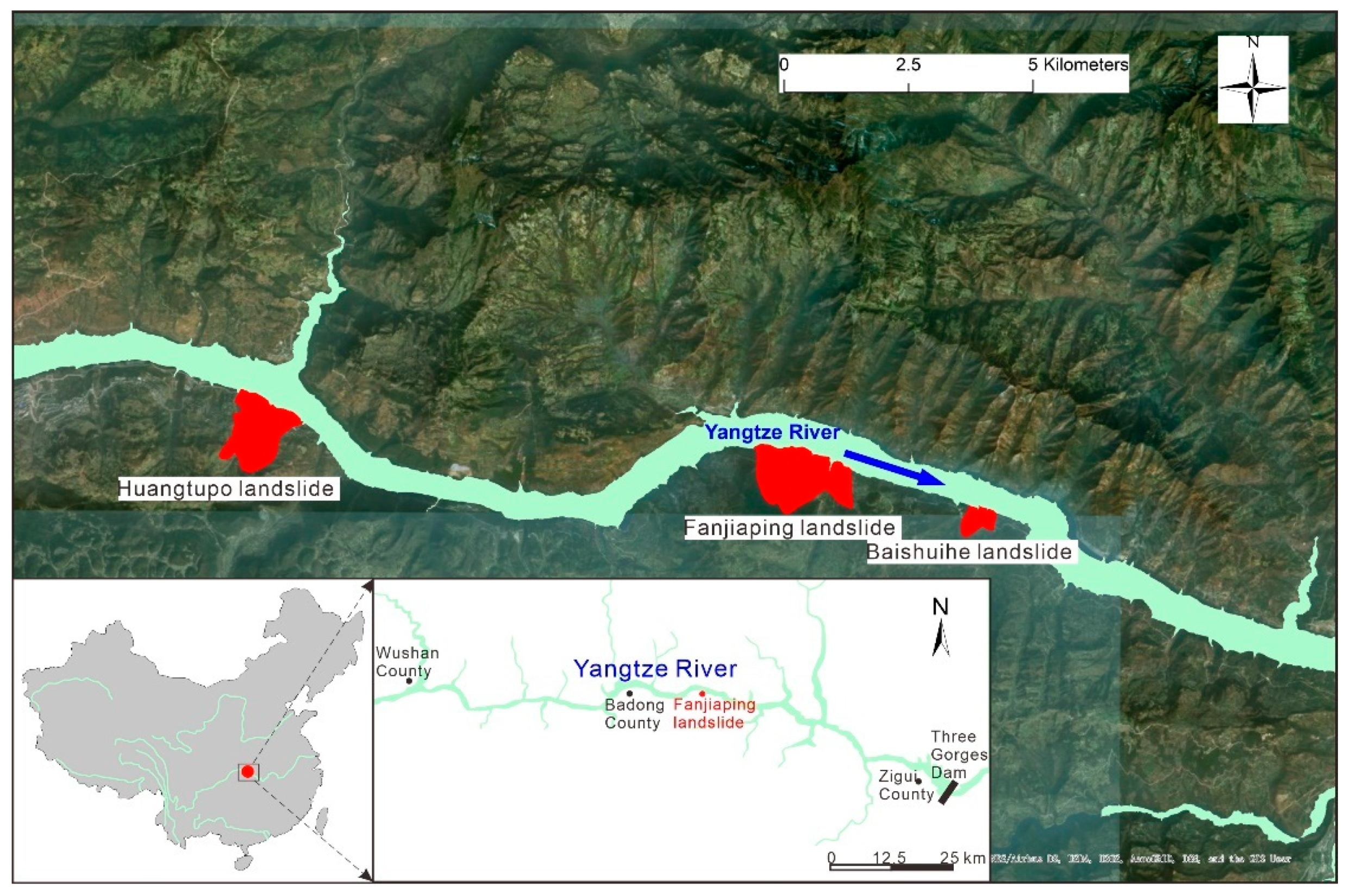
3. Case Study: Fanjiaping Landslide
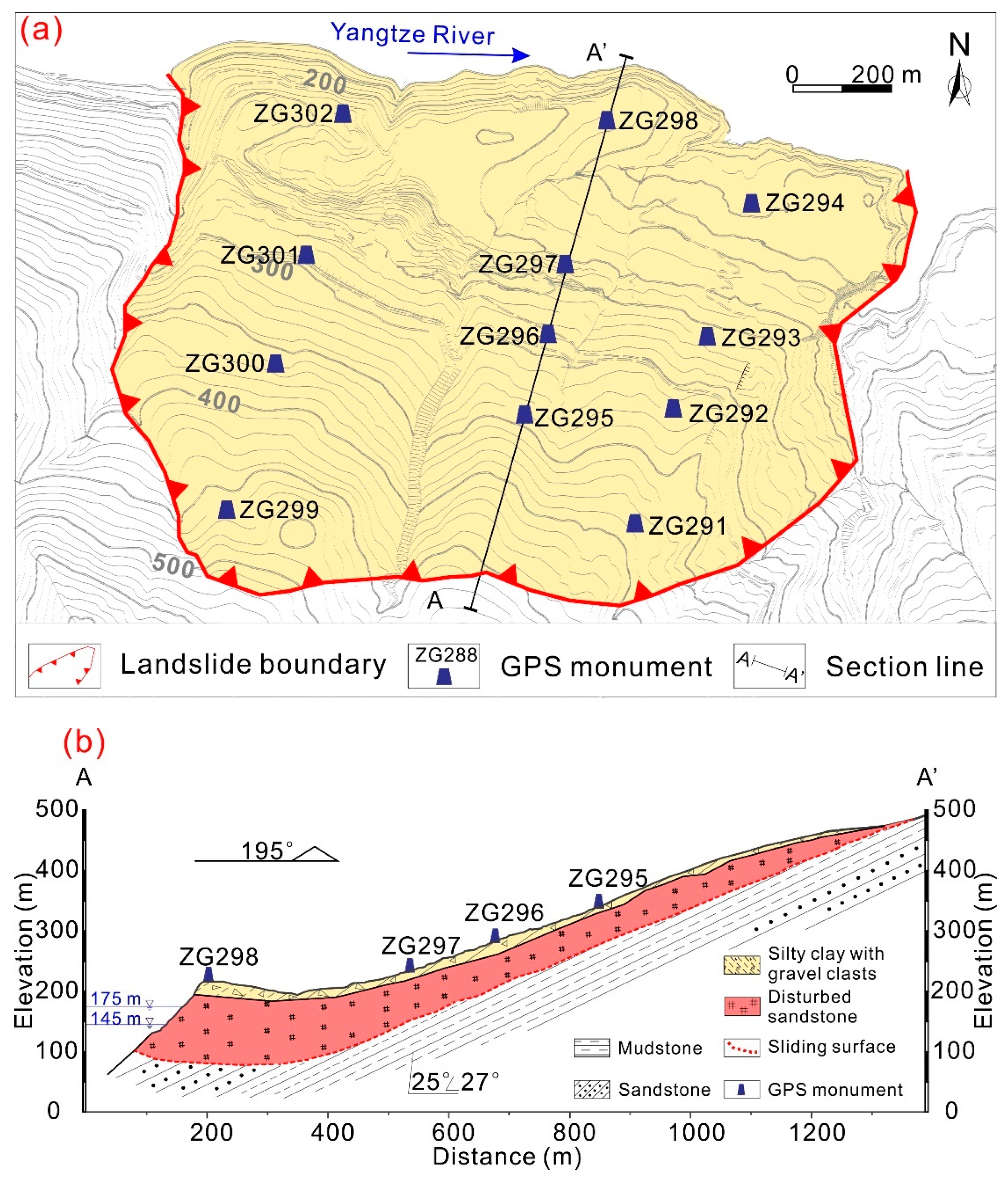
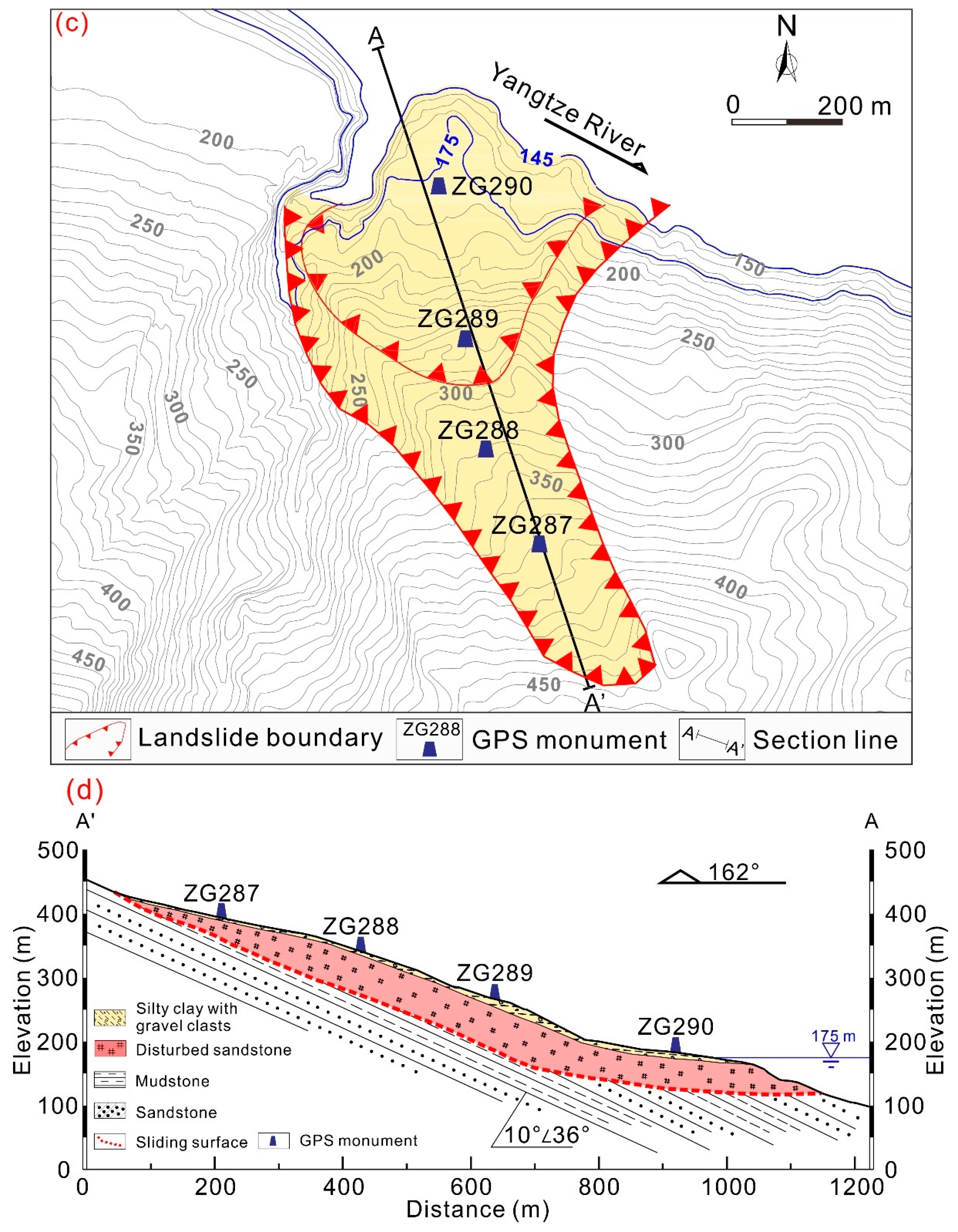
3.1. Features of the Fanjiaping Landslide
3.2. Input Data
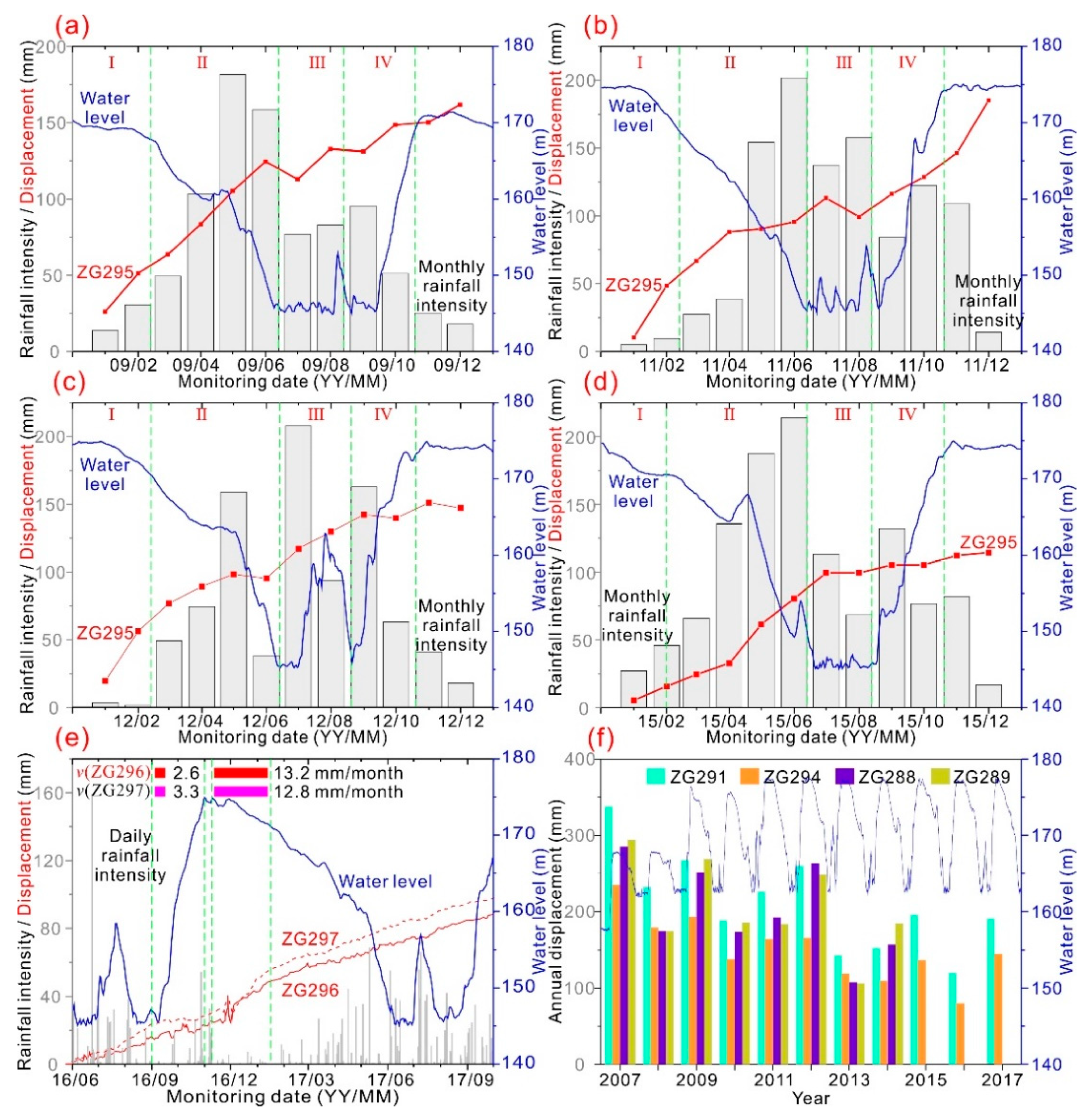
3.3. Triggering Factors of the Landslide Movements
3.4. QRNNs-KDE-Based Method for Ensemble Prediction
3.4.1. Data Splitting and Normalization
3.4.2. QRNN Modelling
3.4.3. PDF Estimation by KDE
3.4.4. Final Ensemble Prediction
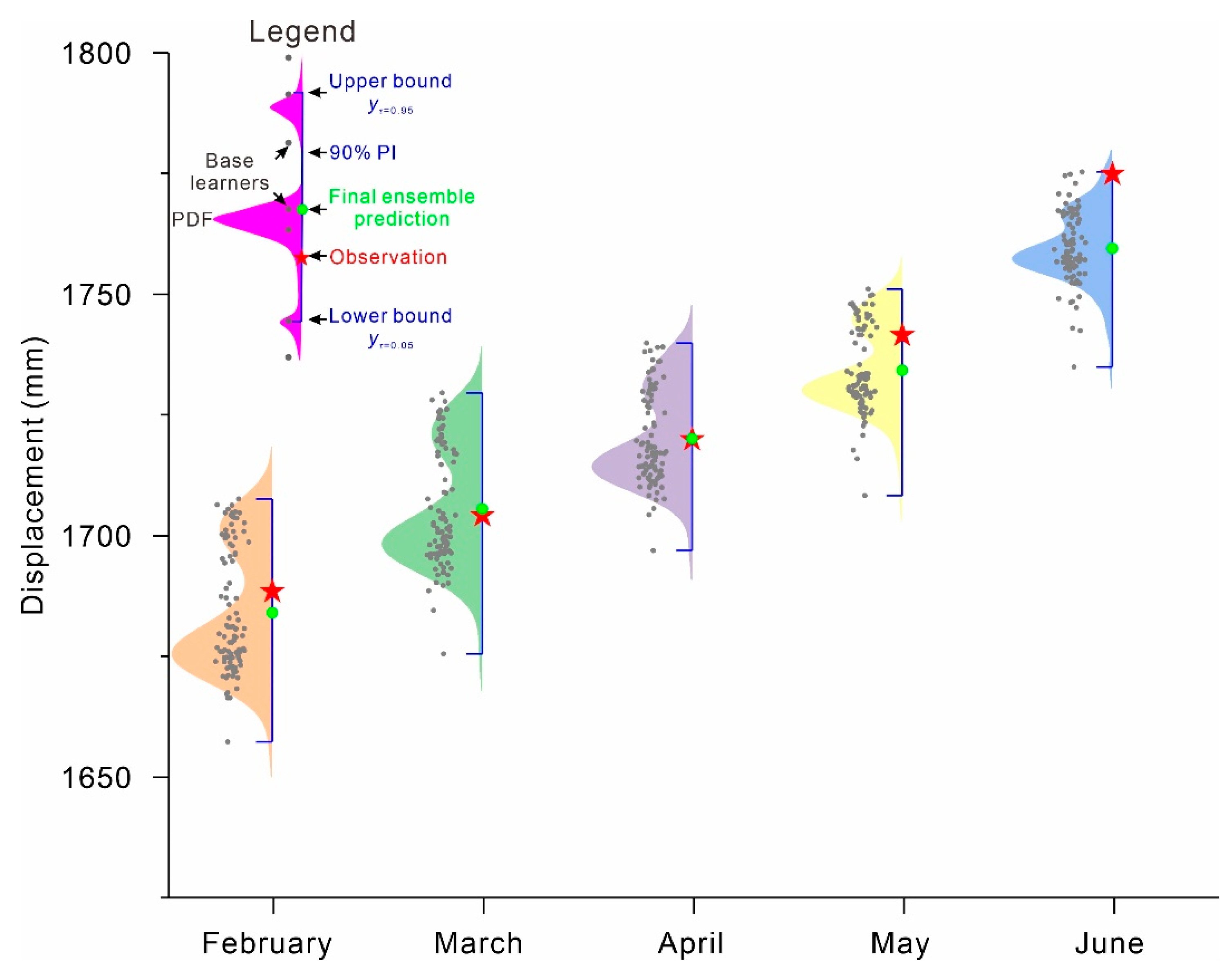
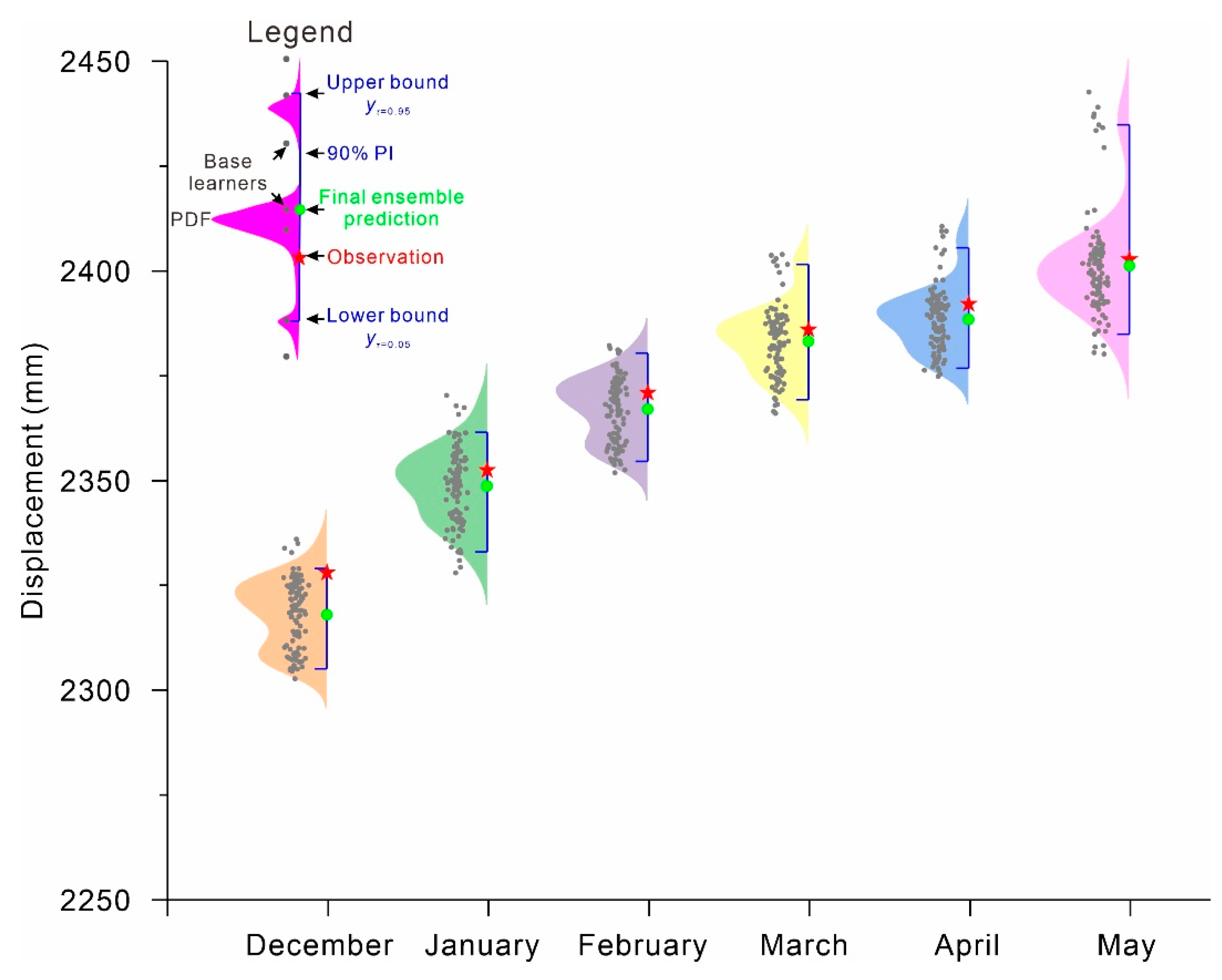
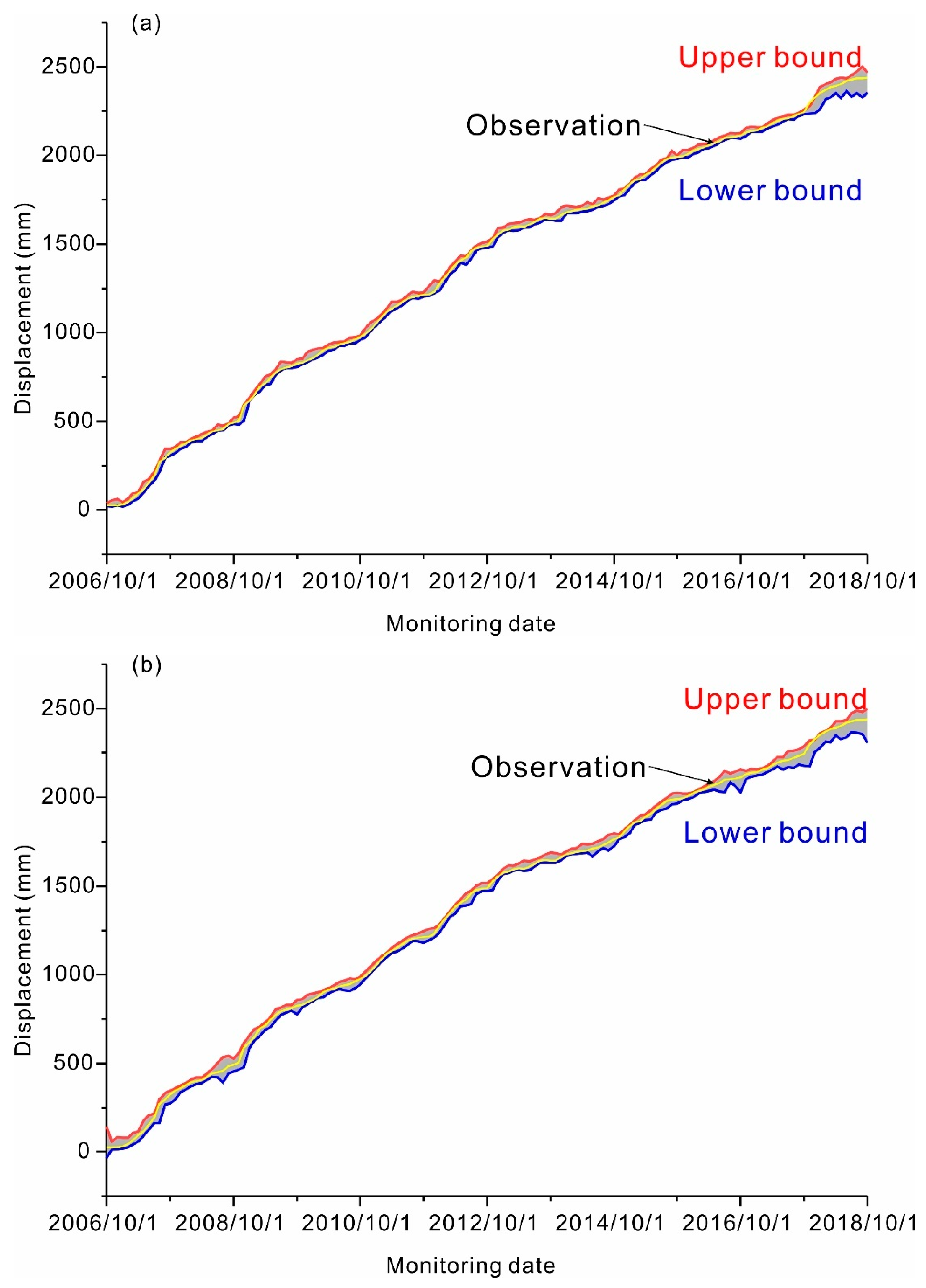
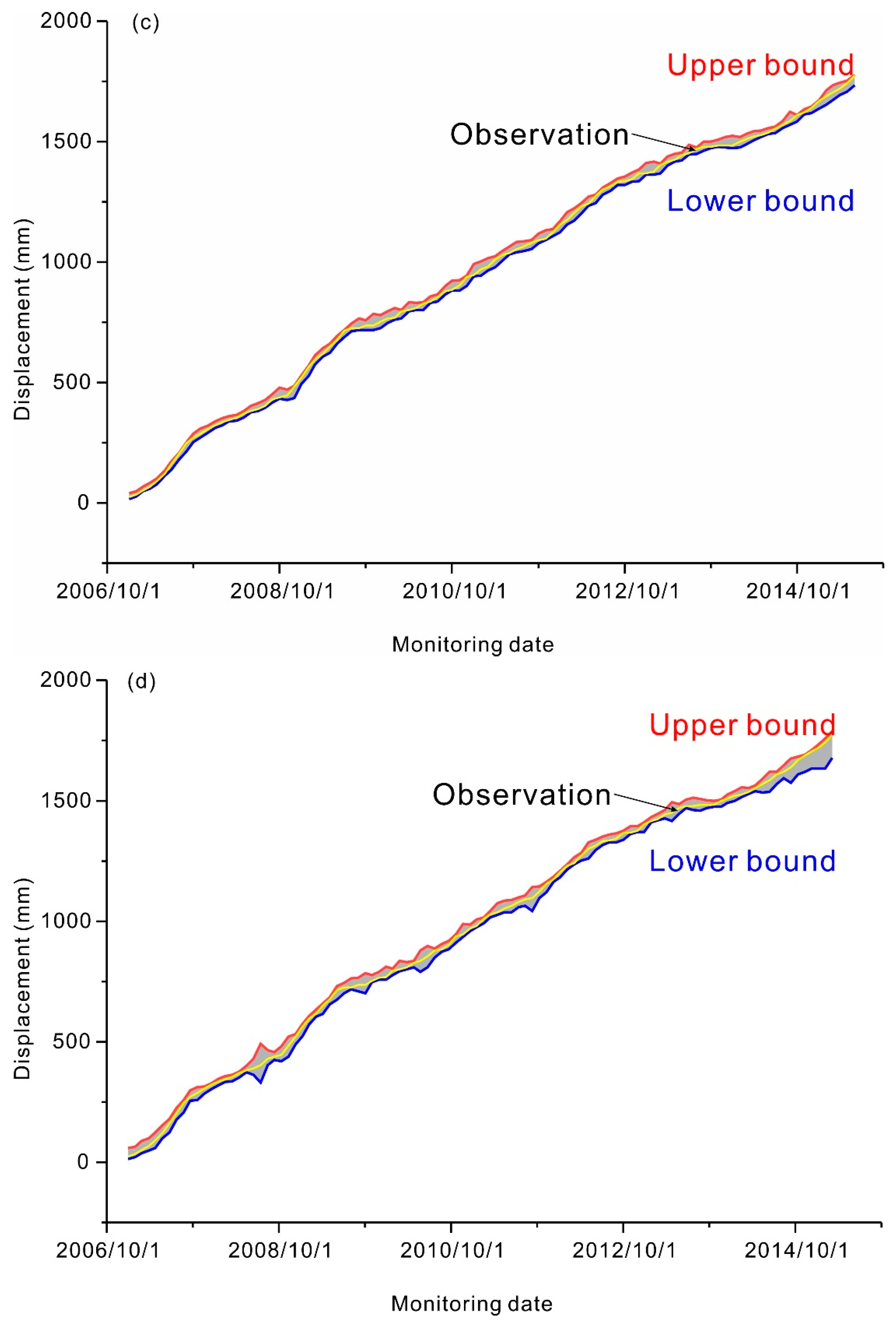
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- CRED. EM-DAT: International Disaster Database. Available online: https://public.emdat.be/data (accessed on 9 June 2020).
- Wang, Y.; Tang, H.; Wen, T.; Ma, J. Direct Interval Prediction of Landslide Displacements Using Least Squares Support Vector Machines. Complexity 2020, 2020, 7082594. [Google Scholar] [CrossRef]
- Ma, J.W.; Niu, X.X.; Tang, H.M.; Wang, Y.K.; Wen, T.; Zhang, J.R. Displacement Prediction of a Complex Landslide in the Three Gorges Reservoir Area (China) Using a Hybrid Computational Intelligence Approach. Complexity 2020, 2020, 2624547. [Google Scholar] [CrossRef]
- Ma, J.W.; Tang, H.M.; Liu, X.; Wen, T.; Zhang, J.R.; Tan, Q.W.; Fan, Z.Q. Probabilistic forecasting of landslide displacement accounting for epistemic uncertainty: A case study in the Three Gorges Reservoir area, China. Landslides 2018, 15, 1145–1153. [Google Scholar] [CrossRef]
- Pinto, F.; Guerriero, L.; Revellino, P.; Grelle, G.; Senatore, M.R.; Guadagno, F.M. Structural and lithostratigraphic controls of earth-flow evolution, Montaguto earth flow, Southern Italy. J. Geol. Soc. Lond. 2016, 173, 649. [Google Scholar] [CrossRef]
- Guerriero, L.; Diodato, N.; Fiorillo, F.; Revellino, P.; Grelle, G.; Guadagno, F.M. Reconstruction of long-term earth-flow activity using a hydroclimatological model. Nat. Hazards 2015, 77, 1–15. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R.; Schulz, W.H.; Fielding, E.J. Four-dimensional surface motions of the Slumgullion landslide and quantification of hydrometeorological forcing. Nat. Commun. 2020, 11, 2792. [Google Scholar] [CrossRef]
- Ma, J.W.; Tang, H.M.; Hu, X.L.; Bobet, A.; Zhang, M.; Zhu, T.W.; Song, Y.J.; Ez Eldin, M.A.M. Identification of causal factors for the Majiagou landslide using modern data mining methods. Landslides 2017, 14, 311–322. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gili, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Li, S.H.; Wu, L.Z.; Chen, J.J.; Huang, R.Q. Multiple data-driven approach for predicting landslide deformation. Landslides 2020, 17, 709–718. [Google Scholar] [CrossRef]
- Saito, M. Forecasting the time of occurrence of a slope failure. In Proceedings of the 6th International Congress of Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; pp. 537–541. [Google Scholar]
- Hayashi, S.; Komamura, F.; Park, B.W.; Yamamori, T. On the forecast of time to failure of slope-Approximate forecast in the early period of the tertiary creep. J. Jpn. Landslide Soc. 1988, 25, 11–16. [Google Scholar] [CrossRef]
- Federico, A.; Popescu, M.; Fidelibus, C.; Interno, G. On the prediction of the time of occurrence of a slope failure: A review. In Proceedings of the 9th International Symposium on Landslides, Rio de Janeiro, Brazil, 28 June–2 July 2004; pp. 979–983. [Google Scholar]
- Ma, J.W.; Tang, H.M.; Liu, X.; Hu, X.L.; Sun, M.J.; Song, Y.J. Establishment of a deformation forecasting model for a step-like landslide based on decision tree C5.0 and two-step cluster algorithms: A case study in the Three Gorges Reservoir area, China. Landslides 2017, 14, 1275–1281. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.M.; Wang, Y.K.; Lin, C.Y.; Xiong, C.R. Landslide displacement prediction using the GA-LSSVM model and time series analysis: A case study of Three Gorges Reservoir, China. Nat. Hazards Earth Syst. Sci. 2017, 17, 2181–2198. [Google Scholar] [CrossRef]
- Huang, F.M.; Yin, K.L.; Zhang, G.R.; Gui, L.; Yang, B.B.; Liu, L. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory. Environ. Earth Sci. 2016, 75, 1376. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.P.; Zhang, G.D.; Xue, Y.D. Probabilistic prediction of slope failure time. Eng. Geol. 2020, 271, 105586. [Google Scholar] [CrossRef]
- Yao, W.; Zeng, Z.G.; Lian, C. Generating probabilistic predictions using mean-variance estimation and echo state network. Neurocomputing 2017, 219, 536–547. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Zhu, Y.J. Ensemble forecast: A new approach to uncertainty and predictability. Adv. Atmos. Sci. 2005, 22, 781–788. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sust. Energ. Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Rigamonti, M.; Baraldi, P.; Zio, E.; Roychoudhury, I.; Goebel, K.; Poll, S. Ensemble of optimized echo state networks for remaining useful life prediction. Neurocomputing 2018, 281, 121–138. [Google Scholar] [CrossRef]
- Kim, M.-J.; Kang, D.-K. Ensemble with neural networks for bankruptcy prediction. Expert Syst. Appl. 2010, 37, 3373–3379. [Google Scholar] [CrossRef]
- Prayogo, D.; Cheng, M.-Y.; Wu, Y.-W.; Tran, D.-H. Combining machine learning models via adaptive ensemble weighting for prediction of shear capacity of reinforced-concrete deep beams. Eng. Comput. Ger. 2019, 36, 1135–1153. [Google Scholar] [CrossRef]
- Chen, K.; Jiang, J.; Zheng, F.; Chen, K. A novel data-driven approach for residential electricity consumption prediction based on ensemble learning. Energy 2018, 150, 49–60. [Google Scholar] [CrossRef]
- Lee, D.; Baldick, R. Short-Term Wind Power Ensemble Prediction Based on Gaussian Processes and Neural Networks. IEEE Trans. Smart Grid 2014, 5, 501–510. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, Q.; Wang, H.; Deng, M. A Machine Learning Ensemble Approach Based on Random Forest and Radial Basis Function Neural Network for Risk Evaluation of Regional Flood Disaster: A Case Study of the Yangtze River Delta, China. Int. J. Environ. Res. Public Health 2020, 17, 49. [Google Scholar] [CrossRef]
- Di Napoli, M.; Carotenuto, F.; Cevasco, A.; Confuorto, P.; Di Martire, D.; Firpo, M.; Pepe, G.; Raso, E.; Calcaterra, D. Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 2020. [Google Scholar] [CrossRef]
- Srivastav, R.K.; Sudheer, K.P.; Chaubey, I. A simplified approach to quantifying predictive and parametric uncertainty in artificial neural network hydrologic models. Water Resour. Res. 2007, 43, W10407. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet-bootstrap-ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; He, J.; Sudheer, K.P.; Tay, J.-H. Potential application of wavelet neural network ensemble to forecast streamflow for flood management. J. Hydrol. 2016, 536, 161–173. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, W.H.; Zhang, L.M.; Huang, H.W. Characterising geotechnical model uncertainty by hybrid Markov Chain Monte Carlo simulation. Comput. Geotech. 2012, 43, 26–36. [Google Scholar] [CrossRef]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. UK 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Xu, Q.F.; Liu, X.; Jiang, C.X.; Yu, K.M. Quantile autoregression neural network model with applications to evaluating value at risk. Appl. Soft Comput. 2016, 49, 1–12. [Google Scholar] [CrossRef]
- Donaldson, R.G.; Kamstra, M. Forecast combining with neural networks. J. Forecast. 1996, 15, 49–61. [Google Scholar] [CrossRef]
- Charlton, T.S.; Rouainia, M. Probabilistic capacity analysis of suction caissons in spatially variable clay. Comput. Geotech. 2016, 80, 226–236. [Google Scholar] [CrossRef]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects; Springer: New York, NY, USA, 2017. [Google Scholar]
- Zhang, S.; Ma, J.W.; Tang, H.M. Estimation of Risk Thresholds for a Landslide in the Three Gorges Reservoir Based on a KDE-Copula-VaR Approach. Geofluids 2020, 2020, 8030264. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Wang, Y.L.; Dong, Z.Y.; Wong, K.P. A hybrid approach for probabilistic forecasting of electricity price. IEEE Trans. Smart Grid 2014, 5, 463–470. [Google Scholar] [CrossRef]
- Wang, Y.K.; Tang, H.M.; Wen, T.; Ma, J.W. A hybrid intelligent approach for constructing landslide displacement prediction intervals. Appl. Soft Comput. 2019, 81, 105506. [Google Scholar] [CrossRef]
- Zhang, L.; Liao, M.S.; Balz, T.; Shi, X.G.; Jiang, Y.N. Monitoring landslide activities in the Three Gorges area with multi-frequency satellite SAR data sets. In Modern Technologies for Landslide Monitoring and Prediction; Scaioni, M., Ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2015; pp. 181–208. [Google Scholar] [CrossRef]
- Fan, J.H.; Qiu, K.T.; Xia, Y.; Li, M.; Lin, H.; Zhang, H.T.; Tu, P.F.; Liu, G.; Shu, S.Q. InSAR monitoring and synthetic analysis of the surface deformation of Fanjiaping landslide in the Three Gorges Reservoir area. Geol. Bull. China 2017, 36, 1665–1673. [Google Scholar]
- Guerriero, L.; Coe, J.A.; Revellino, P.; Grelle, G.; Pinto, F.; Guadagno, F.M. Influence of slip-surface geometry on earth-flow deformation, Montaguto earth flow, southern Italy. Geomorphology 2014, 219, 285–305. [Google Scholar] [CrossRef]
- Guerriero, L.; Bertello, L.; Cardozo, N.; Berti, M.; Grelle, G.; Revellino, P. Unsteady sediment discharge in earth flows: A case study from the Mount Pizzuto earth flow, southern Italy. Geomorphology 2017, 295, 260–284. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Proceedings of the Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Du, J.; Yin, K.L.; Lacasse, S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China. Landslides 2013, 10, 203–218. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Maximum number of iterations | 5000 | Penalty for weight decay regularization | 1 |
| Number of quantiles | 99 | Number of input nodes | 7 |
| Number of repeated trials | 5 | Number of hidden nodes | 5 |
| Monitoring Point | Model | BP | RBF | ELM | SVM | QRNNs-KDE | |
|---|---|---|---|---|---|---|---|
| Index | |||||||
| ZG289 | R2 | 0.99730 | 0.99992 | 0.99785 | 0.99993 | 0.99997 | |
| MSE | 3192.07 | 99.54 | 2538.74 | 78.12 | 30.69 | ||
| RMSE | 56.50 | 9.98 | 50.39 | 8.84 | 5.54 | ||
| NRMSE | 0.032263 | 0.005697 | 0.028772 | 0.005047 | 0.003163 | ||
| MAPE | 2.74 | 2.00 | 1.57 | 1.27 | 1.17 | ||
| ZG291 | R2 | 0.99991 | 0.99759 | 0.99991 | 0.99995 | 0.99997 | |
| MSE | 206.32 | 5684.98 | 215.41 | 119.75 | 70.15 | ||
| RMSE | 14.36 | 75.40 | 14.68 | 10.94 | 8.38 | ||
| NRMSE | 0.005953 | 0.031251 | 0.006083 | 0.004536 | 0.003471 | ||
| MAPE | 3.97 | 1.96 | 2.59 | 2.33 | 0.41 | ||
| Monitoring Point | Index | PICP | NPIW | CWC | |
|---|---|---|---|---|---|
| Model | |||||
| ZG289 | Bootstrap-ELM-ANN | 100% | 0.27 | 0.2071 | |
| QRNNs-KDE | 100% | 0.0215 | 0.1661 | ||
| ZG291 | Bootstrap-ELM-ANN | 99% | 0.024 | 0.143 | |
| QRNNs-KDE | 99% | 0.018 | 0.085 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Liu, X.; Niu, X.; Wang, Y.; Wen, T.; Zhang, J.; Zou, Z. Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique. Int. J. Environ. Res. Public Health 2020, 17, 4788. https://doi.org/10.3390/ijerph17134788
Ma J, Liu X, Niu X, Wang Y, Wen T, Zhang J, Zou Z. Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique. International Journal of Environmental Research and Public Health. 2020; 17(13):4788. https://doi.org/10.3390/ijerph17134788
Chicago/Turabian StyleMa, Junwei, Xiao Liu, Xiaoxu Niu, Yankun Wang, Tao Wen, Junrong Zhang, and Zongxing Zou. 2020. "Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique" International Journal of Environmental Research and Public Health 17, no. 13: 4788. https://doi.org/10.3390/ijerph17134788
APA StyleMa, J., Liu, X., Niu, X., Wang, Y., Wen, T., Zhang, J., & Zou, Z. (2020). Forecasting of Landslide Displacement Using a Probability-Scheme Combination Ensemble Prediction Technique. International Journal of Environmental Research and Public Health, 17(13), 4788. https://doi.org/10.3390/ijerph17134788









