Analyzing Factors Associated with Fatal Road Crashes: A Machine Learning Approach
Abstract
1. Introduction
2. Data Description
3. Method
3.1. Model Description
3.2. Data Pre-Processing
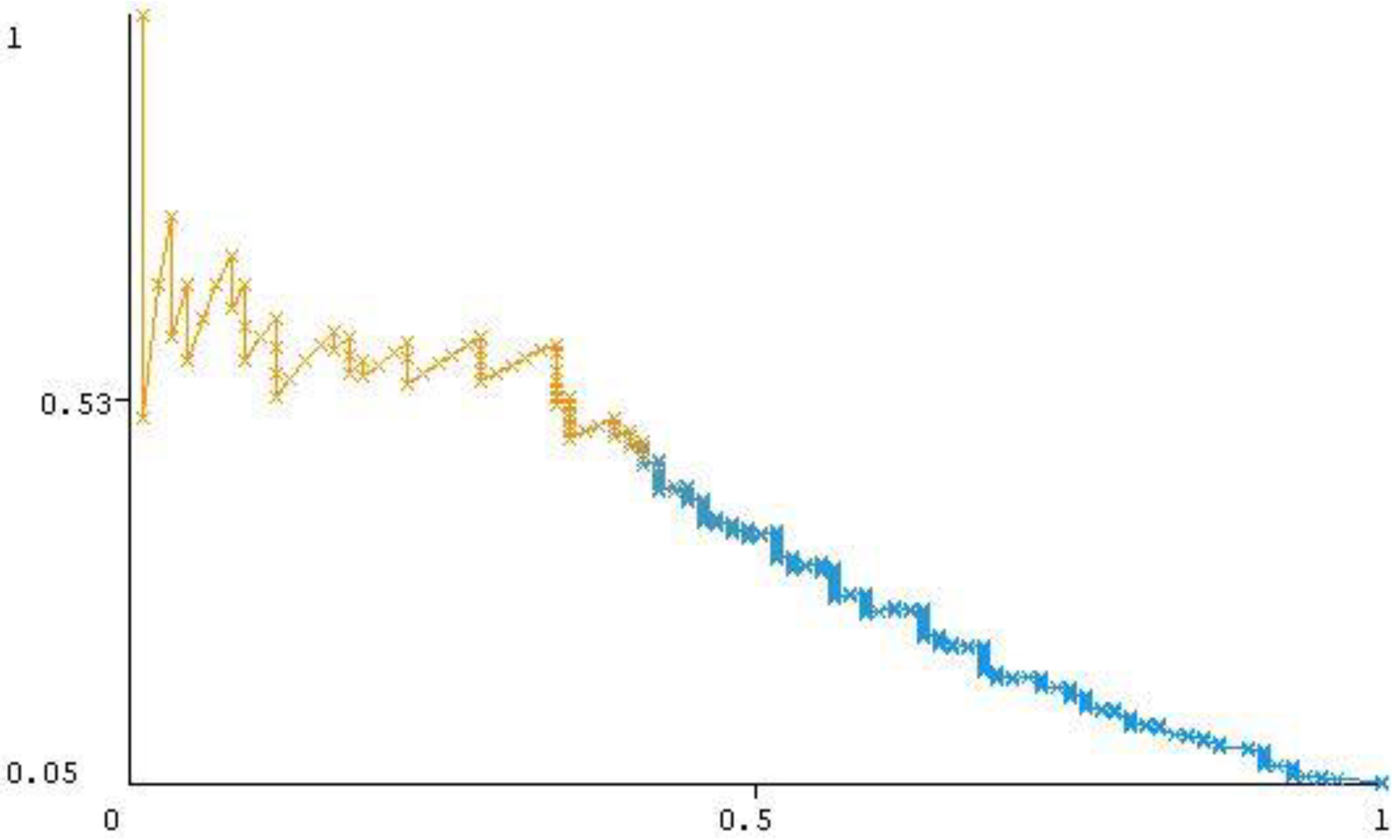
3.3. Metrics Evaluation
4. Results
4.1. Model Development
- Sequential minimal optimization (SMO).
- Random forest.
- Artificial neural network (ANN).
- Logistic regression.
- Naïve Bayes.
4.2. Model Performance
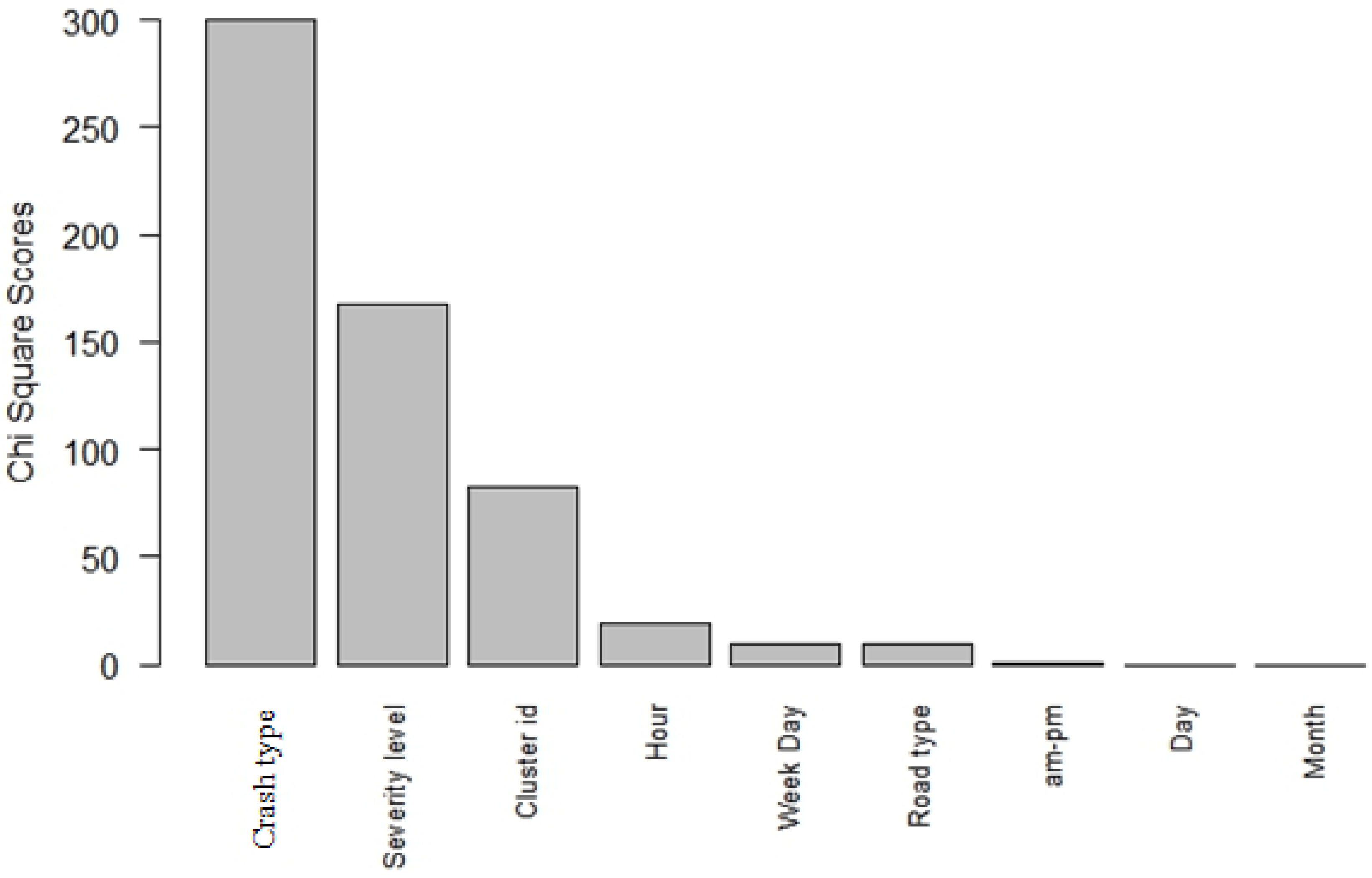
4.3. Attribute Evaluation Analysis
- Crash type: ‘Vehicle–pedestrian’ type was the strongest predictor of fatal road crashes. ‘Truck–bike’ type was the second strongest predictor of fatal road crashes within the crash type category.
- Injury severity level: The severity level variable was a major contributor to fatal crashes.
- Spatial cluster ID: Densely populated areas and the presence of major highway crossings proved to be correlated with increased traffic fatalities.
- Hour of road crash: Time of the day, more specifically 3 am, was highly correlated with fatality occurrence.
- Day of the week. Friday and Sunday were the two strong factors affecting the occurrence of fatal road injuries.
- Road type: Motorways are the main road types correlated with fatal crashes.
- AM-PM and day and month of the year were the least influencing factors on the fatality of the road crash.
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- World Health Organization (WHO). Global Status Report in Road Safety; World Health Organization (WHO): Geneva, Switzerland, 2018. [Google Scholar]
- Rolison, J.J.; Regev, S.; Moutari, S.; Feeney, A. What are the factors that contribute to road accidents? An assessment of law enforcement views, ordinary drivers’ opinions, and road accident records. Accid. Anal. Prev. 2018, 115, 11–24. [Google Scholar] [CrossRef] [PubMed]
- Altwaijri, S.; Quddus, M.A.; Bristow, A. Factors affecting severity of traffic crashes in Riyadh city. In Proceedings of the Transportation Research Board 90th Annual Meeting, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- Keall, M.; Frith, W.J.; Patterson, T.L. The influence of alcohol, age and number of passengers on the night-time risk of driver fatal injury in New Zealand. Accid. Anal. Prev. 2004, 36, 49–61. [Google Scholar] [CrossRef]
- Zajac, S.; Ivan, J.N. Factors influencing injury severity ofmotor vehicle-crossing pedestrian crashes in rural Connecticut. Accid. Anal. Prev. 2002, 35, 369–379. [Google Scholar] [CrossRef]
- Bédard, M.; Guyatt, G.H.; Stones, M.J.; Hirdes, J.P. The independent contribution of driver, crash, and vehicle characteristics to driver fatalities. Accid. Anal. Prev. 2002, 34, 717–727. [Google Scholar] [CrossRef]
- Valent, F.; Schiava, F.; Savonitto, C.; Gallo, T.; Brusaferro, S.; Barbone, F. Risk factors for fatal road traffic accidents in Udine, Italy. Accid. Anal. Prev. 2002, 34, 71–84. [Google Scholar] [CrossRef]
- Yau, K.K.; Yau, K.W.K. Risk factors affecting the severity of single vehicle traffic accidents in Hong Kong. Accid. Anal. Prev. 2004, 36, 333–340. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.S. Using logistic regression to estimate the influence of accident factors on accident severity. Accid. Anal. Prev. 2002, 34, 729–741. [Google Scholar] [CrossRef]
- Tay, R.; Choi, J.; Kattan, L.; Khan, A. A multinomial logit model of pedestrian—Vehicle crash severity. Int. J. Sustain. Transp. 2011, 5, 233–249. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Abdelwahab, H.T. Predicting injury severity levels in traffic crashes: A modeling comparison. J. Transp. Eng. 2004, 130, 204–210. [Google Scholar] [CrossRef]
- Abdel-Aty, M. Analysis of driver injury severity levels at multiple locations using ordered probit models. J. Saf. Res. 2003, 34, 597–603. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; Liang, F. Crash injury severity analysis using bayesian ordered probit models. J. Transp. Eng. 2009, 135, 18–25. [Google Scholar] [CrossRef]
- El Tayeb, A.; Pareek, V.; Araar, A. Applying association rules mining algorithms for traffic accidents in Dubai. Int. J. Soft Comput. Eng. 2015, 5, 2231–2307. [Google Scholar]
- Bigham, B. Road accident data analysis: A data mining approach. Indian J. Sci. Res. 2014, 3, 437–443. [Google Scholar]
- Aci, Ç. Predicting the severity of motor vehicle accident injuries in Adana-Turkey using machine learning methods and detailed meteorological data. Int. J. Intell. Syst. Appl. Eng. 2018, 1, 72–79. [Google Scholar] [CrossRef]
- Akgüngör, A.P.; Doğan, E. An artificial intelligent approach to traffic accident estimation: Model development and application. Transport 2009, 24, 135–142. [Google Scholar] [CrossRef]
- Ghandour, A.; Hammoud, H.; Telesca, L. Transportation hazard spatial analysis using crowd-sourced social network data. Phys. A Stat. Mech. Appl. 2019, 520, 309–316. [Google Scholar] [CrossRef]
- Webb, G.; Zheng, Z. Multi-strategy ensemble learning: Reducing error by combining ensemble learning tech-niques. IEEE Trans. Knowl. Data Eng. 2004, 16, 980–991. [Google Scholar] [CrossRef]
- Graczyk, M.; Lasota, T.; Trawinski, B.; Trawinski, K. Comparison of bagging, boosting and stacking ensembles applied to real estate appraisal. In Intelligent Information and Database Systems; Springer: Berlin/Heiderberg, Germany, 2010; pp. 340–350. [Google Scholar]
- Ganganwar, V. An overview of classification algorithms for imbalanced datasets. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 42–47. [Google Scholar]
- Chawla, N.; Bowyer, K.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Anguita, D.; Ghelardoni, L.; Ghio, A.; Oneto, L.; Ridella, S. The ‘K’in K-fold cross validation. In Proceedings of the ESANN 20th European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2012. [Google Scholar]
- Marzban, C. The ROC curve and the area under it as performance measures. Am. Meteorol. Soc. 2004, 9, 1106–1114. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning (ICML ’06), New York, NY, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Boyd, K.; Eng, K.H.; Page, D. Area under the precision-recall curve: Point estimates and confidence intervals. In Machine Learning and Knowledge Discovery in Databases; Lecture Notes in Computer Science; Blockeel, H., Kersting, K., Nijssen, S., Železný, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8190. [Google Scholar]
- Koch, J.R.L.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.; Witten, I. The WEKA Workbench. In Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Boyd, K.; Costa, V.S.; Davis, J.; Page, D. Unachievable region in precision-recall space and its effect on empirical evaluation. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, Scotland, 26 June–1 July 2012. [Google Scholar]
- Saito, T.; Rehmsmeier, M. The precision-recall plot is more informative than the roc plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.; Lloyd, M.; Sargent, G.; Feleke, R.; Mindell, J.S. Are head injuries to cyclists an important cause of death in road travel fatalities? J. Transp. Health 2018, 10, 178–185. [Google Scholar] [CrossRef]
- Al-Hajj, S.; Arjinian, S.; Hamadeh, Z.; Al-Zaghrini, E.; El-Asmar, K. Child transport injuries and deaths in Lebanon: Assessing the burden to implement safety strategies and shape policies. BMJ Open 2020. (accepted). [Google Scholar]
- Ackaah, W.; Adonteng, D.O. Analysis of fatal road traffic crashes in Ghana. Int. J. Inj. Control. Saf. Promot. 2011, 18, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Tulu, G.S.; Washington, S.; Haque, M.; King, M. Injury severity of pedestrians involved in road traffic crashes in Addis Ababa, Ethiopia. J. Transp. Saf. Secur. 2017, 9, 47–66. [Google Scholar] [CrossRef]
- Teye-Kwadjo, E. Risk factors for road transport–related injury among pedestrians in rural Ghana: Implications for road safety education. Health Educ. J. 2017, 76, 880–890. [Google Scholar] [CrossRef]
- Verzosa, N.; Miles, R. Severity of road crashes involving pedestrians in Metro Manila, Philippines. Accid. Anal. Prev. 2016, 94, 216–226. [Google Scholar] [CrossRef]
- Goniewicz, K.; Goniewicz, M.; Pawłowski, W.; Fiedor, P. Road accident rates: Strategies and programmes for improving road traffic safety. Eur. J. Trauma Emerg. Surg. 2015, 42, 433–438. [Google Scholar] [CrossRef]
- Buehler, R.; Pucher, J. Trends in walking and cycling safety: Recent evidence from high-income countries, with a focus on the United States and Germany. Am. J. Public Health 2016, 107, 281–287. [Google Scholar] [CrossRef]
- Talbot, R.; Reed, S.; Christie, N.; Barnes, J.; Thomas, P. Fatal and serious collisions involving pedal cyclists and trucks in London between 2007 and 2011. Traffic Inj. Prev. 2017, 18, 657–665. [Google Scholar] [CrossRef] [PubMed]
- Barman, D.D.; Karnaboopathy, R. Study of the pattern and injury severity score of fatal blunt abdominal injuries sustained in road traffic accident. J. Indian Acad. Forensic Med. 2019, 41, 158. [Google Scholar] [CrossRef]
- Vardhana, T.M.; Kumaran, M.; Reddy, A.; Naveen, N.; Arun, M.; Kagne, R.N. Profile of fatal road traffic accidents at puducherry-an autopsy based study. Indian J. Forensic Med. Toxicol. 2018, 12, 31. [Google Scholar] [CrossRef]
- Ghandour, A.; Lovallo, M.; Telesca, L. Time-clustering behavior and cycles in the time dynamics of car accident sequences in Lebanon. Phys. A Stat. Mech. Appl. 2019, 516, 178–184. [Google Scholar] [CrossRef]
- Plainis, S.; Murray, I.J.; Pallikaris, I.G. Road traffic casualties: Understanding the night-time death toll. Inj. Prev. 2006, 12, 125–128. [Google Scholar] [CrossRef] [PubMed]
- Abegaz, T.; Berhane, Y.; Worku, A.; Assrat, A.; Assefa, A. Effects of excessive speeding and falling asleep while driving on crash injury severity in Ethiopia: A generalized ordered logit model analysis. Accid. Anal. Prev. 2014, 71, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Algora-Buenafé, A.F.; Suasnavas-Bermúdez, P.R.; Merino-Salazar, P.; Gómez-García, A.R. Epidemiological study of fatal road traffic accidents in ecuador. Australas. Med. J. 2017, 10. [Google Scholar] [CrossRef]
- Gopaul, C.D.; Singh-Gopaul, A.; Sutherland, J.M.; Rostant, L.V.; Ebi, K.L.; Chadee, D.D. The epidemiology of fatal road traffic collisions in Trinidad and Tobago, West Indies (2000–2011). Glob. Health Action 2016, 9. [Google Scholar] [CrossRef]
- Ampanozi, G.; Kovatsi, L.; Smyrnakis, E.; Zaggelidou, E.; Gavana, M.; Papadakis, N.; Benos, A. Analysis of fatal motor vehicle collisions: Evidence from Central Macedonia, Greece. Hippokratia 2011, 15, 32–36. [Google Scholar]
- Qirjako, G.; Burazeri, G.; Hysa, B.; Roshi, E. Factors associated with fatal traffic accidents in Tirana, Albania: Cross-sectional study. Croat. Med. J. 2008, 49, 734–740. [Google Scholar] [CrossRef]
- Quezon, E.; Wedajo, T.; Mohammed, M. Analysis of road traffic accident related of geometric design parameters in Alamata-Mehoni-Hewane section. Int. J. Sci. Eng. Res. 2017, 8, 874–881. [Google Scholar]
| Variable | Range |
|---|---|
| Input Variables | |
| Month | 1–12 |
| Day | 1–31 |
| Day of the Week | Monday–Sunday |
| Hour of Crash | 0–23 |
| AM/PM | am, pm |
| Crash Type | Vehicle–Vehicle, Vehicle–Truck, Vehicle–Pedestrian, Vehicle–Motorcycle, Vehicle–Barrier, Truck–Truck, Truck–Motorcycle, Truck–Barrier, Motorcycle–Motorcycle, Motorcycle–Barrier, Other |
| Injury Severity Level | No Apparent-Injury, Minor Injury, Serious Injury |
| Road Type | Motorway, Trunk, Primary, Secondary, Tertiary, Unclassified |
| Spatial Cluster ID | 1–10 |
| Output Variable | |
| Fatality occurrence | Fatal, Not Fatal |
| F1-Score | AUC-PR | Kappa | |
|---|---|---|---|
| SMO | 0.493 | 0.276 | 0.4678 |
| Random Forest | 0.453 | 0.376 | 0.4258 |
| ANN | 0.385 | 0.291 | 0.3462 |
| Logistic Regression | 0.455 | 0.361 | 0.4309 |
| Naïve Bayes | 0.313 | 0.337 | 0.294 |
| F1-Score | AUC-PR | Kappa | |
|---|---|---|---|
| Bagging J48 100 decision trees | 0.464 | 0.382 | 0.4365 |
| Vote SMO with Bagging J48 | 0.511 | 0.402 | 0.4882 |
| Vote SMO with Bagging J48 | |
|---|---|
| F1-score | 0.435 |
| AUC-PR | 0.368 |
| Kappa | 0.4067 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghandour, A.J.; Hammoud, H.; Al-Hajj, S. Analyzing Factors Associated with Fatal Road Crashes: A Machine Learning Approach. Int. J. Environ. Res. Public Health 2020, 17, 4111. https://doi.org/10.3390/ijerph17114111
Ghandour AJ, Hammoud H, Al-Hajj S. Analyzing Factors Associated with Fatal Road Crashes: A Machine Learning Approach. International Journal of Environmental Research and Public Health. 2020; 17(11):4111. https://doi.org/10.3390/ijerph17114111
Chicago/Turabian StyleGhandour, Ali J., Huda Hammoud, and Samar Al-Hajj. 2020. "Analyzing Factors Associated with Fatal Road Crashes: A Machine Learning Approach" International Journal of Environmental Research and Public Health 17, no. 11: 4111. https://doi.org/10.3390/ijerph17114111
APA StyleGhandour, A. J., Hammoud, H., & Al-Hajj, S. (2020). Analyzing Factors Associated with Fatal Road Crashes: A Machine Learning Approach. International Journal of Environmental Research and Public Health, 17(11), 4111. https://doi.org/10.3390/ijerph17114111






