The Spread of the Covid-19 Pandemic in Time and Space
Abstract
1. Introduction
2. Methodology and Results
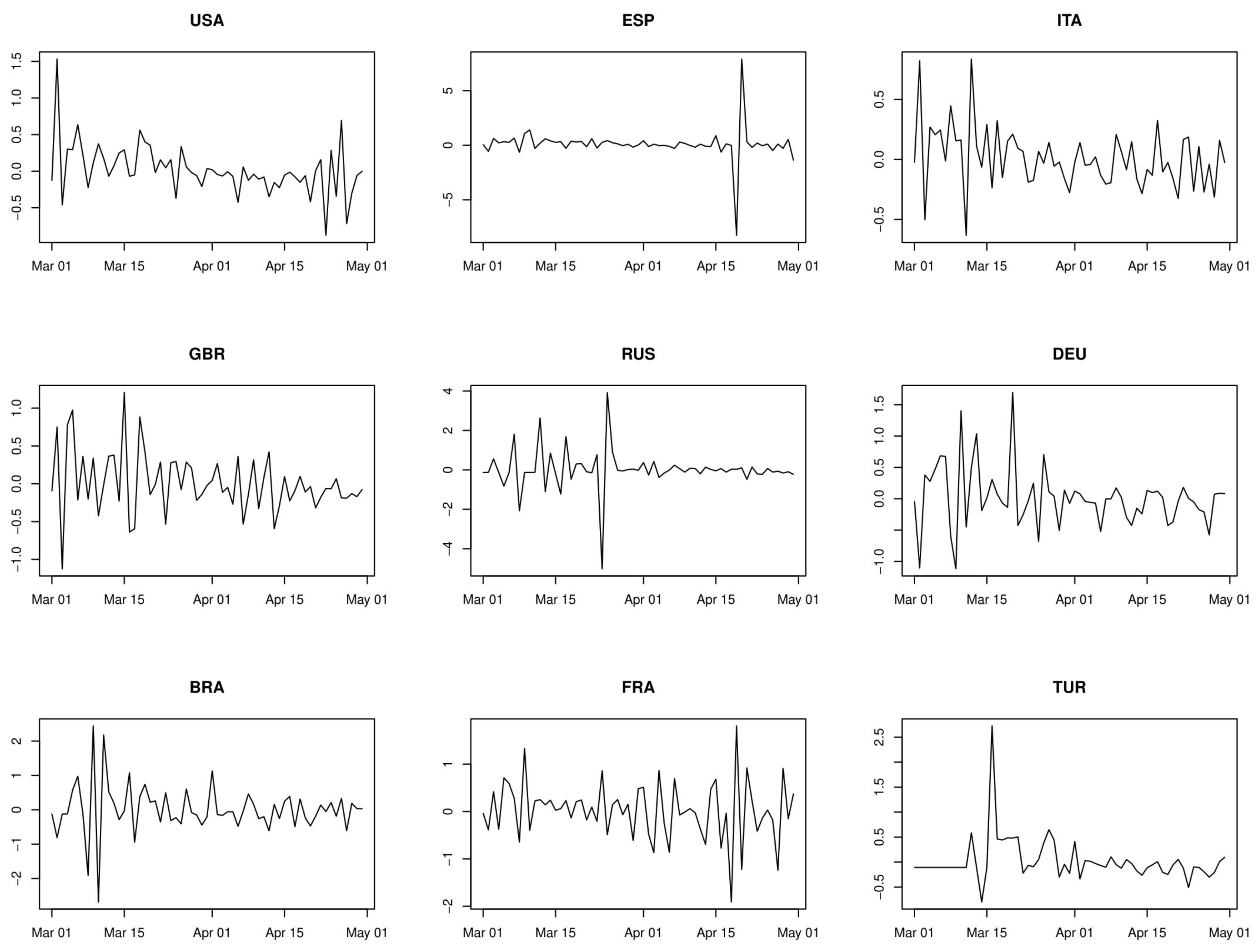
2.1. Univariate Analysis
- First order serial correlations of growth rates are negative.
- For the countries with AR(2) dynamics, there are stochastic cycles in growth rates with an average length of about three days.
- The spatial autocorrelation coefficient is strongly significant.
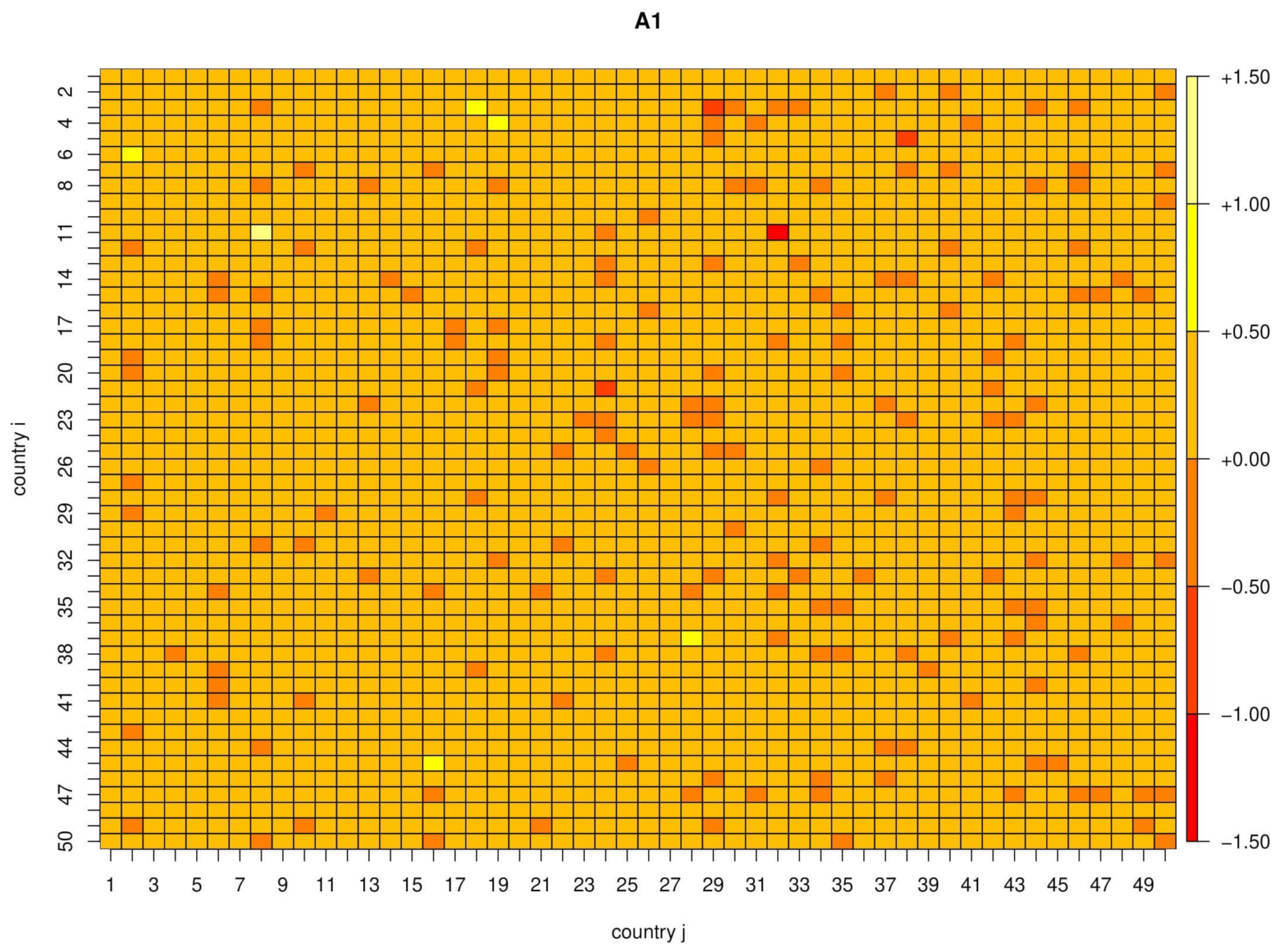
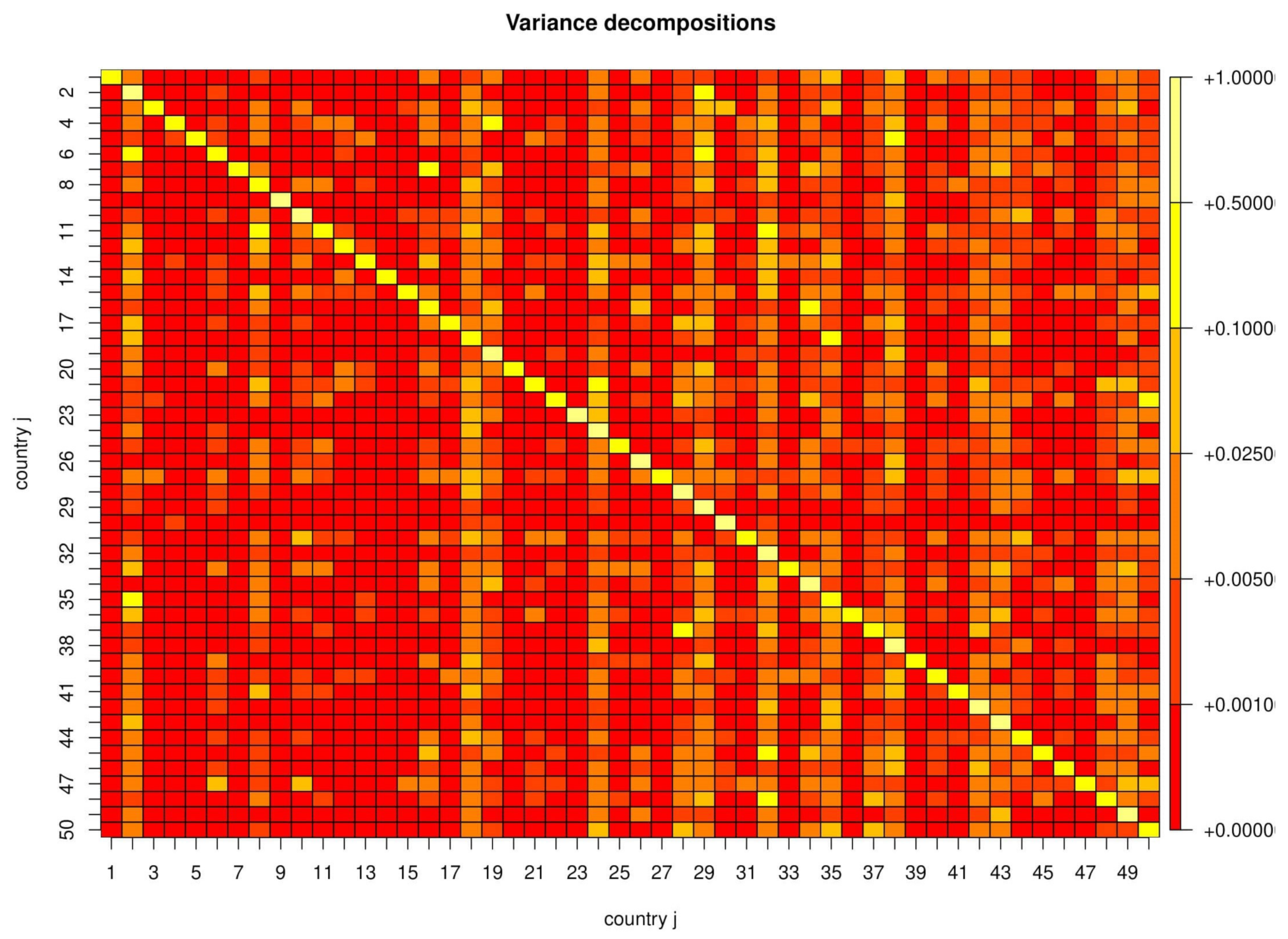
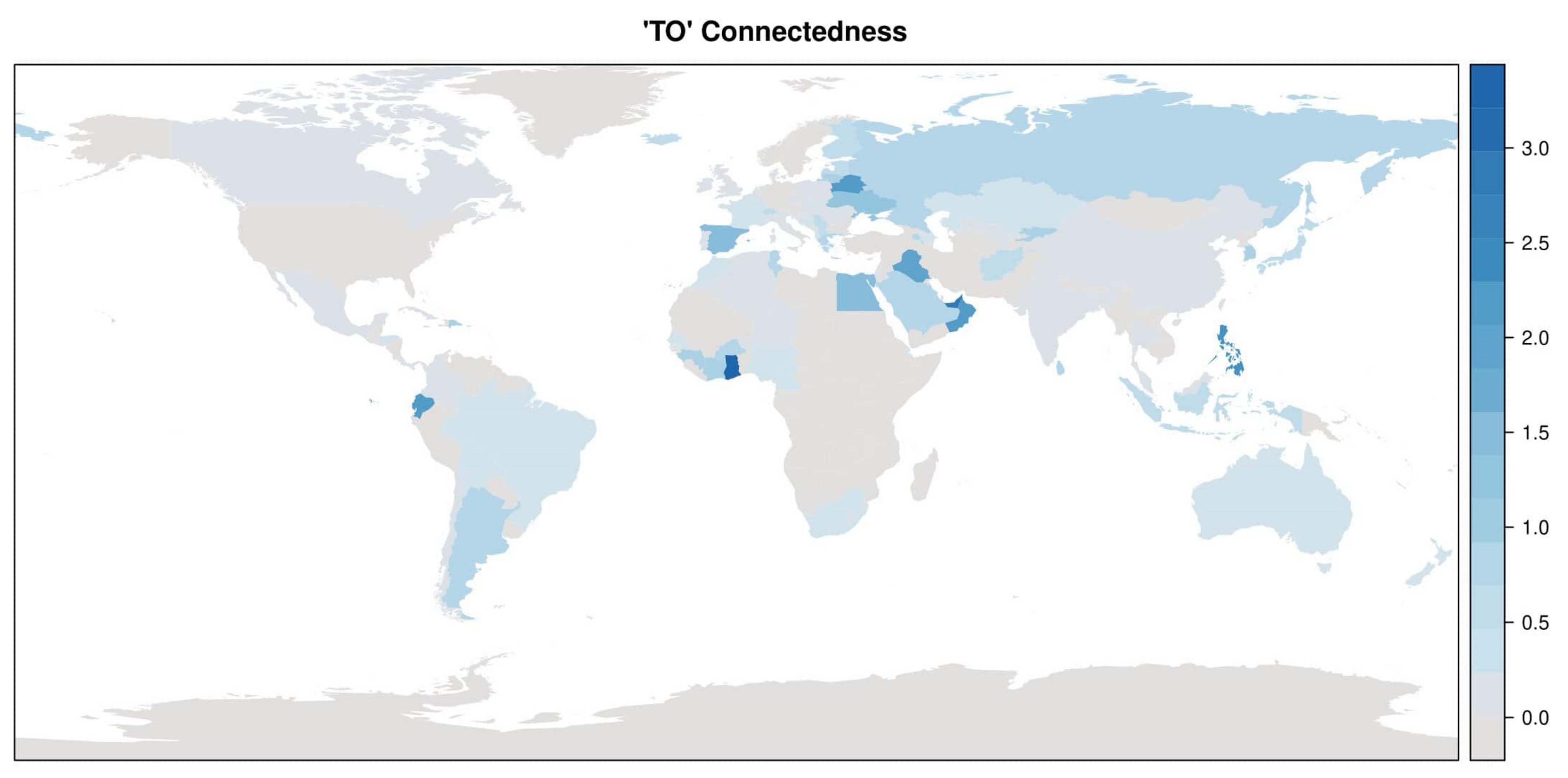
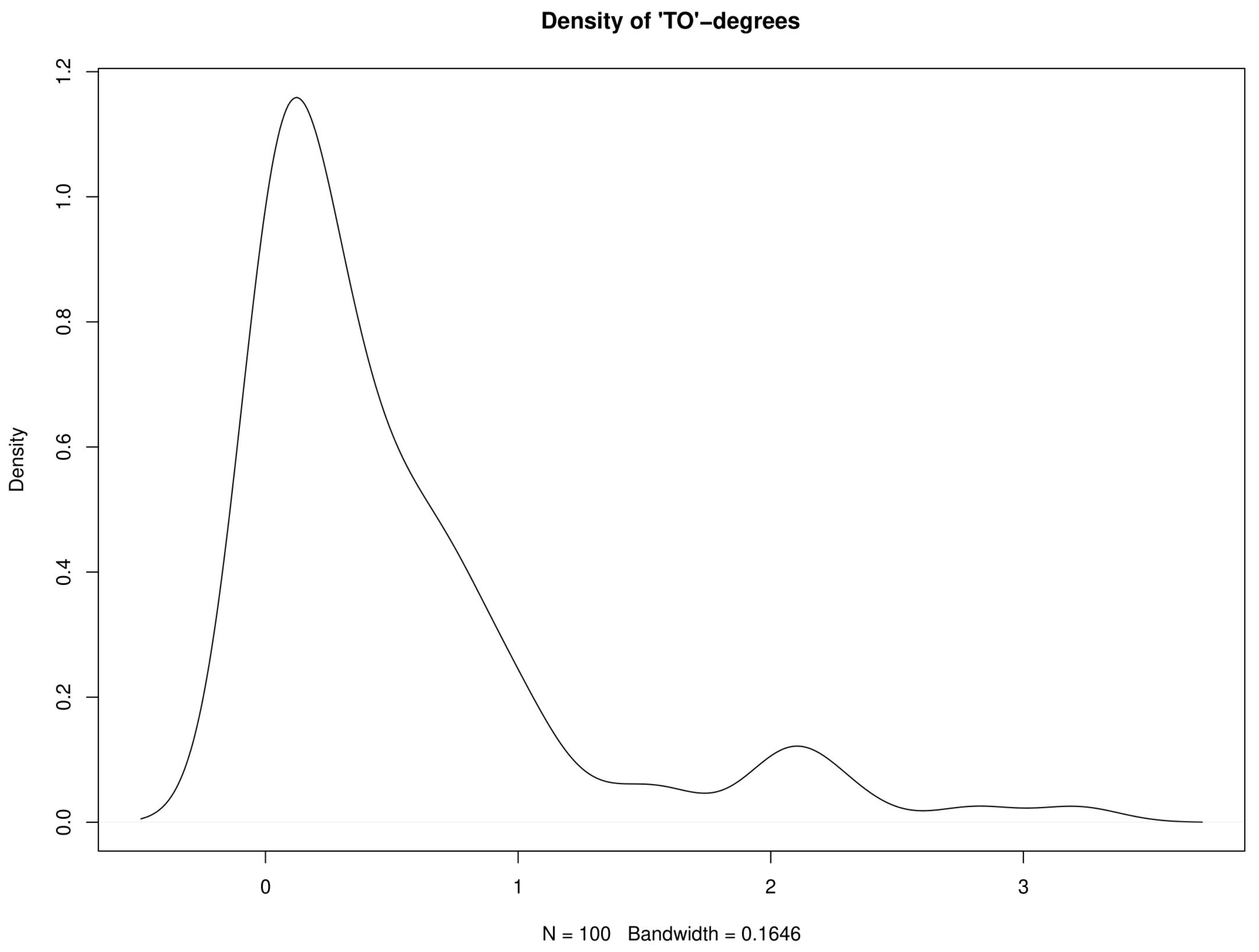
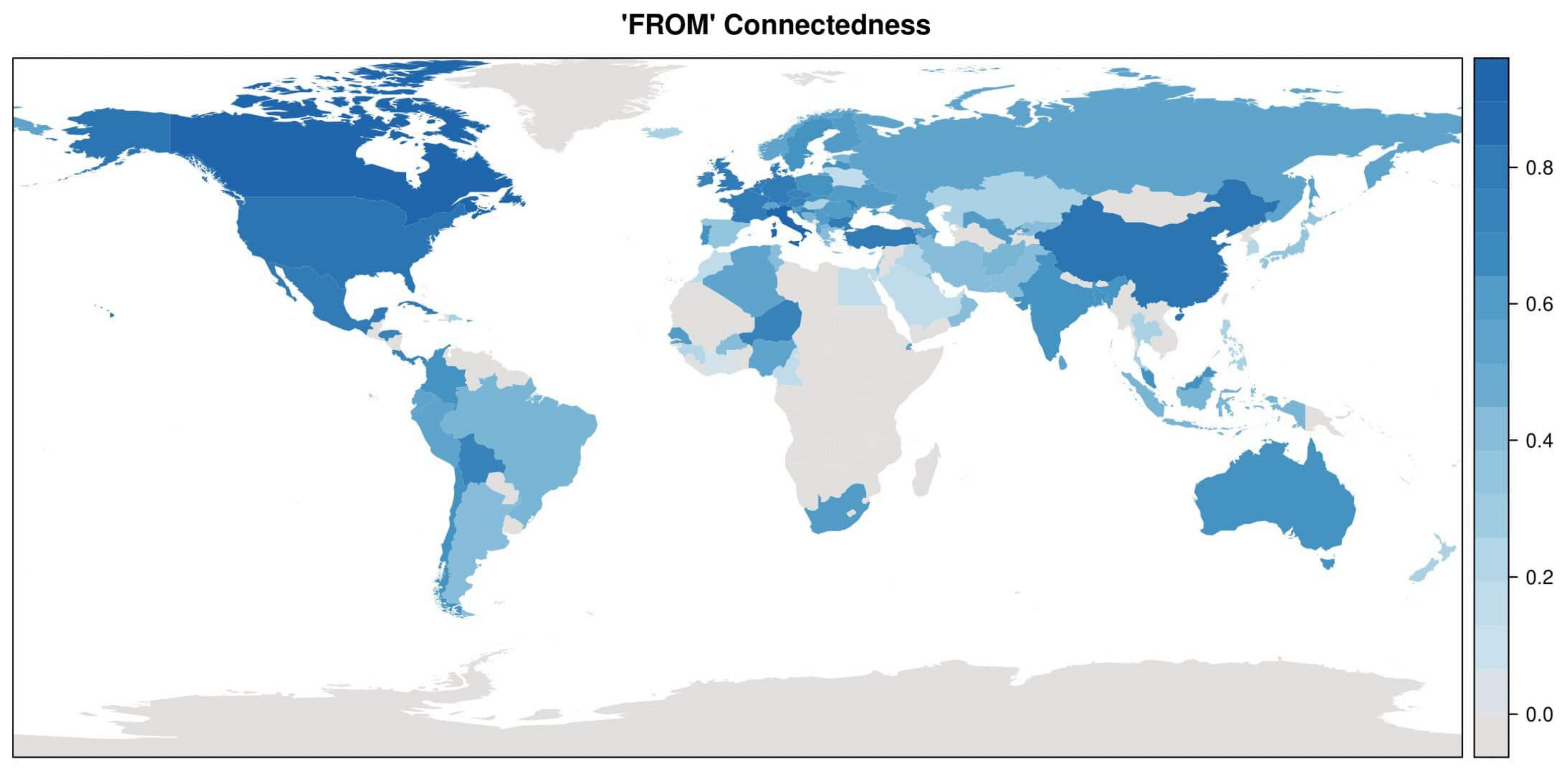
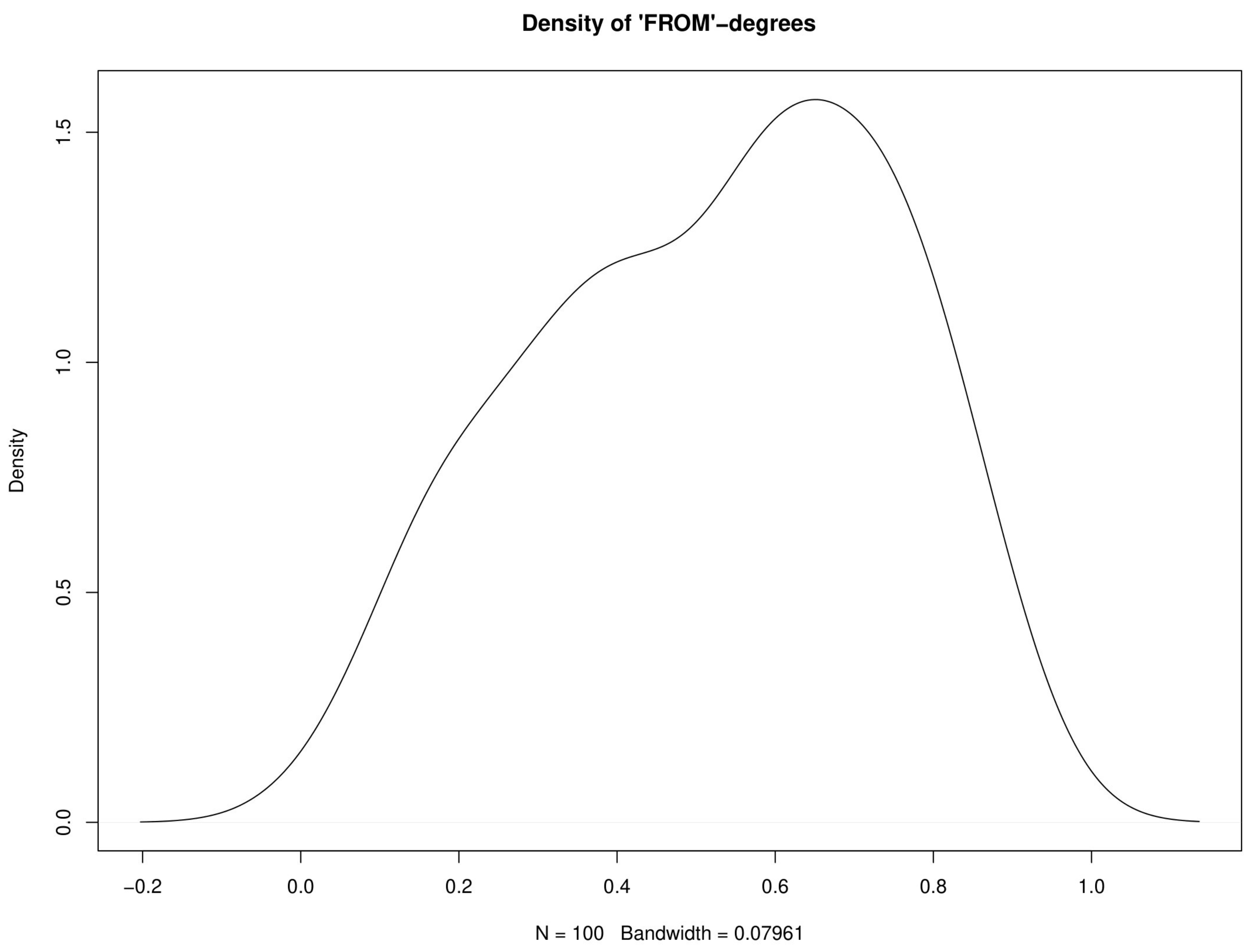
2.2. Multivariate Analysis
3. Conclusions
Funding
Conflicts of Interest
Appendix
| Country | Mu | Alpha1 | Alpha2 | K | Acf1 | Acf2 | |
|---|---|---|---|---|---|---|---|
| 1 | USA | 0.1190 | NA | NA | NA | −0.5812 | 0.1025 |
| 2 | ESP | 0.0551 | −0.6357 | −0.3070 | 2.879772 | −0.4078 | −0.0964 |
| 3 | ITA | 0.0197 | −0.2187 | NA | NA | −0.3080 | −0.1204 |
| 4 | GBR | 0.0994 | −0.2747 | −0.3170 | 3.457548 | −0.4656 | −0.1669 |
| 5 | DEU | −0.0483 | NA | NA | NA | −0.7526 | 0.4425 |
| 6 | FRA | 0.0591 | −0.5001 | NA | NA | −0.5180 | 0.0404 |
| 7 | TUR | 0.1290 | 0.2093 | NA | NA | −0.4603 | 0.1770 |
| 8 | RUS | 0.1454 | −0.6229 | −0.3060 | 2.897091 | −0.2381 | −0.1603 |
| 9 | IRN | 0.0153 | −0.7193 | −0.3499 | 2.824746 | −0.3826 | −0.2127 |
| 10 | BRA | 0.1456 | −0.5581 | NA | NA | −0.7432 | 0.4734 |
| 11 | CAN | 0.0951 | −0.3906 | NA | NA | −0.4648 | −0.0175 |
| 12 | BEL | 0.0951 | NA | NA | NA | −0.3717 | −0.1870 |
| 13 | NLD | 0.0705 | NA | NA | NA | −0.1379 | 0.0532 |
| 14 | PER | 0.1315 | −0.7798 | −0.3740 | 2.777552 | −0.4865 | −0.0313 |
| 15 | IND | 0.1246 | −0.7751 | −0.1902 | 2.357376 | −0.4758 | −0.1840 |
| 16 | CHE | 0.0532 | −0.6605 | −0.1818 | 2.557440 | −0.5581 | 0.1938 |
| 17 | PRT | 0.1035 | −0.4378 | NA | NA | −0.2475 | −0.1414 |
| 18 | ECU | 0.0618 | −0.3215 | −0.3590 | 3.410295 | −0.6846 | 0.3053 |
| 19 | SAU | 0.1182 | −0.7888 | −0.5028 | 2.908032 | −0.5923 | 0.0215 |
| 20 | SWE | 0.0980 | −0.2257 | NA | NA | −0.3906 | 0.0849 |
| 21 | IRL | 0.0965 | −0.3648 | NA | NA | −0.4258 | 0.0670 |
| 22 | MEX | 0.1077 | −0.3284 | −0.1960 | 3.220894 | −0.4257 | −0.0989 |
| 23 | PAK | 0.1142 | −0.6143 | −0.3125 | 2.919015 | −0.5396 | 0.1344 |
| 24 | SGP | 0.0764 | −0.6688 | −0.3331 | 2.870741 | −0.4410 | 0.0195 |
| 25 | CHL | 0.1154 | −0.4258 | NA | NA | −0.5679 | 0.1749 |
| 26 | ISR | 0.0548 | −0.8392 | −0.2685 | 2.498557 | −0.4177 | 0.1557 |
| 27 | AUT | 0.0481 | −0.2929 | −0.2300 | 3.340180 | −0.5234 | 0.3204 |
| 28 | JPN | 0.0409 | −0.3556 | −0.3084 | 3.312745 | −0.6871 | 0.3177 |
| 29 | BLR | 0.1105 | −0.5120 | −0.3774 | 3.140573 | −0.2509 | −0.0071 |
| 30 | QAT | 0.0925 | −0.8442 | −0.3308 | 2.623628 | −0.2274 | 0.2722 |
| 31 | POL | 0.0897 | −0.4912 | NA | NA | −0.7159 | 0.4200 |
| 32 | ARE | 0.1035 | −0.9655 | −0.4536 | 2.651255 | −0.4971 | 0.0442 |
| 33 | ROU | 0.0913 | −0.4175 | NA | NA | −0.2366 | −0.2829 |
| 34 | IDN | 0.0779 | −0.7072 | −0.3386 | 2.825275 | −0.4945 | −0.1337 |
| 35 | UKR | 0.0000 | −0.5586 | −0.3737 | 3.071974 | −0.3739 | 0.0234 |
| 36 | DNK | 0.0709 | −0.1745 | 0.2325 | NaN | −0.5398 | −0.0478 |
| 37 | SRB | 0.0927 | −0.5346 | −0.3479 | 3.078214 | −0.5001 | 0.1388 |
| 38 | PHL | 0.0922 | −0.8493 | −0.3343 | 2.622693 | −0.0336 | −0.0254 |
| 39 | NOR | 0.0357 | −0.7009 | −0.4292 | 2.942658 | −0.6548 | 0.2291 |
| 40 | CZE | 0.0534 | −0.2509 | NA | NA | −0.5757 | 0.3656 |
| 41 | BGD | 0.1039 | −0.6032 | −0.2978 | 2.913854 | −0.6575 | 0.1833 |
| 42 | KOR | −0.0693 | −0.7663 | −0.3236 | 2.720150 | −0.5332 | 0.0641 |
| 43 | DOM | 0.0833 | −0.6311 | −0.2695 | 2.825041 | −0.5545 | 0.0766 |
| 44 | AUS | 0.0237 | −0.4603 | NA | NA | −0.4901 | −0.0438 |
| 45 | PAN | 0.0827 | −0.3611 | NA | NA | −0.6513 | 0.3146 |
| 46 | COL | 0.0933 | −0.6590 | −0.2212 | 2.677165 | −0.5283 | 0.0350 |
| 47 | MYS | 0.0402 | −0.8145 | −0.4581 | 2.834799 | −0.5329 | 0.0334 |
| 48 | ZAF | 0.0934 | −0.7034 | −0.2244 | 2.609739 | −0.6558 | 0.2550 |
| 49 | EGY | 0.0804 | −0.7420 | −0.5007 | 2.959918 | −0.3648 | 0.2310 |
| 50 | FIN | 0.0510 | −0.7983 | −0.4787 | 2.874698 | −0.6616 | 0.2868 |
References
- Li, S.; Wang, Y.; Xue, J.; Zhao, N.; Zhu, T. The Impact of COVID-19 Epidemic Declaration on Psychological Consequences: A Study on Active Weibo Users. Int. J. Environ. Res. Public Health 2020, 17, 2032. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pan, R.; Wan, X.; Tan, Y.; Xu, L.; Ho, C.S.; Ho, R.C. Immediate Psychological Responses and Associated Factors during the Initial Stage of the 2019 Coronavirus Disease (COVID-19) Epidemic among the General Population in China. Int. J. Environ. Res. Public Health 2020, 17, 1729. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ma, Z.F. Impact of the COVID-19 Pandemic on Mental Health and Quality of Life among Local Residents in Liaoning Province, China: A Cross-Sectional Study. Int. J. Environ. Res. Public Health 2020, 17, 2381. [Google Scholar] [CrossRef] [PubMed]
- McAleer, M. Prevention Is Better Than the Cure: Risk Management of COVID-19. J. Risk Financ. Manag. 2020, 13, 46. [Google Scholar] [CrossRef]
- Li, S.; Linton, O. When Will the Covid-19 Pandemic Peak? Cambridge INET Working Paper Series 2020/11. Available online: https://www.inet.econ.cam.ac.uk/research-papers/wp-abstracts?wp=2011 (accessed on 27 May 2020).
- Yue, X.-G.; Shao, X.-F.; Li, R.Y.M.; Crabbe, M.J.C.; Mi, L.; Hu, S.; Baker, J.S.; Liu, L.; Dong, K. Risk Prediction and Assessment: Duration, Infections, and Death Toll of the COVID-19 and Its Impact on China’s Economy. J. Risk Financ. Manag. 2020, 13, 66. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, Z.; Yue, X.-G.; McAleer, M. Risk Management of COVID-19 by Universities in China. J. Risk Financ. Manag. 2020, 13, 36. [Google Scholar] [CrossRef]
- Yue, X.G.; Shao, X.F.; Li, R.Y.; Crabbe, M.J.; Mi, L.; Hu, S.; Baker, J.S.; Liang, G. Risk Management Analysis for Novel Coronavirus in Wuhan, China. J. Risk Financ. Manag. 2020, 13, 22. [Google Scholar] [CrossRef]
- Liu, W.; Yue, X.-G.; Tchounwou, P.B. Response to the COVID-19 Epidemic: The Chinese Experience and Implications for Other Countries. Int. J. Environ. Res. Public Health 2020, 17, 2304. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-L.; McAleer, M.; Ramos, V. A Charter for Sustainable Tourism after COVID-19. Sustainability 2020, 12, 3671. [Google Scholar] [CrossRef]
- Chang, C.-L.; McAleer, M. Alternative Global Health Security Indexes for Risk Analysis of COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 3161. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Z. Strengths, Weaknesses, Opportunities and Threats (SWOT) Analysis of China’s Prevention and Control Strategy for the COVID-19 Epidemic. Int. J. Environ. Res. Public Health 2020, 17, 2235. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Chen, H. Modeling the epidemic dynamics and control of COVID-19 outbreak in China. Quant. Biol. 2020, 8, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Wang, J.; Zhang, M.; Wang, X. Using Social Media to Mine and Analyze Public Opinion Related to COVID-19 in China. Int. J. Environ. Res. Public Health 2020, 17, 2788. [Google Scholar] [CrossRef] [PubMed]
- Di Gennaro, F.; Pizzol, D.; Marotta, C.; Antunes, M.; Racalbuto, V.; Veronese, N.; Smith, L. Coronavirus Diseases (COVID-19) Current Status and Future Perspectives: A Narrative Review. Int. J. Environ. Res. Public Health 2020, 17, 2690. [Google Scholar] [CrossRef] [PubMed]
- Wei, X. Spatial Panel VAR and Application to Forecast Influenza Incidence Rates of US States, SSRN Discussion Paper 2015. Available online: https://ssrn.com/abstract=2646870 (accessed on 27 May 2020).
- Elhorst, J.P. Specification and estimation of spatial panel data models. Int. Reg. Sci. Review. 2003, 26, 244–268. [Google Scholar] [CrossRef]
- Beenstock, M.; Felsenstein, D. Spatial Vector Autoregressions. Spat. Econ. Anal. 2007, 2(2), 167–196. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. Spatial panels: Random components versus fixed effects. Int. Econ. Rev. 2012, 53, 1369–1412. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Verlag: New York, NY, USA, 2005. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the lasso. J. R. Stat. Soc. Ser. B. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R; Springer Verlag: New York, NY, USA, 2013. [Google Scholar]
- Baltagi, B.H.; Song, S.H.; Jung, B.; Koh, W. Testing panel data regression models with spatial and serial error correlation. J. Econom. 2007, 140, 5–51. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafner, C.M. The Spread of the Covid-19 Pandemic in Time and Space. Int. J. Environ. Res. Public Health 2020, 17, 3827. https://doi.org/10.3390/ijerph17113827
Hafner CM. The Spread of the Covid-19 Pandemic in Time and Space. International Journal of Environmental Research and Public Health. 2020; 17(11):3827. https://doi.org/10.3390/ijerph17113827
Chicago/Turabian StyleHafner, Christian M. 2020. "The Spread of the Covid-19 Pandemic in Time and Space" International Journal of Environmental Research and Public Health 17, no. 11: 3827. https://doi.org/10.3390/ijerph17113827
APA StyleHafner, C. M. (2020). The Spread of the Covid-19 Pandemic in Time and Space. International Journal of Environmental Research and Public Health, 17(11), 3827. https://doi.org/10.3390/ijerph17113827




