Sustainable Water Resource Management of Regulated Rivers under Uncertain Inflow Conditions Using a Noisy Genetic Algorithm
Abstract
:1. Introduction
2. Methods
2.1. E-Flow Allocation
E-Flow Policies
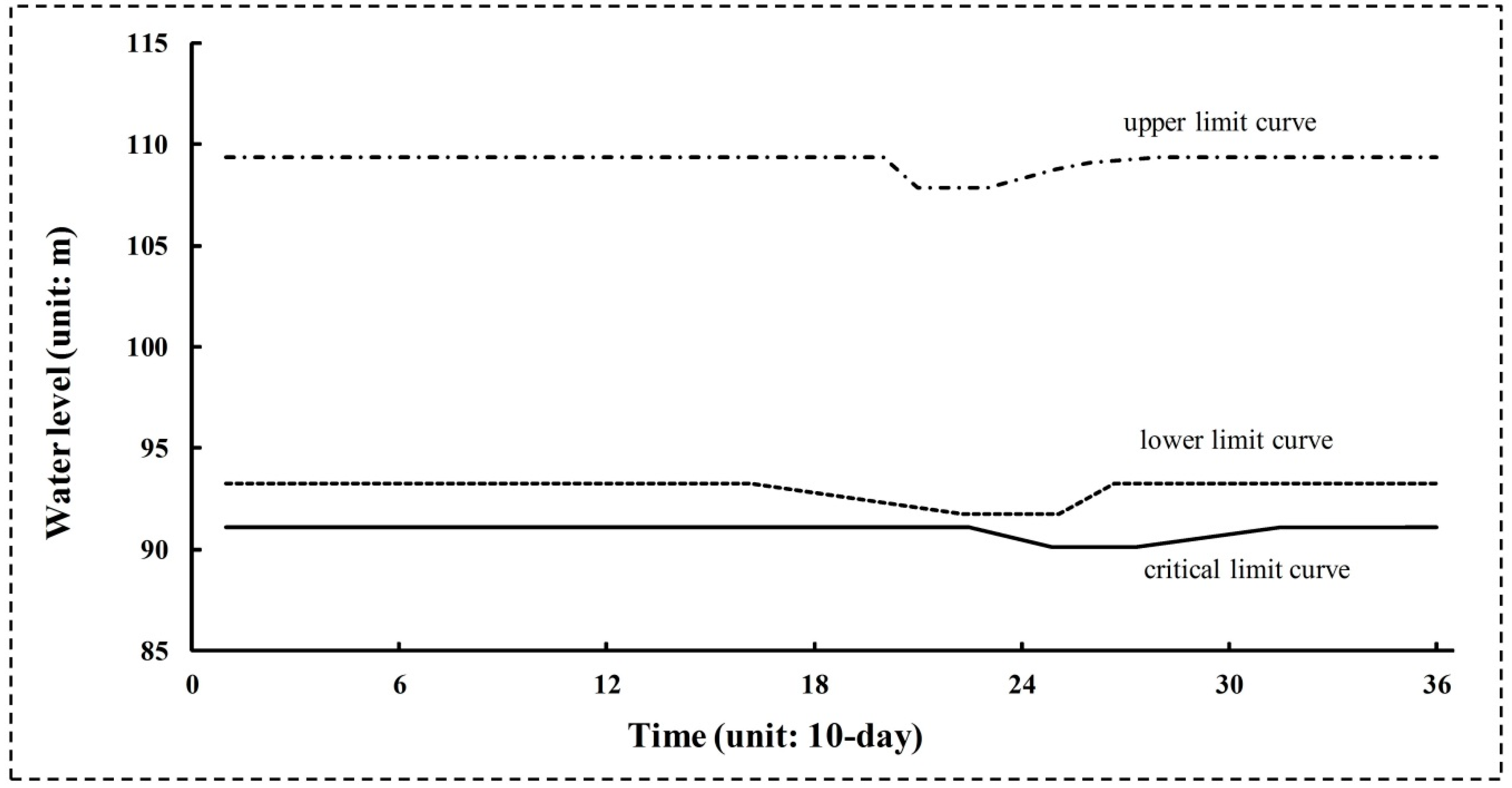
2.2. Reservoir Operation Model
2.3. Optimization Methods
2.3.1. Monte Carlo Genetic Algorithm
2.3.2. The Noisy Genetic Algorithm (NGA)
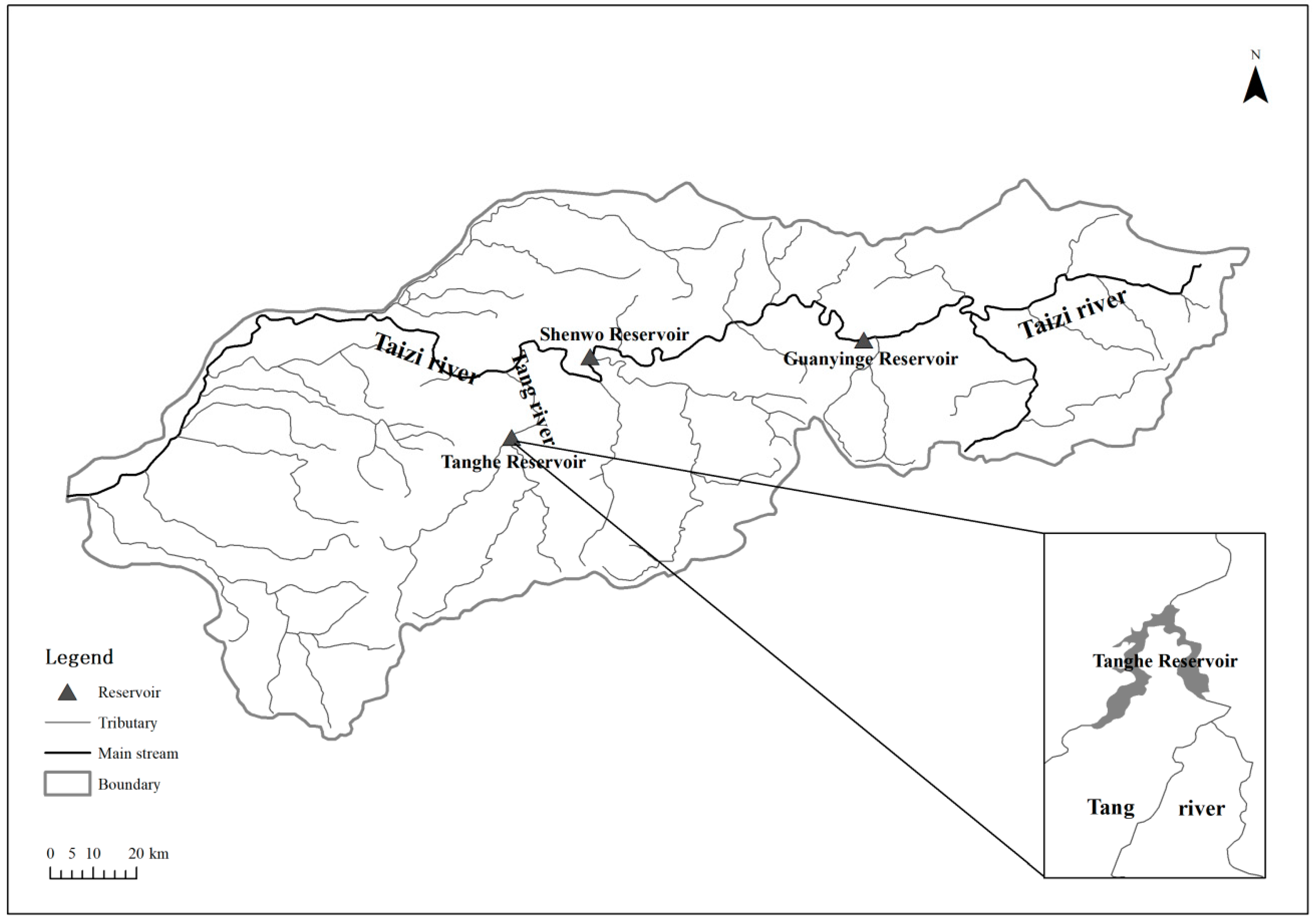
3. Case Study
4. Results and Discussion
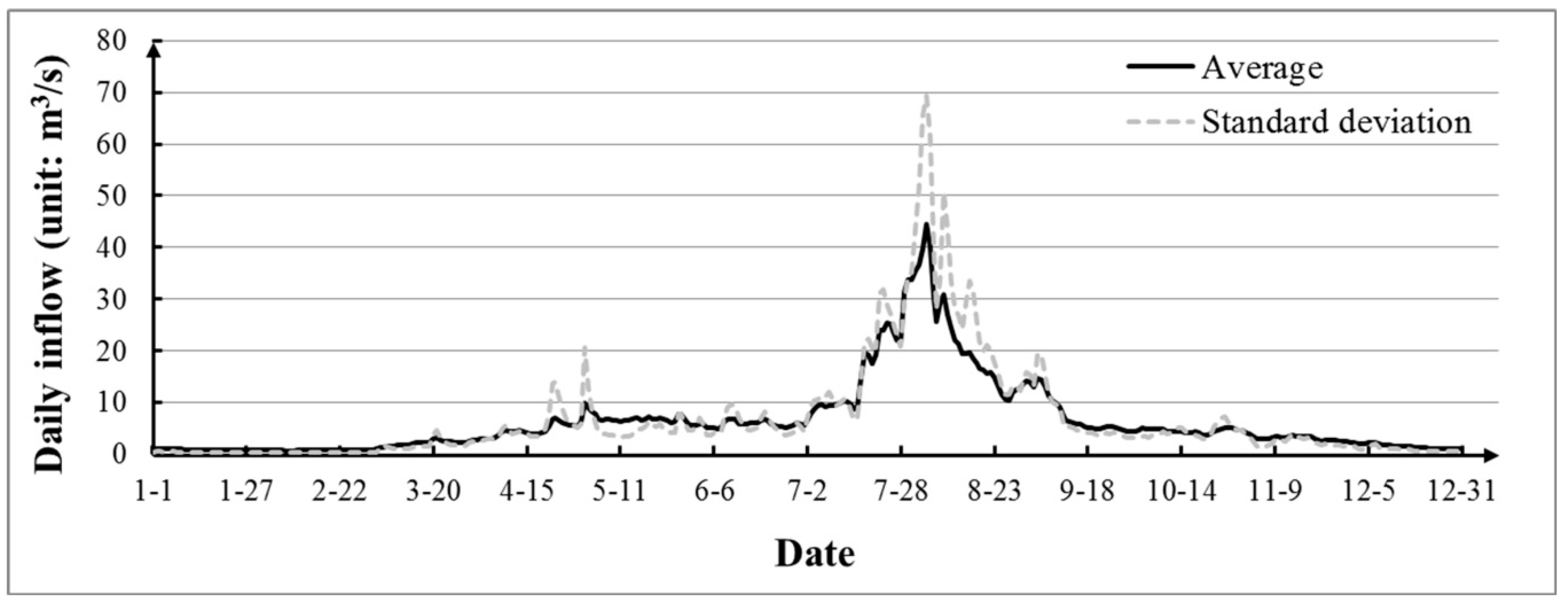
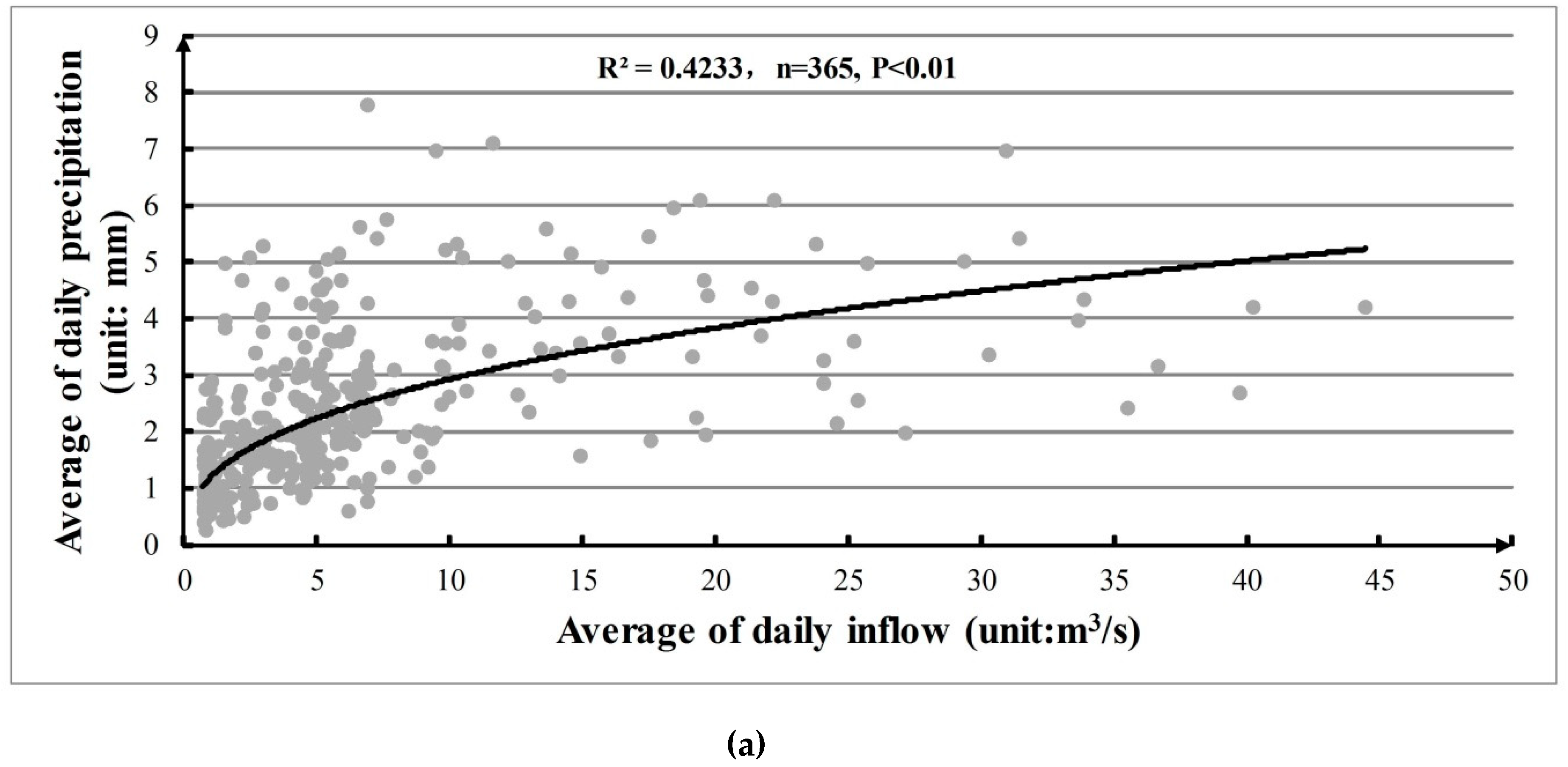
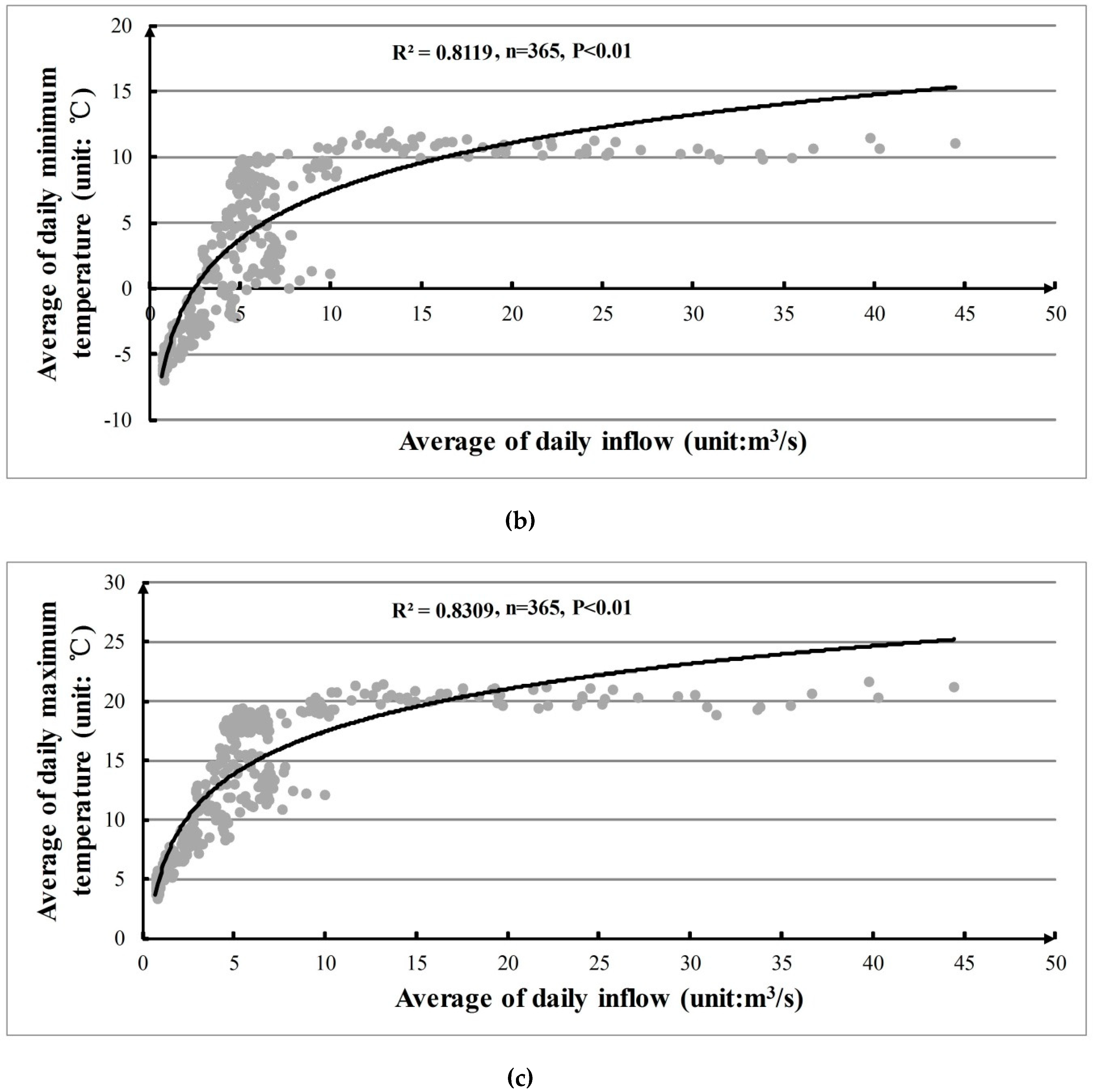
4.1. Analysis of Historical Inflow
4.2. Performance Tests for Monte Carlo GA and NGA
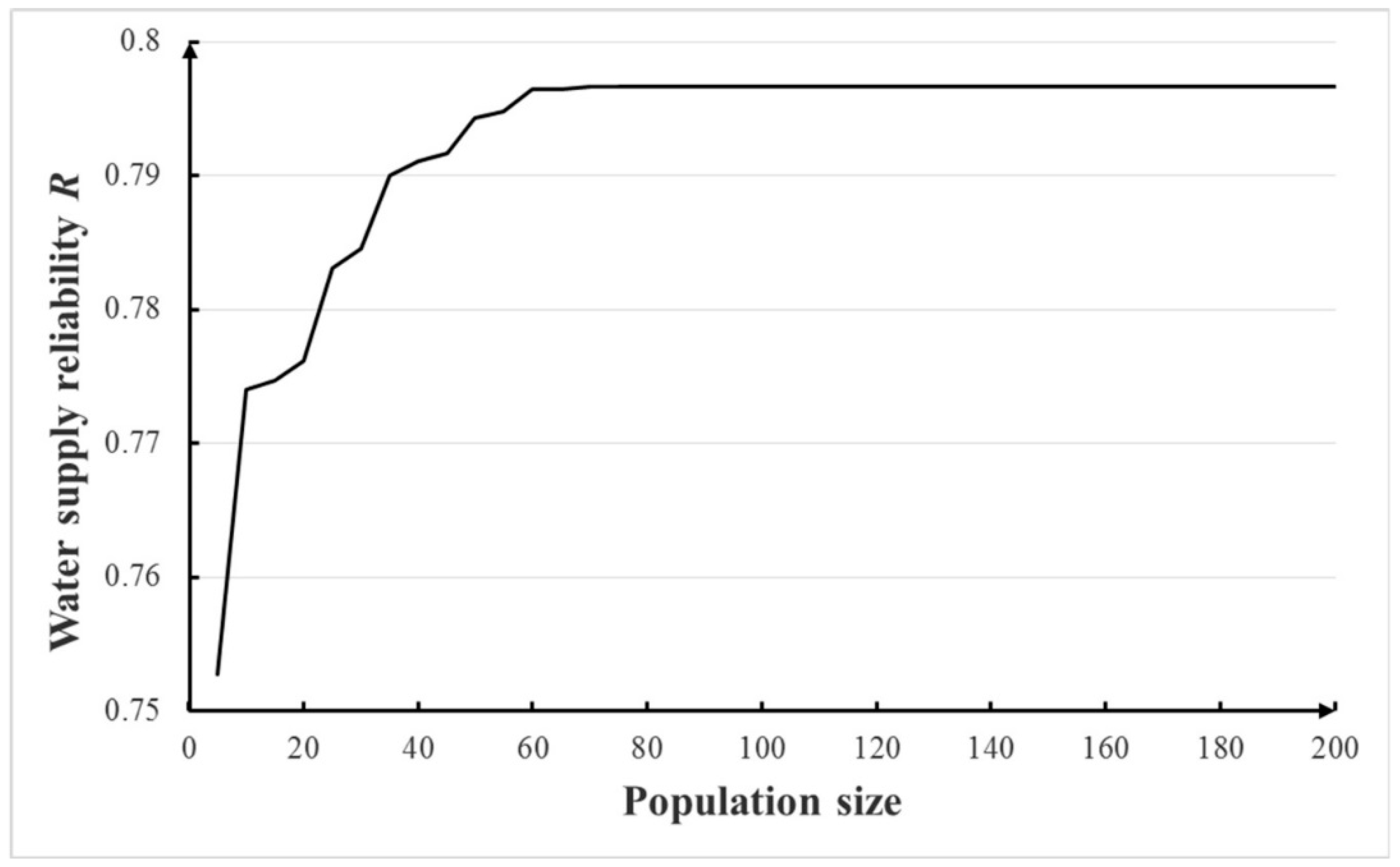
4.2.1. Parameter Setting for the Monte Carlo GA
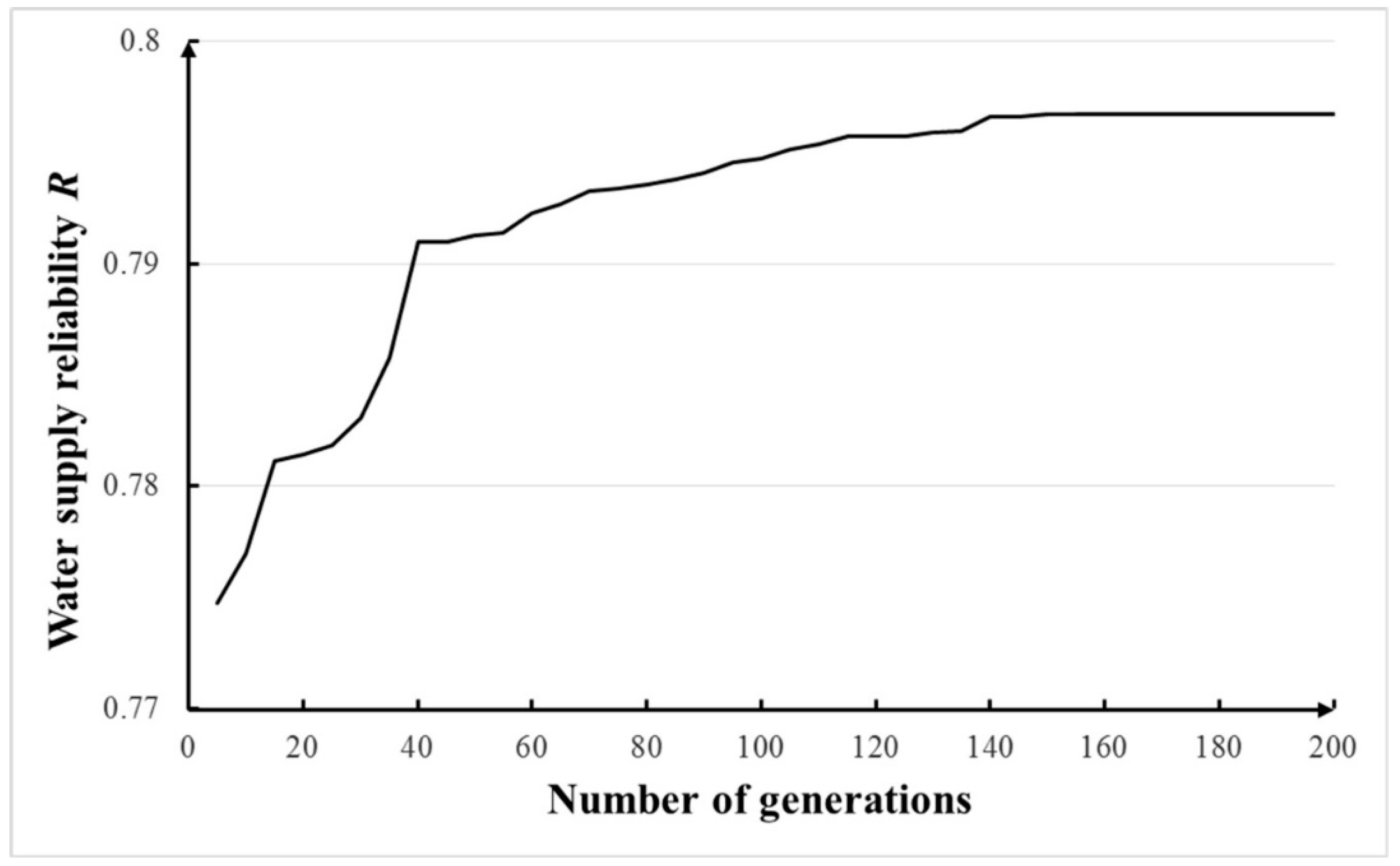
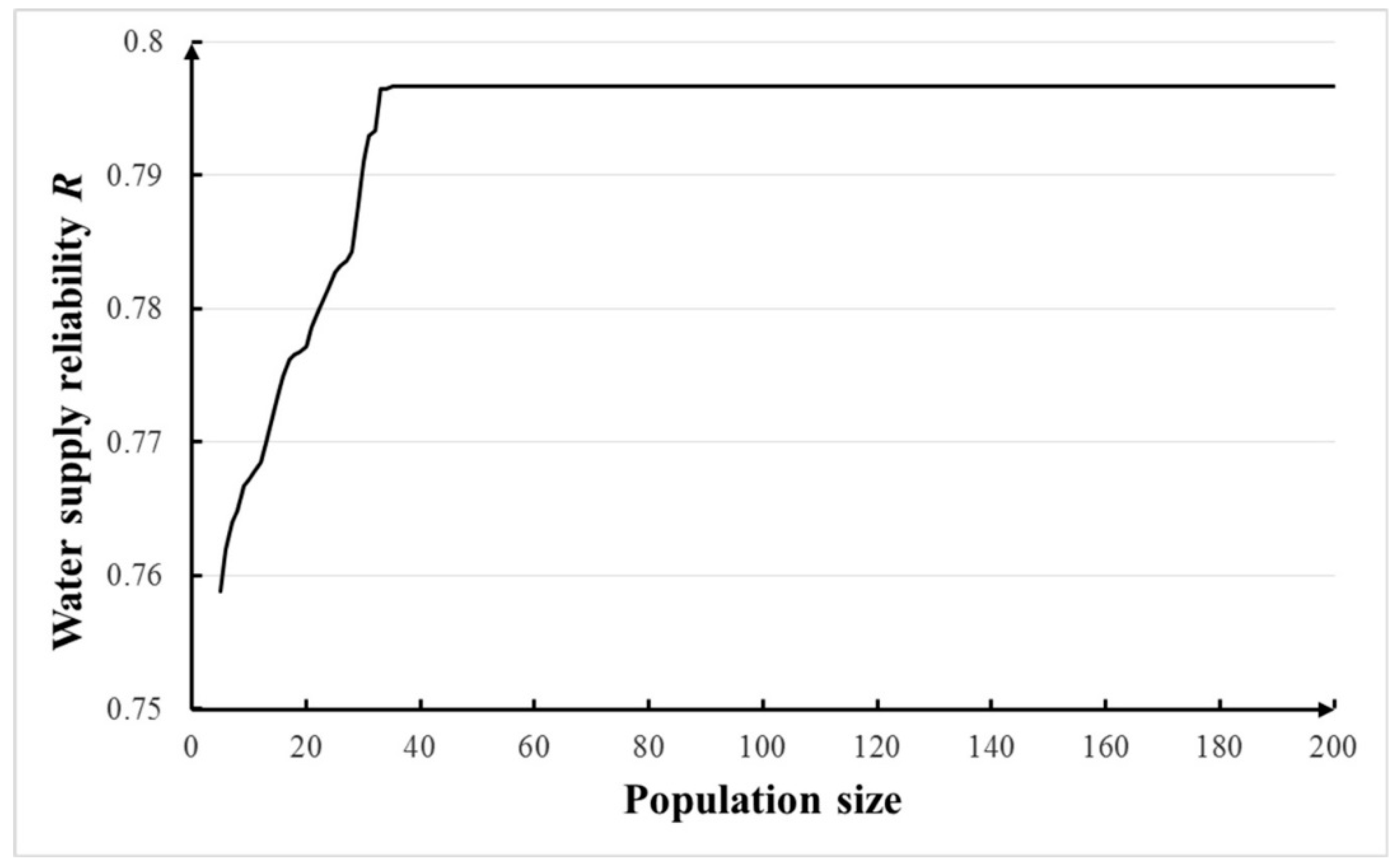
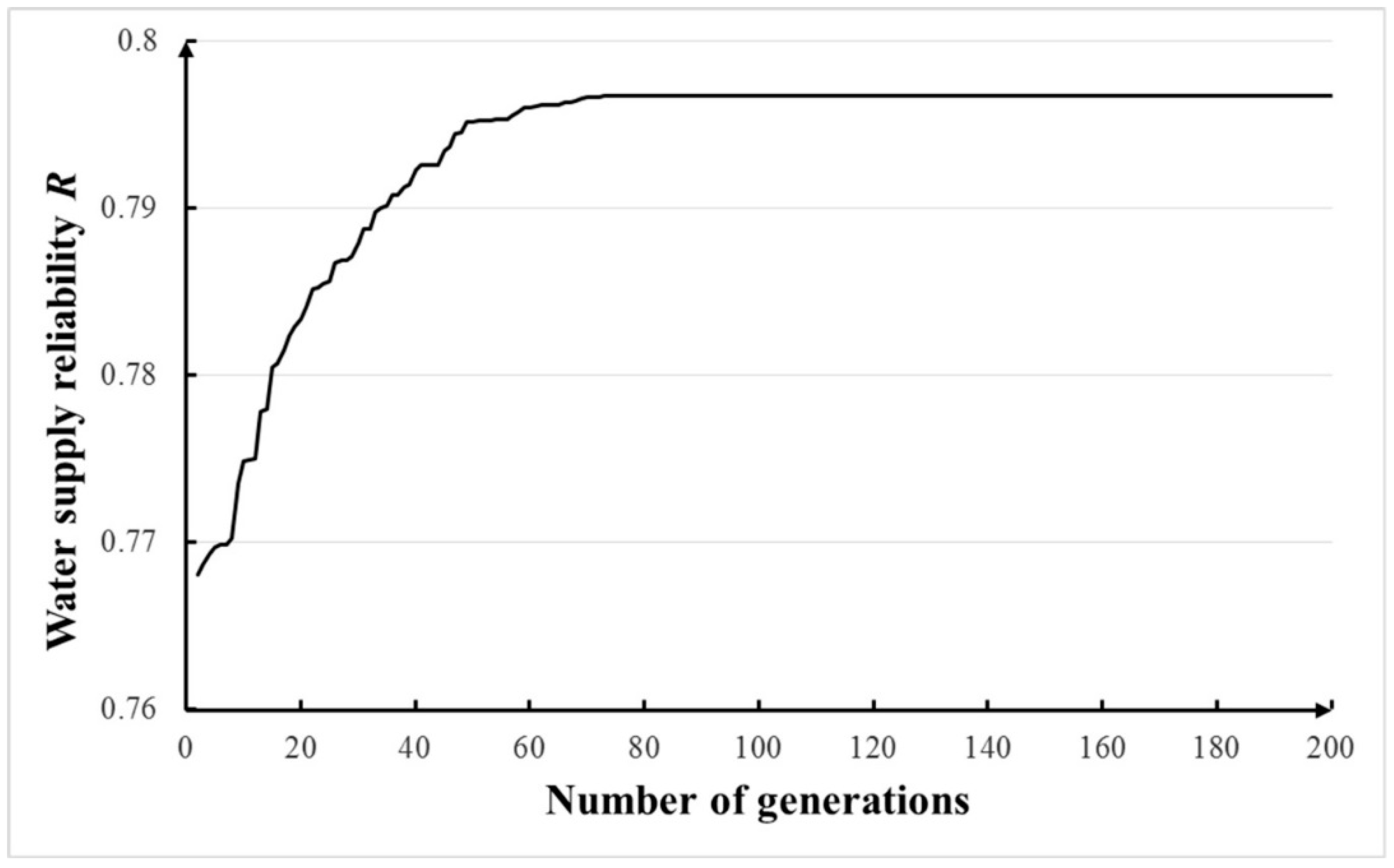
4.2.2. Parameter Setting for the NGA
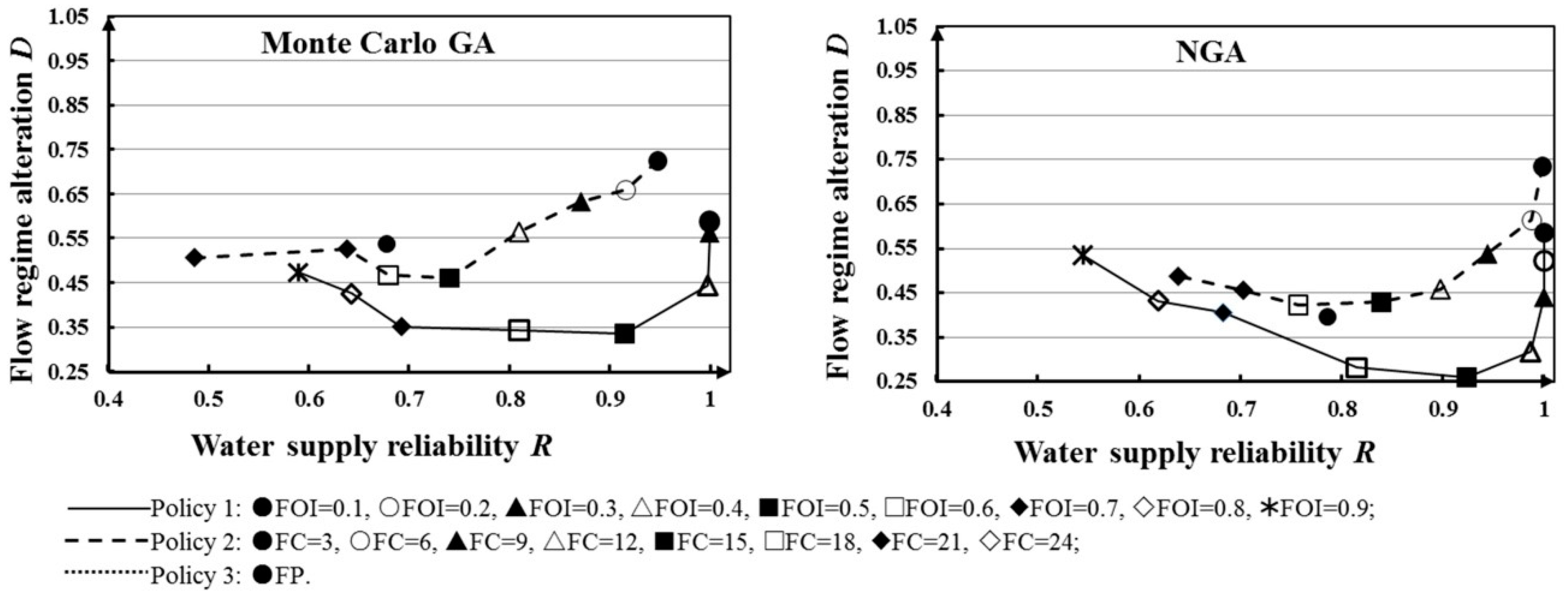
4.3. Comparison of the Two Stochastic Models
4.3.1. Optimization Based on the Average and Standard Deviation of Historical Inflows
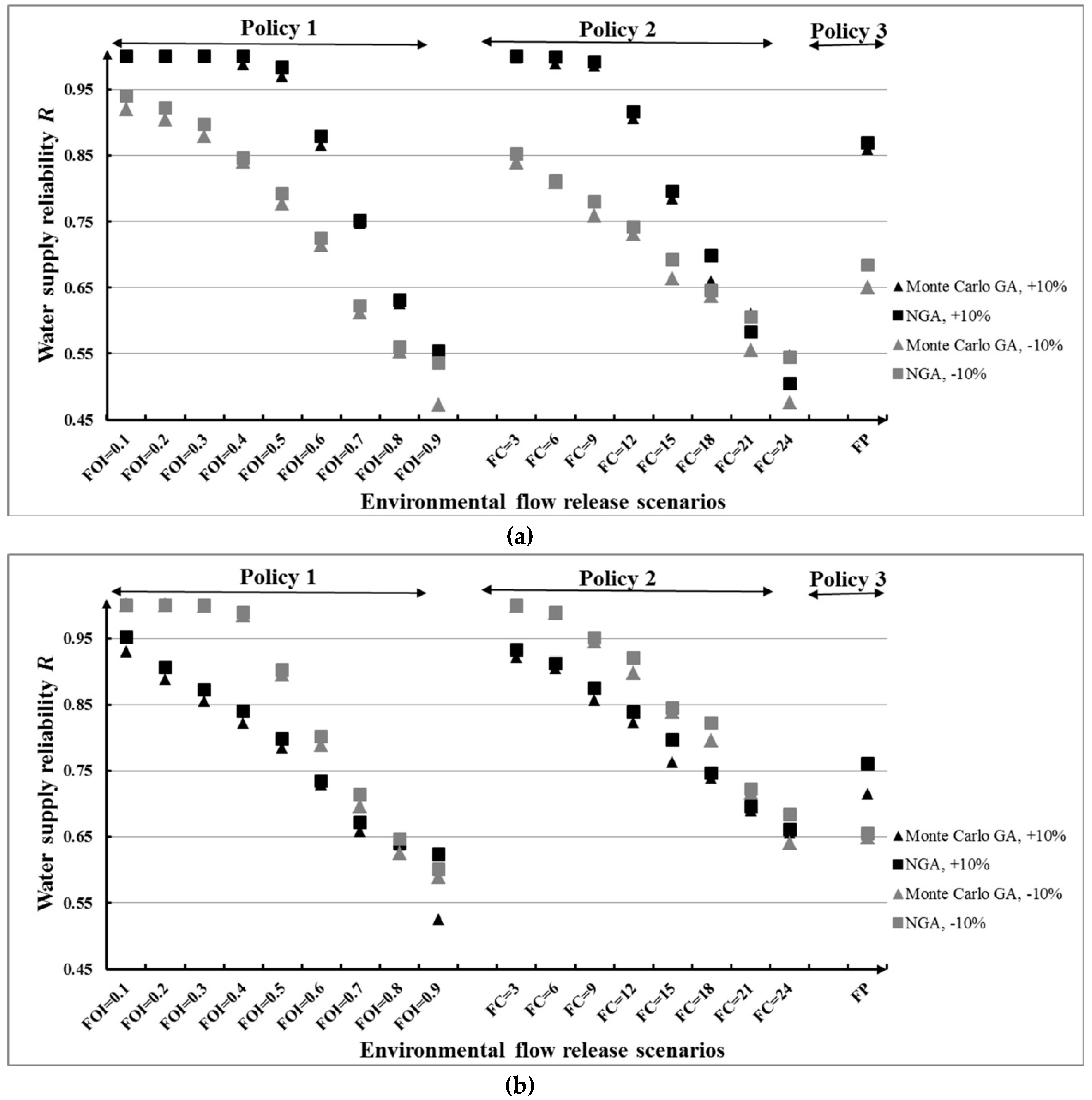
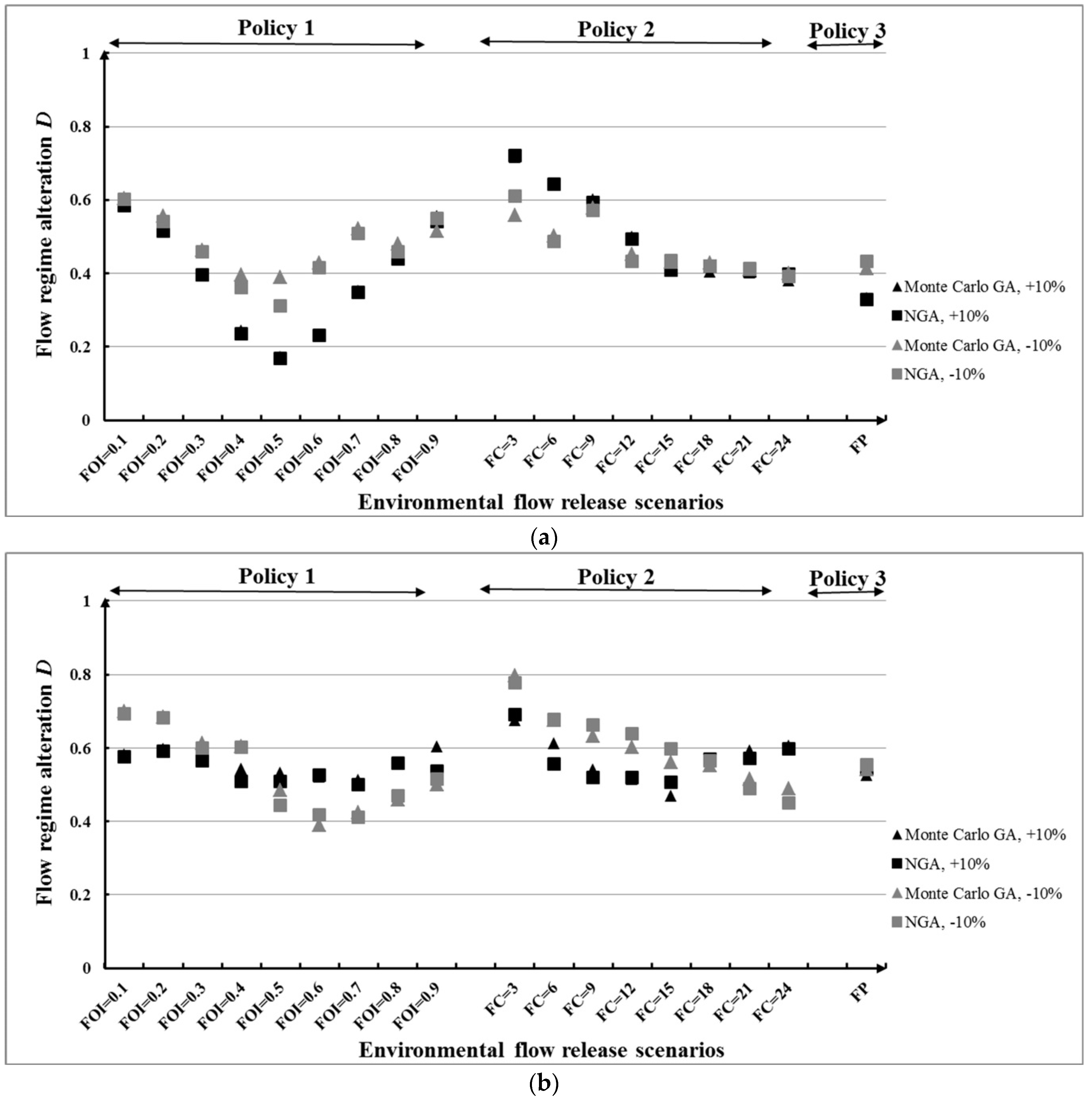
4.3.2. Optimization Based on Changed Average and Standard Deviation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Poff, N.L.R.; Schmidt, J.C. How dams can go with the flow. Science 2016, 353, 1099–1100. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Chen, H.; Xia, F.; Wang, Z.; Mei, K.; Shang, X.; Liu, Y.; Dahlgren, R.A.; Zhang, M.; Huang, H. Assessment of Long-Term Watershed Management on Reservoir Phosphorus Concentrations and Export Fluxes. Int. J. Environ. Res. Public Health 2018, 15, 2169. [Google Scholar] [CrossRef] [PubMed]
- Arias, M.E.; Cochrane, T.A.; Kummu, M.; Lauri, H.; Koponen, J.; Holtgrieve, G.; Piman, T. Impacts of hydropower and climate change on drivers of ecological productivity of Southeast Asia’s most important wetland. Ecol. Model. 2014, 272, 252–263. [Google Scholar] [CrossRef]
- Poff, N.L.; Zimmerman, J.K.H. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshw. Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
- Yin, X.A.; Mao, X.F.; Pan, B.Z.; Zhao, Y.W. Suitable range of reservoir storage capacities for environmental flow provision. Ecol. Eng. 2015, 76, 122–129. [Google Scholar] [CrossRef]
- Yu, C.X.; Yin, X.A.; Yang, Z.F.; Cai, Y.P.; Sun, T. A shorter time step for eco-friendly reservoir operation does not always produce better water availability and ecosystem benefits. J. Hydrol. 2016, 540, 900–913. [Google Scholar] [CrossRef]
- Chen, Q.W.; Chen, D.; Li, R.N.; Ma, J.F.; Blanckaert, K. Adapting the operation of two cascaded reservoirs for ecological flow requirement of a de-watered river channel due to diversion-type hydropower stations. Ecol. Model. 2013, 252, 266–272. [Google Scholar] [CrossRef]
- Suen, J.P. Determining the ecological flow regime for existing reservoir operation. Water Resour. Manag. 2011, 25, 817–835. [Google Scholar] [CrossRef]
- Shiau, J.T.; Wu, F.C. Optimizing environmental flows for multiple reaches affected by a multipurpose reservoir system in Taiwan: Restoring natural flow regimes at multiple temporal scales. Water Resour. Res. 2013, 49, 565–584. [Google Scholar] [CrossRef] [Green Version]
- Alemu, E.T.; Palmer, R.N.; Polebitski, A.; Meaker, B. Decision support system for optimizing reservoir operations using ensemble streamflow predictions. J. Water Res. Plan. Manag. 2010, 137, 72–82. [Google Scholar] [CrossRef]
- Yin, X.A.; Yang, Z.F.; Yang, W.; Zhao, Y.W.; Chen, H. Optimized reservoir operation to balance human and riverine ecosystem needs: Model development, and a case study for the Tanghe reservoir, Tang river basin, China. Hydrol. Process. 2010, 24, 461–471. [Google Scholar] [CrossRef]
- Yin, X.A.; Yang, Z.F.; Petts, G.E. Optimizing environmental flows below Dams. River Res. Appl. 2012, 28, 703–716. [Google Scholar] [CrossRef]
- He, S.; Yin, X.A.; Yu, C.; Xu, Z.; Yang, Z. Quantifying parameter uncertainty in reservoir operation associated with environmental flow management. J. Clean. Prod. 2018, 176, 1271–1282. [Google Scholar] [CrossRef]
- Cardwell, H.; Jager, H.I.; Sale, M.J. Designing instream flows to satisfy fish and human water needs. J. Water Res. Plan. Manag. 1996, 122, 356–363. [Google Scholar] [CrossRef]
- Jager, H.I.; Smith, B.T. Sustainable reservoir operation: Can we generate hydropower and preserve ecosystem values? River Res. Appl. 2008, 24, 340–352. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Res. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Soncini-Sessa, R.; Weber, E.; Castelletti, A. Integrated and Participatory Water Resources Management-Theory; Elsevier: Amsterdan, North Holland, The Netherlands, 2007. [Google Scholar]
- Sangiorgio, M.; Guariso, G. NN-based implicit stochastic optimization of multi-reservoir systems management. Water 2018, 10, 303. [Google Scholar] [CrossRef]
- Datta, B.; Burges, S.J. Short-term, single, multiple-purpose reservoir operation: Importance of loss functions and forecast errors. Water Resour. Res. 1984, 20, 1167–1176. [Google Scholar] [CrossRef]
- Datta, B.; Houck, M.H. A stochastic optimization model for real-time operation of reservoirs using uncertain forecasts. Water Resour. Res. 1984, 20, 1039–1046. [Google Scholar] [CrossRef]
- Celeste, A.B.; Billib, M. Evaluation of stochastic reservoir operation optimization models. Adv. Water Resour. 2009, 32, 1429–1443. [Google Scholar] [CrossRef]
- Coulibalya, P.; Anctilb, F.; Bobeec, B. Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J. Hydrol. 2000, 230, 244–257. [Google Scholar] [CrossRef]
- Karamouz, M.; Vasiliadis, H.V. Bayesian stochastic optimization of reservoir operation using uncertain forecasts. Water Resour. Res. 1992, 28, 1221–1232. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.M.; Yang, D.W. Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv. Water Resour. 2011, 34, 495–504. [Google Scholar] [CrossRef]
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; Dos Reis, A.A. Short-term reservoir optimization for flood mitigation under meteorological and hydrological forecast uncertainty. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef]
- Smalley, J.B.; Minsker, B.; Goldberg, D.E. Risk-based in situ bioremediation design using a noisy genetic algorithm. Water Resour. Res. 2000, 36, 3043–3052. [Google Scholar] [CrossRef] [Green Version]
- Ines, A.V.M.; Mohanty, B.P. Parameter conditioning with a noisy Monte Carlo genetic algorithm for estimating effective soil hydraulic properties from space. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Pal, S.K.; Wang, P.P. Genetic Algorithms for Pattern Recognition; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chan Hilton, A.B.; Culver, T.B. Groundwater remediation design under uncertainty using genetic algorithms. J. Water Resour. Plan. Manag. 2005, 131, 25–34. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, C.; Chien, C.C.; Zheng, L. A comparative study of Monte Carlo simple genetic algorithm and noisy genetic algorithm for cost-effective sampling network design under uncertainty. Adv. Water Resour. 2006, 29, 899–911. [Google Scholar] [CrossRef]
- Singh, A.; Minsker, B.S. Uncertainty-based multiobjective optimization of groundwater remediation design. Water Resour. Res. 2008, 44, W02404. [Google Scholar] [CrossRef]
- Yan, S.; Minsker, B. Applying dynamic surrogate models in noisy genetic algorithms to optimize groundwater remediation designs. J. Water Res. Plan. Manag. 2010, 137, 284–292. [Google Scholar] [CrossRef]
- Yun, R.; Singh, V.P.; Dong, Z.C. Long-Term Stochastic Reservoir Operation Using a Noisy Genetic Algorithm. Water Resour. Manag. 2010, 24, 3159–3172. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A method for assessing hydrologic alteration within ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of conventional rule curves coupled with hedging rules for reservoir operation. J. Water Res. Plan. Manag. 2013, 140, 693–698. [Google Scholar] [CrossRef]
- Tennant, D.L. Instream flow regimens for fish, wildlife, recreation and related environmental resources. Fisheries 1976, 1, 6–10. [Google Scholar] [CrossRef]
- Vogel, R.M.; Sieber, J.; Archfield, S.A.; Smith, M.P.; Apse, C.D.; Huber-Lee, A. Relations among storage, yield, and instream flow. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; McPhee, J.; Yeh, W.W. A diversified multi-objective GA for optimizing reservoir rule curves. Adv. Water Resour. 2007, 30, 1082–1093. [Google Scholar] [CrossRef]
- Ostadrahimi, L.; Mariño, M.A.; Afshar, A. Multi-reservoir operation rules: Multi-swarm PSO-based optimization approach. Water Resour. Manag. 2012, 26, 407–427. [Google Scholar] [CrossRef]
- Aizawa, A.N.; Wah, B.W. Scheduling of genetic algorithms in a noisy environment. Evol. Comput. 1994, 2, 97–122. [Google Scholar] [CrossRef]
- Miller, B.L.; Goldberg, D.E. Genetic algorithms, selection schemes, and the varying effects of noise. Evol. Comput. 1996, 4, 113–131. [Google Scholar] [CrossRef]
- Das, I. Robustness optimization for constrained nonlinear programming problem. Eng. Opt. 2000, 32, 585–618. [Google Scholar] [CrossRef]
- Branke, J. Evolutionary Optimization in Dynamic Environments; Kluwer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
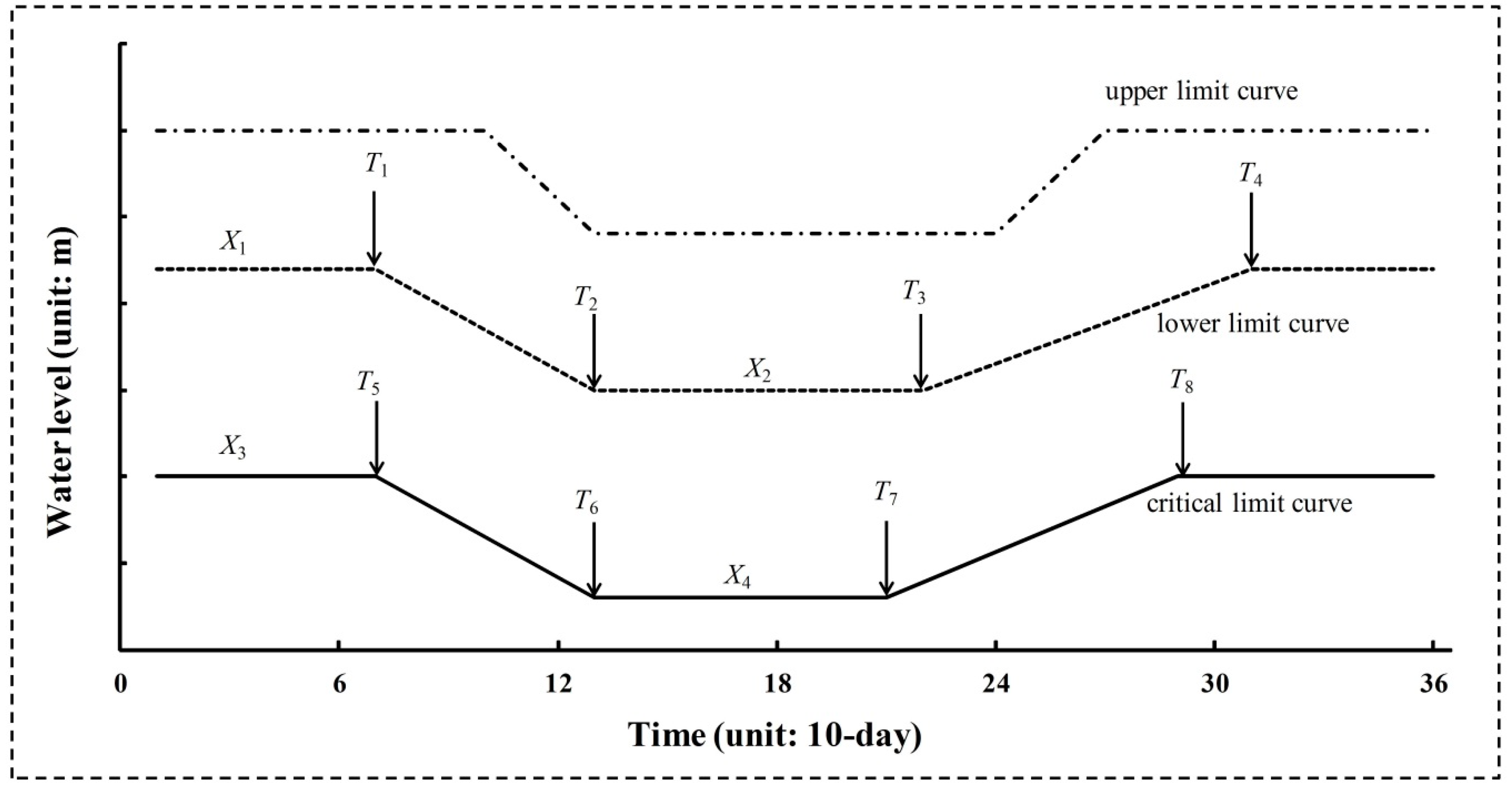
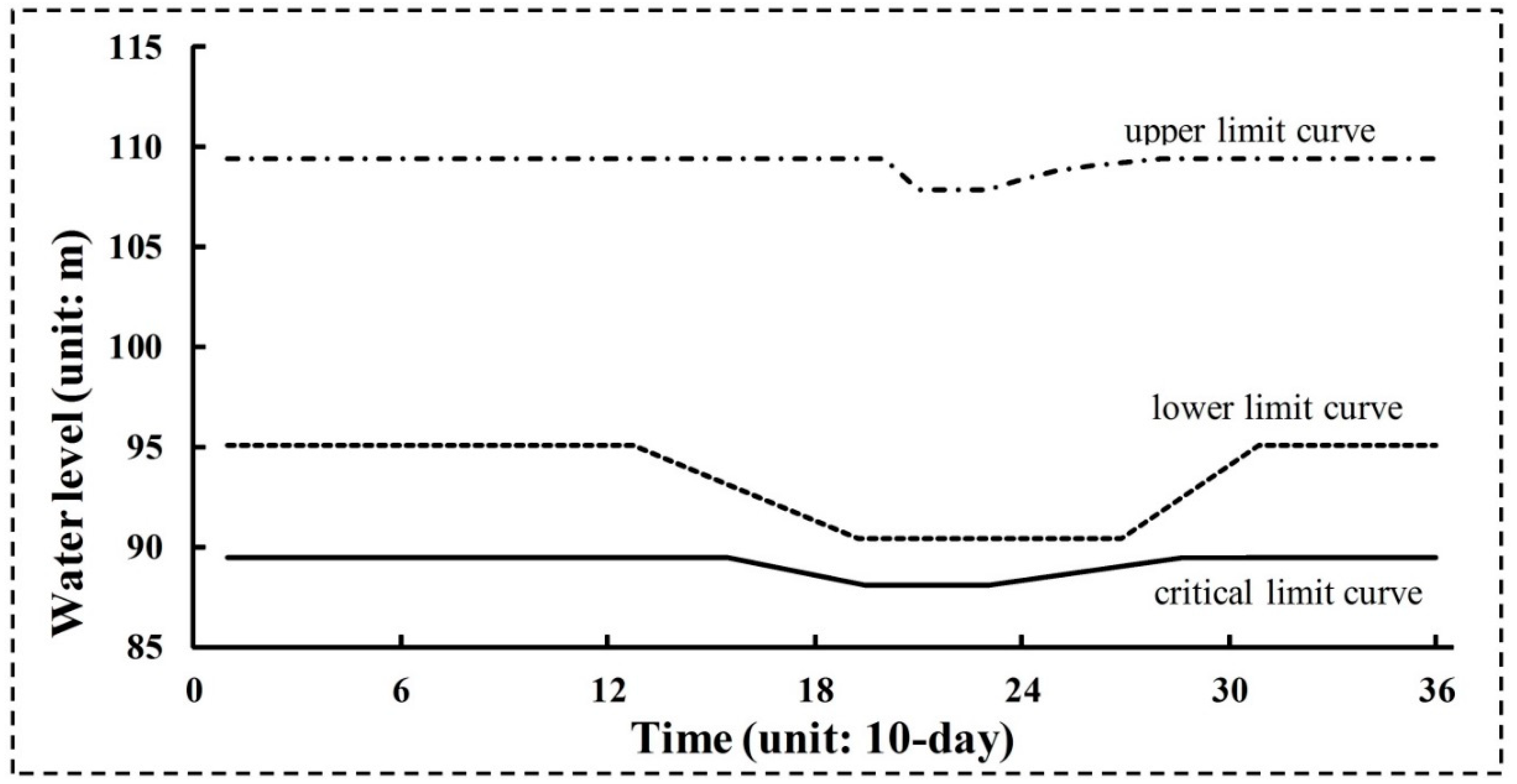
| Policy | Scenarios | Hypothesized Conditions |
|---|---|---|
| 1. Fraction of Inflow (FOI) | Scenario 1, FOI = 0.1; Scenario 2, FOI = 0.2; ⁞ Scenario 9, FOI = 0.9. | This policy offers a promising way that allows for extensive trade-offs between water supply for human and environmental flow requirement. |
| 2. Flow Components (FC) | Scenario 1, 10% of ADF as e-flow during dry season and 30% during the wet season, and 3*1 high-flow events; Scenario 2, 10% of ADF as e-flow during dry season and 30% during the wet season, and 3*2 high-flow events; ⁞ Scenario N (N = INT[the total number of high-flow events/3]), 10% of ADF as e-flow during dry season, 30% during the wet season, and 3*N high-flow events. | This policy attempts to provide occasional high-flow releases for habitat improvement. |
| 3. Four-period release approach (FP) | Scenario 1, (i) Floods: bankfull discharge as e-flow; (ii) Base flows: 10% of ADF as e-flow during the dry season and 30% of ADF during the wet season; (iii) Extreme low flows: e-flow equals to the reservoir inflow; (iv) High-flow pulses: all high-flow are released. | This policy attempts to provide the full range of natural flow regime alterations, including floods and droughts, in which the riverine ecosystem is adapted. |
| IHA Group | Hydrological Indicators |
|---|---|
| Group 1: Magnitude of monthly water conditions | Mean value for each calendar month. |
| Group 2: Magnitude and duration of annual extreme water conditions | Annual minima 1-day means; Annual maxima 1-day means; Annual minima 3-day means; Annual maxima 3-day means; Annual minima 7-day means; Annual maxima 7-day means; Annual minima 30-day means; Annual maxima 30-day means; Annual minima 90-day means; Annual maxima 90-day means. |
| Group 3: Timing of annual extreme water conditions | Julian date of each annual 1 day maximum; Julian date of each annual l day minimum. |
| Group 4: Frequency and duration of high and low pulses | No. of high pulses each year; No. of low pulses each year; Mean duration of high pulses within each year; Mean duration of low pulses within each year. |
| Group 5: Rate and frequency of water condition changes | Means of all positive differences between consecutive daily means; Means of all negative differences between consecutive daily values; Number of rises; Number of falls. |
| Component and Parameter | Type and Value | Component and Parameter | Type and Value |
|---|---|---|---|
| Representation | Real | Crossover | Scattered, 0.7 |
| Selection | Tournament, 4 | Mutation | Uniform, 0.08 |
| Policy | Stochastic Model | ||
|---|---|---|---|
| Monte Carlo GA | NGA | ||
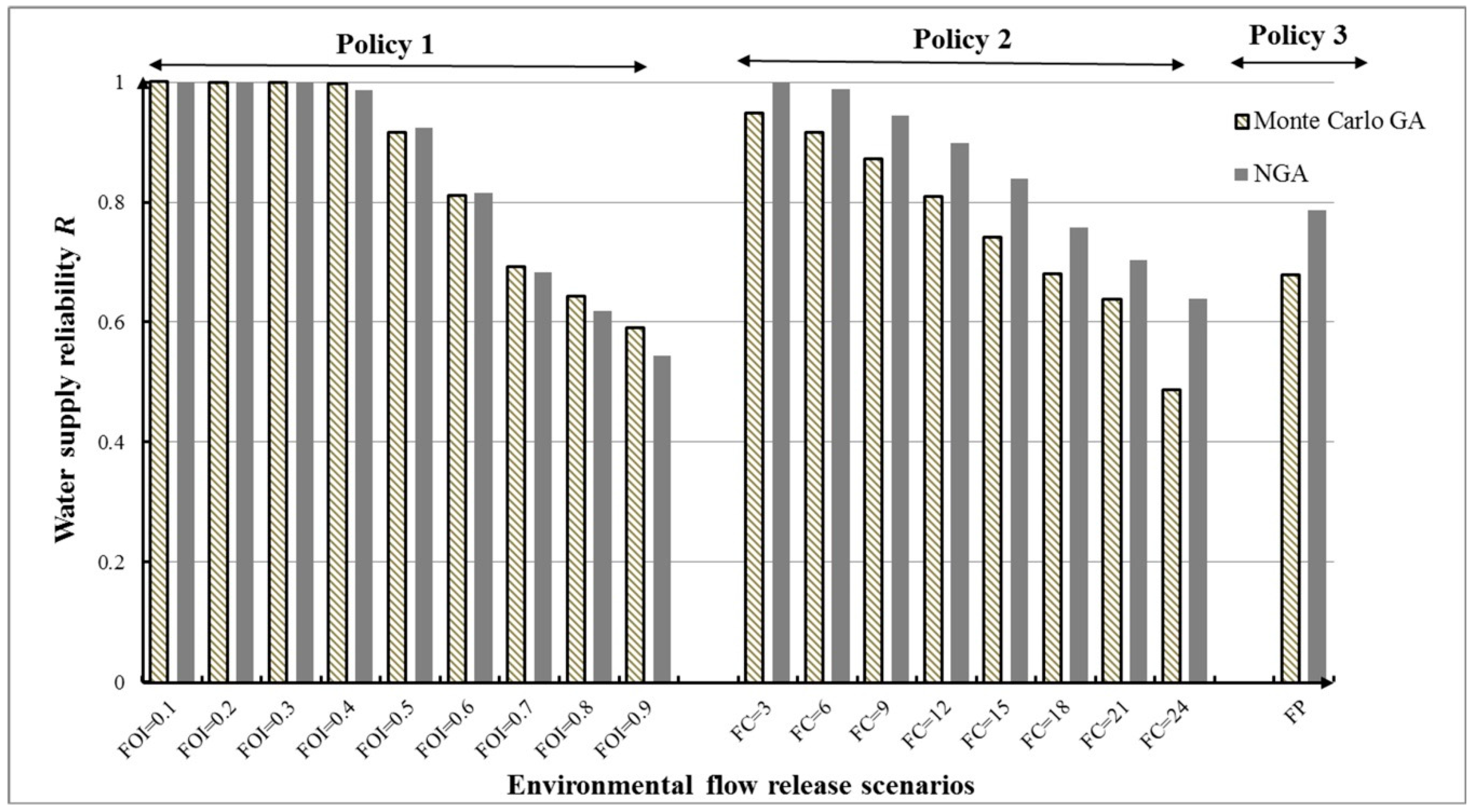
| 1 | FOI = 0.1 | 1 | 1 |
| FOI = 0.2 | 0.9996 | 1 | |
| FOI = 0.3 | 0.9995 | 1 | |
| FOI = 0.4 | 0.9976 | 0.9867 | |
| FOI = 0.5 | 0.9151 | 0.9237 | |
| FOI = 0.6 | 0.8099 | 0.8148 | |
| FOI = 0.7 | 0.6925 | 0.683 | |
| FOI = 0.8 | 0.6425 | 0.619 | |
| FOI = 0.9 | 0.5895 | 0.5447 | |
| 2 | FC = 3 | 0.9479 | 0.9987 |
| FC = 6 | 0.9162 | 0.9879 | |
| FC = 9 | 0.8713 | 0.9443 | |
| FC = 12 | 0.8096 | 0.8977 | |
| FC = 15 | 0.7405 | 0.8395 | |
| FC = 18 | 0.6795 | 0.7574 | |
| FC = 21 | 0.6382 | 0.703 | |
| FC = 24 | 0.4862 | 0.6386 | |
| 3 | FP | 0.6778 | 0.7863 |
| Policy | Stochastic Model | ||
|---|---|---|---|
| Monte Carlo GA | NGA | ||
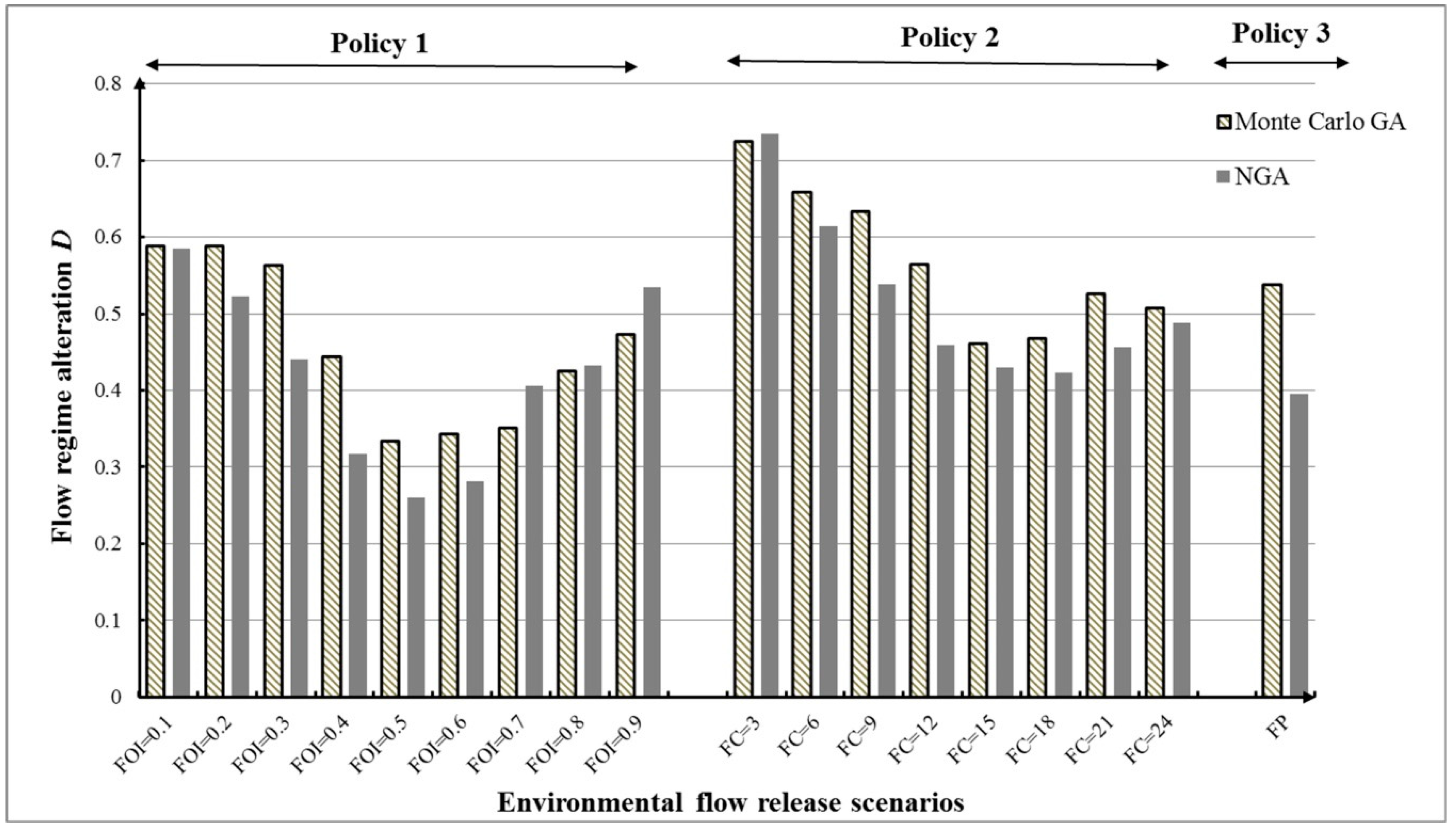
| 1 | FOI = 0.1 | 0.5875 | 0.5854 |
| FOI = 0.2 | 0.5875 | 0.5229 | |
| FOI = 0.3 | 0.5625 | 0.4403 | |
| FOI = 0.4 | 0.4438 | 0.3174 | |
| FOI = 0.5 | 0.3344 | 0.2597 | |
| FOI = 0.6 | 0.3431 | 0.2813 | |
| FOI = 0.7 | 0.3513 | 0.4056 | |
| FOI = 0.8 | 0.4250 | 0.4326 | |
| FOI = 0.9 | 0.4731 | 0.5347 | |
| 2 | FC = 3 | 0.7250 | 0.7347 |
| FC = 6 | 0.6588 | 0.6139 | |
| FC = 9 | 0.6325 | 0.5382 | |
| FC = 12 | 0.5644 | 0.4583 | |
| FC = 15 | 0.4606 | 0.4292 | |
| FC = 18 | 0.4669 | 0.4229 | |
| FC = 21 | 0.5263 | 0.4563 | |
| FC = 24 | 0.5069 | 0.4875 | |
| 3 | FP | 0.5375 | 0.3958 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Yin, X.; Yang, Z.; Dang, Z. Sustainable Water Resource Management of Regulated Rivers under Uncertain Inflow Conditions Using a Noisy Genetic Algorithm. Int. J. Environ. Res. Public Health 2019, 16, 868. https://doi.org/10.3390/ijerph16050868
Yu C, Yin X, Yang Z, Dang Z. Sustainable Water Resource Management of Regulated Rivers under Uncertain Inflow Conditions Using a Noisy Genetic Algorithm. International Journal of Environmental Research and Public Health. 2019; 16(5):868. https://doi.org/10.3390/ijerph16050868
Chicago/Turabian StyleYu, Chunxue, Xinan Yin, Zhifeng Yang, and Zhi Dang. 2019. "Sustainable Water Resource Management of Regulated Rivers under Uncertain Inflow Conditions Using a Noisy Genetic Algorithm" International Journal of Environmental Research and Public Health 16, no. 5: 868. https://doi.org/10.3390/ijerph16050868
APA StyleYu, C., Yin, X., Yang, Z., & Dang, Z. (2019). Sustainable Water Resource Management of Regulated Rivers under Uncertain Inflow Conditions Using a Noisy Genetic Algorithm. International Journal of Environmental Research and Public Health, 16(5), 868. https://doi.org/10.3390/ijerph16050868





