Investigation of Intense Precipitation from Tropical Cyclones during the 21st Century by Dynamical Downscaling of CCSM4 RCP 4.5
Abstract
1. Introduction
- The resolution in the simulation outer domain should be fine enough to resolve TCs;
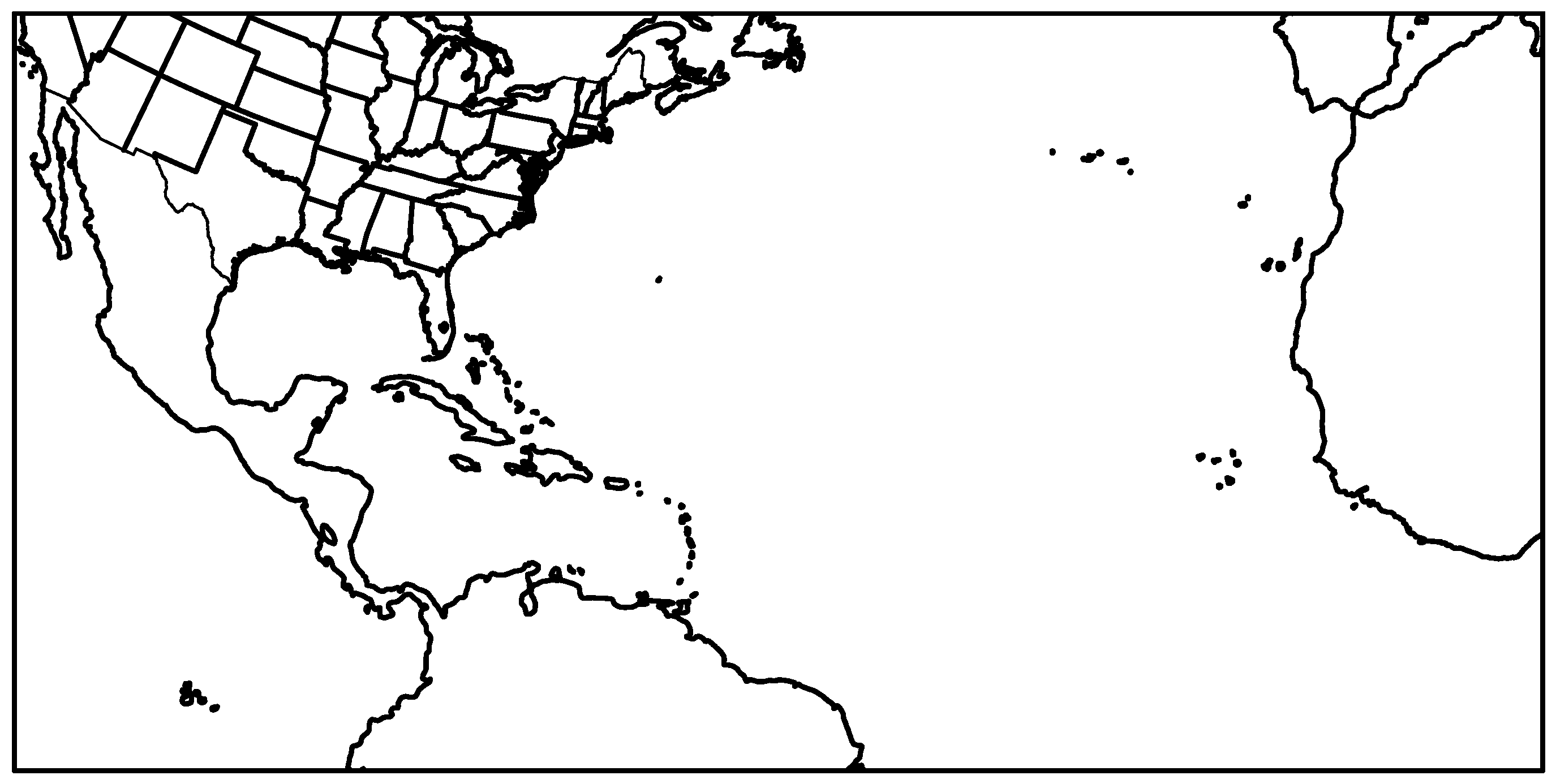
- The outer domain should be large enough for several reasons. First, for the simulation of Atlantic TCs, the region of formation of African easterly waves should be included in the outer domain because these waves play an important role in the formation of TCs. Second, if the outer domain is too small, it will be too closely coupled with the driving GCM, and consequently unable to capture upscale interactions. This can be all the more problematic if the GCM is biased;
- The presence of bias in the driving GCM may prevent the RAM from generating its own TCs. In this case, it is necessary to remove the bias from the IBCs. In particular, in their study, Done et al. [16] found that the simulations driven directly by CCSM3 produced too strong large-scale flow at upper-levels over the tropical North Atlantic which was responsible for generating anomalously strong wind shear, thus preventing the genesis of TCs. They had to perform a bias correction of the driving GCM before running the model because no TCs were simulated with the biased IBCs. This bias correction was performed by expressing the 6-hourly CCSM3 data and the 6-hourly National Centers for Environmental Prediction (NCEP)/ National Center for Atmospheric Research (NCAR) Reanalysis Project (NNRP) data as the sum of a background state plus a perturbation. The background state was obtained by averaging over the 20-yr period from 1975 to 1994. Afterwards, the bias was removed by replacing the background state of CCSM3 by the background state of NNRP. They found that the wind shear over the tropical Atlantic was significantly improved when the NRCM was run with the bias-corrected IBCs, which allowed the genesis of TCs.
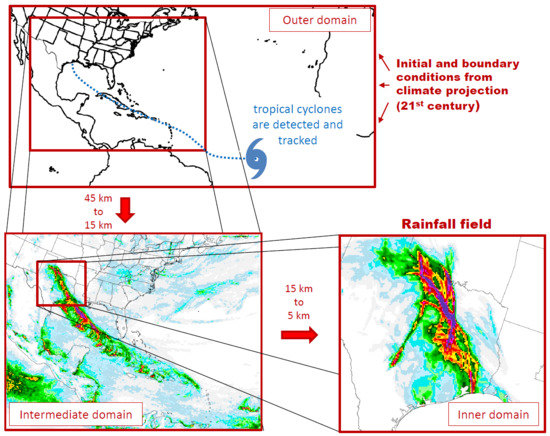
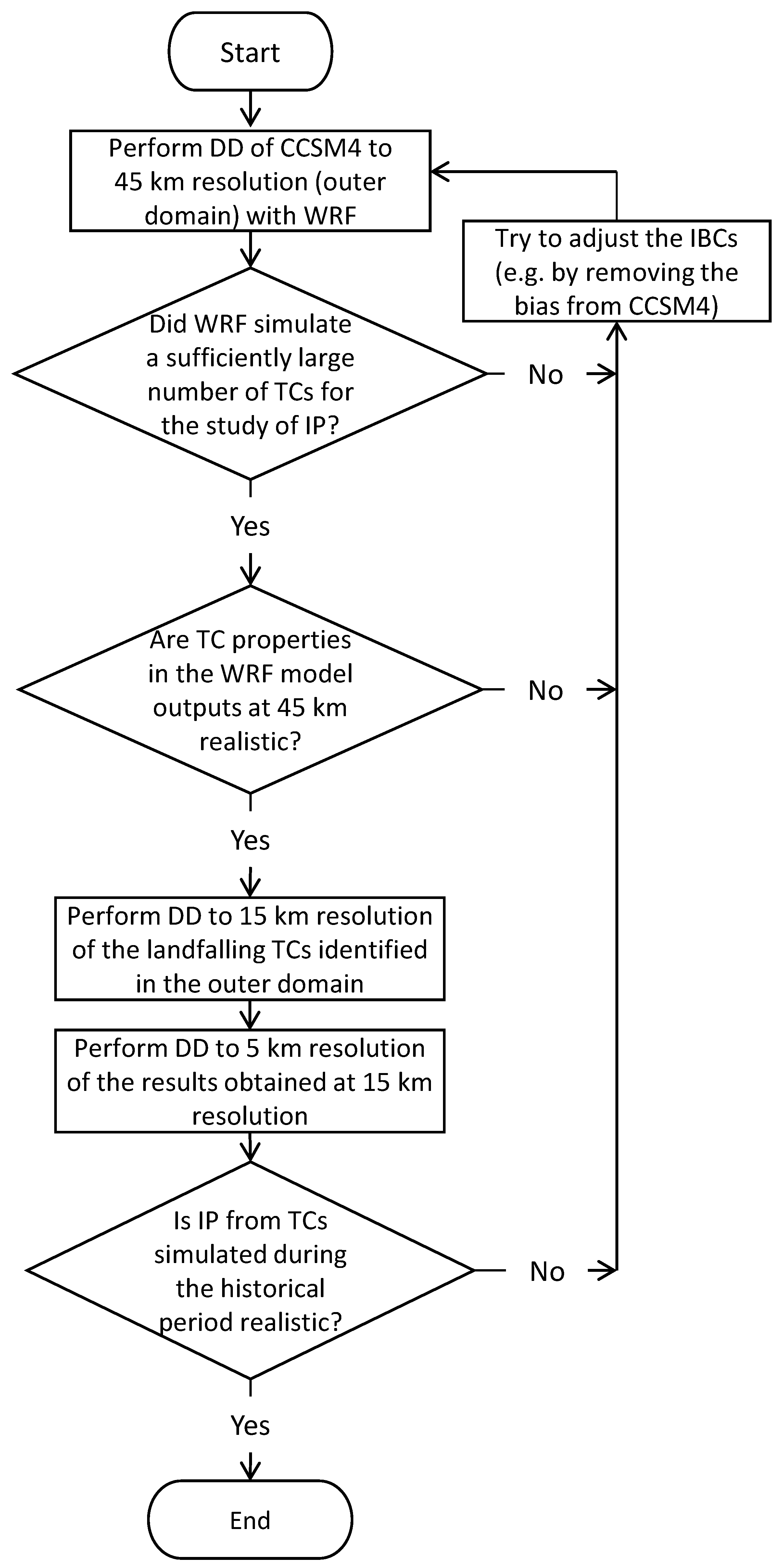
2. Modeling Framework
- Perform the DD of CCSM4 with the WRF model at 45 km horizontal resolution with the domain shown in Figure 1 for all hurricane seasons during the period 2005–2100. One hurricane season was defined as the time period between the beginning of July and the end of November;
- Examine the WRF model outputs from the previous step to assess whether the model generated a sufficiently large number of TCs, including a sufficiently large number of landfalling TCs for the study of IP over the eastern and southern U.S. in the future. If so, one can go to the next step. It is noted that since the focus of this study is on IP rather than TC climatology (i.e., TC frequency, geographical distribution, seasonal variability, etc.), it is less problematic if the number of TCs simulated by the WRF model is less or more than it should be. There should be, however, substantially more TCs in the WRF model outputs than in CCSM4, since the scarcity of TCs in CCSM4 was the main reason for adopting this DD alternative. If the model fails to produce enough TCs, additional work is required. For example, following the discussion in Section 1, one may try to remove the bias from CCSM4 and run the WRF model with the unbiased IBCs;
- Examine the TCs in the WRF model outputs to assess whether their properties (e.g., MTSWS) are realistic. For example, did the model generate a population of TCs that is overall too strong, or too weak? If not, one can go to the next step. Otherwise, additional work is required, which again may involve trying to remove the bias from CCSM4 and run the WRF model with the unbiased IBCs;
- Perform DD to 15 km horizontal resolution of the TCs identified in Step 2;
- Perform DD to 5 km horizontal resolution of the results from Step 4;
- Validate the WRF model performance in simulating IP from TCs during the historical period (corresponding to 2005–2017 in this study). This step is necessary if one wants to confidently use the WRF model previsions of future IP from TCs.
3. Detection and Tracking of Tropical Cyclones
4. Calculation of the Properties of Tropical Cyclones
4.1. Calculation of the CPD and TCCHL
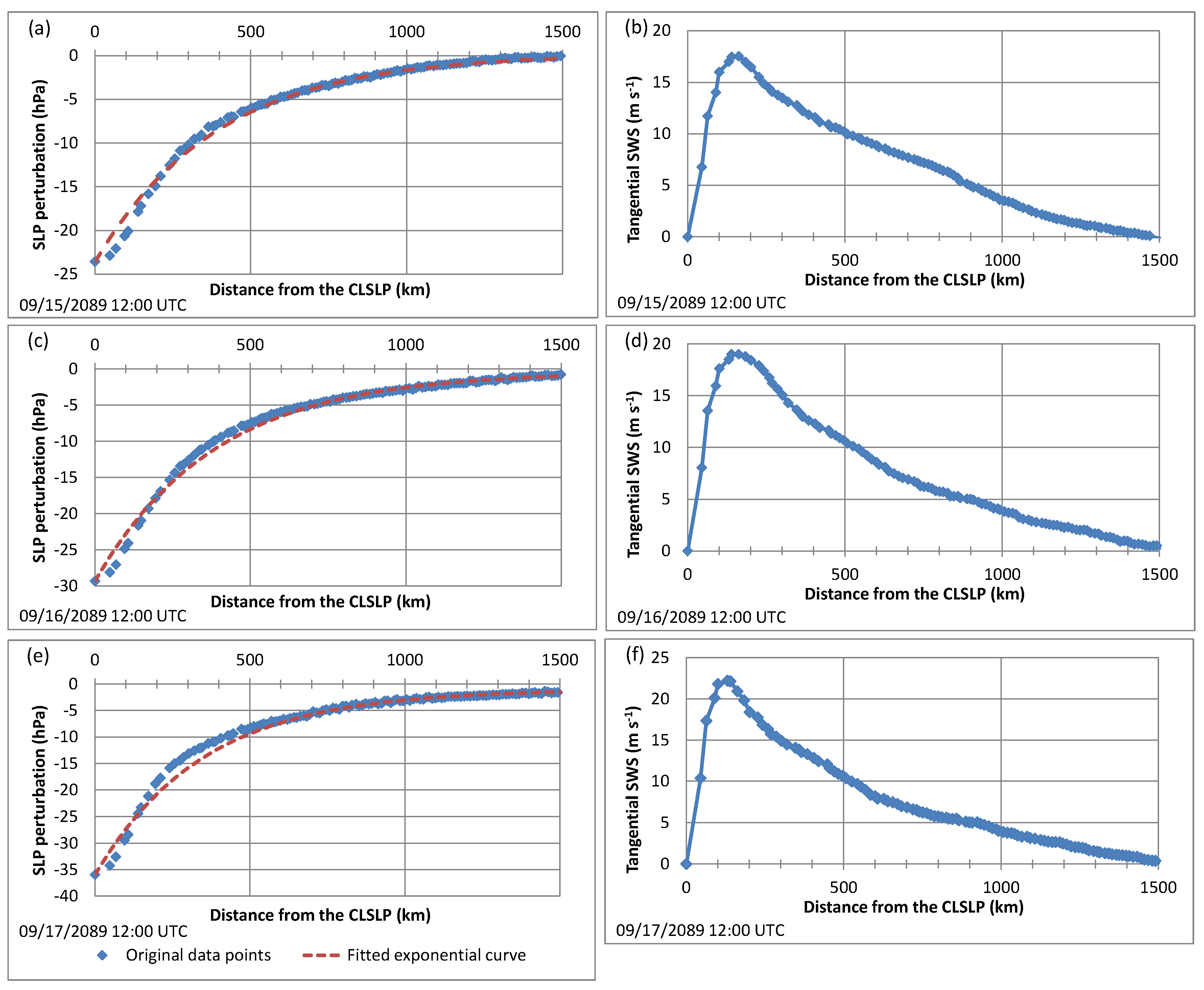
4.2. Calculation of the MTSWS and RMTSWS
4.3. Calculation of the TC Depth
4.4. Comparison of TC Properties between CFSR and the WRF Model Outputs during the Period 2005–2017
5. Dynamical Downscaling to 15 km and 5 km Resolutions
6. Intense Precipitation from Tropical Cyclones during the 21st Century
6.1. What Is Intense Precipitation?
6.2. Validation of the WRF Model Performance in Simulating IP from TCs during the Period 2005–2017
6.3. Evolution of IP from TCs during the 21st Century
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CCSM | Community Climate System Model |
| CCSM3 | CCSM version 3 |
| CCSM4 | CCSM version 4 |
| CFSR | Climate Forecast System Reanalysis |
| CLSLP | center of low sea level pressure |
| CPD | central pressure deficit |
| DD | dynamical downscaling |
| DTA | detection and tracking algorithm |
| GCM | general circulation model |
| GFDL | Geophysical Fluid Dynamics Laboratory |
| IBC | initial and boundary condition |
| IP | intense precipitation |
| MTSWS | maximum tangential surface wind speed |
| NCAR | National Center for Atmospheric Research |
| NCEP | National Centers for Environmental Prediction |
| NNRP | NCEP/NCAR Reanalysis Project |
| NOAA | National Oceanic and Atmospheric Administration |
| NRCM | Nested Regional Climate Model |
| PD | precipitation depth |
| PGW-DD | pseudo-global warming dynamical downscaling |
| PS | parameterization scheme |
| RAM | regional atmospheric model |
| RCP | Representative Concentration Pathway |
| RMTSWS | radius of maximum tangential surface wind speed |
| SLP | sea level pressure |
| SWS | surface wind speed |
| TC | tropical cyclone |
| TCCHL | TC characteristic horizontal length |
| TS | tropical storm |
| UTC | Coordinated Universal Time |
| WRF | Weather Research and Forecasting |
Appendix A. Simulation Start and End Dates for Dynamical Downscaling of the 64 Landfalling Tropical Cyclones to 15 km and 5 km Resolutions
| Event # | Simulation Start Date for Intermediate Domain | Simulation End Date for Intermediate Domain | Simulation Start Date for Inner Domain | Simulation End Date for Inner Domain |
|---|---|---|---|---|
| 1 | 08/11/2005 18:00 | 08/25/2005 18:00 | 08/14/2005 12:00 | 08/18/2005 12:00 |
| 2 | 08/27/2005 12:00 | 09/10/2005 12:00 | 08/29/2005 18:00 | 09/02/2005 18:00 |
| 3 | 08/14/2006 12:00 | 08/28/2006 12:00 | 08/17/2006 06:00 | 08/21/2006 06:00 |
| 4 | 08/12/2009 06:00 | 08/26/2009 06:00 | 08/14/2009 06:00 | 08/19/2009 12:00 |
| 5 | 09/10/2010 18:00 | 09/24/2010 18:00 | 09/13/2010 12:00 | 09/16/2010 12:00 |
| 6 | 08/02/2011 06:00 | 08/16/2011 06:00 | 08/04/2011 00:00 | 08/07/2011 00:00 |
| 7 | 08/22/2012 18:00 | 09/05/2012 18:00 | 08/24/2012 18:00 | 08/27/2012 18:00 |
| 8 | 08/26/2012 18:00 | 09/09/2012 18:00 | 08/30/2012 00:00 | 09/02/2012 00:00 |
| 9 | 08/13/2013 18:00 | 08/27/2013 18:00 | 08/17/2013 12:00 | 08/21/2013 12:00 |
| 10 | 08/28/2015 12:00 | 09/11/2015 12:00 | 08/30/2015 00:00 | 09/02/2015 18:00 |
| 11 | 08/28/2017 00:00 | 09/11/2017 00:00 | 08/31/2017 00:00 | 09/03/2017 18:00 |
| 12 | 07/30/2020 12:00 | 08/13/2020 12:00 | 08/05/2020 18:00 | 08/09/2020 12:00 |
| 13 | 09/15/2020 06:00 | 09/29/2020 06:00 | 09/20/2020 18:00 | 09/23/2020 18:00 |
| 14 | 08/07/2021 18:00 | 08/21/2021 18:00 | 08/10/2021 18:00 | 08/13/2021 18:00 |
| 15 | 08/15/2021 18:00 | 08/29/2021 18:00 | 08/20/2021 00:00 | 08/23/2021 18:00 |
| 16 | 08/27/2021 06:00 | 09/10/2021 06:00 | 08/28/2021 06:00 | 08/31/2021 06:00 |
| 17 | 10/11/2021 00:00 | 10/25/2021 00:00 | 10/15/2021 06:00 | 10/18/2021 06:00 |
| 18 | 09/03/2024 00:00 | 09/17/2024 00:00 | 09/04/2024 18:00 | 09/08/2024 00:00 |
| 19 | 09/10/2024 06:00 | 09/24/2024 06:00 | 09/15/2024 00:00 | 09/18/2024 00:00 |
| 20 | 08/22/2025 06:00 | 09/05/2025 06:00 | 08/25/2025 00:00 | 08/28/2025 06:00 |
| 21 | 09/03/2027 18:00 | 09/17/2027 18:00 | 09/07/2027 00:00 | 09/10/2027 18:00 |
| 22 | 09/02/2028 00:00 | 09/16/2028 00:00 | 09/07/2028 00:00 | 09/10/2028 00:00 |
| 23 | 08/19/2030 00:00 | 09/02/2030 00:00 | 08/21/2030 12:00 | 08/25/2030 18:00 |
| 24 | 08/29/2031 00:00 | 09/12/2031 00:00 | 09/02/2031 00:00 | 09/05/2031 12:00 |
| 25 | 09/23/2032 00:00 | 10/07/2032 00:00 | 09/27/2032 18:00 | 09/30/2032 18:00 |
| 26 | 08/26/2033 12:00 | 09/09/2033 12:00 | 08/28/2033 12:00 | 09/01/2033 00:00 |
| 27 | 09/03/2033 00:00 | 09/17/2033 00:00 | 09/04/2033 06:00 | 09/08/2033 00:00 |
| 28 | 09/21/2033 18:00 | 10/05/2033 18:00 | 09/23/2033 18:00 | 09/26/2033 18:00 |
| 29 | 09/04/2034 06:00 | 09/18/2034 06:00 | 09/07/2034 18:00 | 09/10/2034 18:00 |
| 30 | 07/17/2037 18:00 | 07/31/2037 18:00 | 07/19/2037 06:00 | 07/23/2037 00:00 |
| 31 | 09/23/2037 06:00 | 10/07/2037 06:00 | 09/26/2037 12:00 | 09/29/2037 12:00 |
| 32 | 08/30/2038 18:00 | 09/13/2038 18:00 | 09/02/2038 12:00 | 09/05/2038 12:00 |
| 33 | 09/03/2038 00:00 | 09/17/2038 00:00 | 09/08/2038 00:00 | 09/11/2038 00:00 |
| 34 | 07/12/2040 00:00 | 07/26/2040 00:00 | 07/19/2040 12:00 | 07/22/2040 12:00 |
| 35 | 08/21/2043 06:00 | 09/04/2043 06:00 | 08/24/2043 06:00 | 08/27/2043 06:00 |
| 36 | 08/26/2043 06:00 | 09/09/2043 06:00 | 09/02/2043 12:00 | 09/05/2043 12:00 |
| 37 | 08/20/2047 18:00 | 09/03/2047 18:00 | 08/25/2047 00:00 | 08/28/2047 00:00 |
| 38 | 08/24/2047 12:00 | 09/07/2047 12:00 | 09/04/2047 06:00 | 09/07/2047 12:00 |
| 39 | 09/23/2048 00:00 | 10/07/2048 00:00 | 09/29/2048 00:00 | 10/02/2048 00:00 |
| 40 | 08/31/2049 12:00 | 09/14/2049 12:00 | 09/03/2049 18:00 | 09/09/2049 06:00 |
| 41 | 09/26/2050 00:00 | 10/10/2050 00:00 | 09/27/2050 18:00 | 09/30/2050 18:00 |
| 42 | 08/28/2052 00:00 | 09/11/2052 00:00 | 08/31/2052 00:00 | 09/03/2052 12:00 |
| 43 | 08/30/2057 00:00 | 09/13/2057 00:00 | 09/01/2057 06:00 | 09/04/2057 12:00 |
| 44 | 09/27/2057 18:00 | 10/11/2057 18:00 | 10/01/2057 00:00 | 10/04/2057 00:00 |
| 45 | 09/09/2062 06:00 | 09/23/2062 06:00 | 09/12/2062 06:00 | 09/15/2062 06:00 |
| 46 | 09/13/2064 18:00 | 09/27/2064 18:00 | 09/17/2064 18:00 | 09/21/2064 12:00 |
| 47 | 08/16/2066 18:00 | 08/30/2066 18:00 | 08/19/2066 18:00 | 08/22/2066 18:00 |
| 48 | 08/22/2066 06:00 | 09/05/2066 06:00 | 08/24/2066 12:00 | 08/27/2066 12:00 |
| 49 | 08/26/2067 12:00 | 09/09/2067 12:00 | 08/30/2067 00:00 | 09/02/2067 06:00 |
| 50 | 08/12/2068 18:00 | 08/26/2068 18:00 | 08/16/2068 06:00 | 08/19/2068 18:00 |
| 51 | 08/24/2068 00:00 | 09/07/2068 00:00 | 08/29/2068 00:00 | 09/01/2068 00:00 |
| 52 | 08/29/2071 12:00 | 09/12/2071 12:00 | 09/01/2071 00:00 | 09/04/2071 00:00 |
| 53 | 09/17/2073 18:00 | 10/01/2073 18:00 | 09/23/2073 00:00 | 09/27/2073 00:00 |
| 54 | 08/04/2078 00:00 | 08/18/2078 00:00 | 08/06/2078 06:00 | 08/09/2078 06:00 |
| 55 | 09/07/2080 00:00 | 09/21/2080 00:00 | 09/11/2080 12:00 | 09/14/2080 18:00 |
| 56 | 09/18/2080 12:00 | 10/02/2080 12:00 | 09/22/2080 00:00 | 09/25/2080 00:00 |
| 57 | 09/24/2081 00:00 | 10/08/2081 00:00 | 10/02/2081 12:00 | 10/05/2081 12:00 |
| 58 | 09/14/2085 12:00 | 09/28/2085 12:00 | 09/20/2085 06:00 | 09/26/2085 00:00 |
| 59 | 08/18/2088 00:00 | 09/01/2088 00:00 | 08/22/2088 12:00 | 08/26/2088 12:00 |
| 60 | 08/30/2088 06:00 | 09/13/2088 06:00 | 09/02/2088 12:00 | 09/07/2088 06:00 |
| 61 | 09/13/2089 00:00 | 09/27/2089 00:00 | 09/16/2089 00:00 | 09/19/2089 00:00 |
| 62 | 09/17/2089 06:00 | 10/01/2089 06:00 | 09/22/2089 00:00 | 09/25/2089 06:00 |
| 63 | 08/16/2092 12:00 | 08/30/2092 12:00 | 08/18/2092 00:00 | 08/23/2092 12:00 |
| 64 | 08/18/2098 18:00 | 09/01/2098 18:00 | 08/25/2098 00:00 | 08/28/2098 00:00 |
Appendix B. Plots of the Inner-Domain Precipitation Depth Fields of the 64 Landfalling Tropical Cyclones during the Period 2005–2100
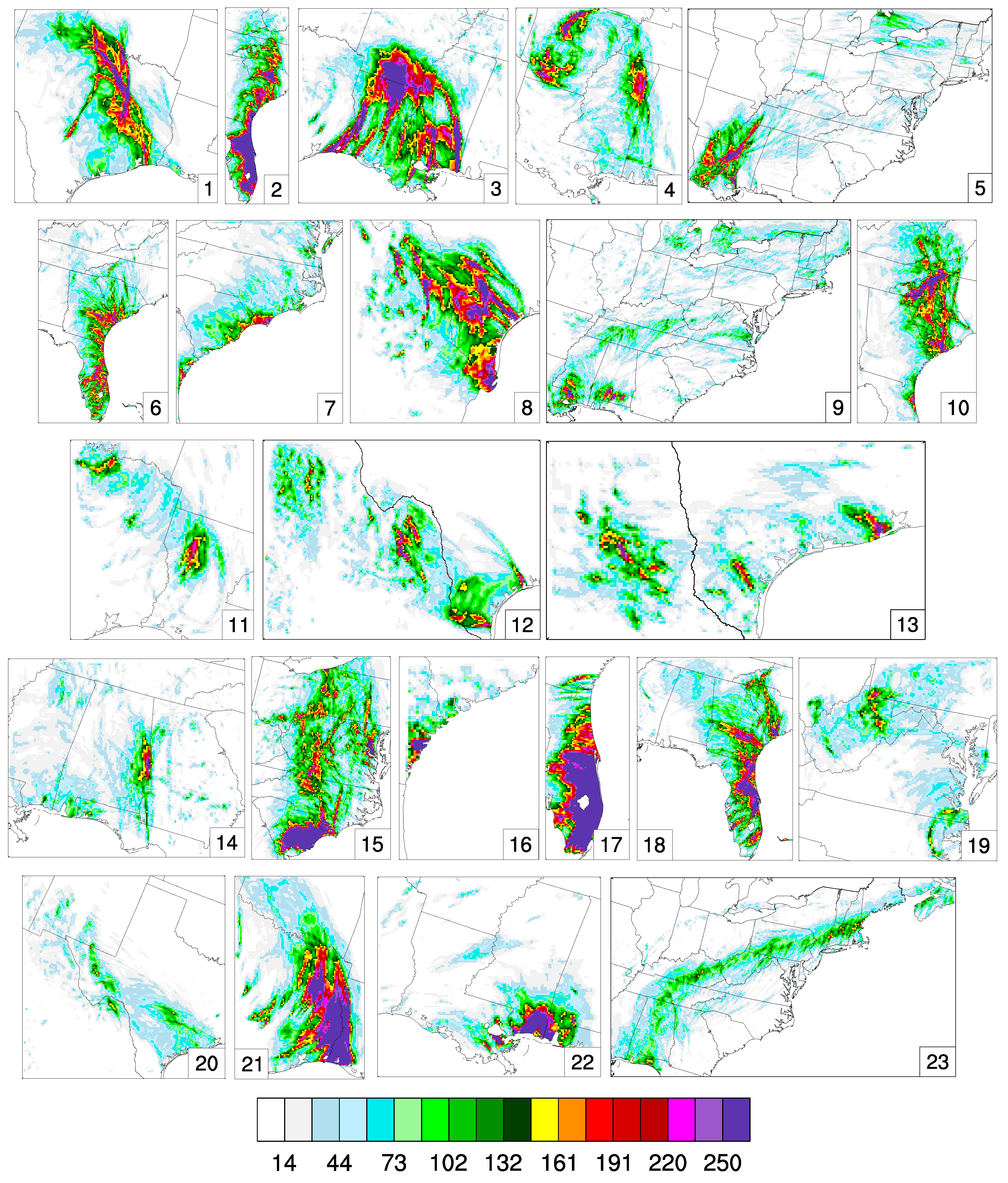
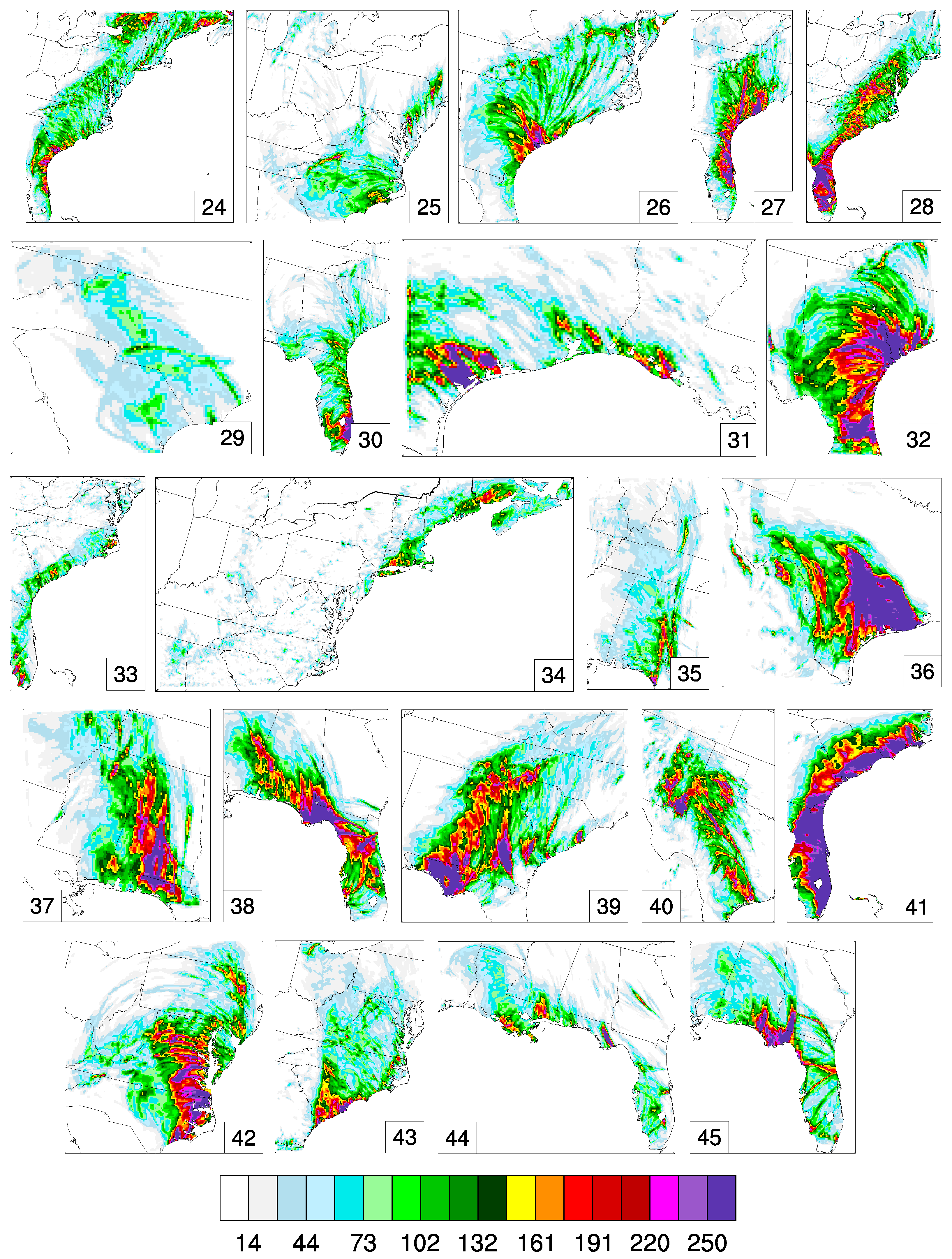
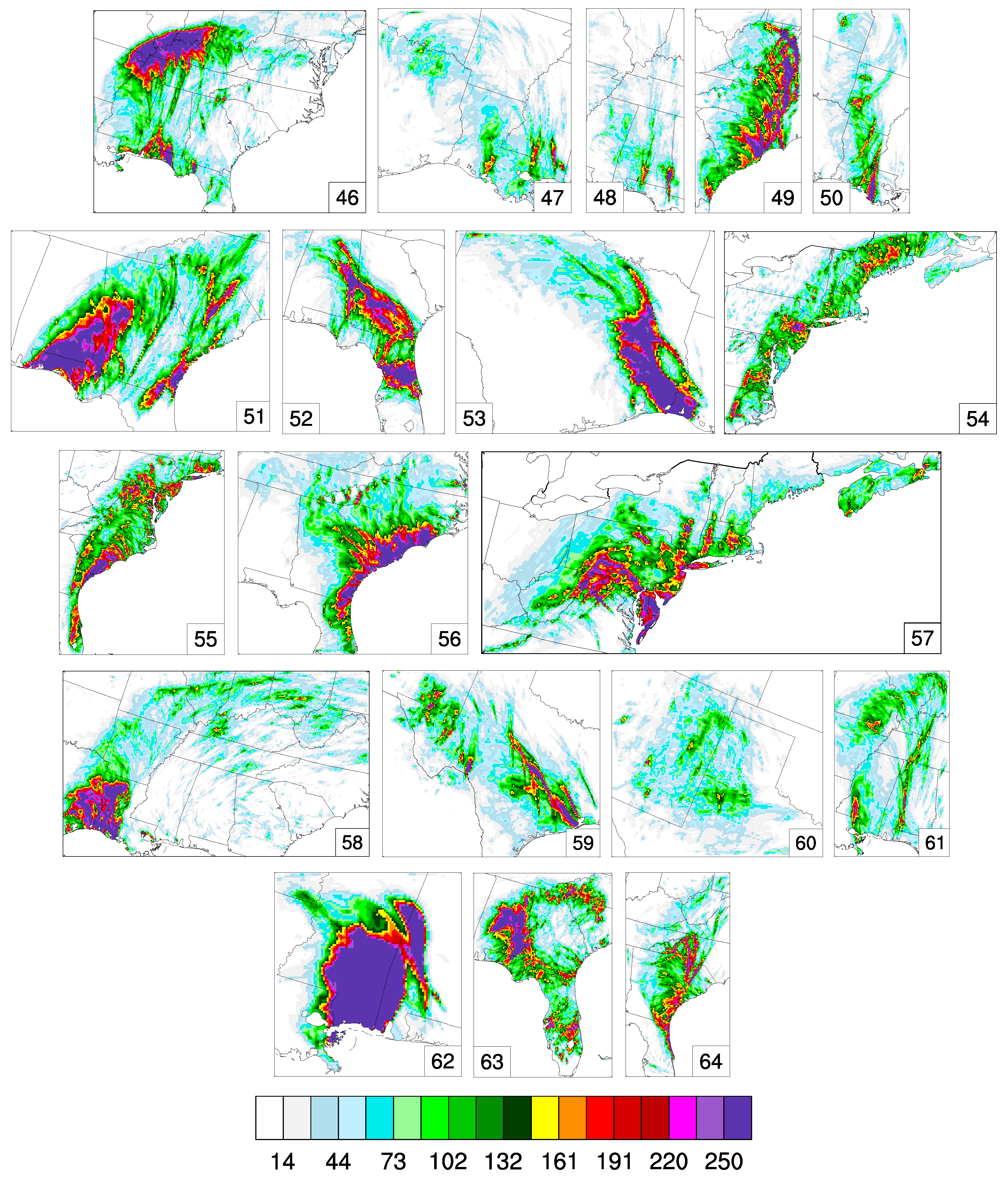
References
- Gray, W.M. Hurricanes: Their formation, structure and likely role in the tropical circulation. In Meteorology over the Tropical Oceans, Royal Meteorological Society, James Glaisher House, Grenville Place, Bracknell; Shaw, D.B., Ed.; James Glaisher House: Berkshire, UK, 1979; pp. 155–218. [Google Scholar]
- Ryan, B.F.; Watterson, I.G.; Evans, J.L. Tropical cyclone frequencies inferred from Gray’s yearly genesis parameter: Validation of GCM tropical climates. Geophys. Res. Lett. 1992, 19, 1831–1834. [Google Scholar] [CrossRef]
- Watterson, I.G.; Evans, J.L.; Ryan, B.F. Seasonal and Interannual Variability of Tropical Cyclogenesis: Diagnostics from Large-Scale Fields. J. Clim. 1995, 8, 3052–3066. [Google Scholar] [CrossRef]
- Bengtsson, L.; Hodges, K.I.; Esch, M.; Keenlyside, N.; Kornblueh, L.; Luo, J.J.; Yamagata, T. How may tropical cyclones change in a warmer climate? Tellus A Dyn. Meteorol. Oceanogr. 2007, 59, 539–561. [Google Scholar] [CrossRef]
- Emanuel, K.A. Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proc. Natl. Acad. Sci. USA 2013. [Google Scholar] [CrossRef] [PubMed]
- Bengtsson, L.; Botzet, M.; Esch, M. Will greenhouse gas-induced warming over the next 50 years lead to higher frequency and greater intensity of hurricanes? Tellus A 1996, 48, 57–73. [Google Scholar] [CrossRef]
- Broccoli, A.J.; Manabe, S. Can existing climate models be used to study anthropogenic changes in tropical cyclone climate? Geophys. Res. Lett. 1990, 17, 1917–1920. [Google Scholar] [CrossRef]
- Oouchi, K.; Yoshimura, J.; Yoshimura, H.; Mizuta, R.; Kusunoki, S.; Noda, A. Tropical cyclone climatology in a global-warming climate as simulated in a 20 km-mesh global atmospheric model: Frequency and wind intensity analyses. J. Meteorol. Soc. Jpn. Ser. II 2006, 84, 259–276. [Google Scholar] [CrossRef]
- Schott, T.; Landsea, C.; Hafele, G.; Lorens, J.; Taylor, A.; Thurm, H.; Ward, B.; Willis, M.; Zaleski, W. The Saffir-Simpson Hurricane Wind Scale. 2012. Available online: https://www.nhc.noaa.gov/pdf/sshws.pdf (accessed on 18 February 2019).
- Murakami, H.; Wang, Y.; Yoshimura, H.; Mizuta, R.; Sugi, M.; Shindo, E.; Adachi, Y.; Yukimoto, S.; Hosaka, M.; Kusunoki, S.; et al. Future Changes in Tropical Cyclone Activity Projected by the New High-Resolution MRI-AGCM. J. Clim. 2012, 25, 3237–3260. [Google Scholar] [CrossRef]
- Knutson, T.R.; Sirutis, J.J.; Garner, S.T.; Vecchi, G.A.; Held, I.M. Simulated reduction in Atlantic hurricane frequency under twenty-first-century warming conditions. Nat. Geosci. 2008, 1, 359. [Google Scholar] [CrossRef]
- Bender, M.A.; Knutson, T.R.; Tuleya, R.E.; Sirutis, J.J.; Vecchi, G.A.; Garner, S.T.; Held, I.M. Modeled Impact of Anthropogenic Warming on the Frequency of Intense Atlantic Hurricanes. Science 2010, 327, 454–458. [Google Scholar] [CrossRef] [PubMed]
- Knutson, T.R.; Sirutis, J.J.; Vecchi, G.A.; Garner, S.; Zhao, M.; Kim, H.S.; Bender, M.; Tuleya, R.E.; Held, I.M.; Villarini, G. Dynamical Downscaling Projections of Twenty-First-Century Atlantic Hurricane Activity: CMIP3 and CMIP5 Model-Based Scenarios. J. Clim. 2013, 26, 6591–6617. [Google Scholar] [CrossRef]
- Wright, D.B.; Knutson, T.R.; Smith, J.A. Regional climate model projections of rainfall from U.S. landfalling tropical cyclones. Clim. Dyn. 2015, 45, 3365–3379. [Google Scholar] [CrossRef]
- Kawase, H.; Yoshikane, T.; Hara, M.; Kimura, F.; Yasunari, T.; Ailikun, B.; Ueda, H.; Inoue, T. Intermodel variability of future changes in the Baiu rainband estimated by the pseudo global warming downscaling method. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Done, J.M.; Holland, G.J.; Bruyère, C.L.; Leung, L.R.; Suzuki-Parker, A. Modeling high-impact weather and climate: Lessons from a tropical cyclone perspective. Clim. Chang. 2015, 129, 381–395. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Davis, C.A.; Fasullo, J. Water and energy budgets of hurricanes: Case studies of Ivan and Katrina. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Davis, C.; Wang, W.; Chen, S.S.; Chen, Y.; Corbosiero, K.; DeMaria, M.; Dudhia, J.; Holland, G.; Klemp, J.; Michalakes, J.; et al. Prediction of Landfalling Hurricanes with the Advanced Hurricane WRF Model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef]
- Fierro, A.O.; Rogers, R.F.; Marks, F.D.; Nolan, D.S. The Impact of Horizontal Grid Spacing on the Microphysical and Kinematic Structures of Strong Tropical Cyclones Simulated with the WRF-ARW Model. Mon. Weather Rev. 2009, 137, 3717–3743. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, X.; Davis, C.; Tuttle, J.; Holland, G.; Fitzpatrick, P.J. Experiments of Hurricane Initialization with Airborne Doppler Radar Data for the Advanced Research Hurricane WRF (AHW) Model. Mon. Weather Rev. 2009, 137, 2758–2777. [Google Scholar] [CrossRef]
- Khain, A.; Lynn, B.; Dudhia, J. Aerosol Effects on Intensity of Landfalling Hurricanes as Seen from Simulations with the WRF Model with Spectral Bin Microphysics. J. Atmos. Sci. 2010, 67, 365–384. [Google Scholar] [CrossRef]
- Lin, N.; Smith, J.A.; Villarini, G.; Marchok, T.P.; Baeck, M.L. Modeling Extreme Rainfall, Winds, and Surge from Hurricane Isabel (2003). Weather Forecast. 2010, 25, 1342–1361. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747. [Google Scholar] [CrossRef] [PubMed]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5. [Google Scholar] [CrossRef]
- Clarke, L.; Edmonds, J.; Jacoby, H.; Pitcher, H.; Reilly, J.; Richels, R. Scenarios of Greenhouse Gas Emissions and Atmospheric Concentrations; U.S. Department of Energy at DigitalCommons@University of Nebraska: Lincoln, RI, USA, 2007. [Google Scholar]
- Gentry, M.S.; Lackmann, G.M. Sensitivity of Simulated Tropical Cyclone Structure and Intensity to Horizontal Resolution. Mon. Weather Rev. 2010, 138, 688–704. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.G.; Marks, F.; Zhang, X.; Bao, J.W.; Yeh, K.S.; Atlas, R. The Experimental HWRF System: A Study on the Influence of Horizontal Resolution on the Structure and Intensity Changes in Tropical Cyclones Using an Idealized Framework. Mon. Weather Rev. 2011, 139, 1762–1784. [Google Scholar] [CrossRef]
- Murakami, H.; Sugi, M. Effect of Model Resolution on Tropical Cyclone Climate Projections. SOLA 2010, 6, 73–76. [Google Scholar] [CrossRef]
- Roberts, M.J.; Vidale, P.L.; Mizielinski, M.S.; Demory, M.E.; Schiemann, R.; Strachan, J.; Hodges, K.; Bell, R.; Camp, J. Tropical Cyclones in the UPSCALE Ensemble of High-Resolution Global Climate Models. J. Clim. 2015, 28, 574–596. [Google Scholar] [CrossRef]
- Strachan, J.; Vidale, P.L.; Hodges, K.; Roberts, M.; Demory, M.E. Investigating Global Tropical Cyclone Activity with a Hierarchy of AGCMs: The Role of Model Resolution. J. Clim. 2013, 26, 133–152. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Kristovich, D.A.R.; Gleason, B.; Stoecker, L.; Smith, R. Meteorological Causes of the Secular Variations in Observed Extreme Precipitation Events for the Conterminous United States. J. Hydrometeorol. 2012, 13, 1131–1141. [Google Scholar] [CrossRef]
- Schumacher, R.S.; Johnson, R.H. Organization and Environmental Properties of Extreme-Rain-Producing Mesoscale Convective Systems. Mon. Weather Rev. 2005, 133, 961–976. [Google Scholar] [CrossRef]
- Hershfield, D.M. Estimating the probable maximum precipitation. J. Hydraul. Div. 1961, 87, 99–116. [Google Scholar]
- Stevenson, S.N.; Schumacher, R.S. A 10-Year Survey of Extreme Rainfall Events in the Central and Eastern United States Using Gridded Multisensor Precipitation Analyses. Mon. Weather Rev. 2014, 142, 3147–3162. [Google Scholar] [CrossRef]
- Lin, Y.; Mitchell, K.E. The NCEP stage II/IV hourly precipitation analyses: Development and applications. In Proceedings of the 19th Conference on Hydrology, American Meteorological Society, San Diego, CA, USA, 9–13 January 2005. [Google Scholar]
- Lin, Y. GCIP/EOP Surface: Precipitation NCEP/EMC 4KM Gridded Data (GRIB) Stage IV Data. Version 1.0. UCAR/NCAR—Earth Observing Laboratory. Available online: https://doi.org/10.5065/D6PG1QDD (accessed on 18 February 2019).
- Kursinski, A.L.; Mullen, S.L. Spatiotemporal Variability of Hourly Precipitation over the Eastern Contiguous United States from Stage IV Multisensor Analyses. J. Hydrometeorol. 2008, 9, 3–21. [Google Scholar] [CrossRef]
- Moore, B.J.; Mahoney, K.M.; Sukovich, E.M.; Cifelli, R.; Hamill, T.M. Climatology and Environmental Characteristics of Extreme Precipitation Events in the Southeastern United States. Mon. Weather Rev. 2015, 143, 718–741. [Google Scholar] [CrossRef]
- Herschfield, D. Rainfall Frequency atlas of the United States; Technical Papers of the U.S. Department of Commerce’s Weather Bureau; US Department of Commerce: Gaithersburg, MD, USA, 1961; Volume 40.
- World Meteorological Organization. Manual on Estimation of Probable Maximum Precipitation (PMP); WMO-No. 1045; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Mure-ravaud, M. On the Maximization of Precipitation from Tropical Cyclones in the Context of Climate Change. Ph.D. Thesis, University of California, Davis, CA, USA, 2019. [Google Scholar]

| Parameterization | Name of the Scheme |
|---|---|
| Microphysics | WRF double moment 6-class (WDM6) |
| Cumulus a | New Simplified Arakawa-Schubert (SAS) |
| Planetary Boundary Layer | Mellor-Yamada-Janjic (MYJ) |
| Longwave Radiation | Rapid Radiative Transfer Model (RRTM) |
| Shortwave Radiation | Dudhia |
| Land Surface | Unified Noah land-surface model |
| Surface Layer | Monin-Obukhov (Janjic Eta) |
| Year | TC Strength ≥ TS | TC Strength ≥ Hurricane | TC Strength = Major Hurricane (Category 3, 4 and 5) | |||
|---|---|---|---|---|---|---|
| Reported | Detected | Reported | Detected | Reported | Detected | |
| 2004 | 15 | 8 | 9 | 7 | 6 | 5 |
| 2005 | 28 | 12 | 15 | 10 | 7 | 6 |
| 2006 | 10 | 4 | 5 | 3 | 2 | 2 |
| 2007 | 15 | 1 | 6 | 1 | 2 | 1 |
| 2008 | 16 | 9 | 8 | 7 | 5 | 5 |
| 2009 | 9 | 4 | 3 | 3 | 2 | 2 |
| 2010 | 19 | 7 | 12 | 5 | 5 | 4 |
| 2011 | 19 | 6 | 7 | 5 | 4 | 3 |
| 2012 | 19 | 7 | 10 | 7 | 2 | 2 |
| 2013 | 14 | 3 | 2 | 1 | 0 | 0 |
| 2014 | 8 | 5 | 6 | 5 | 2 | 2 |
| 2015 | 11 | 5 | 4 | 4 | 2 | 2 |
| 2016 | 15 | 7 | 7 | 5 | 4 | 3 |
| 2017 | 17 | 6 | 10 | 6 | 6 | 5 |
| average per year | 15.4 | 6 | 7.4 | 4.9 | 3.5 | 3 |
| TC Property | WRF Model Outputs | CFSR |
|---|---|---|
| (45 km Resolution) | ||
| CPD (mbar) | 17.8 | 15.4 |
| MTSWS (m s) | 14.3 | 13.8 |
| RMTSWS (km) | 135 | 158 |
| TCCHL (km) | 387 | 467 |
| TC depth (km) | 11.0 | 12.9 |
| (a) Mean | WRF Model Outputs | Stage IV (Observation) | |
| All TCs | TC Strength ≥ TS Strength | TC Strength ≥ Hurricane Strength | |
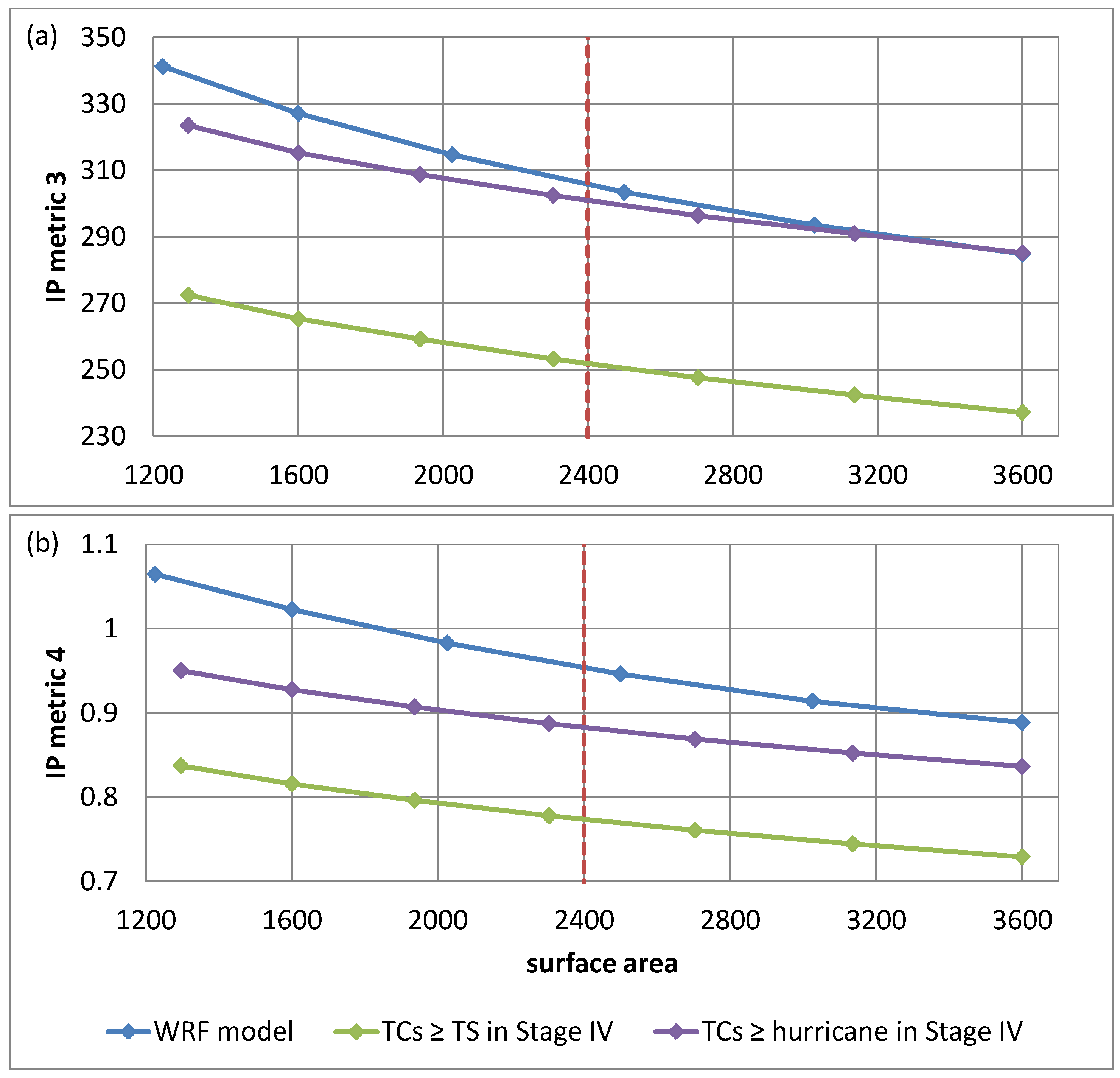
| IP Metric 1 (km2) | 4.54 × 103 | 3.12 × 103 | 5.20 × 103 |
| IP Metric 2 (km2) | 1.06 × 105 | 1.43 × 105 | 1.76 × 105 |
| (b) StandardDeviation | WRF Model Outputs | Stage IV (Observation) | |
| All TCs | TC Strength ≥ TS Strength | TC Strength ≥ Hurricane Strength | |
| IP Metric 1 (km2) | 7.73 × 103 | 7.01 × 103 | 9.37 × 103 |
| IP Metric 2 (km2) | 6.44 × 104 | 8.74 × 104 | 6.87 × 104 |
| Metric | Most Extreme | Obtained for TC No. |
|---|---|---|
| Value | (See Table A1) | |
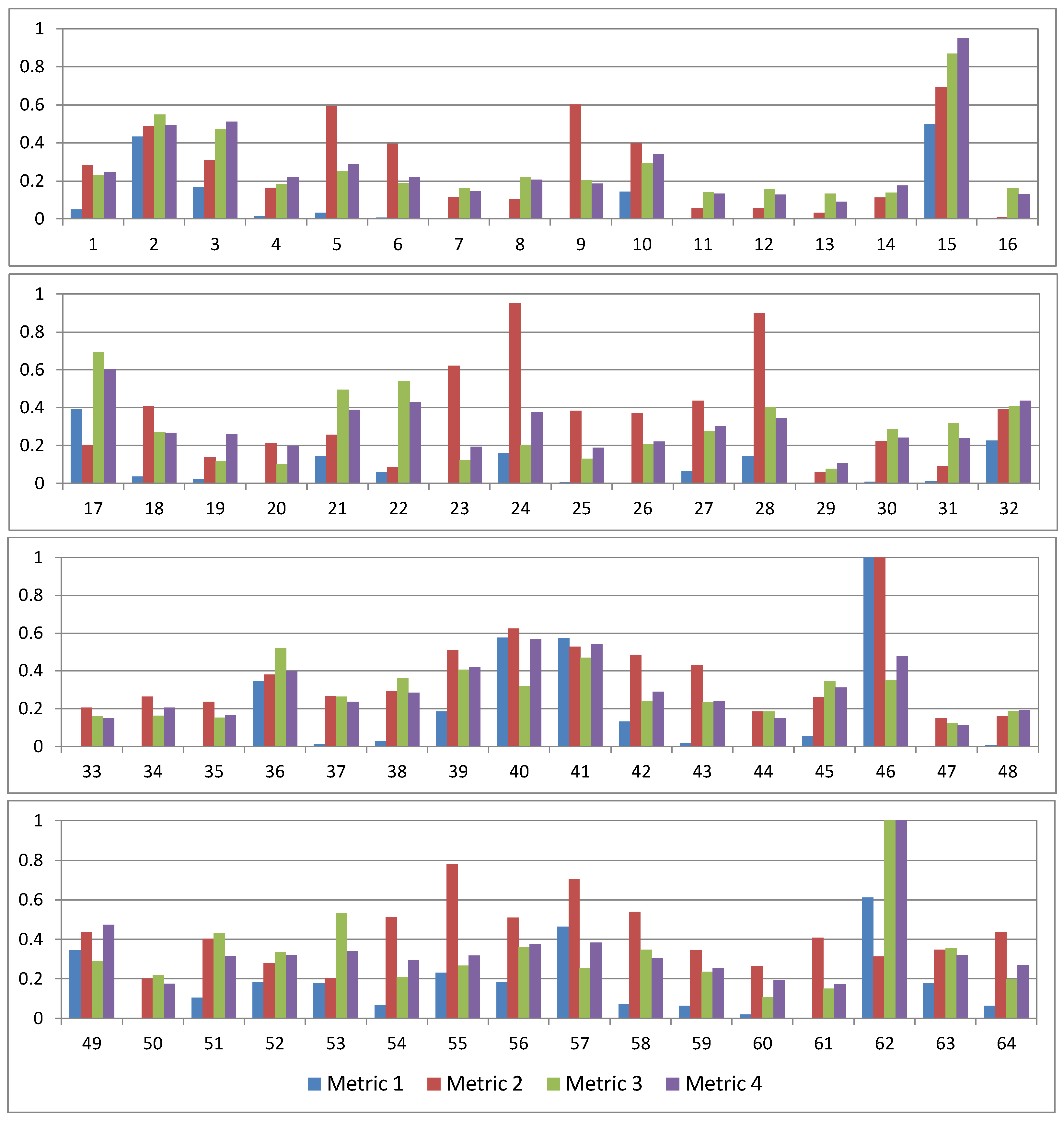
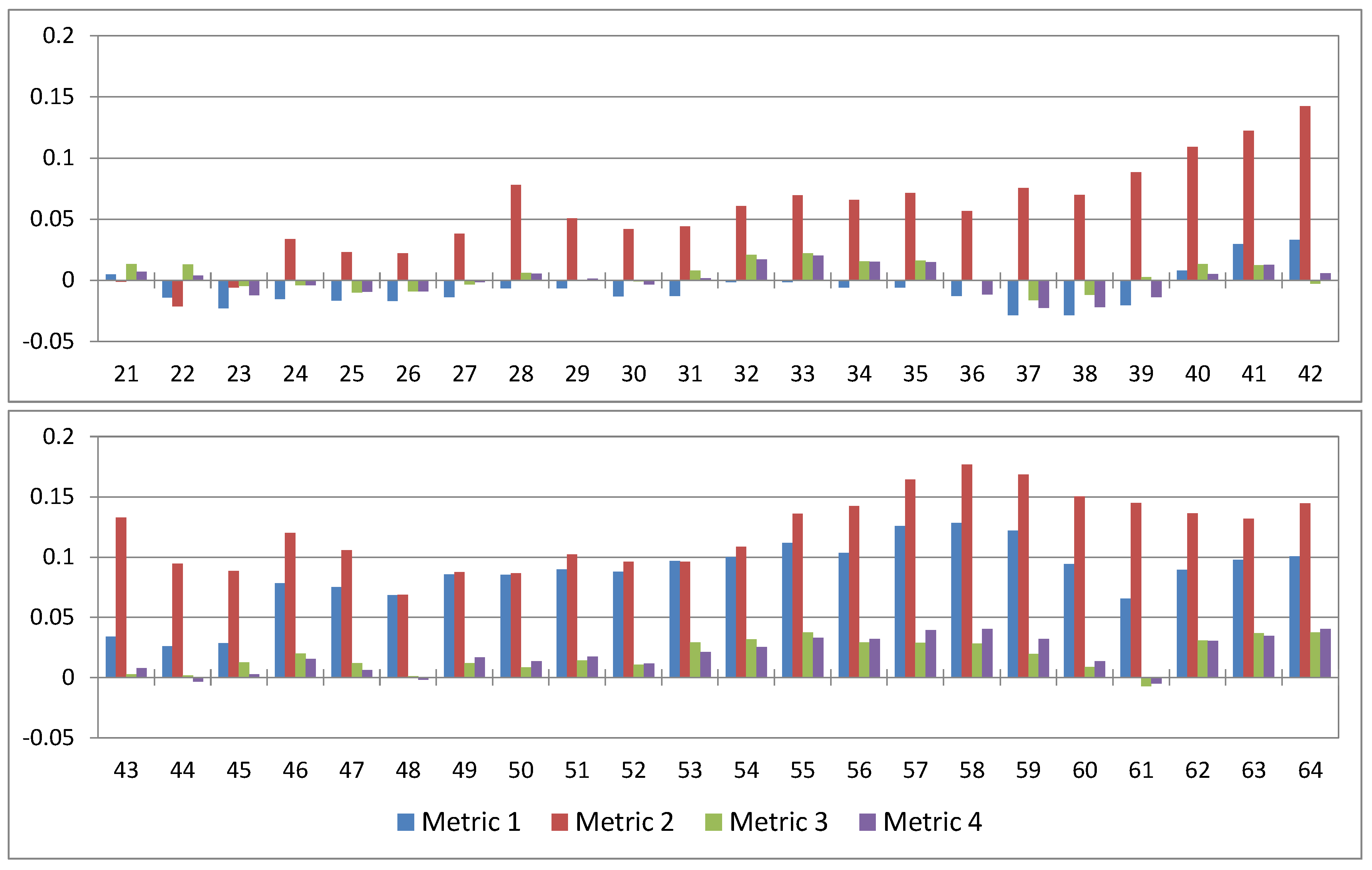
| 1 | 58.30 × 103 km2 | 46 |
| 2 | 331.4 × 103 km2 | 46 |
| 3 | 1152 mm | 62 |
| 4 | 3.48 | 62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mure-Ravaud, M.; Kavvas, M.L.; Dib, A. Investigation of Intense Precipitation from Tropical Cyclones during the 21st Century by Dynamical Downscaling of CCSM4 RCP 4.5. Int. J. Environ. Res. Public Health 2019, 16, 687. https://doi.org/10.3390/ijerph16050687
Mure-Ravaud M, Kavvas ML, Dib A. Investigation of Intense Precipitation from Tropical Cyclones during the 21st Century by Dynamical Downscaling of CCSM4 RCP 4.5. International Journal of Environmental Research and Public Health. 2019; 16(5):687. https://doi.org/10.3390/ijerph16050687
Chicago/Turabian StyleMure-Ravaud, Mathieu, M. Levent Kavvas, and Alain Dib. 2019. "Investigation of Intense Precipitation from Tropical Cyclones during the 21st Century by Dynamical Downscaling of CCSM4 RCP 4.5" International Journal of Environmental Research and Public Health 16, no. 5: 687. https://doi.org/10.3390/ijerph16050687
APA StyleMure-Ravaud, M., Kavvas, M. L., & Dib, A. (2019). Investigation of Intense Precipitation from Tropical Cyclones during the 21st Century by Dynamical Downscaling of CCSM4 RCP 4.5. International Journal of Environmental Research and Public Health, 16(5), 687. https://doi.org/10.3390/ijerph16050687