Incineration Kinetic Analysis of Upstream Oily Sludge and Sectionalized Modeling in Differential/Integral Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
2.2. Apparatus and Methods
3. Results and Discussion
3.1. Sectionalized Rules and Peak-Thermal Kinetic Analysis
3.1.1. Characteristics of the Upstream Oily Sludge
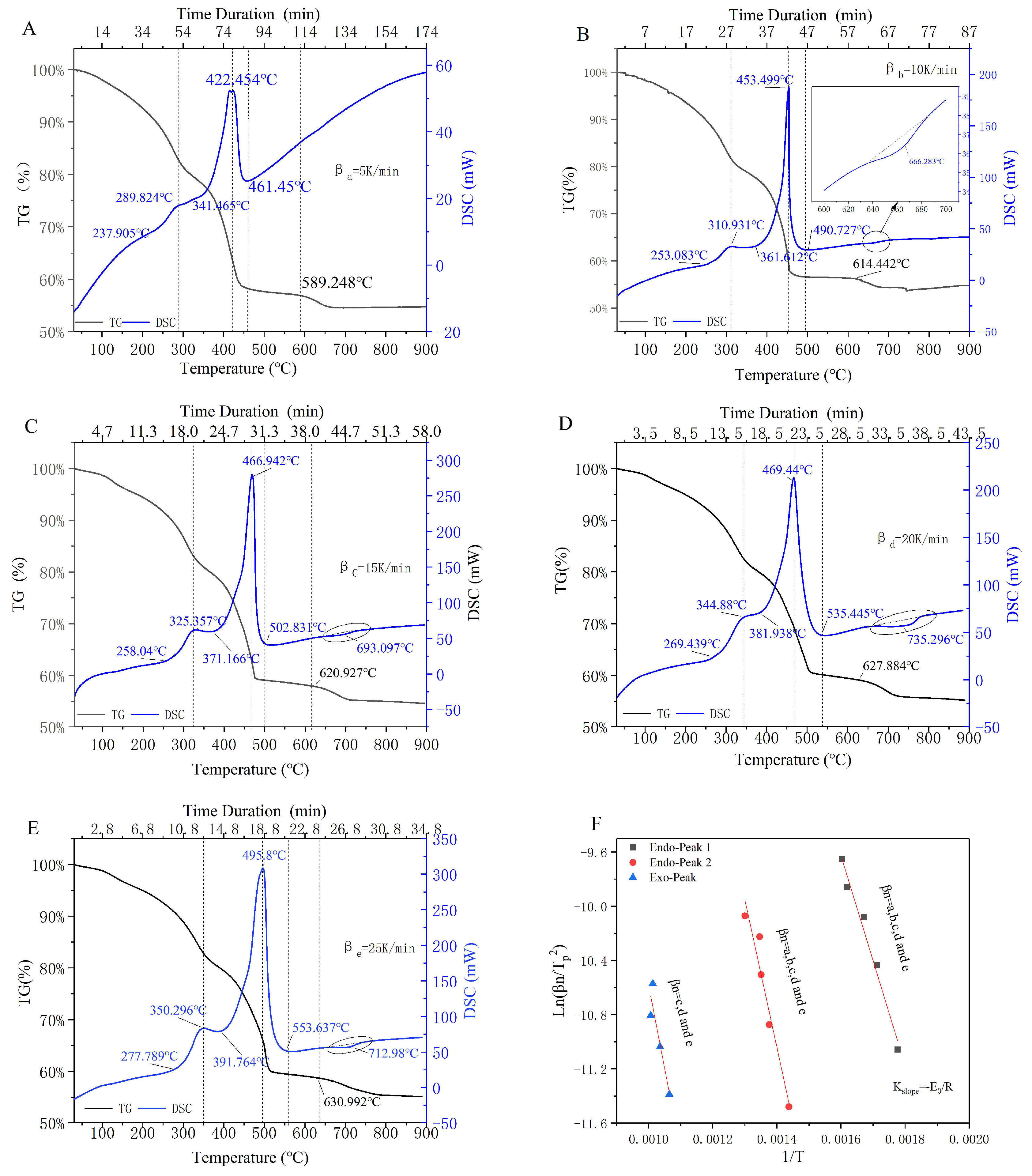
3.1.2. Sectionalized Rules for the Incineration Process of Upstream Oily Sludge
3.1.3. Peak-Thermal Kinetic Analysis of Endothermic/Exothermic Reactions
3.2. The Reasoning Process of the Modeling Method Applied for Oily Sludge Incineration
3.2.1. The Reasoning Process of Differential Methods
3.2.2. The Reasoning Process of Integral Methods
3.3. The Incineration Kinetic Analysis and Model of Stage One
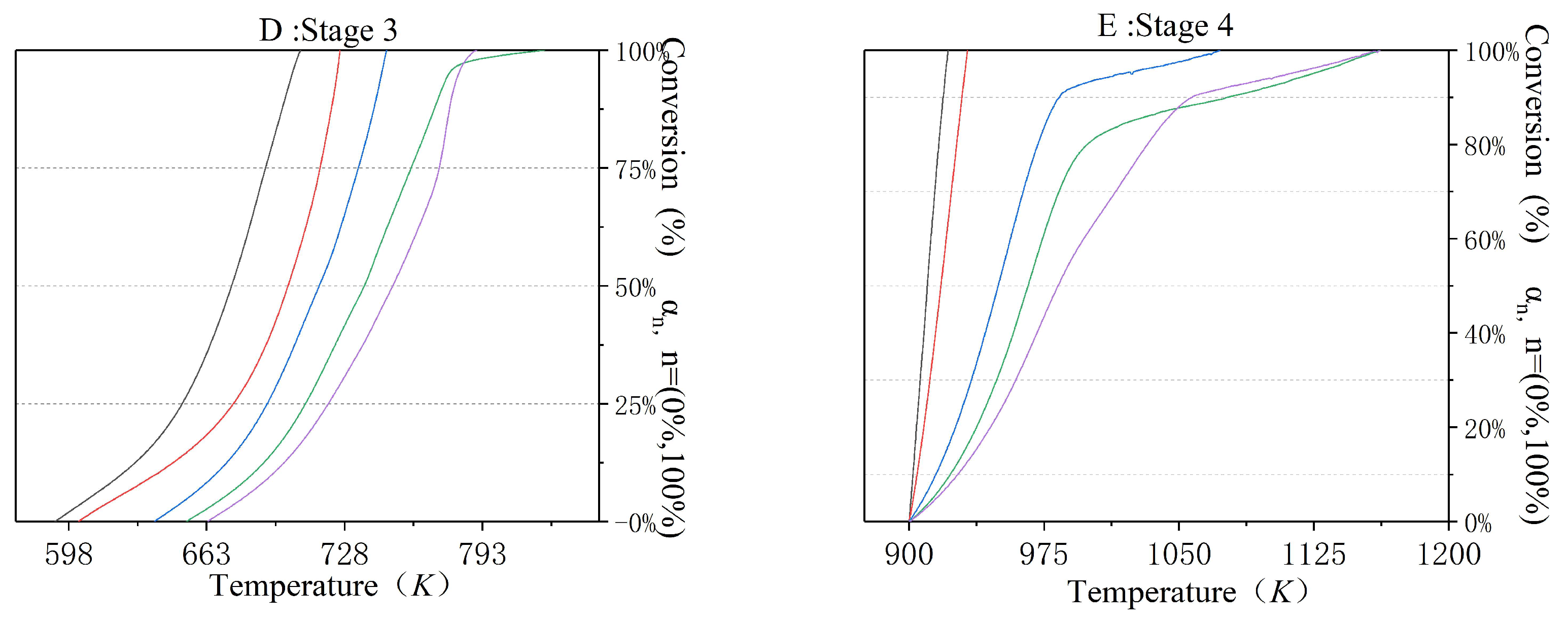
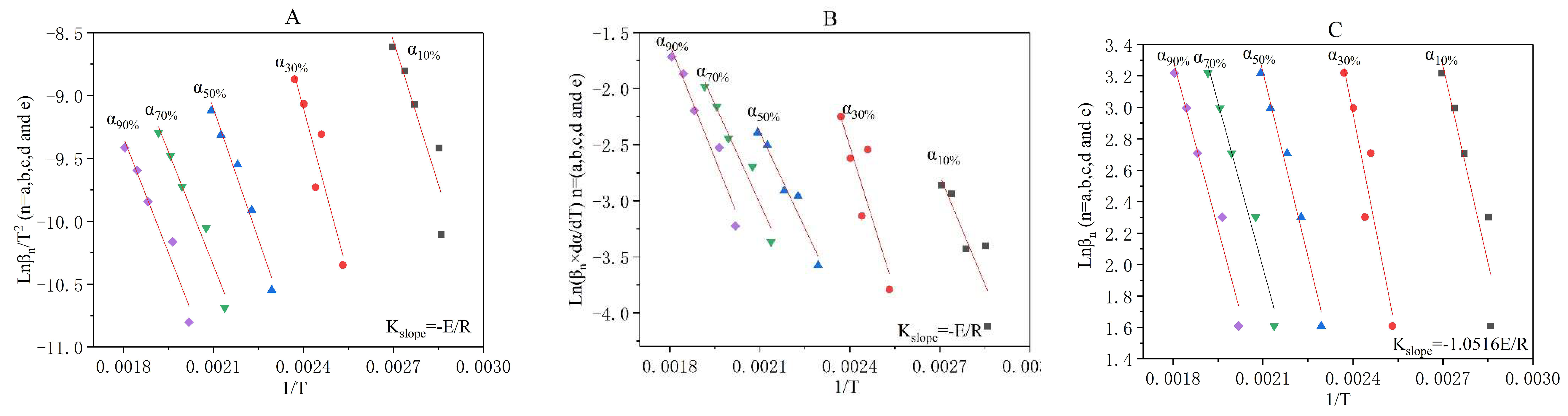
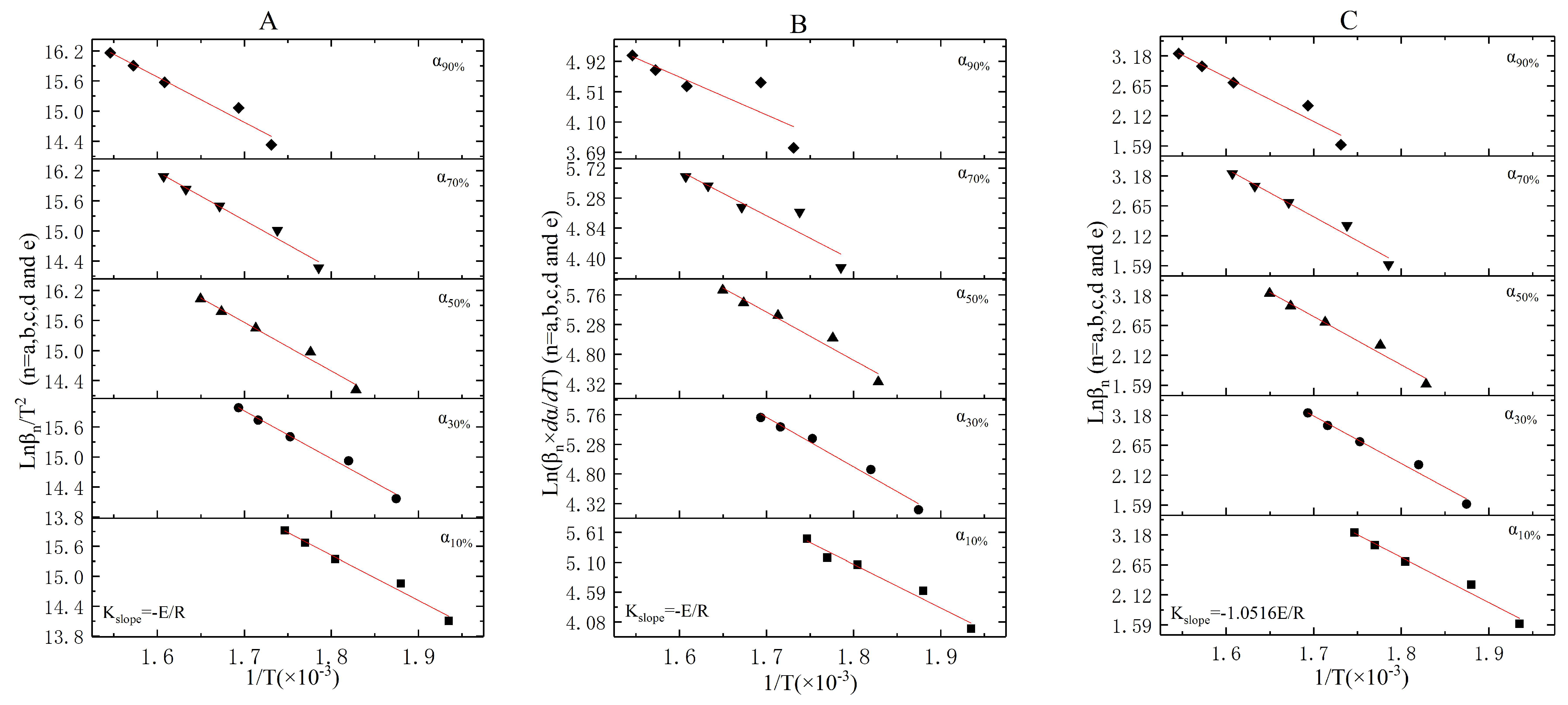
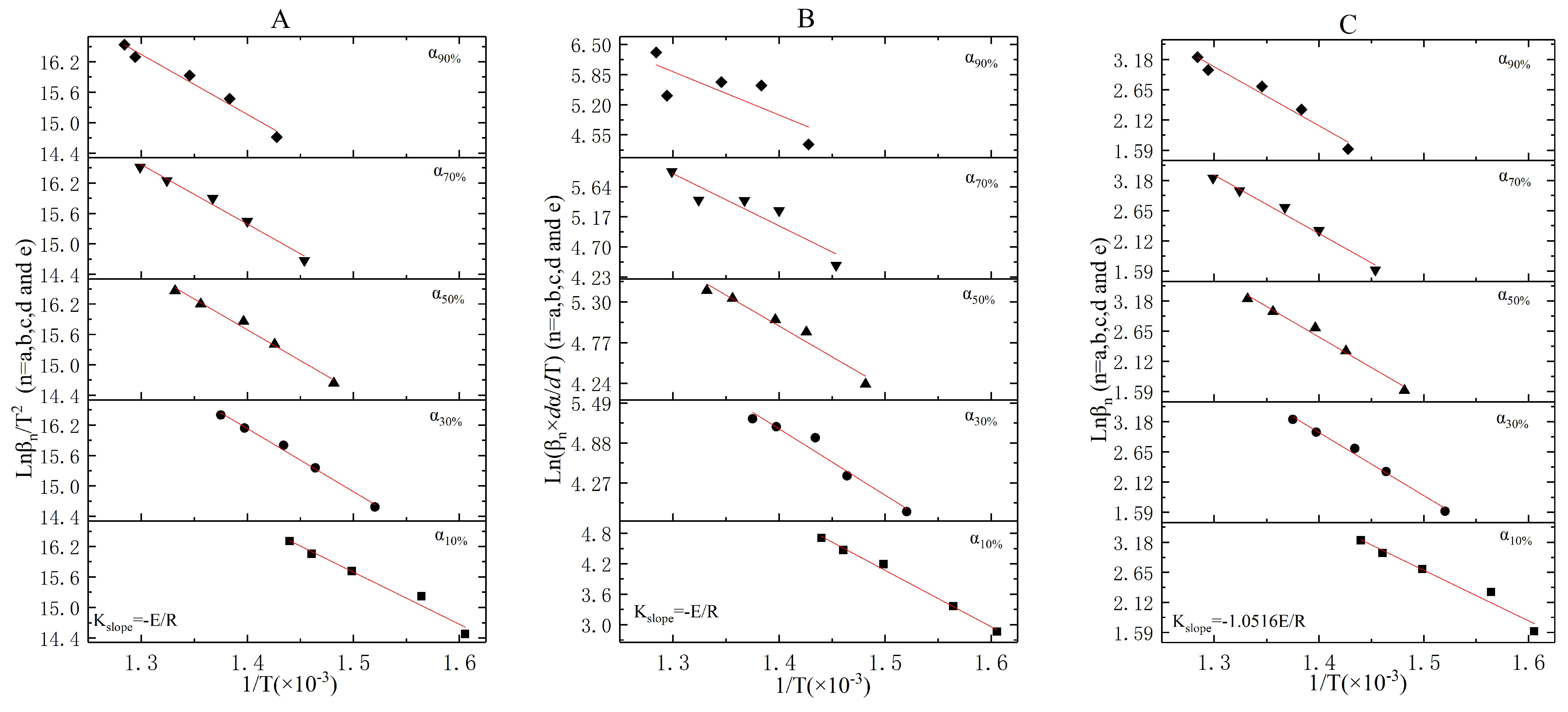
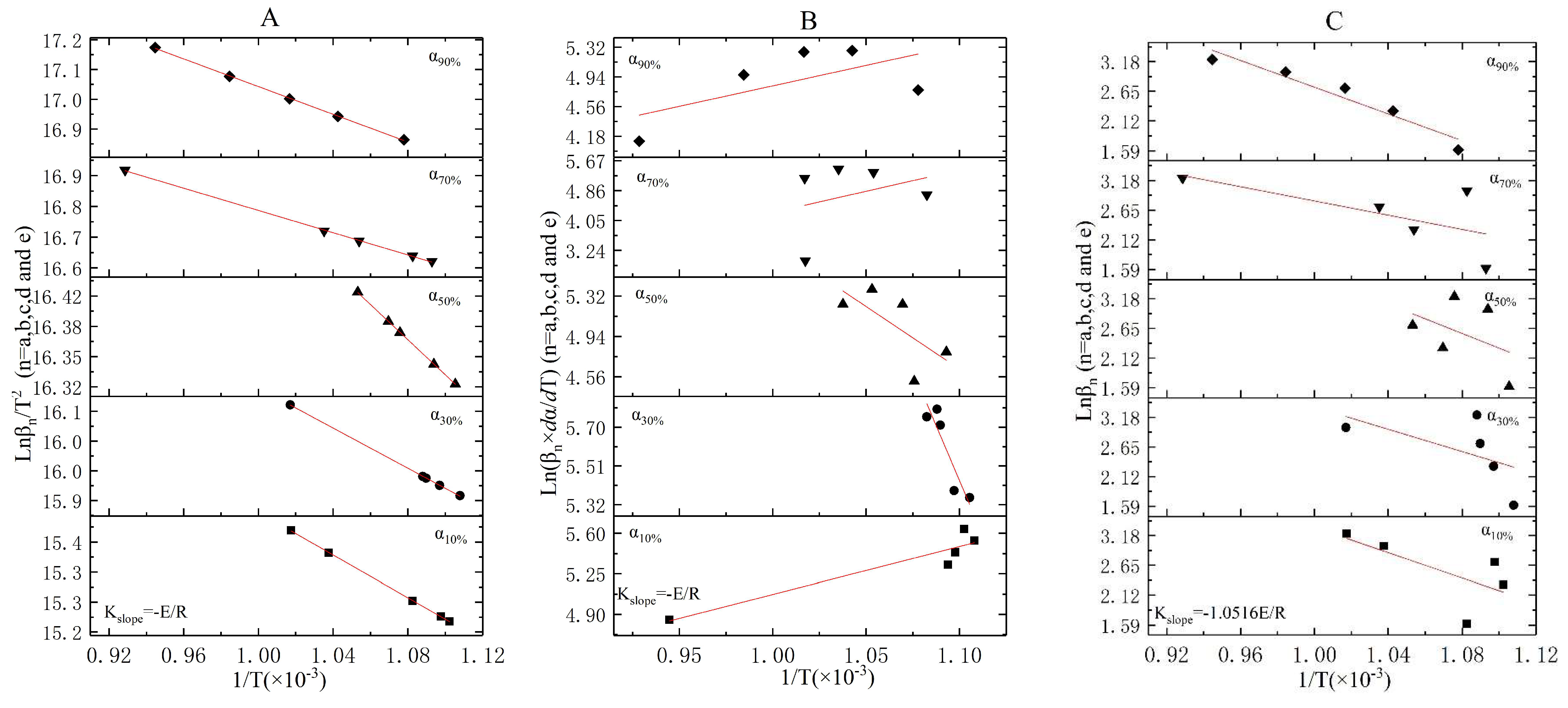
3.4. The Incineration Kinetic Analysis and Model of Stages Two, Three, and Four
3.5. The Judgement of Sectionalized Modeling in Differential/Integral Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, G.; Li, J.; Zeng, G. Recent development in the treatment of oily sludge from petroleum industry: A review. J. Hazard. Mater. 2013, 261, 470–490. [Google Scholar] [CrossRef] [PubMed]
- Mrayyan, B.; Battikhi, M.N. Biodegradation of total organic carbon (TOC) in Jordanian petroleum sludge. J. Hazard. Mater. 2005, 120, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Al-Futaisi, A.; Jamrah, A.; Yaghi, B.; Taha, R. Assessment of alternative management techniques of tank bottom petroleum sludge in Oman. J. Hazard. Mater. 2007, 141, 557–564. [Google Scholar] [CrossRef]
- Greg, M.H.; Robert, A.H.; Zdenek, D. Paraffinic sludge reduction in crude oil storage tanks through the use of shearing and resuspension. Acta Montanistica Slovaca 2004, 9, 184–188. [Google Scholar]
- Lima, T.M.S.; Fonseca, A.F.; Leão, B.A.; Mounteer, A.H.; Tótola, M.R.; Borges, A.C. Oil recovery from fuel oil storage tank sludge using biosurfactants. J. Bioremediat. Biodegrad. 2011, 2, 125. [Google Scholar]
- Tang, J.; Lu, X.; Sun, Q.; Zhu, W. Aging effect of petroleum hydrocarbons in soil under different attenuation conditions. Agric. Ecosyst. Environ. 2012, 149, 109–117. [Google Scholar] [CrossRef]
- Cuypers, C.; Pancras, T.; Grotenhuis, T.; Rulkens, W. The estimation of PAH bioavailability in contaminated sediments using hydroxypropyl-beta-cyclodextrin and Triton X-100 extraction techniques. Chemosphere 2002, 46, 1235–1245. [Google Scholar] [CrossRef]
- Wang, J.; Yin, J.; Ge, L.; Shao, J.; Zheng, J. Characterization of Oil Sludges from Two Oil Fields in China. Energy Fuels 2010, 24, 973–978. [Google Scholar] [CrossRef]
- Long, X.; Zhang, G.; Shen, C.; Sun, G.; Wang, R.; Yin, L.; Meng, Q. Application of rhamnolipid as a novel biodemulsifier for destabilizing waste crude oil. Bioresour. Technol. 2013, 131, 1–5. [Google Scholar] [CrossRef]
- Gong, B.; Deng, Y.; Yang, Y.; Tan, S.N.; Liu, Q.; Yang, W. Solidification and Biotoxicity Assessment of Thermally Treated Municipal Solid Waste Incineration (MSWI) Fly Ash. Int. J. Environ. Res. Public Health 2017, 14, 626. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, X.; Zhou, L.; Han, X.; Cui, Z. Pyrolysis treatment of oil sludge and model-free kinetics analysis. J. Hazard. Mater. 2009, 161, 1208–1215. [Google Scholar] [CrossRef] [PubMed]
- Shie, J.; Chang, C.; Lin, J.; Wu, C.; Lee, D. Resources recovery of oil sludge by pyrolysis: Kinetics study. J. Chem. Technol. Biotechnol. 2000, 75, 443–450. [Google Scholar] [CrossRef]
- Schmidt, H.; Kaminsky, W. Pyrolysis of oil sludge in a fluidised bed reactor. Chemosphere 2001, 45, 285–290. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Li, L.H.; Zhang, J.S.; Ma, C.; Wu, X. Solidification of oily sludge. Pertol. Sci. Technol. 2018, 36, 273–279. [Google Scholar] [CrossRef]
- Stasiuk, E.N.; Schramm, L.L. The influence of solvent and demulsifier additions on nascent froth formation during flotation recovery of Bitumen from Athabasca oil sands. Fuel Process. Technol. 2001, 73, 95–110. [Google Scholar] [CrossRef]
- Zubaidy, E.; Abouelnasr, D. Fuel recovery from waste oily sludge using solvent extraction. Process Saf. Environ. Prot. 2010, 88, 318–326. [Google Scholar] [CrossRef]
- Rocha, O.; Dantas, R.; Duarte, M.; Duarte, M.; Silva, V. Oil sludge treatment by photocatalysis applying black and white light. Chem. Eng. J. 2010, 157, 80–85. [Google Scholar] [CrossRef]
- Nii, S.; Kikumoto, S.; Tokuyama, H. Quantitative approach to ultrasonic emulsion separation. Ultrason. Sonochem. 2009, 16, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Christofi, N.; Ivshina, I.B. A review: Microbial surfactants and their use in field studies of soil remediation. J. Appl. Microbiol. 2002, 93, 915–929. [Google Scholar] [CrossRef]
- Lima, T.; Procópio, L.; Brandão, F.; Leão, B.; Tótola, M.; Borges, A. Evaluation of bacterial surfactant toxicity towards petroleum degrading microorganisms. Bioresour. Technol. 2011, 102, 2957–2964. [Google Scholar] [CrossRef]
- Mater, L.; Sperb, R.M.; Madureira, L.; Rosin, A.; Correa, A.; Radetski, C.M. Proposal of a sequential treatment methodology for the safe reuse of oil sludge-contaminated soil. J. Hazard. Mater. B 2006, 136, 967–971. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Jiang, X.; Zhou, L.; Wang, H.; Han, X. Co-firing of oil sludge with coal–water slurry in an industrial internal circulating fluidized bed boiler. J. Hazard. Mater. 2009, 167, 817–823. [Google Scholar] [CrossRef] [PubMed]
- Sankaran, S.; Pandey, S.; Sumathy, K. Experimental investigation on waste heat recovery by refinery oil sludge incineration using fluidised-bed technique. J. Environ. Sci. Health 1998, 33, 829–845. [Google Scholar] [CrossRef]
- Scala, F.; Chirone, R. Fluidized bed combustion of alternative solid fuels. Exp. Therm. Fluid Sci. 2004, 28, 691–699. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, X.; Liu, J. Characteristics of oily sludge combustion in circulating fluidized beds. J. Hazard. Mater. 2009, 170, 175–179. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Liu, J.; Gao, F.; Zhou, J.; Cen, K. The slurrying properties of slurry fuels made of petroleum coke and petrochemical sludge. Fuel Process. Technol. 2012, 104, 57–66. [Google Scholar] [CrossRef]
- Yue, Q.; Zhao, Y.; Li, Q.; Li, W.; Gao, B.; Han, S.; Qi, Y.; Yu, H. Research on the characteristics of red mud granular adsorbents (RMGA) for phosphate removal. J. Hazard. Mater. 2010, 176, 741–748. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Dai, B.; He, S.; Wu, S.; Huang, J.; Xi, F. Effect of chemical constituents of oxytetracycline mycelia residue and dredged sediments on characteristics of ultra-lightweight ceramsite. J. Taiwan Inst. Chem. Eng. 2016, 65, 225–232. [Google Scholar] [CrossRef]
- Qi, Y.; Yue, Q.; Han, S.; Yue, M.; Gao, B. Preparation and mechanism of ultra-lightweight ceramics produced from sewage sludge. J. Hazard. Mater. 2010, 176, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.N.; Font, R.; Esperanza, M.M. Thermogravimetric Kinetic Model of the Combustion of a Varnish Waste Based on Polyurethane. Energy Fuels 2001, 15, 848–855. [Google Scholar] [CrossRef]
- Hui, W.; Qing, W.; Jia, H.; Zhan, M.; Jin, S. Study on the Pyrolytic Behaviors and Kinetics of Rigid Polyurethane Foams. Procedia Eng. 2013, 52, 377–385. [Google Scholar]
- Lefebvre, J.; Duquesne, S.; Mamleev, V.; le Bras, M.; Delobel, R. Study of the kinetics of pyrolysis of a rigid polyurethane foam: Use of the invariant kinetics parameters method. Polym. Adv. Technol. 2003, 14, 796–801. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, D.; Li, M.; He, J.; Gao, Z.; Zhou, Y.; Sun, J. Pyrolytic behavior of waste extruded polystyrene and rigid polyurethane by multi kinetics methods and Py-GC/MS. Fuel 2018, 222, 11–20. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. 1965, 6, 183–195. [Google Scholar] [CrossRef]
- Coat, A.W.; Redfern, J.P. Kinetic Parameters from Thermogravimetric Data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Orava, J.; Greer, A.L. Kissinger method applied to the crystallization of glass-forming liquids: Regimes revealed by ultra-fast-heating calorimetry. Thermochim. Acta 2015, 603, 63–68. [Google Scholar] [CrossRef]
- Font, R.; Garrido, M.A. Friedman and n-reaction order methods applied to pine needles and polyurethane thermal decompositions. Thermochim. Acta 2018, 660, 124–133. [Google Scholar] [CrossRef]
- Flynn, J.H. The ‘Temperature Integral’—Its use and abuse. Thermochim. Acta 1997, 300, 83–92. [Google Scholar] [CrossRef]
- Lima, A.C.R.; China, B.L.F.; Jawada, Z.A. Kinetic analysis of rice husk pyrolysis using Kissinger-Akahira-Sunose (KAS) method. Procedia Eng. 2016, 148, 1247–1251. [Google Scholar] [CrossRef]
- Opfermann, J.; Kaisersberger, E. An advantageous variant of the Ozawa-Flynn-Wall analysis. Thermochim. Acta 1992, 203, 167–175. [Google Scholar] [CrossRef]

| Materials | Atmosphere | Thermal Test Method | Modeling Method | Basic Three Elements | Reference |
|---|---|---|---|---|---|
| Oil sludge, Phenolic plastic | Nitrogen | TGA/DTG | Integral | [11,34] | |
| Oil sludge | Nitrogen | TGA | Differential | , A and n | [12] |
| Polyurethane Foams | Nitrogen | TGA | Differential | [30,31] | |
| Chalcogenide Ge2Sb2Te5 | Nitrogen | DSC | Integral | [36] | |
| Polyurethane | Nitrogen | TGA | Differential | , A and n | [37] |
| Rice husk | Nitrogen | TGA | Integral | [39] |
| Parameters | Heating Values (MJ/Kg, dry basis) | Ash Content (wt.%, dry basis) | Moisture (wt.%) | Bulk Density (kg/m³) |
|---|---|---|---|---|
| Values | 35.45 ± 3.64 | 57.56 ± 1.23 | 3.24 ± 1.08 | 1366.25 ± 46.73 |
| Parameters | Stage 1 | Stage 2 | Stage 3 | Stage 4 | |
|---|---|---|---|---|---|
| DSC | Endo/Exo 1 | ND 2 | Exo | Exo | Endo |
| TGA | Weight Loss | 10% | 10% | 20% | 5% |
| Peak temperature at (K) | ND | 562.974 | 695.604 | ND | |
| ND | 584.081 | 726.649 | 939.433 | ||
| ND | 598.507 | 740.092 | 965.624 | ||
| ND | 618.030 | 742.590 | 993.691 | ||
| ND | 623.446 | 768.950 | 987.380 | ||
| Ep (KJ/mol) | ND | 64.43 ± 5.34 | 90.71 ± 13.35 | 102.11 ± 28.93 | |
| R2 | ND | 0.9798 | 0.9389 | 0.8616 | |
(×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3.26 | 349.781 | 3.33 | 350.605 | 2.16 | 358.763 | 2.65 | 365.125 | 2.29 | 369.640 | |
| 4.51 | 394.986 | 4.35 | 409.822 | 5.24 | 406.490 | 3.64 | 416.323 | 4.22 | 421.908 | |
| 5.59 | 435.879 | 5.19 | 448.973 | 3.63 | 458.567 | 4.09 | 470.557 | 3.66 | 477.807 | |
| 6.90 | 467.820 | 6.75 | 481.817 | 5.78 | 501.161 | 5.77 | 511.133 | 5.51 | 521.753 | |
| 7.97 | 495.421 | 7.99 | 509.078 | 7.42 | 531.442 | 7.73 | 541.839 | 7.19 | 553.763 | |
| KAS Method | FWO Method | Firedman Method | ||||
|---|---|---|---|---|---|---|
| R2 | R2 | R2 | ||||
| 59.26 ± 15.62 | 0.8453 | 65.84 ± 14.79 | 0.8676 | 53.56 ± 17.26 | 0.7572 | |
| 56.83 ± 17.05 | 0.8622 | 63.51 ± 16.13 | 0.8818 | 45.41 ± 23.09 | 0.7633 | |
| 54.53 ± 5.44 | 0.9738 | 61.93 ± 5.11 | 0.9798 | 47.32 ± 5.83 | 0.9571 | |
| 54.04 ± 5.15 | 0.9691 | 60.45 ± 4.83 | 0.9774 | 49.06 ± 9.38 | 0.9558 | |
| 53.78 ± 6.24 | 0.9565 | 60.24 ± 5.87 | 0.9685 | 55.80 ± 7.08 | 0.9555 | |
| Parameters | Reaction Order (n) | Pre-Exponential Factor (ln A) | Coefficient of Determination (R2) |
|---|---|---|---|
| 0.97 ± 0.28 | 13.72 ± 0.44 | 0.9236 | |
| 0.87 ± 0.25 | 13.79 ± 0.40 | 0.9202 | |
| 0.85 ± 0.29 | 13.46 ± 0.45 | 0.9012 | |
| 0.81 ± 0.30 | 13.42 ± 0.47 | 0.8766 | |
| 0.82 ± 0.30 | 13.32 ± 0.45 | 0.8868 | |
| Average | 0.82 ± 0.30 | 13.32 ± 0.45 | 0.9023 |
| Stage | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | (×10−3) | (K) | ||
| Stage 2 | 10.57 | 516.785 | 10.08 | 531.892 | 10.49 | 554.185 | 8.89 | 565.030 | 9.81 | 572.626 | |
| Stage 3 | 3.51 | 622.887 | 2.89 | 639.315 | 4.39 | 667.270 | 4.36 | 684.588 | 4.43 | 694.448 | |
| Stage 4 | 50.82 | 902.590 | 21.16 | 904.648 | 8.05 | 914.979 | 5.77 | 923.805 | 4.72 | 927.736 | |
| Stage 2 | 13.60 | 533.479 | 13.03 | 549.453 | 14.35 | 570.510 | 12.99 | 582.810 | 12.09 | 590.517 | |
| Stage 3 | 9.25 | 657.685 | 7.96 | 682.952 | 9.50 | 697.241 | 8.41 | 715.626 | 7.60 | 727.265 | |
| Stage 4 | 56.23 | 907.129 | 21.91 | 911.520 | 12.60 | 934.999 | 10.61 | 948.819 | 7.82 | 959.173 | |
| Stage 2 | 15.53 | 546.946 | 15.83 | 563.042 | 15.21 | 583.725 | 13.97 | 597.489 | 13.73 | 606.171 | |
| Stage 3 | 13.73 | 674.935 | 13.56 | 701.422 | 10.61 | 716.113 | 10.48 | 737.392 | 9.32 | 750.831 | |
| Stage 4 | 45.91 | 911.038 | 30.19 | 917.644 | 14.53 | 949.547 | 11.59 | 965.994 | 7.69 | 983.627 | |
| Stage 2 | 14.17 | 560.069 | 15.98 | 575.404 | 11.44 | 598.262 | 11.76 | 612.476 | 10.76 | 622.225 | |
| Stage 3 | 16.51 | 687.783 | 19.34 | 714.310 | 15.14 | 731.354 | 11.44 | 755.153 | 14.27 | 769.902 | |
| Stage 4 | 41.20 | 914.145 | 31.44 | 923.775 | 12.63 | 963.750 | 9.04 | 983.212 | 5.73 | 1015.759 | |
| Stage 2 | 8.51 | 577.680 | 10.3 | 590.512 | 6.53 | 621.731 | 6.09 | 635.915 | 5.94 | 646.828 | |
| Stage 3 | 15.38 | 700.390 | 27.47 | 722.863 | 19.72 | 743.134 | 11.03 | 772.596 | 22.36 | 778.701 | |
| Stage 4 | 25.62 | 919.106 | 32.64 | 929.565 | 6.11 | 982.866 | 0.97 | 1076.961 | 2.45 | 1058.503 | |
| Stage | KAS Method | Friedman Method | FWO Method | ||||
|---|---|---|---|---|---|---|---|
| R2 | R2 | R2 | |||||
| Stage 2 | 75.40 ± 5.81 | 0.9825 | 61.80 ± 6.34 | 0.9693 | 62.84 ± 5.53 | 0.9772 | |
| 79.10 ± 5.56 | 0.9854 | 66.58 ± 5.84 | 0.9774 | 69.77 ± 5.31 | 0.9810 | ||
| 80.59 ± 5.88 | 0.9843 | 64.64 ± 7.59 | 0.9602 | 67.25 ± 5.62 | 0.9795 | ||
| 80.29 ± 6.81 | 0.9789 | 54.68 ± 11.97 | 0.8743 | 66.74 ± 6.50 | 0.9723 | ||
| 75.16 ± 8.69 | 0.9614 | 42.63 ± 15.31 | 0.7210 | 61.57 ± 8.26 | 0.9487 | ||
| Stage 3 | 94.42 ± 8.09 | 0.9738 | 92.41 ± 4.07 | 0.9942 | 70.83 ± 7.71 | 0.9654 | |
| 103.31 ± 5.03 | 0.9930 | 84.01 ± 10.33 | 0.9565 | 87.32 ± 4.85 | 0.9908 | ||
| 100.83 ± 6.18 | 0.9888 | 66.66 ± 7.83 | 0.9602 | 84.63 ± 5.94 | 0.9853 | ||
| 97.26 ± 6.77 | 0.9857 | 67.74 ± 15.01 | 0.8703 | 80.98 ± 6.52 | 0.9808 | ||
| 98.28 ± 9.40 | 0.9732 | 77.59 ± 35.79 | 0.6103 | 81.76 ± 8.99 | 0.9647 | ||
| Stage 4 | 15.68 ± 0.074 | 0.9999 | −34.35 ± 6.88 | 0.8925 | 89.05 ± 56.65 | 0.4516 | |
| 15.71 ± 0.073 | 0.9999 | 179.03 ± 45.85 | 0.8355 | 78.65 ± 66.51 | 0.3179 | ||
| 15.40 ± 0.068 | 0.9999 | 92.93 ± 60.19 | 0.4687 | 103.69 ± 127.91 | 0.1797 | ||
| 16.54 ± 0.197 | 0.9996 | 95.77 ± 170.19 | 0.0955 | 50.20 ± 33.35 | 0.4303 | ||
| 16.46 ± 0.195 | 0.9996 | −43.57±31.13 | 0.3949 | 94.35 ± 14.70 | 0.9321 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, X.; Qi, Y.; Xi, F. Incineration Kinetic Analysis of Upstream Oily Sludge and Sectionalized Modeling in Differential/Integral Method. Int. J. Environ. Res. Public Health 2019, 16, 384. https://doi.org/10.3390/ijerph16030384
Zhang Y, Wang X, Qi Y, Xi F. Incineration Kinetic Analysis of Upstream Oily Sludge and Sectionalized Modeling in Differential/Integral Method. International Journal of Environmental Research and Public Health. 2019; 16(3):384. https://doi.org/10.3390/ijerph16030384
Chicago/Turabian StyleZhang, Yanqing, Xiaohui Wang, Yuanfeng Qi, and Fei Xi. 2019. "Incineration Kinetic Analysis of Upstream Oily Sludge and Sectionalized Modeling in Differential/Integral Method" International Journal of Environmental Research and Public Health 16, no. 3: 384. https://doi.org/10.3390/ijerph16030384
APA StyleZhang, Y., Wang, X., Qi, Y., & Xi, F. (2019). Incineration Kinetic Analysis of Upstream Oily Sludge and Sectionalized Modeling in Differential/Integral Method. International Journal of Environmental Research and Public Health, 16(3), 384. https://doi.org/10.3390/ijerph16030384





