A Biophysical Analysis on the Arm Stroke Efficiency in Front Crawl Swimming: Comparing Methods and Determining the Main Performance Predictors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Procedures
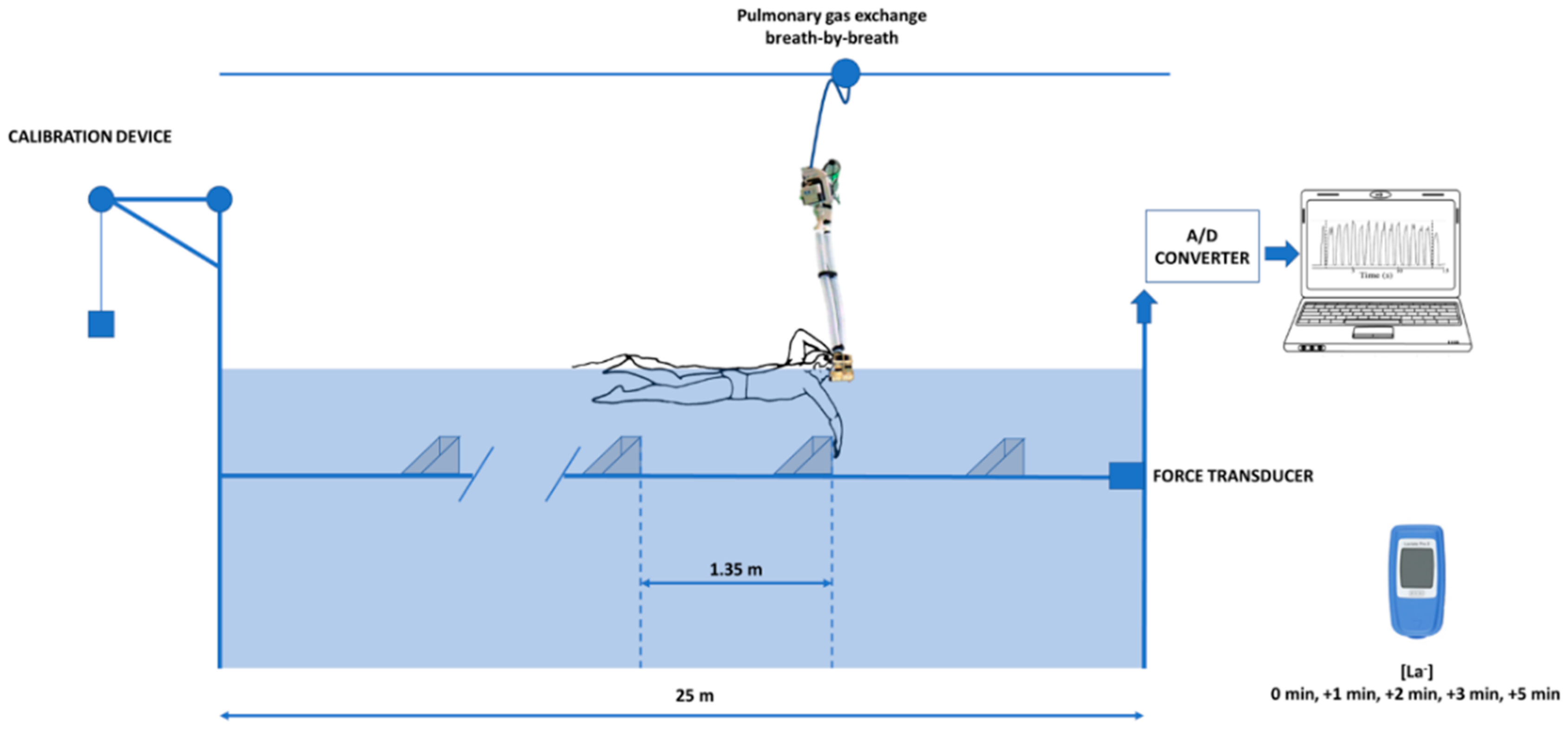
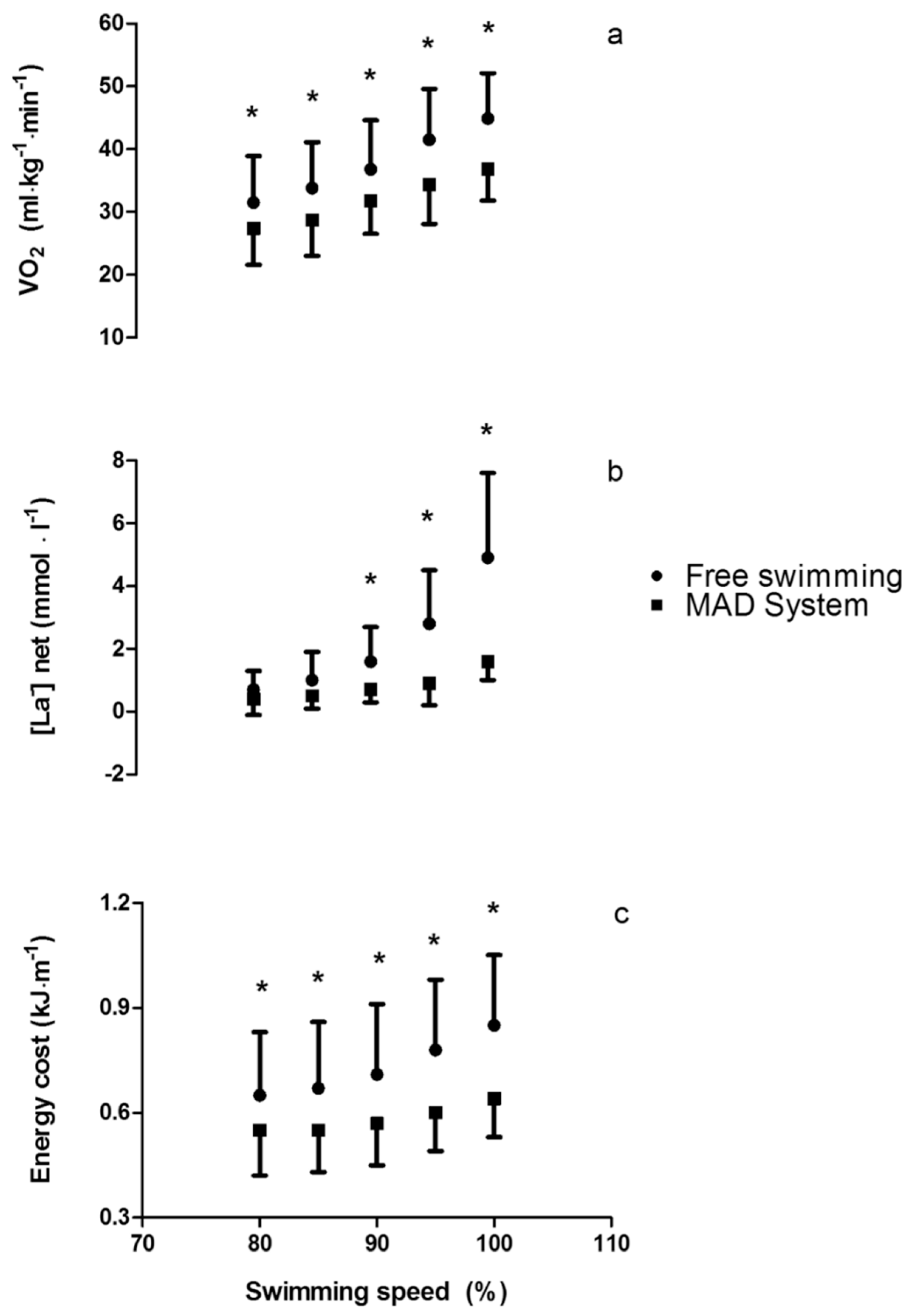
2.3. Physiological Assessments
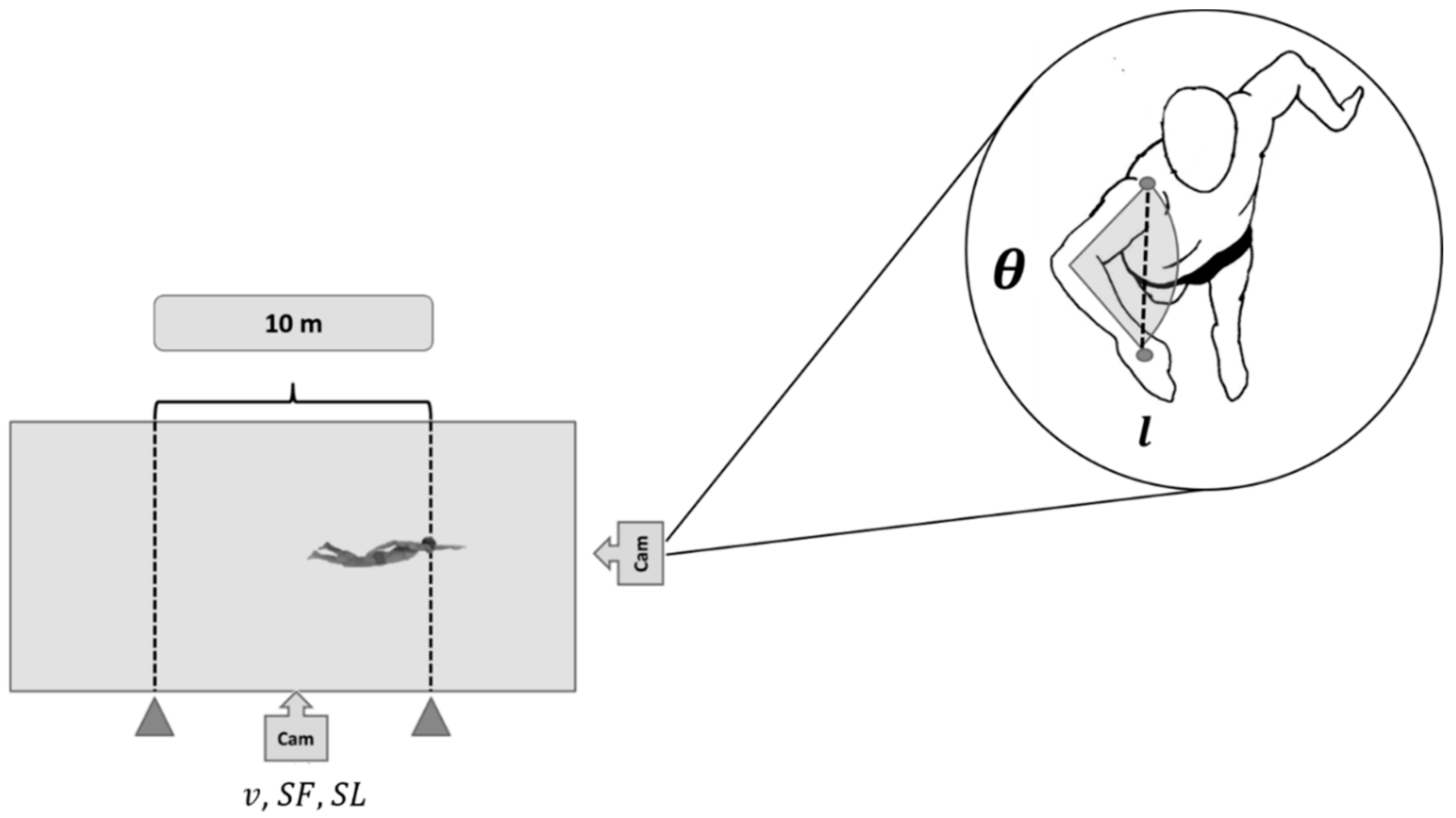
2.4. Biomechanical Assessments in Free-Swimming
2.5. Biomechanical Assessments on the MAD System
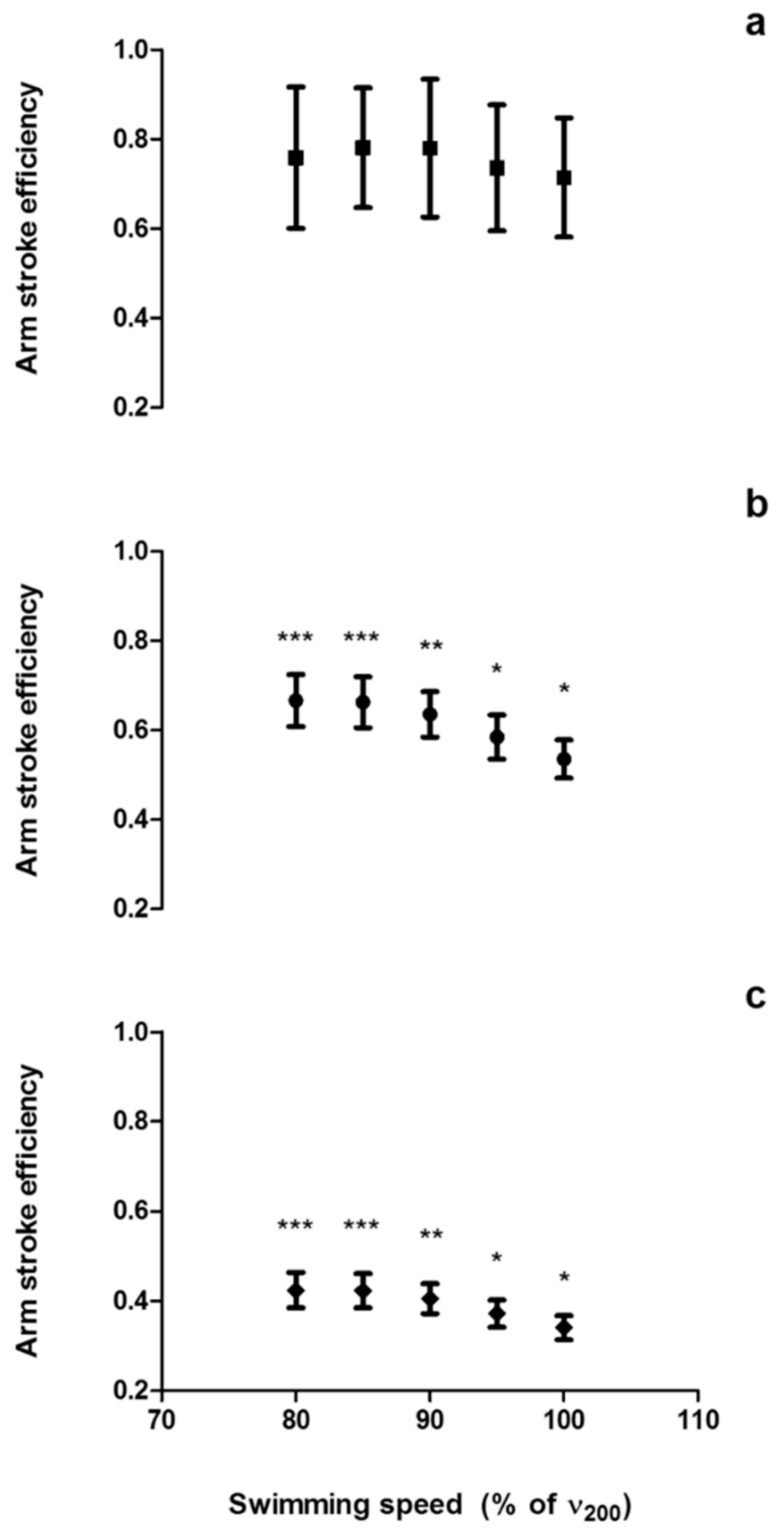
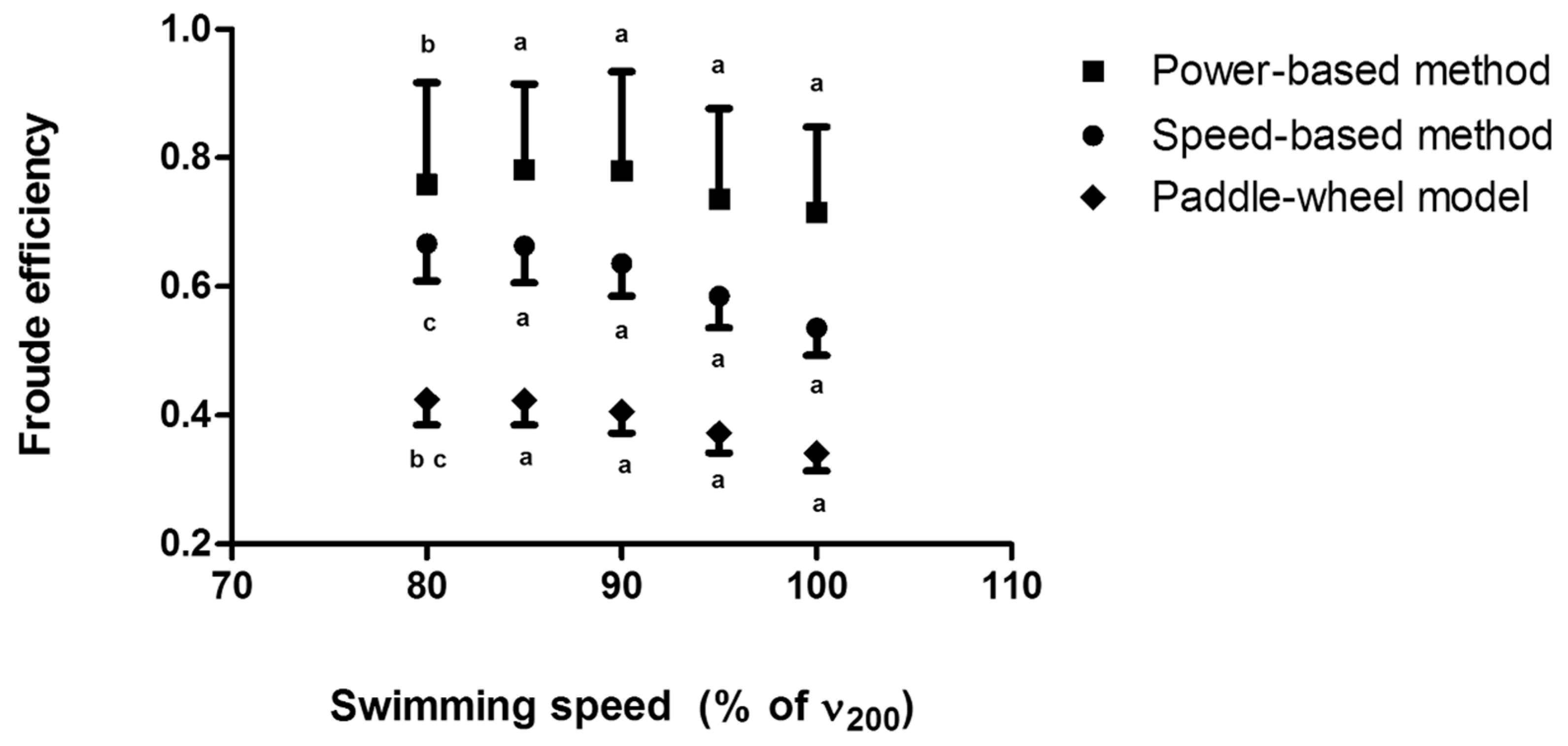
2.6. Speed-Based Efficiency
2.7. Paddle-Wheel Efficiency
2.8. Power-Based Efficiency
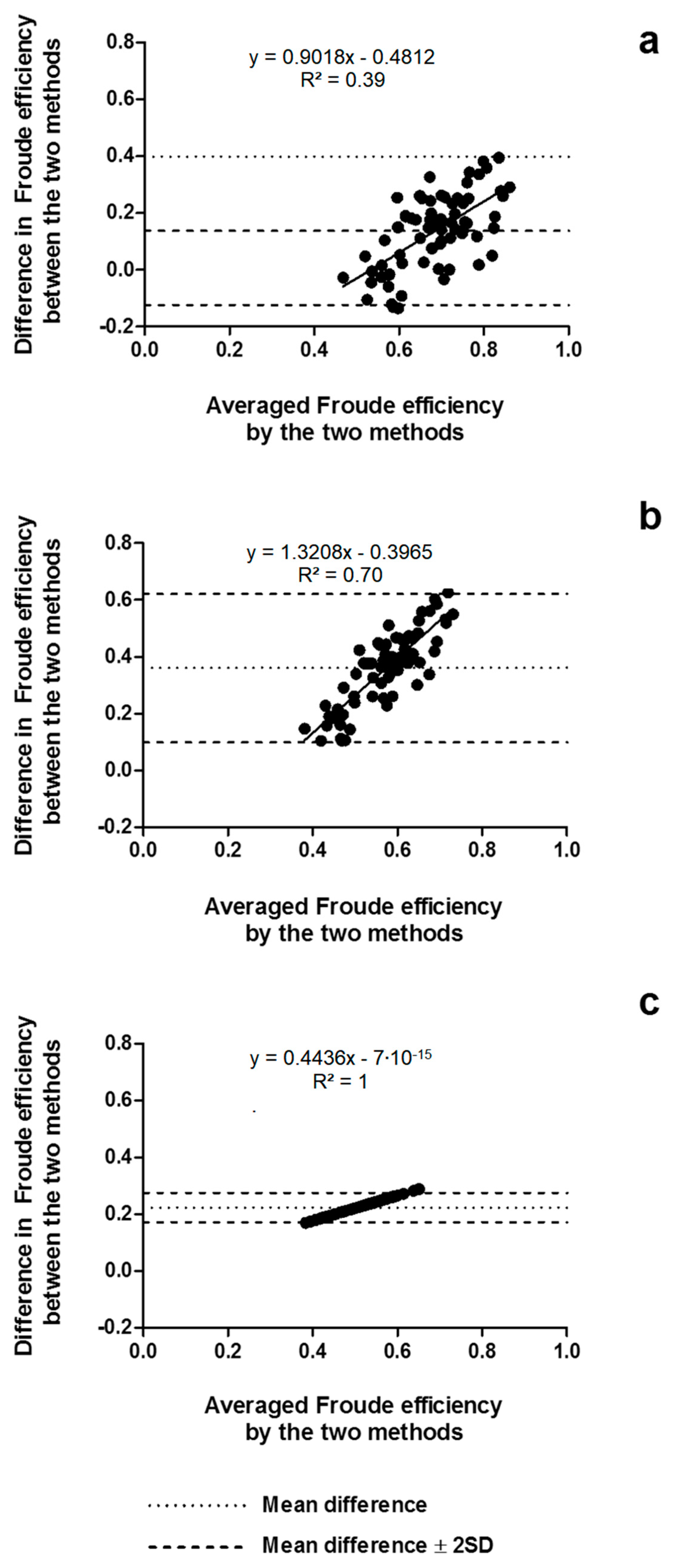
2.9. Statistical Analysis
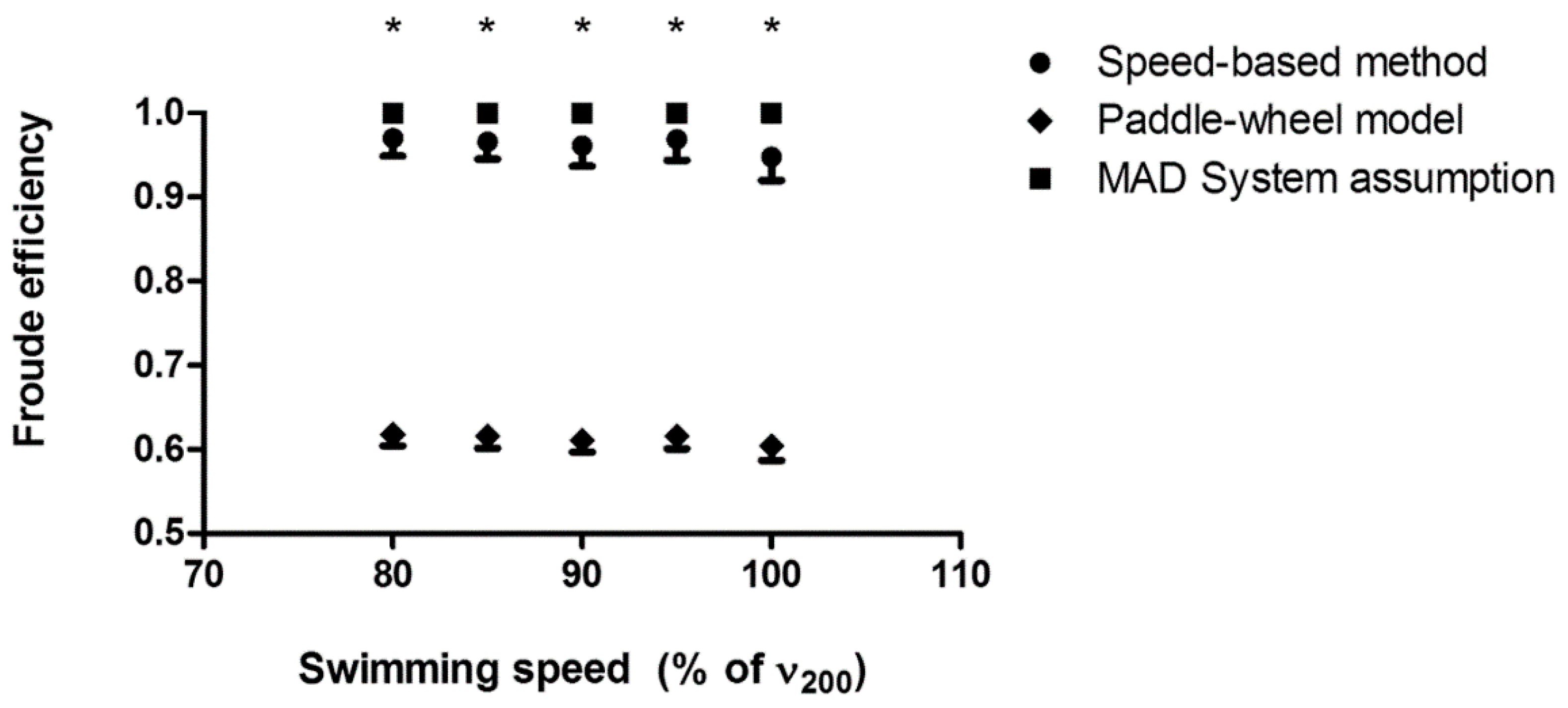
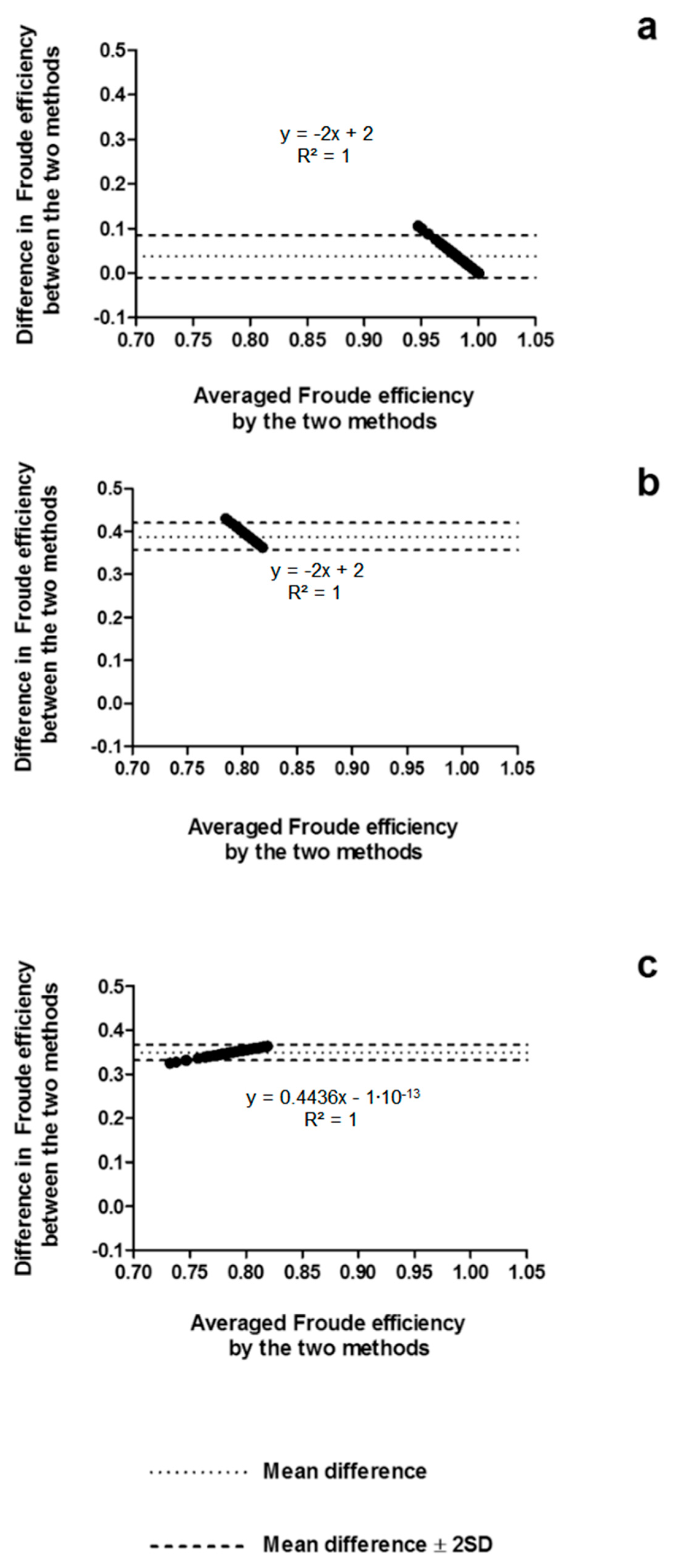
3. Results
4. Discussion
4.1. Arm Stroke Efficiency in the MAD System and Free-Swimming Conditions
4.2. Biophysical Adaptations to Enhance Efficiency
4.3. Biophysical Predictors of Maximal Swimming Speed
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Toussaint, H.M.; Janssen, T.; Kluft, M. The influence of paddles on propulsion. Swim. Tech. 1989, 26, 28–32. [Google Scholar]
- Zamparo, P.; Turri, E.; Peterson Silveira, R.; Poli, A. The interplay between arms-only propelling efficiency, power output and speed in mater swimmers. Eur. J. Appl. Physiol. 2014, 114, 1259–1268. [Google Scholar] [CrossRef] [PubMed]
- Toussaint, H.M.; Beelen, A.; Rodenburg, A.; Sargeant, A.J.; De Groot, G.; Hollander, A.P.; Van Ingen Schenau, G.J. Propelling efficiency on front-crawl swimming. J. Appl. Physiol. 1988, 65, 2506–2512. [Google Scholar] [CrossRef] [PubMed]
- Martin, R.B.; Yeater, R.A.; White, M.K. A simple analytical model for the crawl stroke. J. Biomech. 1981, 14, 539–548. [Google Scholar] [CrossRef]
- Zamparo, P.; Pendergast, D.R.; Mollendorf, J.; Termin, A.; Minetti, A.E. An energy balance of front crawl. Eur. J. Appl. Physiol. 2005, 94, 134–144. [Google Scholar] [CrossRef]
- Toussaint, H.M.; Carol, A.; Kranenborg, H.; Truijens, M.J. Effect of fatigue on stroking characteristics in an arms-only 100-m front-crawl race. Med. Sci. Sports Exerc. 2006, 38, 1635–1642. [Google Scholar] [CrossRef]
- Figueiredo, P.; Zamparo, P.; Sousa, A.; Vilas-Boas, J.P.; Fernandes, R.J. An energy balance of the 200 m front crawl race. Eur. J. Appl. Physiol. 2011, 111, 767–777. [Google Scholar] [CrossRef]
- Hollander, A.P.; Toussaint, H.M.; De Groot, G.; Van Ingen Schenau, G.J. Active drag and swimming performance. NZJ Sports Med. 1985, 13, 110–113. [Google Scholar]
- Seifert, L.; Schnitzler, C.; Bideault, G.; Alberty, M.; Chollet, D.; Toussaint, H.M. Relationships between coordination, active drag and propelling efficiency in crawl. Hum. Mov. Sci. 2015, 39, 55–64. [Google Scholar] [CrossRef]
- Toussaint, H.M. Differences in propelling efficiency between competitive and triathlon swimmers. Med. Sci. Sports Exerc. 1990, 22, 409–415. [Google Scholar] [CrossRef]
- Toussaint, H.M.; Knops, W.; de Groot, G.; Hollander, A.P. The mechanical efficiency of front crawl swimming. Med. Sci. Sport Exerc. 1990, 22, 402–408. [Google Scholar] [CrossRef]
- Toussaint, H.M.; Vervoorn, K. Effects of specific high resistance training in the water on competitive swimmers. Int. J. Sports Med. 1990, 11, 228–233. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, J.; Toubekis, A.G.; Figueiredo, P.; de Jesus, K.; Toussaint, H.M.; Alves, F.; Vilas-Boas, J.P.; Fernandes, R.J. Biophysical Determinants of Front Crawl Swimming at Moderate and Severe Intensities. Int. J. Sports Physiol. Perform. 2017, 12, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Di Prampero, P.E.; Pendergast, D.R.; Wilson, D.R.; Rennie, D.W. Blood lactic acid concentrations in high velocity swimming. In Swimming Medicine IV; Eriksson, B., Furberg, B., Eds.; University Park Press: Baltimore, MD, USA, 1978; pp. 249–261. [Google Scholar]
- Thelevein, X.; Daily, D.; Persyn, U. Measurement of total energy use in the evaluation of competitive swimmers. In Current Topics in Sports Medicine; Bachl, N., Prakup, L., Suckert, R., Eds.; Urban & Schawarzenerg: Wien, Austria, 1984; pp. 668–676. [Google Scholar]
- Capelli, C.; Pendergast, D.; Termin, B. Energetics of swimming at maximal speeds in humans. Eur. J. Appl. Physiol. Occup. Physiol. 1988, 78, 385–393. [Google Scholar] [CrossRef]
- Di Prampero, P.E. The energy cost of human locomotion on land and Water. Int. J. Sports Med. 1986, 7, 55–72. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Zamparo, P. Effects of age and gender on the propelling efficiency of the arm stroke. Eur. J. Appl. Physiol. 2006, 94, 134–144. [Google Scholar] [CrossRef]
- Zamparo, P.; Lazzer, S.; Antoniazzi, C.; Cedolin, S.; Avon, R.; Lesa, C. The interplay between propelling efficiency, hydrodynamic position and energy cost of front crawl in 8 to 19-year-old swimmers. Eur. J. Appl. Physiol. 2008, 104, 689–699. [Google Scholar] [CrossRef]
- Peterson Silveira, R.; Castro, F.A.S.; Figueiredo, P.; Vilas-Boas, J.P.; Zamparo, P. The effects of leg kick on the swimming speed and on arm stroke efficiency in front crawl. Int. J. Sports Physiol. Perform. 2017, 12, 728–735. [Google Scholar] [CrossRef]
- Chollet, D.; Chalies, S.; Chatard, J.C. A new index of coordination for the crawl: Description and usefulness. Int. J. Sports Med. 2000, 21, 54–59. [Google Scholar] [CrossRef]
- Gatta, G.; Cortesi, M.; Swaine, I.; Zamparo, P. Mechanical power, thrust power and propelling efficiency: Relationships with elite sprint swimming performance. J. Sports Sci. 2018, 36, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Zamparo, P.; Swaine, I.L. Mechanical and propelling efficiency in swimming derived from exercise using a laboratory-based whole-body swimming ergometer. J. Appl. Physiol. 2012, 113, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Gastin, P.B. Energy system interaction and relative contribution during maximal exercise. Sports Med. 2001, 31, 725–741. [Google Scholar] [CrossRef] [PubMed]
- Alexander, R.M. Swimming. In Mechanics and Energetics of Animal Locomotion; Alexander, R.M., Goldspink, G., Eds.; Chapman and Hall: London, UK, 1977; pp. 222–248. [Google Scholar]
- Daniel, T.L. Efficiency in aquatic locomotion: Limitations from single cells to animals. In Efficiency and Economy in Animal Physiology; Blake, R.W., Ed.; Cambridge University Press: Cambridge, UK, 1991; pp. 83–96. [Google Scholar]
- Zamparo, P.; Gatta, G.; Pendergast, D.; Capelli, C. Active and passive drag: The role of trunk incline. Eur. J. Appl. Physiol. 2009, 106, 195–205. [Google Scholar] [CrossRef]
- Zamparo, P.; Capelli, C.; Pendergast, D. Energetics of swimming: A historical perspective. Eur. J. Appl. Physiol. 2010, 111, 367–378. [Google Scholar] [CrossRef]
- Pendergast, D.; Zamparo, P.; di Prampero, P.E.; Capelli, C.; Cerretelli, P.; Termin, A.; Craig, A., Jr.; Bushnell, D.; Paschke, D.; Mollendorf, J. Energy balance of human locomotion in water. Eur. J. Appl. Physiol. 2003, 90, 377–386. [Google Scholar] [CrossRef]
- Di Prampero, P.E.; Pendergast, D.R.; Zamparo, P. Swimming economy (energy cost) and efficiency. In World Book of Swimming: From Science to Performance; Seifert, L., Chollet, D., Mujika, I., Eds.; Nova Science Publishers: New York, NY, USA, 2011; pp. 297–312. [Google Scholar]
- Pendergast, D.; Zamparo, P. Balance of biomechanical and physiological contributions to swimming performance. Port. J. Sport Sci. 2011, 11, (Suppl.3), 51–59. [Google Scholar]
- Figueiredo, P.; Pendergast, D.R.; Vilas-Boas, J.P.; Fernandes, R.J. Interplay of biomechanical, energetic, coordinative, and muscular factors in a 200 m front crawl swim. BioMed Res. Int. 2013, 2013, 897232. [Google Scholar] [CrossRef]
- Zamparo, P.; Gatta, G.; di Prampero, P.E. The determinants of performance in master swimmers: An analysis of master world records. Eur. J. Appl. Physiol. 2012, 12, 3511–3518. [Google Scholar] [CrossRef]
| Step | Swimming Speed (% and m·s−1) | Active Drag (N) | Speed-Specific Drag | Stroke Frequency (Hz) | Stroke Length (m) | (W) | (W) | (W) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Both Conditions | Both Conditions | Both Conditions | Free-Swimming | MAD System | Free-Swimming | MAD System | Free-Swimming | MAD System | Free-Swimming | MAD System | Free-Swimming | MAD System | ||
| 1 | 80% | 1.09 ± 0.09 b | 43.0 ± 11.1 b | 36.6 ± 9.4 | 0.49 ± 0.04 a,b | 0.40 ± 0.03 a,b | 2.22 ± 0.23 a c | 2.70 ± 0.00 a | 72 ± 23 a,b | 47 ± 14 a,b | 47 ± 14 b | 47 ± 14 b | 25 ± 11 a,b | 0 ± 0 a |
| 2 | 85% | 1.15 ± 0.09 b | 47.7 ± 11.7 b | 35.9 ± 8.3 | 0.53 ± 0.04 a,b | 0.42 ± 0.04 a,b | 2.20 ± 0.17 a c | 2.70 ± 0.00 a | 85 ± 28 a,b | 55 ± 16 a,b | 55 ± 16 b | 55 ± 16 b | 30 ± 13 a,b | 0 ± 0 a |
| 3 | 90% | 1.22 ± 0.10 b | 52.6 ± 12.3 b | 35.4 ± 7.5 | 0.58 ± 0.06 a,b | 0.45 ± 0.04 a,b | 2.12 ± 0.15 a c | 2.70 ± 0.00 a | 104 ± 33 a,b | 65 ± 18 a,b | 65 ± 18 b | 65 ± 18 b | 39 ± 16 a,b | 0 ± 0 a |
| 4 | 95% | 1.29 ± 0.10 b | 57.7 ± 13.3 b | 34.8 ± 6.7 | 0.65 ± 0.07 a,b | 0.47 ± 0.04 a,b | 1.97 ± 0.14 a,b | 2.70 ± 0.00 a | 130 ± 42 a,b | 75 ± 21 a,b | 75 ± 21 b | 75 ± 21 b | 55 ± 22 a,b | 0 ± 0 a |
| 5 | 100% | 1.35 ± 0.10 b | 63.3 ± 14.4 b | 34.4 ± 6.2 | 0.76 ± 0.08 a,b | 0.51 ± 0.04 a,b | 1.79 ± 0.11 a,b | 2.70 ± 0.00 a | 165 ± 52 a,b | 87 ± 24 a,b | 87 ± 24 b | 87 ± 24 b | 78 ± 29 a,b | 0 ± 0 a |
| Step | (W) | (W) | (W) | Aerobic Contribution (%) | Anaerobic Contribution (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Free Swimming | MAD System | Free Swimming | MAD System | Free Swimming | MAD System | Free Swimming | MAD System | Free Swimming | MAD System | |
| 1 | 702 ± 222 a c | 598 ± 166 a c | 15 ± 15 c | 9 ± 10 e | 716 ± 230 a c | 600 ± 173 a b | 98 ± 1 c | 99 ± 1 d | 2 ± 1 c | 1 ± 1 d |
| 2 | 759 ± 241 a c | 629 ± 171 a c | 23 ± 25 c | 10 ± 10 e | 782 ± 255 a c | 648 ± 181 a b | 97 ± 2 c | 99 ± 1 d | 3 ± 2 c | 1 ± 1 d |
| 3 | 833 ± 260 a b | 699 ± 160 a b | 39 ± 31 a b | 16 ± 11 a d | 873 ± 283 a b | 707 ± 186 a b | 96 ± 2 a b | 98 ± 1 a d | 4 ± 2 a b | 2 ± 1 d |
| 4 | 948 ± 276 a b | 763 ± 186 a b | 71 ± 52 a b | 23 ± 21 a d | 1018 ± 316 a b | 784 ± 192 a b | 94 ± 3 a b | 97 ± 2 a d | 6 ± 3 a b | 3 ± 2 d |
| 5 | 1032 ± 270 a b | 824 ± 166 a b | 130 ± 88 a b | 40 ± 20 a b | 1162 ± 337 a b | 877 ± 193 a b | 90 ± 5 a b | 96 ± 2 a b | 10 ± 5 a b | 4 ± 2 d |
| Parameter | Loading Values | |
|---|---|---|
| Principal Component 1 | Principal Component 2 | |
| Shoulder to hand distance | 0.77 | 0.44 |
| Stroke frequency | 0.67 | −0.25 |
| Stroke length | −0.13 | 0.44 |
| Active drag | 0.84 * | 0.45 |
| Power to overcome drag | 0.88 * | 0.37 |
| Speed-specific drag | 0.41 | 0.80 ** |
| Arm stroke efficiency | −0.87 ** | −0.12 |
| External mechanical power | 0.92 ** | 0.33 |
| Power wasted to the water | 0.94 * | 0.30 |
| Aerobic metabolic power | 0.94 * | 0.07 |
| Anaerobic metabolic power | 0.77 | −0.59 |
| Total metabolic power | 0.96 ** | −0.09 |
| Oxygen uptake | 0.88 * | 0.15 |
| Blood lactate concentration | 0.70 | −0.64 |
| Energy cost | 0.93 ** | −0.10 |
| Aerobic contribution | −0.61 | 0.71 |
| Anaerobic contribution | 0.61 | −0.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peterson Silveira, R.; Soares, S.M.; Zacca, R.; Alves, F.B.; Fernandes, R.J.; Castro, F.A.d.S.; Vilas-Boas, J.P. A Biophysical Analysis on the Arm Stroke Efficiency in Front Crawl Swimming: Comparing Methods and Determining the Main Performance Predictors. Int. J. Environ. Res. Public Health 2019, 16, 4715. https://doi.org/10.3390/ijerph16234715
Peterson Silveira R, Soares SM, Zacca R, Alves FB, Fernandes RJ, Castro FAdS, Vilas-Boas JP. A Biophysical Analysis on the Arm Stroke Efficiency in Front Crawl Swimming: Comparing Methods and Determining the Main Performance Predictors. International Journal of Environmental Research and Public Health. 2019; 16(23):4715. https://doi.org/10.3390/ijerph16234715
Chicago/Turabian StylePeterson Silveira, Ricardo, Susana Maria Soares, Rodrigo Zacca, Francisco B. Alves, Ricardo J. Fernandes, Flávio Antônio de Souza Castro, and João Paulo Vilas-Boas. 2019. "A Biophysical Analysis on the Arm Stroke Efficiency in Front Crawl Swimming: Comparing Methods and Determining the Main Performance Predictors" International Journal of Environmental Research and Public Health 16, no. 23: 4715. https://doi.org/10.3390/ijerph16234715
APA StylePeterson Silveira, R., Soares, S. M., Zacca, R., Alves, F. B., Fernandes, R. J., Castro, F. A. d. S., & Vilas-Boas, J. P. (2019). A Biophysical Analysis on the Arm Stroke Efficiency in Front Crawl Swimming: Comparing Methods and Determining the Main Performance Predictors. International Journal of Environmental Research and Public Health, 16(23), 4715. https://doi.org/10.3390/ijerph16234715










