1. Introduction
Emergency management is crucial to preventing potential risks in urban communities [
1]. In high-density urban communities, efficient, safe and timely evacuation is important for guaranteeing the safety of residents in emergencies [
2,
3].
Various emergency evacuation studies have been done all over the world. Many researchers conducted small-scale evacuations inside single buildings [
4,
5,
6], while many other scholars developed evacuation optimization models on large-scale evacuations as well [
7,
8,
9]. However, only a few studies have attempted to analyze emergency evacuations in urban residential communities with a consideration for residents’ behaviors from a microscopic perspective. Most of the previous studies have concentrated on risk assessments of evacuations [
10,
11] or personnel evacuation simulations within buildings [
12,
13]. Due to the complexity of resident structure in urban communities, residents may have various behavioral responses to emergencies. Moreover, members in a family focus on each other to ensure the safety of family members [
14,
15,
16]. Therefore, the evacuation processes in communities is quite different from the evacuations in office buildings, subway stations and other public places.
Previous studies in emergency evacuations have provided evidence that some occupants may not evacuate immediately and attempt to confirm and evaluate the risk of emergency events [
17]. Moreover, people may fight a fire or help others [
18,
19] when encountering an emergency, such as a fire. The importance of estimating the components of evacuation time, like authorities’ decision time, warning dissemination time, household preparation time, and evacuation travel time, has been recognized for approximately 40 years. Urbanik et al. [
20] proposed a basic formulation and Urbanik [
21,
22] updated it. Lindell and Perry [
23] and Lindell and Prater [
24] critiqued transportation engineers assumptions about evacuation time components. Lindell et al. [
25] summarized the state-of-the-art in large scale evacuations and Lindell et al. [
26] reported empirical departure times for a flash flood evacuation. There is also empirical data from tsunami evacuation studies by Blake et al. [
27], Goto et al. [
28], Lindell et al. [
29], and Sun et al. [
30,
31,
32]. Although little attention has been paid to evaluating the pre-evacuation time, the issue of community evacuations was studied by Lindell et al. [
25]. Lindell et al. [
26] addressed the predictors of evacuation delay from a flash flood. This study indicated that pre-evacuation delays often occurred in evacuations due to the differences in behavioral responses to emergencies, which may be influenced by the factors relating to characteristics of occupants, buildings and emergencies [
33,
34,
35].
Furthermore, due to the urgency and complexity of emergencies, the evacuation processes have a great deal of uncertainty. However, some possible situations of an evacuation have been neglected in traditional evacuations, particularly in the estimation of evacuation times. The neglect may cause inaccuracy in estimating personal evacuation times and the total evacuation time. To reduce the uncertainty, parameter sensitivity analysis is a critical step in determining values of important parameters, which have a significant impact on the simulation results. Among existing methods of sensitivity analysis, the one-at-a-time (OAT) method has been commonly used [
36,
37]. This method has a simple calculation procedure and is easy to be understood. It is suitable for conducting a parameter sensitivity analysis for evacuation simulations.
People’s responses to emergencies are generally based on the effect of psychology, evacuation environment, etc. However, people’s behavior intentions largely determine actual behaviors according to the theory of reasoned action (TRA) [
38]. Meanwhile, general research findings might not permit researchers to conduct specific studies about emergency management for specific behaviors of residents in communities. A survey demonstrated a significant degree of correspondence between respondents’ evacuation expectations and actual behaviors [
39]. Behavioral expectations have a limitation in that it cannot assess people’s moment-to-moment responses to actual evacuation situations or warning messages, behavioral tendencies and perceptional responses on evacuation decisions, which they have not previously encountered. However, actual evacuation studies and hypothetical evacuation studies identify the same predictors of evacuation decisions. A lot of similarity between responses to hypothetical scenarios and those of actual evacuations were indicated by Huang et al. [
40]. Based on the behavioral expectations and actual evacuation behavior studies, the questionnaire in this study was conducted on the basis of behavioral expectations.
Considering the limitations of existing studies, a new evacuation simulation method, which considers the pre-evacuation times of residents in urban residential communities, is proposed in this study. This paper tries to address an evacuation problem in a vertical building evacuation followed by a small-scale horizontal pedestrian area evacuation. In this method, a predictive model based on the Random Forest (RF) algorithm was built to forecast pre-evacuation times. It was able to conduct the training and verification of pre-evacuation behavioral information obtained by questionnaires and estimate the delay times for different residents. The method also integrated indoor and outdoor evacuation processes. A case study in Pudong New District, Shanghai, China was conducted to demonstrate the feasibility of the method. With the evacuation simulation result (including the total evacuation time, the congestion time and the congestion degree), analysis in the study area and a comparison with the scenario, which did not consider pre-evacuation time, the advantage of this method was demonstrated.
2. Methodology
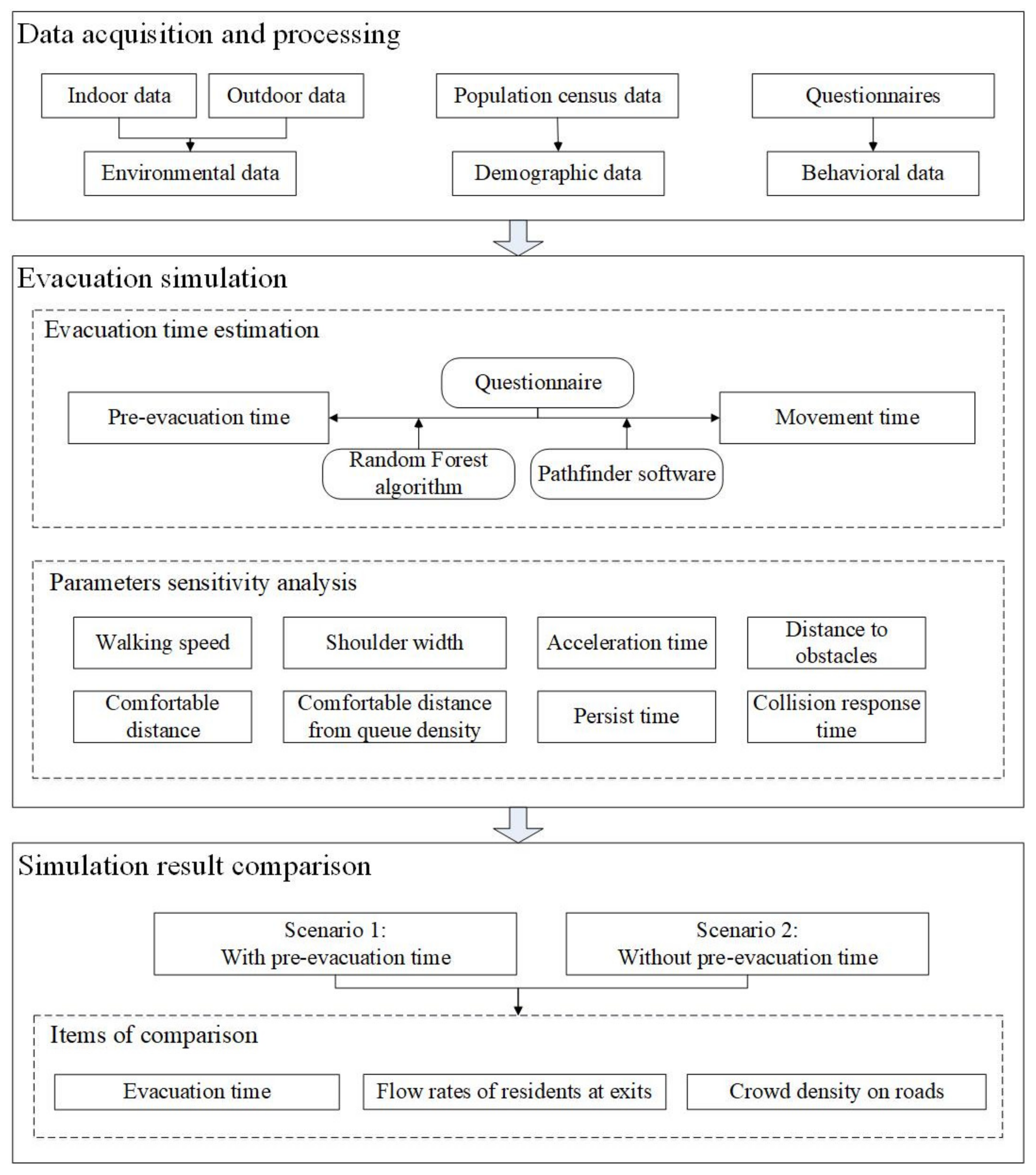
Figure 1 illustrates the framework of the proposed method, which describes the evacuation simulation procedure. There are three parts of the framework as follows:
2.1. Data Acquisition and Processing
2.1.1. Environmental Data
Environmental data were mainly obtained to construct the evacuation space during emergency evacuation simulations, which included two parts: indoor data and outdoor data.
(1) Indoor Data
Indoor data comprised of house types, corridors and stairways. These data was obtained from real estate companies or construction planning bureaus. Due to the characteristics of buildings such as floors, materials and electrical equipment, evacuations within buildings are more complex than the outside, particularly in high-rise buildings [
41]. The human behaviors in buildings is one of the key factors affecting the evacuation time [
42].
(2) Outdoor Data
Outdoor data included community roads, building layouts and exits that was acquired from community layout plans and aerial images. The layout of buildings in a community can directly affect the spatial distribution of residents. Moreover, the layout of the road network also has significant impacts on the efficiency of evacuation [
43].
2.1.2. Demographic Data
Demographic data, including gender ratio and the age structure of residents, had a significant impact on the results of evacuation simulations. The residential population distribution data was generated from the population census data or the actual population data acquired by field surveys.
2.1.3. Behavioral Data
The evacuation behavior is an important factor, which affects the evacuation time. For instance, Wang et al. [
44] described the individual level data needed for a pedestrian evacuation model of an environmental hazard (tsunami). Evacuation behaviors are very complex and they are reflected mainly in the pre-evacuation time and route planning. Compared to emergency evacuations in schools, office buildings, supermarkets or other public spaces, emergency evacuations in residential communities involve different types of residents and complex social relationships. Pre-evacuation behavioral data was collected using questionnaires. Respondents had to answer questions focused on personal information and pre-evacuation behaviors. The questionnaire is presented in
Appendix A for reference, including the following information:
- (1)
Basic personal information, including gender, age, education, physical condition, family members, evacuation training experience and so on.
- (2)
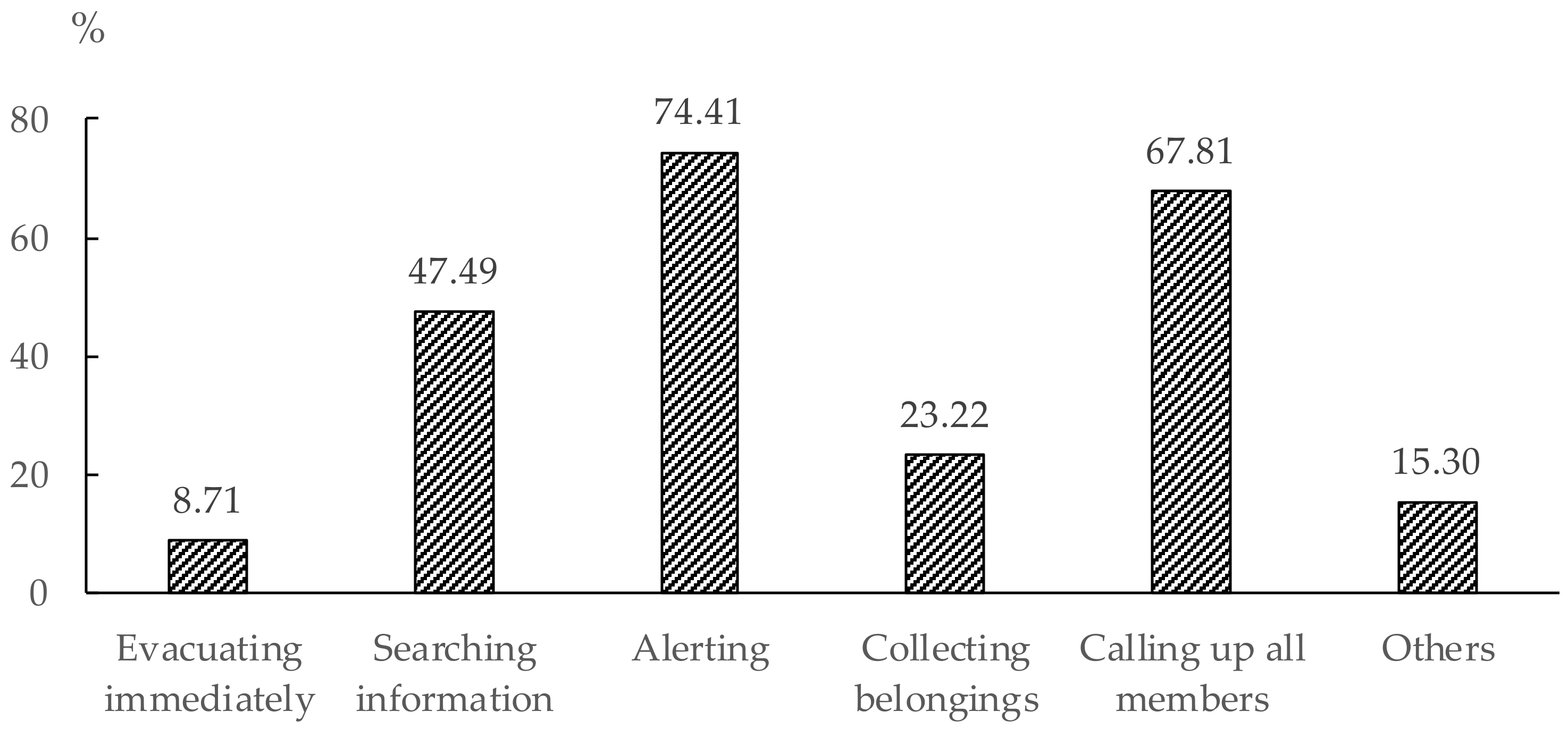
Personal behavior at the initial stage of an emergency, including the first reaction when an emergency occurs, and his/her estimation of the pre-evacuation time.
- (3)
Personal behavior during an evacuation, including the choice of stairways and the route selection when congested.
2.2. Evacuation Simulation
In general, there are two main types of emergency evacuation simulation methods: evacuation drills and computer-based evacuation simulations. Evacuation drills are reliable methods and the results are more realistic. However, it is costly to utilize such time-consuming and laborious methods to conduct evacuation simulations with tracking and recording the behaviors and trajectories of evacuees. Moreover, evacuation behaviors are quite complex and may be different even in the same scenario, which greatly affects route selection, evacuation time and efficiency [
45]. Therefore, in this study the computer-based evacuation simulation method was chosen, which used a typical simulation software, Pathfinder, to conduct emergency evacuation simulations.
Pathfinder is an agent-based egress and human movement simulator. The evacuation simulation of Pathfinder provides two primary modes: SFPE mode and Steering mode, and a number of virtual residents can be set up based on complex evacuation rules to walk. An evacuation simulation environment can be built in a graphical interface, including the layout of community, floors, stairways, entrances and exits of buildings. Once the environment is built, properties of residents can be set, such as walking speed, shoulder width, acceleration time, and some behavior characteristics such as pre-evacuation time and designation points. After these basic parameters have been set the evacuation simulation can be conducted.
Because various factors can affect evacuation times in realistic situations, it is necessary to make several assumptions to simplify the scenario of evacuation simulation. Firstly, the delays due to authorities’ decision time and warning dissemination time were not considered in this study. Secondly, to eliminate common causes of delays such as reuniting separated family members in departure time [
26,
46], the time devoted to evacuation was a weeknight, when all residents were at home before the evacuation. The third assumption was that we did not consider complex conditions such as incomplete compliance and evacuation shadow [
26], incomplete warning reception, attention, and comprehension, as well as physical mobility limitations [
47,
48]. The last assumption was that no one was overtaken by the hazard, such as a wildfire and tsunami.
2.3. Evacuation Time Estimation
Evacuation time is one of the most important factors that measures the efficiency of evacuation. Relevant studies believe that saving evacuation time is the primary goal in evacuation optimization [
49,
50,
51]. Due to the uncertainty of emergencies, it poses a great threat to personnel safety if residents take a long-term detention. In this study, the evacuation time was divided into two parts, these were pre-evacuation time and movement time. The pre-evacuation time was related to personal characteristics, psychology, disaster experience, social relations and so on. Simultaneously, the movement time depended on many factors, such as the crowd density, personal walking speed, and the widths of exits. In general, the total evacuation time can be calculated using the following equation:
where
is the total evacuation time;
is the pre-evacuation time which represents the time interval between the time of receiving a warning and the beginning of movement;
represents the movement time during evacuation, that is, the time from leaving home to reaching the safe place.
To calculate
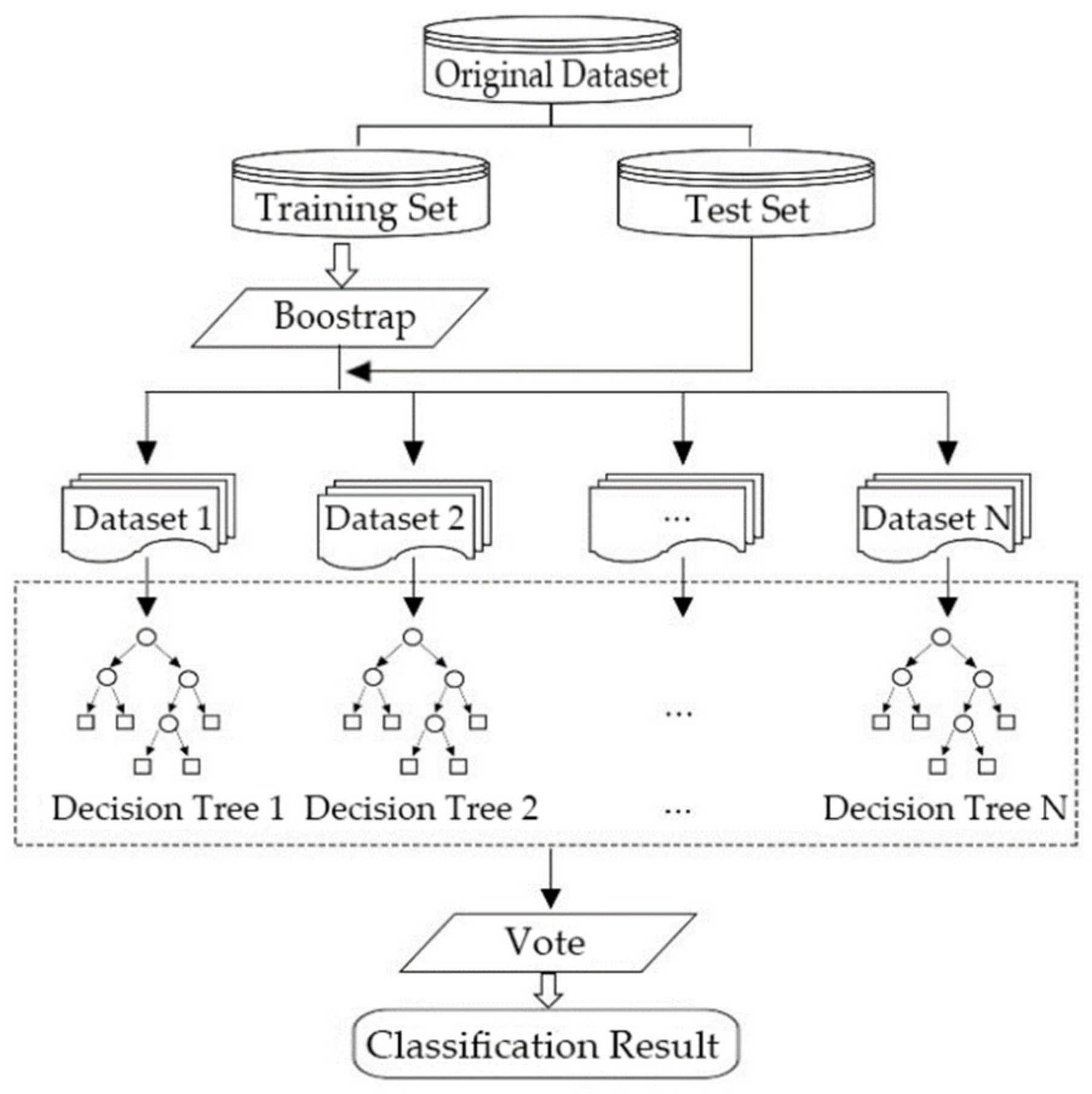
accurately, a predictive model based on the Random Forest (RF) algorithm was built to predict the pre-evacuation time based on behavioral characteristics of residents. The RF algorithm is a machine learning algorithm proposed by Leo Breiman [
52], which can be regarded as an extension of Breiman’s bootstrap aggregation idea [
53] and is inspired by random subspace [
54] and earlier work about shape classification [
55].
A RF is composed of multiple decision trees. A decision tree is a tree-like model that uses a branching method to illustrate every possible outcome of a decision. The tree consists of directed edges and nodes, including a root node, branch nodes, and leaf nodes. The root node is an aggregation of training data. The branch nodes represent the principles of classification. The data which arrive at the branch nodes will be classified by rules. Leaf nodes represent the final classification results. Each path from the root node to a leaf node represents a classification process.
This study assumes an unknown connection relation between the p-dimensional input vector and the output variable . The set of possible values of is denoted by . The goal is to predict based on the classification models with the variable .
The training and classification process of the RF algorithm includes three steps shown in
Figure 2:
(1) Using the Bootstrap method to take samples for N times from the training set to generate N datasets after dividing the original dataset into the training set and test set.
(2) Constructing N decision trees as classification models
to classify N datasets. For the
th tree, a random vector
is generated. On the condition of sufficient trees,
. A set of models depend on the values of
can be presented as follows:
where
is the
th tree;
is the number of trees;
is the random vector which is independently distributed with
but with the same distribution.
N classification results will be generated in this step, respectively.
(3) Voting the N classification results and using the most frequently predicted class as the final output result without pruning of the decision trees. The decision for voting is shown in Equation (3):
where
is an ensemble classification model, which represents the most frequently predicted class;
means the prediction of the variable
using the
th tree with the variable
;
is the indicator function.
With the aforementioned voting procedure, the final classification result can be generated.
In this study, the objective of using the RF algorithm was to predict the pre-evacuation time of residents based on the individual information of residents. Questionnaires were designed to collect residents’ information for surveying pre-evacuation behaviors. Some questions were set as input variables and the answer about pre-evacuation time was chosen to be the output variable in RF. The major questions involved in the prediction model are listed in
Table 1.
After estimating the pre-evacuation time, the movement time in evacuation ( in Equation (1)) was also measured by evacuation simulations. The evacuation simulation software Pathfinder was utilized to simulate the emergency evacuation process of residents.
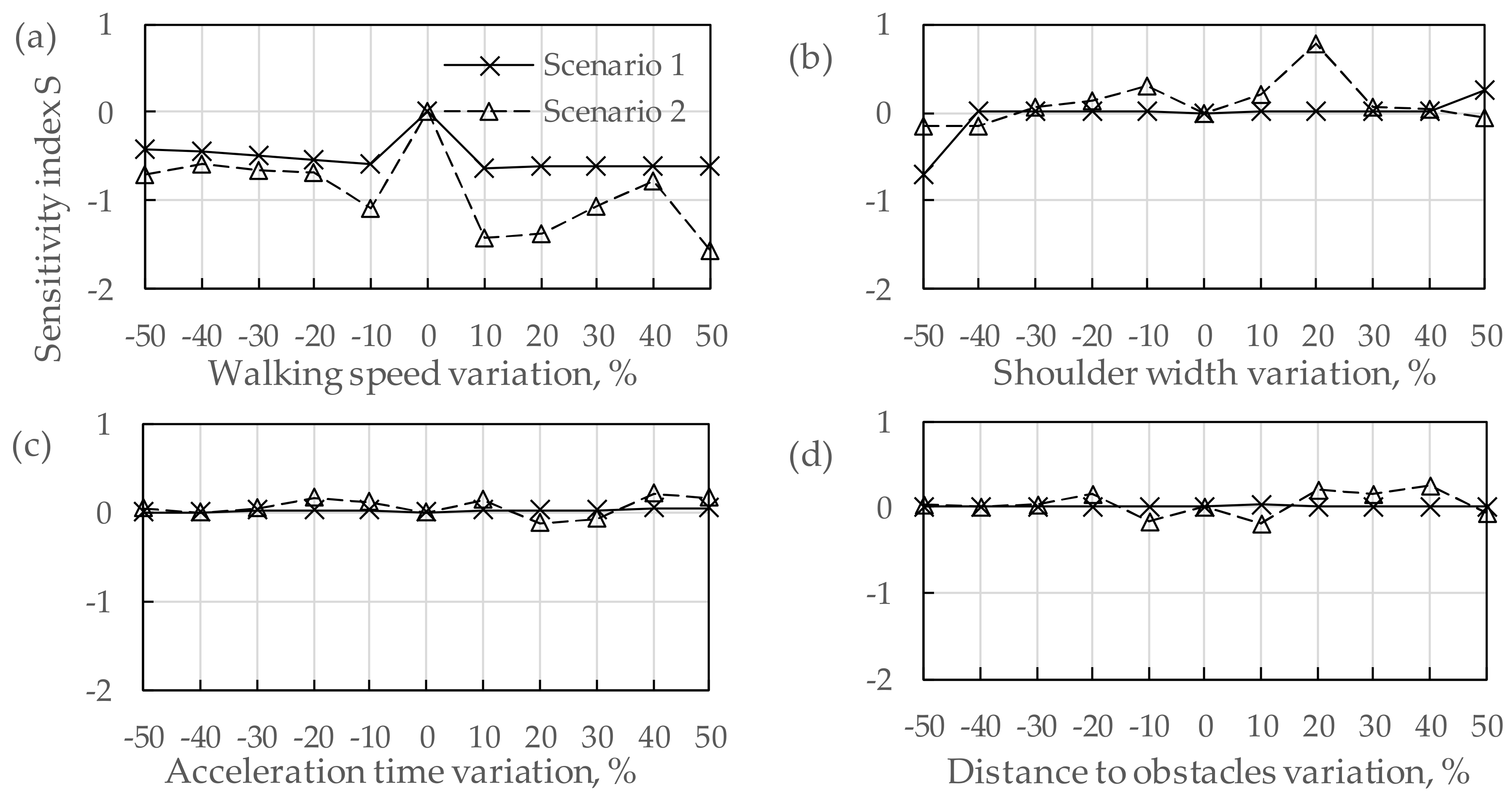
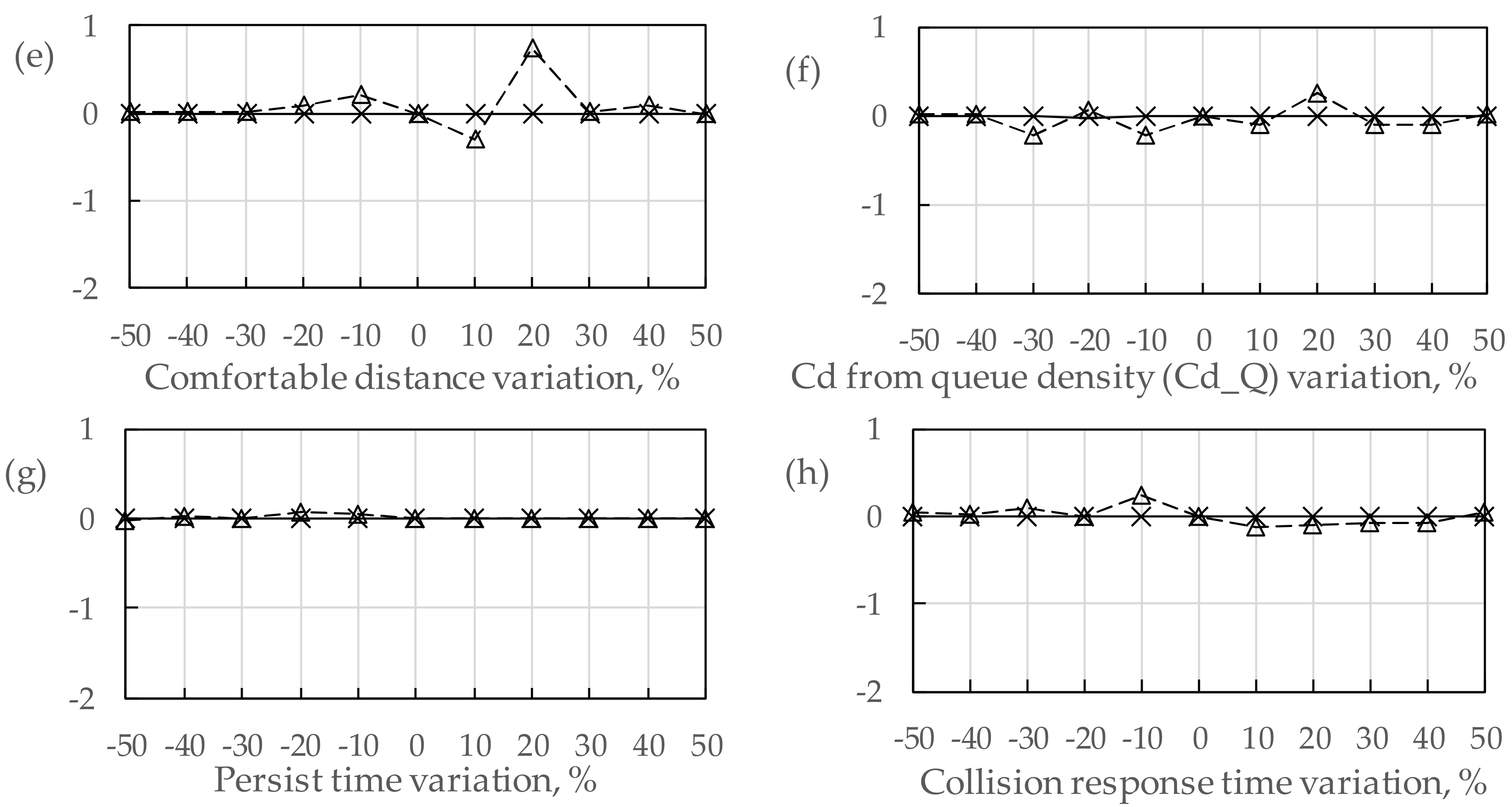
2.4. Parametric Sensitivity Analysis
Due to the urgency of emergency events and the complexity of the evacuation procedure, the estimation of evacuation time involved some uncertain parameters in evacuation simulations, including the spatial distribution and attributes of residents, such as walking speed and shoulder width.
Under most circumstances, it is impossible to conduct an enormous amount of evacuation drills to analyze the uncertainty in evacuation. Meanwhile, value setting of critical parameters cannot be determined by subjective judgments or default values in evacuation software. In such a case, sensitivity analysis methods can deal with parameter uncertainty problems effectively. Typically, it is one of the key modules in most model development processes [
56,
57], which can reduce the complexity of a model by describing how important the input variables are to the output variables quantitatively.
In the research field of sensitivity analysis, various kinds of methods have been proposed, such as Monte Carlo simulation and one-factor-at-a-time (OAT). OAT is one of the most commonly used methods, which has a simple calculation procedure and is easy to be understood. OAT-based parameter sensitivity analysis examines the influence of the perturbation of a single parameter on the output, while others remain constant. It can determine which input parameters
have greater impacts on the output result
by observing the influence of perturbation of parameter values on the result. The degree of influence can be expressed as the un-normalized sensitivity index
as follows [
58]:
where
is the
th input parameter and
is the output result.
Based on Equation (4), the normalized sensitivity index
[
59] can be utilized to eliminate the difference in input parameters
with different units and magnitudes. The equation of the normalized sensitivity index can be expressed as follows:
According to the definition of the partial derivative, the normalized sensitivity index was only applicable to the small variation (
) in the input parameter. Therefore, the method of local sensitivity analysis was used in this study, that is, adding a stepwise percentage change on the value of input parameters, and then the effect on the output was observed [
60].
The sensitivity index
can be calculated by the following equations:
where
is the
th percentage changed value of the
th input parameter;
is the increment/decrement of value change of the
th input parameter compared with the original value of this parameter;
is the output result (the total evacuation time in this study) with the
th percentage value change of the
th input parameter;
is the value change of the output result when compared with the original result when making the
th percentage value change of the
th input parameter;
is the original value of the
th input parameter; IPC is the increment of percentage change (10% in this study);
is the
th integer value ranging from range
min to range
max; range
min and range
max were −5 and 5 in this study, respectively. With different
, stepwise percentage change on the value of input parameters could be conducted and the OAT sensitivity analysis could be carried out.
2.5. Simulation Result Comparison
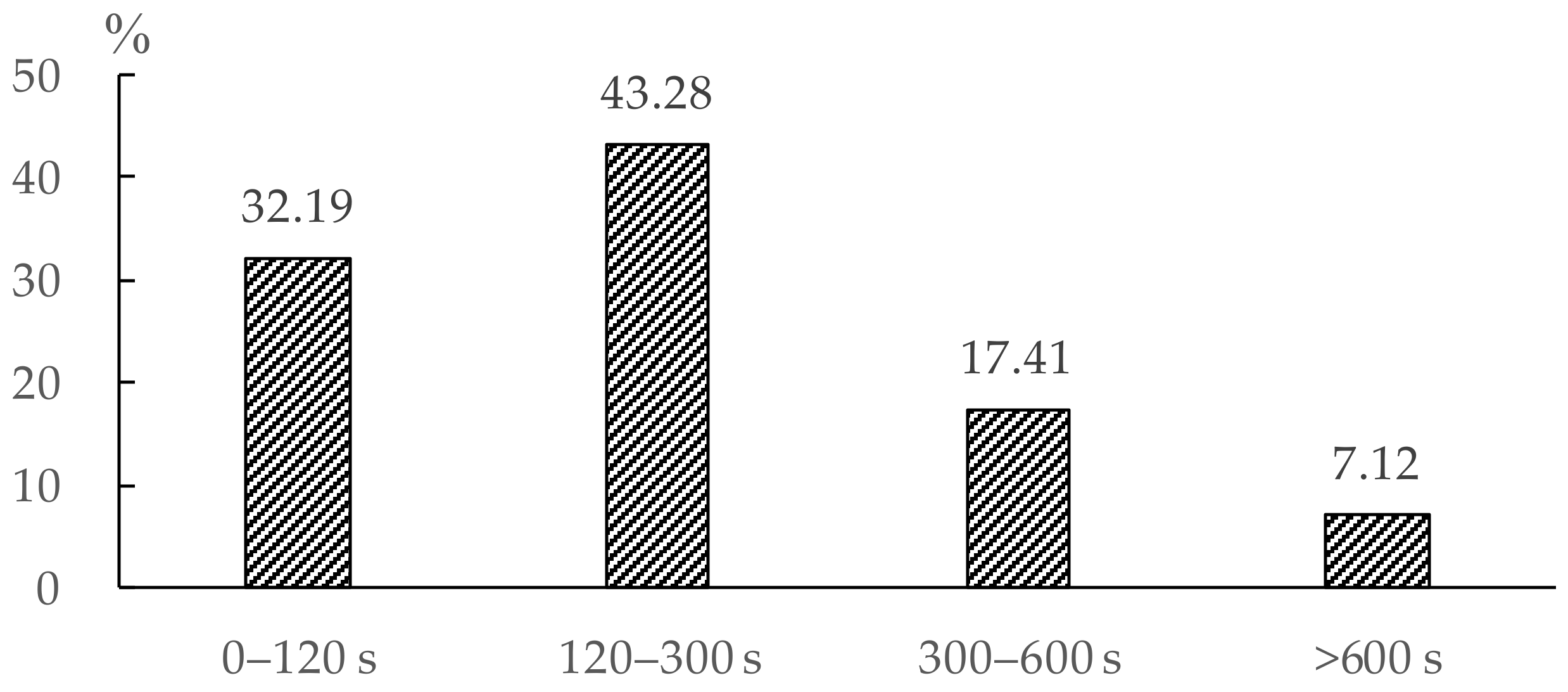
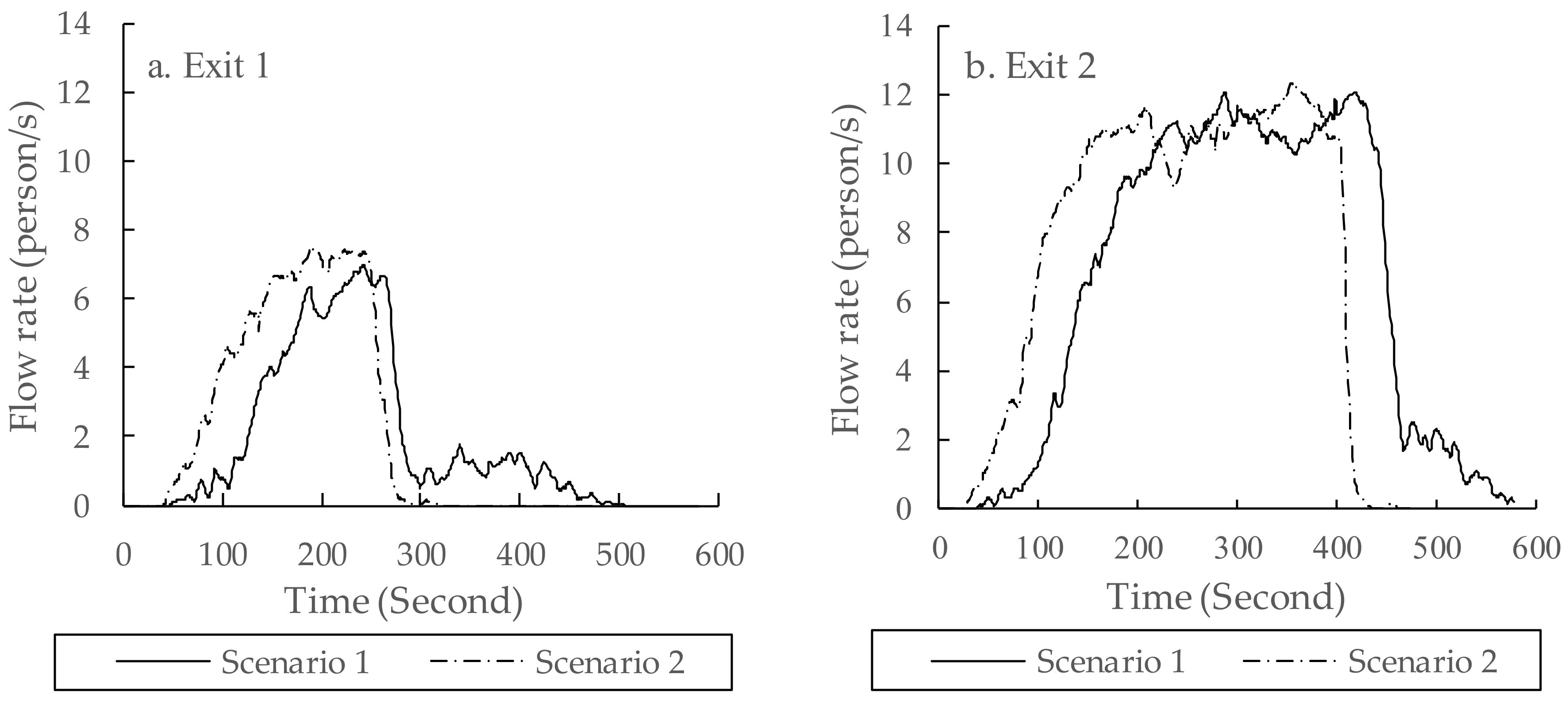
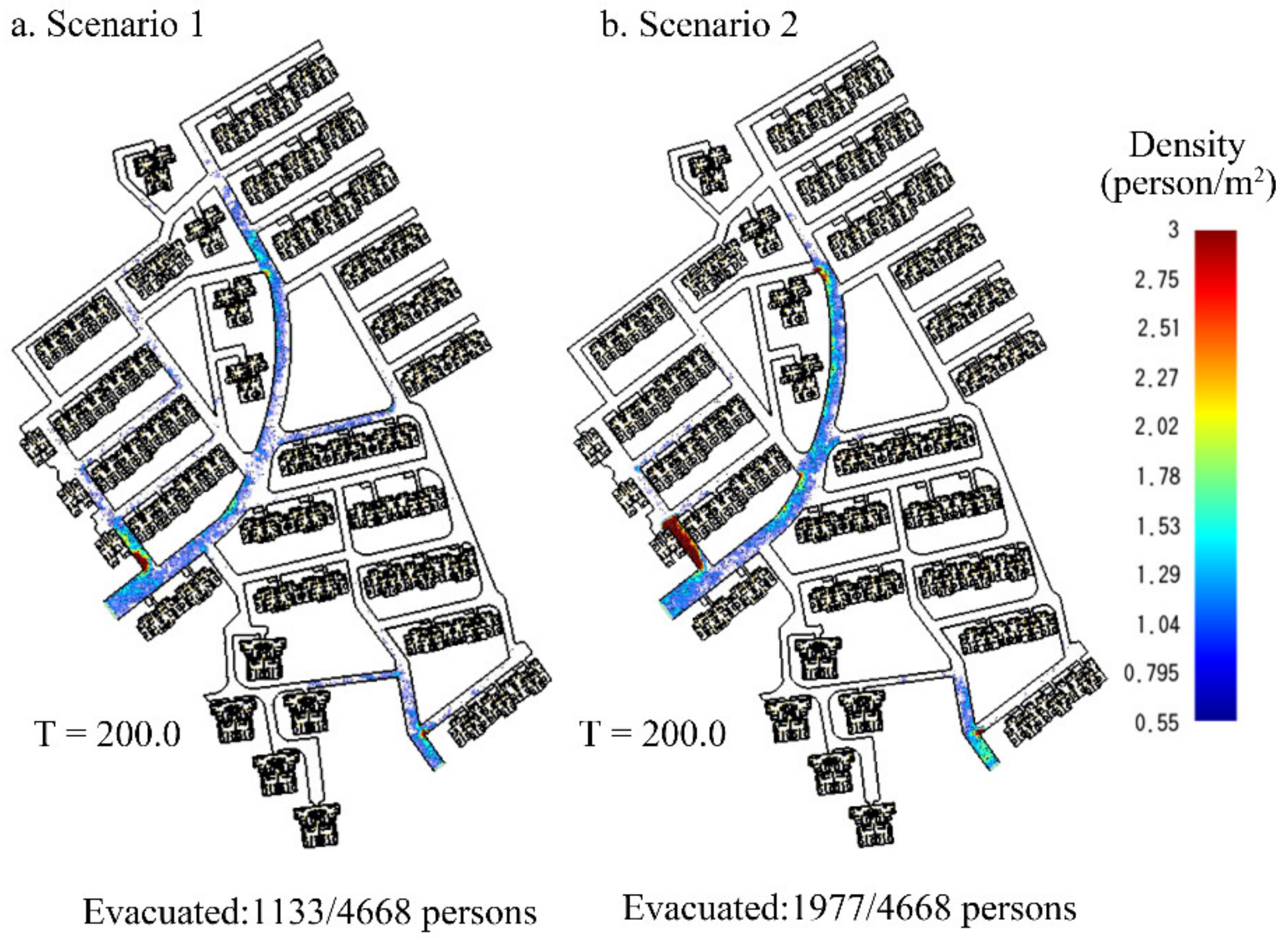
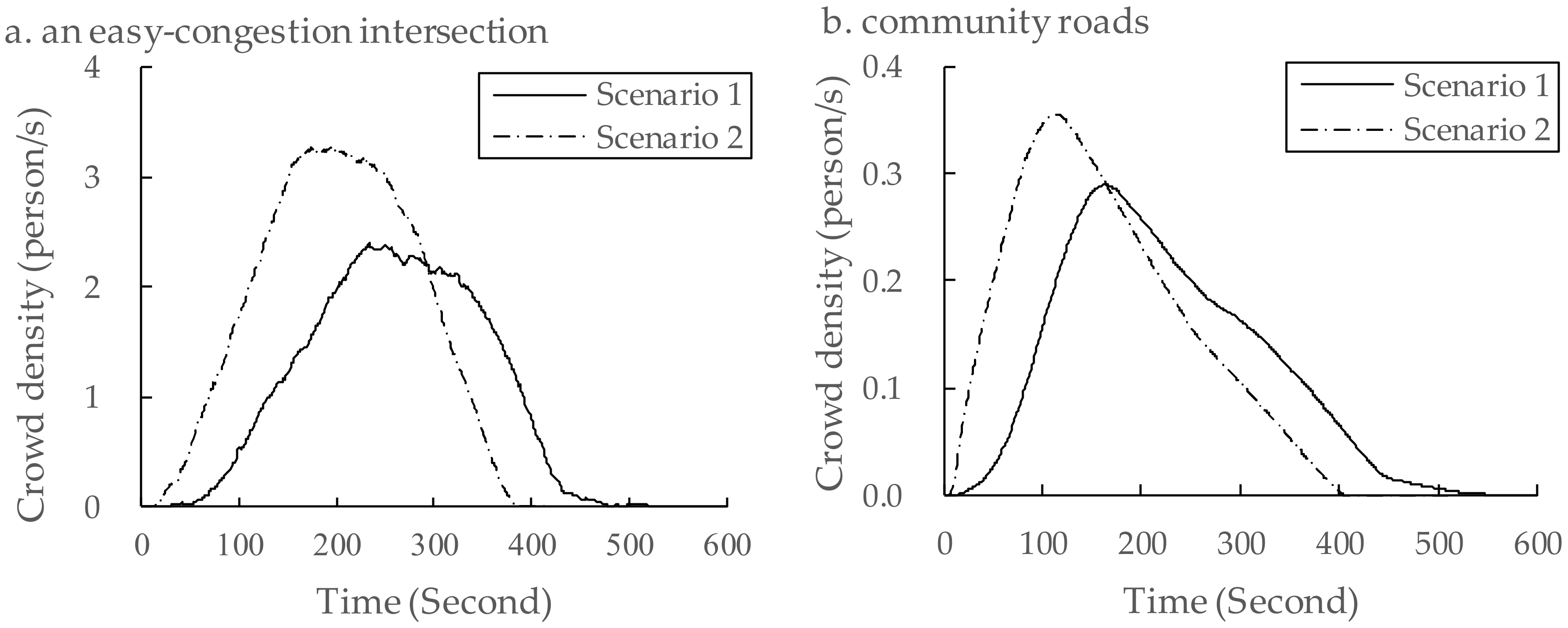
In this study, two different scenarios were preset for evacuation simulations. Scenario one considered the pre-evacuation behaviors of residents, while Scenario two neglected the pre-evacuation times and all the residents started to be evacuated at the same time. With the evacuation simulations of these two scenarios, their simulation results were compared to quantitatively analyze the impact of pre-evacuation time on the evacuation procedure. The comparison had different items, including “evacuation time”, “flow rates of residents at exits” and “crowd density on roads”. With such a detailed comparison, the significance of pre-evacuation estimation for the evacuation simulation in a community can be demonstrated.
4. Discussion
With the analysis of the simulation result in
Section 3.3, it can be judged that the pre-evacuation estimation can improve the estimation procedure of the start time, end time, changing flow rate and spatio-temporal crowd density.
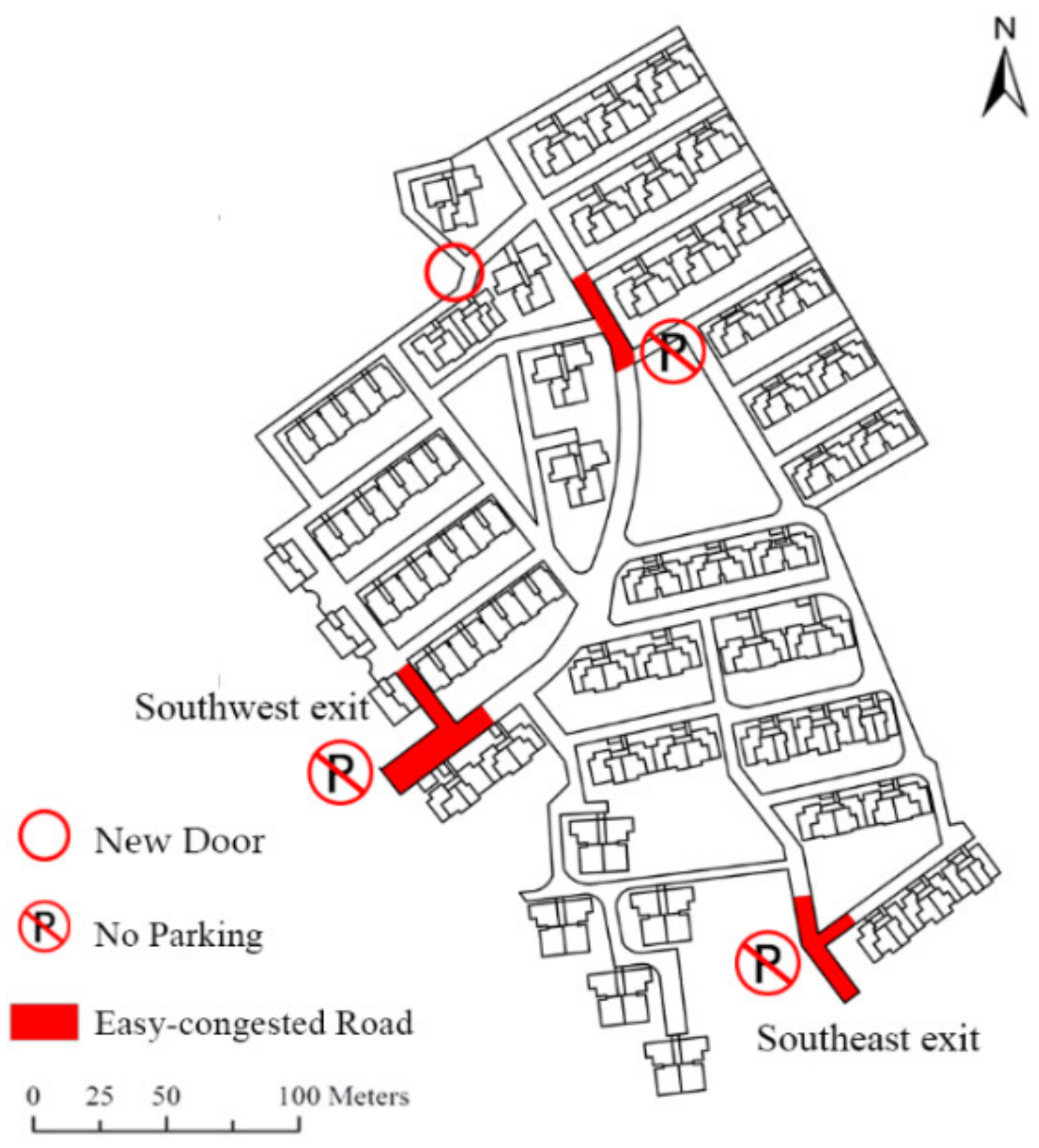
In this study, we also tried to propose some evacuation management strategies and recommendations for emergency management after the case study: (1) Three easy-congested road sections (
Figure 11) should be set as no-parking zones to prohibit car parking. This is of great significance for the safety and efficiency of an emergency evacuation. (2) Taking traffic dispersion measures at critical road sections. Guide signs or LED display screens which are designed to guide the residents and enable them to evacuate rationally should be placed at the major road sections. (3) Opening a new North exit. The new exit can relieve the road evacuation pressure of the southern region, effectively reducing the crowd degree in evacuation and decrease the total evacuation time.
Compared with other existing relevant research, although it is not the first evacuation simulation which includes the pre-departure evacuation time estimation component [
26], the main contributions of this study are as follows: (1) The proposed method can predict short pre-evacuation times in emergency evacuation simulations in urban communities, which is more realistic than traditional simulation methods. (2) The pre-evacuation times of residents are predicted on the basis of questionnaires by the Random Forest (RF) algorithm and can get qualified prediction accuracy. (3) It integrates three-dimensional building evacuation with an outdoor pedestrian evacuation simulation process in an urban residential community. (4) A sensitivity analysis is integrated into the method to assess the extent to which variation in each key parameter produces corresponding variation in the estimation of the total evacuation time. (5) Based on the spatial mapping of the simulation results, some management strategies are proposed to improve management of an evacuation.
The method proposed in this study has some limitations in the following aspects. Firstly, this method was based on ultra-detailed data on residents and buildings, including the three-dimensional information of buildings and behaviors of residents. This may be a time-consuming and difficult task to simulate evacuation with ultra-detailed data in a large area. Moreover, the field survey may only cover a small percentage of residents for obtaining the data source to estimate the pre-evacuation time if the study area is large. Secondly, we made some simplified assumptions for conducting our method, which may have been different to a realistic condition. This study did not consider some complex conditions, including some common causes of delays such as reuniting separated family members during departure time, incomplete compliance and evacuation shadow, physical mobility limitations, etc. In the future, we will improve this method to simulate more complex evacuation behaviors on a larger spatial scale.
5. Conclusions
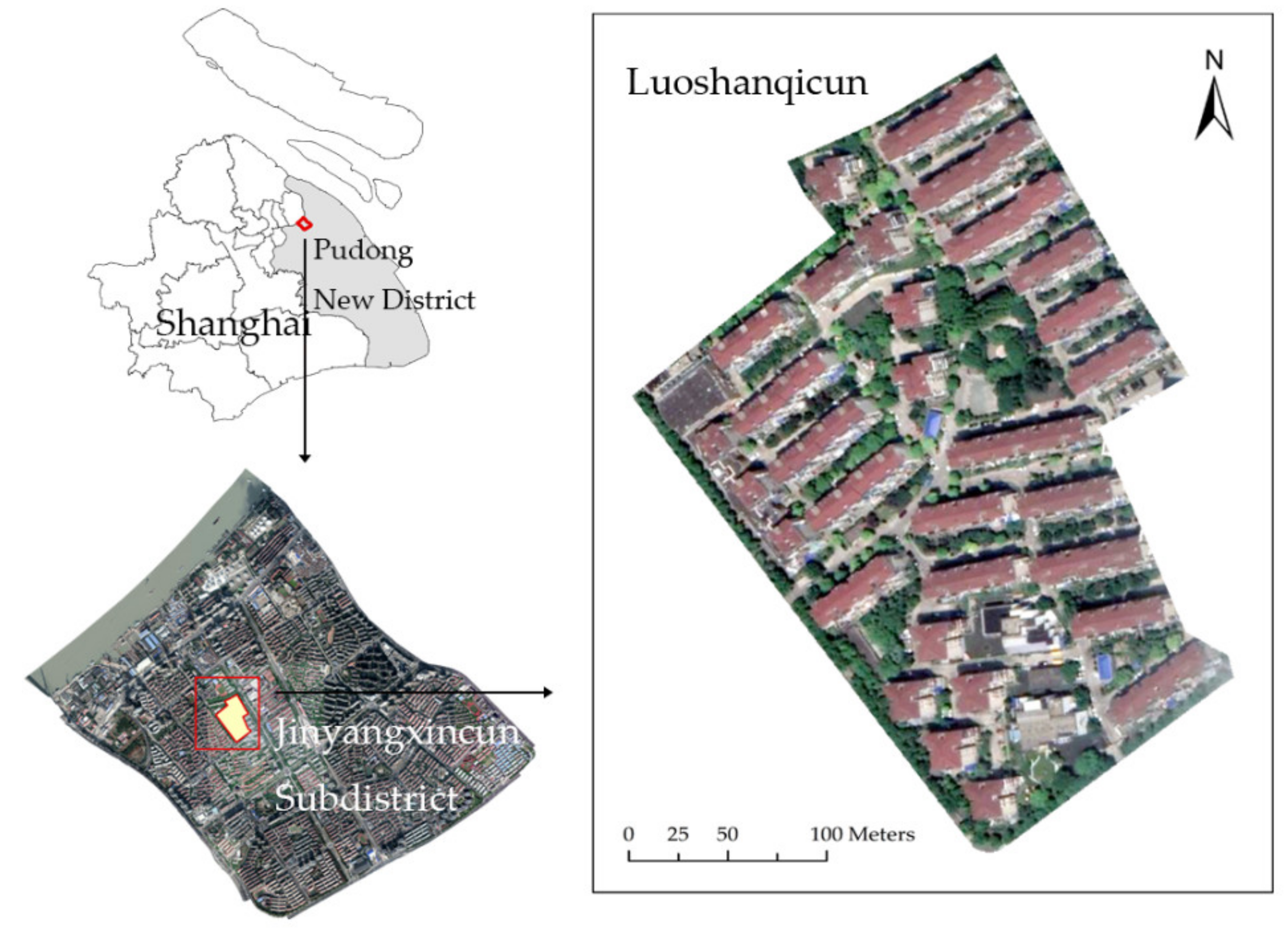
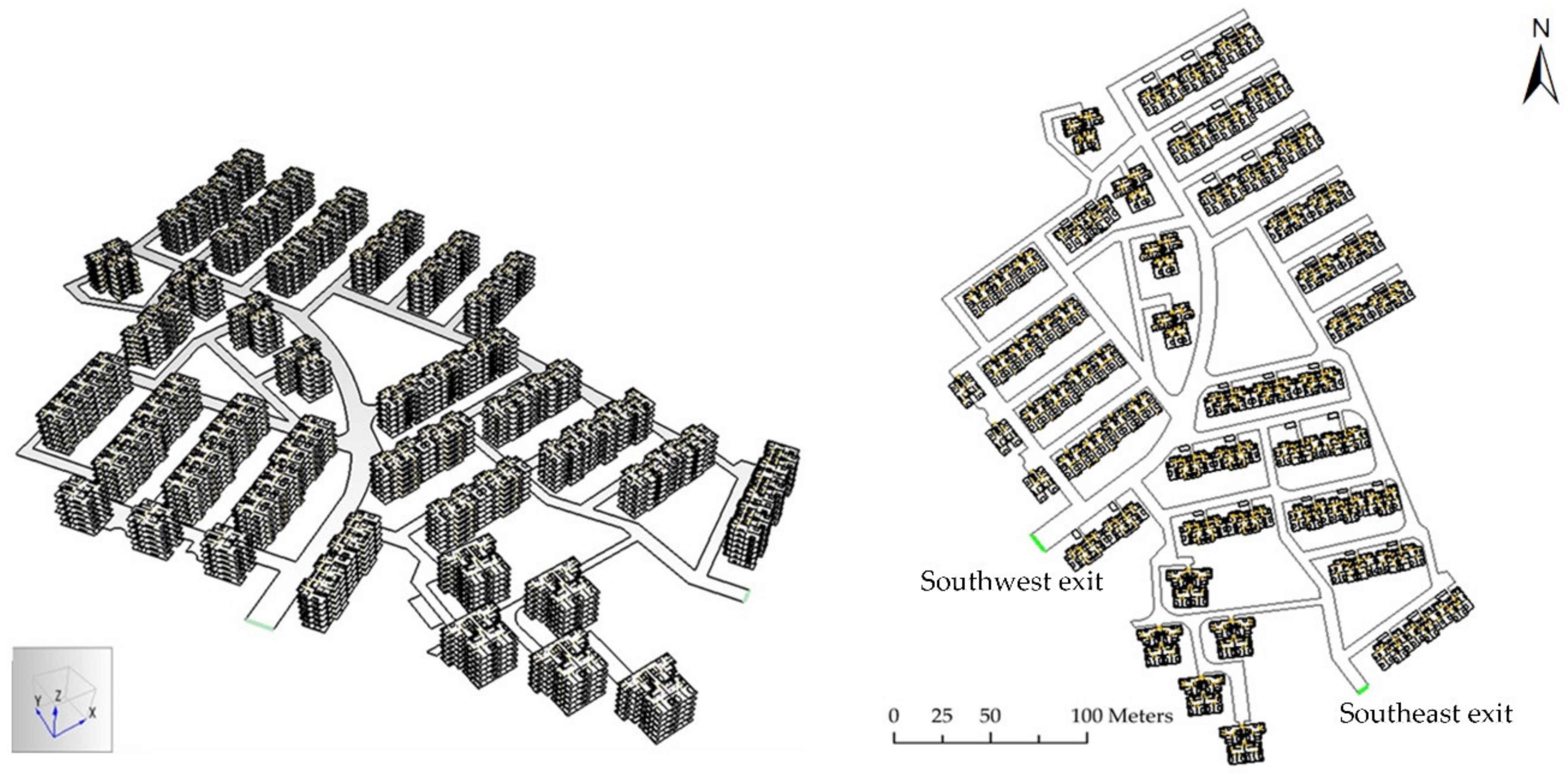
This study proposed a new method to address the evacuation problem of a vertical building evacuation followed by a small-scale horizontal pedestrian area evacuation, which integrated the pre-evacuation time estimation and made evacuation simulations in urban residential communities more realistic. The pre-evacuation times of residents were predicted by the Random Forest (RF) algorithm on the basis of residents’ pre-evacuation behavior data obtained by field surveys. The proposed method also involved a sensitivity analysis to estimate the sensitivity of different evacuation simulation parameters based on the one-at-a-time (OAT) method. The evacuation simulation results can be used to identify potential evacuation problems and help decision-making in evacuation management. To demonstrate the feasibility of this study, a case study was carried out in Luoshanqicun Community, Pudong New District, Shanghai, China. There are 51 residential buildings and more than 4000 residents in this community, which is a typical scale for a community. On this scale, it is also suitable for collecting sufficient survey data from the residents. We collected the residents’ pre-evacuation behavioral data from a field survey by means of questionnaires and simulated the evacuation process of all the residents in the study area. According to the simulation results, such as evacuation time estimation, flow rate calculation and crowd density estimation, it was found that the pre-evacuation times had significant impacts on the simulation procedure. The analysis results proved that the proposed method could get better simulation results than traditional simulation methods. On the basis of the simulation and analysis results, the potential evacuation problems in the study area were also discussed, and some evacuation management strategies were proposed to support emergency management. The case study illustrated the practicality of the proposed method. The method may be applied in other similar case studies with relevant population census data and investigations.