On Dam-Break Flow Routing in Confluent Channels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Model
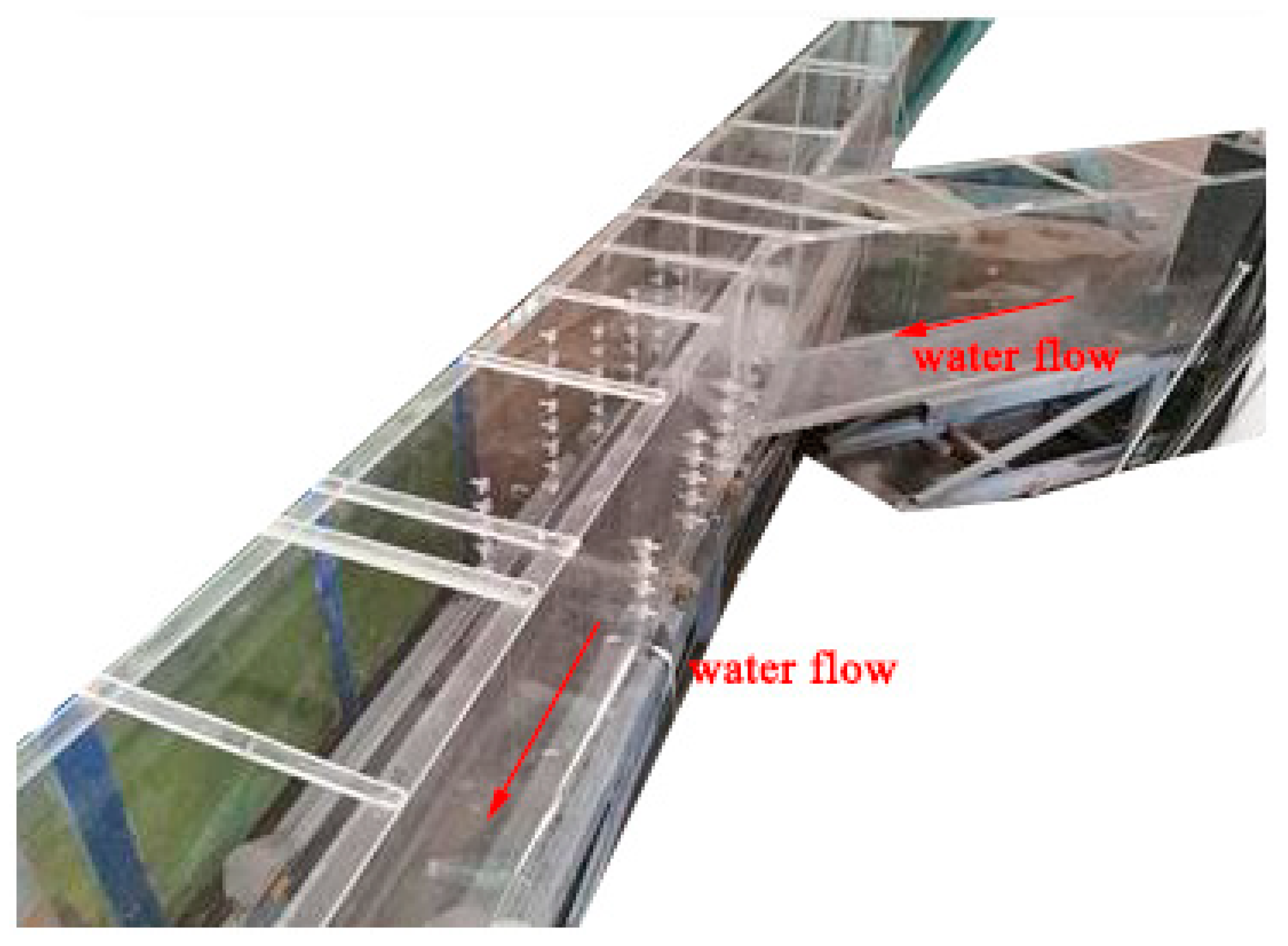
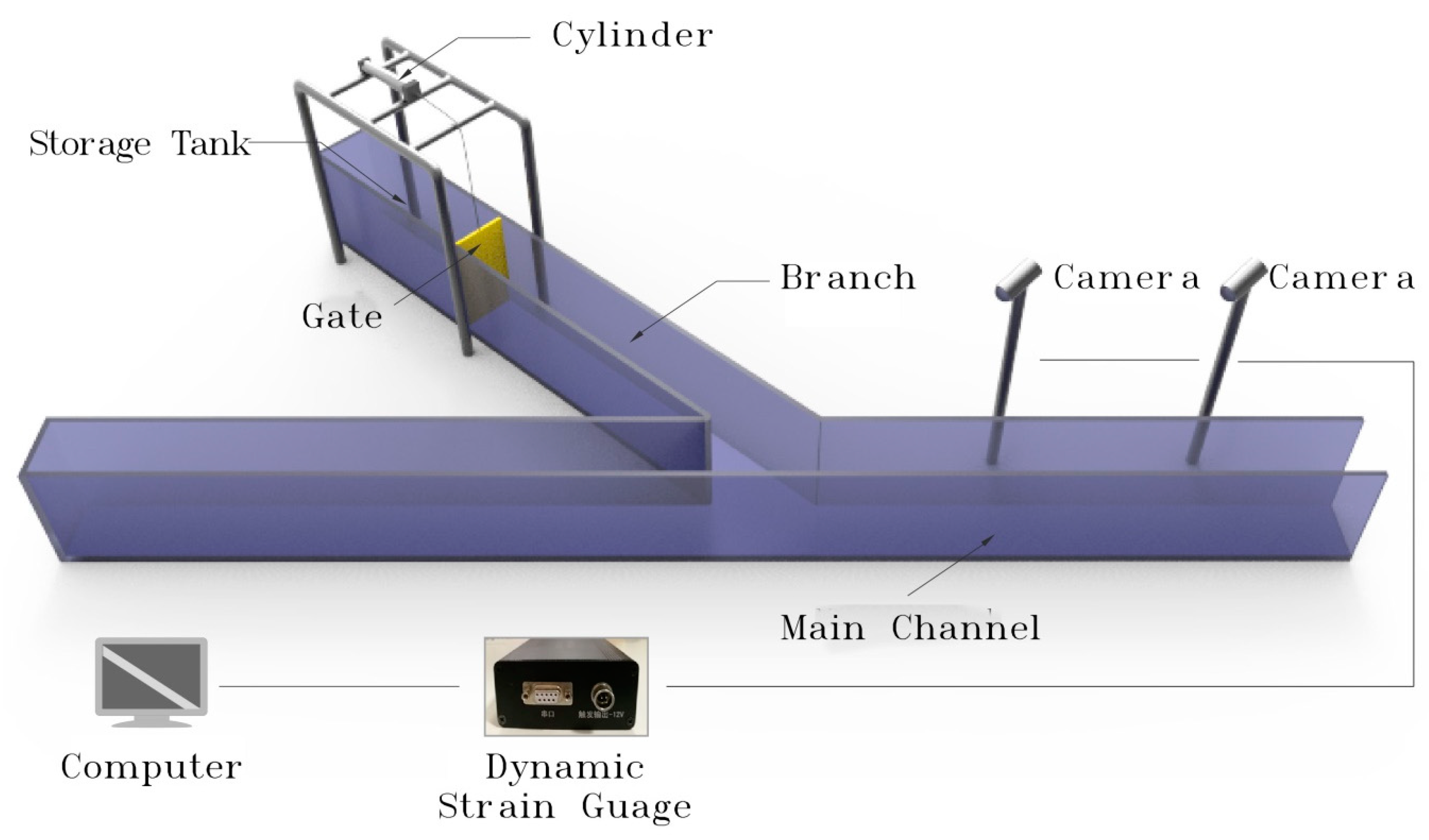
2.1.1. Arrangement of Test Apparatus
2.1.2. Test Methods
2.1.3. Test Conditions and Placement of Measuring Points
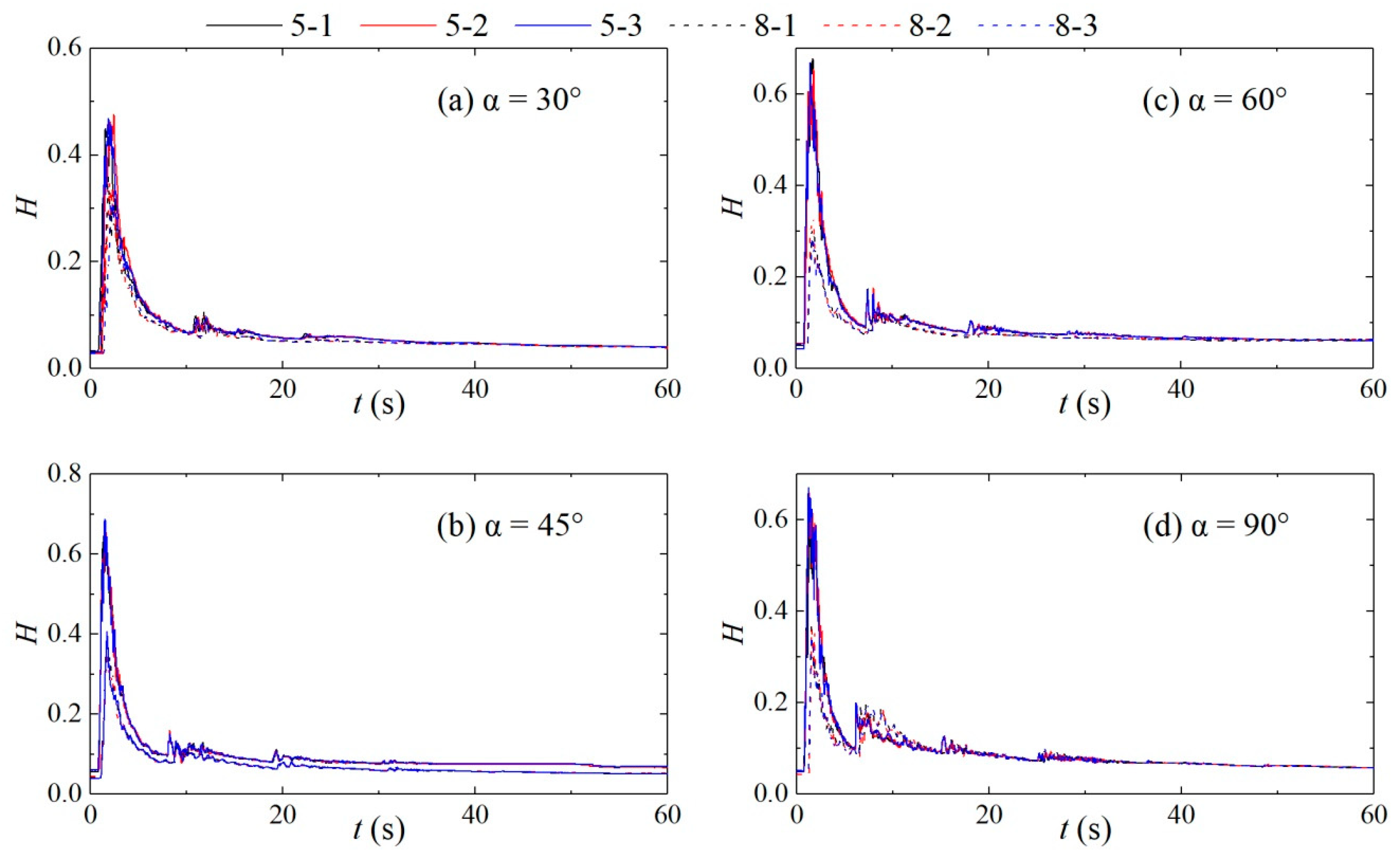
2.1.4. Verification of Test Repeatability
2.2. Numerical Model
2.2.1. Turbulence Model and Free Surface
2.2.2. Computational Domain, Boundary Conditions, and Initial Conditions
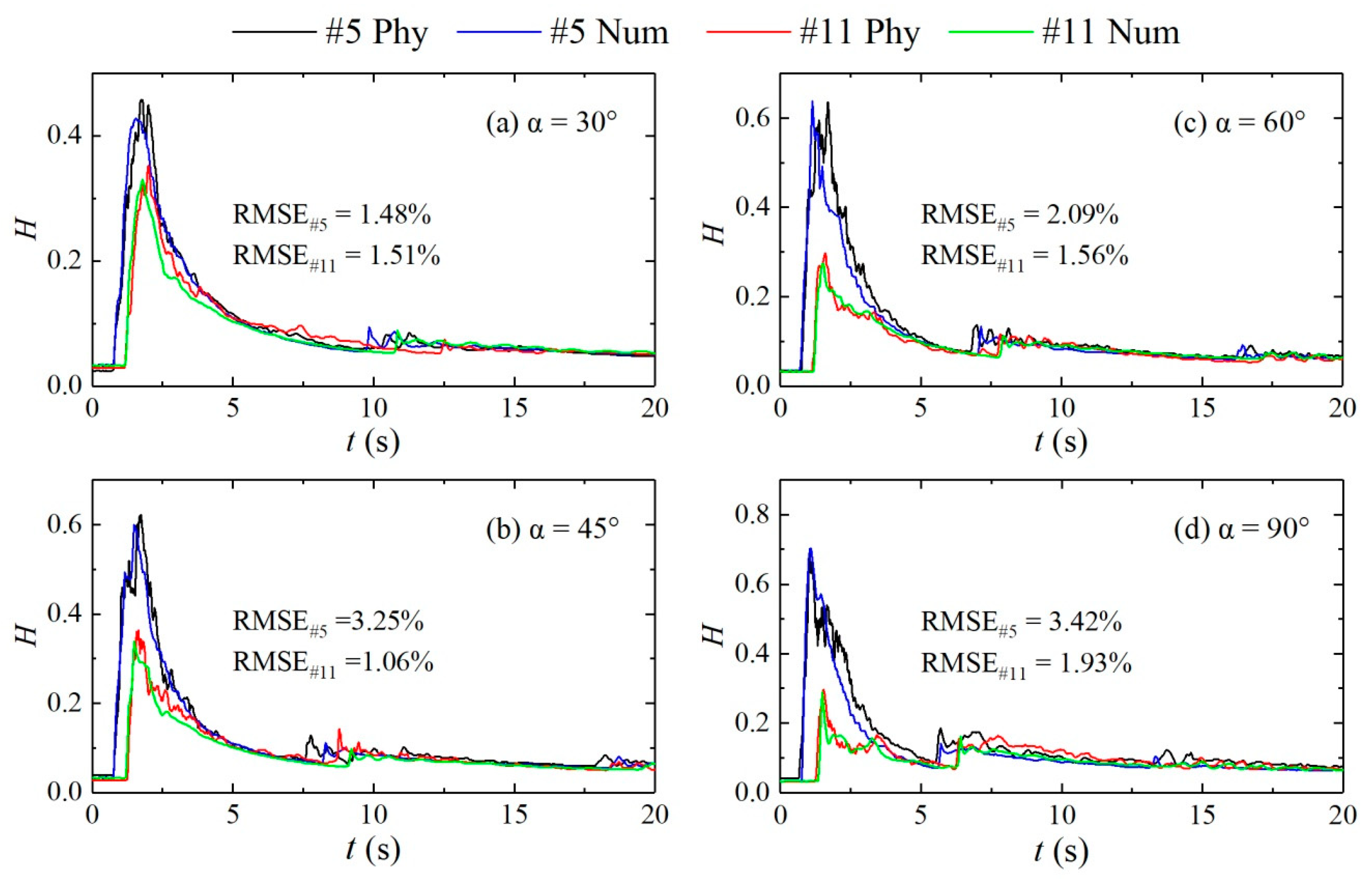
2.2.3. Reliability Analysis of Numerical Simulation Results
3. Results and Discussion
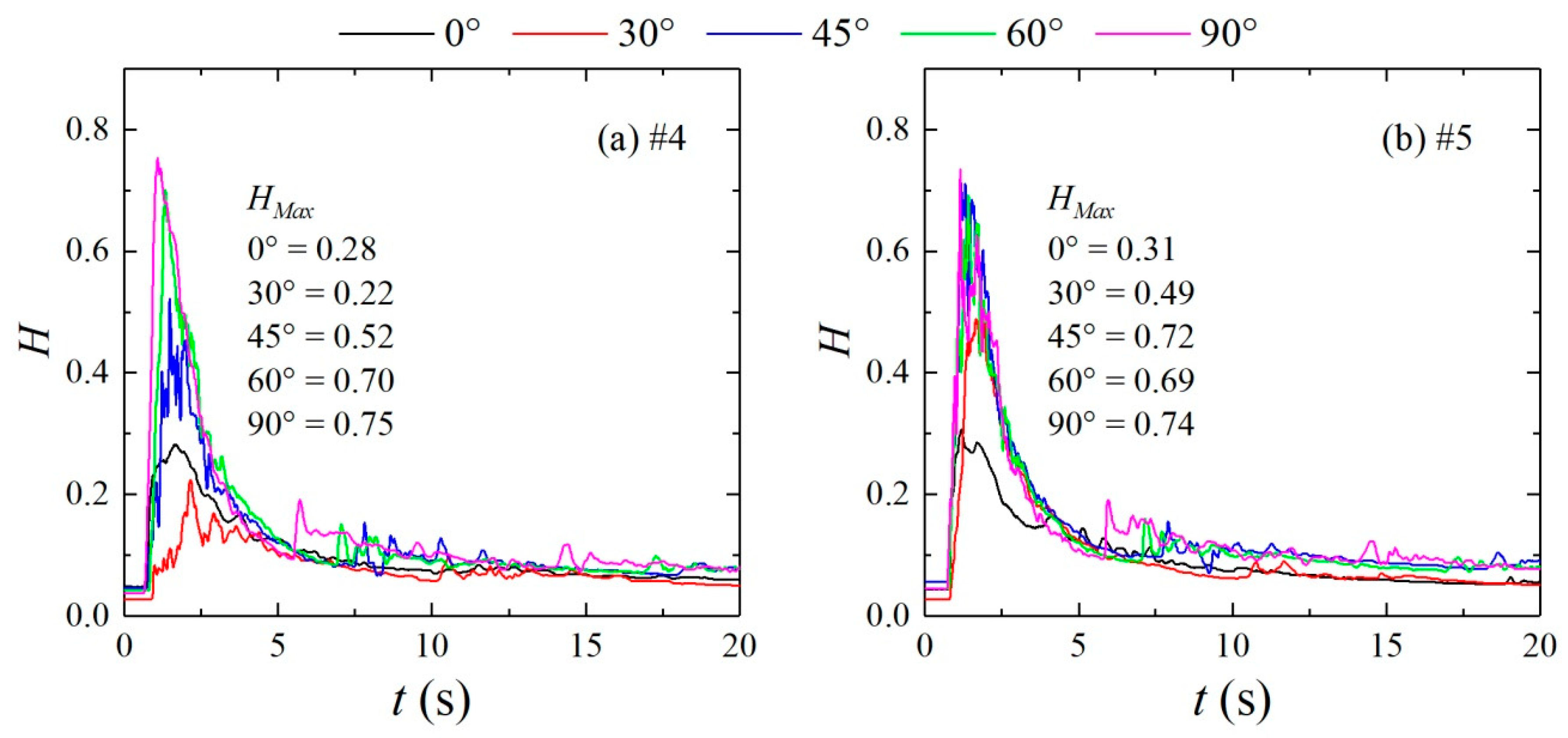
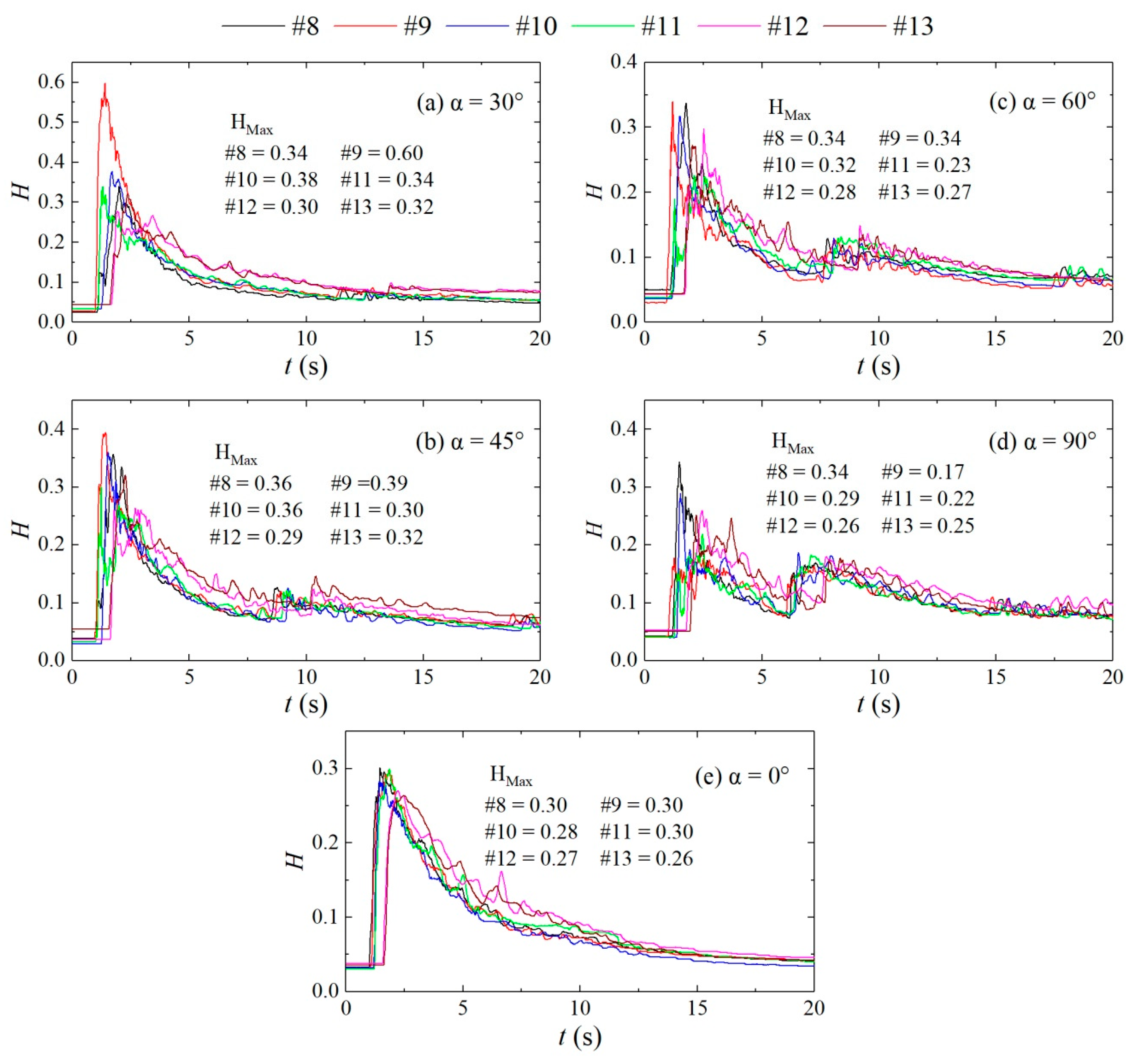
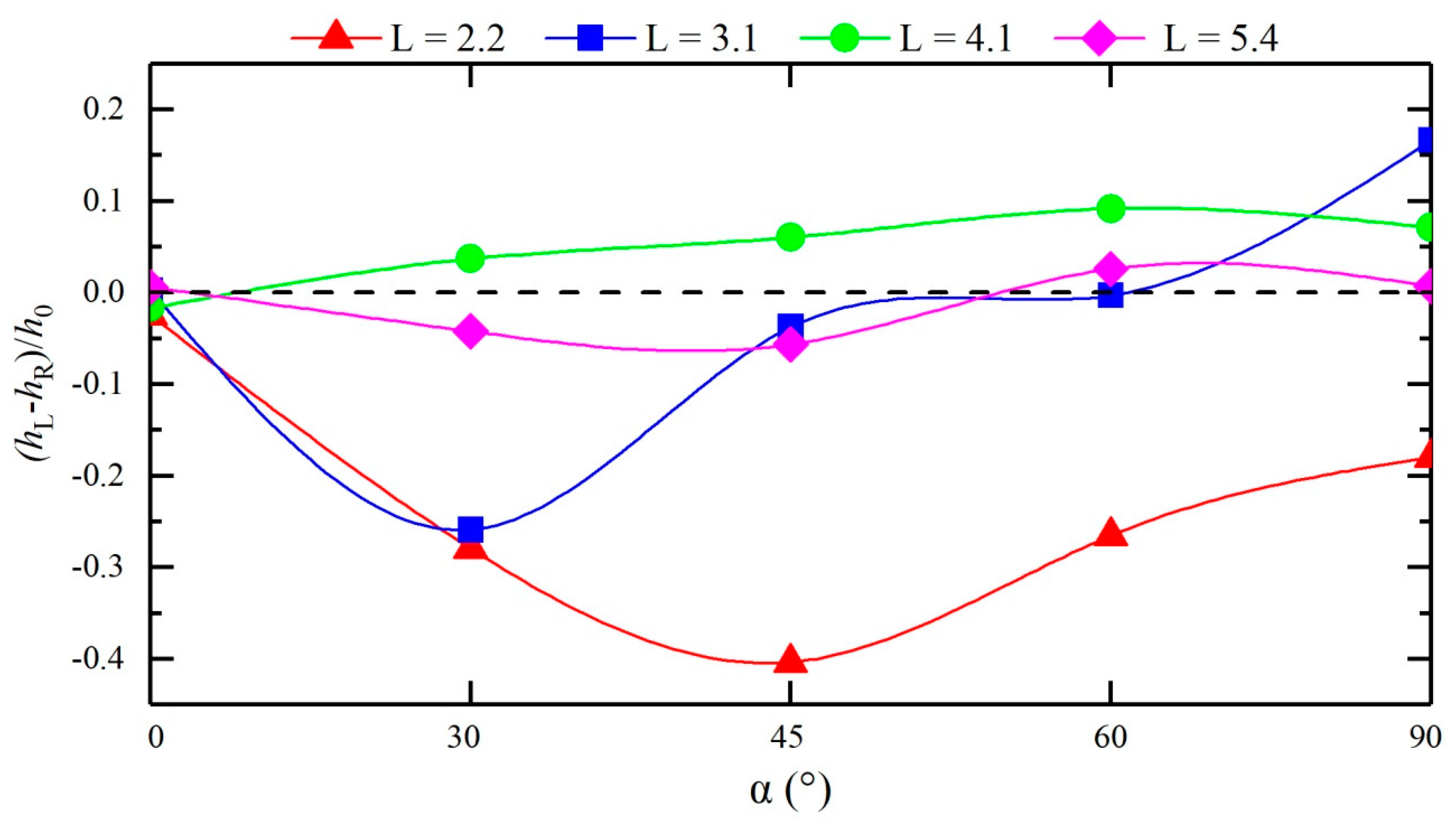
3.1. Water Level Variation
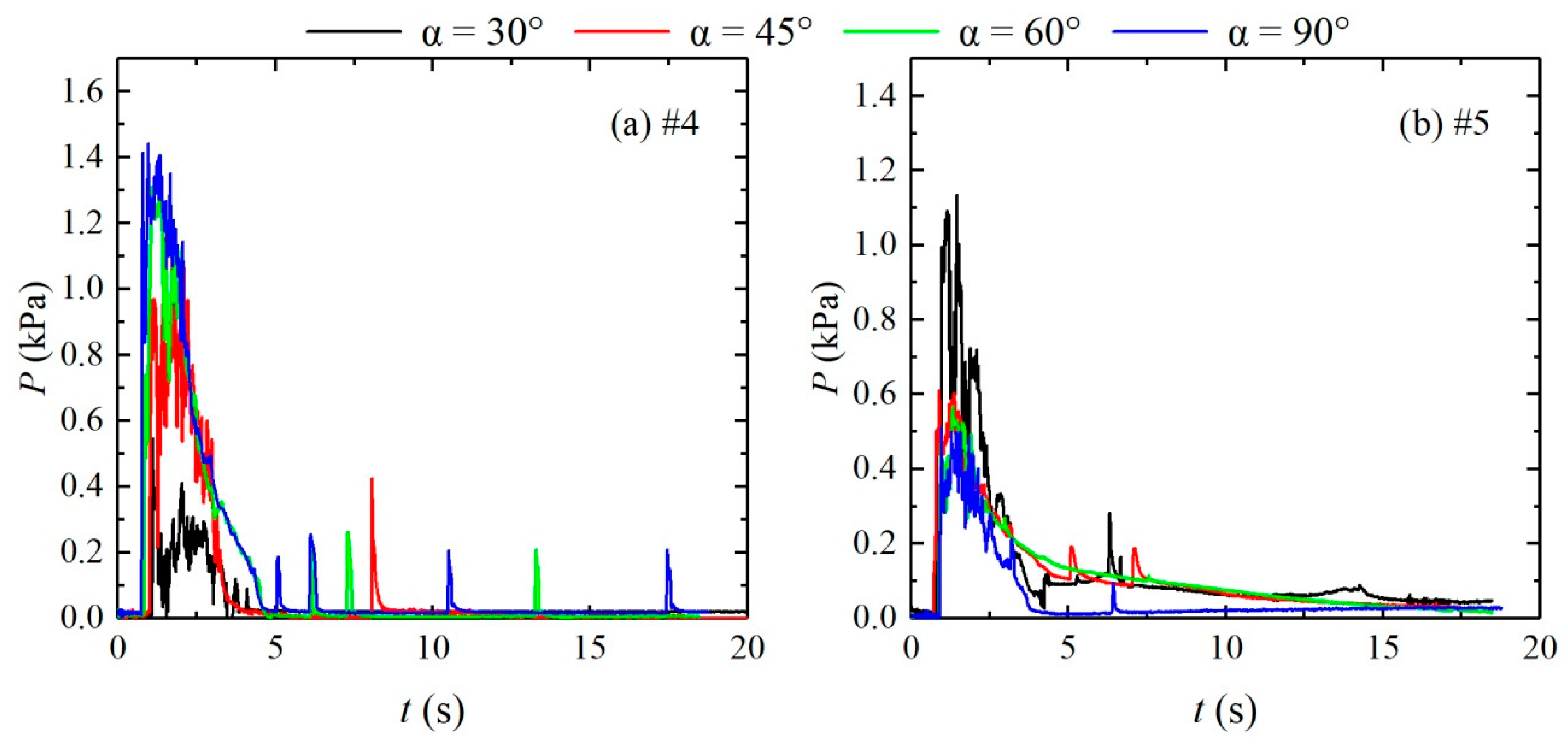
3.2. Pressure Variation
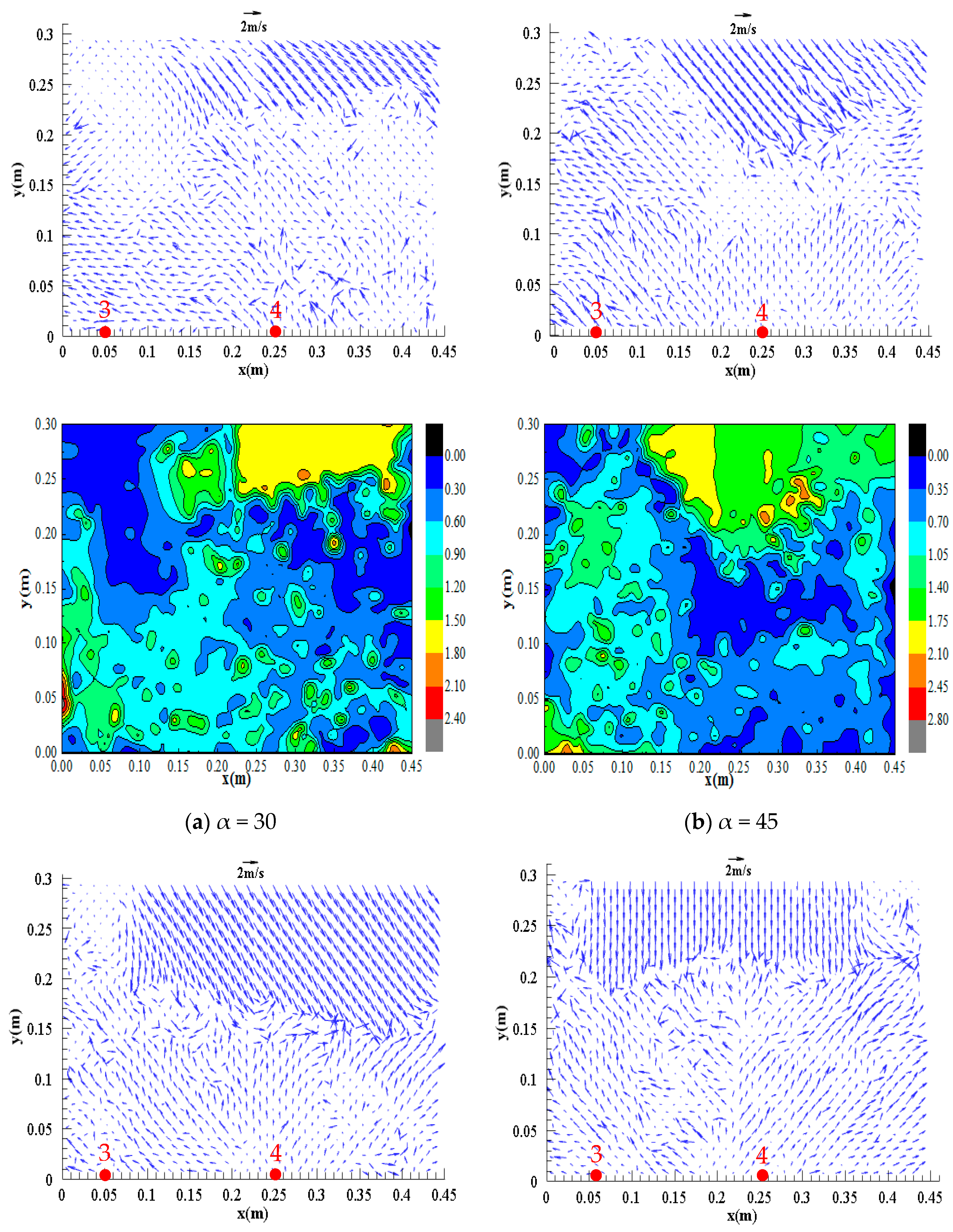
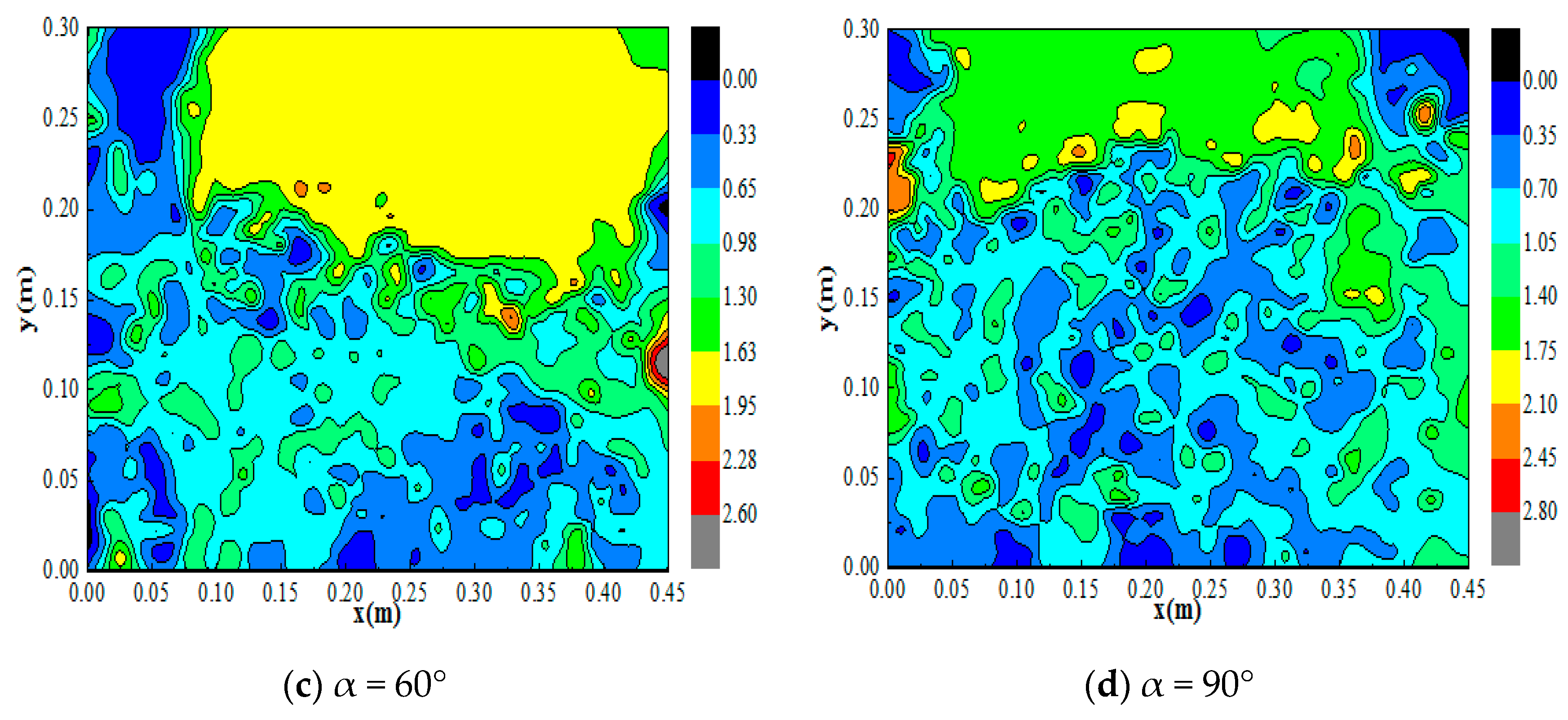
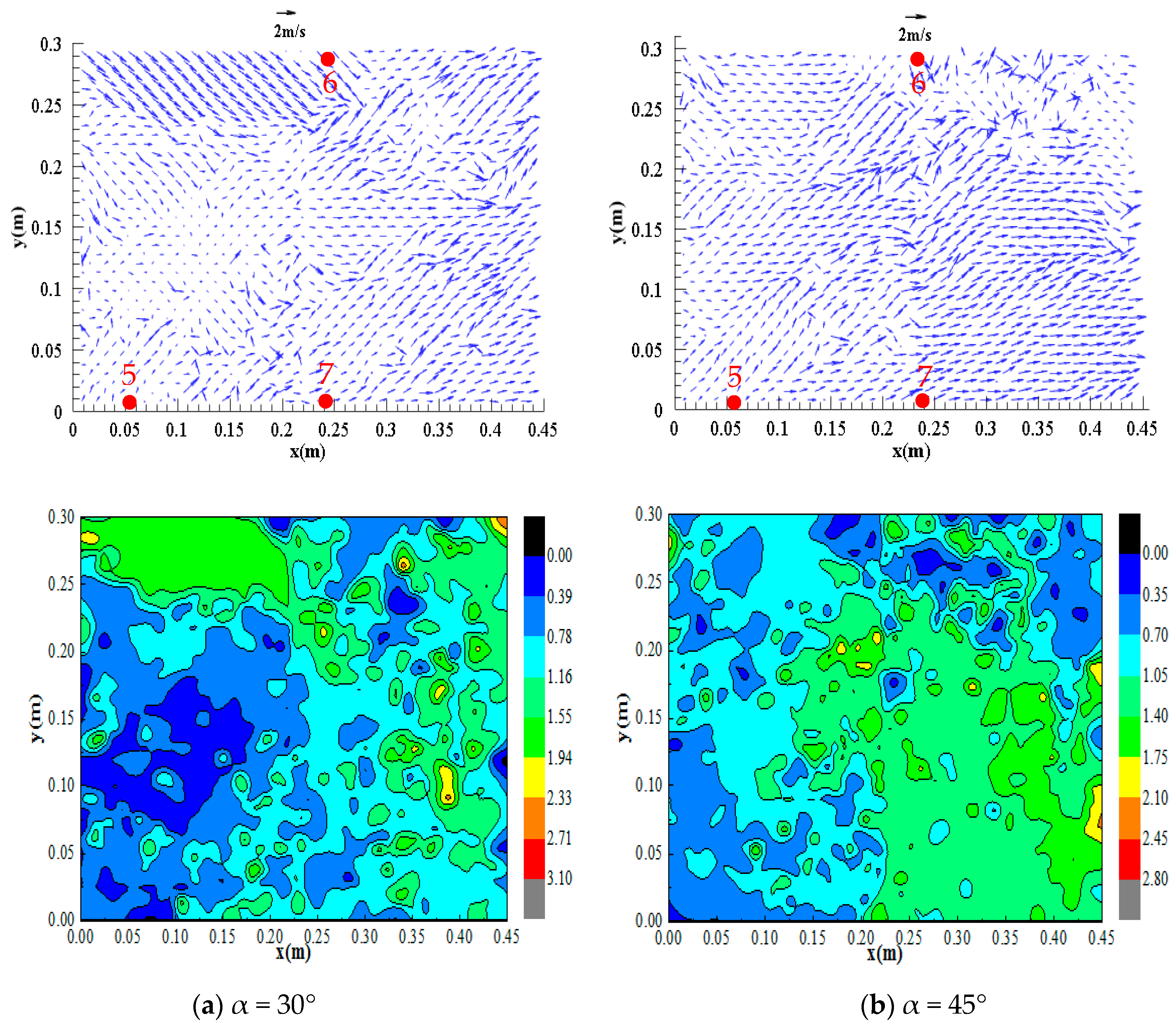
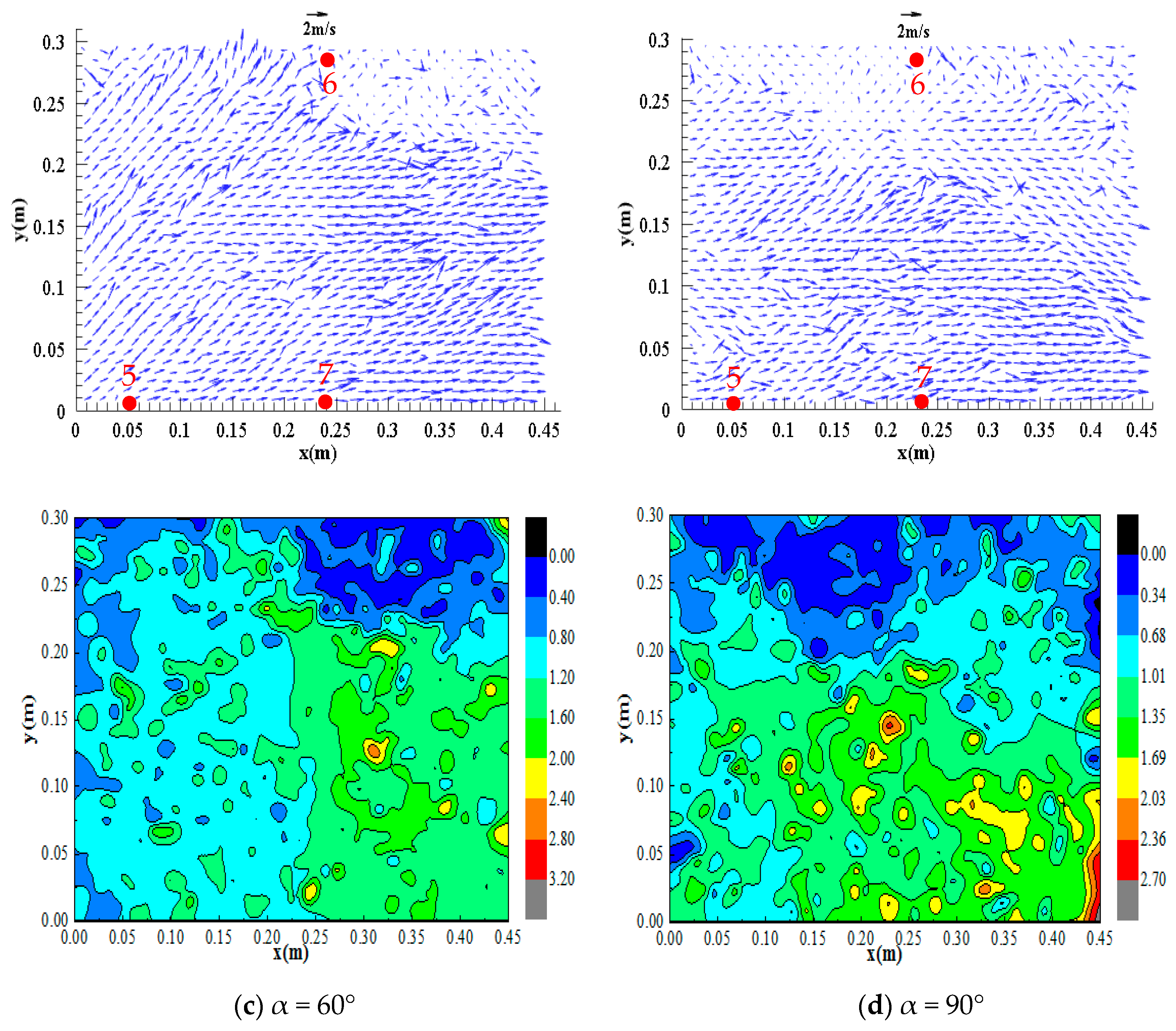
3.3. Flow Field
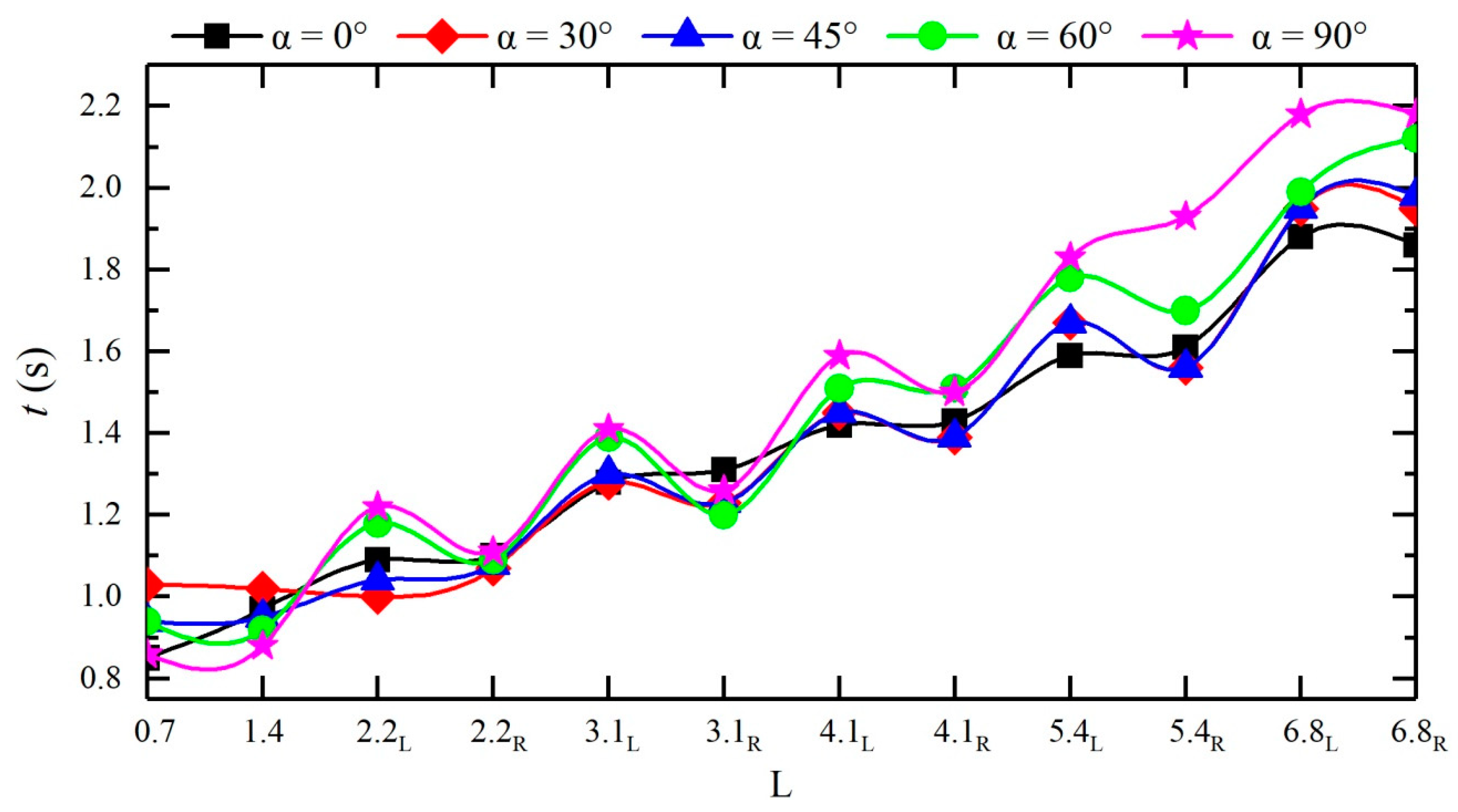
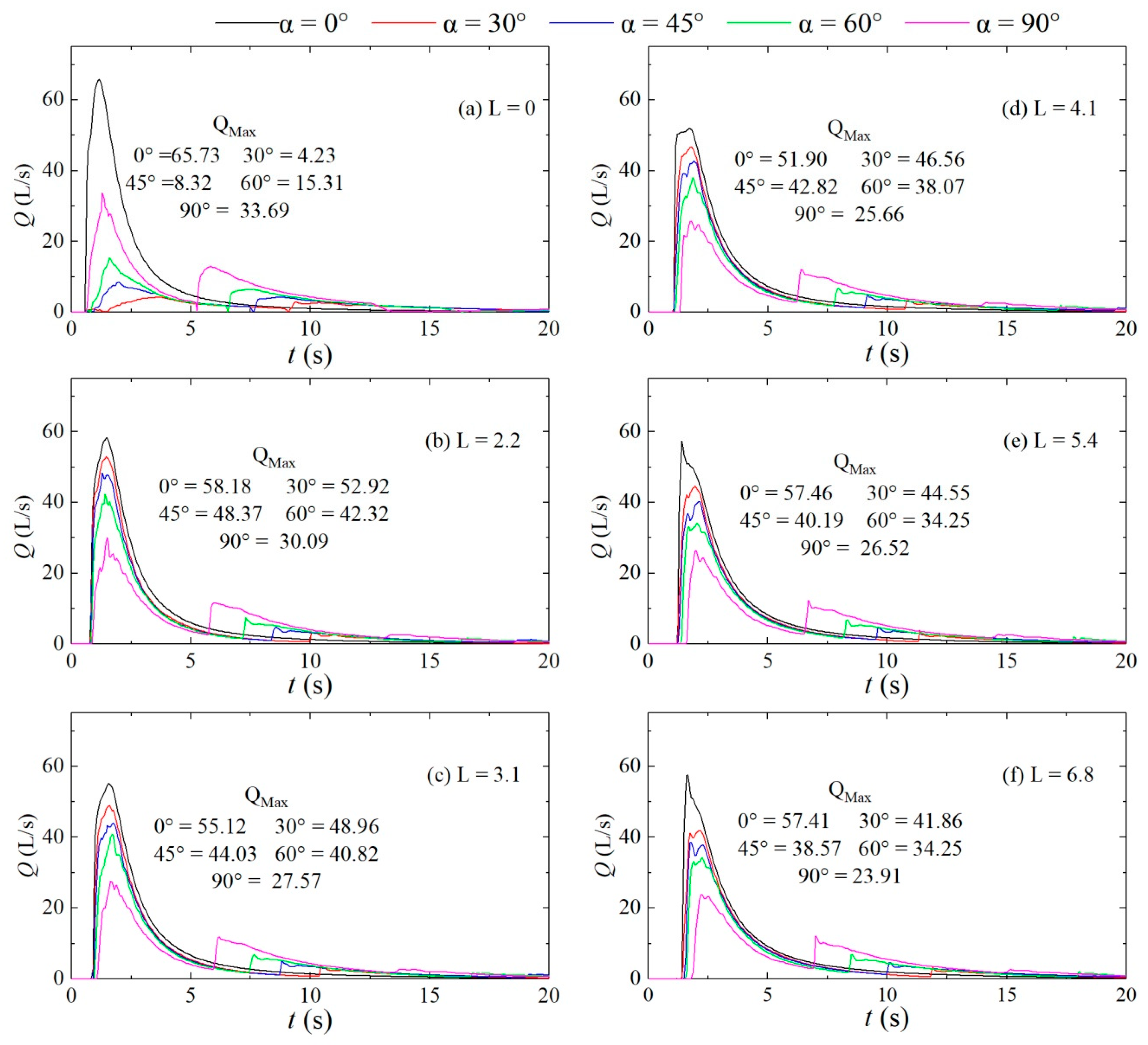
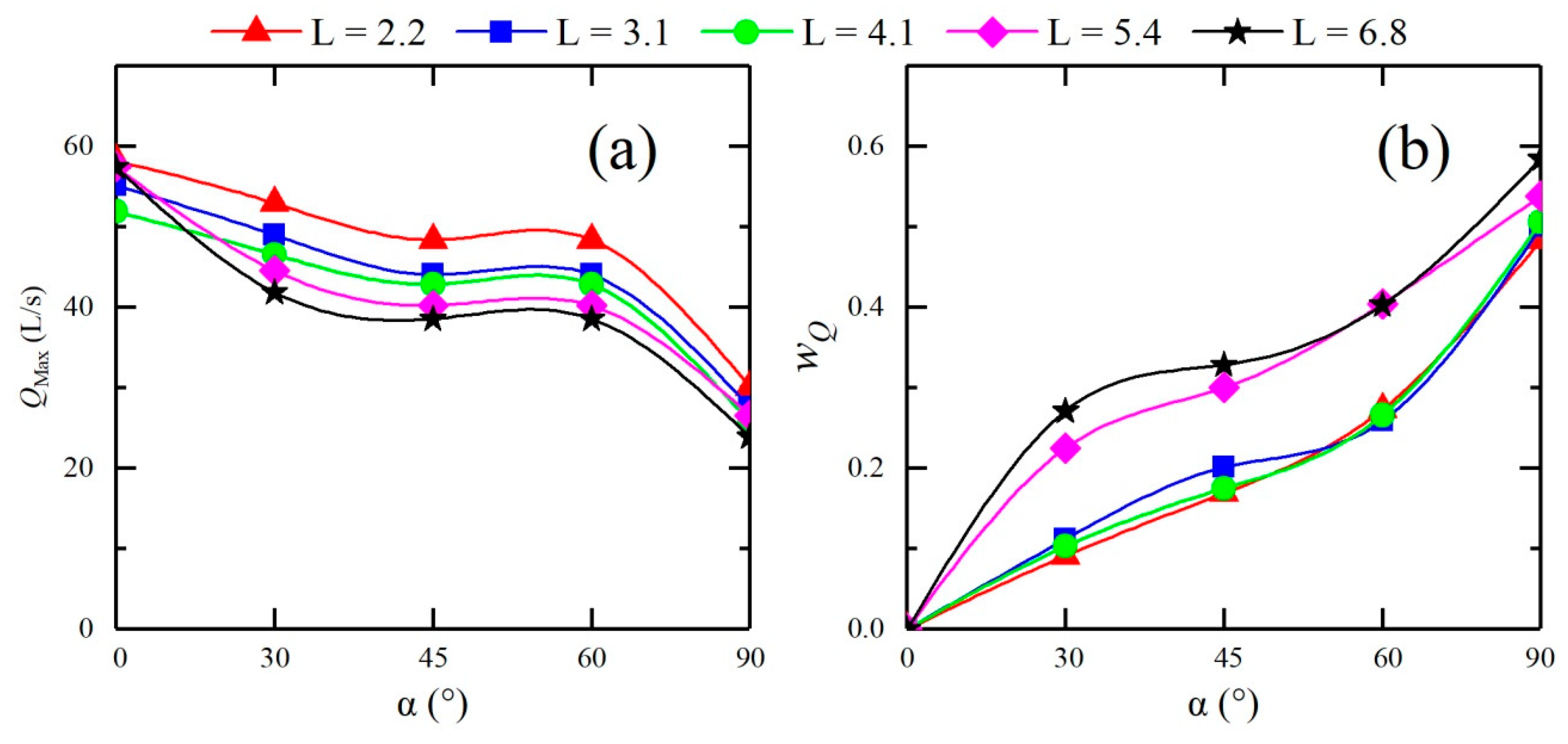
3.4. Flow Discharge
4. Conclusions
- (1)
- Compared with that of the straight channel, as the confluence angle increases, the maximum pressure at the confluence increases, the peak value point and flow impact point move upstream, and the impact point of the downstream straight section moves upstream.
- (2)
- The flow regime is relatively turbulent at the confluence and is evenly distributed in the downstream straight section. Additionally, the flow velocity at the inlet of the confluence section is relatively high, and the flow velocity at the flow impact location is lower than that at the inlet and in the downstream straight section; as the confluence angle increases, the flood impact point moves upstream, and the impact range decreases.
- (3)
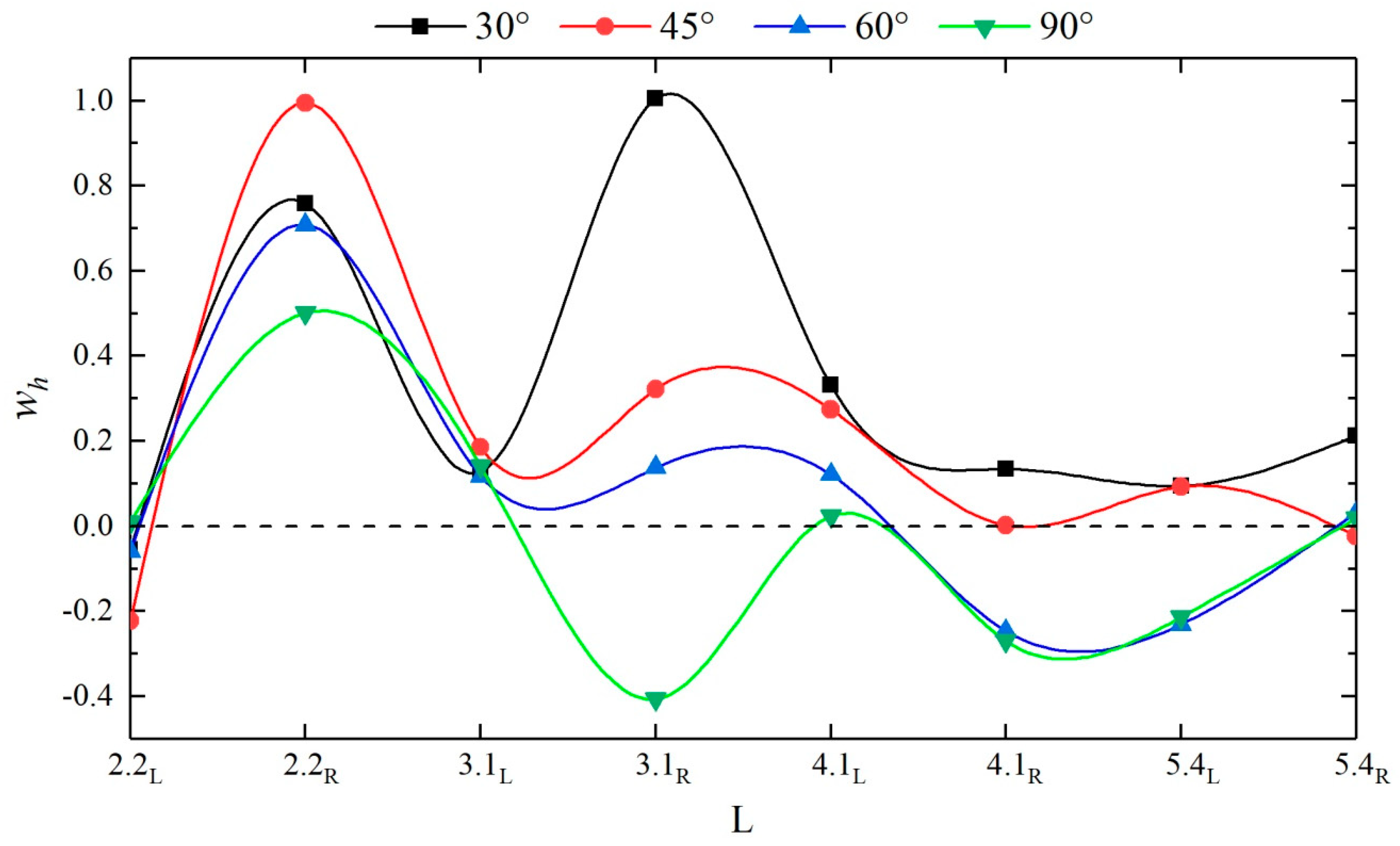
- A wave peak factor wh was introduced to reveal the influence of the confluence angle on the peak of the downstream straight section. The confluence angle increases the wave peaks at the measuring points by approximately 0.19% to 99.49%, and the smaller the confluence angle is, the more significant the enhancement effect is. In comparison, when the confluence angle has an abatement effect on the wave peak values, the reduction is in the range of approximately 1.82% to 40.70%, and the larger the confluence angle is, the greater the abatement effect is.
- (4)
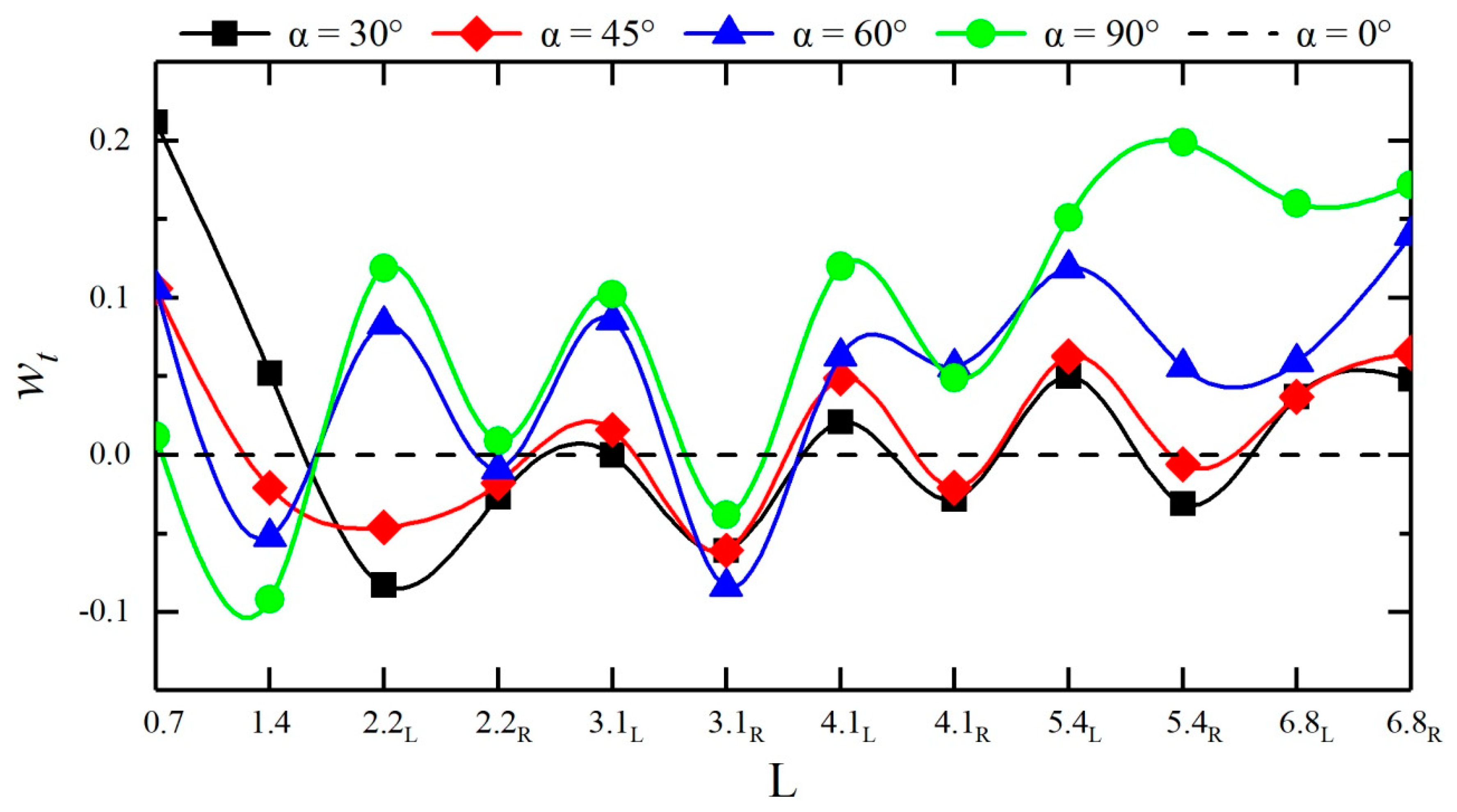
- A rise time retardation factor wt and a discharge peak reduction factor wQ were introduced to reveal the influence of the confluence angle on the dam-break flood routing. The larger the confluence angle is, the more pronounced the retardation effect on the dam-break flood routing is, and the greater the abatement effect on the peak flood discharge is. Compared with that of the straight channel, the flood arrival time is delayed by approximately 0.91% to 21.18%, and the flow discharge is reduced by approximately 9.05% to 58.36%.
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.H.; Li, G.B. Computational Research on the Flow Characteristics at the Confluences Reach of Main Stream and Tributary Stream. Master’s Thesis, Master of Science in Engineering, Nanjing Hydraulic Research Institute, Nanjing, China, July 2007. [Google Scholar]
- Yang, Z.Y.; Yang, Z.C. 3D Numerical Simulation of Hydraulic Characteristics in Confluence between Main Stream and Tributary. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, June 2013. [Google Scholar]
- Lauber, G.; Hager, W.H. Experiments to Dambreak Wave: Horizontal Channel. J. Hydraul. Res. 2010, 36, 291–307. [Google Scholar] [CrossRef]
- Lauber, G.; Hager, W.H. Experiments to Dambreak Wave: Sloping Channel. J. Hydraul. Res. 2010, 36, 761–773. [Google Scholar] [CrossRef]
- Marra, D.; Earl, T.; Ancey, C. Experimental Investigations of Dam Break Flows down an Inclined Channel. In Proceedings of the 34th International Association of Hydro-Environmental Engineering and Research, Brisbane, Australia, 26 June–1 July 2011; Volume 6, pp. 26–71. [Google Scholar]
- Von Hafen, H.; Goseberg, N.; Stolle, J.; Nistor, I. Gate-Opening Criteria for Generating Dam-Break Waves. J. Hydraul. Eng. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Soares Frazao, S.; Zech, Y. Dam Break in Channels with 90° Bend. J. Hydraul. Eng. 2002, 128, 956–968. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and Numerical Assessment of the Shallow Water Model for Two-Dimensional Dam-Break Type Problems. J. Hydraul. Res. 2010, 33, 843–864. [Google Scholar] [CrossRef]
- Macchione, F.; Morelli, M.A. Practical Aspects in Comparing Shock-Capturing Schemes for Dam Break Problems. J. Hydraul. Eng. 2003, 129, 187–195. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, J.; Li, T. Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data. Appl. Sci. 2018, 8, 2456. [Google Scholar] [CrossRef]
- Ghaitanellis, A. Modelling Flows Involving Highly Dynamic Interactions between Granular Material and Water with SPH. In Proceedings of the 38th IAHR World Congress, Panama, Panama, 1–6 September 2019; pp. 5052–5061. [Google Scholar]
- Liu, T.; Guo, W.; Zhan, L. Experimental Study of the Velocity Profile at 90°Open Channel Confluence. Adv. In Water Sci. 2009, 20, 485–489. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X.; Guo, W. Experimental Study on Flow Characteristics of Open Channel Confluence at Junction Angle 30°. J. Yangtze River Sci. Res. Inst. 2007, 24, 75–78. [Google Scholar] [CrossRef]
- Wang, C.H.; Li, G.C. The Modelling of Basin Flood. J. Hydraul. Eng. 1996, 3, 44–50. [Google Scholar] [CrossRef]
- Shi, A.; Teng, M.H.; Sou, I.M. Propagation of Long Water Waves through Branching Channels. J. Eng. Mech. 2005, 131, 859–871. [Google Scholar] [CrossRef]
- Marsooli, R.; Wu, W. 3-D Finite-Volume Model of Dam-Break Flow over Uneven Beds Based on VOF Method. Adv. Water Resour. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, J.P.; Zhang, J.M. Multispeed Lattice Boltzmann Model with Space-Filling Lattice for Transcritical Shallow Water Flows. Math. Probl. In Eng. 2017, 2017, 8917360. [Google Scholar] [CrossRef]
- Eaket, J.; Hicks, F.E.; Peterson, A.E. Use of Stereoscopy for Dam Break Flow Measurement. J. Hydraul. Eng. 2005, 131, 24–29. [Google Scholar] [CrossRef]
- Aleixo, R.; Soares-Frazao, S.; Zech, Y. Velocity-Field Measurements in a Dam-Break Flow Using a PTV Voronoi Imaging Technique. Exp. In Fluids 2010, 50, 1633–1649. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel Approach for Dam Break Flow Modeling Using Computational Intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Hosseini Boosari, S. Predicting the Dynamic Parameters of Multiphase Flow in CFD (Dam-Break Simulation) Using Artificial Intelligence-(Cascading Deployment). Fluids 2019, 4, 44. [Google Scholar] [CrossRef]
- Weber, L.J.; Schumate, E.D.; Mawer, N. Experiments on Flow at a 90° Open-Channel Junction. J. Hydraul. Eng. 2001, 127, 340–350. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Capart, H. Riemann Wave Description of Erosional Dam-Break Flows. J. Fluid Mech. 2002, 461, 183–228. [Google Scholar] [CrossRef]
- Soares-Frazao, S. Experiments of Dam-Break Wave Over a Triangular Bottom Sill. J. Hydraul. Res. 2010, 45, 19–26. [Google Scholar] [CrossRef]
- Soares Frazao, S.; Zech, Y. Experimental Study of Dam-Break Flow against an Isolated Obstacle. J. Hydraul. Res. 2010, 45, 27–36. [Google Scholar] [CrossRef]
- Kocaman, S.; Ozmen Cagatay, H. Investigation of Dam-Break Induced Shock Waves Impact on a Vertical Wall. J. Hydrol. 2015, 525, 1–12. [Google Scholar] [CrossRef]
- Yang, Q.; Lu, W.; Zhou, S.; Wang, X. Impact of Dissipation and Dispersion Terms on Simulations of Open-Channel Confluence Flow Using Two-Dimensional Depthaveragedmodel. Hydrol. Process. 2014, 28, 3230–3240. [Google Scholar] [CrossRef]
- Lan, B. The Comprehensive Analysis of the Special Property at the Tributary Junction of Mountain River. J. Chongqing Jiaotong Inst. 1998, 17, 91–96. [Google Scholar]
- Larocque, L.A.; Imran, J.; Chaudhry, M.H. 3D Numerical Simulation of Partial Breach Dam-Break Flow Using the LES and k–ϵ Turbulence Models. J. Hydraul. Res. 2013, 51, 145–157. [Google Scholar] [CrossRef]
- LaRocque, L.A.; Imran, J.; Chaudhry, M.H. Experimental and Numerical Investigations of Two-Dimensional Dam-Break Flows. J. Hydraul. Eng. 2013, 139, 569–579. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
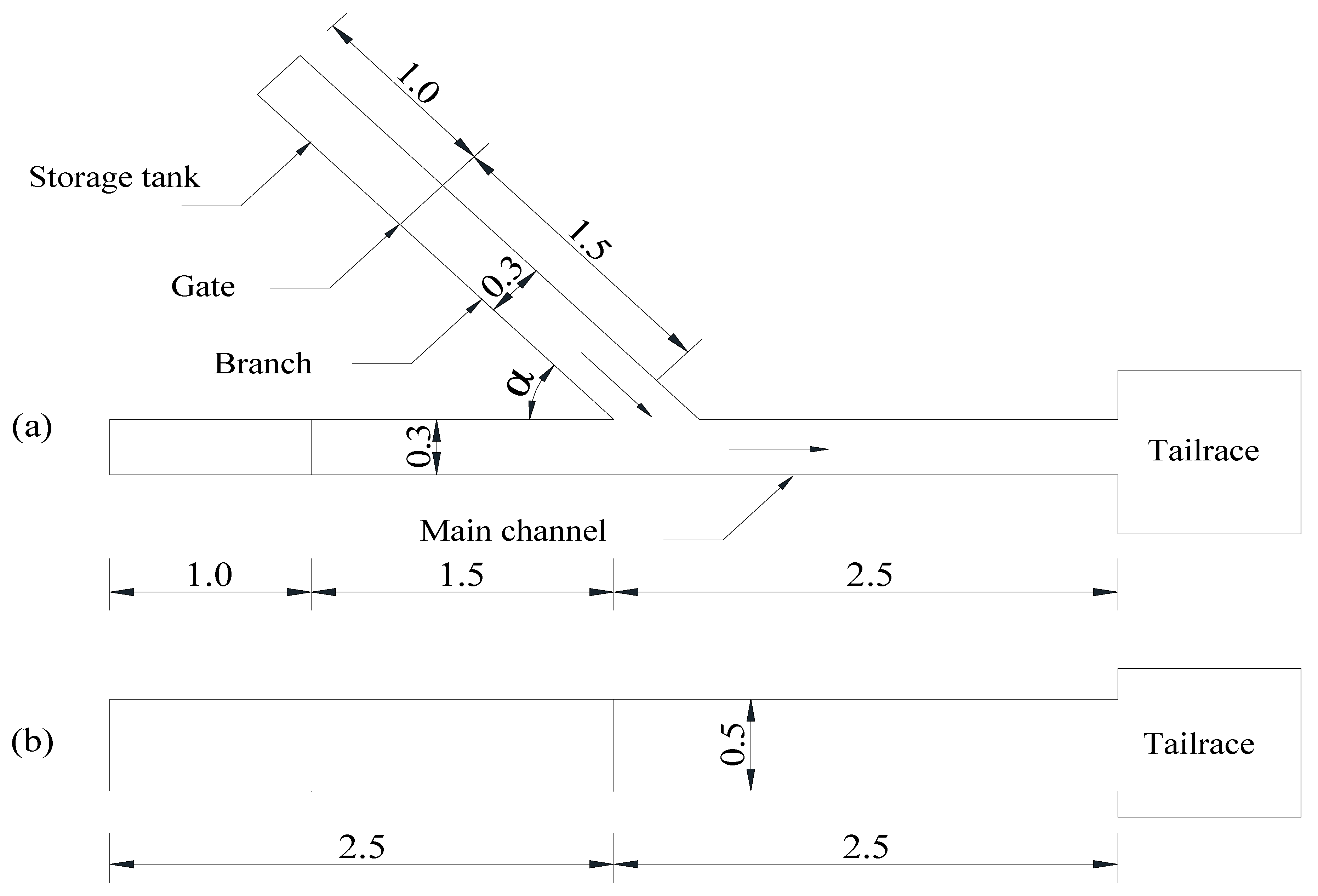
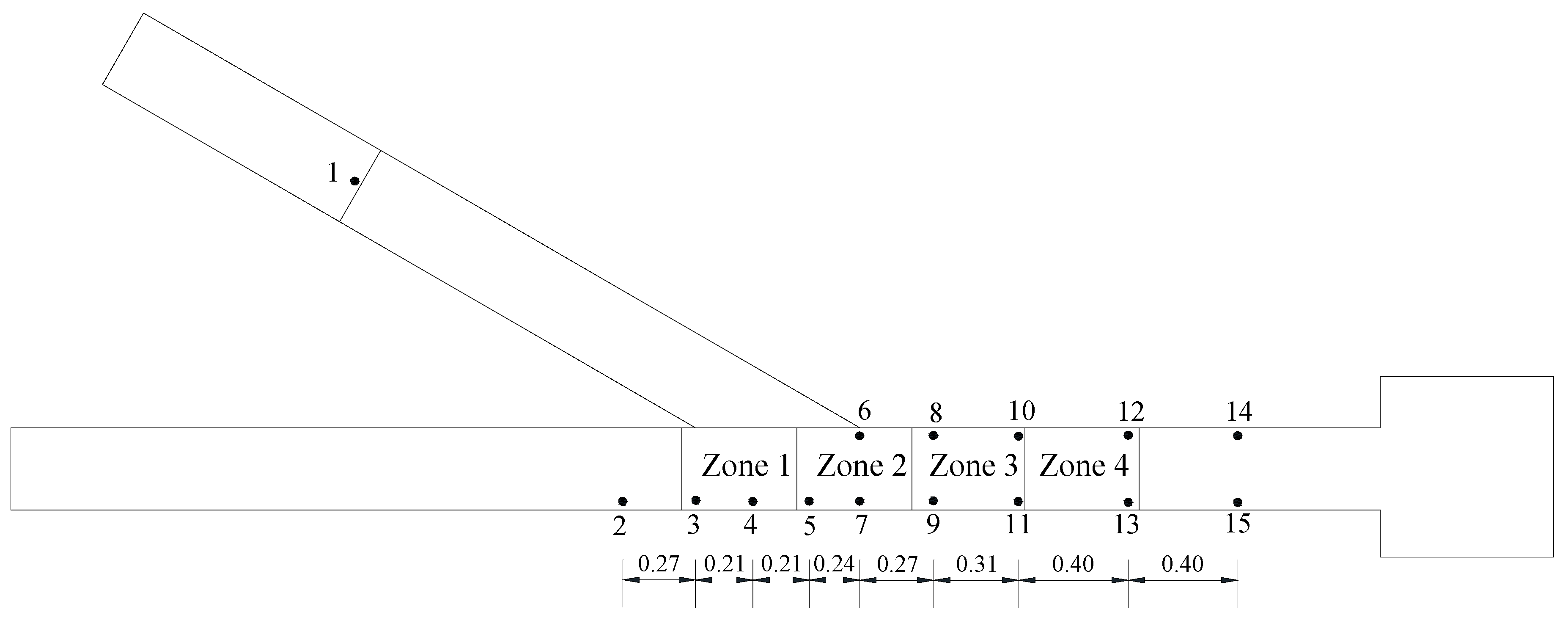
| Upstream Water Level | Confluence Angles | ||||
|---|---|---|---|---|---|
| 30° | 45° | 60° | 90° | 0° (Straight) | |
| 0.30 (m) | #1 | #2 | #3 | #4 | #5 |
| 0.40 (m) | #6 | #7 | #8 | #9 | #10 |
| 0.45 (m) | #11 | #12 | #13 | #14 | #15 |
| Baffles | 1 | 2 | 3 | 4 | 5 | 6 |
| L | 0 | 2.2 | 3.1 | 4.1 | 5.4 | 6.8 |
| Measuring Points | Confluence Angles | |||
|---|---|---|---|---|
| 30° | 45° | 60° | 90° | |
| #3 | 0.002 | 0.303 | 0.448 | 0.733 |
| #4 | 0.546 | 1.154 | 1.321 | 1.443 |
| #5 | 1.134 | 0.611 | 0.569 | 0.511 |
| #6 | 0.510 | 0.413 | 0.550 | 0.652 |
| #7 | 1.010 | 0.856 | 0.640 | 0.565 |
| #8 | 0.577 | 0.486 | 0.729 | 0.451 |
| #9 | 0.543 | 0.304 | 0.390 | 0.153 |
| #10 | 0.661 | 0.362 | 0.598 | 0.114 |
| #11 | 0.257 | 0.652 | 0.614 | 0.336 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Li, Y.; Tian, Z.; Fan, Q. On Dam-Break Flow Routing in Confluent Channels. Int. J. Environ. Res. Public Health 2019, 16, 4384. https://doi.org/10.3390/ijerph16224384
Chen S, Li Y, Tian Z, Fan Q. On Dam-Break Flow Routing in Confluent Channels. International Journal of Environmental Research and Public Health. 2019; 16(22):4384. https://doi.org/10.3390/ijerph16224384
Chicago/Turabian StyleChen, Sihan, Yingjin Li, Zhong Tian, and Qiang Fan. 2019. "On Dam-Break Flow Routing in Confluent Channels" International Journal of Environmental Research and Public Health 16, no. 22: 4384. https://doi.org/10.3390/ijerph16224384
APA StyleChen, S., Li, Y., Tian, Z., & Fan, Q. (2019). On Dam-Break Flow Routing in Confluent Channels. International Journal of Environmental Research and Public Health, 16(22), 4384. https://doi.org/10.3390/ijerph16224384





