Quick Analysis of Organic Amendments via Portable X-ray Fluorescence Spectrometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Portable X-ray Fluorescence (PXRF) Analysis
2.2. Samples
2.3. Statistical Data Analysis
3. Results and Discussion
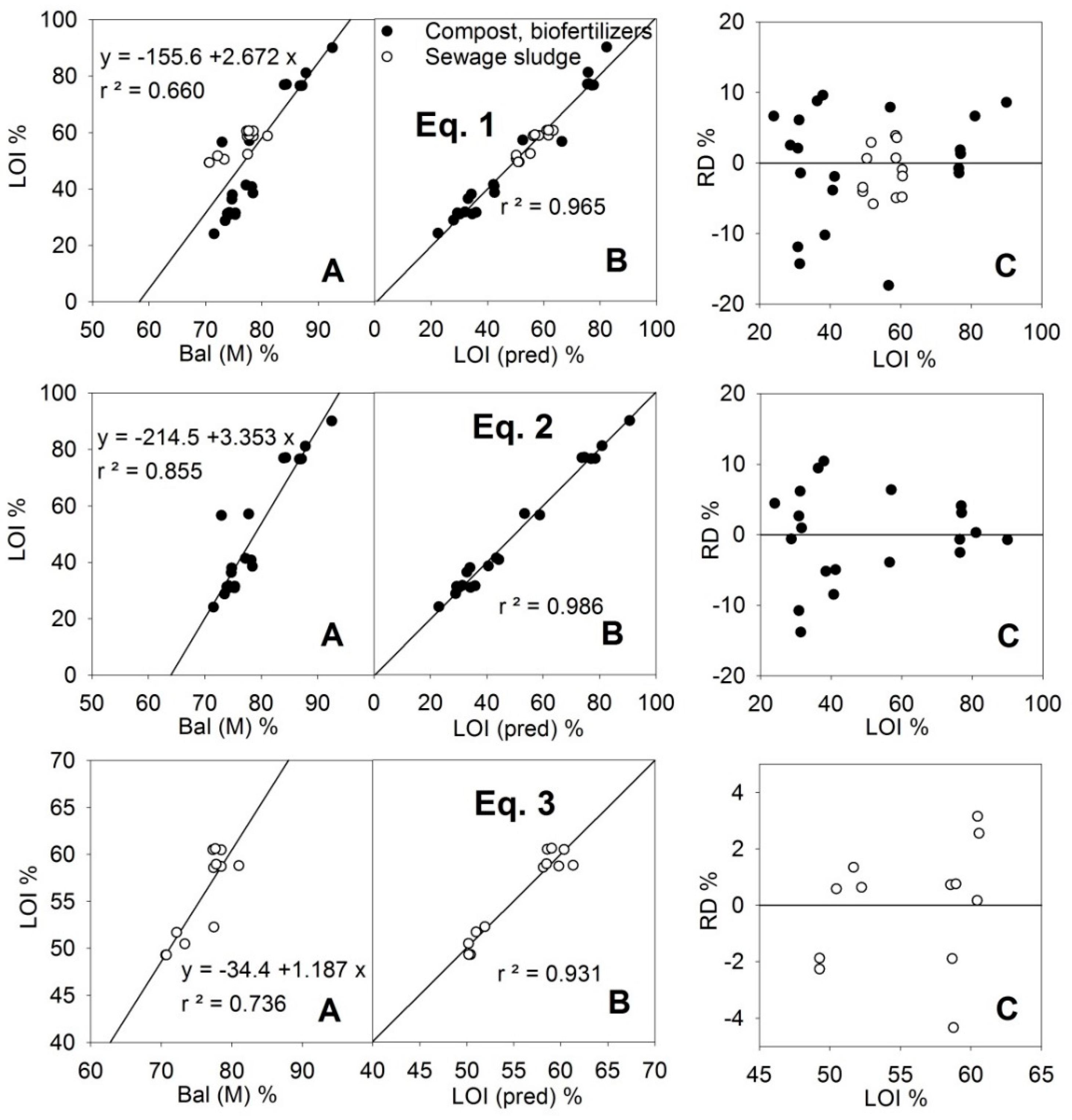
3.1. Loss on Ignition (LOI)
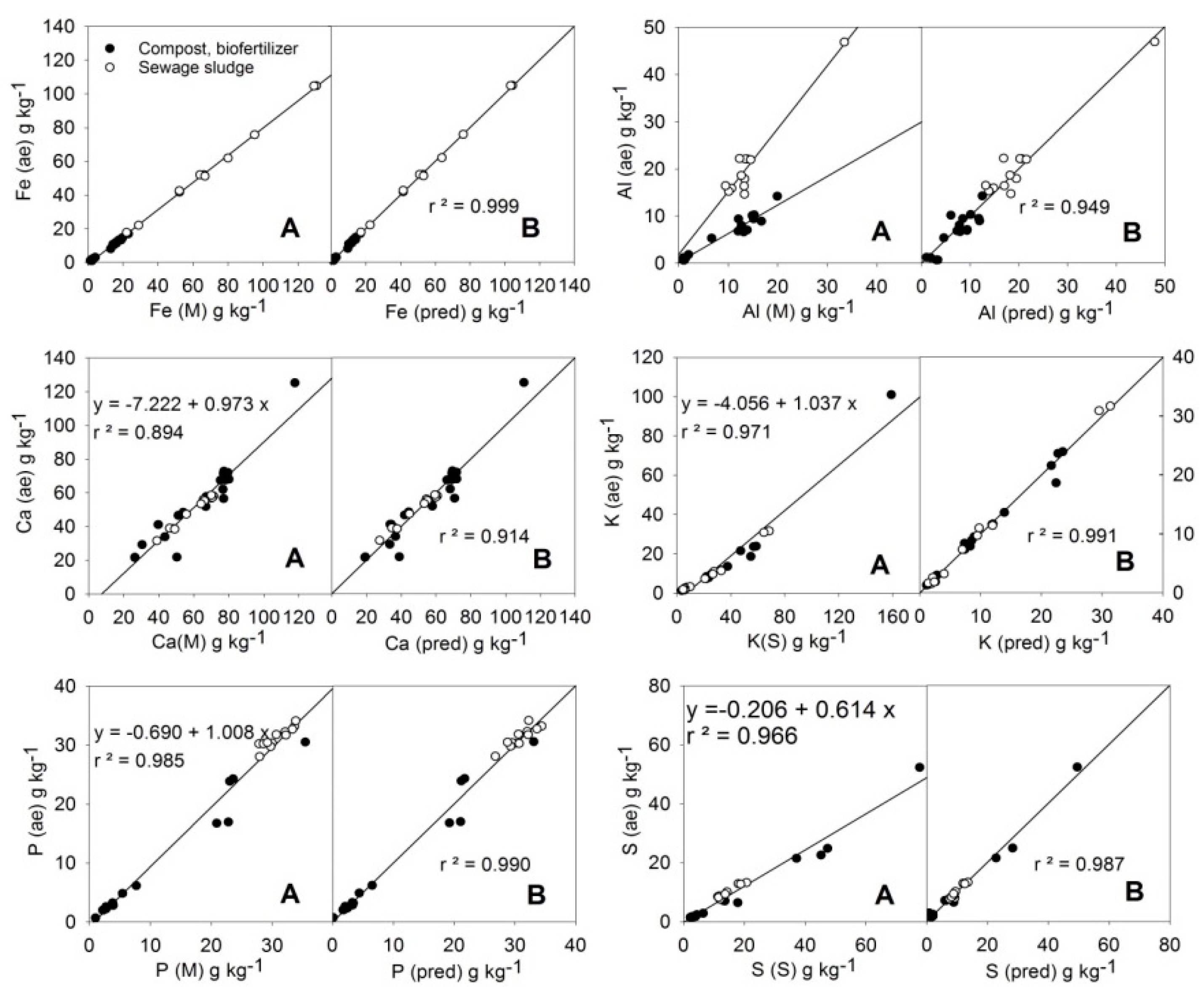
3.2. Macroelements (Fe, Al, Ca, K, P, S)
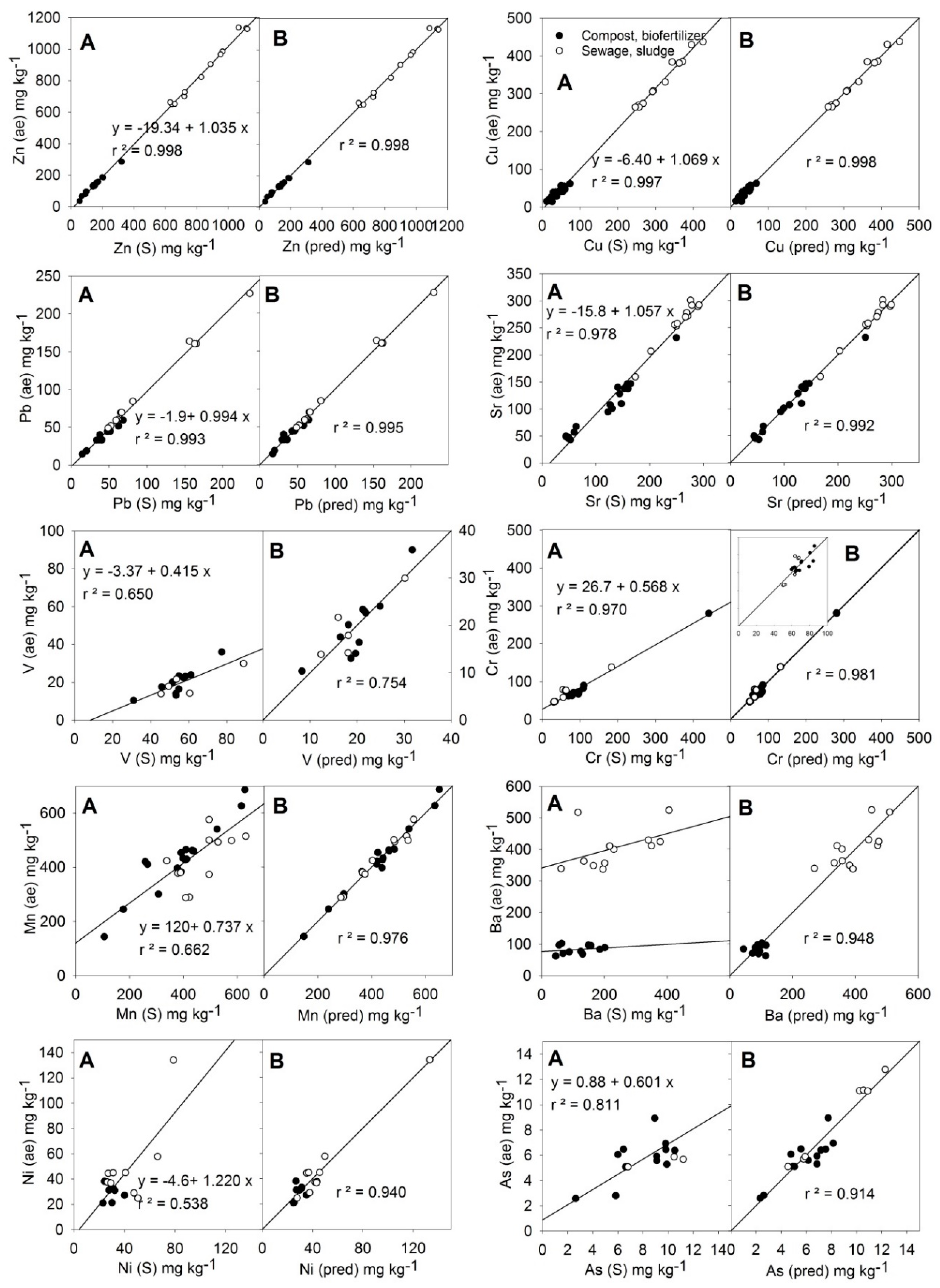
3.3. Trace Elements
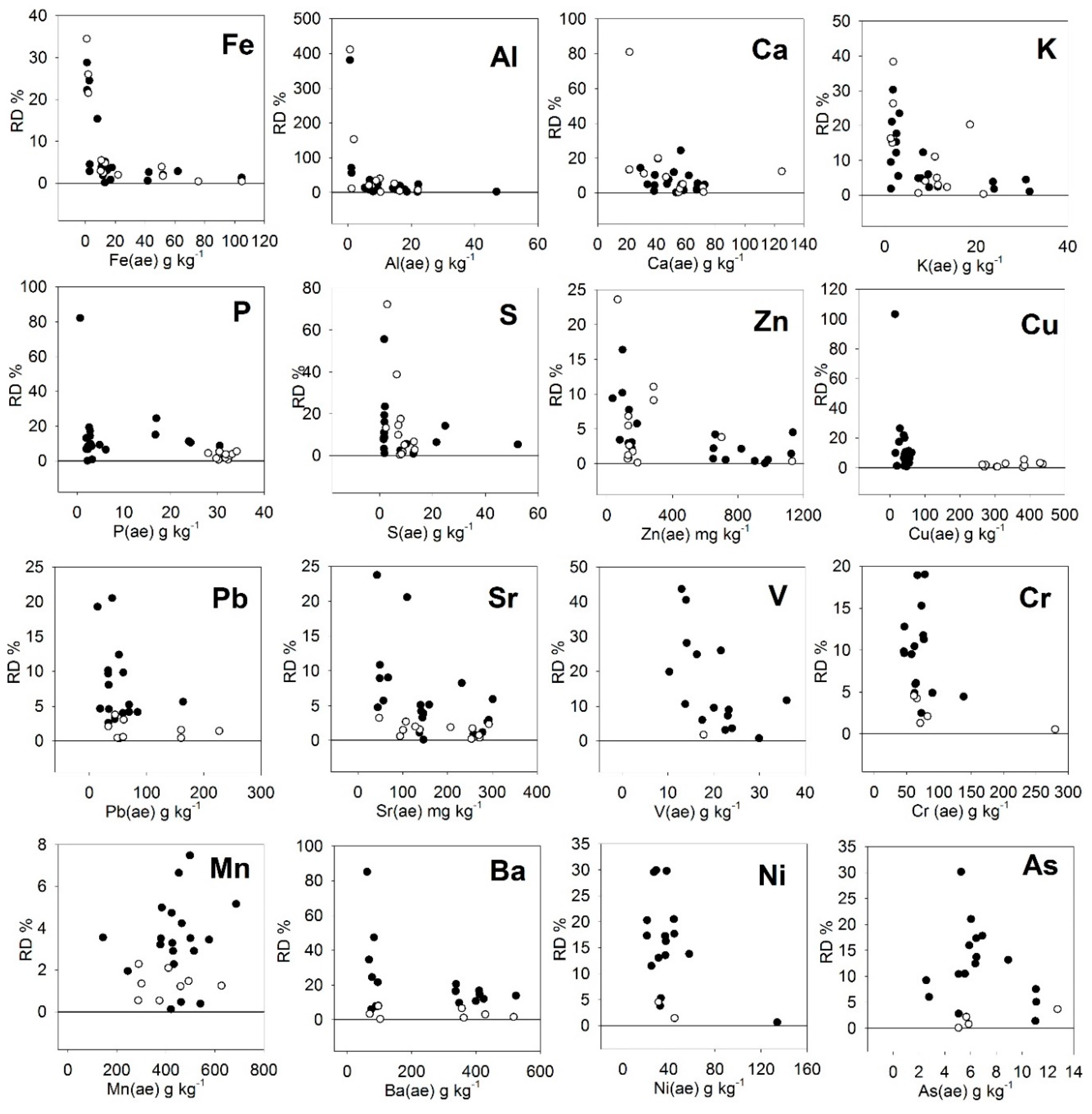
3.4. Deviations of Results
3.5. Practical Implications of this Study
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ICPMS | Inductively coupled plasma—Mass Spectrometry |
| ICP-OES | Inductively coupled plasma—Optical emission spectrometry |
| ISE | International Soil Exchange |
| LOI | Loss on ignition |
| MARSEP | Manure and Refuse Sample Exchange Programme |
| PXRF | Portable X-ray fluorescence |
| RD | Relative difference: difference, as percentage, between the predicted and actual values |
| RSD | Relative standard deviation |
References
- Martellozzo, F.; Landry, J.S.; Plouffe, D.; Seufert, V.; Rowhani, P.; Ramankutty, N. Urban agriculture: A global analysis of the space constraint to meet urban vegetable demand. Environ. Res. Lett. 2014, 9, 064025. [Google Scholar] [CrossRef]
- Meharg, A.A. Perspective: City farming needs monitoring. Nature 2016, 531, S60. [Google Scholar] [CrossRef] [PubMed]
- FAO. HABITAT III. Revised Zero Draft of the New Urban Agenda. In Proceedings of the United Nations Conference on Housing and Sustainable Urban Development, Quito, Ecuador, 18 June 2016. [Google Scholar]
- Pfeiffer, A.; Silva, E.; Colquhoun, J. Innovation in urban agricultural practices: Responding to diverse production environments. Renew. Agric. Food Syst. 2015, 30, 79–91. [Google Scholar] [CrossRef]
- Rogus, S.; Dimitri, C. Agriculture in urban and peri-urban areas in the United States: Highlights from the census of agriculture. Renew. Agric. Food Syst. 2015, 30, 64–78. [Google Scholar] [CrossRef]
- Pearson, L.J.; Pearson, L.; Pearson, C.J. Sustainable urban agriculture: Stocktake and opportunities. Int. J. Agric. Sustain. 2010, 8, 7–19. [Google Scholar] [CrossRef]
- Johnson, M.S.; Lathuillière, M.J.; Tooke, T.R.; Coops, N.C. Attenuation of urban agricultural production potential and crop water footprint due to shading from buildings and trees. Environ. Res. Lett. 2015, 10, 064007. [Google Scholar] [CrossRef]
- Mok, H.F.; Williamson, V.G.; Grove, J.R.; Burry, K.; Barker, S.F.; Hamilton, A.J. Strawberry fields forever? Urban agriculture in developed countries: A review. Agron. Sustain. Dev. 2014, 34, 21–43. [Google Scholar] [CrossRef]
- Alloway, B.J. Contamination of soils in domestic gardens and allotments: A brief overview. Land Contam. Reclam. 2004, 12, 179–187. [Google Scholar] [CrossRef]
- Wei, B.; Yang, L. A review of heavy metal contaminations in urban soils, urban road dusts and agricultural soils from China. Microchem. J. 2010, 94, 99–107. [Google Scholar] [CrossRef]
- Young, K.E.; Evans, C.A.; Hodges, K.V.; Bleacher, J.E.; Graff, T.G. A review of the handheld X-ray fluorescence spectrometer as a tool for field geologic investigations on Earth and in planetary surface exploration. Appl. Geochem. 2016, 72, 77–87. [Google Scholar] [CrossRef]
- Weindorf, D.C.; Bakr, N.; Zhu, Y. Advances in Portable X-ray Fluorescence (PXRF) for Environmental, Pedological, and Agronomic Applications. Adv. Agron. 2014, 128, 1–45. [Google Scholar]
- Shand, C.A.; Wendler, R. Portable X-ray fluorescence analysis of mineral and organic soils and the influence of organic matter. J. Geochem. Explor. 2014, 143, 31–42. [Google Scholar] [CrossRef]
- Li, F.; Lu, A.; Wang, J. Modeling of Chromium, Copper, Zinc, Arsenic and Lead Using Portable X-ray Fluorescence Spectrometer Based on Discrete Wavelet Transform. Intern. J. Environ. Res. Public Health 2017, 14, 1163. [Google Scholar] [CrossRef] [PubMed]
- EPA. Method 6200: Field Portable X-ray Fluorescence Spectrometry for the Determination of Elemental Concentrations in Soil and Sediment. Available online: https://www.epa.gov/sites/production/files/2015-12/documents/6200.pdf (accessed on 15 February 2019).
- ISO. Soil quality—Screening Soils for Selected Elements by Energy-Dispersive X-ray Fluorescence Spectrometry Using a Handheld or Portable Instrument. Available online: https://www.iso.org/standard/53490.html (accessed on 12 February 2019).
- Caporale, A.G.; Adamo, P.; Capozzi, F.; Langella, G.; Terribile, F.; Vingiani, S. Monitoring metal pollution in soils using portable-XRF and conventional laboratory-based techniques: Evaluation of the performance and limitations according to metal properties and sources. Sci. Total Environ. 2018, 643, 516–526. [Google Scholar] [CrossRef]
- Sharma, A.; Weindorf, D.C.; Wang, D.; Chakraborty, S. Characterizing soils via portable X-ray fluorescence spectrometer: 4. Cation exchange capacity (CEC). Geoderma 2015, 239–240, 130–134. [Google Scholar] [CrossRef]
- Manohara, B.; Belagali, S.L. Evaluation of energy dispersive scanning electron microscopy and X-ray fluorescence techniques for analysis of compost quality. Anal. Methods 2017, 9, 253–258. [Google Scholar] [CrossRef]
- Weindorf, D.C.; Sarkar, R.; Dia, M.; Haggard, B.; McWhirt, A.; Wooten, A.; Wang, H.; Chang, Q. Correlation of X-ray Fluorescence Spectrometry and Inductively Coupled Plasma Atomic Emission Spectroscopy for Elemental Determination in Composted Products. Compost Sci. Util. 2008, 16, 79–82. [Google Scholar] [CrossRef]
- Weindorf, D.C.; Chakraborty, S.; Li, B.; Deb, S.; Singh, A.; Kusi, N.Y. Compost salinity assessment via portable X-ray fluorescence (PXRF) spectrometry. Waste Manag. 2018, 78, 158–163. [Google Scholar] [CrossRef]
- McWhirt, A.; Weindorf, D.C.; Zhu, Y. Rapid analysis of elemental concentrations in compost via portable x-ray fluorescence spectrometry. Compost Sci. Util. 2012, 20, 185–193. [Google Scholar] [CrossRef]
- Havukainen, J.; Hiltunen, J.; Puro, L.; Horttanainen, M. Applicability of a field portable X-ray fluorescence for analyzing elemental concentration of waste samples. Waste Manag. 2019, 83, 6–13. [Google Scholar] [CrossRef]
- Healy, M.G.; Fenton, O.; Forrestal, P.J.; Danaher, M.; Brennan, R.B.; Morrison, L. Metal concentrations in lime stabilised, thermally dried and anaerobically digested sewage sludges. Waste Manag. 2016, 48, 404–408. [Google Scholar] [CrossRef] [PubMed]
- Houba, V.J.G.; Uittenbogaard, J.; Pellen, P. Wageningen Evaluating Programmes for Analytical Laboratories (WEPAL), organization and purpose. Commun. Soil Sci. Plant Anal. 1996, 27, 421–431. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). Soil Improvers and Growing Media—Extraction of Aqua Regia Soluble Elements, EN 13650; British Standards Institution: London, UK, 2001. [Google Scholar]
- European Committee for Standardization (CEN). Sludge, Treated Biowaste and Soil-Digestion of Aqua Regia Soluble Fractions of Elements, EN 16174; British Standards Institution: London, UK, 2012. [Google Scholar]
- Cofino, W.P.; Van Stokkum, I.H.M.; Wells, D.E.; Ariese, F.; Wegener, J.W.M.; Peerboom, R.A.L. A new model for the inference of population characteristics from experimental data using uncertainties. Application to interlaboratory studies. Chemom. Intell. Lab. Syst. 2000, 53, 37–55. [Google Scholar] [CrossRef]
- International Soil Analytical Exchange (ISE). Quarterlyy Report 2017.2; International Soil Analytical Exchange: Wageningen, The Netherlands, 2017. [Google Scholar]
- International Association of Geoanalysts. Reference Material Data Sheet SdAR-M2 Metal-Rich Sediment; International Association of Geoanalysts: Nottingham, UK, 2015. [Google Scholar]
- Wageningen Evaluating Programmes for Analytical Laboratories (WEPAL). MARSEP. Available online: http://www.wepal.nl/website/products/MARSEP.htm (accessed on 6 May 2019).
- Andrade, R.; Silva, S.H.G.; Weindorf, D.C.; Chakraborty, S.; Faria, W.M.; Mesquita, L.F.; Guilherme, L.R.G.; Curi, N. Assessing models for prediction of some soil chemical properties from portable X-ray fluorescence (pXRF) spectrometry data in Brazilian Coastal Plains. Geoderma 2020, 357, 113957. [Google Scholar] [CrossRef]
- Silva, S.H.G.; dos Santos Teixeira, A.F.; de Menezes, M.D.; Guilherme, L.R.G.; de Souza Moreira, F.M.; Curi, N. Multiple linear regression and random forest to predict and map soil properties using data from portable X-ray fluorescence spectrometer (pXRF). Ciênc. Agrotec. 2017, 41, 648–664. [Google Scholar] [CrossRef]
- MetcalfandEddy, I. Wastewater Engineering: Treatment, Disposal and Reuse, 3rd ed.; McGraw-Hill Ltd.: New Delhi, India, 1991. [Google Scholar]
- Nawar, S.; Delbecque, N.; Declercq, Y.; De Smedt, P.; Finke, P.; Verdoodt, A.; Van Meirvenne, M.; Mouazen, A.M. Can spectral analyses improve measurement of key soil fertility parameters with X-ray fluorescence spectrometry? Geoderma 2019, 350, 29–39. [Google Scholar] [CrossRef]
- Kabata-Pendias, A.; Pendias, H. Trace Elements in Soils ad Plants, 4th ed.; CRC Press: Boca Raton, FL, USA, 2011; p. 432. [Google Scholar]
- Thermo Scientific. Thermo Scientific. Thermo Scientific Niton XRF Analyzers, Certificate of Analysis. In Part Number 143-00131, Rev. D.; Thermo Scientific: Boston, MA, USA, 2016. [Google Scholar]
- European Union. Regulation (EU) 2019/1009 of the European Parliament and of the Council of 5 June 2019 Laying down Rules on the Making Available on the Market of EU Fertilising Products and Amending Regulations (EC) No 1069/2009 and (EC) No 1107/2009 and Repealing Regulation (EC) No 2003/2003. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32019R1009 (accessed on 17 July 2019).
- Tóth, T.; Kovács, Z.A.; Rékási, M. XRF-measured rubidium concentration is the best predictor variable for estimating the soil clay content and salinity of semi-humid soils in two catenas. Geoderma 2019, 342, 106–108. [Google Scholar] [CrossRef]
| Samples | Method Soil | Method Mining | ||||||
|---|---|---|---|---|---|---|---|---|
| N 1 | Min | Max | Mean | N 1 | Min | Max | Mean | |
| LOI 2 | 32 | 24.1 | 90.0 | 52.0 | ||||
| Bal 3 | 32 | 70.6 | 92.5 | 77.7 | ||||
| As | 20 | 2.6 | 18.5 | 9.8 | 14 | 4.7 | 10.0 | 7.2 |
| Ba | 23 | 45.4 | 406 | 177 | 24 | 79.5 | 489 | 244 |
| Cr | 21 | 30.4 | 441 | 94.0 | 25 | 92.6 | 326 | 170 |
| Cu | 31 | 12.0 | 426 | 150.6 | 27 | 29.2 | 768 | 294 |
| Mn | 28 | 106 | 631 | 418 | 27 | 105 | 680 | 312 |
| Mo | 23 | 3.2 | 22.7 | 5.2 | 10 | 2.9 | 16.2 | 5.0 |
| Ni | 18 | 23.0 | 78.6 | 36.8 | <LOD | <LOD | <LOD | |
| Pb | 25 | 14.3 | 236 | 69.8 | 24 | 12.9 | 240 | 66.3 |
| Rb | 32 | 8.7 | 59.9 | 26.8 | 32 | 4.3 | 38.0 | 17.2 |
| Sr | 32 | 44.2 | 292 | 170 | 32 | 44.6 | 296 | 172 |
| Ti | 32 | 68.5 | 4142 | 1664 | 32 | 97.7 | 2669 | 1200 |
| V | 16 | 31.0 | 88.8 | 56.0 | 24 | 42.5 | 157 | 82.7 |
| Zn | 32 | 55.5 | 1122 | 419 | 32 | 59.0 | 1364 | 502 |
| Zr | 32 | 4.46 | 128 | 59.3 | 32 | 3.8 | 120 | 51.7 |
| Al 4 | 30 | 1.0 | 33.5 | 11.4 | ||||
| Ca 4 | 32 | 33.6 | 145 | 79.2 | 32 | 26.4 | 118 | 61.0 |
| Cl 4 | 32 | 0.30 | 10.3 | 2.57 | ||||
| Fe 4 | 32 | 0.9 | 147 | 29.9 | 32 | 1.4 | 130 | 33.3 |
| K 4 | 32 | 3.74 | 159 | 28.5 | 32 | 2.56 | 94.9 | 15.9 |
| Mg 4 | 12 | 3.10 | 7.19 | 4.33 | ||||
| P 4 | 32 | 1.01 | 35.4 | 17.1 | ||||
| S 4 | 32 | 2.22 | 77.6 | 14.6 | 32 | 3.64 | 92.8 | 18.0 |
| Si 4 | 32 | 4.08 | 159 | 59.2 | ||||
| Equation | p Values | Paired t-test | ||||||
|---|---|---|---|---|---|---|---|---|
| p(A) | p(B) | p(C) | p(D) | r | Mean | Sd 4 | ||
| (1) 2,3 | 0.000 | 0.000 | 0.000 | 0.982 | 52.0 | 3.31 | ||
| (2) | 0.000 | 0.000 | 0.000 | 0.000 | 0.993 | 49.8 | 2.53 | |
| (3) | 0.000 | 0.000 | 0.019 | 0.965 | 55.8 | 1.24 | ||
| Cert 1 | Mining | Soil | ||||||
|---|---|---|---|---|---|---|---|---|
| Value | Value | sd 2 | RD(%) 3 | Value | sd 2 | RD(%) 3 | ||
| Fe | ISE 859 | 42.0 | 46.4 | 1.9 | 10.6 | 37.7 | 0.1 | −10.2 |
| SdAR_M2 | 18.4 | 18.5 | 0.1 | 0.3 | 13.9 | 0.1 | −24.3 | |
| Al | ISE 859 | 55.3 | 37.5 | 0.1 | −32.2 | - | - | - |
| SdAR_M2 | 66.0 | 46.8 | 0.5 | −29.0 | - | - | - | |
| Ca | ISE 859 | 33.9 | 35.0 | 0.0 | 3.1 | 39.5 | 0.2 | 16.6 |
| SdAR_M2 | 6.00 | 5.72 | 0.1 | −4.7 | 5.45 | 0.0 | -8.7 | |
| K | ISE 859 | 15.3 | 12.3 | 0.0 | −19.2 | 18.5 | 0.0 | 21.5 |
| SdAR_M2 | 41.5 | 32.7 | 0.3 | −21.2 | 40.1 | 0.2 | -8.7 | |
| P | ISE 859 | 4.08 | 4.09 | 0.03 | 0.3 | - | - | - |
| SdAR_M2 | 0.35 | 0.58 | 0.11 | 68.3 | - | - | - | |
| S | ISE 859 | 11.7 | 17.9 | 0.1 | 53.4 | 11.5 | 0.5 | −1.1 |
| SdAR_M2 | 0.97 | 1.56 | 0.04 | 60.6 | 1.19 | 0.08 | 22.6 | |
| Si | ISE 859 | 213.0 | 167.5 | 0.3 | −21.3 | - | - | - |
| SdAR_M2 | 343.3 | 304.5 | 1.1 | −11.3 | - | - | - | |
| Mg | ISE 859 | 8.42 | 5.42 | 0.45 | −35.7 | - | - | - |
| SdAR_M2 | 2.95 | - | - | - | - | - | - | |
| Equation 1 | p Values | ||||||
|---|---|---|---|---|---|---|---|
| p(B) | p(C) | p(D) | r | Mean 2 | N 4 | ||
| (4) | 0.000 | 0.005 | 1.000 | 25.9 | 32 | ||
| (5) | 0.000 | 0.000 | 0.974 | 12.0 | 30 | ||
| (6) | 0.000 | 0.017 | 0.956 | 52.1 | 32 | ||
| (7) | 0.000 | 0.000 | 0.000 | 0.995 | 9.53 | 31 | |
| (8) | 0.000 | 0.001 | 0.995 | 16.6 | 32 | ||
| (9) 3 | 0.000 | 0.001 | 0.011 | 0.994 | 8.30 | 31 | |
| Paired Differences | 99% CID 3 | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Sd 1 | sEM 2 | Lower | Upper | t | Df 4 | Sig 5 | |
| Fe | 0.000 | 0.77 | 0.14 | −0.37 | 0.37 | 0.000 | 31 | 1.000 |
| Al | 0.000 | 2.17 | 0.40 | −1.09 | 1.09 | 0.000 | 29 | 1.000 |
| Ca | 0.000 | 6.52 | 1.15 | −3.16 | 3.16 | 0.000 | 31 | 1.000 |
| K | 0.000 | 1.34 | 0.24 | −0.66 | 0.66 | 0.000 | 30 | 1.000 |
| P | 0.000 | 1.37 | 0.24 | −0.67 | 0.67 | 0.000 | 31 | 1.000 |
| S | 0.000 | 1.13 | 0.20 | −0.56 | 0.56 | 0.000 | 30 | 1.000 |
| Zn | 0.000 | 0.77 | 0.14 | −0.37 | 0.37 | 0.000 | 31 | 1.000 |
| Cu | 0.000 | 7.53 | 1.30 | −3.58 | 3.58 | 0.000 | 30 | 1.000 |
| Pb | 0.000 | 3.72 | 0.74 | −2.08 | 2.08 | 0.000 | 24 | 1.000 |
| Sr | 0.000 | 7.74 | 1.37 | −3.76 | 3.76 | 0.000 | 31 | 1.000 |
| V | 0.000 | 3.32 | 0.83 | −2.45 | 2.45 | 0.000 | 15 | 1.000 |
| Cr | 0.000 | 6.82 | 1.49 | −4.24 | 4.24 | 0.000 | 20 | 1.000 |
| Mn | 0.000 | 17.7 | 3.35 | −9.27 | 9.27 | 0.000 | 27 | 1.000 |
| Ba | 0.000 | 39.0 | 8.13 | −22.9 | 22.9 | 0.000 | 22 | 1.000 |
| Ni | 0.000 | 6.14 | 1.44 | −4.20 | 4.20 | 0.000 | 17 | 1.000 |
| As | 0.000 | 1.08 | 0.24 | −0.69 | 0.69 | 0.000 | 19 | 1.000 |
| Equation 1 | p Values | ||||||
|---|---|---|---|---|---|---|---|
| p(B) | p(C) | p(D) | r | Mean 2 | N 4 | ||
| (10) | 0.000 | 0.999 | 414.7 | 32 | |||
| (11) | 0.000 | 0.004 | 0.999 | 154.6 | 31 | ||
| (12) | 0.000 | 0.005 | 0.998 | 67.5 | 25 | ||
| (13) | 0.000 | 0.000 | 0.996 | 164.0 | 32 | ||
| (14) | 0.000 | 0.035 | 0.868 | 19.8 | 16 | ||
| (15) | 0.000 | 0.005 | 0.991 | 80.1 | 21 | ||
| (16) | 0.000 0.000 | 0.000 0.000 | 0.000 | 0.988 | 428.2 | 28 | |
| (17) | 0.000 | 0.000 | 0.000 | 0.973 | 250.9 | 23 | |
| (18) | 0.000 | 0.000 | 0.000 | 0.970 | 40.3 | 18 | |
| (19) 3 | 0.000 | 0.058 ns | 0.921 | 6.80 | 20 | ||
| Rsd (%) 1 | Content for RSD < 20% 2 | EU Limit | Actual Values | |||
|---|---|---|---|---|---|---|
| n > 20% 3 | Average RD (%) | Average RD-n(%) 4 | ||||
| LOI 5 | 6.4 | 16.6 | 27 7 | 0 | 5.1 | 5.1 |
| Fe 5 | 3.0 | 3.9 | 6 | 7.4 | 3.1 | |
| Al 5 | 18.1 | 10.9 | 13 | 47.9 | 7.5 | |
| Ca 5 | 12.5 | 32.6 | 2 | 9.7 | 6.9 | |
| K 5 | 14.1 | 6.7 | 16.6 7 | 6 | 10.4 | 6.5 |
| P 5 | 8.3 | 6.9 | 8.7 7 | 2 | 9.8 | 6.9 |
| S 5 | 13.6 | 5.7 | 4 | 12.5 | 7.3 | |
| Zn 6 | 0.18 | 3.9 | 800 8 | 1 | 4.5 | 3.9 |
| Cu 6 | 4.9 | 37.7 | 300 8 | 3 | 9.8 | 5.5 |
| Pb 6 | 5.5 | 18.6 | 120 8 | 1 | 5.7 | 5.0 |
| Sr 6 | 4.7 | 38.7 | 2 | 4.6 | 3.4 | |
| V 6 | 16.8 | 16.6 | 5 | 15.4 | 7.6 | |
| Cr 6 | 8.5 | 34.1 | 0 | 8.1 | 8.1 | |
| Mn 6 | 4.1 | 88.5 | 0 | 3.1 | 3.1 | |
| Ba 6 | 15.5 | 195 | 6 | 16.2 | 8.2 | |
| Ni 6 | 15.2 | 30.7 | 50 8 | 5 | 14.8 | 10.5 |
| As 6 | 15.9 | 5.4 | 40 8 | 2 | 10.0 | 8.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Núñez, R.; Ajmal-Poley, F.; González-Pérez, J.A.; Bello-López, M.A.; Burgos-Doménech, P. Quick Analysis of Organic Amendments via Portable X-ray Fluorescence Spectrometry. Int. J. Environ. Res. Public Health 2019, 16, 4317. https://doi.org/10.3390/ijerph16224317
López-Núñez R, Ajmal-Poley F, González-Pérez JA, Bello-López MA, Burgos-Doménech P. Quick Analysis of Organic Amendments via Portable X-ray Fluorescence Spectrometry. International Journal of Environmental Research and Public Health. 2019; 16(22):4317. https://doi.org/10.3390/ijerph16224317
Chicago/Turabian StyleLópez-Núñez, Rafael, Fátima Ajmal-Poley, José A. González-Pérez, Miguel Angel Bello-López, and Pilar Burgos-Doménech. 2019. "Quick Analysis of Organic Amendments via Portable X-ray Fluorescence Spectrometry" International Journal of Environmental Research and Public Health 16, no. 22: 4317. https://doi.org/10.3390/ijerph16224317
APA StyleLópez-Núñez, R., Ajmal-Poley, F., González-Pérez, J. A., Bello-López, M. A., & Burgos-Doménech, P. (2019). Quick Analysis of Organic Amendments via Portable X-ray Fluorescence Spectrometry. International Journal of Environmental Research and Public Health, 16(22), 4317. https://doi.org/10.3390/ijerph16224317







