Estimation of the Spatial Suitability of Winter Tourism Destinations Based on Copula Functions
Abstract
1. Introduction
2. Materials and Methods
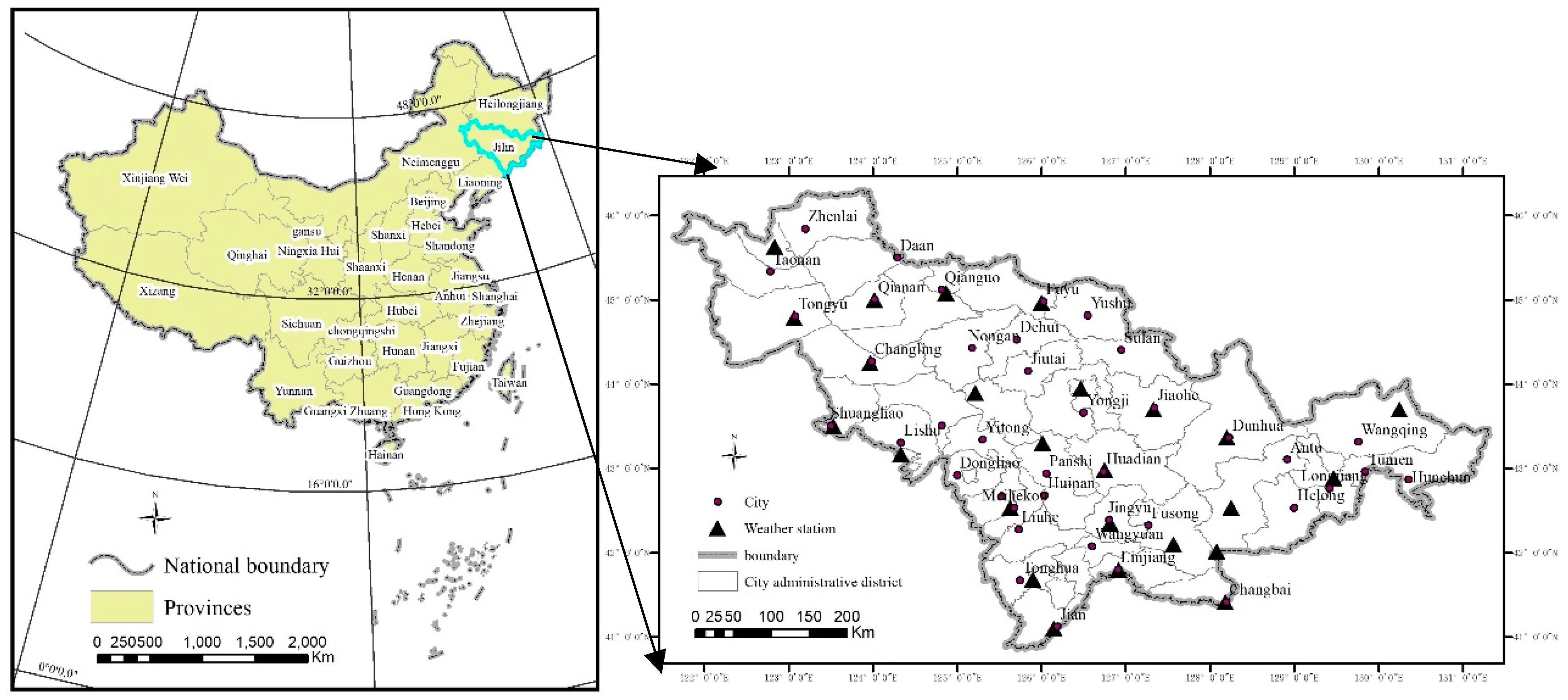
2.1. Study Area
2.2. Methods
2.2.1. Meteorological Suitability Index (MSI)
2.2.2. Snow Abundance Index (SAI)
2.2.3. Copula Function
- (1)
- ;
- (2)
- ;
- (3)
- For all and , .
3. Results
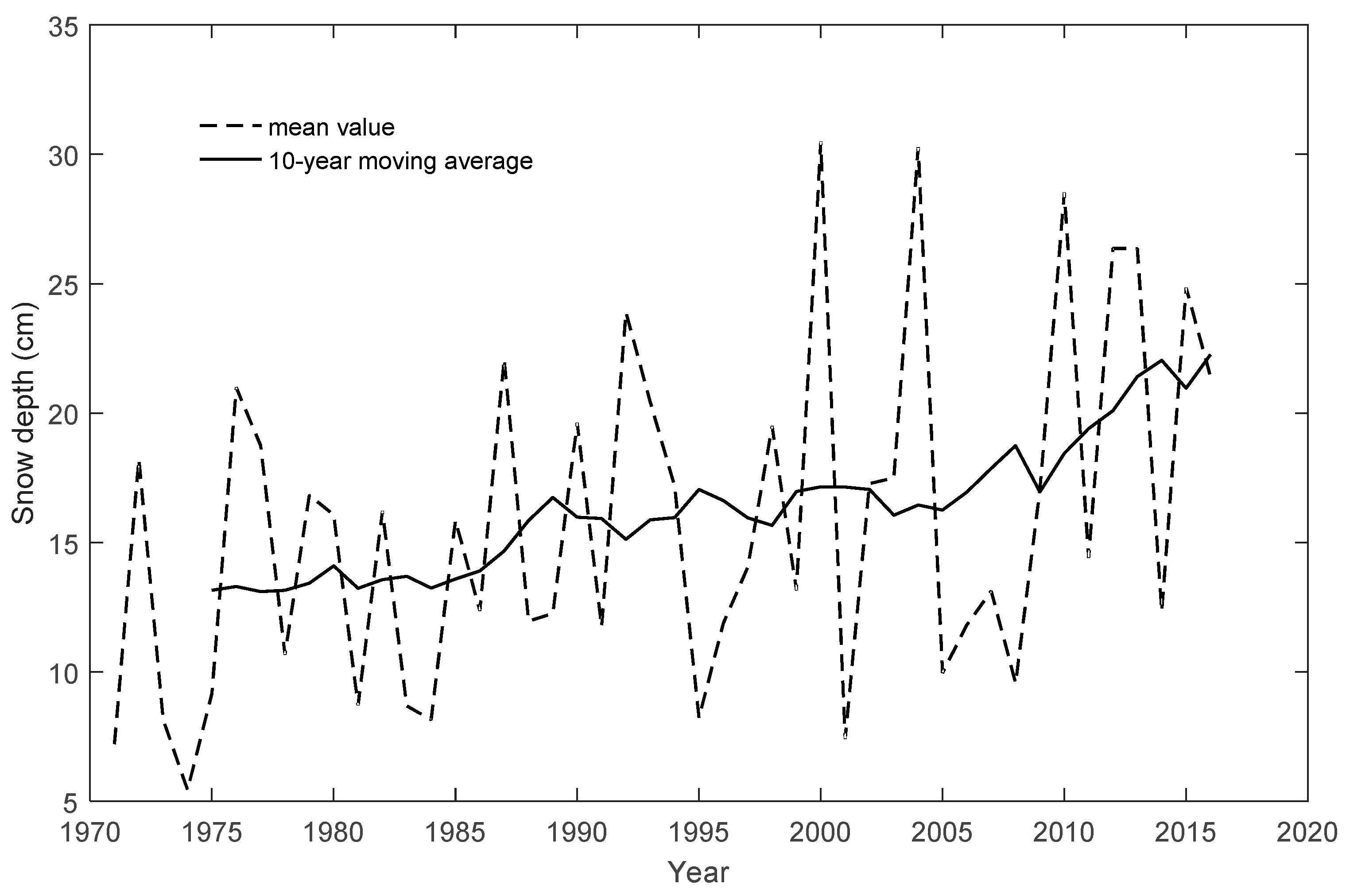
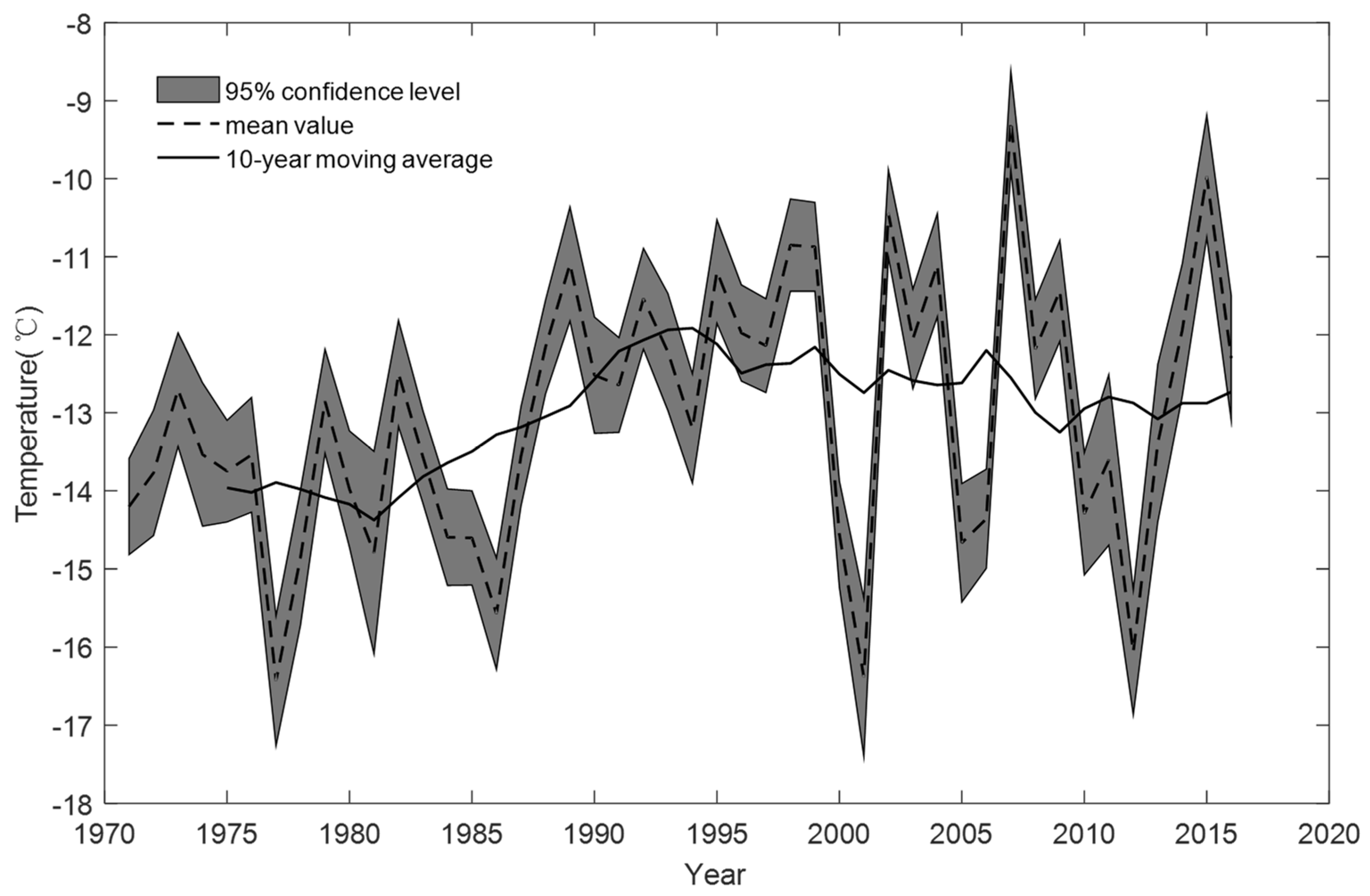
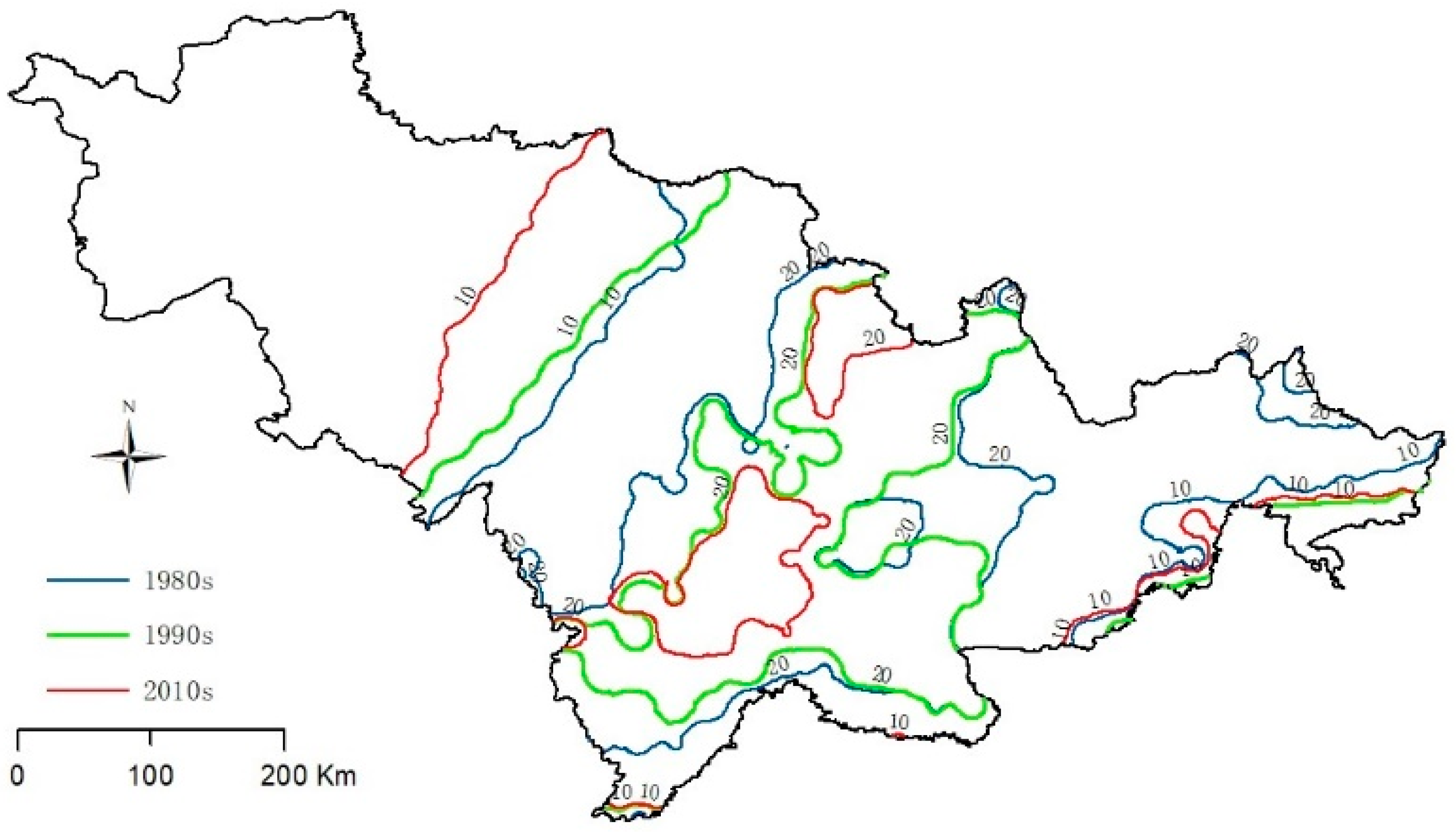
3.1. Changing Temperature and Snowfall under Climate Change
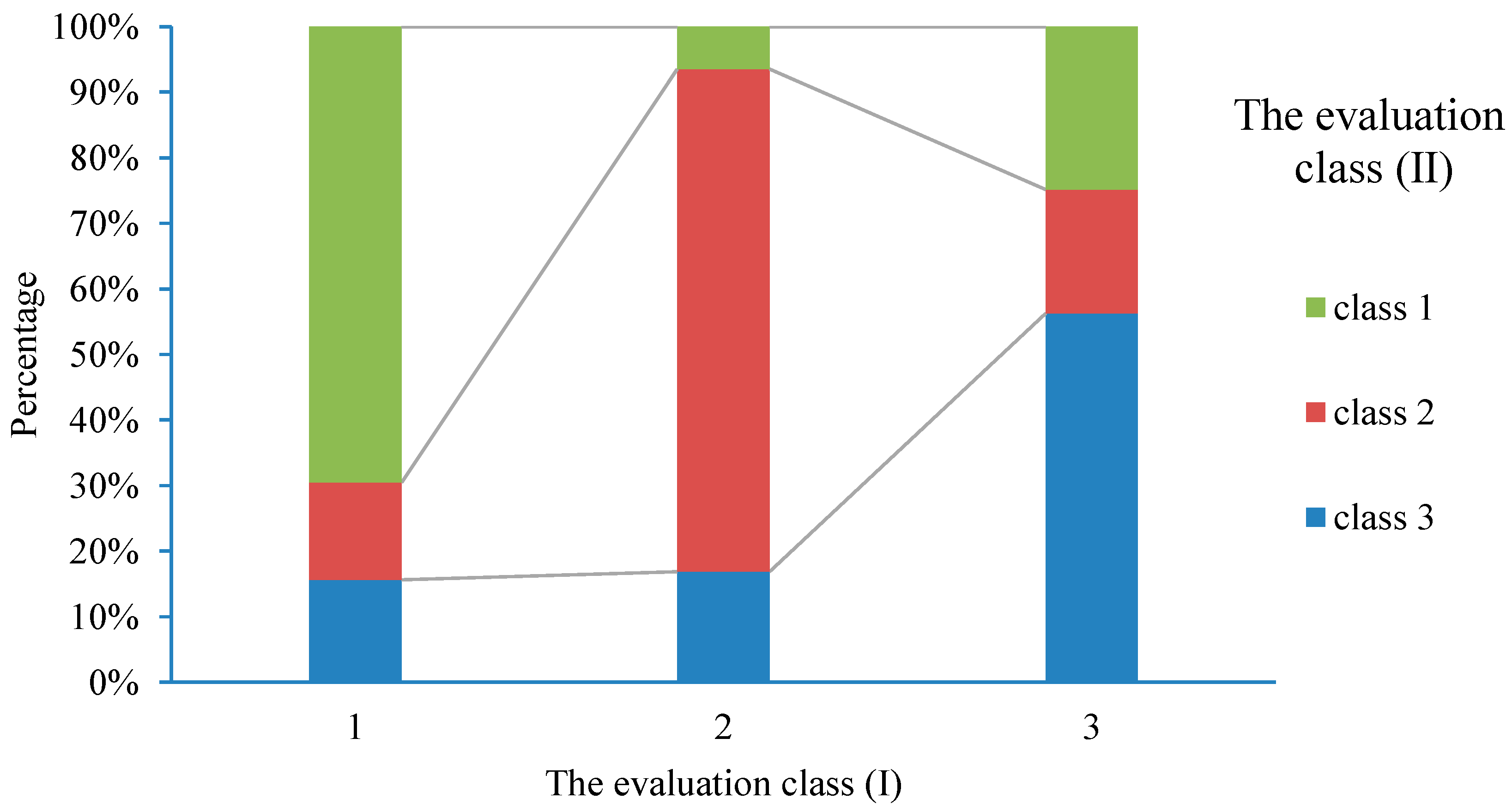
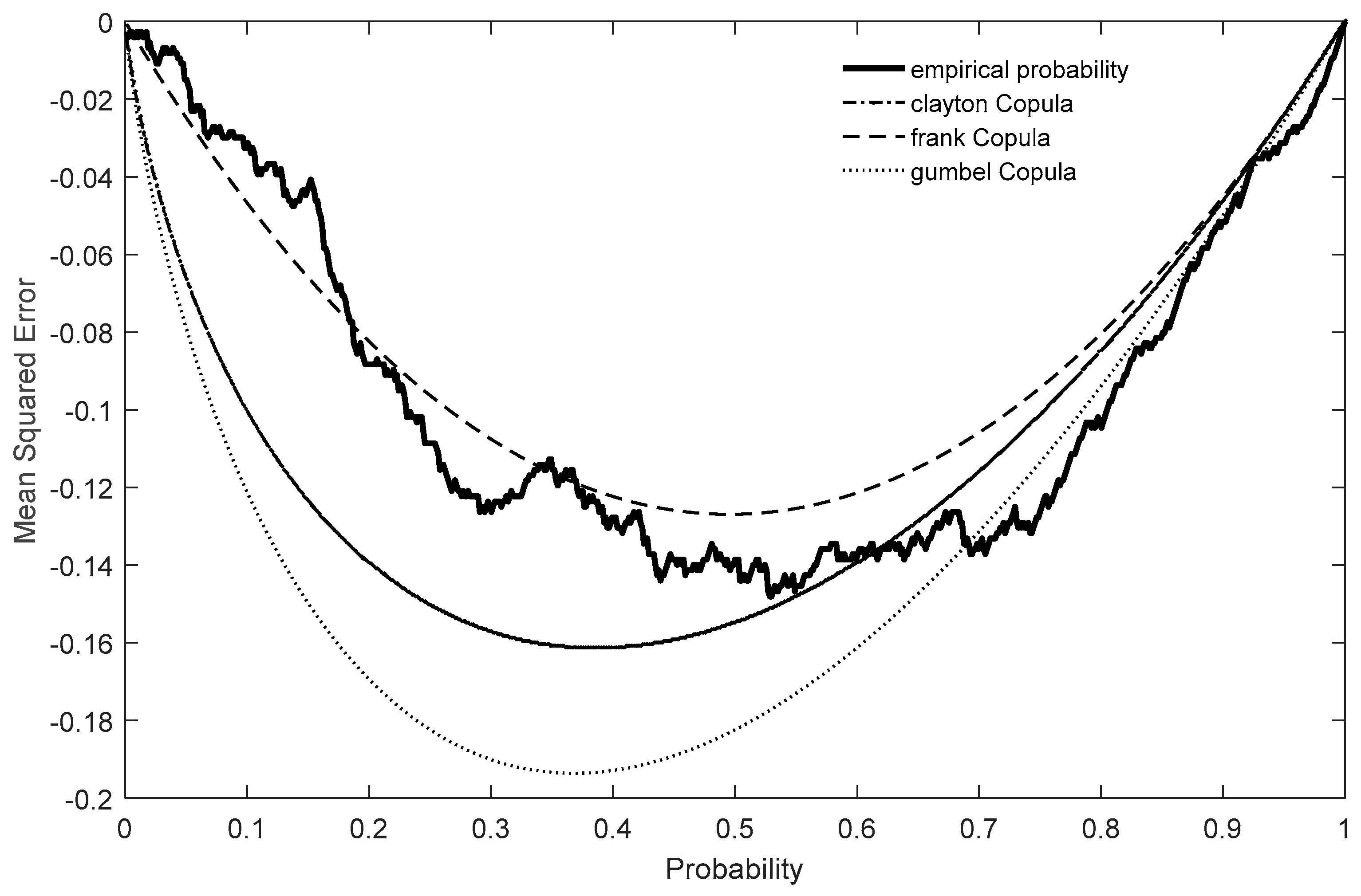
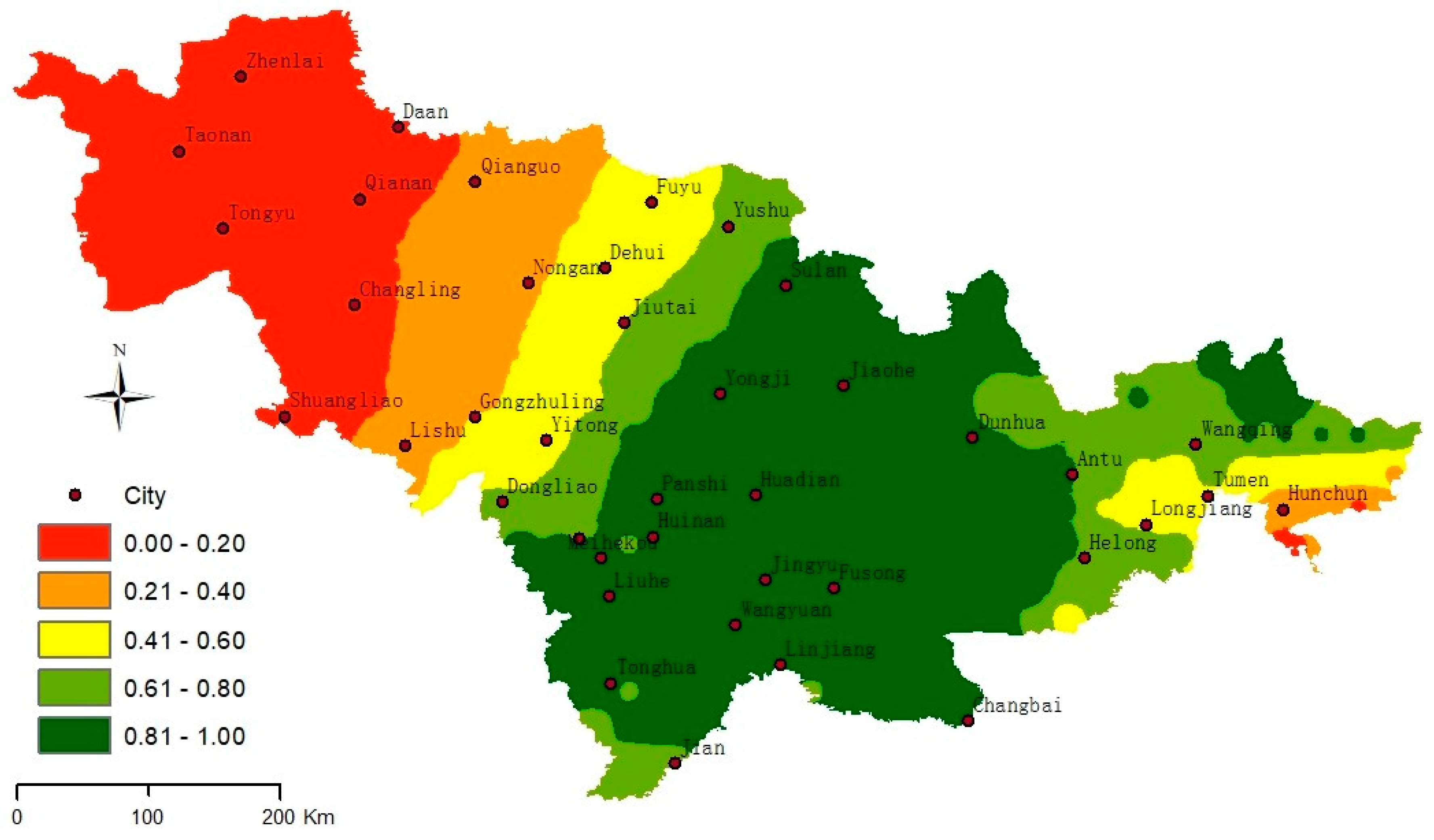
3.2. The SAI and SMI Joint Probability
4. Discussion
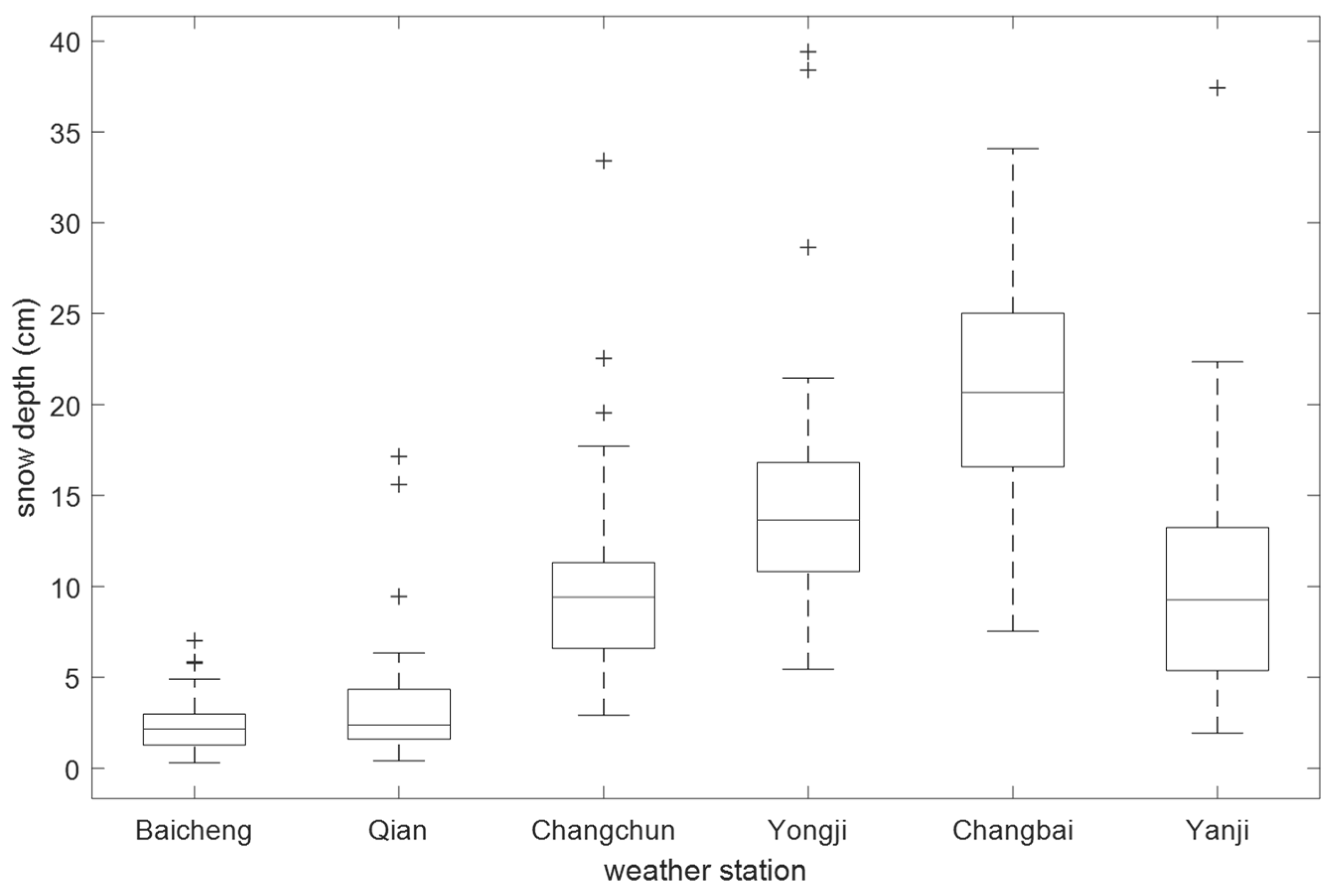
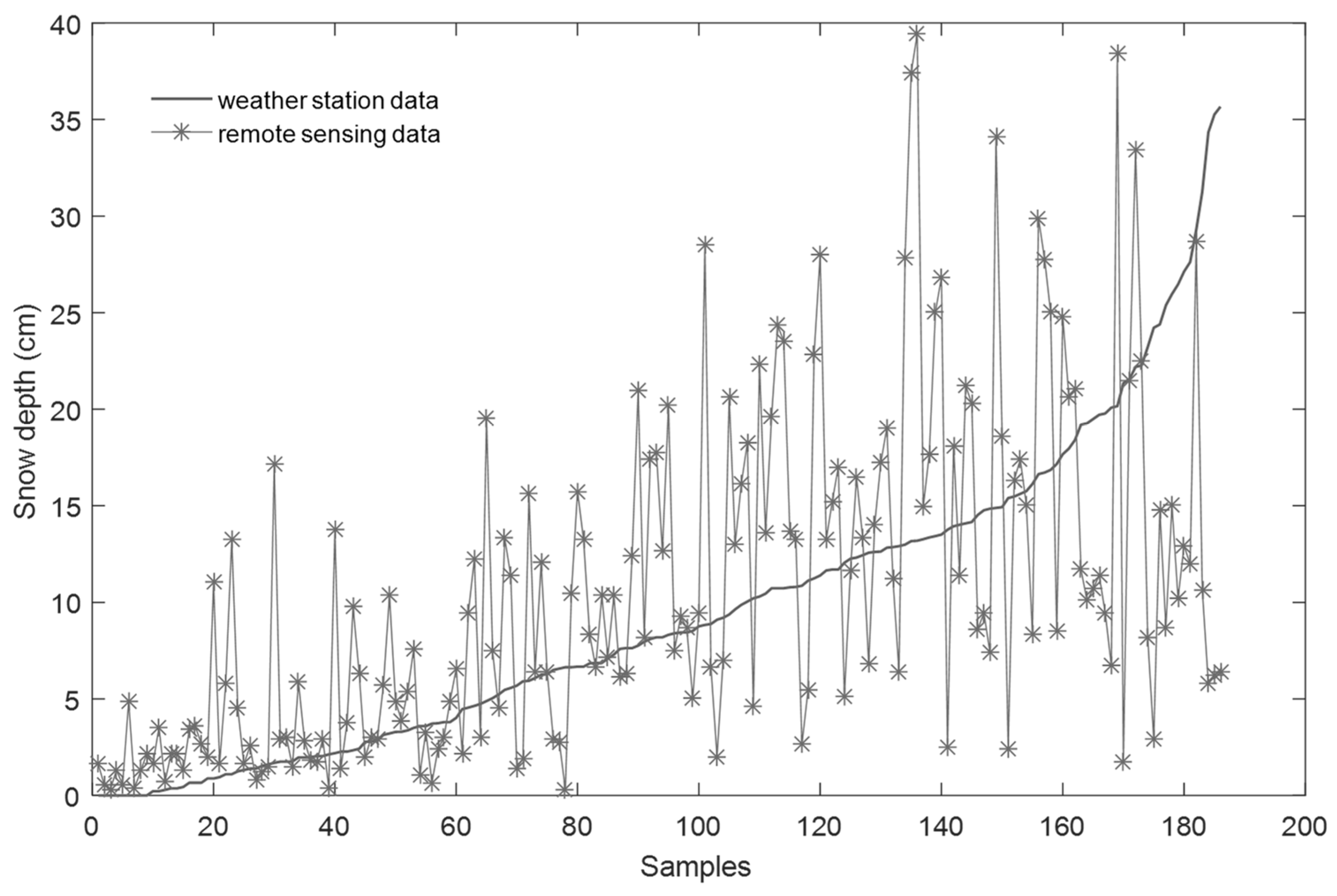
4.1. Spatial Snow DEPTH verification
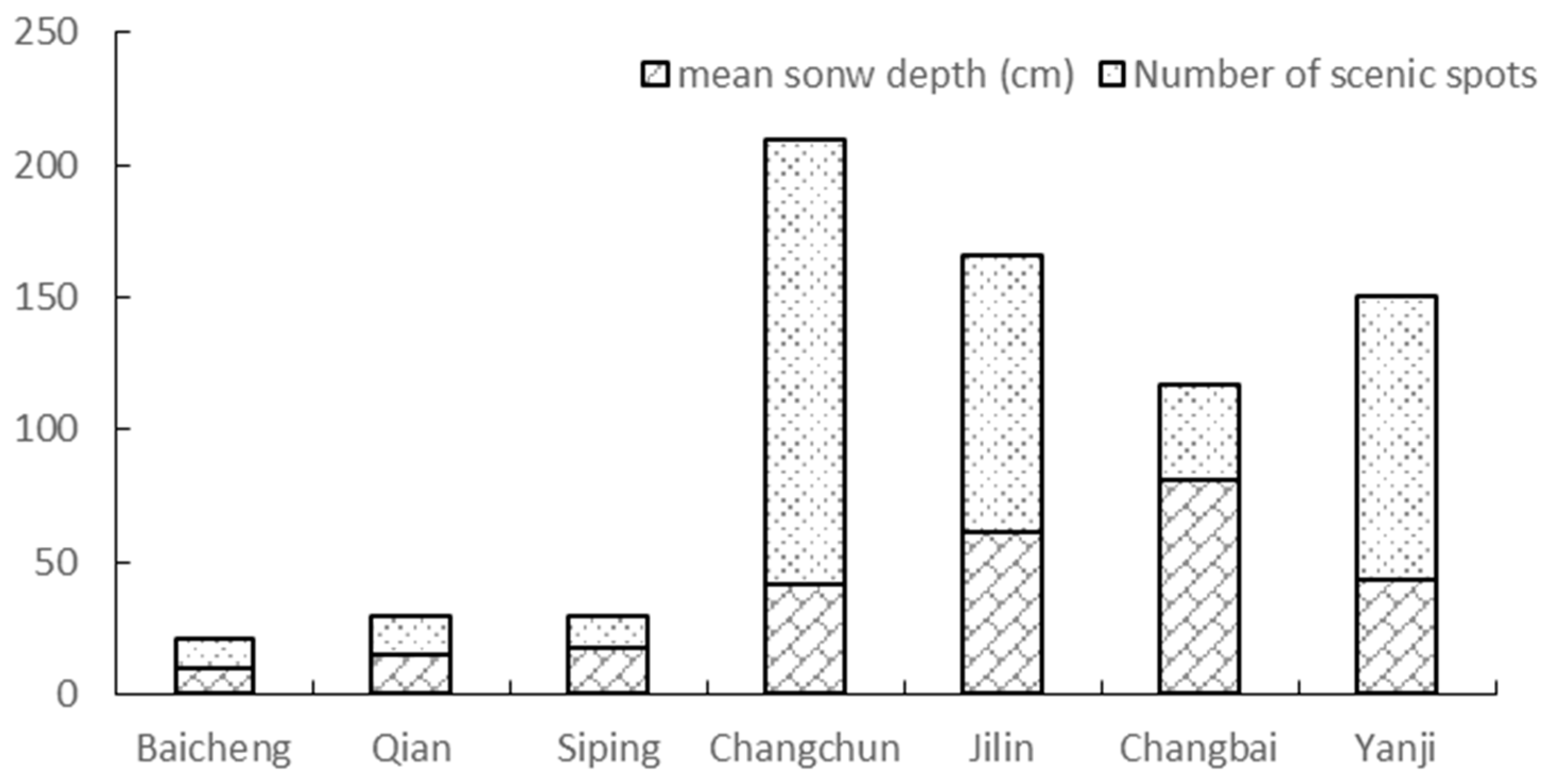
4.2. Winter Tourism Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Becken, S. The Importance of Climate and Weather for Tourism; Technical Report Lincoln University; Lincoln University: Christchurch, New Zealand, 2013. [Google Scholar]
- Falk, M. A dynamic panel data analysis of snow depth and winter tourism. Tourism Manag. 2010, 31, 912–924. [Google Scholar] [CrossRef]
- Schwirplies, C.; Ziegler, A. Adaptation of future travel habits to climate change-A micro econometric analysis of tourists from Germany. Tourism Econ. 2017, 23, 1275–1295. [Google Scholar] [CrossRef]
- Falk, M.; Lin, X. The declining dependence of ski lift operators on natural snow conditions. Tourism Econ. 2018, 24, 662–676. [Google Scholar] [CrossRef]
- Wu, B.; Wei, Q.H. White Book on Skiing Industry in China. 2017. Available online: https://www.wenzikong.cc (accessed on 15 August 2018).
- Scott, D.; Lemieux, C. Weather and climate information for tourism. Procedia Environ. Sci. 2010, 1, 146–183. [Google Scholar] [CrossRef]
- Cools, M.; Moons, E.; Wets, G. Assessing the impact of weather on traffic intensity. Weather Clim. Soc. 2010, 2, 60–68. [Google Scholar] [CrossRef]
- Conradt, S. Flexible weather index-based insurance design. Clim. Risk Manag. 2015, 10, 106–117. [Google Scholar] [CrossRef]
- Zhou, W.; Shi, J.; Haizhen, M.U. Climate change characteristics of winter temperature and precipitation in eastern china. Res. Sci. 2010, 32, 1088–1096. [Google Scholar]
- Damm, A.; Köberl, J.; Prettenthaler, F.; Töglhofer, C. Economic Impacts of Climate Change on Winter Tourism: Challenges for Ski Area Operators. EGU Gen. Assem. Conf. 2012, 14, 9287. [Google Scholar]
- Scott, D.; McBoyle, G.; Mills, B. Climate change and the skiing industry in southern Ontario (Canada): Exploring the importance of snowmaking as a technical adaptation. Clim. Res. 2003, 23, 171. [Google Scholar] [CrossRef]
- Laternser, M.; Schneebeli, M. Long-term snow climate trends of the Swiss Alps (1931–99). Int. J. Climatol. 2003, 23, 733–750. [Google Scholar] [CrossRef]
- Gajićčapka, M.; Srnec, L. Response of snow parameters relevant for winter tourism to climate change. In Proceedings of the International Congress of Biometeorology Harmony Within Nature Proceedings, Tokyo, Japan, 22–26 September 2008. [Google Scholar]
- Hoffmann, V.H.; Sprengel, D.C.; Ziegler, A.; Kolb, M.; Abegg, B. Determinants of corporate adaptation to climate change in winter tourism: An econometric analysis. Glob. Environ. Chang. 2009, 19, 256–264. [Google Scholar] [CrossRef]
- Dingeldey, A.; Soboll, A. The future impact of climate change on alpine winter tourism: A high-resolution simulation system in the German and Austrian alps. J. Sustain. Tourism 2012, 20, 101–120. [Google Scholar]
- Gonseth, C. Impact of snow variability on the Swiss winter tourism sector: Implications in an era of climate change. Clim. Chang. 2013, 119, 307–320. [Google Scholar] [CrossRef]
- Bonzanigo, L.; Giupponi, C.; Balbi, S. Sustainable tourism planning and climate change adaptation in the Alps: A case study of winter tourism in mountain communities in the Dolomites. J. Sustain. Tourism 2016, 24, 637–652. [Google Scholar] [CrossRef]
- Steiger, R. The impact of climate change on ski season length and snowmaking requirements in Tyrol. Aust. Clim. Res. 2010, 43, 251. [Google Scholar] [CrossRef]
- Pütz, M.; Gallati, D.; Kytzia, S.; Elsasser, H.; Lardelli, C.; Teich, M. Winter tourism, climate change, and snowmaking in the Swiss Alps: tourists’ attitudes and regional economic impacts. Mountain Res. Dev. 2011, 31, 357–362. [Google Scholar] [CrossRef]
- Rixen, C.; Teich, M.; Lardelli, C.; Gallati, D.; Pohl, M.; Pütz, M. Winter tourism and climate change in the Alps: An assessment of resource consumption, snow reliability, and future snowmaking potential. Mountain Res. Dev. 2011, 31, 229–236. [Google Scholar] [CrossRef]
- Koenig, U.; Abegg, B. Impacts of climate change on winter tourism in the Swiss Alps. J. Sustain. Tourism 1997, 5, 46–58. [Google Scholar] [CrossRef]
- Scott, D.; McBoyle, G. Climate change adaptation in the ski industry. Mitig. Adapt. Strat. Glob. Chang. 2007, 12, 1411. [Google Scholar] [CrossRef]
- Scott, D.; Dawson, J.; Jones, B. Climate change vulnerability of the US northeast winter recreation- tourism sector. Mitig. Adapt. Strat. Glob. Chang. 2008, 13, 577–596. [Google Scholar] [CrossRef]
- Winter, C. Tourism and climate change: Risks and opportunities. Ann. Tourism Res. 2008, 35, 614–616. [Google Scholar] [CrossRef]
- Ogrin, M.; Ogrin, D.; Rodman, N.; Močnik, M.; Vengar, R.; Smolej, A. Climate change and the future of winter tourism in slovenia. Hrvatski Geografski Glas. 2011, 73, 215–228. [Google Scholar] [CrossRef]
- Wolfsegger, C.; Gössling, S.; Scott, D.; Gössling, S.; Scott, D. Climate change risk appraisal in the Austrian ski industry. Tourism Rev. Int. 2008, 12, 13–23. [Google Scholar] [CrossRef]
- Ponspons, M.; Johnson, P.A.; Rosascasals, M.; Sureda, B.; Jover, È. Modeling climate change effects on winter ski tourism in Andorra. Clim. Res. 2012, 54, 197–207. [Google Scholar] [CrossRef]
- Pröbstl, U.; Prutsch, A.; Formayer, H.; Landauer, M.; Grabler, K.; Kulnig, A. Climate change in winter sport destinations: Transdisciplinary research for implementing sustainable tourism. Sustain. Tourism 2013, 3, 165–173. [Google Scholar]
- Tranos, E.; Davoudi, S. The regional impact of climate change on winter tourism in Europe. Tourism Plan. Dev. 2014, 11, 163–178. [Google Scholar] [CrossRef]
- Falk, M.; Lin, X. Sensitivity of winter tourism to temperature increases over the last decades. Econ. Model. 2018, 71, 174–183. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Wang, Y.; Zhou, X.Y.; Cui, Y.; Liu, Y.L.; Shi, D.M.; Yu, H.M.; Liu, Y.Y. Changes in climatic factors and extreme climate events in Northeast China during 1961–2010. Adv. Clim. Chang. Res. 2013, 4, 92–102. [Google Scholar]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR Derived Global Snow Cover Parameters. Ann. Glaciol. 2016, 9, 39–44. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T.J. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
- Zhen, L.I.; Shao, Y.; Zhou, J.; Tian, B.; Chen, Q. Snow-depth retrieval algorithms on MEMLS. J. Remote. Sens. 2013, 17, 1993–2002. [Google Scholar]
- Terjung, W.T. Physiologic climates of the conterminous United States: A bioclimatic classification based on man. Ann. Assoc. Am. Geogr. 1966, 5, 141–179. [Google Scholar] [CrossRef]
- Cai, X. Golden section, the optimization of environmental factors for human body. Chin. J. Clin. Rehabil. 2006, 10, 227–228. [Google Scholar]
- China Meteorological Administration, QXT 386-2017. Available online: http://www.cma.gov.cn/root7/auto13139/201801/t20180117_460483.html (accessed on 10 October 2018).
- Elsasser, H.; Messerli, P. The vulnerability of the snow industry in the Swiss Alps. Mountain. Res. Dev. 2001, 21, 335–339. [Google Scholar] [CrossRef]
- Elsasser, H.; Bürki, R. Climate change as a threat to tourism in the Alps. Clim. Res. 2002, 20, 253–257. [Google Scholar] [CrossRef]
- Yang, J.; Wan, C. Progress in research on the impacts of global climate change on winter ski tourism. Adv. Clim. Change Res. 2010, 1, 55–62. [Google Scholar] [CrossRef]
- Brouder, P.; Lundmark, L. Climate change in Northern Sweden: Intra-regional perceptions of vulnerability among winter-oriented tourism businesses. J. Sustain. Tourism 2011, 19, 919–933. [Google Scholar] [CrossRef]
- Steiger, R. Scenarios for skiing tourism in Austria: Integrating demographics with an analysis of climate change. J. Sustain. Tourism 2012, 20, 867–882. [Google Scholar] [CrossRef]
- Wang, L. A summery on the ice-snow tourism development research at home and abroad. Ecol. Econ. 2010, 11, 66–69. (In Chinese) [Google Scholar]
- Liu, W.J.; Jiang, M.M. Value and value system construction of the ice snow tourism resources. China Winter Sports 2016, 38, 90–93. (In Chinese) [Google Scholar]
- Cheng, Z.H.; Liu, K.; Sun, J. The comprehensive evaluation of suitability of ice-snow tourism base in China. Resour. Sci. 2016, 38, 2233–2243. (In Chinese) [Google Scholar]
- Che, T.; Dai, L. Long-term snow depth dataset of China. Cold Arid Reg. Sci. Data Center Lanzhou 2014. [Google Scholar] [CrossRef]
- Gao, F.; Xie, Y.; Piao, J.H.; Li, T. The relationship of meteorological condition and ski sport. Jilin Weather 2017, 1, 21–25. (In Chinese) [Google Scholar]
- Ming, J.; Chen, X.I.; Meng, M.; Xu, J.-Q. The influence of air temperature variety on skiing in heilongjiang province. J. Harbin Inst. Phys. Educ. 2008, 26, 107–110. (In Chinese) [Google Scholar]
- Richins, H.; Hull, J.S.; Richins, H. Mountain Tourism: Experiences, Communities, Environments and Sustainable Futures; CABI Publishing: Oxfordshire, UK, 2016. [Google Scholar]
- National Tourism Administration. Quality Classification of Tourist Skiing Grounds (LB/T037-2014); National Tourism Administration: Beijing, China, 2014.
- Witmer, U. Erfassung, Bearbeitung und Kartierung von Schneedaten in der Schweiz; Geographica Bernensia G25, Geographical Institiute, University of Bern: Bern, Switzerland, 1986. [Google Scholar]
- Li, X.F.; Zheng, X.M.; Wu, L.L.; Zhao, K.; Jiang, T.; Gu, L.J. Effects of snow cover on ground thermal regime: A case study in Heilongjiang Province of China. Chin. Geogr. Sci. 2016, 26, 527–538. [Google Scholar] [CrossRef]
- Goda, K.; Ren, J.D. Assessment of seismic loss dependence using copula. Risk. Anal. 2010, 30, 1076–1091. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Wang, L.F.; Zeng, J.C.; Hong, Y. Estimation of distribution algorithm based on copula theory. In Exploitation of Linkage Learning in Evolutionary Algorithms. Evolutionary Learning and Optimization; Springer: Berlin, Germany, 2009; pp. 1057–1063. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science Business Media Inc.: New York, NY, USA, 2006; ISBN 978-1-4419-2109-3. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Lecture Notes in Statistics: New York, NY, USA, 1999. [Google Scholar]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis: Part 2—A copula-based approach with mixed marginal distributions. J. Flood Risk Manag. 2009, 2, 32–44. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate flood frequency analysis using the gumbel–hougaard copula. J. Hydrol. Eng. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.; Bobée, B.; Legendre, P.; Bruneau, P. The gumbel mixed model for flood frequency analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Zhao, D.; Zheng, D.; Wu, S. Climate changes in northeastern China during last four decades. Chin. Geogr. Sci. 2007, 17, 317. [Google Scholar] [CrossRef]
- Rutty, M.; Scott, D.; Johnson, P.; Pons, M.; Steiger, R.; Vilella, M. Using ski industry response to climatic variability to assess climate change risk: An analogue study in eastern Canada. Tourism Manag. 2017, 58, 196–204. [Google Scholar] [CrossRef]
- Wobus, C.; Small, E.E.; Hosterman, H.; Mills, D.; Stein, J.; Rissing, M.; Jones, R.; Duckworth, M.; Hall, R.; Kolian, M.; Creason, J.; Martinich, J. Projected climate change impacts on skiing and snowmobiling: A case study of the United States. Glob. Environ. Chang. 2017, 45, 1–14. [Google Scholar] [CrossRef]
- Mayer, M.; Demiroglu, O.C.; Ozcelebi, O. Microclimatic volatility and elasticity of glacier skiing demand. Sustainability 2018, 10, 3536. [Google Scholar] [CrossRef]
- Gao, F.; Wang, T.Y.; Li, D.H.; Wang, Y. Analysis of Winter Climate Change in Jilin Province in Recent 53 Years. Jilin Weather 2015, 3, 31–34. (In Chinese) [Google Scholar]
| Factors | High | Middle | Low |
|---|---|---|---|
| H(°C) | [−12, −8] | [−16, −12) OR (−8, 2] | >2 OR < −16 |
| W(m/s) | <5.4 | [5.4, 10.7] | >5 |
| H(%) | [50, 60] | [30, 50) OR (60, 80] | >80 OR < 30 |
| V(km) | >1 | [0.5, 1] | <0.5 |
| Factors | High | Middle | Low |
|---|---|---|---|
| H(°C) | |||
| W(m/s) | |||
| H(%) | |||
| V(km) |
| Kinds | ||||
|---|---|---|---|---|
| Frank | ||||
| Clayton | ||||
| Gumbel |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Di, H.; Liu, X. Estimation of the Spatial Suitability of Winter Tourism Destinations Based on Copula Functions. Int. J. Environ. Res. Public Health 2019, 16, 186. https://doi.org/10.3390/ijerph16020186
Cai W, Di H, Liu X. Estimation of the Spatial Suitability of Winter Tourism Destinations Based on Copula Functions. International Journal of Environmental Research and Public Health. 2019; 16(2):186. https://doi.org/10.3390/ijerph16020186
Chicago/Turabian StyleCai, Weiying, Hui Di, and Xingpeng Liu. 2019. "Estimation of the Spatial Suitability of Winter Tourism Destinations Based on Copula Functions" International Journal of Environmental Research and Public Health 16, no. 2: 186. https://doi.org/10.3390/ijerph16020186
APA StyleCai, W., Di, H., & Liu, X. (2019). Estimation of the Spatial Suitability of Winter Tourism Destinations Based on Copula Functions. International Journal of Environmental Research and Public Health, 16(2), 186. https://doi.org/10.3390/ijerph16020186





