Noise Disturbances and Calls for Police Service in València (Spain): A Logistic Model with Spatial and Temporal Effects
Abstract
:1. Introduction
2. Materials and Methods
2.1. Binomial Logistic Model
2.2. Model Parameters Interpretation
2.3. Neighborhood Structure
2.4. Data
2.5. Data Transformation and Variables
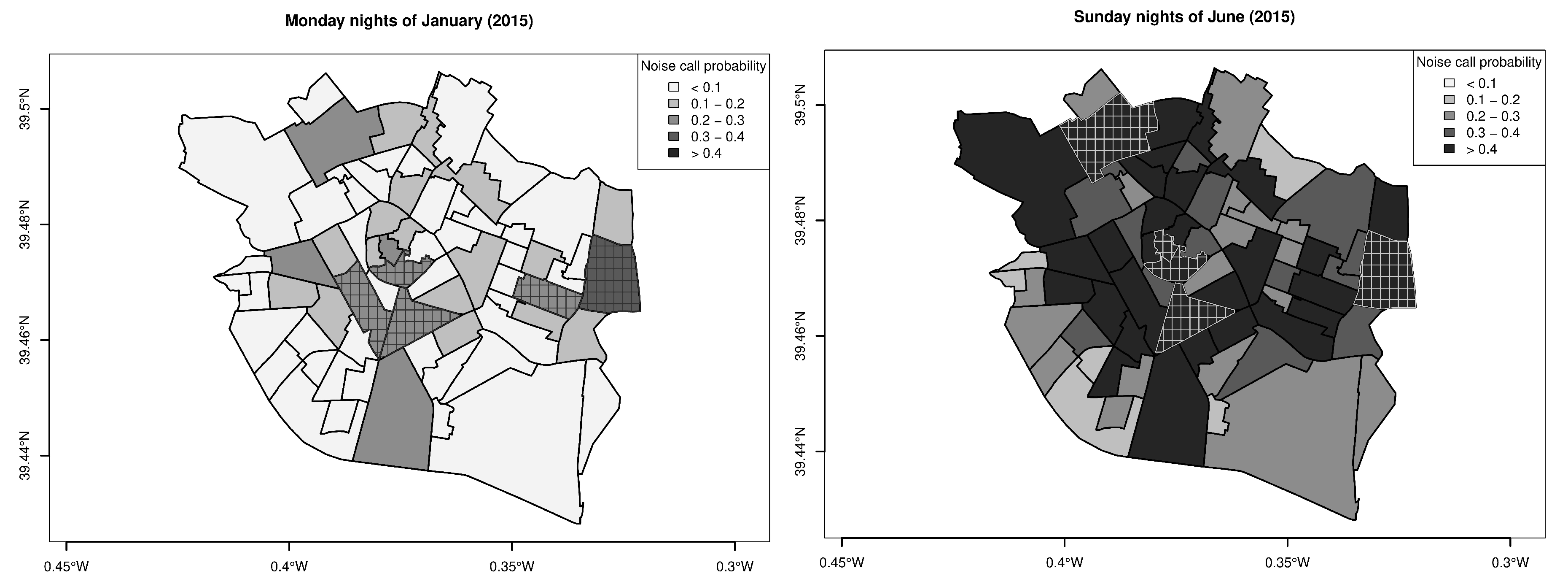
3. Results
- the presence of spatial and temporal (weekday, month and period) effects,
- the effect that incidents happened one or two weeks earlier in the borough neighborhoods, noise, and in the borough itself, noise, have on what occurs now in the borough, and
- the effect that a set of variables linked to the borough has on the occurrence of noise incidents.
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Borough | 2014 | 2015 | Borough | 2014 | 2015 |
|---|---|---|---|---|---|
| 11 LA SEU | 203 | 92 | 85 FAVARA | 47 | 111 |
| 12 LA XEREA | 123 | 62 | 91 LA RAIOSA | 134 | 82 |
| 13 EL CARME | 286 | 199 | 92 L’HORT DE SENABRE | 149 | 151 |
| 14 EL PILAR | 219 | 297 | 93 LA CREU COBERTA | 76 | 44 |
| 15 EL MERCAT | 461 | 380 | 94 SANT MARCEL·LÍ | 79 | 102 |
| 16 SANT FRANCESC | 370 | 374 | 95 CAMÍ REAL | 48 | 62 |
| 21 RUSSAFA | 600 | 608 | 101 MONT-OLIVET | 197 | 98 |
| 22 EL PLA DEL REMEI | 104 | 136 | 102 EN CORTS | 171 | 137 |
| 23 LA GRAN VIA | 149 | 107 | 103 MALILLA | 202 | 290 |
| 31 EL BOTÀNIC | 124 | 143 | 104 LA FONTETA S. LLUÍS | 21 | 24 |
| 32 LA ROQUETA | 118 | 83 | 105 NA ROVELLA | 132 | 172 |
| 33 LA PETXINA | 228 | 155 | 106 LA PUNTA | 46 | 85 |
| 34 ARRANCAPINS | 327 | 293 | 107 CIUTAT DE LES ARTS I DE LES CIÈNCIES | 117 | 121 |
| 41 CAMPANAR | 145 | 159 | 111 EL GRAU | 211 | 237 |
| 42 LES TENDETES | 66 | 98 | 112 EL CABANYAL-EL CANYAMELAR | 614 | 659 |
| 43 EL CALVARI | 75 | 34 | 113 LA MALVA-ROSA | 194 | 145 |
| 44 SANT PAU | 130 | 121 | 114 BETERÓ | 78 | 41 |
| 51 MARXALENES | 120 | 233 | 115 NATZARET | 71 | 75 |
| 52 MORVEDRE | 203 | 177 | 121 AIORA | 294 | 292 |
| 53 TRINITAT | 129 | 121 | 122 ALBORS | 106 | 99 |
| 54 TORMOS | 113 | 86 | 123 LA CREU DEL GRAU | 123 | 114 |
| 55 SANT ANTONI | 90 | 103 | 124 CAMÍ FONDO | 47 | 48 |
| 61 EXPOSICIÓ | 62 | 36 | 125 PENYA-ROJA | 252 | 272 |
| 62 MESTALLA | 320 | 344 | 131 L’ILLA PERDUDA | 98 | 88 |
| 63 JAUME ROIG | 101 | 88 | 132 CIUTAT JARDÍ | 287 | 260 |
| 64 CIUTAT UNIVERSITÀRIA | 47 | 71 | 133 L’AMISTAT | 135 | 114 |
| 71 NOU MOLES | 299 | 251 | 134 LA BEGA BAIXA | 100 | 58 |
| 72 SOTERNES | 44 | 18 | 135 LA CARRASCA | 41 | 13 |
| 73 TRES FORQUES | 205 | 160 | 141 BENIMACLET | 315 | 286 |
| 74 LA FONTSANTA | 63 | 90 | 142 CAMÍ DE VERA | 43 | 7 |
| 75 LA LLUM | 29 | 21 | 151 ORRIOLS | 234 | 195 |
| 81 PATRAIX | 205 | 186 | 152 TORREFIEL | 311 | 247 |
| 82 SANT ISIDRE | 88 | 68 | 153 SANT LLORENÇ | 67 | 30 |
| 83 VARA DE QUART | 65 | 152 | 161 BENICALAP | 486 | 393 |
| 84 SAFRANAR | 65 | 114 | 162 CIUTAT FALLERA | 75 | 30 |
References
- Basner, M.; Babisch, W.; Davis, A.; Brink, M.; Clark, C.; Janssen, S.; Stansfeld, S. Auditory and non-auditory effects of noise on health. Lancet 2014, 383, 1325–1332. [Google Scholar] [CrossRef]
- Stallen, P.J.M. A theoretical framework for environmental noise annoyance. Noise Health 1999, 1, 69–80. [Google Scholar] [PubMed]
- Stansfeld, S.A.; Berglund, B.; Clark, C.; Lopez-Barrio, I.; Fischer, P.; Öhrström, E.; Haines, M.M.; Head, J.; Hygge, S.; van Kamp, I.; et al. Aircraft and road traffic noise and children’s cognition and health: A cross-national study. Lancet 2005, 365, 1942–1949. [Google Scholar] [CrossRef]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135142. [Google Scholar] [CrossRef] [PubMed]
- Huss, A.; Spoerri, A.; Egger, M.; Röösli, M. Aircraft noise, air pollution, and mortality from myocardial infarction. Epidemiology 2010, 21, 829–836. [Google Scholar] [CrossRef] [PubMed]
- Münzel, T.; Schmidt, F.P.; Steven, S.; Herzog, J.; Daiber, A.; Sørensen, M. Environmental Noise and the Cardiovascular System. J. Am. Coll. Cardiol. 2018, 71, 688–697. [Google Scholar] [CrossRef]
- Orban, E.; McDonald, K.; Sutcliffe, R.; Hoffmann, B.; Fuks, K.B.; Dragano, N.; Viehmann, A.; Erbel, R.; Jöckel, K.H.; Pundt, N.; et al. Residential road traffic noise and high depressive symptoms after five years of follow-up: Results from the Heinz Nixdorf recall study. Environ. Health Perspect. 2015, 124, 578–585. [Google Scholar] [CrossRef]
- Klompmaker, J.O.; Hoek, G.; Bloemsma, L.D.; Wijga, A.H.; van den Brink, C.; Brunekreef, B.; Lebret, E.; Gehring, U.; Janssen, N.A.H. Associations of combined exposures to surrounding green, air pollution and traffic noise on mental health. Environ. Int. 2019, 129, 525–537. [Google Scholar] [CrossRef]
- WHO Regional Office for Europe. Environmental Noise Guidelines for the European Region; Publications WHO Regional Office for Europe: Copenhagen, Denmark, 2018; ISBN 978 92 890 5356 3. Available online: http://www.euro.who.int/pubrequest (accessed on 6 August 2019).
- Green Paper on Future Noise Policy. COM (96) 540 Final. 4 November 1996. Available online: http://aei.pitt.edu/1204/ (accessed on 6 August 2019).
- Iftimi, A.; Montes, F.; Seguí, L. Análisis de la percepción del ruido en la ciudad de València en los años 2014-15; IUSTEL: Madrid, Spain, 2018. [Google Scholar]
- Banbury, S.P.; Macken, W.J.; Tremblay, S.; Jones, D.M. Auditory distraction and short-term memory: Phenomena and practical implications. Hum. Factors 2001, 43, 12–29. [Google Scholar] [CrossRef]
- Antolos, D.; Liu, D.; Ludu, A.; Vincenzi, D.A. Burglary Crime Analysis Using Logistic Regression. In Human Interface and the Management of Information. Information and Interaction for Learning, Culture, Collaboration and Business, Proceedings of the 15th International Conference, HCI International 2013, Las Vegas, NV, USA, 21–26 July 2013; Yamamoto, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Part III; pp. 549–558. [Google Scholar] [CrossRef] [Green Version]
- Rummens, A.; Hardyns, W.; Pauwels, L. The use of predictive analysis in spatiotemporal crime forecasting: Building and testing a model in an urban context. Appl. Geogr. 2017, 86, 255–261. [Google Scholar] [CrossRef]
- Braithwaite, A.; Johnson, S.D. The Battle for Baghdad: Testing Hypotheses About Insurgency From Risk Heterogeneity, Repeat Victimization, and Denial Policing Approaches. Terror. Political Violence 2015, 21, 112–132. [Google Scholar] [CrossRef]
- Statistics Office of València City Council. Anuari Estadístic de la Ciutat de València; València City Council: València, Spain, 2015. [Google Scholar]
- Agresti, A. Categorical Data Analysis; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cliff, A.; Ord, J. Spatial Autocorrelation; Pion: London, UK, 1973. [Google Scholar]
- Statistics Office of València City Council. Àrees Vulnerables a la Ciutat de València; València City Council: València, Spain, 2016. [Google Scholar]
- Pedrero-García, E. Nightlife and alcohol consumption among youths: the botellón phenomenon in Spain. SAGE Open 2018, 8. [Google Scholar] [CrossRef]
- Seguí, L. El botellón. Alcohol 2018. submitted. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: http://www.R-project.org/ (accessed on 6 August 2019).
- Wei, T.; Simko, V. R Package “corrplot”: Visualization of a Correlation Matrix (Version 0.84). 2017. Available online: https://github.com/taiyun/corrplot (accessed on 6 August 2019).
- Lee, E.Y.; Jerrett, M.; Ross, Z.; Coogan, P.F.; Seto, E.Y. Assessment of traffic-related noise in three cities in the United States. Environ. Res. 2014, 132, 182–189. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, I.; Foraster, M.; Basagaña, X.; Corradi, E.; Deltell, A.; Morelli, X.; Phuleria, H.C.; Ragettli, M.S.; Rivera, M.; Thomasson, A.; et al. Application of land use regression modelling to assess the spatial distribution of road traffic noise in three European cities. J. Expo. Sci. Environ. Epidemiol. 2015, 25, 97–105. [Google Scholar] [CrossRef]
- Lagonigro, R.; Martori, J.C.; Apparicio, P. Environmental noise inequity in the city of Barcelona. Transp. Res. Part D Transp. Environ. 2018, 63, 309–319. [Google Scholar] [CrossRef]
- Martín, M.A.; Tarrero, A.; González, J.; Machimbarrena, M. Exposure-effect relationships between road traffic noise annoyance and noise cost valuations in Valladolid, Spain. Appl. Acoust. 2006, 67, 945–958. [Google Scholar] [CrossRef]
- Dale, L.M.; Goudreau, S.; Perron, S.; Ragettli, M.S.; Hatzopoulou, M.; Smargiassi, A. Socioeconomic status and environmental noise exposure in Montreal, Canada. BMC Public Health 2015, 15, 205. [Google Scholar] [CrossRef]
- Ragettli, M.S.; Goudreau, S.; Plante, C.; Fournier, M.; Hatzopoulou, M.; Perron, S.; Smargiassi, A. Statistical modeling of the spatial variability of environmental noise levels in Montreal, Canada, using noise measurements and land use characteristics. J. Expo. Sci. Environ. Epidemiol. 2015, 26, 597–605. [Google Scholar] [CrossRef]
- Sakieh, Y.; Jaafari, S.; Ahmadi, M.; Danekar, A. Green and calm: Modeling the relationships between noise pollution propagation and spatial patterns of urban structures and green covers. Urban For. Urban Green. 2017, 24, 195–211. [Google Scholar] [CrossRef]
- Diggle, P.J.; Moraga, P.; Rowlingson, B.M.; Taylor, B.M. Spatial and Spatio-Temporal Log-Gaussian Cox Processes: Extending the Geostatistical Paradigm. Stat. Sci. 2013, 28, 542–563. [Google Scholar] [CrossRef] [Green Version]
- Iftimi, A.; van Lieshout, M.N.M.; Montes, F. A multi-scale area-interaction model for spatio-temporal point patterns. Spat. Stat. 2018, 26, 38–55. [Google Scholar] [CrossRef] [Green Version]

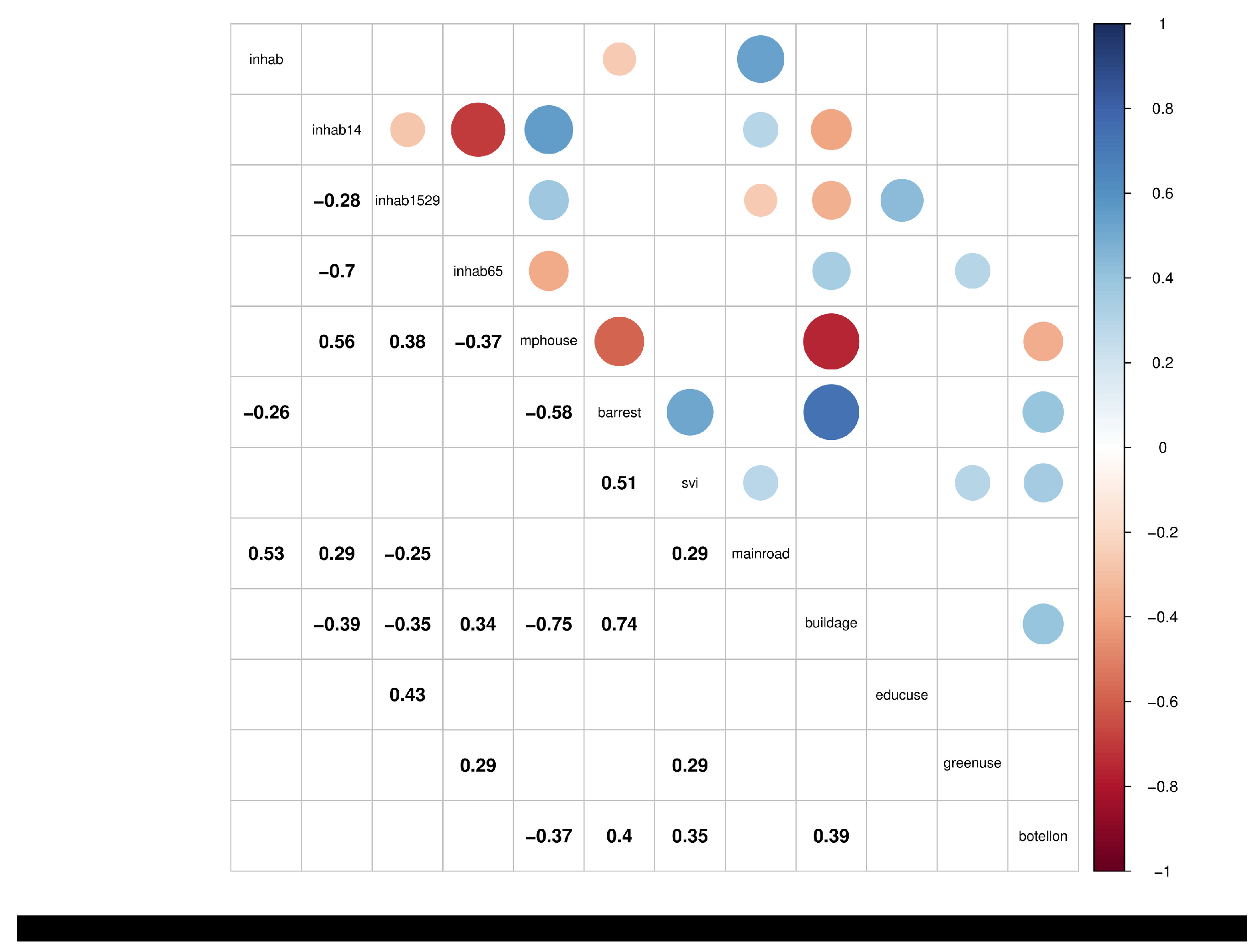
| Variable | Meaning |
|---|---|
| (1) weekday | day of the week |
| (2) month | month of the year |
| (3) period | period of the day |
| (4) noise | number of noise calls 1 week before in the borough |
| (5) noise | number of noise calls 2 weeks before in the borough |
| (6) noise | number of noise calls 1 week before in the 1 lag borough neighborhood |
| (7) noise | number of noise calls 1 week before in the 2 lag borough neighborhood |
| (8) noise | number of noise calls 2 week before in the 1 lag borough neighborhood |
| (9) noise | number of noise calls 2 week before in the 2 lag borough neighborhood |
| (10) district | district to which the borough belongs to |
| (11) inhab | number of inhabitants in the borough |
| (12) inhab14 | percentage of inhabitants in the borough aged under 15 |
| (13) inhab1529 | percentage of inhabitants in the borough aged between 15 and 29 |
| (14) inhab65 | percentage of inhabitants in the borough aged 65 or over |
| (15) mphouse | average number of members per household |
| (16) barrest | number of bars and restaurants per 100 inhabitants in the borough |
| (17) svi | socio-economic vulnerability index |
| (18) mainroad | number of km of non-pedestrian main road located in the borough |
| (19) buildage | average age of the buildings located in the borough |
| (20) educuse | percentage of land in the borough dedicated to educational use (undergraduate and university level) |
| (21) greenuse | percentage of land in the borough dedicated to green areas |
| (22) botellón | binary variable indicating if the practice of “botellón” is usual in the borough |
| (23) noise | number of noise calls in the borough |
| Df | Deviance | Resid Df | Resid Dev | p-Value | |
|---|---|---|---|---|---|
| NULL | 100239 | 88,454.79 | |||
| weekday | 6 | 1692.29 | 100233 | 86,762.50 | 0.00 |
| month | 11 | 918.26 | 100222 | 85,844.23 | 0.00 |
| period | 1 | 1409.47 | 100221 | 84,434.76 | 0.00 |
| noisebin | 1 | 319.50 | 100220 | 84,115.26 | 0.00 |
| noisebin | 1 | 361.51 | 100219 | 83,753.75 | 0.00 |
| noisebin | 1 | 255.37 | 100218 | 83,498.38 | 0.00 |
| noisebin | 1 | 1.85 | 100217 | 83,496.53 | 0.17 |
| noisebin | 1 | 393.44 | 100216 | 83,103.09 | 0.00 |
| noisebin | 1 | 18.69 | 100215 | 83,084.39 | 0.00 |
| district | 15 | 296.35 | 100188 | 77,919.11 | 0.00 |
| log(inhab) | 1 | 2320.00 | 100214 | 80,764.40 | 0.00 |
| inhab14 | 1 | 180.97 | 100213 | 80,583.42 | 0.00 |
| inhab1529 | 1 | 381.78 | 100212 | 80,201.65 | 0.00 |
| inhab65 | 1 | 29.17 | 100211 | 80,172.47 | 0.00 |
| mphouse | 1 | 1111.22 | 100210 | 79,061.26 | 0.00 |
| barrest | 1 | 365.69 | 100209 | 78,695.57 | 0.00 |
| svi | 1 | 167.76 | 100208 | 78,527.81 | 0.00 |
| mainroad | 1 | 43.18 | 100207 | 78,484.63 | 0.00 |
| buildage | 1 | 60.84 | 100206 | 78,423.79 | 0.00 |
| educuse | 1 | 10.04 | 100205 | 78,413.74 | 0.00 |
| greenuse | 1 | 109.99 | 100204 | 78,303.75 | 0.00 |
| botellón | 1 | 88.30 | 100203 | 78,215.46 | 0.00 |
| Variable | SE | p-Value | 95% CI | |||
|---|---|---|---|---|---|---|
| Lower | Upper | |||||
| Monday | −0.89 | 0.04 | 0.00 | 0.41 | 0.38 | 0.44 |
| Tuesday | −0.83 | 0.04 | 0.00 | 0.43 | 0.40 | 0.46 |
| Wednesday | −0.76 | 0.03 | 0.00 | 0.47 | 0.43 | 0.50 |
| Thursday | −0.70 | 0.03 | 0.00 | 0.50 | 0.46 | 0.53 |
| Friday | −0.45 | 0.03 | 0.00 | 0.64 | 0.60 | 0.68 |
| Saturday | −0.08 | 0.03 | 0.01 | 0.92 | 0.87 | 0.98 |
| Sunday | ||||||
| January | −1.00 | 0.05 | 0.00 | 0.37 | 0.33 | 0.40 |
| February | −0.83 | 0.05 | 0.00 | 0.43 | 0.40 | 0.47 |
| March | −0.55 | 0.04 | 0.00 | 0.58 | 0.53 | 0.62 |
| April | −0.65 | 0.04 | 0.00 | 0.52 | 0.48 | 0.57 |
| May | −0.44 | 0.04 | 0.00 | 0.65 | 0.59 | 0.70 |
| June | ||||||
| July | −0.28 | 0.04 | 0.00 | 0.75 | 0.70 | 0.81 |
| August | −0.48 | 0.04 | 0.00 | 0.62 | 0.57 | 0.67 |
| September | −0.35 | 0.04 | 0.00 | 0.70 | 0.65 | 0.76 |
| October | −0.49 | 0.04 | 0.00 | 0.61 | 0.56 | 0.66 |
| November | −0.74 | 0.04 | 0.00 | 0.47 | 0.43 | 0.52 |
| December | −0.78 | 0.04 | 0.00 | 0.46 | 0.42 | 0.50 |
| night | 0.63 | 0.02 | 0.00 | 1.88 | 1.81 | 1.96 |
| noisebin | 0.13 | 0.02 | 0.00 | 1.14 | 1.08 | 1.19 |
| noisebin | 0.20 | 0.02 | 0.00 | 1.22 | 1.17 | 1.28 |
| noisebin | 0.07 | 0.02 | 0.00 | 1.08 | 1.03 | 1.12 |
| noisebin | −0.03 | 0.03 | 0.40 | 0.97 | 0.90 | 1.04 |
| noisebin | 0.18 | 0.02 | 0.00 | 1.20 | 1.14 | 1.25 |
| noisebin | 0.10 | 0.04 | 0.00 | 1.11 | 1.03 | 1.19 |
| log(inhab) | 0.93 | 0.03 | 0.00 | 2.52 | 2.39 | 2.65 |
| inhab14 | 0.13 | 0.01 | 0.00 | 1.14 | 1.11 | 1.17 |
| inhab1529 | 0.12 | 0.01 | 0.00 | 1.13 | 1.10 | 1.16 |
| inhab65 | 0.04 | 0.01 | 0.00 | 1.04 | 1.03 | 1.05 |
| mphouse | −2.04 | 0.16 | 0.00 | 0.13 | 0.09 | 0.17 |
| barrest | 0.18 | 0.02 | 0.00 | 1.20 | 1.15 | 1.24 |
| svi | −0.38 | 0.03 | 0.00 | 0.68 | 0.64 | 0.73 |
| mainroad | 0.02 | 0.01 | 0.06 | 1.02 | 1.00 | 1.03 |
| buildage | −0.00 | 0.00 | 0.00 | 1.00 | 0.99 | 1.00 |
| educuse | 0.01 | 0.00 | 0.00 | 1.01 | 1.00 | 1.01 |
| greenuse | −0.02 | 0.00 | 0.00 | 0.98 | 0.98 | 0.99 |
| botellón | 0.29 | 0.03 | 0.00 | 1.33 | 1.25 | 1.42 |
| District 1 | ||||||
| District 2 | −0.76 | 0.07 | 0.00 | 0.47 | 0.40 | 0.53 |
| District 3 | −1.02 | 0.07 | 0.00 | 0.36 | 0.31 | 0.42 |
| District 4 | −1.05 | 0.10 | 0.00 | 0.35 | 0.28 | 0.42 |
| District 5 | −1.07 | 0.10 | 0.00 | 0.34 | 0.28 | 0.41 |
| District 6 | −0.81 | 0.10 | 0.00 | 0.44 | 0.35 | 0.54 |
| District 7 | −1.23 | 0.11 | 0.00 | 0.29 | 0.23 | 0.35 |
| District 8 | −1.22 | 0.11 | 0.00 | 0.30 | 0.23 | 0.36 |
| District 9 | −1.38 | 0.11 | 0.00 | 0.25 | 0.20 | 0.30 |
| District 10 | −1.10 | 0.10 | 0.00 | 0.33 | 0.27 | 0.40 |
| District 11 | −1.29 | 0.11 | 0.00 | 0.28 | 0.22 | 0.34 |
| District 12 | −1.04 | 0.10 | 0.00 | 0.35 | 0.28 | 0.43 |
| District 13 | −1.13 | 0.11 | 0.00 | 0.32 | 0.25 | 0.39 |
| District 14 | −1.47 | 0.12 | 0.00 | 0.23 | 0.18 | 0.29 |
| District 15 | −1.37 | 0.13 | 0.00 | 0.25 | 0.19 | 0.32 |
| District 16 | −1.23 | 0.12 | 0.00 | 0.29 | 0.22 | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seguí, L.; Iftimi, A.; Briz-Redón, Á.; Martínez-Garay, L.; Montes, F. Noise Disturbances and Calls for Police Service in València (Spain): A Logistic Model with Spatial and Temporal Effects. Int. J. Environ. Res. Public Health 2019, 16, 2815. https://doi.org/10.3390/ijerph16162815
Seguí L, Iftimi A, Briz-Redón Á, Martínez-Garay L, Montes F. Noise Disturbances and Calls for Police Service in València (Spain): A Logistic Model with Spatial and Temporal Effects. International Journal of Environmental Research and Public Health. 2019; 16(16):2815. https://doi.org/10.3390/ijerph16162815
Chicago/Turabian StyleSeguí, Lia, Adina Iftimi, Álvaro Briz-Redón, Lucía Martínez-Garay, and Francisco Montes. 2019. "Noise Disturbances and Calls for Police Service in València (Spain): A Logistic Model with Spatial and Temporal Effects" International Journal of Environmental Research and Public Health 16, no. 16: 2815. https://doi.org/10.3390/ijerph16162815
APA StyleSeguí, L., Iftimi, A., Briz-Redón, Á., Martínez-Garay, L., & Montes, F. (2019). Noise Disturbances and Calls for Police Service in València (Spain): A Logistic Model with Spatial and Temporal Effects. International Journal of Environmental Research and Public Health, 16(16), 2815. https://doi.org/10.3390/ijerph16162815





