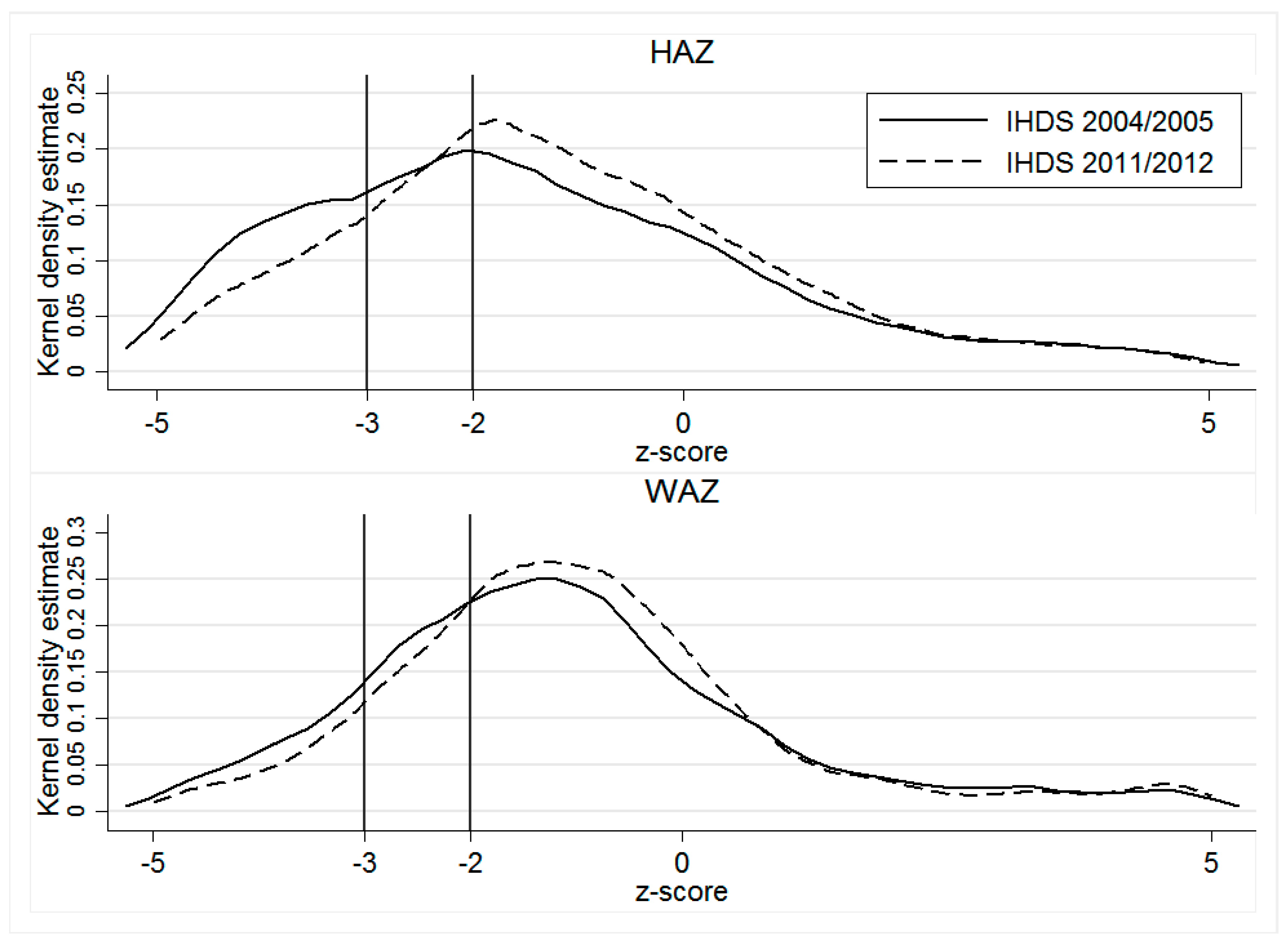
3.1. Data
The data for this analysis are taken from the IHDS 2004–2005 and 2011–2012, a collaborative research program between researchers from the National Council of Applied Economic Research, New Delhi, and the University of Maryland. This nationally representative multi-topic survey was administered to households in 1503 villages and 971 urban neighborhoods across India and the sample includes 384 districts out of a total of 593 identified in 2001 census. Villages and urban blocks (comprising of 150–200 households) form the primary sampling unit (PSU) from which the households are selected [
40]. Urban and rural PSUs are selected using a different design. Specifically, to draw a random sample of urban households, all urban areas in a state are listed in the order of their size with the number of blocks drawn from each urban area allocated based on probability proportional to size [
40]. When the numbers of blocks for each urban area are fixed, the enumeration blocks are then selected randomly with the assistance from Registrar General of India. Drawing on these Census Enumeration Blocks of about 150–200 households, a complete household listing is conducted and a household sample of 15 households is selected within each block. For sampling purposes, some smaller states are merged with nearby larger states. Nevertheless, the rural sample encompasses about half the households that are interviewed initially by NCAER in 1993–1994 in a survey titled Human Development Profile of India (HDPI) and the other half of the samples are drawn from both districts surveyed in HDPI as well as from the districts located in the states and union territories not covered in HDPI [
40]. The first phase, IHDS-I (2004–2005), comprised two one-hour interviews with each household on topics such as health status, education, employment, economic status, marriage, fertility, gender relations, and social capital. The second phase, IHDS-II, was conducted between 2011–2012. A detailed description of sampling design and data quality is available in Reference [
40]. All individual- and household-level data are available for public use [
41].
Our sample is restricted to those households with children born in the five years prior to the survey, where information was available on all our variables of interest. Because data on certain outcome variables of interest are limited, our final pooled sample contains 6445 observations for stunting, 7634 observations for underweight, and 5693 observations for the CIAF.
3.2. Study Variables
3.2.1. Dependent Variables
In keeping with the World Health Organization’s reference standards [
42], we measure children’s nutritional outcomes conventionally using z-scores of height-for-age (HAZ) and weight for age (WAZ). According to Waterlow et al. [
43], the height-for-age z-score, expressed in standard deviations from the reference population mean, is a good indicator of nutritional status. Whereas HAZ measures long-term nutrition by showing the cumulative effects of growth deficiency (often associated with chronic insufficient food intake, frequent infections, sustained incorrect feeding practices, and/or low socio-economic family status), WAZ reflects both acute and chronic undernutrition, making it a better single indicator of childhood undernutrition [
44].
Children with z-score values below −2 (below −3) of the reference population are considered undernourished (severely undernourished) [
42]. However, because these conventional undernutrition measures reflect different aspects of anthropometric failure, they cannot individually determine the overall prevalence of child undernutrition in a population, and may underestimate the true extent of undernutrition, primarily due to the overlapping of children into multiple categories of anthropometric failure [
45,
46,
47,
48]. For instance, underweight cannot identify children who are suffering from underweight combined with stunting and/or wasting [
46,
47]. We address this shortcoming using Svedberg’s [
48] CIAF, an aggregated single anthropometric proxy for the overall estimation of malnourished children. In our analysis, we combine Nandy et al.’s [
45] Group Y, underweight only, with six of Svedberg’s groups [
48]: Group A, no failure; Group B, wasting only; Group C, wasting and underweight; Group D, wasting, stunting, and underweight; Group E, stunting and underweight; and Group F, stunting only (see
Table A1 for a detailed classification). CIAF is thus a binary variable for which 0 indicates no failure, and 1 signals one or more anthropometric failures.
3.2.2. Explanatory Variables
Maternal characteristics. We control for mother’s education using four categories: No education, primary, secondary, tertiary and above. As a proxy for mother’s health, we include her BMI measured in kg/m2 (categorizing into three groups: Underweight for BMI < 18.5, normal for 18.5 ≤ BMI ≤ 24.9 and overweight/obesity for BMI ≥ 25).
Economic characteristics. A household’s economic status is measured using the household wealth index, which is a categorical variable divided into five population quintiles from the poorest 20% to the wealthiest 20% of households [
49]. This index is calculated with Principle Component Analyses (PCA) using 33 dichotomous items measuring household ownership of assets and housing quality. Relative to income and consumption, this measure of wealth is less volatile and thus arguably a better long-run measure of household economic status.
Maternal autonomy. A key advantage of our dataset is the rich array of attitudinal questions that are available on married women’s decision-making authority in the household. Autonomy is regarded as a multidimensional construct, encompassing dimensions such as the ability to make purchases, control over resources, decision-making autonomy both relating to own health care or child’s medical needs [
50]. We therefore categorize maternal autonomy into:
Decision-making autonomy: A female respondent (child’s mother) is assumed to have decision-making autonomy if she was involved in decision-making either on her own or in conjunction with another household member on: (i) What is to be cooked, (ii) making expensive purchases, (iii) the number of children to have, and (iv) children’s medical needs (decide what to do when a child falls sick).
Mobility autonomy: The child’s mother is assumed to have mobility autonomy if she can go on her own: (i) To visit relatives/friends, (ii) to the local health center, and (iii) to the local grocery store.
These individual responses are coded as binary indicators which we use to construct two factors: Maternal autonomy in decision-making and mobility using PCA.
Hygiene characteristics. We include three binary variables that capture the level of sanitation and hygiene practiced in the household: Drinking water source (1 if the household’s drinking water is piped or supplied by tube well or hand pump, 0 otherwise), access to a flushing toilet (1 = yes, 0 = no), and hand-washing behavior (1 = yes, 0 = no).
Regional characteristics. The 24 Indian states are classified into six regions as per the regional definitions used in the IHDS data (see
Table A2). These are: North (comprising of the states of Jammu and Kashmir, Himachal Pradesh, Punjab, Chandigarh, Uttaranchal, Uttar Pradesh, Haryana and Delhi); Central (Chhattisgarh and Madhya Pradesh); East (Bihar, West Bengal, Jharkhand, Odisha); South (Andhra Pradesh, Karnataka, Kerala, Tamil Nadu and Pondicherry); North East (Sikkim, Arunachal Pradesh, Nagaland, Manipur, Mizoram, Tripura, Meghalaya and Assam); and West (Rajasthan, Goa, Maharashtra, Daman and Diu, Dadar and Nagar Haveli and Gujarat). The descriptive analysis of regional changes in child nutrition are based on these six regions.
Other characteristics. Our specifications also include controls for child’s age (in years) and gender (1 = male and 0 = female), father’s education levels (a categorical variable, 1 = no education, 2 = primary, 3 = secondary and 4 = tertiary and above), religion (a categorical variable, 1 = Hindu, 2 = Muslim and 3 = others), caste (a categorical variables, 1 = other, 2 = other backward and 3 = scheduled caste/tribe) and a binary variable for rural residence (1 = rural and 0 = urban).
3.3. Estimation Procedure
Blinder-Oaxaca (BO) decomposition. We use BO decomposition to explain changes in the nutritional measures HAZ and WAZ as a function of selected explanatory factors. The BO decomposition quantifies the distribution differences of factors that explain the average gap, and also identifies differences in these factors’ effects [
51]. The total difference in mean z-scores of our three measures of child undernutrition can be decomposed as follows:
where
is a vector of the averaged values of the independent variables and
is a vector of the coefficient estimates for wave
i (here,
i = 2004/2005, 2011/2012).
Re-centred influence function regression (RIFR) decomposition. Because covariate and coefficient contributions may differ between the median and tails of the childhood undernutrition distribution, we use RIFR decomposition [
52] to investigate the contributions of demographic and socio-economic characteristics at different quantiles of the unconditional marginal distribution. The RIFR method involves a two-step procedure: First, we calculate an influence function (IF) at each quantile
of the distribution of the outcome variable (z-score of child undernutrition), as follows:
where
represents the unconditional
quantile of the
z-score,
is the unconditional density of the
z-score at the
quantile, and
is an indicator function for whether the outcome variable is smaller or equal to the
quantile. For each quantile, the coefficient on
X for waves 2004/2005 and 2011/2012 are then estimated by regressing the RIF on
X:
where
is the unconditional
quantile of the
z-score for wave 2004/05 and 2011/12, respectively.
is the coefficient of the unconditional quantile regression, which captures the marginal effect of a change in the distribution of
X on the unconditional quantile of the
z-score.
In the second step, we employ the BO decomposition strategy at different quantiles (25%, 50%, and 75%) calculated by the RIFR:
Both the explained and unexplained parts are then decomposed into the contributions of each covariate at the quantile in Equation (5), which is in effect analogous to the BO decomposition in Equation (1).
Fairlie’s (1999) non-linear decomposition. Applying standard BO decomposition to a linear probability model provides misleading estimates for binary dependent variables, particularly if the group differences for an influential independent variable are relatively large [
39]. It is therefore preferable to apply a relatively straightforward simulation technique for non-linear decomposition. Accordingly, we estimate the contributions of socio-economic and demographic factors to identified differences in our key undernutrition indicators by employing a non-linear decomposition approach for binary dependent variables. Stunting, underweight, and CIAF are the dependent variables, so the decomposition for the non-linear equation,
, can be expressed as:
where
denotes the sample size of each wave (
j = 2004/2005, 2011/2012). The function
represents a probit model. Two aspects are worth noting: First, the BO decomposition in Equation (1) is a special case of Equation (6) where
. Second, in Equations (1) and (6), the first (explained) term on the right indicates the contribution resulting from a difference in the distribution of the determinant of
X, and the second (unexplained) term refers to the part attributable to a difference in the effect of the determinants. Equally noteworthy, the second term captures all the potential effects of differences in unobservables [
39]. In keeping with previous research using decomposition, we focus on the explained terms and their disaggregated contribution for individual covariates, which result primarily from the difficulty of interpreting the unexplained part [
53]. The contribution of a variable is given by the average change in the function if that variable is changed while all other variables remain the same. For severe childhood undernutrition in terms of
HAZ and
WAZ, we use the same specification as in Equation (6).
One potential concern related to Fairlie’s sequential decomposition is path dependence, the possibility that changing the order of variables in the decomposition may produce different results [
39,
54]. We therefore test the sensitivity of decomposition estimates to variable re-ordering by randomizing their order in the decomposition [
39] using 1000 replications, the minimum number recommended for most applications [
39]. As a robustness check, we also perform an analysis using 5000 replications. These results are not reported here but are available on request.
When reporting the decomposition results for these three decomposition methods, we categorize the disaggregated contributions of the determinants in the explained part into five main dimensions depicted above, namely: Maternal autonomy, maternal characteristics, household economic status, hygiene, and other.