A GIS-Based Artificial Neural Network Model for Spatial Distribution of Tuberculosis across the Continental United States
Abstract
1. Introduction
2. Material and Methods
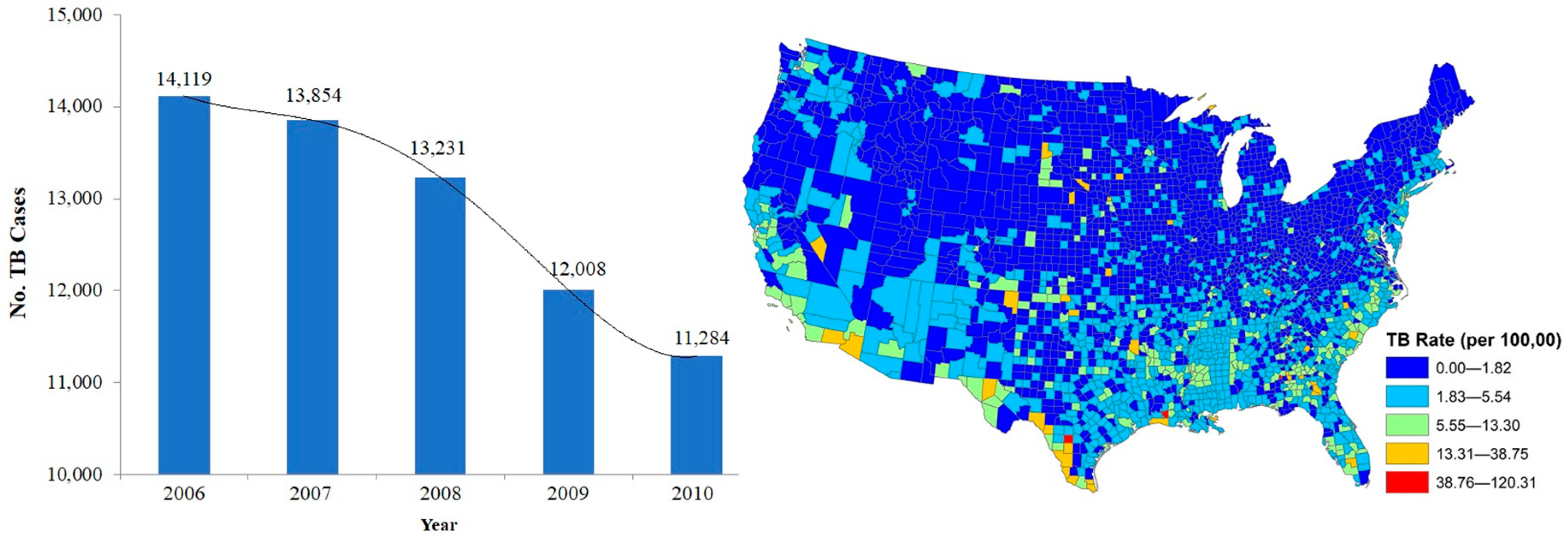
2.1. Tuberculosis Data
2.2. Explanatory Data
2.3. Global and Local Clustering
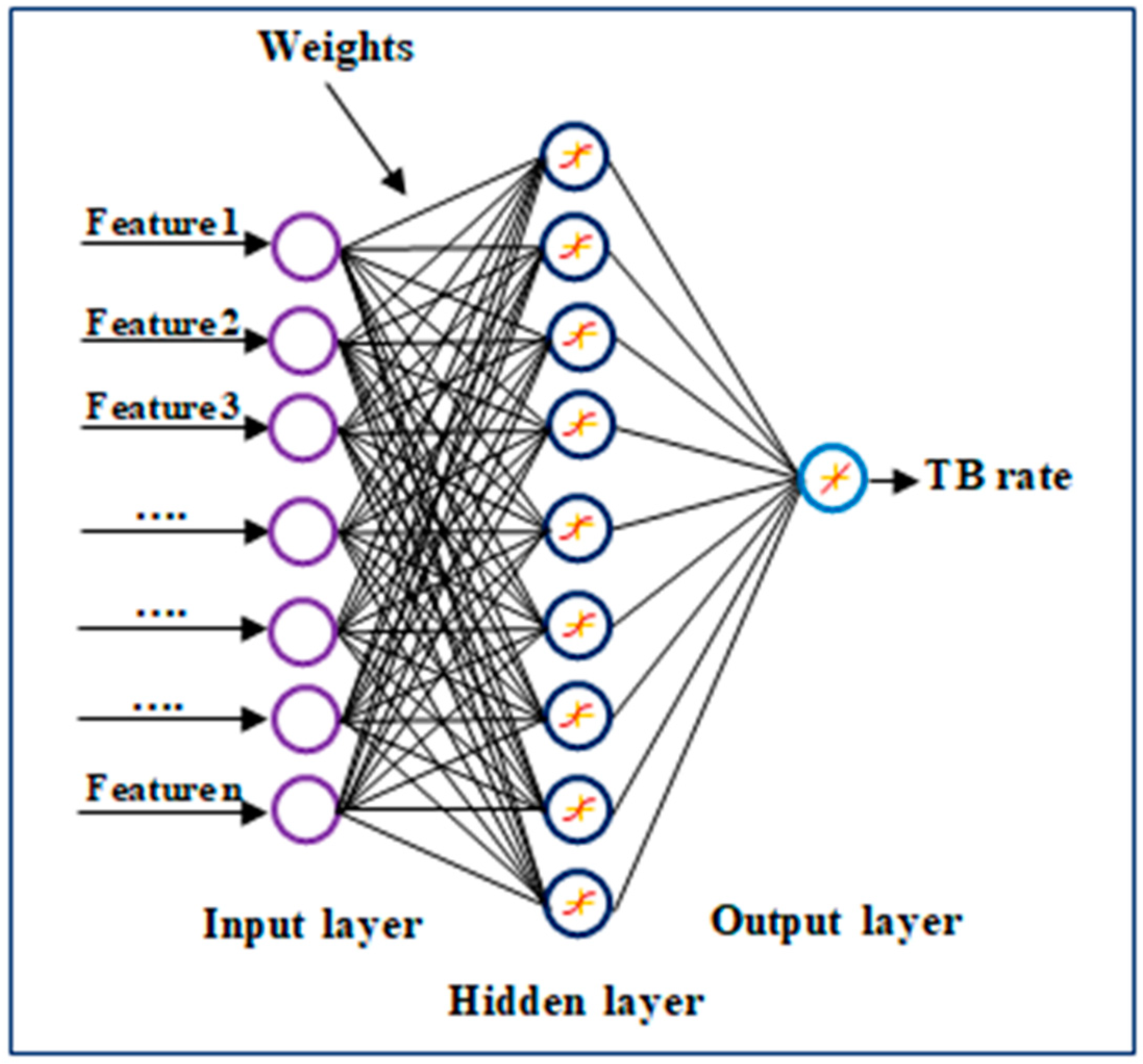
2.4. Artificial Neural Networks
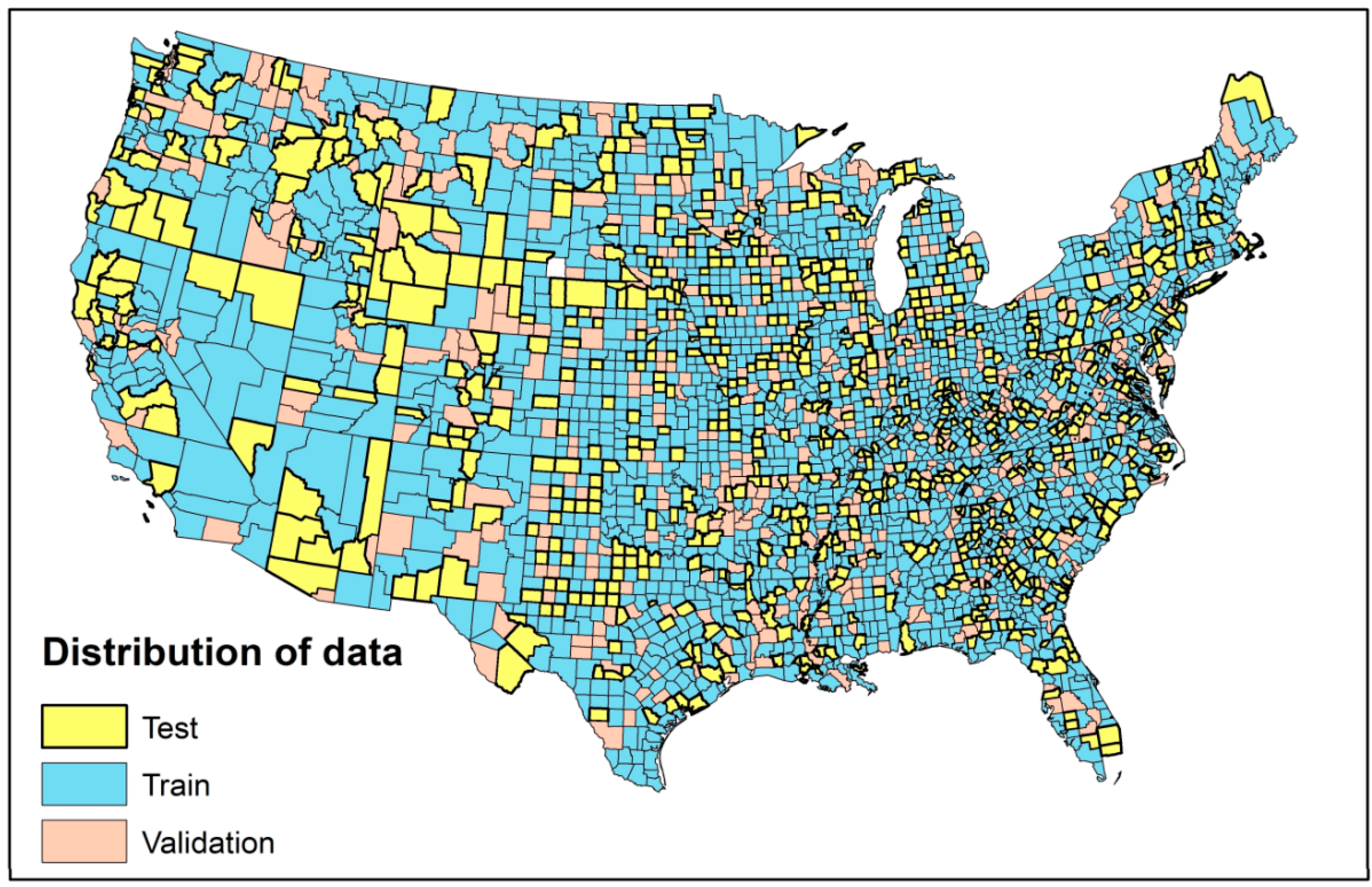
2.5. Model Pre-Processing
2.6. Model Evaluation
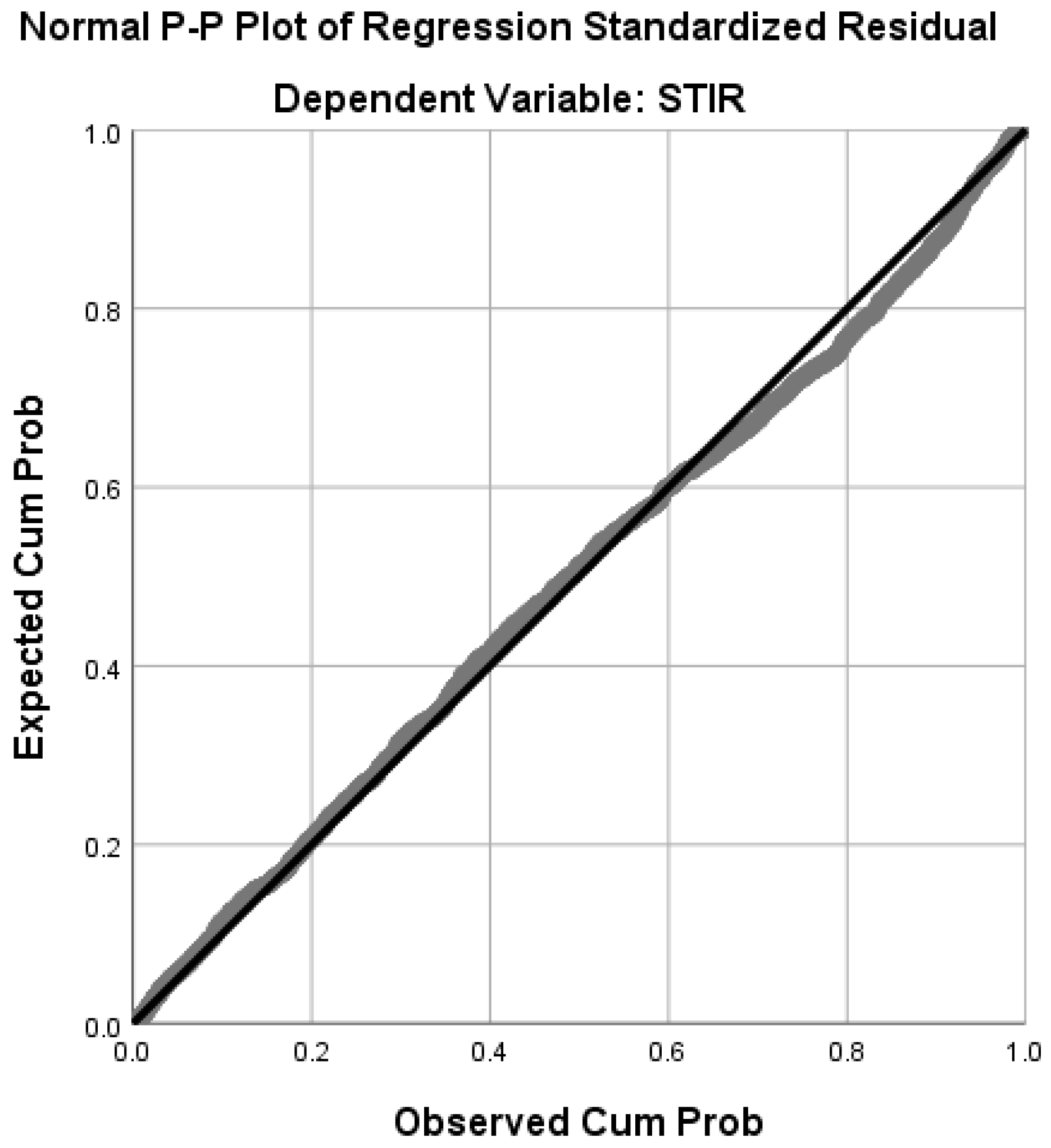
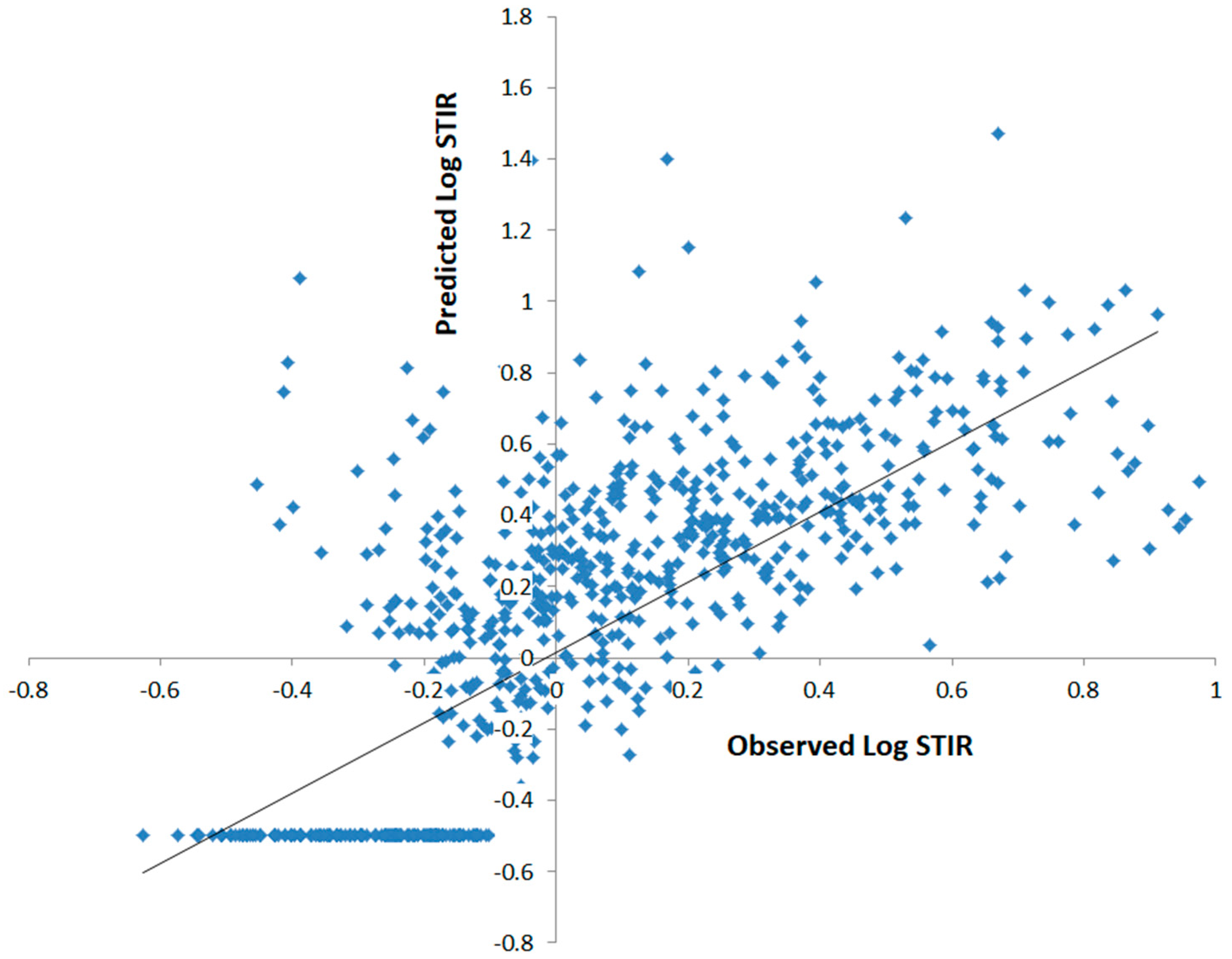
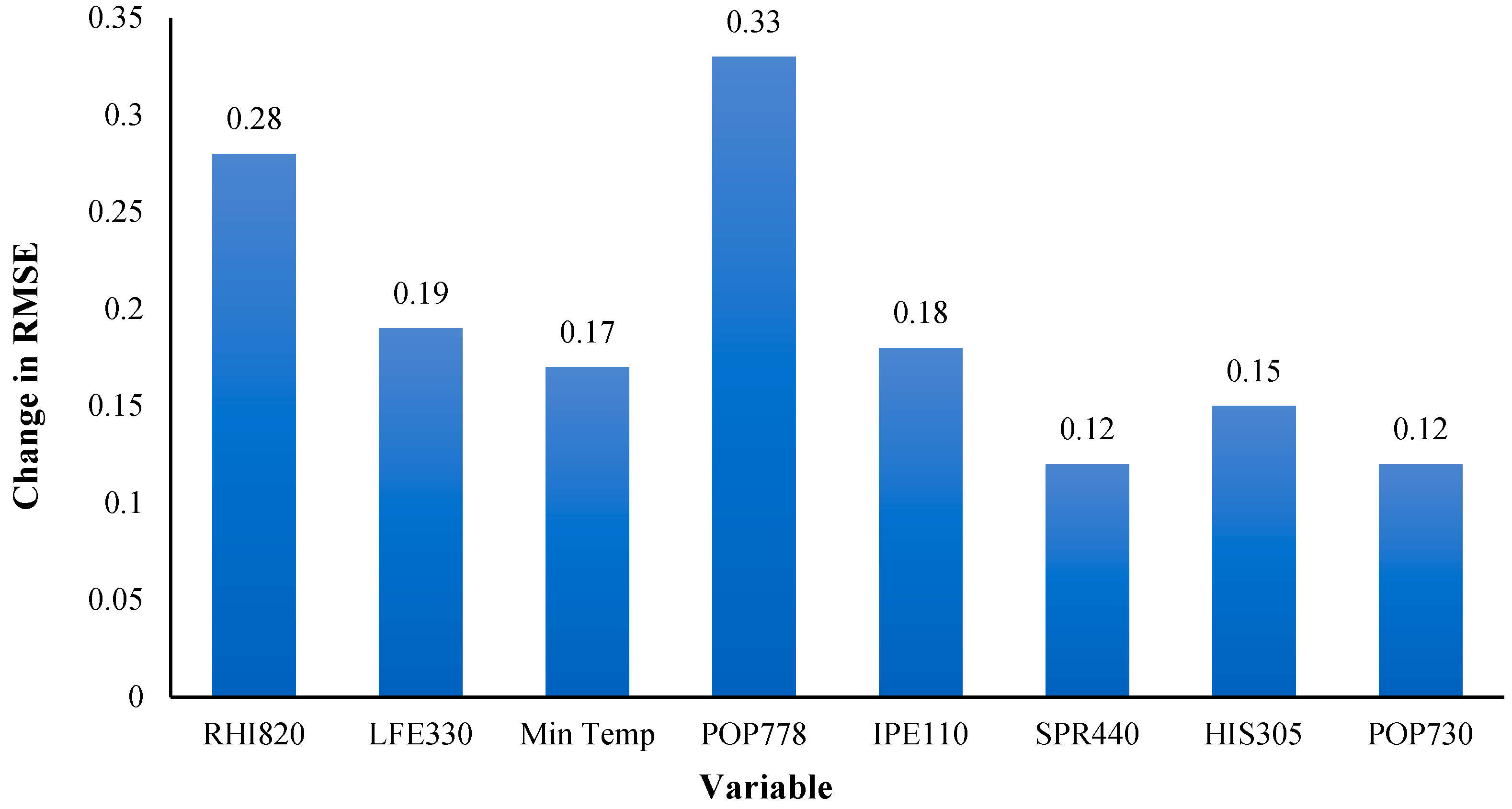
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lalvani, A.; Pathan, A.A.; Durkan, H.; Wilkinson, K.A.; Whelan, A.; Deeks, J.J.; Reece, W.H.; Latif, M.; Pacvol, G.; Hill, A.V. Enhanced contact tracing and spatial tracking of Mycobacterium tuberculosis infection by enumeration of antigen-specific T cells. Lancet 2001, 357, 2017–2021. [Google Scholar] [CrossRef]
- Sreeramareddy, C.T.; Kumar, H.H.; Arokiasamy, J.T. Prevalence of self-reported tuberculosis, knowledge about tuberculosis transmission and its determinants among adults in India: Results from a nation-wide cross-sectional household survey. BMC Infect. Dis. 2013, 13, 16. [Google Scholar]
- Smith, I. Mycobacterium tuberculosis pathogenesis and molecular determinants of virulence. Clin. Microbiol. Rev. 2003, 16, 463–496. [Google Scholar] [CrossRef]
- Whalen, C.; Horsburgh, C.R.; Hom, D.; Lahart, C.; Simberkoff, M.; Ellner, J. Accelerated course of human immunodeficiency virus infection after tuberculosis. Am. J. Respir. Crit. Care Med. 1995, 151, 129–135. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Report 2017. Available online: www.who.int/tb/publications/global_report/en/ (accessed on 12 July 2017).
- Thomas, T.Y.; Rajagopalan, S. Tuberculosis and aging: A global health problem. Clin. Infect. Dis. 2001, 33, 1034–1039. [Google Scholar]
- Figueroa-Munoz, J.I.; Ramon-Pardo, P. Tuberculosis control in vulnerable groups. Bull. World Health Organ. 2008, 86, 733–735. [Google Scholar] [CrossRef]
- Schmit, K.M.; Wansaula, Z.; Pratt, R.; Price, S.F.; Langer, A.J. Tuberculosis-United States, 2016. MMWR. Morb. Mortal. Wkl. Rep. 2017, 66, 289–294. [Google Scholar] [CrossRef]
- Hill, A.N.; Becerra, J.E.; Castro, K.G. Modelling tuberculosis trends in the USA. Epidemiol. Infect. 2012, 140, 1862–1872. [Google Scholar] [CrossRef]
- Sun, W.; Gong, J.; Zhou, J.; Zhao, Y.; Tan, J.; Ibrahim, A.N.; Zhou, Y. A spatial, social and environmental study of tuberculosis in China using statistical and GIS technology. Int. J. Environ. Res. Public Health 2015, 12, 1425–1448. [Google Scholar] [CrossRef]
- Cantwell, M.F.; Mckenna, M.T.; Mccray, E.; Onorato, I.M. Tuberculosis and race/ethnicity in the United States: Impact of socioeconomic status. Am. J. Respir. Crit. Care Med. 1998, 157, 1016–1020. [Google Scholar] [CrossRef]
- Wubuli, A.; Xue, F.; Jiang, D.; Yao, X.; Upur, H.; Wushouer, Q. Socio-demographic predictors and distribution of pulmonary tuberculosis (TB) in Xinjiang, China: A spatial analysis. PLoS ONE 2015, 10, e0144010. [Google Scholar] [CrossRef] [PubMed]
- Mahara, G.; Yang, K.; Chen, S.; Wang, W.; Guo, X. Socio-Economic Predictors and Distribution of Tuberculosis Incidence in Beijing, China: A Study Using a Combination of Spatial Statistics and GIS Technology. Med. Sci. 2018, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Harling, G.; Castro, M.C. A spatial analysis of social and economic determinants of tuberculosis in Brazil. Health Place 2014, 25, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Krieger, N.; Chen, J.T.; Waterman, P.D.; Rehkopf, D.H.; Subramanian, S.V. Race/ethnicity, gender, and monitoring socioeconomic gradients in health: A comparison of area-based socioeconomic measures—The public health disparities geocoding project. Am. J. Public Health 2003, 93, 1655–1671. [Google Scholar] [CrossRef] [PubMed]
- Kistemann, T.; Munzinger, A.; Dangendorf, F. Spatial patterns of tuberculosis incidence in Cologne (Germany). Soc. Sci. Med. 2002, 55, 7–19. [Google Scholar] [CrossRef]
- Jia, Z.W.; Jia, X.W.; Liu, Y.X.; Dye, C.; Chen, F.; Chen, C.S.; Zhang, W.-Y.; Li, X.-W.; Cao, W.-C.; Liu, H.L. Spatial analysis of tuberculosis cases in migrants and permanent residents, Beijing, 2000–2006. Emerg. Infect. Dis. 2008, 14, 1413. [Google Scholar] [CrossRef] [PubMed]
- Hawker, J.I.; Bakhshi, S.S.; Ali, S.; Farrington, C.P. Ecological analysis of ethnic differences in relation between tuberculosis and poverty. BMJ 1999, 319, 1031–1034. [Google Scholar] [CrossRef] [PubMed]
- Mollalo, A.; Alimohammadi, A.; Shahrisvand, M.; Shirzadi, M.R.; Malek, M.R. Spatial and statistical analyses of the relations between vegetation cover and incidence of cutaneous leishmaniasis in an endemic province, northeast of Iran. Asian Pac. J. Trop. Dis. 2014, 4, 176. [Google Scholar] [CrossRef]
- Mollalo, A.; Khodabandehloo, E. Zoonotic cutaneous leishmaniasis in northeastern Iran: A GIS-based spatio-temporal multi-criteria decision-making approach. Epidemiol. Infect. 2016, 144, 2217–2229. [Google Scholar] [CrossRef]
- Shaweno, D.; Karmakar, M.; Alene, K.A.; Ragonnet, R.; Clements, A.C.; Trauer, J.M.; Denholm, J.T.; McBryde, E.S. Methods used in the spatial analysis of tuberculosis epidemiology: A systematic review. BMC Med. 2018, 16, 193. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models, 4th ed.; Irwin: Chicago, IL, USA, 1996. [Google Scholar]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Sadeghian, A.; Lim, D.; Karlsson, J.; Li, J. Automatic target recognition using discrimination based on optimal transport. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2604–2608. [Google Scholar]
- Mollalo, A.; Sadeghian, A.; Israel, G.D.; Rashidi, P.; Sofizadeh, A.; Glass, G.E. Machine learning approaches in GIS-based ecological modeling of the sand fly Phlebotomus papatasi, a vector of zoonotic cutaneous leishmaniasis, Golestan province, Iran. Acta Trop. 2018, 188, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Shirzadi, M.R.; Mollalo, A.; Yaghoobi-Ershadi, M.R. Dynamic relations between incidence of zoonotic cutaneous leishmaniasis and climatic factors in Golestan Province, Iran. J Arthropod Borne Dis. 2015, 9, 148. [Google Scholar] [PubMed]
- Vahedi, B.; Kuhn, W.; Ballatore, A. Question-based spatial computing—A case study. In Geospatial Data in a Changing World; Springer: Cham, Switzerland, 2016; pp. 37–50. [Google Scholar]
- Hatami, M.; Ameri Siahooei, E. Examines criteria applicable in the optimal location new cities, with approach for sustainable urban development. Middle-East, J. Sci. Res. 2013, 14, 734–743. [Google Scholar]
- Bagheri, M.; Bazvand, A.; Ehteshami, M. Application of artificial intelligence for the management of landfill leachate penetration into groundwater, and assessment of its environmental impacts. J. Clean. Prod. 2017, 149, 784–796. [Google Scholar] [CrossRef]
- Sadeghian, A.; Sundaram, L.; Wang, D.; Hamilton, W.; Branting, K.; Pfeifer, C. Semantic edge labeling over legal citation graphs. In Proceedings of the Workshop on Legal Text, Document, and Corpus Analytics (LTDCA-2016), San Diego, CA, USA, 17 June 2016; pp. 70–75. [Google Scholar]
- Janalipour, M.; Mohammadzadeh, A. A fuzzy-ga based decision making system for detecting damaged buildings from high-spatial resolution optical images. Remote Sens. 2017, 9, 349. [Google Scholar] [CrossRef]
- Shafieardekani, M.; Hatami, M. Forecasting Land Use Change in suburb by using Time series and Spatial Approach; Evidence from Intermediate Cities of Iran. Eur. J. Sci. Res. 2013, 116, 199–208. [Google Scholar]
- Rajabi, M.; Mansourian, A.; Pilesjö, P.; Bazmani, A. Environmental modelling of visceral leishmaniasis by susceptibility-mapping using neural networks: A case study in north-western Iran. Geosp. Health 2014, 9, 179–191. [Google Scholar] [CrossRef] [PubMed]
- Mollalo, A.; Alimohammadi, A.; Khoshabi, M. Spatial and spatio-temporal analysis of human brucellosis in Iran. Trans. R. Soc. Trop. Med. Hyg. 2014, 108, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Sordo, M. Introduction to neural networks in healthcare. Open Clin. 2002, 1–7. Available online: http://www.openclinical.org/docs/int/neuralnetworks011.pdf (accessed on 25 July 2018).
- Aburas, H.M.; Cetiner, B.G.; Sari, M. Dengue confirmed-cases prediction: A neural network model. Expert Syst. Appl. 2010, 37, 4256–4260. [Google Scholar] [CrossRef]
- Laureano-Rosario, A.E.; Duncan, A.P.; Mendez-Lazaro, P.A.; Garcia-Rejon, J.E.; Gomez-Carro, S.; Farfan-Ale, J.; Savic, D.A.; Muller-Karger, F.E. Application of Artificial Neural Networks for Dengue Fever Outbreak Predictions in the Northwest Coast of Yucatan, Mexico and San Juan, Puerto Rico. Trop. Med. Infect. Dis. 2018, 3, 5. [Google Scholar] [CrossRef] [PubMed]
- Xue, H.; Bai, Y.; Hu, H.; Liang, H. Influenza activity surveillance based on multiple regression model and artificial neural network. IEEE Access 2018, 6, 563–575. [Google Scholar] [CrossRef]
- Murray, E.J.; Marais, B.J.; Mans, G.; Beyers, N.; Ayles, H.; Godfrey-Faussett, P.; Wallmas, S.; Bond, V. A multidisciplinary method to map potential tuberculosis transmission ‘hot spots’ in high-burden communities. Int. J. Tuberc. Lung Dis. 2009, 13, 767–774. [Google Scholar] [PubMed]
- Mullins, J.; Lobato, M.N.; Bemis, K.; Sosa, L. Spatial clusters of latent tuberculous infection, Connecticut, 2010–2014. Int. J. Tuberc. Lung Dis. 2018, 22, 165–170. [Google Scholar] [CrossRef] [PubMed]
- Bennett, R.J.; Brodine, S.; Waalen, J.; Moser, K.; Rodwell, T.C. Prevalence and treatment of latent tuberculosis infection among newly arrived refugees in San Diego County, January 2010–October 2012. Am. J. Public Health 2014, 104, e95–e102. [Google Scholar] [CrossRef] [PubMed]
- Feske, M.L.; Teeter, L.D.; Musser, J.M.; Graviss, E.A. Including the third dimension: A spatial analysis of TB cases in Houston Harris County. Tuberculosis 2011, 91, S24–S33. [Google Scholar] [CrossRef]
- Scales, D.; Brownstein, J.S.; Khan, K.; Cetron, M.S. Toward a county-level map of tuberculosis rates in the US. Am. J. Prev. Med. 2014, 46, e49. [Google Scholar] [CrossRef]
- HealthMap. Available online: https://healthmap.org/tb (accessed on 25 July 2018).
- American Community Survey (ASC). Available online: https://www.census.gov/programs-surveys/acs/ (accessed on 25 July 2018).
- Center for Disease Control and Prevention (CDC) Wonder. Available online: http://wonder.cdc.gov/ (accessed on 25 July 2018).
- García-Elorriaga, G.; Del Rey-Pineda, G. Type 2 diabetes mellitus as a risk factor for tuberculosis. J. Mycobac. Dis. 2014, 4, 144. [Google Scholar]
- The National Map. Available online: http://nationalmap.gov/ (accessed on 25 July 2018).
- The US Census Bureau. Available online: https://www.census.gov/ (accessed on 25 July 2018).
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An introduction to spatial data analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Mollalo, A.; Blackburn, J.K.; Morris, L.R.; Glass, G.E. A 24-year exploratory spatial data analysis of Lyme disease incidence rate in Connecticut, USA. Geosp. Health 2017, 12. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Mollalo, A.; Alimohammadi, A.; Shirzadi, M.R.; Malek, M.R. Geographic information system-based analysis of the spatial and spatio-temporal distribution of zoonotic cutaneous leishmaniasis in Golestan Province, north-east of Iran. Zoonoses Public Health 2015, 62, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. Local spatial statistics: An overview. Spat. Anal. 1996, 374, 261–277. [Google Scholar]
- Civco, D.L. Artificial neural networks for land-cover classification and mapping. Int. J. Geogr. Inf. Sci. 1993, 7, 173–186. [Google Scholar] [CrossRef]
- Woods, K.; Bowyer, K.W. Generating ROC curves for artificial neural networks. IEEE Trans. Med. Imaging 1997, 16, 329–337. [Google Scholar] [CrossRef]
- Huang, G.B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–281. [Google Scholar] [CrossRef]
- Yilmaz, I.; Kaynar, O. Multiple regression, ANN (RBF, MLP) and ANFIS models for prediction of swell potential of clayey soils. Expert Syst. Appl. 2011, 38, 5958–5966. [Google Scholar] [CrossRef]
- Behrang, M.A.; Assareh, E.; Ghanbarzadeh, A.; Noghrehabadi, A.R. The potential of different artificial neural network (ANN) techniques in daily global solar radiation modeling based on meteorological data. Solar Energy 2010, 84, 1468–1480. [Google Scholar] [CrossRef]
- Karlik, B.; Olgac, A.V. Performance analysis of various activation functions in generalized MLP architectures of neural networks. In. J. Artif. Intell. Expert Syst. 2011, 1, 111–122. [Google Scholar]
- Zadeh, M.R.; Amin, S.; Khalili, D.; Singh, V.P. Daily outflow prediction by multi layer perceptron with logistic sigmoid and tangent sigmoid activation functions. Water Resour. Manag. 2010, 24, 2673–2688. [Google Scholar] [CrossRef]
- Bagheri, M.; Mirbagheri, S.A.; Ehteshami, M.; Bagheri, Z. Modeling of a sequencing batch reactor treating municipal wastewater using multi-layer perceptron and radial basis function artificial neural networks. Process Saf. Environ. Prot. 2015, 93, 111–123. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Riedmiller, M. Advanced supervised learning in multi-layer perceptrons-from backpropagation to adaptive learning algorithms. Comput. Stand. Interfaces 1994, 16, 265–278. [Google Scholar] [CrossRef]
- Shanker, M.; Hu, M.Y.; Hung, M.S. Effect of data standardization on neural network training. Omega 1996, 24, 385–397. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Park, M.Y.; Hastie, T. L1-regularization path algorithm for generalized linear models. J. R. Stat. Soc. Ser. B 2007, 69, 659–677. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Multivariate hyperbolic tangent neural network approximation. Comput. Math. Appl. 2011, 61, 809–821. [Google Scholar] [CrossRef]
- Singh, P.; Deo, M.C. Suitability of different neural networks in daily flow forecasting. App. Soft Comput. 2007, 7, 968–978. [Google Scholar] [CrossRef]
- Institute of Medicine: Ending Neglect: The Elimination of Tuberculosis in the United States; National Academy Press: Washington, DC, USA, 2000.
- Georgia Tuberculosis Report (2017). Available online: https://dph.georgia.gov/sites/dph.georgia.gov/files/2016%20GA%20TB%20Report%20FINAL.pdf (accessed on 25 November 2018).
- Florida Tuberculosis Report (2016). Available online: http://www.floridahealth.gov/diseases-and-conditions/tuberculosis/tb-statistics/index.html (accessed on 25 November 2018).
- Onozuka, D.; Hagihara, A. The association of extreme temperatures and the incidence of tuberculosis in Japan. Int. J. Biometeorol. 2015, 59, 1107–1114. [Google Scholar] [CrossRef] [PubMed]
- Mourtzoukou, E.G.; Falagas, M.E. Exposure to cold and respiratory tract infections. Int. J. Tuberc. Lung Dis. 2007, 11, 938–943. [Google Scholar] [PubMed]
- Khalid, A.; Baqai, T.; Bukhari, M.; Khan, M.M. Comparison of the incidence of tuberculosis in different geographical zones in the state of Jammu and Kashmir. Pak. J. Chest 2015, 19, 1–7. [Google Scholar]
- McKenna, M.T.; McCray, E.; Onorato, I. The epidemiology of tuberculosis among foreign-born persons in the United States, 1986 to 1993. N. Engl. J. Med. 1995, 332, 1071–1076. [Google Scholar] [CrossRef] [PubMed]
- Ho, M.J. Sociocultural aspects of tuberculosis: A literature review and a case study of immigrant tuberculosis. Soc. Sci. Med. 2004, 59, 753–762. [Google Scholar] [CrossRef] [PubMed]
- Weis, S.E.; Moonan, P.K.; Pogoda, J.M.; Turk, L.E.; King, B.; Freeman-Thompson, S.; Burgess, G. Tuberculosis in the foreign-born population of Tarrant county, Texas by immigration status. Am. J. Respir. Crit. Care Med. 2001, 164, 953–957. [Google Scholar] [CrossRef] [PubMed]
- Munch, Z.; Van Lill, S.W.P.; Booysen, C.N.; Zietsman, H.L.; Enarson, D.A.; Beyers, N. Tuberculosis transmission patterns in a high-incidence area: A spatial analysis. Int. J. Tuberc. Lung Dis. 2003, 7, 271–277. [Google Scholar] [PubMed]
- Dos Santos, M.A.; Albuquerque, M.F.; Ximenes, R.A.; Lucena-Silva, N.L.; Braga, C.; Campelo, A.R.; Dantas, O.M.; Montarroyos, U.R.; Souza, W.V.; Kawasaki, A.M.; et al. Risk factors for treatment delay in pulmonary tuberculosis in Recife, Brazil. BMC Public Health 2005, 5, 25. [Google Scholar] [CrossRef]
- Jakubowiak, W.M.; Bogorodskaya, E.M.; Borisov, E.S.; Danilova, D.I.; Kourbatova, E.K. Risk factors associated with default among new pulmonary TB patients and social support in six Russian regions. Int. J. Tuberc. Lung Dis. 2007, 11, 46–53. [Google Scholar]
- Djibuti, M.; Mirvelashvili, E.; Makharashvili, N.; Magee, M.J. Household income and poor treatment outcome among patients with tuberculosis in Georgia: A cohort study. BMC Public Health 2014, 14, 88. [Google Scholar] [CrossRef]
- Bamrah, S.; Yelk Woodruff, R.S.; Powell, K.; Ghosh, S.; Kammerer, J.S.; Haddad, M.B. Tuberculosis among the homeless, United States, 1994–2010. Int. J. Tuberc. Lung Dis. 2013, 17, 1414–1419. [Google Scholar] [CrossRef] [PubMed]
- Mapping and Analyzing Race and Ethnicity. Available online: https://www2.census.gov/programs-surveys/sis/activities/geography/hg-2_teacher.pdf (accessed on 25 November 2018).
- Centers for Disease Control and Prevention. Trends in tuberculosis—United States, 2010. MMWR. Morb. Mortal. Wkl. Rep. 2011, 60, 333. [Google Scholar]
- Lam, H.K.; Ling, S.H.; Leung, F.H.; Tam, P.K.S. Tuning of the structure and parameters of neural network using an improved genetic algorithm. In Proceedings of the 27th IEEE Annual Conference of the Industrial Electronics Society, IECON’01, Denver, CO, USA, 29 November–2 December 2001; Volume 1, pp. 25–30. [Google Scholar]
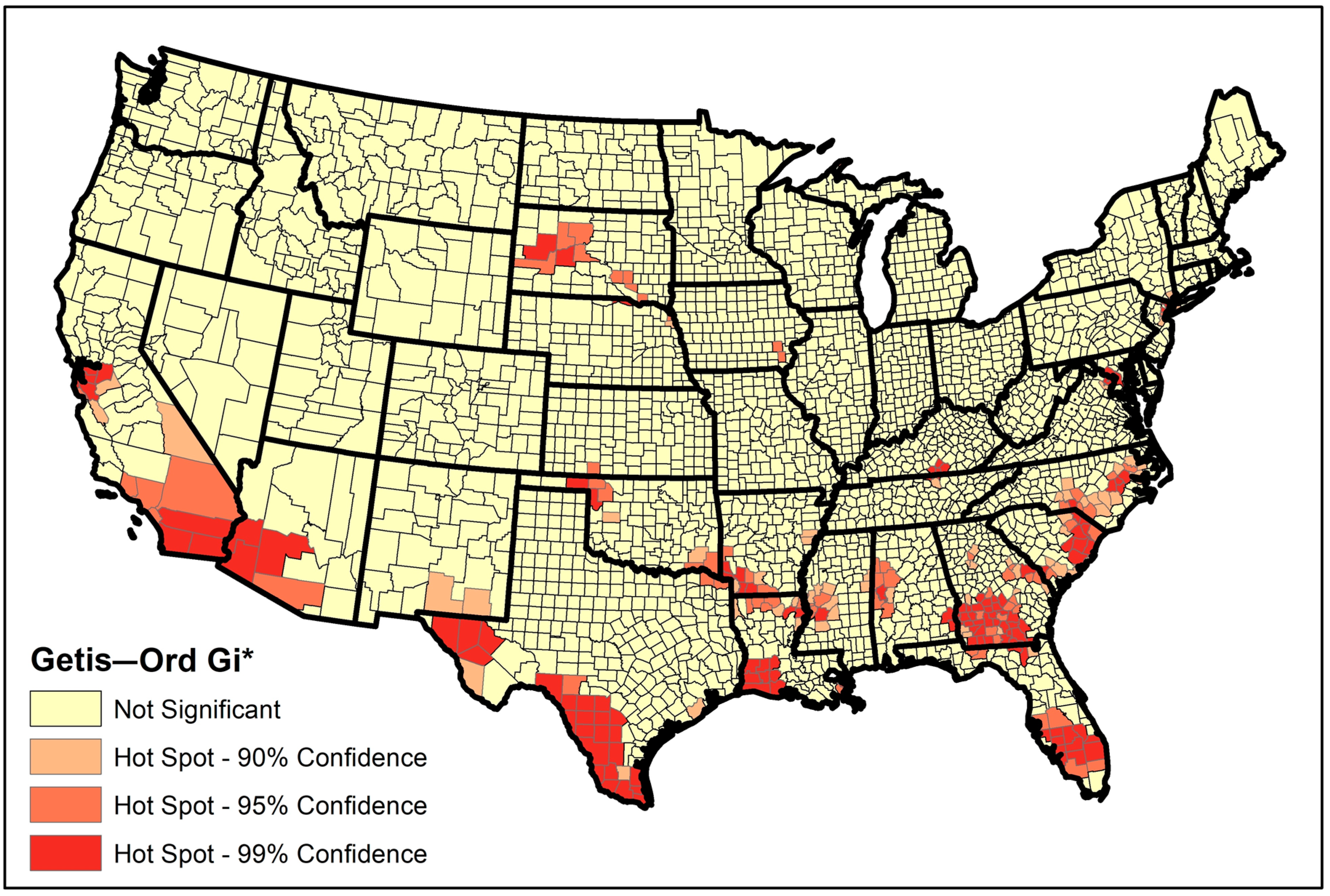
| Rank | State | No. Hotspot Counties | Percentage (#hotspots/#counties) |
|---|---|---|---|
| 1 | Georgia | 57 | 35.8% |
| 2 | Texas | 30 | 11.8% |
| 3 | North Carolina | 23 | 23.0% |
| 4 | Louisiana | 22 | 34.3% |
| 5 | Florida | 20 | 29.9% |
| 6 | California | 17 | 22.7% |
| 7 | South Carolina | 17 | 37% |
| 8 | Arkansas | 12 | 16.0% |
| 9 | Mississippi | 12 | 14.6% |
| 10 | Alabama | 10 | 14.9% |
| POP730 | LFE330 | IPE110 | POP778 | Min Temp | SPR440 | HIS305 | RHI820 | |
|---|---|---|---|---|---|---|---|---|
| POP730 | 1.000 | 0.051 | 0.041 | 0.064 | −0.124 | −0.078 | −0.138 | −0.024 |
| LFE330 | 0.051 | 1.000 | 0.018 | 0.057 | 0.136 | −0.499 | −0.186 | −0.040 |
| IPE110 | 0.041 | 0.018 | 1.000 | 0.266 | −0.231 | −0.108 | 0.066 | 0.384 |
| POP778 | 0.064 | 0.057 | 0.266 | 1.000 | −0.005 | 0.091 | −0.390 | 0.248 |
| Min Temp | −0.124 | 0.136 | −0.231 | −0.005 | 1.000 | 0.066 | −0.032 | 0.308 |
| SPR440 | −0.078 | −0.499 | −0.108 | 0.091 | 0.066 | 1.000 | −0.015 | 0.003 |
| HIS305 | −0.138 | −0.186 | 0.066 | −0.390 | −0.032 | −0.015 | 1.000 | 0.403 |
| RHI820 | −0.024 | −0.040 | 0.384 | 0.248 | 0.308 | 0.003 | 0.403 | 1.000 |
| R | R Square | Adjusted R Square | Change Statistics | Durbin–Watson | |||||
|---|---|---|---|---|---|---|---|---|---|
| R Square Change | F | df1 | df2 | Sig. | |||||
| LR | 0.666 a | 0.443 | 0.440 | 0.443 | 184.246 | 8 | 1854 | 0.000 | 2.041 |
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | 95.0% Confidence Interval for B | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|---|
| Variables | B | Beta | Lower Bound | Upper Bound | Tolerance | VIF | ||
| (Constant) | 0.001 | 0.009 | 0.993 | −0.198 | 0.200 | |||
| RHI820 | −0.007 | −0.294 | −11.117 | 0.000 | −0.009 | −0.006 | 0.429 | 2.328 |
| LFE330 | −0.023 | −0.166 | −7.929 | 0.000 | −0.029 | −0.017 | 0.683 | 1.463 |
| Min Temp | 0.013 | 0.210 | 9.809 | 0.000 | 0.010 | 0.016 | 0.653 | 1.532 |
| POP778 | 0.083 | 0.282 | 12.621 | 0.000 | 0.070 | 0.095 | 0.602 | 1.661 |
| IPE110 | 0.012 | 0.140 | 6.662 | 0.000 | 0.008 | 0.015 | 0.677 | 1.477 |
| SPR440 | −0.009 | −0.097 | −4.703 | 0.000 | −0.013 | −0.005 | 0.701 | 1.426 |
| HIS305 | −0.019 | −0.145 | −5.976 | 0.000 | −0.026 | −0.013 | 0.508 | 1.968 |
| POP730 | −0.015 | −0.080 | −4.489 | 0.000 | −0.021 | −0.008 | 0.950 | 1.053 |
| Model | Training | Cross-Validation | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | R | MAE | RMSE | R | MAE | RMSE | R | |
| LR | 0.27 | 0.35 | 0.66 | 0.27 | 0.36 | 0.65 | 0.28 | 0.36 | 0.61 |
| MLP (1 hidden layer) | 0.25 | 0.33 | 0.70 | 0.26 | 0.35 | 0.67 | 0.27 | 0.35 | 0.63 |
| MLP (2 hidden layers) | 0.26 | 0.34 | 0.69 | 0.26 | 0.35 | 0.65 | 0.27 | 0.36 | 0.62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mollalo, A.; Mao, L.; Rashidi, P.; Glass, G.E. A GIS-Based Artificial Neural Network Model for Spatial Distribution of Tuberculosis across the Continental United States. Int. J. Environ. Res. Public Health 2019, 16, 157. https://doi.org/10.3390/ijerph16010157
Mollalo A, Mao L, Rashidi P, Glass GE. A GIS-Based Artificial Neural Network Model for Spatial Distribution of Tuberculosis across the Continental United States. International Journal of Environmental Research and Public Health. 2019; 16(1):157. https://doi.org/10.3390/ijerph16010157
Chicago/Turabian StyleMollalo, Abolfazl, Liang Mao, Parisa Rashidi, and Gregory E. Glass. 2019. "A GIS-Based Artificial Neural Network Model for Spatial Distribution of Tuberculosis across the Continental United States" International Journal of Environmental Research and Public Health 16, no. 1: 157. https://doi.org/10.3390/ijerph16010157
APA StyleMollalo, A., Mao, L., Rashidi, P., & Glass, G. E. (2019). A GIS-Based Artificial Neural Network Model for Spatial Distribution of Tuberculosis across the Continental United States. International Journal of Environmental Research and Public Health, 16(1), 157. https://doi.org/10.3390/ijerph16010157






