Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Data Processing
- change-point detection and modeling of each segment with an AR model;
- calculation of kernel density estimation (KDE) of the AR model parameters (qualitative analysis);
- calculation of p-value histograms of the parameters obtained from the AR model (quantitative analysis).
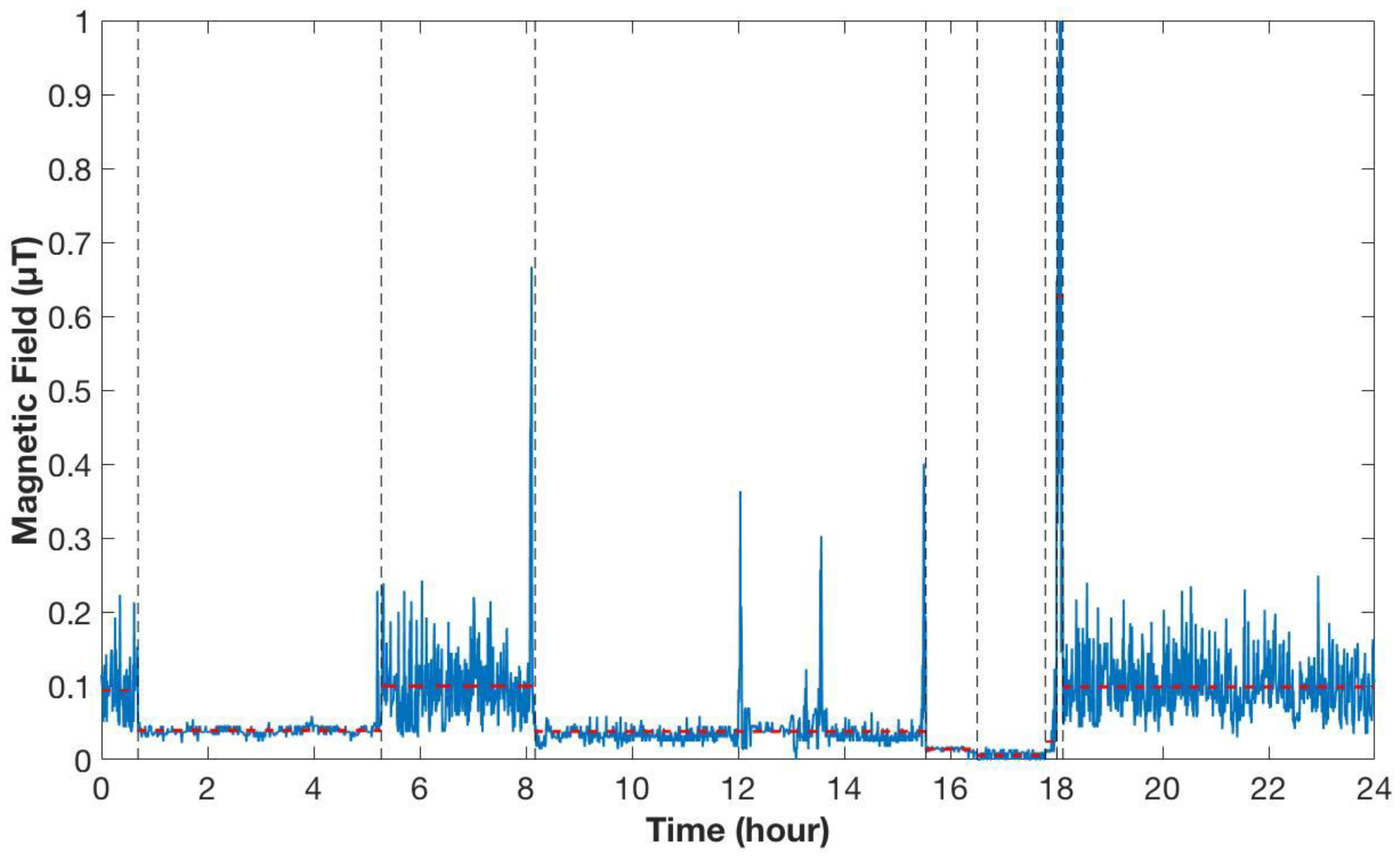
2.2.1. Change-Point Detection and AR Modeling
- find the periods of stability and homogeneity in the behavior of the time series;
- identify the change-points;
- represent the regularities and features of each segments (estimate the model of each segment by parameters like change-points location, segment mean and variance, and segment duration for each day of recording).
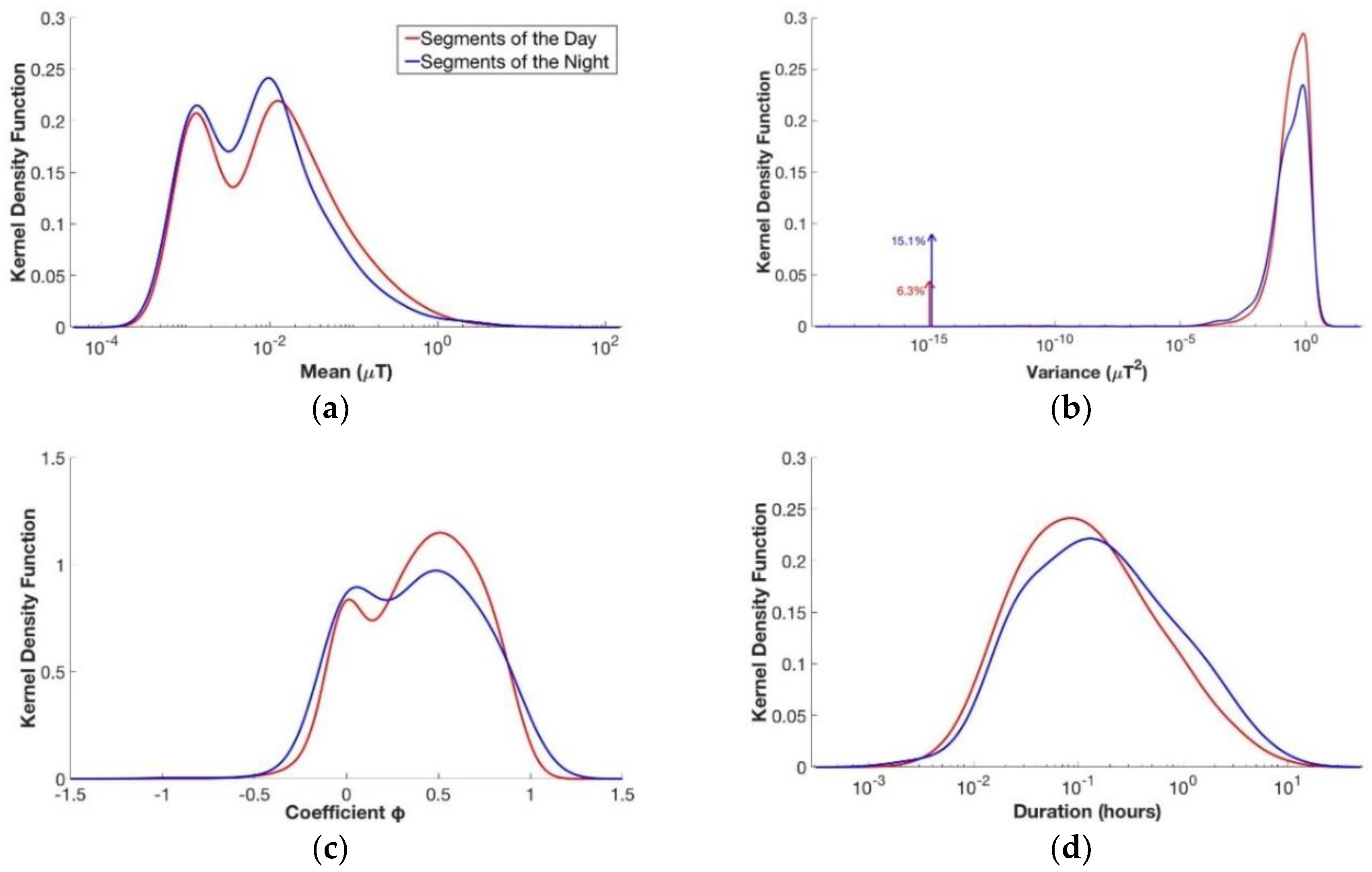
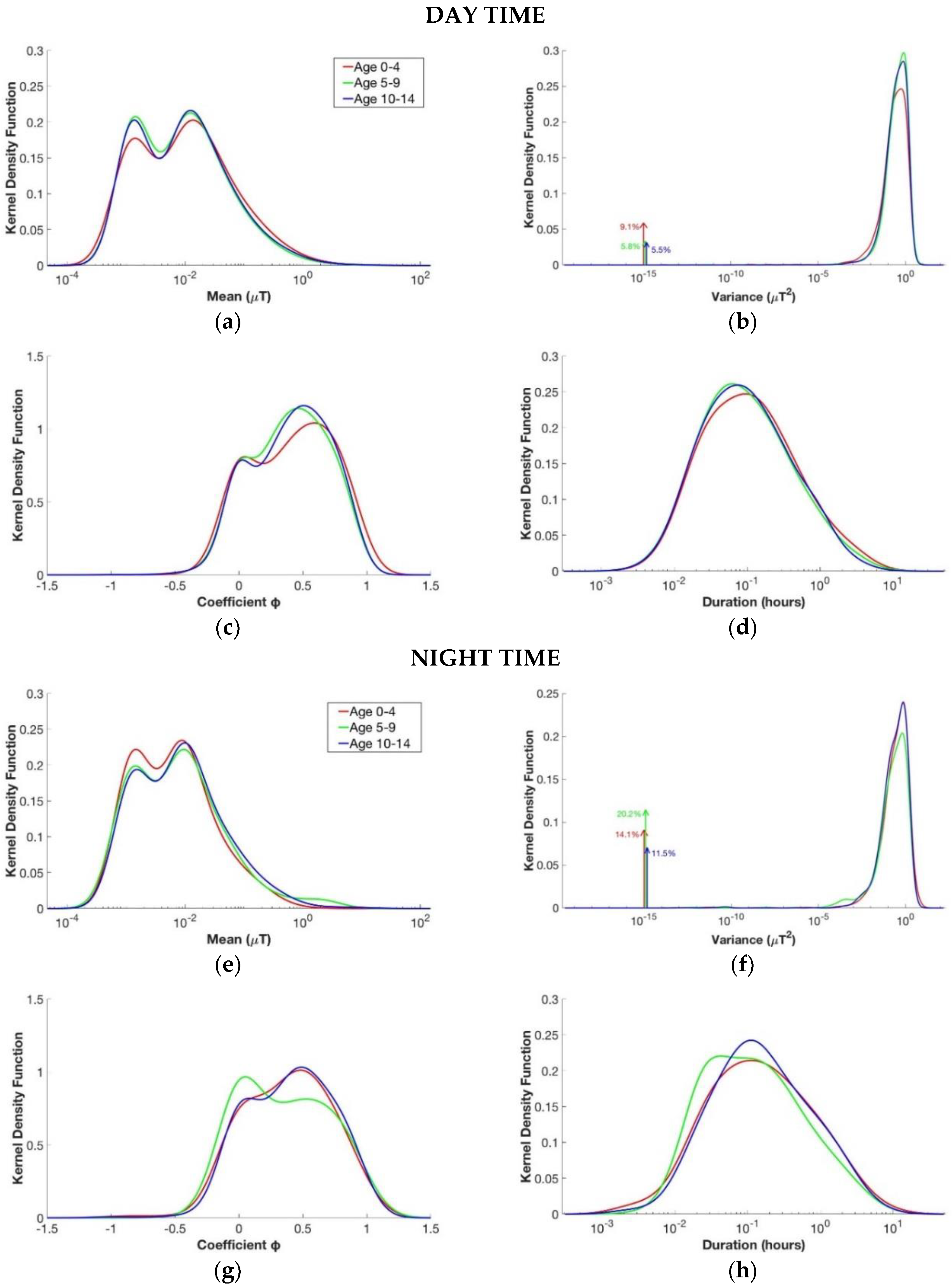
- the mean of the stationary process (μ);
- the variance of the stationary process (σ2);
- the coefficient of the AR model of order 1 (ϕ);
- the duration of the stationary process (T).
2.2.2. Calculation of Kernel Density Estimations of the Four Parameters
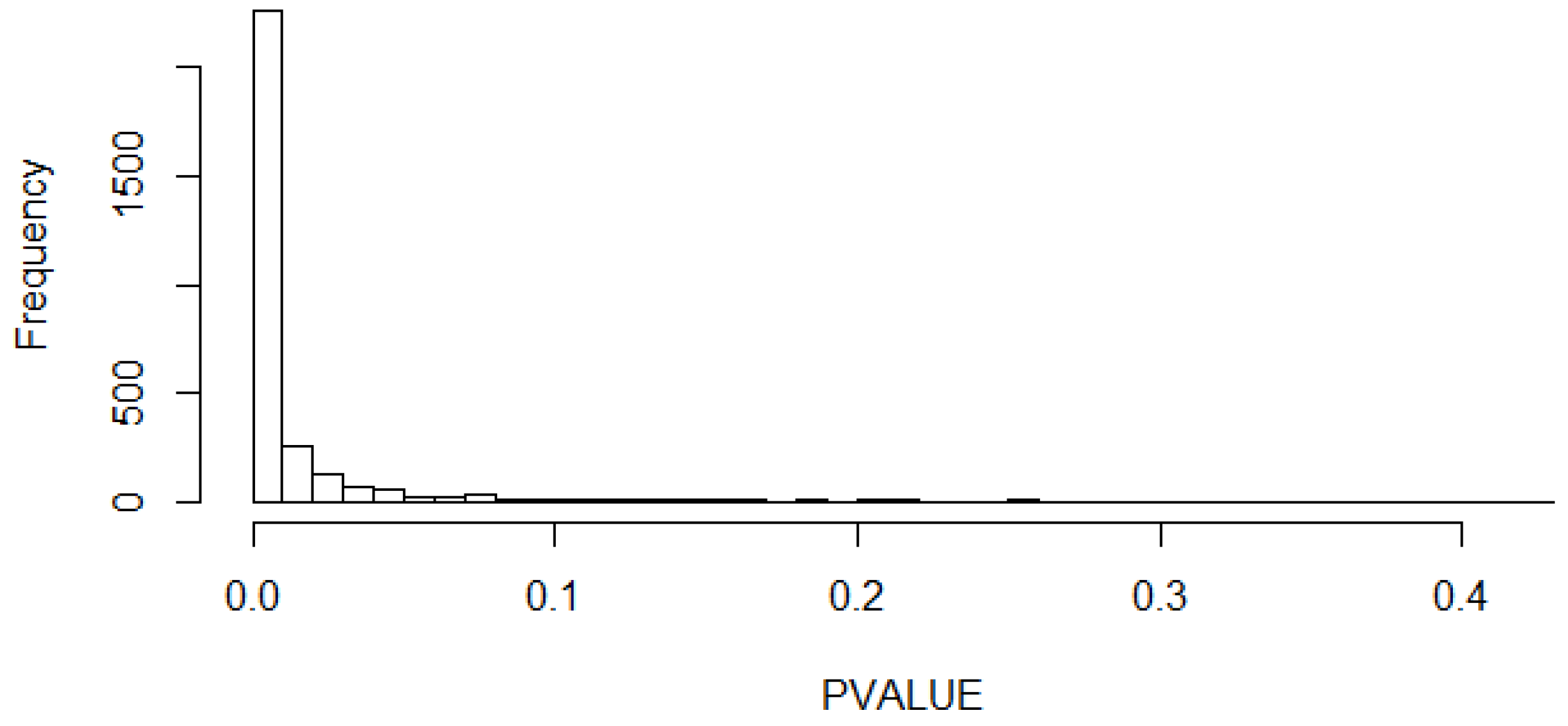
2.2.3. Calculation of p-Value Histograms of the 4 Parameters
2.3. Data Analysis
- Segments regarding daytime (from 07:00 to 21:00 h) and segments regarding night time recordings (from 21:01 to 06:59 h) considering the whole database.
- Segments divided by the children’s age from whole database. Three groups were analyzed: children from 0 to 4 (these data were only from the EXPERS database), children from 5 to 9, and children from 10 to 14.
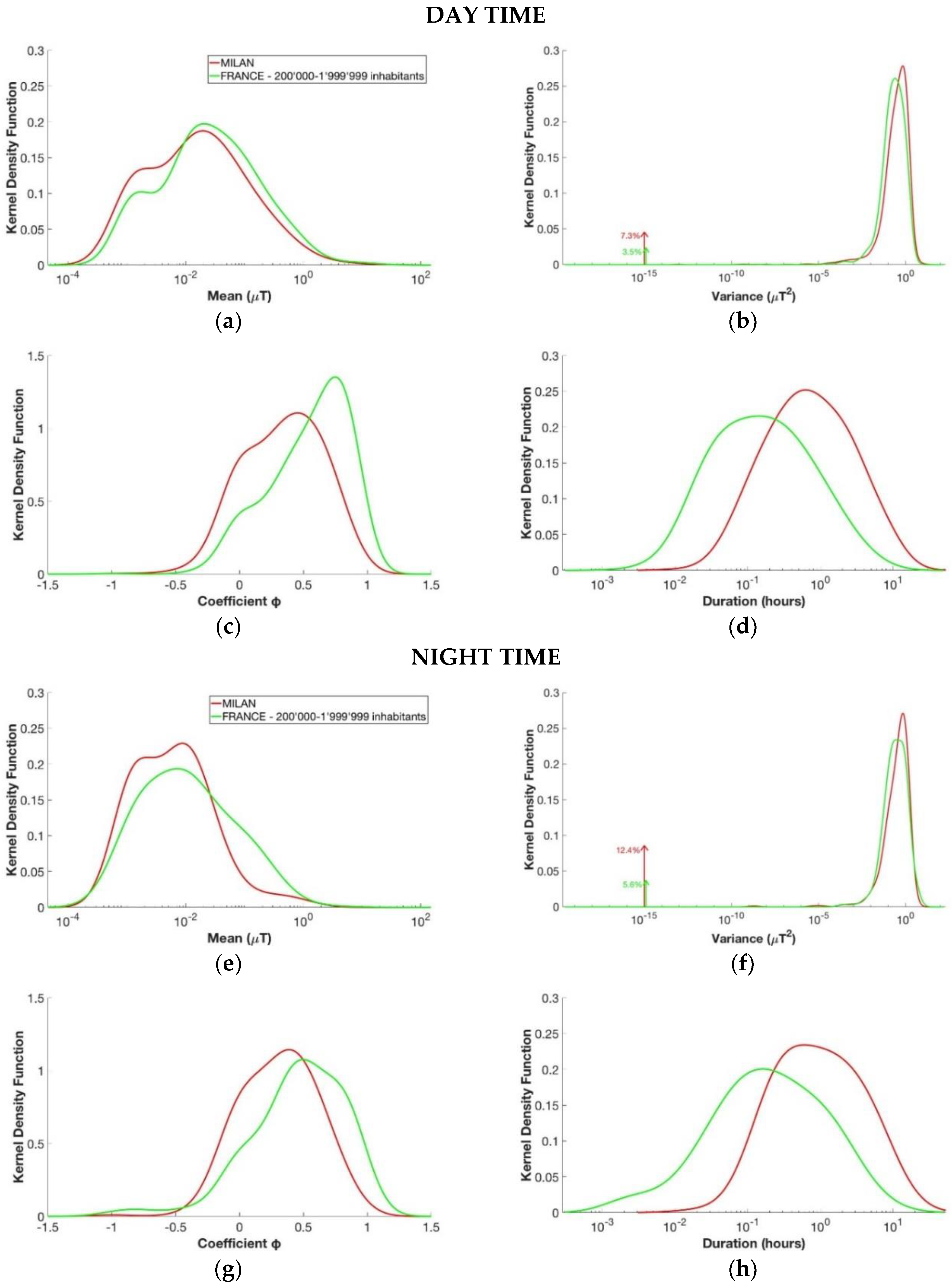
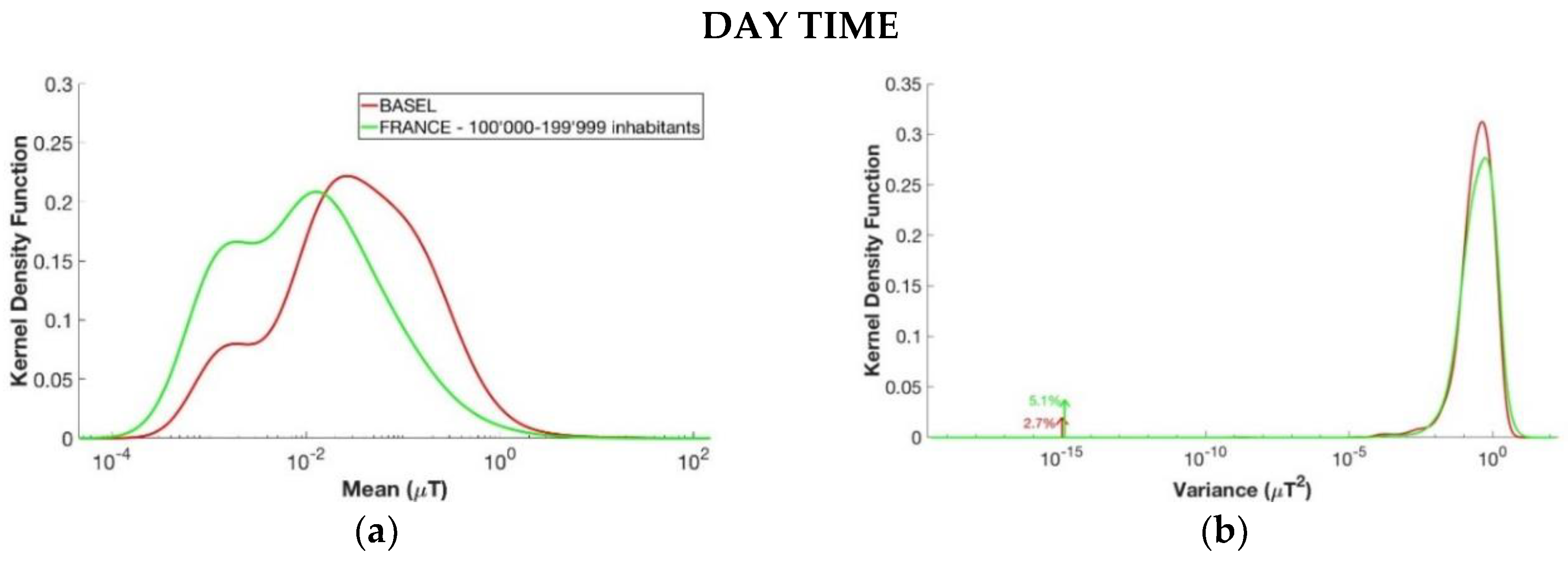
- Segments divided by the number of inhabitants of the town where the children were living. In this case, the ARIMMORA database was split into segments regarding the measurements in Milan and the ones in Basel. The EXPERS database was split into segments regarding the measurements in Paris and in the rural area (less than 2000 inhabitants), and into different groups based on the number of town’s inhabitants, as shown in Table 2.
- Segments divided by the distance between the children’s domicile and the nearest ML/LV substation. As can seen from Table 2, for this last analysis, only the EXPERS database was considered. The EXPERS database was split into three groups. The first group collected the segments obtained from recordings of children whose domicile was at least 40 m away from the substation; the second group were the segments obtained from the children’s recordings where the substation is less than 40 m away from the children’s domicile; the last group were the segments obtained from the children’s recordings where the substation is in the same building of children’s domicile or adjacent.
3. Results and Discussion
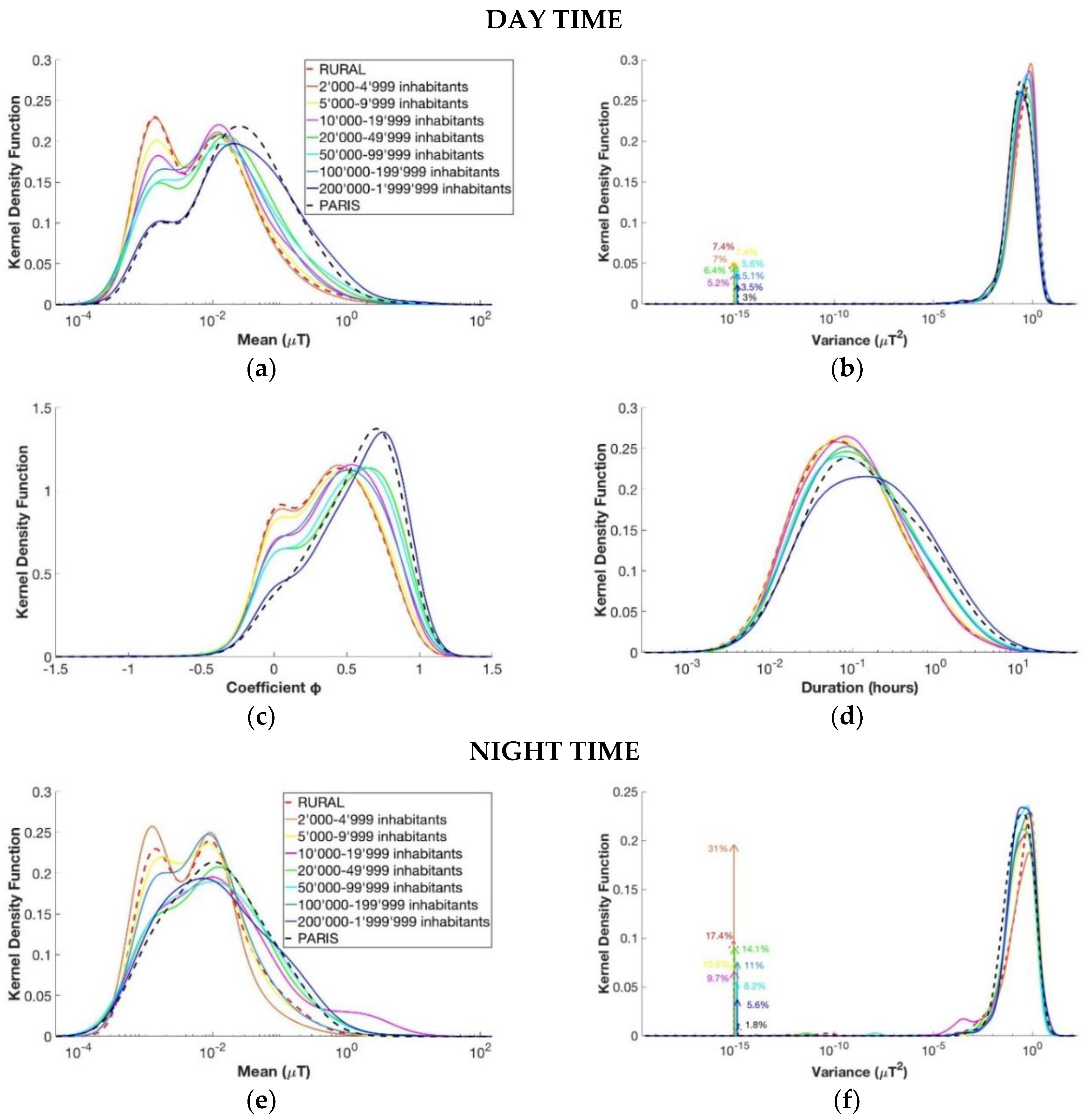
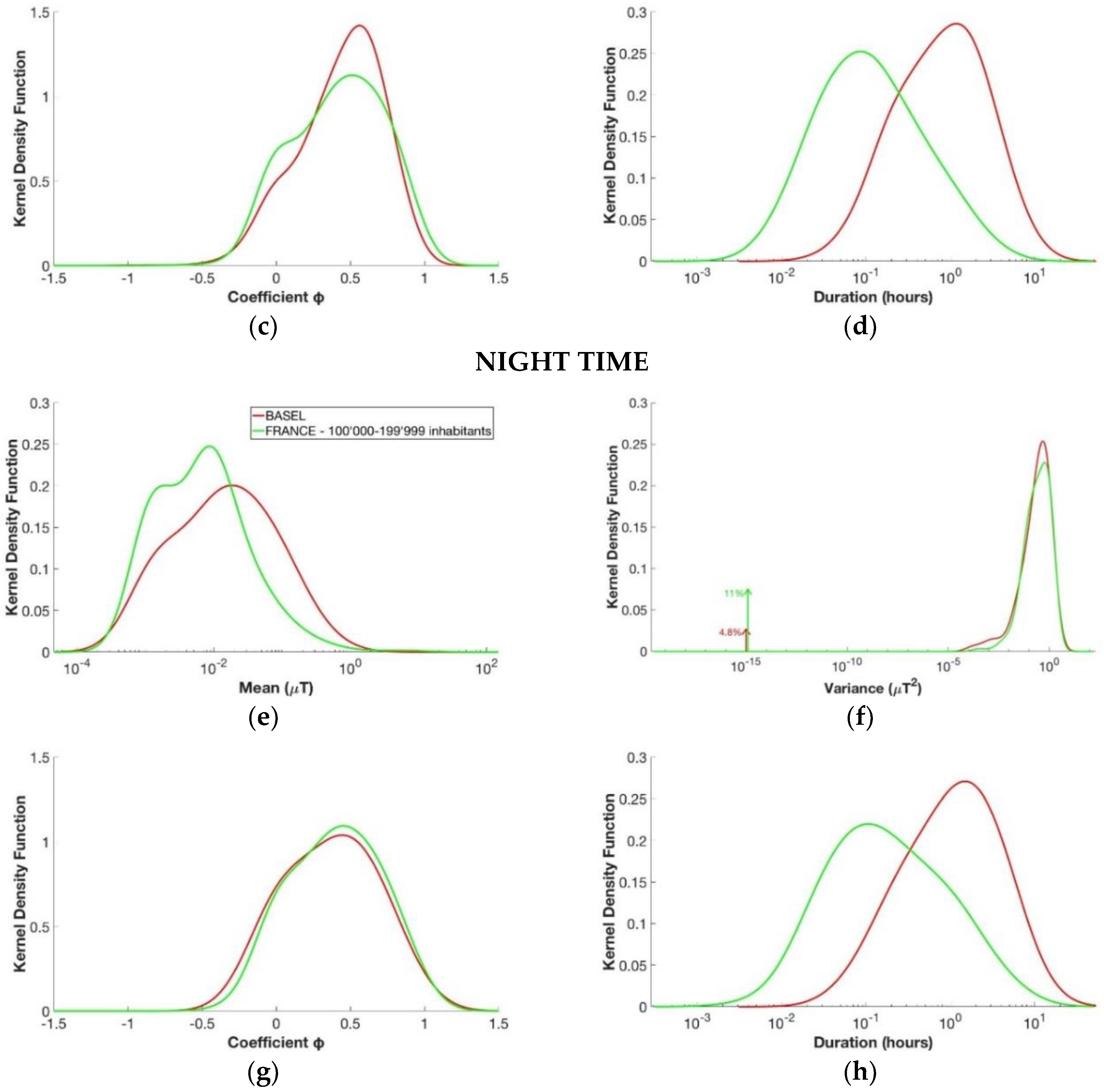
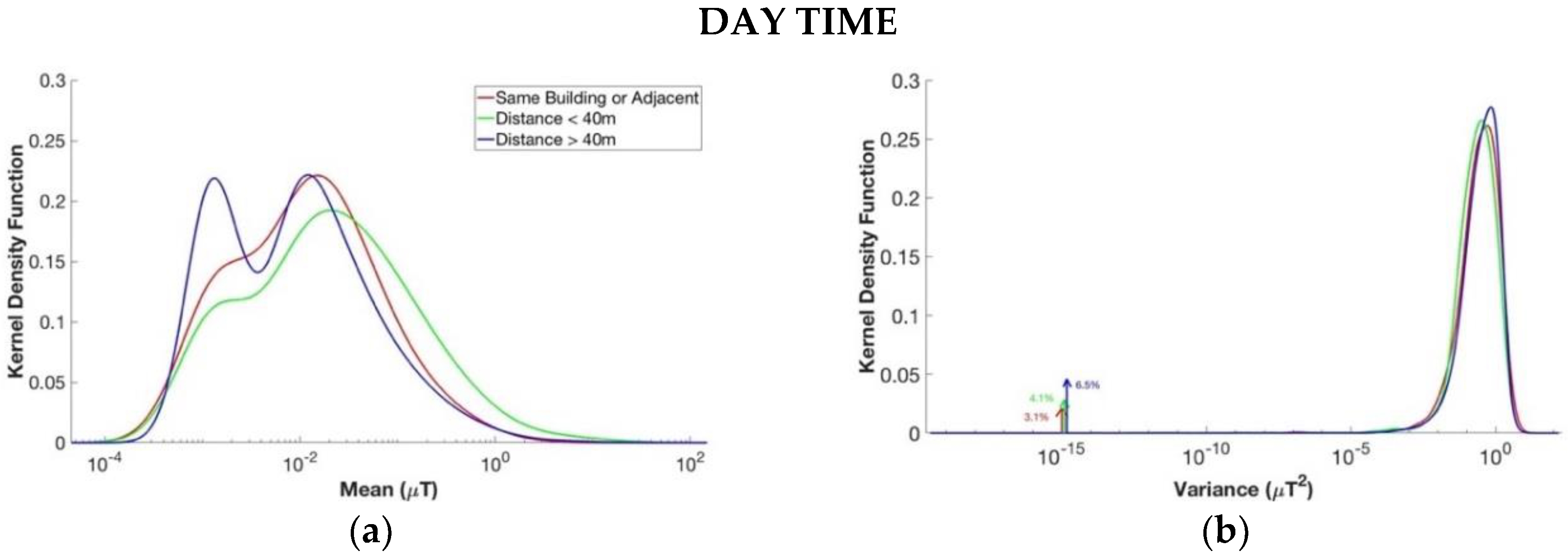
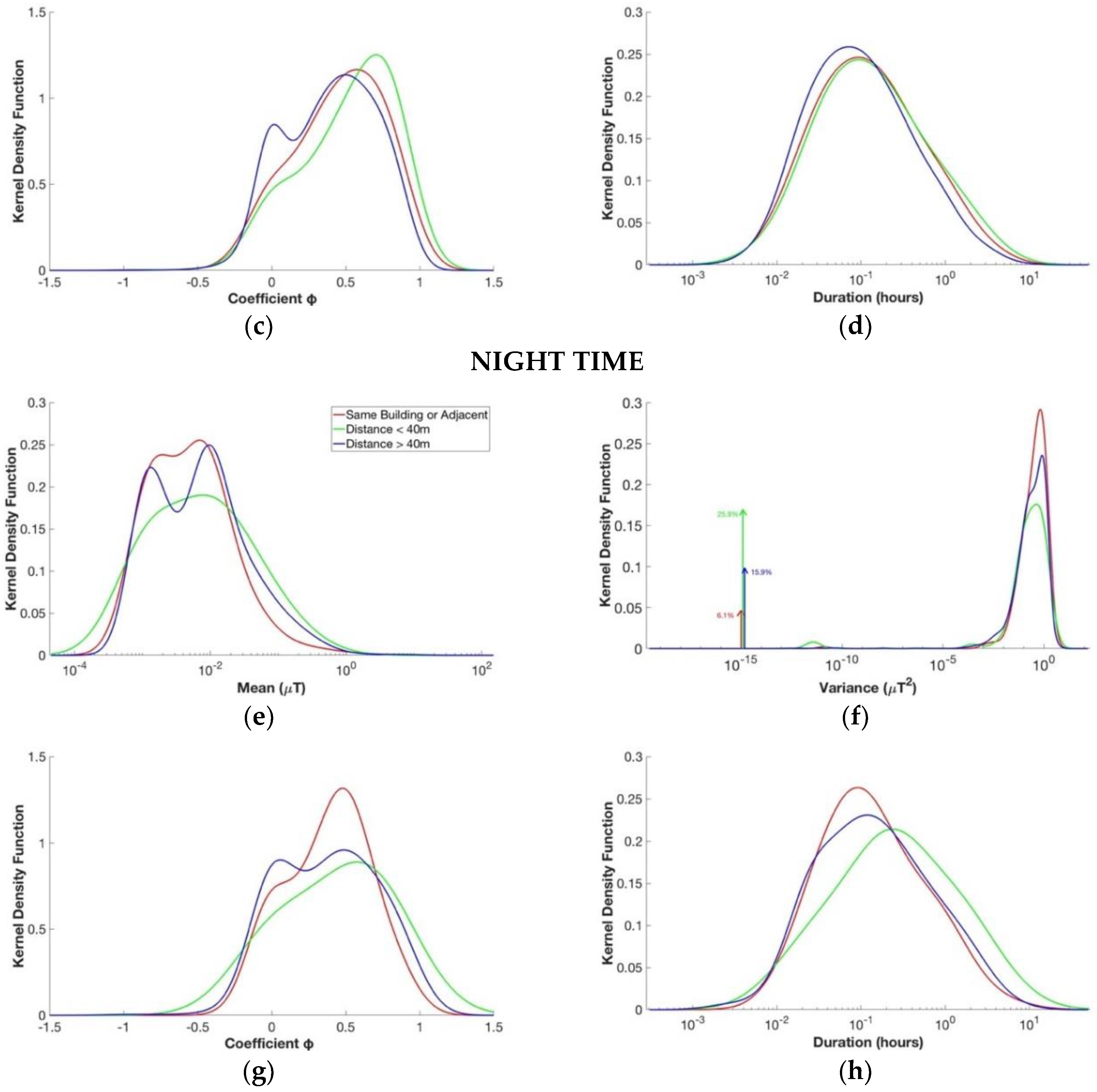
3.1. Daytime Versus Nighttime
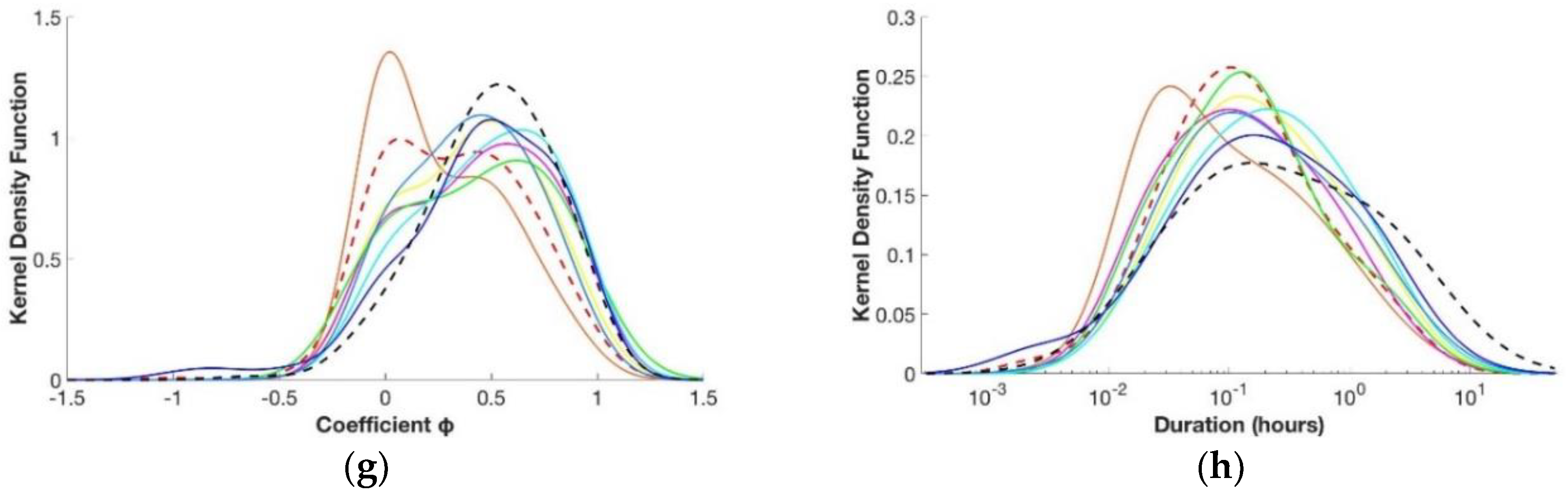
3.2. Children’s Age
3.3. Number of Inhabitants
3.4. Distance from ML/LV Substation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wertheimer, N.; Leeper, E.D. Electrical wiring configurations and childhood cancer. Am. J. Epidemiol. 1979, 109, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Greenland, S.; Sheppard, A.R.; Kaune, W.T.; Poole, C.; Kelsh, M.A. A pooled analysis of magnetic fields, wire codes, and childhood leukemia. Epidemiology 2000, 11, 624–634. [Google Scholar] [CrossRef] [PubMed]
- Ahlbom, A.; Day, N.; Feychting, M.; Roman, E.; Skinner, J.; Dockerty, J.; Linet, M.; McBride, M.; Michaelis, J.; Olsen, J.H.; et al. A pooled analysis of magnetic fields and childhood leukaemia. Br. J. Cancer 2000, 83, 692–698. [Google Scholar] [CrossRef] [PubMed]
- Kheifets, L.; Ahlbom, A.; Crespi, C.M.; Draper, G.; Hagihara, J.; Lowenthal, R.M.; Mezei, G.; Oksuzyan, S.; Schüz, J.; Swanson, J.; et al. Pooled analysis of recent studies on magnetic fields and childhood leukaemia. Br. J. Cancer 2010, 103, 1128–1135. [Google Scholar] [CrossRef] [PubMed]
- Steliarova-Foucher, E.; Stiller, C.; Kaatsch, P.; Berrino, F.; Coebergh, J.W.; Lacour, B.; Perkin, M. Geographical patterns and time trends of cancer incidence and survival among children and adolescents in Europe since the 1970s (the ACCIS project): An epidemiological study. Lancet 2004, 36, 2097–2105. [Google Scholar] [CrossRef]
- IARC Working Group on the Evaluation of Carcinogenic Risks to Humans. Non-Ionizing Radiation, Part 1: Static and extremely low frequency (ELF) electric and magnetic fields. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; IARC Press: Lyon, France, 2002; Volume 80. [Google Scholar]
- Schüz, J.; Dasenbrock, C.; Ravazzani, P.; Röösli, M.; Schär, P.; Bounds, P.L.; Erdmann, F.; Borkhardt, A.; Cobaleda, C.; Fedrowitz, M.; et al. Extremely low-frequency magnetic fields and risk of childhood leukemia: A risk assessment by the ARIMMORA consortium. Bioelectromagnetics 2016, 37, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Forssén, U.M.; Ahlbom, A.; Feychting, M. Relative contribution of residential and occupational magnetic field exposure over twenty-four hours among people living close to and far from a power line. Bioelectromagnetics 2002, 23, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Vistnes, A.I.; Ramberg, G.B.; Bjørnevik, L.R.; Tynes, T.; Haldorsen, T. Exposure of children to residential magnetic fields in Norway: Is proximity to power lines an adequate predictor of exposure? Bioelectromagnetics 1997, 18, 47–57. [Google Scholar] [CrossRef]
- Friedman, D.R.; Hatch, E.E.; Tarone, R.; Kaune, W.T.; Kleinerman, R.A.; Wacholder, S.; Boice, J.D., Jr.; Linet, M.S. Childhood exposure to magnetic fields: Residential area measurements compared to personal dosimetry. Epidemiology 1996, 7, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Foliart, D.E.; Iriye, R.N.; Tarr, K.J.; Silva, J.M.; Kavet, R.; Ebi, K.L. Alternative magnetic field exposure metrics: Relationship to TWA, appliance use, and demographic characteristics of children in a leukemia survival study. Bioelectromagnetics 2001, 22, 574–580. [Google Scholar] [CrossRef] [PubMed]
- Foliart, D.E.; Iriye, R.N.; Silva, J.M.; Mezei, G.; Tarr, K.J.; Ebi, K.L. Correlation of year-to-year magnetic field exposure metrics among children in a leukemia survival study. J. Expo. Anal. Environ. Epidemiol. 2002, 12, 441–447. [Google Scholar] [CrossRef] [PubMed]
- Kaune, W.T. Assessing human exposure to power-frequency electric and magnetic fields. Environ. Health Perspect. 1993, 101 (Suppl. 4), 121–133. [Google Scholar] [CrossRef] [PubMed]
- Deadman, J.E.; Armstrong, B.G.; McBride, M.L.; Gallagher, R.; Thériault, G. Exposures of children in Canada to 60-Hz magnetic and electric fields. Scand. J. Work Environ. Health 1999, 25, 368–375. [Google Scholar] [CrossRef] [PubMed]
- McBride, M.L.; Gallagher, R.P.; Thériault, G.; Armstrong, B.G.; Tamaro, S.; Spinelli, J.J.; Deadman, J.E.; Fincham, S.; Robson, D.; Choi, W. Power-frequency electric and magnetic fields and risk of childhood leukemia in Canada. Am. J. Epidemiol. 1999, 149, 831–842. [Google Scholar] [CrossRef] [PubMed]
- Li, C.Y.; Mezei, G.; Sung, F.C.; Silva, M.; Chen, P.C.; Lee, P.C.; Chen, L.M. Survey of residential extremely-low-frequency magnetic field exposure among children in Taiwan. Environ. Int. 2007, 33, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Lin, I.F.; Li, C.Y.; Wang, J.D. Analysis of individual- and school-level clustering of power frequency magnetic fields. Bioelectromagnetics 2008, 29, 564–570. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.H.; Ju, M.N.; Myung, S.H.; Shin, K.Y.; Hwang, G.H.; Park, J.H. Development of a New Personal Magnetic Field Exposure Estimation Method for Use in Epidemiological EMF Surveys among Children under 17 Years of Age. J. Electr. Eng. Technol. 2012, 7, 376–383. [Google Scholar] [CrossRef]
- ICNIRP—International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz to 100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar]
- Schüz, J.; Grigat, J.P.; Brinkmann, K.; Michaelis, J. Residential magnetic fields as a risk factor for childhood acute leukaemia: Results from a German population-based case-control study. Int. J. Cancer 2001, 91, 728–735. [Google Scholar] [CrossRef]
- Calvente, I.; Dávila-Arias, C.; Ocón-Hernández, O.; Pérez-Lobato, R.; Ramos, R.; Artacho-Cordón, F.; Olea, N.; Núñez, M.I.; Fernández, M.F. Characterization of indoor extremely low frequency and low frequency electromagnetic fields in the INMA-Granada cohort. PLoS ONE 2014, 9, e106666. [Google Scholar] [CrossRef] [PubMed]
- Liorni, I.; Parazzini, M.; Struchen, B.; Fiocchi, S.; Röösli, M.; Ravazzani, P. Children’s personal exposure measurements to extremely low frequency magnetic fields in Italy. Int. J. Environ. Res. Public Health 2016, 13, 549. [Google Scholar] [CrossRef] [PubMed]
- Struchen, B.; Liorni, I.; Parazzini, M.; Gängler, S.; Ravazzani, P.; Röösli, M. Analysis of personal and bedroom exposure to ELF-MFs in children in Italy and Switzerland. J. Expo. Sci. Environ. Epidemiol. 2016, 26, 586–596. [Google Scholar] [CrossRef] [PubMed]
- Magne, I.; Souques, M.; Bureau, I.; Duburcq, A.; Remy, E.; Lambrozo, J. Exposure of children to extremely low frequency magnetic fields in France: Results of the EXPERS study. J. Expo. Sci. Environ. Epidemiol. 2017, 27, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Tolba, H.; Le Brusquet, L.; Parazzini, M.; Fiocchi, S.; Chiaramello, E.; Ravazzani, P.; Röösli, M.; Magne, I.; Souques, M. Modelling the Extremely Low Frequencies Magnetic Fields Times Series Exposure by Segmentation. In Proceedings of the 11ème Congrès National de Radioprotection, Lille, France, 7 June 2017. [Google Scholar]
- Fryzlewicz, P. Wild binary segmentation for multiple change-point detection. Ann. Stat. 2014, 42, 2243–2281. [Google Scholar] [CrossRef]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal detection of changepoints with a linear computational cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Lavielle, M. Using penalized contrasts for the change-point problem. Signal Process. 2005, 85, 1501–1510. [Google Scholar] [CrossRef]
- Davis, R.A.; Lee, T.C.M.; Rodriguez-Yam, G.A. Structural break estimation for nonstationary time series models. J. Am. Stat. Assoc. 2006, 101, 223–239. [Google Scholar] [CrossRef]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall: Englewood Cliffs, NJ, USA, 1993; Volume 104. [Google Scholar]
- Scott, A.J.; Knott, M. A Cluster Analysis Method for Grouping Means in the Analysis of Variance. Biometrics 1974, 30, 507–512. [Google Scholar] [CrossRef]
- Olshen, A.B.; Venkatraman, E.S.; Lucito, R.; Wigler, M. Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics 2004, 5, 557–572. [Google Scholar] [CrossRef] [PubMed]
- Killick, R.; Eckley, I. Changepoint: An R package for changepoint analysis. J. Stat. Softw. 2014, 58, 1–19. [Google Scholar] [CrossRef]
- Jackson, B.; Scargle, J.D.; Barnes, D.; Arabhi, S.; Alt, A.; Gioumousis, P.; Gwin, E.; Sangtrakulcharoen, P.; Tan, L.; Tsai, T.T. An algorithm for optimal partitioning of data on an interval. IEEE Signal Process. Lett. 2005, 12, 105–108. [Google Scholar] [CrossRef]
- Silverman, B. Density Estimation for Statistics and Data Analysis; Chapman Hall: London, UK, 1986; Volume 37, pp. 1–22. [Google Scholar] [CrossRef]
- Scott, D.W.; Sain, S.R. Multi-dimensional Density Estimation. Handb. Stat. 2005, 24, 229–261. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice and Visualization; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Baringhaus, L.; Franz, C. On a new multivariate two-sample test. J. Multivar. Anal. 2004, 88, 190–206. [Google Scholar] [CrossRef]
- Hu, X.; Gadbury, G.L.; Xiang, Q.; Allison, D.B. Illustrations on Using the Distribution of a P-value in High Dimensional Data Analyses. Adv. Appl. Stat. Sci. 2010, 1, 191–213. [Google Scholar] [PubMed]
- Storey, J.D.; Tibshirani, R. Statistical significance for genomewide studies. Proc. Natl. Acad. Sci. USA 2003, 100, 9440–9445. [Google Scholar] [CrossRef] [PubMed]
| ARIMMORA Database | EXPERS Database | ||
|---|---|---|---|
| Milan | Basel | Paris | France |
| Winter: 86 recordings | Winter: 79 recordings | 29 recordings | 948 recordings |
| Summer: 86 recordings | Summer: 80 recordings | ||
| 331 recordings from 166 children | 977 recordings from 977 children | ||
| Type of Comparison | ARIMMORA Database | EXPERS Database | ||
|---|---|---|---|---|
| Day vs. Night | 682 days | Day: 4129 segments Night: 693 segments | 767 days | Day: 38,742 segments |
| Night: 8906 segments | ||||
| Age’s Groups | 0–4 years 0 days | No Registrations | 0–4 years 175 days | Day: 7538 segments |
| Night: 1901 segments | ||||
| 5–9 years 405 days | Day: 2386 segments Night: 372 segments | 5–9 years 244 days | Day: 12,381 segments | |
| Night: 3066 segments | ||||
| 10–14 years 277 days | Day: 1743 segments | 10–14 years 348 days | Day: 18,823 segments | |
| Night: 321 segments | Night: 3939 segments | |||
| Number of Inhabitants | Milan 366 days | Day: 2271 segments Night: 485 segments | Paris 28 days | Day: 1023 segments |
| Night: 168 segments | ||||
| Rural Area 176 days | Day: 9868 segments | |||
| Night: 2069 segments | ||||
| 2000–4999 inhab. 121 days | Day: 6845 segments | |||
| Night: 1579 segments | ||||
| 5000–9999 inhab. 86 days | Day: 4987 segments | |||
| Night: 822 segments | ||||
| Basel 316 days | Day: 1858 segments Night: 208 segments | 10,000–19,999 inhab. 103 days | Day: 5776 segments | |
| Night: 1372 segments | ||||
| 20,000–49,999 inhab. 90 days | Day: 3940 segments | |||
| Night: 1158 segments | ||||
| 50,000–99,999 inhab. 62 days | Day: 2617 segments | |||
| Night: 671 segments | ||||
| 100,000–199,999 inhab. 44 days | Day: 2052 segments | |||
| Night: 509 segments | ||||
| 200,000–1,999,999 inhab. 54 days | Day: 1634 segments | |||
| Night: 558 segments | ||||
| Distance from MV/LV (20 kV/400 V) substation | Not Available | >40 m 726 days | Day: 37,124 segments | |
| Night: 8277 segments | ||||
| <40 m 21 days | Day: 762 segments | |||
| Night: 174 segments | ||||
| Same Building or Adjacent 19 days | Day: 842 segments | |||
| Night: 263 segments | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonato, M.; Parazzini, M.; Chiaramello, E.; Fiocchi, S.; Le Brusquet, L.; Magne, I.; Souques, M.; Röösli, M.; Ravazzani, P. Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling. Int. J. Environ. Res. Public Health 2018, 15, 1963. https://doi.org/10.3390/ijerph15091963
Bonato M, Parazzini M, Chiaramello E, Fiocchi S, Le Brusquet L, Magne I, Souques M, Röösli M, Ravazzani P. Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling. International Journal of Environmental Research and Public Health. 2018; 15(9):1963. https://doi.org/10.3390/ijerph15091963
Chicago/Turabian StyleBonato, Marta, Marta Parazzini, Emma Chiaramello, Serena Fiocchi, Laurent Le Brusquet, Isabelle Magne, Martine Souques, Martin Röösli, and Paolo Ravazzani. 2018. "Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling" International Journal of Environmental Research and Public Health 15, no. 9: 1963. https://doi.org/10.3390/ijerph15091963
APA StyleBonato, M., Parazzini, M., Chiaramello, E., Fiocchi, S., Le Brusquet, L., Magne, I., Souques, M., Röösli, M., & Ravazzani, P. (2018). Characterization of Children’s Exposure to Extremely Low Frequency Magnetic Fields by Stochastic Modeling. International Journal of Environmental Research and Public Health, 15(9), 1963. https://doi.org/10.3390/ijerph15091963











