Spatial Patterns of Urban Wastewater Discharge and Treatment Plants Efficiency in China
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of Indicators and Data Sources
2.2. Exploratory Spatial Data Analysis (ESDA) Method
2.2.1. Super-Efficiency Data Envelopment Analysis (DEA) Model
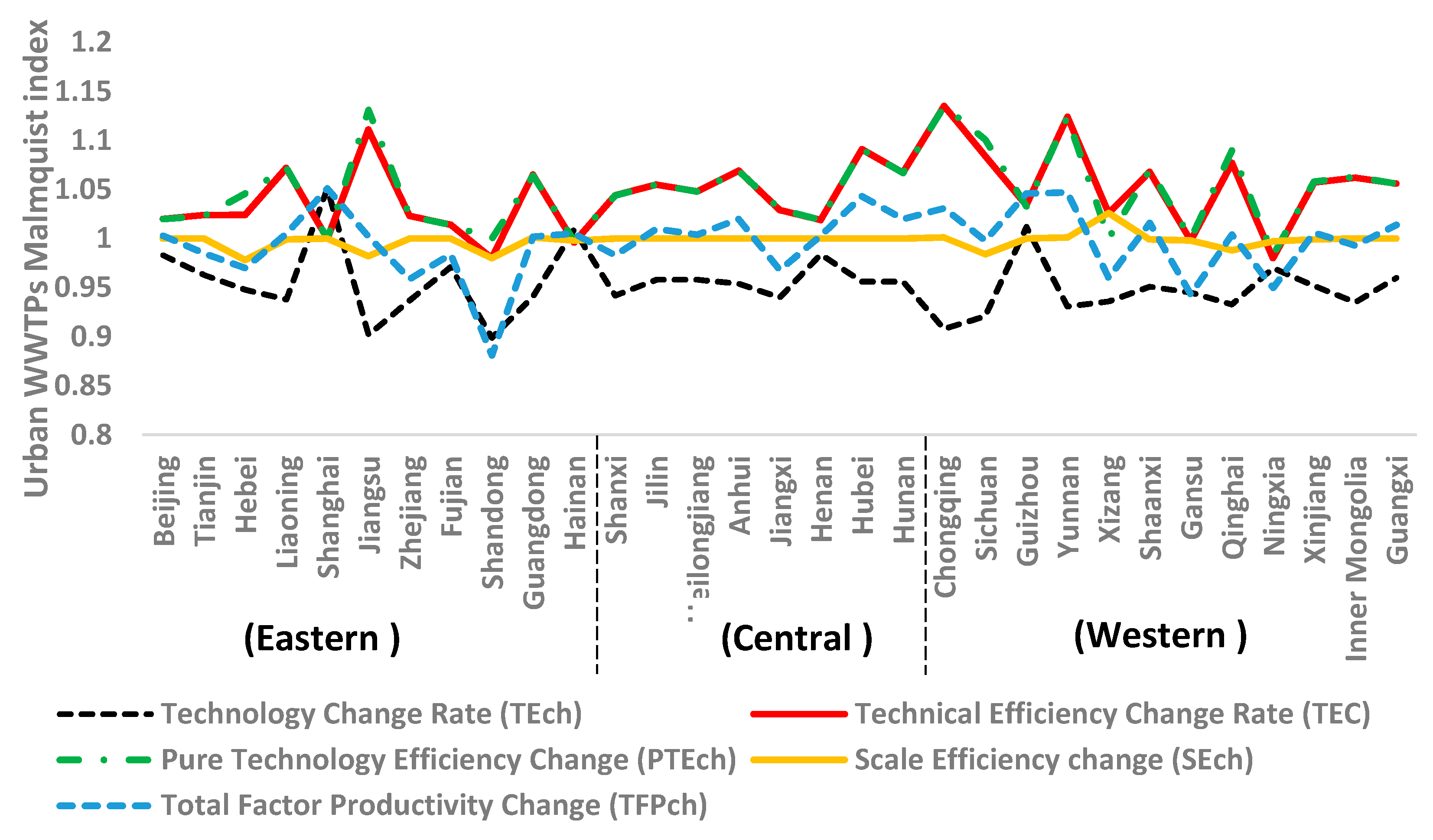
2.2.2. Malmquist Index
3. Results and Discussion
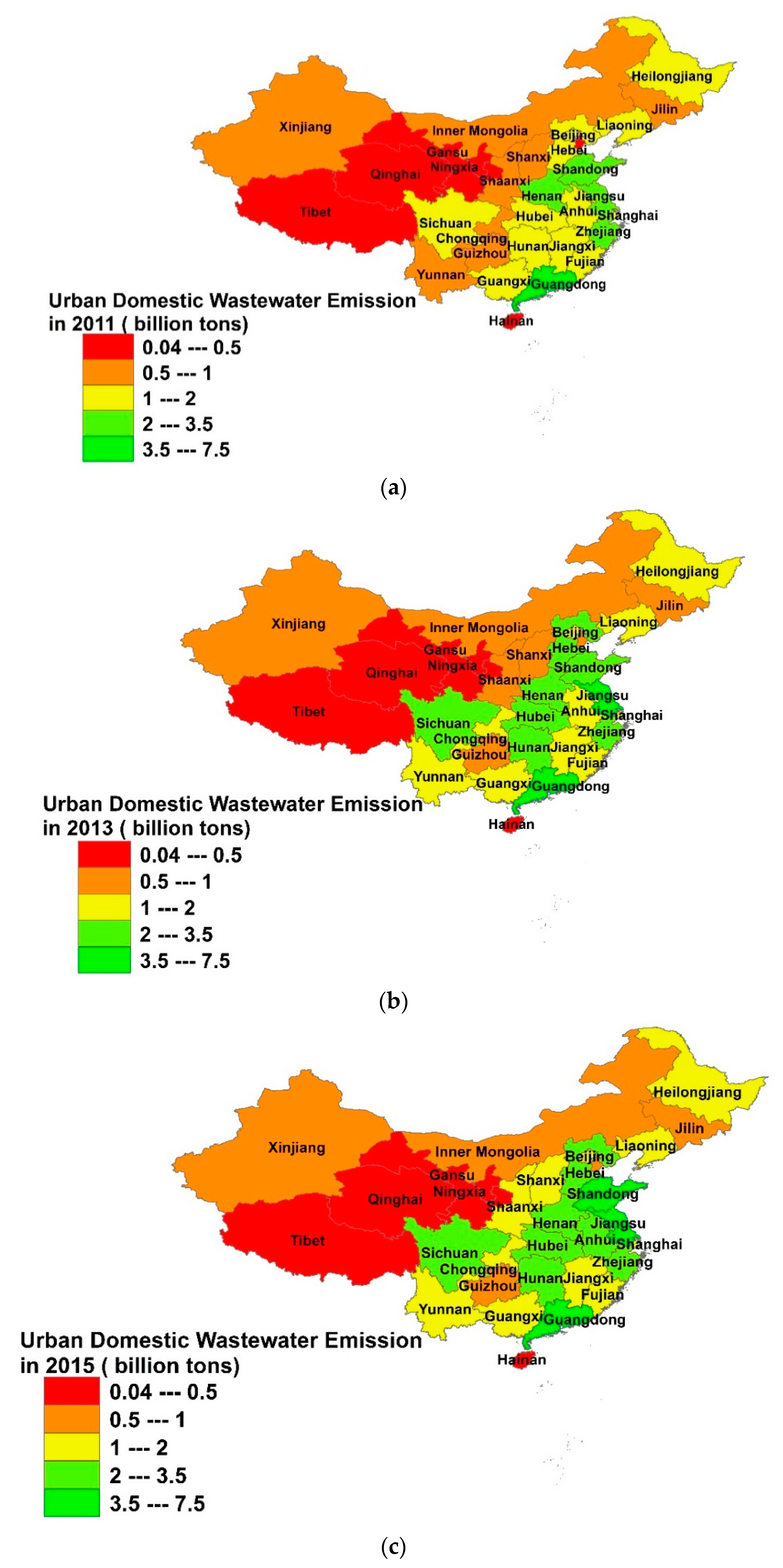
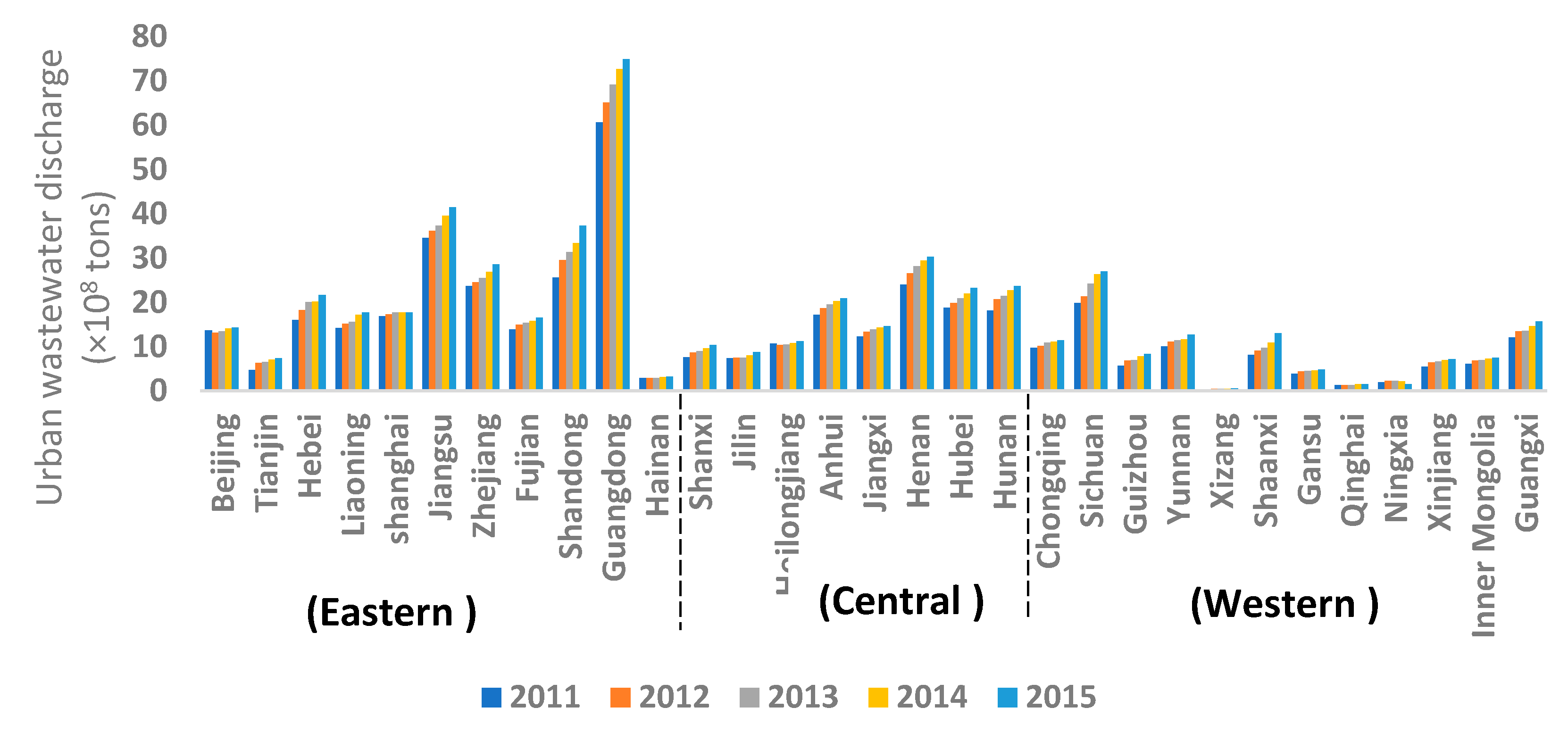
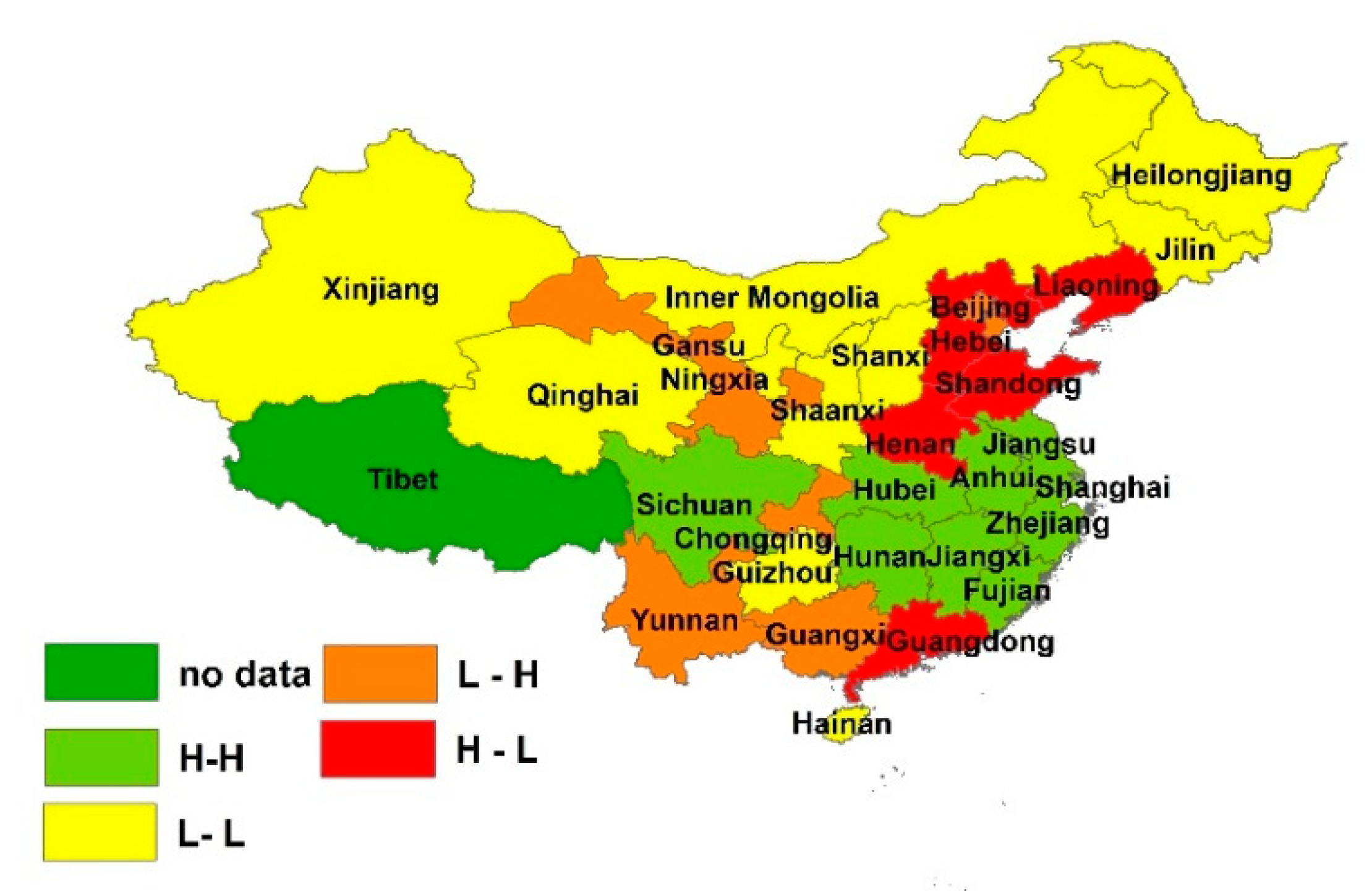
3.1. Spatial Pattern of Provincial Urban Wastewater Discharge
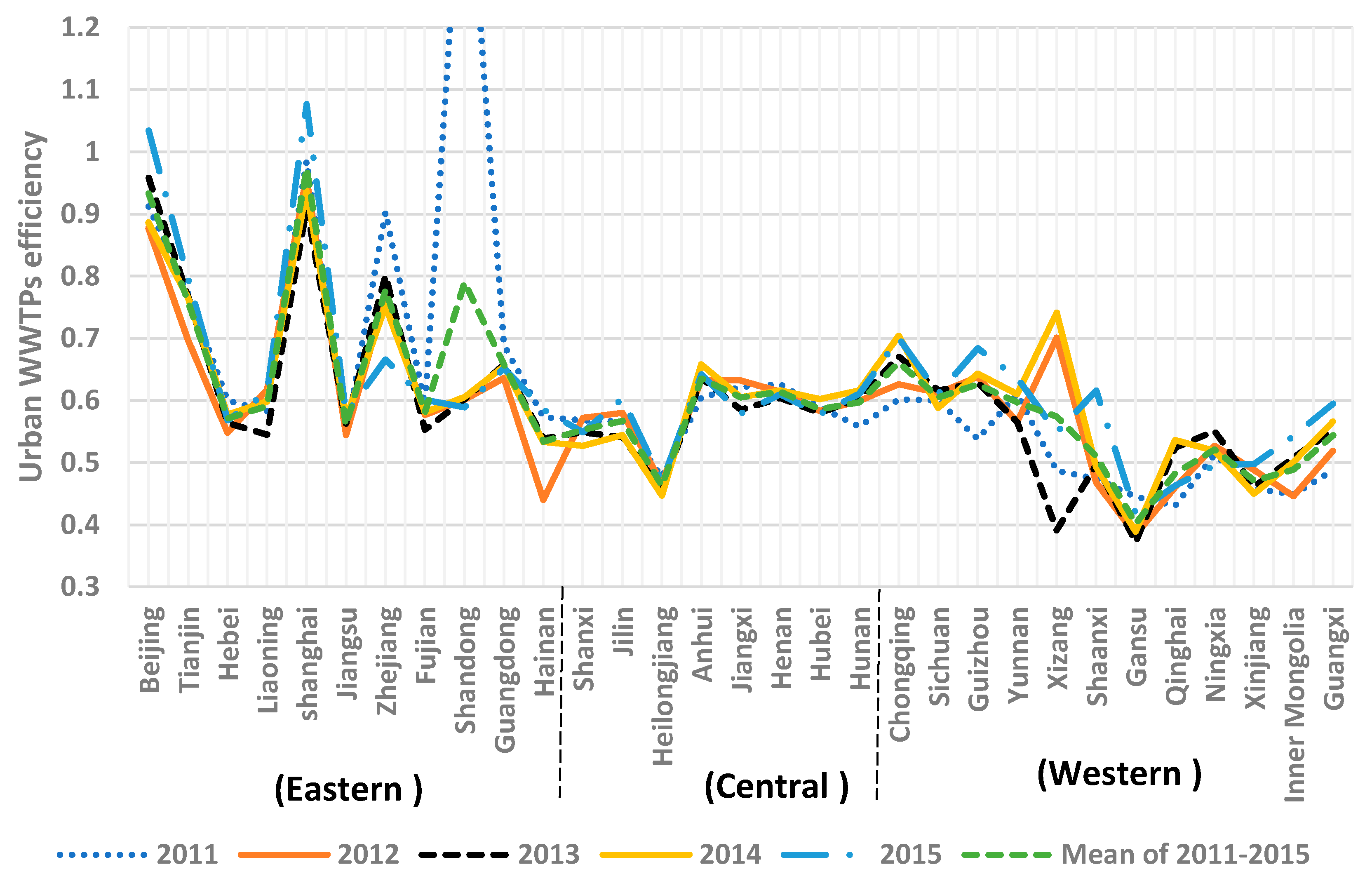
3.2. The Urban WWTPs Efficiency with Super-Efficiency DEA Model
3.3. The Results of the Malmquist Index
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Time | 2011 | 2012 | 2013 | 2014 | 2015 | Mean | |
|---|---|---|---|---|---|---|---|
| Province | |||||||
| Beijing | 0.912 | 0.877 | 0.958 | 0.886 | 1.034 | 0.933 | |
| Tianjin | 0.772 | 0.697 | 0.767 | 0.765 | 0.796 | 0.759 | |
| Hebei | 0.6 | 0.548 | 0.564 | 0.577 | 0.568 | 0.571 | |
| Liaoning | 0.582 | 0.617 | 0.545 | 0.598 | 0.613 | 0.591 | |
| shanghai | 0.985 | 0.96 | 0.909 | 0.937 | 1.077 | 0.974 | |
| Jiangsu | 0.545 | 0.544 | 0.563 | 0.57 | 0.578 | 0.56 | |
| Zhejiang | 0.903 | 0.767 | 0.801 | 0.752 | 0.666 | 0.778 | |
| Fujian | 0.593 | 0.577 | 0.553 | 0.581 | 0.601 | 0.581 | |
| Shandong | 1.552 | 0.601 | 0.602 | 0.605 | 0.589 | 0.79 | |
| Guangdong | 0.689 | 0.636 | 0.658 | 0.655 | 0.652 | 0.658 | |
| Hainan | 0.573 | 0.44 | 0.539 | 0.533 | 0.585 | 0.534 | |
| Eastern average | 0.791 | 0.660 | 0.678 | 0.678 | 0.705 | 0.703 | |
| Shanxi | 0.568 | 0.572 | 0.549 | 0.527 | 0.549 | 0.553 | |
| Jilin | 0.566 | 0.58 | 0.541 | 0.544 | 0.603 | 0.567 | |
| Heilongjiang | 0.477 | 0.467 | 0.455 | 0.447 | 0.469 | 0.463 | |
| Anhui | 0.605 | 0.633 | 0.636 | 0.658 | 0.642 | 0.635 | |
| Jiangxi | 0.622 | 0.632 | 0.585 | 0.605 | 0.579 | 0.605 | |
| Henan | 0.626 | 0.614 | 0.604 | 0.616 | 0.61 | 0.614 | |
| Hubei | 0.589 | 0.583 | 0.58 | 0.602 | 0.578 | 0.586 | |
| Hunan | 0.558 | 0.599 | 0.603 | 0.616 | 0.611 | 0.597 | |
| Median average | 0.577 | 0.585 | 0.569 | 0.577 | 0.580 | 0.578 | |
| Chongqing | 0.602 | 0.626 | 0.671 | 0.704 | 0.7 | 0.661 | |
| Sichuan | 0.6 | 0.612 | 0.616 | 0.588 | 0.611 | 0.605 | |
| Guizhou | 0.538 | 0.638 | 0.629 | 0.643 | 0.684 | 0.626 | |
| Yunnan | 0.611 | 0.565 | 0.565 | 0.61 | 0.636 | 0.597 | |
| Xizang | 0.487 | 0.701 | 0.391 | 0.741 | 0.549 | 0.574 | |
| Shaanxi | 0.474 | 0.468 | 0.497 | 0.493 | 0.616 | 0.51 | |
| Gansu | 0.445 | 0.384 | 0.372 | 0.389 | 0.418 | 0.402 | |
| Qinghai | 0.431 | 0.46 | 0.524 | 0.536 | 0.463 | 0.483 | |
| Ningxia | 0.513 | 0.527 | 0.551 | 0.519 | 0.496 | 0.521 | |
| Xinjiang | 0.458 | 0.488 | 0.461 | 0.45 | 0.498 | 0.471 | |
| Inner Mongolia | 0.449 | 0.446 | 0.508 | 0.501 | 0.543 | 0.489 | |
| Guangxi | 0.488 | 0.519 | 0.552 | 0.566 | 0.595 | 0.544 | |
| Western average | 0.508 | 0.536 | 0.528 | 0.562 | 0.567 | 0.54 | |
| Total average | 0.626 | 0.593 | 0.592 | 0.607 | 0.62 | 0.608 | |
| Productivity | Technology Change Rate (TEch) | Technical Efficiency Change Rate (TEC) | Pure Technology Efficiency Change (PTEch) | Scale Efficiency Change (SEch) | Total Factor Productivity Change (TFPch) |
|---|---|---|---|---|---|
| Beijing | 0.983 | 1.020 | 1.020 | 1.000 | 1.003 |
| Tianjin | 0.963 | 1.024 | 1.023 | 1.000 | 0.985 |
| Hebei | 0.948 | 1.024 | 1.046 | 0.978 | 0.970 |
| Liaoning | 0.938 | 1.072 | 1.072 | 0.999 | 1.005 |
| Shanghai | 1.051 | 1.000 | 1.000 | 1.000 | 1.051 |
| Jiangsu | 0.902 | 1.111 | 1.131 | 0.982 | 1.002 |
| Zhejiang | 0.937 | 1.023 | 1.023 | 1.000 | 0.959 |
| Fujian | 0.971 | 1.014 | 1.014 | 1.000 | 0.984 |
| Shandong | 0.899 | 0.980 | 1.000 | 0.98 | 0.881 |
| Guangdong | 0.941 | 1.065 | 1.064 | 1.001 | 1.002 |
| Hainan | 1.009 | 0.996 | 0.998 | 0.998 | 1.005 |
| Eastern average | 0.958 | 1.030 | 1.036 | 0.994 | 0.986 |
| Shanxi | 0.942 | 1.044 | 1.044 | 1.000 | 0.983 |
| Jilin | 0.958 | 1.055 | 1.055 | 1.000 | 1.010 |
| Heilongjiang | 0.958 | 1.048 | 1.048 | 1.000 | 1.004 |
| Anhui | 0.954 | 1.069 | 1.069 | 1.000 | 1.020 |
| Jiangxi | 0.940 | 1.029 | 1.030 | 1.000 | 0.968 |
| Henan | 0.984 | 1.019 | 1.019 | 1.000 | 1.003 |
| Hubei | 0.956 | 1.091 | 1.091 | 1.000 | 1.043 |
| Hunan | 0.956 | 1.067 | 1.067 | 1.000 | 1.020 |
| Median average | 0.956 | 1.053 | 1.053 | 1.000 | 1.006 |
| Chongqing | 0.908 | 1.135 | 1.135 | 1.001 | 1.031 |
| Sichuan | 0.921 | 1.084 | 1.101 | 0.984 | 0.998 |
| Guizhou | 1.012 | 1.034 | 1.033 | 1.000 | 1.046 |
| Yunnan | 0.931 | 1.124 | 1.124 | 1.001 | 1.047 |
| Xizang | 0.936 | 1.026 | 1.000 | 1.026 | 0.960 |
| Shaanxi | 0.951 | 1.068 | 1.070 | 0.999 | 1.016 |
| Gansu | 0.945 | 0.998 | 1.000 | 0.998 | 0.943 |
| Qinghai | 0.933 | 1.077 | 1.090 | 0.988 | 1.004 |
| Ningxia | 0.970 | 0.980 | 0.983 | 0.997 | 0.950 |
| Xinjiang | 0.952 | 1.057 | 1.058 | 0.999 | 1.006 |
| Inner Mongolia | 0.935 | 1.062 | 1.063 | 1.000 | 0.993 |
| Guangxi | 0.960 | 1.056 | 1.056 | 1.000 | 1.014 |
| Western average | 0.946 | 1.058 | 1.059 | 0.999 | 1.001 |
| Total average | 0.952 | 1.046 | 1.048 | 0.998 | 0.996 |
References
- Zhao, H.; Cui, J.; Wang, S.; Lindley, S. Customizing the coefficients of urban domestic pollutant discharge and their driving mechanisms: Evidence from the Taihu Basin, China. J. Environ. Manag. 2018, 213, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.R.; Chen, J.Y.; Xu, Z.C.; Yang, D.Y.; Lin, K. Emission Characteristic Analysis of Urban Domestic Pollution. Procedia Environ. Sci. 2010, 2, 761–767. [Google Scholar] [CrossRef]
- Chen, K.; Liu, X.; Ding, L.; Huang, G.; Li, Z. Spatial characteristics and driving factors of provincial wastewater discharge in China. Int. J. Environ. Res. Public Health 2016, 13, 1221. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Environmental Protection of the People’s Republic of China. Annual Statistic Report on Environment in China; China Environmental Science Press: Beijing, China, 2015.
- Touaylia, S.; Ghannem, S.; Toumi, H.; Bejaoui, M. Assessment of heavy metals status in northern Tunisia using contamination indices: Case of the Ichkeul steams system. Arab. J. Geosci. 2016, 3, 209–217. [Google Scholar]
- Xin, X.; Huang, G.; Liu, X.; An, C.; Yao, Y.; Weger, H.; Zhang, P.; Chen, X. Molecular toxicity of triclosan and carbamazepine to green algae Chlorococcum sp.: A single cell view using synchrotron-based Fourier transform infrared spectromicroscopy. Environ. Pollut. 2017, 226, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Zhang, J.; Zhu, C.; Hu, Y.; Zhou, L. An assessment of China’s ecological environment quality change and its spatial variation. Acta Geogr. Sin. 2012, 67, 1599–1610. [Google Scholar]
- Geng, Y.; Wang, M.; Sarkis, J.; Xue, B.; Zhang, L.; Fujita, T.; Yu, X.; Ren, W.; Zhang, L.; Dong, H. Spatial-temporal patterns and driving factors for industrial wastewater emission in China. J. Clean. Prod. 2014, 76, 116–124. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Yang, W.N.; Ngo, H.H.; Guo, W.S.; Jin, P.K.; Dzakpasu, M.; Yang, S.J.; Wang, Q.; Wang, X.C.; Ao, D. Current status of urban wastewater treatment plants in China. Environ. Int. 2016, 92–93, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Sancho, F.; Sala-Garrido, R. Technical efficiency and cost analysis in wastewater treatment processes: A DEA approach. Desalination 2009, 249, 230–234. [Google Scholar] [CrossRef]
- Sala-Garrido, R.; Molinos-Senante, M.; Hernández-Sancho, F. Comparing the efficiency of wastewater treatment technologies through a DEA metafrontier model. Chem. Eng. J. 2011, 173, 766–772. [Google Scholar] [CrossRef]
- Lorenzo-Toja, Y.; Vázquez-Rowe, I.; Chenel, S.; Marín-Navarro, D.; Moreira, M.T.; Feijoo, G. Eco-efficiency analysis of Spanish WWTPs using the LCA + DEA method. Water Res. 2015, 68, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Zheng, Q. Energy efficiency evolution of China’s paper industry. J. Clean. Prod. 2017, 140, 1105–1117. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, H. Technology gap and regional energy efficiency in China’s textile industry: A non-parametric meta-frontier approach. J. Clean. Prod. 2016, 137, 21–28. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, Y.; Xu, H. Water use efficiency and related pollutants’ abatement costs of regional industrial systems in China: A slacks-based measure approach. J. Clean. Prod. 2015, 101, 301–310. [Google Scholar] [CrossRef]
- Bian, Y.; Yan, S.; Xu, H. Efficiency evaluation for regional urban water use and wastewater decontamination systems in China: A DEA approach. Resour. Conserv. Recycl. 2014, 83, 15–23. [Google Scholar] [CrossRef]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Golany, B.; Yaako, R. An application procedure of DEA. Omega 1989, 17, 237–250. [Google Scholar] [CrossRef]
- Hernández-Sancho, F.; Molinos-Senante, M.; Sala-Garrido, R. Energy efficiency in Spanish wastewater treatment plants: A non-radial DEA approach. Sci. Total Environ. 2011, 409, 2693–2699. [Google Scholar] [CrossRef] [PubMed]
- Sala-Garrido, R.; Hernández-Sancho, F.; Molinos-Senante, M. Assessing the efficiency of wastewater treatment plants in an uncertain context: A DEA with tolerances approach. Environ. Sci. Policy 2012, 18, 34–44. [Google Scholar] [CrossRef]
- Castellet, L.; Molinos-Senante, M. Efficiency assessment of wastewater treatment plants: A data envelopment analysis approach integrating technical, economic, and environmental issues. J. Environ. Manag. 2016, 167, 160–166. [Google Scholar] [CrossRef] [PubMed]
- Molinos-Senante, M.; Hernández-Sancho, F.; Mocholí-Arce, M.; Sala-Garrido, R. Economic and environmental performance of wastewater treatment plants: Potential reductions in greenhouse gases emissions. Resour. Energy Econ. 2014, 38, 125–140. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China, Ministry of Environmental Protection of China. China Statistic Yearbook on Environment (2011–2015); China Statistica Press: Beijing, China, 2015.
- National Bureau of Statistics of China. China Statistical Yearbook (2011–2015); China Statistica Press: Beijing, China, 2015.
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Per Andersen, N.C.P. A procedure for ranking efficient units in data envelopment analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Douglas, W.; Caves Laurits, R.; Christensen, W.E.D. The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity. Econ. Theory 2012, 50, 1393–1414. [Google Scholar]
- Fjire, R.; Unviersity, S.I.; Grosskopf, S.; Unviersity, S.I.; Lindgren, B.; Economks, H.; Roos, P. Productivity Changes in Swedish Pharamacies 1980–1989: A Non-Parametric Malmquist Approach. J. Product. Anal. 1992, 3, 85–101. [Google Scholar]
- Fisher, I. The Making of Index Numbers; Houghton Mifflin: Boston, MA, USA, 1922. [Google Scholar]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress and efficiency change in Industrialised Countries. Am. Econ. Assoc. 1994, 84, 66–83. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Guo, W.; Dong, J.; Wang, L.; Dai, S. Seasonal and spatial distribution of nonylphenol in Lanzhou Reach of Yellow River in China. Chemosphere 2006, 65, 1445–1451. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Mei, K.; Zhang, Y.; Liao, L.; Long, B.; Dahlgren, R.A.; Zhang, M. Spatial and temporal variations of nitrogen pollution in Wen-Rui Tang River watershed, Zhejiang, China. Environ. Monit. Assess. 2011, 180, 501–520. [Google Scholar] [CrossRef] [PubMed]
- Tao, S.; Li, B.G.; He, X.C.; Liu, W.X.; Shi, Z. Spatial and temporal variations and possible sources of dichlorodiphenyltrichloroethane (DDT) and its metabolites in rivers in Tianjin, China. Chemosphere 2007, 68, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Cheng, X.; Xu, Z.; Han, H.; Zhang, Q. Spatial and temporal patterns of the water quality in the Danjiangkou Reservoir, China. Hydrol. Sci. J. 2009, 54, 124–134. [Google Scholar] [CrossRef]
- Bu, H.; Tan, X.; Li, S.; Zhang, Q. Temporal and spatial variations of water quality in the Jinshui River of the South Qinling Mts., China. Ecotoxicol. Environ. Saf. 2010, 73, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Huang, X.; Liu, Y. Spatial autocorrelation analysis of Chinese inter-provincial industrial chemical oxygen demand discharge. Int. J. Environ. Res. Public Health 2012, 9, 2031–2044. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Shi, P.; Liu, Y. Realizing China’s urban dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Sun, B. The influence of Chinese environmental regulation on corporation innovation and competitiveness. J. Clean. Prod. 2016, 112, 1528–1536. [Google Scholar] [CrossRef]
- Rafiq, S.; Nielsen, I.; Smyth, R. Effect of internal migration on the environment in China. Energy Econ. 2017, 64, 31–44. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Hernández-Sancho, F.; Sala-Garrido, R. Comparing the dynamic performance of wastewater treatment systems: A metafrontier Malmquist productivity index approach. J. Environ. Manag. 2015, 161, 309–316. [Google Scholar] [CrossRef] [PubMed]
- Torregrossa, D.; Marvuglia, A.; Leopold, U. A novel methodology based on LCA + DEA to detect eco-efficiency shifts in wastewater treatment plants. Ecol. Indic. 2018, 94, 7–15. [Google Scholar] [CrossRef]
- Gómez, T.; Gémar, G.; Molinos-Senante, M.; Sala-Garrido, R.; Caballero, R. Assessing the efficiency of wastewater treatment plants: A double-bootstrap approach. J. Clean. Prod. 2017, 164, 315–324. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Gémar, G.; Gómez, T.; Caballero, R.; Sala-Garrido, R. Eco-efficiency assessment of wastewater treatment plants using a weighted Russell directional distance model. J. Clean. Prod. 2016, 137, 1066–1075. [Google Scholar] [CrossRef]
- Guerrini, A.; Romano, G.; Indipendenza, A. Energy efficiency drivers in wastewater treatment plants: A double bootstrap DEA analysis. Sustainability 2017, 9, 1126. [Google Scholar] [CrossRef]
- Zhou, X.; Luo, R.; Yao, L.; Cao, S.; Wang, S.; Lev, B. Assessing integrated water use and wastewater treatment systems in China: A mixed network structure two-stage SBM DEA model. J. Clean. Prod. 2018, 185, 533–546. [Google Scholar] [CrossRef]
| Statistical Description | Input Indicators | Output Indicators | ||||
|---|---|---|---|---|---|---|
| Number of Urban Wastewater Treatment Plants | Treatment Capacity of Urban Wastewater Treatment Plant (×10,000 tons/day) | Annual Operating Expenses (×10,000 CNY) | Actual Treatment Capacity of Urban Wastewater (×10,000 tons) | Removal of Chemical Oxygen Demand from Urban Wastewater (ton) | Removal of Ammonia from Urban Wastewater (ton) | |
| Mean | 173.59 | 531.28 | 120,554.43 | 148,497.81 | 360,704.25 | 32,773.86 |
| Maximum | 797 | 2329 | 524,447.11 | 709,942 | 1,470,883.1 | 146,396 |
| Minimum | 2 | 1 | 162 | 236 | 532.6 | 40.1 |
| Median | 134 | 383 | 87,567.2 | 102,321 | 239,205.8 | 22,648.4 |
| Standard Deviation | 149.94 | 455.72 | 117,992.56 | 136,909.03 | 336,531.03 | 29,502.38 |
| Number of Observations | 155 | 155 | 155 | 155 | 155 | 155 |
| Year | Moran’s I | E(I) | Sd. | P(I) |
|---|---|---|---|---|
| 2011 | 0.188 | −0.034 | 0.106 | 0.018 |
| 2012 | 0.183 | −0.034 | 0.106 | 0.020 |
| 2013 | 0.179 | −0.034 | 0.106 | 0.022 |
| 2014 | 0.18 | −0.034 | 0.106 | 0.022 |
| 2015 | 0.176 | −0.034 | 0.106 | 0.025 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, M.; He, W.; Degefu, D.M.; Liao, Z.; Zhang, Z.; Yuan, L. Spatial Patterns of Urban Wastewater Discharge and Treatment Plants Efficiency in China. Int. J. Environ. Res. Public Health 2018, 15, 1892. https://doi.org/10.3390/ijerph15091892
An M, He W, Degefu DM, Liao Z, Zhang Z, Yuan L. Spatial Patterns of Urban Wastewater Discharge and Treatment Plants Efficiency in China. International Journal of Environmental Research and Public Health. 2018; 15(9):1892. https://doi.org/10.3390/ijerph15091892
Chicago/Turabian StyleAn, Min, Weijun He, Dagmawi Mulugeta Degefu, Zaiyi Liao, Zhaofang Zhang, and Liang Yuan. 2018. "Spatial Patterns of Urban Wastewater Discharge and Treatment Plants Efficiency in China" International Journal of Environmental Research and Public Health 15, no. 9: 1892. https://doi.org/10.3390/ijerph15091892
APA StyleAn, M., He, W., Degefu, D. M., Liao, Z., Zhang, Z., & Yuan, L. (2018). Spatial Patterns of Urban Wastewater Discharge and Treatment Plants Efficiency in China. International Journal of Environmental Research and Public Health, 15(9), 1892. https://doi.org/10.3390/ijerph15091892





