The Adsorptive Removal of Fluoride from Aqueous Solution by Modified Sludge: Optimization Using Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples Collection and Treatment
2.2. Experimental Process
2.2.1. Reagent and Standard Solutions
2.2.2. Adsorption Kinetics and Isotherm
2.2.3. Batch Experiments of Variable Condition
2.2.4. Effect of Co-Existing Anions
2.2.5. The Examination of Removal Efficient from Water
2.3. Analysis
3. Results and Discussion
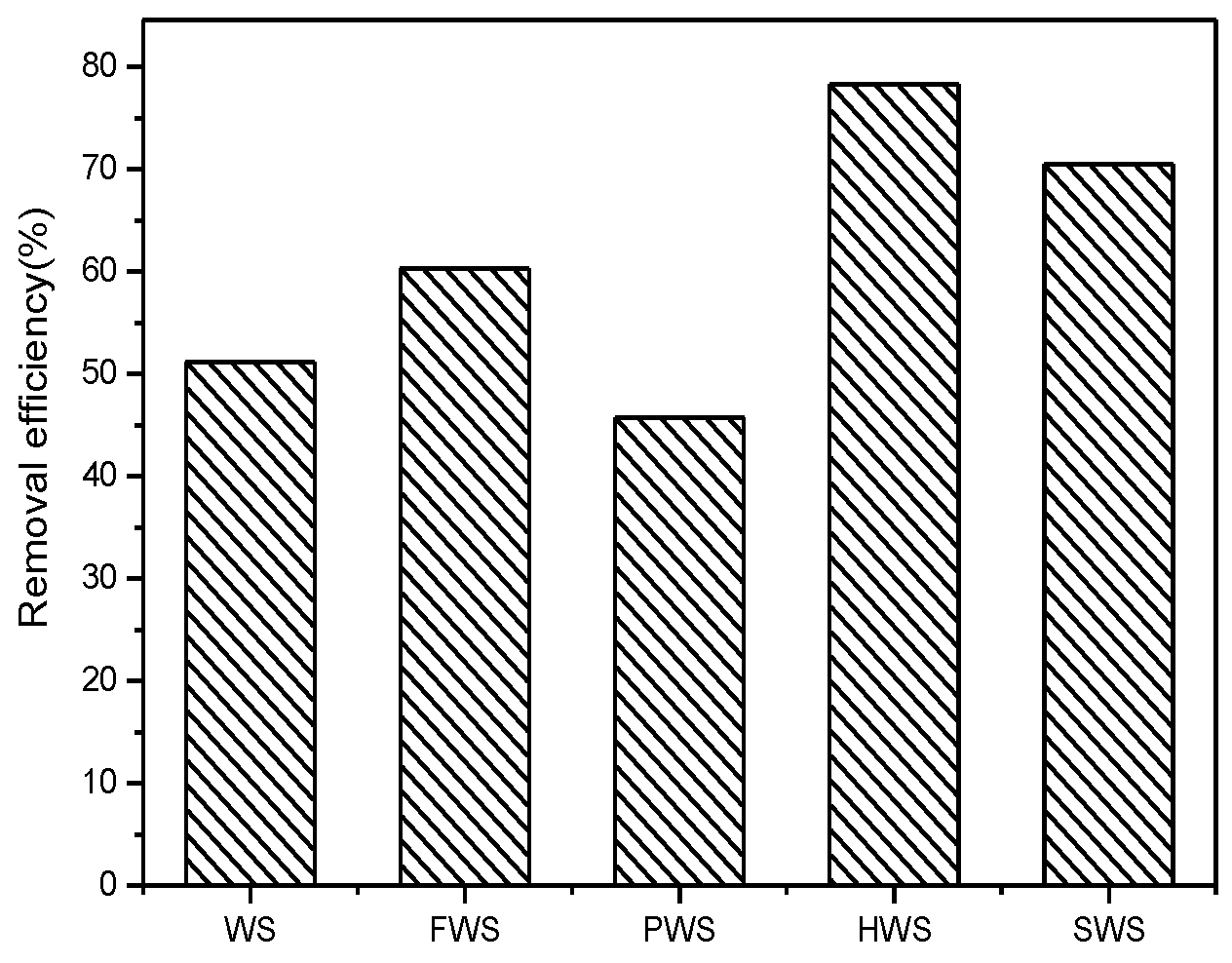
3.1. Effects of Four Treated Sludges when Removing Fluoride
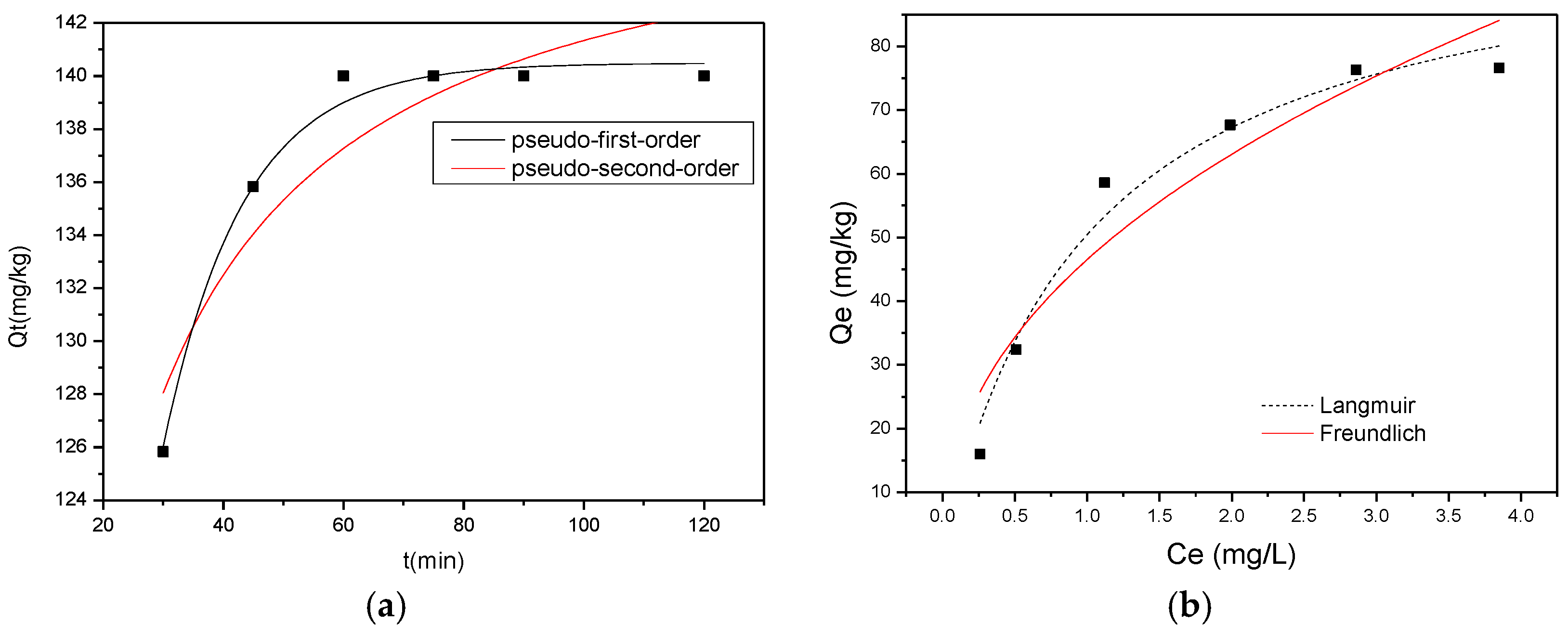
3.2. Equilibrium and Kinetics of Adsorption
3.3. Adsorption Mechanism Analysis
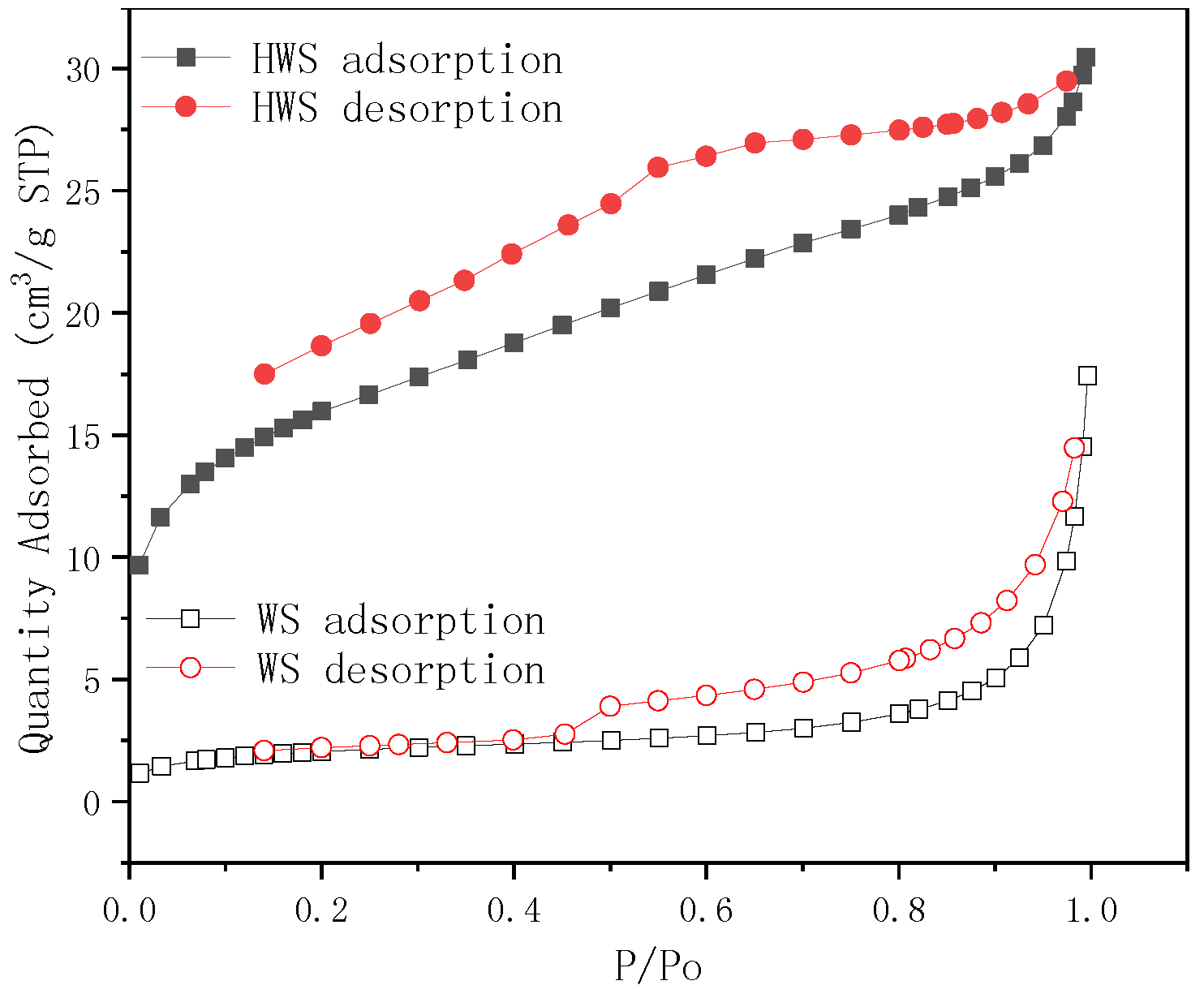
3.3.1. Surface Area Analysis
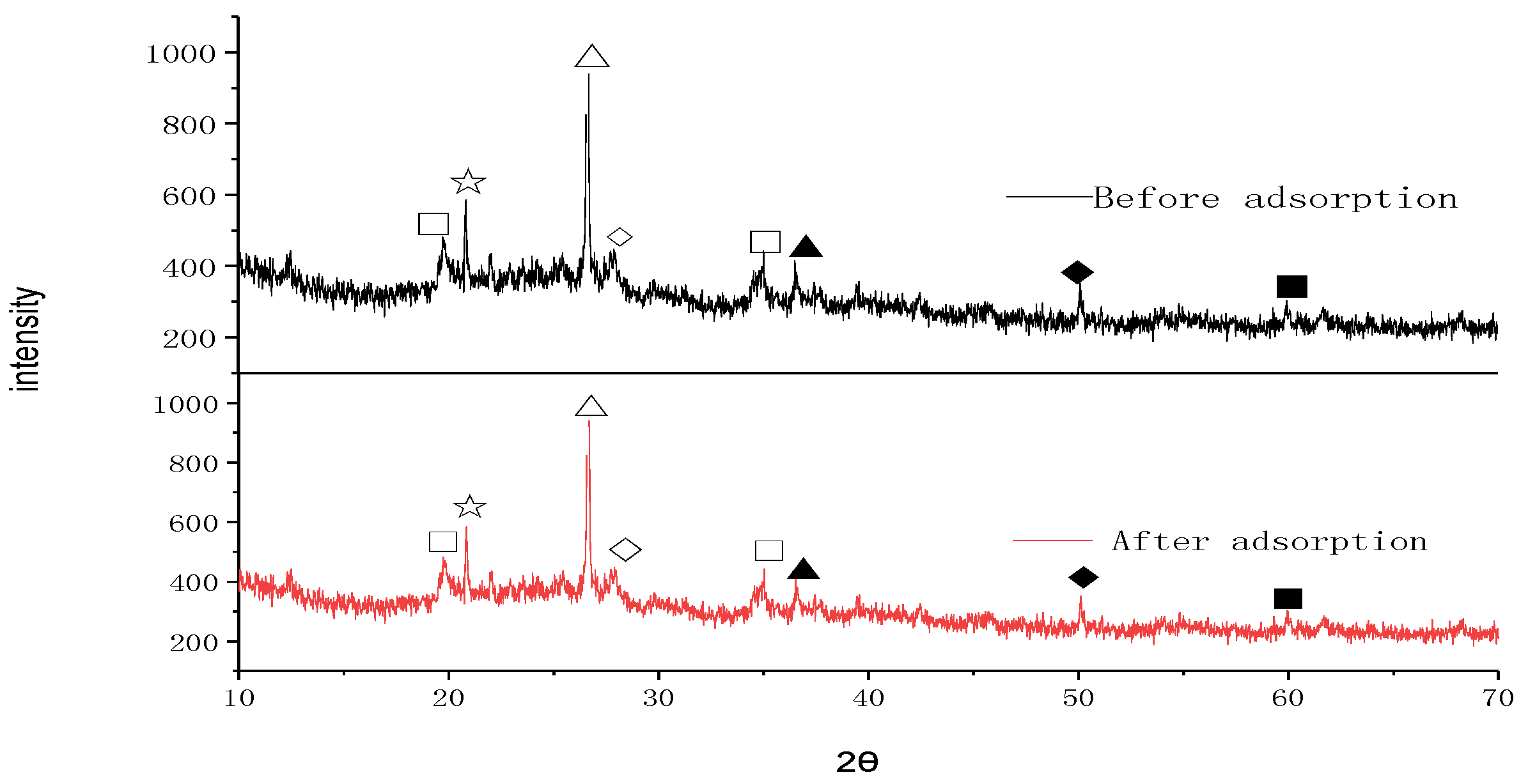
3.3.2. SEM and XRD Studies
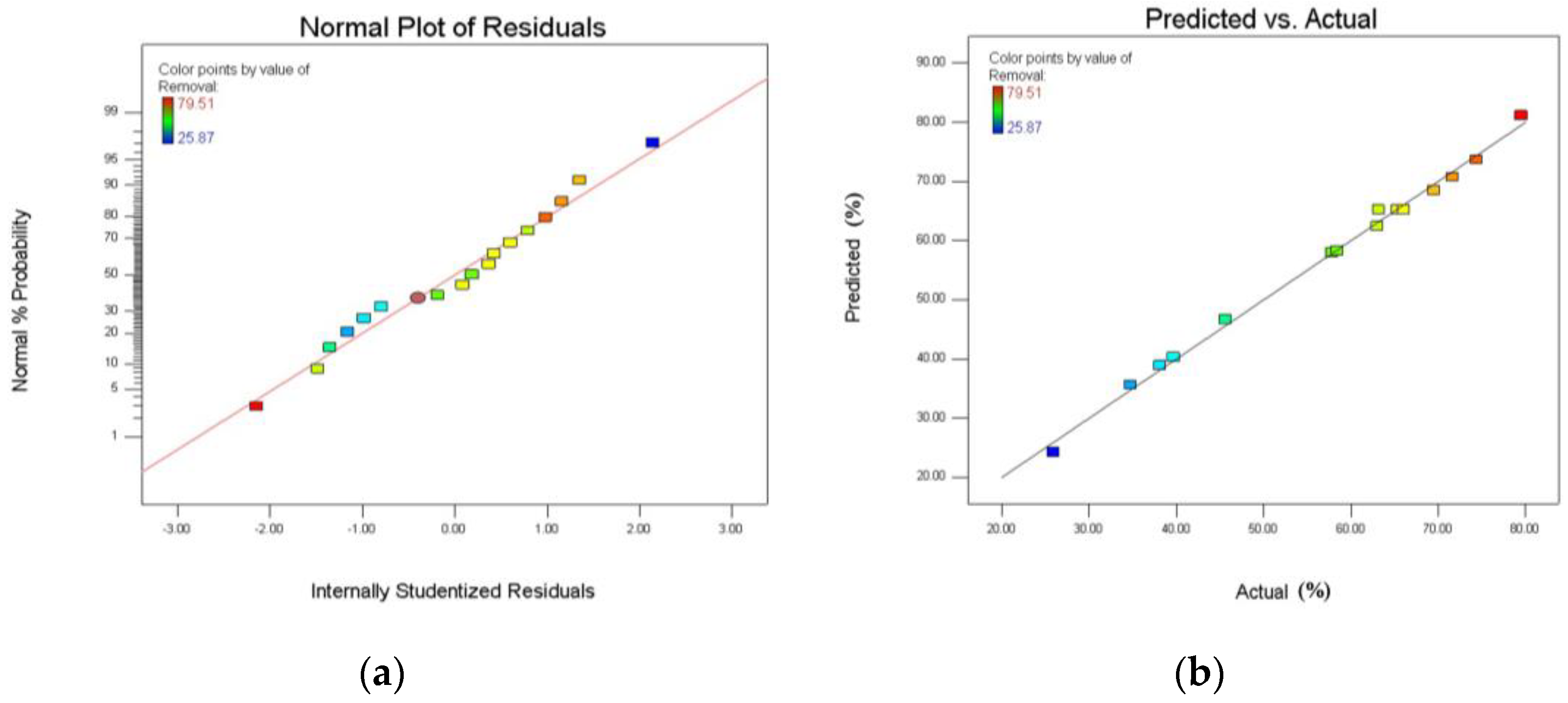
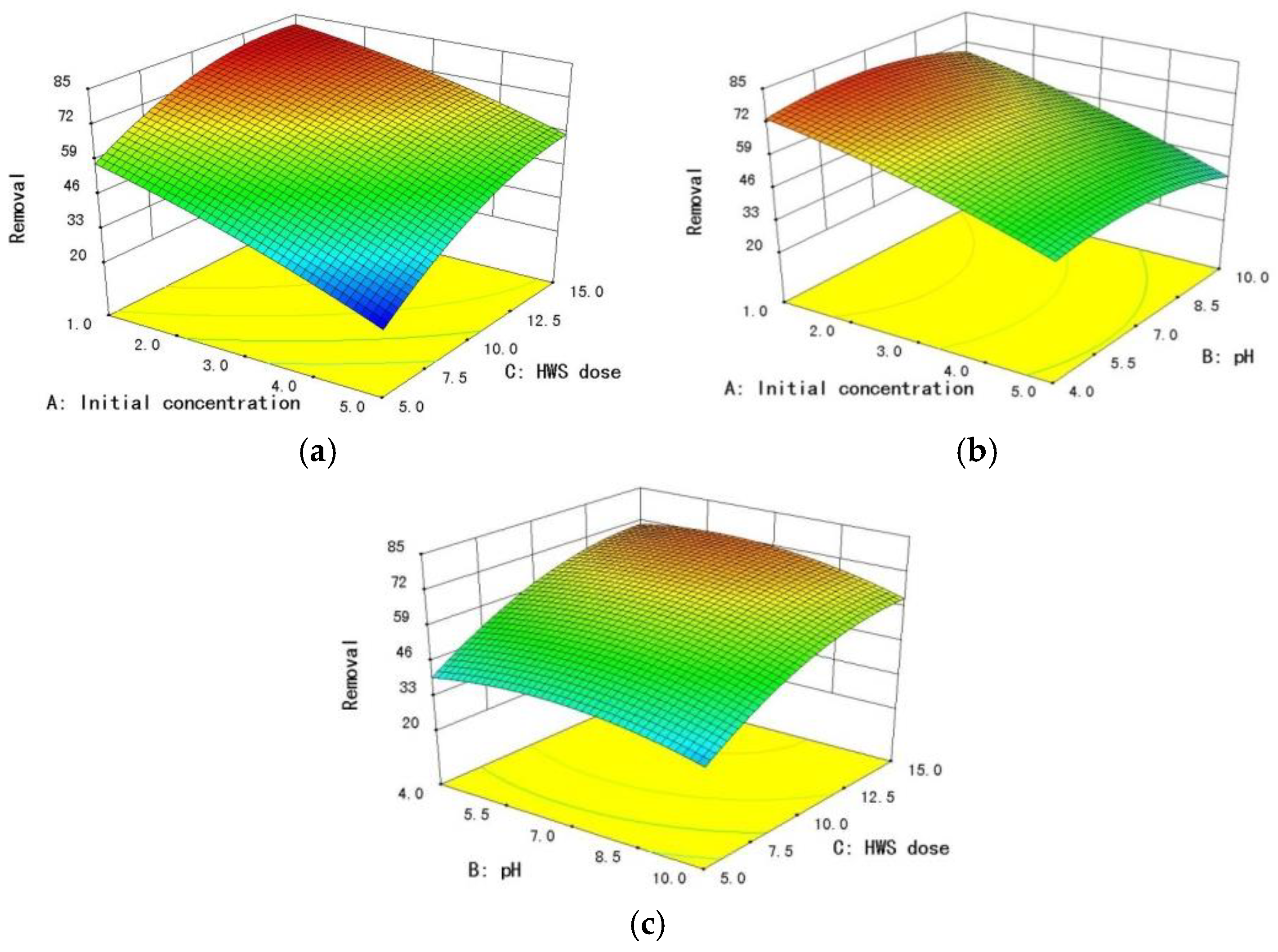
3.4. Effects of Variable Conditions on the Adsorption of Fluoride
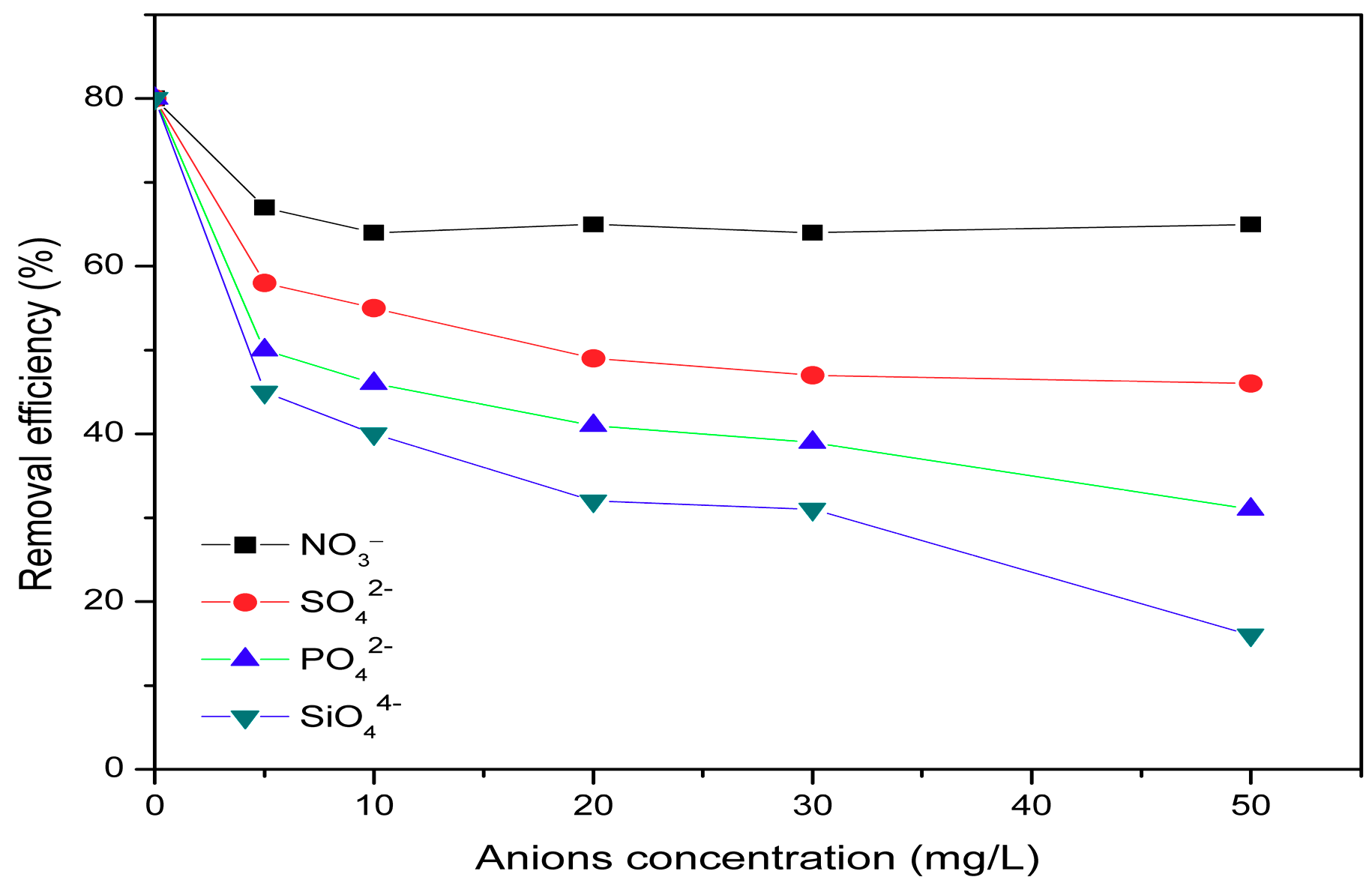
3.5. Effect of Co-Existing Anions
3.6. The Adsorption Efficiency from Water
4. Conclusions
- (1)
- Acid treatment and high temperature ranges found as the conditions for better fluoride sorption and hydrochloric acid treatment will gain the best efficiency for removing fluoride for WS.
- (2)
- A model of adsorption has been proposed for the adsorption of F− onto HWS. The results gained from this study were well described by the theoretical Langmuir isotherms. The values of the equilibrium parameter and RL indicated that the F−/treated HWS system was favorable. Kinetic studies reveal that the adsorption is first order. Thermodynamic parameters were calculated, indicating that the adsorption was spontaneous.
- (3)
- RSM based on BBD was employed to investigate the effects of the three independent variables, namely, HWS dose, pH, and initial concentration on the adsorption of fluoride by HWS. The optimum removal efficiency of fluoride from wastewater using HWS was observed with the help of RSM, and it can reach 81.153% under the optimum condition: HWS dose of 14.10 g/L, at pH = 6.12.
- (4)
- In addition, the results showed that presence of other co-exiting ions, such as SO42−, PO43−, SiO44−, and NO3− anions show a negative effect on the removal of fluoride to varying degrees, in the order SiO44− > PO43− > SO42− > NO3−.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ozsvath, D.L. Fluoride and environmental health: A review. Rev. Environ. Sci. Biol. 2008, 8, 59–79. [Google Scholar] [CrossRef]
- Velazquez-Jimenez, L.H.; Hurt, R.H.; Matos, J.; Rangel-Mendez, J.R. Zirconium-carbon hybrid sorbent for removal of fluoride from water: Oxalic acid mediated Zr(IV) assembly and adsorption mechanism. Environ. Sci. Technol. 2014, 48, 1166–1174. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, M.; Anand, S.; Mishra, B.K.; Giles, D.E.; Singh, P. Review of fluoride removal from drinking water. J. Environ. Manag. 2009, 91, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Aoudj, S.; Drouiche, N.; Hecini, M.; Ouslimane, T.; Palaouane, B. Coagulation as a Post-Treatment Method for the Defluoridation of Photovoltaic Cell Manufacturing Wastewater. Procedia Eng. 2012, 33, 111–120. [Google Scholar] [CrossRef]
- Tor, A. Removal of fluoride from water using anion-exchange membrane under Donnan dialysis condition. J. Hazard. Mater. 2007, 141, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Ho, L.N.; Ishihara, T.; Ueshima, S.; Nishiguchi, H.; Takita, Y. Removal of fluoride from water through ion exchange by mesoporous Ti oxohydroxide. J. Colloid Interface Sci. 2004, 272, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Tripathy, S.S.; Bersillon, J.L.; Gopal, K. Removal of fluoride from drinking water by adsorption onto alum-impregnated activated alumina. Sep. Purif. Technol. 2006, 50, 310–317. [Google Scholar] [CrossRef]
- Yu, X.L.; Tong, S.R.; Ge, M.F.; Zuo, J.C. Removal of fluoride from drinking water by cellulose @ hydroxyapatite nanocomposites. Carbohyd. Polym. 2013, 92, 269–275. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.C.; Xu, J.S.; Wu, B.; Li, Z.G.; Liu, X.T. Enhanced removal of fluoride by polystyrene anion exchanger supported hydrous zirconium oxide nanoparticles. Environ. Sci. Technol. 2013, 47, 9347–9354. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Parker, D.J.; Smith, M.D. Adsorption kinetics of fluoride on low cost materials. Water Res. 2003, 37, 4929–4937. [Google Scholar] [CrossRef] [PubMed]
- Márquez-Mendoza, S.; Jiménez-Reyes, M.; Solache-Ríos, M.; Gutiérrez-Segura, E. Fluoride removal from aqueous solutions by a carbonaceous material from pyrolysis of sewage sludge. Water Air Soil Pollut. 2012, 223, 1959–1971. [Google Scholar] [CrossRef]
- Ghorai, S.; Pant, K.K. Equilibrium, kinetics and breakthrough studies for adsorption of fluoride on activated alumina. Sep. Purif. Technol. 2005, 42, 265–271. [Google Scholar] [CrossRef]
- Xu, Y.M.; Ning, A.R.; Zhao, J. Preparation and defluorination performance of activated cerium(IV) oxidesimcm-41 adsorbent in water. J. Colloid Interface Sci. 2001, 235, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Wajima, T.; Umeta, Y.; Narita, S.; Sugawara, K. Adsorption behavior of fluorideions using a titanium hydroxide-derived adsorbent. Desalination 2009, 113, 1027–1035. [Google Scholar] [CrossRef]
- Turner, B.D.; Binning, P.; Stipp, S.L.S. Fluoride removal by calcite: Evidence for fluorite precipitation and surface adsorption. Environ. Sci. Technol. 2005, 39, 9561–9568. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.S.; Zhao, Y.Q.; Zhao, X.H.; Jeyakumar, L. High Rate Nitrogen Removal in an Alum Sludge-Based Intermittent Aeration Constructed Wetland. Environ. Sci. Technol. 2012, 46, 4583–4590. [Google Scholar] [CrossRef] [PubMed]
- Sujana, M.G.; Thakur, R.S.; Rao, S.B. Removal of Fluoride from aqueous solution by using alum sludge. J. Colloid Interface Sci. 1998, 206, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S.; Kim, D.H.; Yang, J.S.; Baek, K. Adsorption Characteristics of As(III) and As(V) on Alum Sludge from Water Purification Facilities. Sep. Sci. Technol. 2012, 47, 2211–2217. [Google Scholar] [CrossRef]
- Razali, M.; Zhao, Y.Q.; Bruen, M. Effectiveness of a drinking-water treatment sludge in removing different phosphorus species from aqueous solution. Sep. Purif. Technol. 2007, 55, 300–306. [Google Scholar] [CrossRef]
- Wajima, T.; Rakovan, J.F. Removal of fluoride ions using calcined paper sludge. J. Therm. Anal. Calorim. 2013, 113, 1027–1035. [Google Scholar] [CrossRef]
- Nair, A.T.; Ahammed, M.M. The reuse of water treatment sludge as a coagulant for post-treatment of UASB reactor treating urban wastewater. J. Clean. Prod. 2013, 96, 272–281. [Google Scholar] [CrossRef]
- Wahab, M.A.; Jellali, S.; Jedidi, N. Ammonium biosorption onto sawdust: FTIR analysis, kinetics and adsorption isotherms modeling. Bioresour. Technol. 2010, 101, 5070–5075. [Google Scholar] [CrossRef] [PubMed]
- Lv, L.; He, J.; Wei, M.; Evans, D.G.; Zhou, Z. Treatment of high fluoride concentration water by MgAl-CO3 layered double hydroxides: Kinetic and equilibrium studies. Water Res. 2007, 41, 1534–1542. [Google Scholar] [CrossRef] [PubMed]
- Nigussie, W.; Zewge, F.; Chandravanshi, B.S. Removal of excess fluoride from water using waste residue from alum manufacturing process. J. Hazard. Mater. 2007, 147, 954–963. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, Y.; Wu, X. Statistical experiment design approach for the treatment of landfill leachate by photoelectro-Fenton process. J. Environ. Eng. 2012, 138, 278–285. [Google Scholar] [CrossRef]
- Nair, A.T.; Makwana, A.R.; Ahammed, M.M. The use of response surface methodology for modelling and analysis of water and wastewater treatment processes: A review. Environ. Sci. Technol. 2014, 69, 464–478. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.H.; Yang, S.K.; Zhao, Y.; Chen, J. Adsorption behaviors of Oxytetracycline onto sediment in the Weihe River, Shaanxi, China. J. Chem. 2013, 2013, 719–723. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, S.K.; Wang, G.; Han, M. Adsorption behaviors of Acetaminophen onto the colloid in sediment. Pol. J. Environ. Stud. 2015, 24, 411–419. [Google Scholar] [CrossRef]
- Cengeloĝlu, Y.; Kir, E.; ErsÖz, M. Removal of fluoride from aqueous solution by using red mud. Sep. Purif. Technol. 2006, 51, 374–378. [Google Scholar] [CrossRef]
- Gopal, V.; Elango, K.P. Equilibrium, kinetic and thermodynamic studies of adsorption of fluoride onto plaster of Paris. J. Hazard. Mater. 2007, 141, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Samarghandi, M.R.; Khiadani, M.; Foroughi, M.; Nasab, H.Z. Defluoridation of water using activated alumina in presence of natural organic matter via response surface methodology. Environ. Sci. Pollut. R. 2016, 23, 887–897. [Google Scholar] [CrossRef] [PubMed]
- Bashir, M.J.; Isa, M.H.; Kutty, S.R.M.; Awang, Z.B.; Aziz, H.A.; Mohajeri, S. Landfill leachate treatment by electrochemical oxidation. Waste Manag. 2009, 29, 2534–2541. [Google Scholar] [CrossRef] [PubMed]
- Mohajeri, S.; Aziz, H.A.; Isa, M.H.; Zahed, M.A.; Adlan, M.N. Statistical optimization of process parameters for landfill leachate treatment using electro-Fenton technique. J. Hazard. Mater. 2010, 176, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, S.S.; Moghaddam, M.R.A.; Arami, M. Coagulation/flocculation process for dye removal using sludge from water treatment plant: Optimization through response surface methodology. J. Hazard. Mater. 2010, 175, 651–657. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, C.S.; Viswanathan, N.; Meenakshi, S. Defluoridation chemistry of synthetic hydroxyapatite at nano scale: Equilibrium and kinetic studies. J. Hazard. Mater. 2008, 155, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Cui, J.; Wei, Z. Study on the fluoride sorption of various apatite materials in aqueous solution. J. Fluor. Chem. 2009, 130, 1035–1041. [Google Scholar] [CrossRef]
- Kumar, E.; Bhatnagar, A.; Kumar, U.; Sillanpää, M. Defluoridation from aqueous solutions by nano-alumina: Characterization and sorption studies. J. Hazard. Mater. 2011, 186, 1042–1049. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.J.; Tan, Y.; Zhong, M.F. Defluorination of wastewater by calcium chloride modified natural zeolite. Desalination 2011, 276, 246–252. [Google Scholar] [CrossRef]
- Mourabet, M.; Rhilassi, A.E.; Boujaady, H.E.; Bennani-Ziatni, M.; Hamri, R.E.; Taitai, A. Removal of fluoride from aqueous solution by adsorption on apatitic tricalcium phosphate using box–behnken design and desirability function. Appl. Surf. Sci. 2012, 258, 4402–4410. [Google Scholar] [CrossRef]
- Kamble, S.P.; Jagtap, S.; Labhsetwar, N.K.; Thakare, D.; Godfrey, S.; Devotta, S.; Rayalu, S.S. Defluoridation of drinking water using chitin, chitosan and lanthanum-modified chitosan. Chem. Eng. Sci. 2007, 129, 173–180. [Google Scholar] [CrossRef]
- Vinitnantharat, S.; Kositchaiyong, S.; Chiarakorn, S. Removal of fluoride in aqueous solution by adsorption on acid activated water treatment sludge. Appl. Surf. Sci. 2010, 256, 5458–5462. [Google Scholar] [CrossRef]
- Chen, J.X.; Chen, H.H.; Li, X.H.; He, X.J. Preparation and application of zirconium-modified chitosan-zeolite-kaolin composite absorbent for fluoride removal from water. J. Environ. Health 2017, 34, 61–66. (In Chinese) [Google Scholar]
- Malakootian, M.; Moosazadeh, M.; Yousefi, N.; Fatehizadeh, A. Fluoride removal from aqueous solution by pumice: Case study on Kuhbonan water. Afr. J. Environ. Sci. Technol. 2011, 5, 299–306. [Google Scholar]
- Song, R.; Yang, S.K.; Xu, H.Y.; Wang, Z.Z.; Chen, Y.Y.; Wang, Y.Y. Adsorption Behavior and Mechanism for the Uptake of Fluoride Ions by Reed Residues. Int. J. Environ. Res. Public Health 2018, 15, 101. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.Q.; Deng, X.H.; Liu, H.M.; Li, Z.W. Treatment of aqueous solution containing fluoride by absorption process. Technol. Water Treat. 2006, 32, 1–5. (In Chinese) [Google Scholar]
- Bia, G.; de Pauli, C.P.; Borgnino, L. The role of Fe(III)modified montmorillonite on fluoride mobility: Adsorptionexperiments and competition with phosphate. J. Environ. Manag. 2012, 100, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Teutli-Sequeira, A.; Martı’nez-Miranda, V.; Solache-Rı’os, M.; Linares-Herna’ndez, I. Aluminum and lanthanum effects in natural materials on the adsorption of fluoride ions. J. Fluor. Chem. 2013, 148, 6–13. [Google Scholar] [CrossRef]

| Run | x1-Initial Concentration (mg/L) | x2-pH | x3-HWS dose (g/L) | Removal Efficiency (%) | ε | |
|---|---|---|---|---|---|---|
| Yexp | Ypre | |||||
| 1 | 3 | 10 | 5 | 34.72 | 35.61 | −0.89 |
| 2 | 3 | 4 | 15 | 71.62 | 70.73 | 0.89 |
| 3 | 3 | 7 | 10 | 63.17 | 65.20 | −2.03 |
| 4 | 1 | 7 | 5 | 57.84 | 57.98 | −0.14 |
| 5 | 3 | 10 | 15 | 63.03 | 62.42 | 0.61 |
| 6 | 5 | 4 | 10 | 45.65 | 46.68 | −1.03 |
| 7 | 3 | 7 | 10 | 65.32 | 65.20 | 0.12 |
| 8 | 3 | 7 | 10 | 65.71 | 65.20 | 0.51 |
| 9 | 5 | 7 | 5 | 25.87 | 24.23 | 1.64 |
| 10 | 1 | 4 | 10 | 74.42 | 73.67 | 0.75 |
| 11 | 3 | 7 | 10 | 65.78 | 65.20 | 0.58 |
| 12 | 3 | 7 | 10 | 66.03 | 65.20 | 0.83 |
| 13 | 1 | 10 | 10 | 69.53 | 68.49 | 1.04 |
| 14 | 1 | 7 | 15 | 79.51 | 81.15 | −1.64 |
| 15 | 5 | 10 | 10 | 38.12 | 38.87 | −0.75 |
| 16 | 3 | 4 | 5 | 39.68 | 40.29 | −0.61 |
| 17 | 5 | 7 | 15 | 58.45 | 58.31 | 0.14 |
| Samples | F− (mg/L) | SS (mg/L) | pH |
|---|---|---|---|
| W1 | 20.2 | 615.0 | 9.10 |
| W2 | 15.3 | 45.0 | 7.40 |
| W3 | 8.6 | 34.0 | 7.42 |
| Chemical Composition | WS (%) | Alum Sludge(%) [17] |
|---|---|---|
| Al2O3 | 47.56 | 47.20 |
| SiO2 | 28.54 | 1.60 |
| Fe2O3 | 4.30 | 7.18 |
| TiO2 | 1.47 | 20.65 |
| Cl− | 2.14 | - |
| LOI | 14.32 | 19.00 |
| Adsorbent | Qe,exp (mg/g) | Pseudo-First Order | Pseudo-Second Order | ||||
|---|---|---|---|---|---|---|---|
| R2 | K1 (1/h) | Qe,cal (mg/g) | R2 | K2 (kg/mg·h) | Qe,cal (mg/g) | ||
| HWS | 0.1402 | 0.9894 | 0.0757 | 0.1405 | 0.8286 | 1.5 | 0.1479 |
| Langmuir | Freundlich | |||||
|---|---|---|---|---|---|---|
| Qm (mg/g) | b (L/mg) | R2 | RL | KF (mg/g)·(L/mg)1/n | 1/n | R2 |
| 0.24643 | 1.8547 | 0.9959 | 0.7294 | 0.1455 | 0.4165 | 0.9537 |
| Samples | Surface Area (m2/g) | Pore Volume (m3/g) | Average Pore Size (nm) |
|---|---|---|---|
| WS | 6.85680 | 0.000723 | 8.88669 |
| HWS | 53.59230 | 0.006453 | 3.23694 |
| Source | Sum of Squares | df | Mean Square | F-value | p-value p > F | Significance |
|---|---|---|---|---|---|---|
| Model | 3782.08 | 9 | 420.23 | 178.60 | <0.0001 | significant |
| A-initial concentration | 1602.06 | 1 | 1602.06 | 680.88 | <0.0001 | |
| B-pH | 84.31 | 1 | 84.31 | 35.83 | 0.0006 | |
| C-HWS dose | 1638.78 | 1 | 1638.78 | 696.48 | <0.0001 | |
| AB | 1.74 | 1 | 1.74 | 0.74 | 0.4180 | |
| AC | 29.76 | 1 | 29.76 | 12.65 | 0.0093 | |
| BC | 3.29 | 1 | 3.29 | 1.40 | 0.2753 | |
| A2 | 27.56 | 1 | 27.56 | 11.71 | 0.0111 | |
| B2 | 137.45 | 1 | 137.45 | 58.42 | 0.0001 | |
| C2 | 219.85 | 1 | 219.85 | 93.44 | <0.0001 | |
| Residual | 16.47 | 7 | 2.35 | |||
| Lack of Fit | 11.05 | 3 | 3.68 | 2.72 | 0.1792 | not significant |
| Pure Error | 5.42 | 4 | 1.36 | |||
| Cor Total | 3798.55 | 16 |
| Item | Initial Concentration (mg/L) | pH | HWS Dose (g/L) | Removal (%) | Desirability |
|---|---|---|---|---|---|
| Predicted | linear | 6.12 | 14.10 | 81.921 | 0.756 |
| Observed | linear | 6.12 | 14.10 | 81.153 | - |
| Adsorbent | Adsorbent Dose (g/L) | Initial Concentration (mg/L) | Adsorption Capacity (mg/g) | Removal Efficiency (%) |
|---|---|---|---|---|
| HWS | 14.10 | 2.40 | 0.141 | 82.84 |
| 2.00 | 2.40 | 0.625 | 52.08 | |
| 14.10 | 20.20 (W1) | 1.135 | 79.23 | |
| 2.00 | 20.00 (W1) | 2.030 | 20.10 | |
| 14.10 | 15.30 (W2) | 0.866 | 79.81 | |
| 2.00 | 15.30 (W2) | 1.940 | 25.36 | |
| 14.10 | 8.60 (W3) | 0.492 | 80.67 | |
| 2.00 | 8.60 (W3) | 1.535 | 35.70 |
| Adsorbent | Adsorbent Dose (g/L) | Initial Concentration (mg/L) | Adsorption Capacity (mg/g) | Reference |
|---|---|---|---|---|
| Composite absorbent | 1.5 | 5.24 | 3.07 | [42] |
| Pumice | 2.29 | 2.8 | 0.31 | [43] |
| Desugared reed root | 0.1 | 2.4 | 2.136 | [44] |
| Lignite | 3 | 90 | 6.9 | [45] |
| Modified montmorillonite | 1 | 10 | 0.696 | [46] |
| Modified hematite | - | 5.8 | 0.53 | [47] |
| Modified zeolite | - | 0.1 | 1.766 | [38] |
| HWS | 2.0 | 20.2 (W1) | 2.03 | This study |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, S.; Jiang, Q.; Fang, J.; Wang, W.; Wang, Y. The Adsorptive Removal of Fluoride from Aqueous Solution by Modified Sludge: Optimization Using Response Surface Methodology. Int. J. Environ. Res. Public Health 2018, 15, 826. https://doi.org/10.3390/ijerph15040826
Li Y, Yang S, Jiang Q, Fang J, Wang W, Wang Y. The Adsorptive Removal of Fluoride from Aqueous Solution by Modified Sludge: Optimization Using Response Surface Methodology. International Journal of Environmental Research and Public Health. 2018; 15(4):826. https://doi.org/10.3390/ijerph15040826
Chicago/Turabian StyleLi, Ying, Shengke Yang, Qianli Jiang, Jie Fang, Wenke Wang, and Yanhua Wang. 2018. "The Adsorptive Removal of Fluoride from Aqueous Solution by Modified Sludge: Optimization Using Response Surface Methodology" International Journal of Environmental Research and Public Health 15, no. 4: 826. https://doi.org/10.3390/ijerph15040826
APA StyleLi, Y., Yang, S., Jiang, Q., Fang, J., Wang, W., & Wang, Y. (2018). The Adsorptive Removal of Fluoride from Aqueous Solution by Modified Sludge: Optimization Using Response Surface Methodology. International Journal of Environmental Research and Public Health, 15(4), 826. https://doi.org/10.3390/ijerph15040826






