Using Grey Relational Analysis to Evaluate Energy Consumption, CO2 Emissions and Growth Patterns in China’s Provincial Transportation Sectors
Abstract
:1. Introduction
- What are the relationships between energy consumption and CO2 emissions in China’s transport sector at the regional and provincial levels?
- What are the growth patterns of economy, energy and environment (3E) systems for the Chinese provincial transport sectors?
- What are the impacts of interprovincial inequality in economic development and construction of transportation infrastructure on the 3E’s growth pattern over time?
- How the growth disparities of CO2 emissions among eastern, central and western provincial units could be contributed to geography, economy production, energy consumption and transportation activities, respectively?
- Considering the wide variations in the 3E system growth patterns across provincial regions, what clean energy policies should be adopted to mitigate CO2 emissions on the province-by-province basis?
2. Materials and Methods
2.1. Introduction of Grey Relational Analysis
2.2. Grey Relational Analysis in Transportation Sector
2.3. Data Consolidation
3. Results
3.1. The Case with Negative GRGs
3.2. The Case with Positive GRGs
3.3. The Case with Mixed GRGs
4. Discussion
4.1. Development Modes in China’s Provincial Transportation Sectors
4.2. Policy Implications
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baron, R.; Aasrud, A.; Sinton, J.; Campbell, N.; Jiang, K.; Zhuang, X. Policy options for low-carbon power generation in China: Designing an emissions trading system for China’s electricity sector. IEA Energy Pap. 2012. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook. 2011. Available online: https://www.iea.org/newsroom/news/2011/november/world-energy-outlook-2011.html (accesssed on 22 November 2017).
- IEA. CO2 Emissions from Fuel Combustion-Highlights. Available online: http://www.iea.org/media/statistics/co2highlights.pdf (accessed on 22 November 2017).
- Yeung, Y.-M.; Shen, J. Developing China's West: A Critical Path to Balanced National Development; Chinese University Press: Hong Kong, China, 2004. [Google Scholar]
- Sun, Z. Explaining Regional Disparities of China’s Economic Growth: Geography, Policy and Infrastructure. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 2013. [Google Scholar]
- Yuan, C.; Liu, S.; Fang, Z.; Xie, N. The relation between Chinese economic development and energy consumption in the different periods. Energy Policy 2010, 38, 5189–5198. [Google Scholar] [CrossRef]
- Loo, B.P.; Li, L. Carbon dioxide emissions from passenger transport in China since 1949: Implications for developing sustainable transport. Energy Policy 2012, 50, 464–476. [Google Scholar] [CrossRef]
- Zhang, M.; Li, H.; Zhou, M.; Mu, H. Decomposition analysis of energy consumption in Chinese transportation sector. Appl. Energy 2011, 88, 2279–2285. [Google Scholar] [CrossRef]
- Deng, J.-L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Li, P.; Tan, T.; Lee, J. Grey relational analysis of amine inhibition of mild steel corrosion in acids. Corrosion 1997, 53, 186–194. [Google Scholar] [CrossRef]
- Deng, J. Properties of Relational Space for Grey System. In Essential Topics on Grey System Theory and Applications; China Ocean University: Qingdao, China, 1988; pp. 1–13. [Google Scholar]
- Tzeng, G.; Hu, Y. The section of bus system operation and service performance indicators—Application of grey relation analysis. J. Chin. Fuzzy Syst. Assoc. 1996, 2, 73–82. [Google Scholar]
- Chang, Y.; Chen, J. Evaluation criteria and alternatives choice of the grade separated railroad—Applications of grey relation method. Transport. Plan. 1997, 26, 353–378. [Google Scholar]
- Chang, T.; Lin, S. Grey relation analysis of carbon dioxide emissions from industrial production and energy uses in Taiwan. J. Environ. Manag. 1999, 56, 247–257. [Google Scholar] [CrossRef]
- Liang, R.-H. Application of grey relation analysis to hydroelectric generation scheduling. Int. J. Electr. Power Energy Syst. 1999, 21, 357–364. [Google Scholar] [CrossRef]
- Mu, H.; Kondou, Y.; Tonooka, Y.; Sato, Y.; Zhou, W.; Ning, Y.; Sakamoto, K. Grey relative analysis and future prediction on rural household biofuels consumption in China. Fuel Process. Technol. 2004, 85, 1231–1248. [Google Scholar] [CrossRef]
- Lin, S.J.; Lu, I.; Lewis, C. Grey relation performance correlations among economics, energy use and carbon dioxide emission in Taiwan. Energy Policy 2007, 35, 1948–1955. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Tong, L.-I. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers. Manag. 2011, 52, 147–152. [Google Scholar] [CrossRef]
- Pao, H.-T.; Fu, H.-C.; Tseng, C.-L. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model. Energy 2012, 40, 400–409. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Chang, H. Forecasting Carbon Dioxide Emissions in China Using Optimization Grey Model. JCP 2013, 8, 97–101. [Google Scholar] [CrossRef]
- Fan, F.; Lei, Y. Decomposition analysis of energy-related carbon emissions from the transportation sector in Beijing. Transp. Res. Part D Transp. Environ. 2016, 42, 135–145. [Google Scholar] [CrossRef]
- Huang, M.; Wang, B. Factors influencing CO2 emissions in China based on grey relational analysis. Energy Source Part A 2016, 38, 555–561. [Google Scholar] [CrossRef]
- Yuan, C.; Rui, X.; Wu, D.; Jiao, P. Carbon emission reduction pressure index for China’s provincial transport sector based on geographical weighted regression model. China J. Highway Transp. 2016, 29, 262–270. [Google Scholar]
- Yuan, C.; Zhang, S.; Jiao, P.; Wu, D. Temporal and spatial variation and influencing factors research on total factor efficiency for transportation carbon emissions in China. Res. Sci. 2017, 39, 687–697. [Google Scholar]
- Moran, J.; Granada, E.; Miguez, J.L.; Poretiro, J. Use of grey relational analysis to assess and optimize small biomass boilers. Fuel Process. Technol. 2006, 87, 123–127. [Google Scholar] [CrossRef]
- Pai, T.-Y.; Hanaki, K.; Ho, H.-H.; Hsieh, C.-M. Using grey system theory to evaluate transportation effects on air quality trends in Japan. Transp. Res. Part D Transp. Environ. 2007, 12, 158–166. [Google Scholar] [CrossRef]
- Kose, E.; Burmaoglu, S.; Kabak, M. Grey relational analysis between energy consumption and economic growth. Grey Syst. Inf. 2013, 3, 291–304. [Google Scholar] [CrossRef]
- Malekpoor, H.; Chalvatzis, K.; Mishra, N.; Mehlawat, M.K.; Zafirakis, D.; Song, M. Integrated grey relational analysis and multi objective grey linear programming for sustainable electricity generation planning. Ann. Oper. Res. 2017. [Google Scholar] [CrossRef]
- Julong, D. Grey fuzzy forecast and control for grain. J. Huazhong Univ. Sci. Technol. Med. Sci. 1983, 2, 1–8. [Google Scholar]
- CESY. China Energy Statistical Yearbook 1995–2013; China Statistics Press: Beijing, China, 2014; Available online: http://tongji.cnki.net/overseas/engnavi/HomePage.aspx?id=N2012020066&name=YCXME&floor=1 (accessed on 22 November 2017).
- Zhao, M.; Zhang, W.; Yu, L. Carbon emissions from energy consumption in Shanghai City. Res. Environ. Sci. 2009, 22, 984–989. [Google Scholar]
- Paustian, K.; Ravindranath, N.; van Amstel, A. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/ (accessed on 22 November 2017).
- CTCY. Yearbook of China Transportation and Communications. Available online: http://tongji.cnki.net/overseas/engnavi/HomePage.aspx?id=N2011030122&name=YZGJT&floor=1 (accessed on 22 November 2017).
- Yang, Y.; Wang, C.; Liu, W.; Zhou, P. Microsimulation of low carbon urban transport policies in Beijing. Energy Policy 2017, 107, 561–572. [Google Scholar] [CrossRef]
- Wang, Y.; Sperling, D.; Tal, G.; Fang, H. China’s electric car surge. Energy Policy 2017, 102, 486–490. [Google Scholar] [CrossRef]
| Provincial Unit | GCE (Energy Consumption) | GCT (Transportation Turnover) |
|---|---|---|
| Anhui | −0.9755 | 0.7096 |
| Beijing | −0.9768 | −0.6802 |
| Chongqing | −0.9608 | −0.7836 |
| Fujian | −0.9922 | 0.8823 |
| Gansu | −0.9367 | 0.6259 |
| Guangdong | 0.9896 | 0.6743 |
| Guangxi | 0.9900 | −0.7372 |
| Guizhou | −0.9949 | −0.7947 |
| Hainan | −0.9710 | −0.6946 |
| Hebei | −0.9740 | 0.7831 |
| Heilongjiang | −0.9763 | −0.7696 |
| Henan | 0.9872 | 0.7982 |
| Hubei | −0.9586 | −0.7244 |
| Hunan | −0.9785 | −0.7623 |
| Jilin | 0.9520 | −0.7619 |
| Jiangsu | −0.9862 | 0.8387 |
| Jiangxi | 0.9913 | 0.6052 |
| Liaoning | 0.9689 | 0.7202 |
| Inner Mongolia | 0.9758 | −0.8606 |
| Ningxia | −0.9028 | 0.6220 |
| Qinghai | −0.9613 | −0.8760 |
| Shandong | 0.9846 | −0.7696 |
| Shanghai | 0.9845 | 0.6690 |
| Shaanxi | −0.9681 | −0.8623 |
| Shanxi | −0.9562 | −0.7971 |
| Sichuan | −0.9710 | −0.7716 |
| Tianjin | 0.9927 | 0.6787 |
| Xinjiang | −0.9326 | 0.7954 |
| Yunnan | 0.9900 | −0.6747 |
| Zhejiang | −0.9855 | 0.7739 |
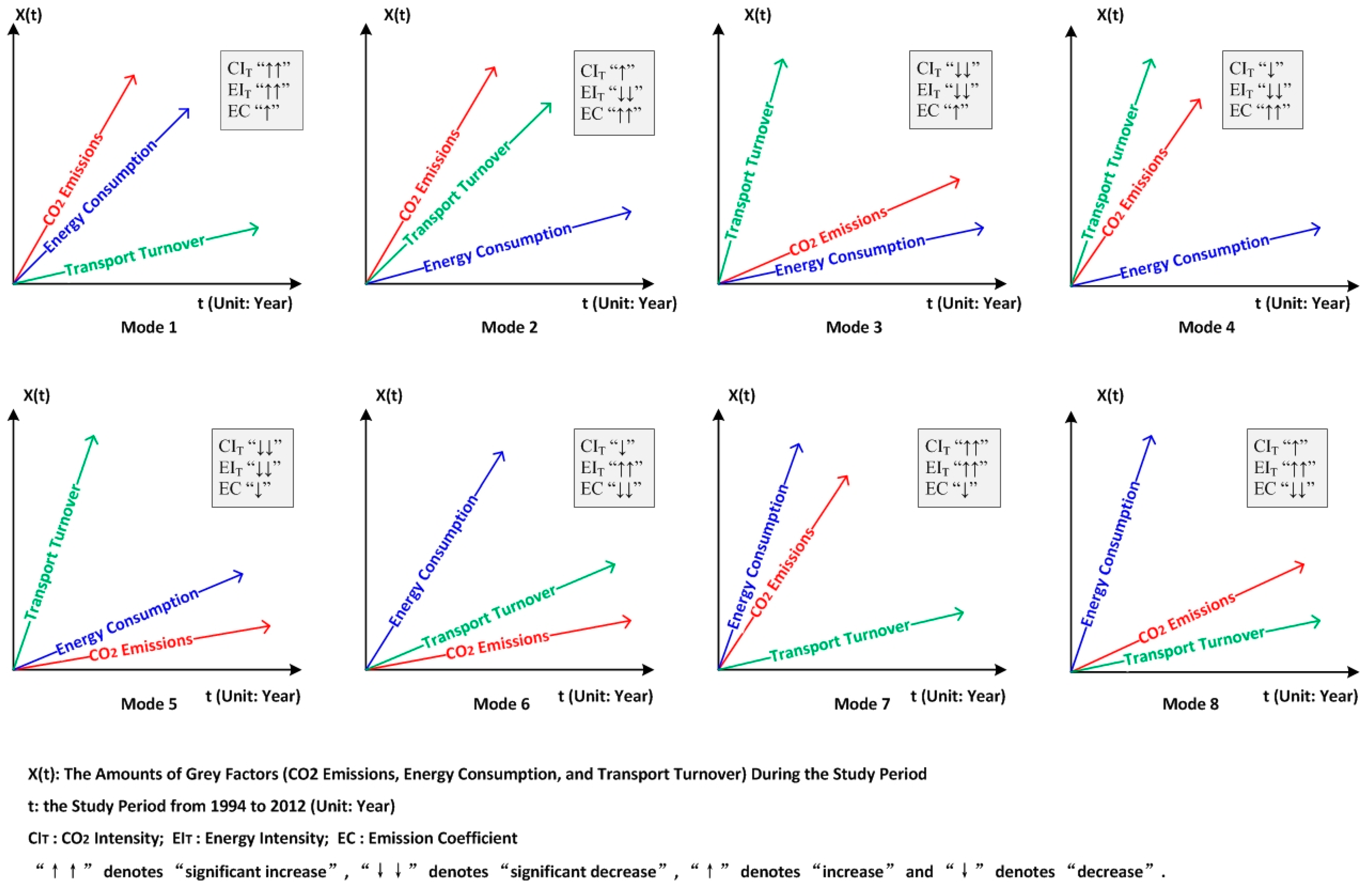
| Development Mode | GRG of Transport Turnover GCT | GRG of Energy Consumption GCE | GRA Comparison | Trend | Provincial Units |
|---|---|---|---|---|---|
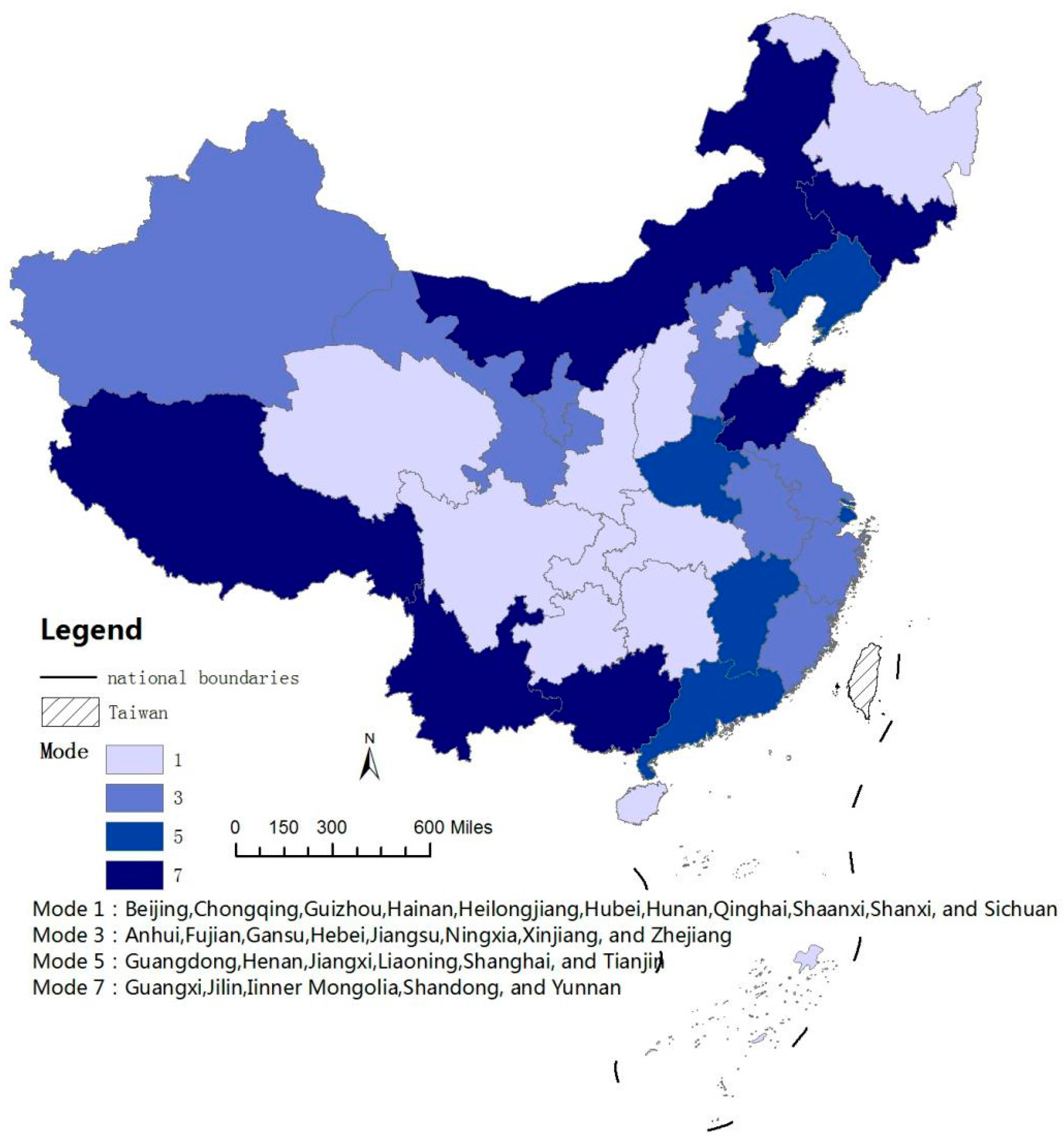
| Mode 1 | <0 | <0 | |GCE| > |GCT| | CIT “↑↑” EIT “↑↑” EC “↑” | Beijing, Chongqing, Guizhou, Hainan, Heilongjiang, Hubei, Hunan, Qinghai, Shaanxi, Shanxi, Sichuan, |
| Mode 2 | <0 | <0 | |GCE| < |GCT| | CIT “↑” EIT “↓↓” EC “↑↑” | N/A |
| Mode 3 | >0 | <0 | |GCE| > |GCT| | CIT “↓↓” EIT “↓↓” EC “↑” | Anhui, Fujian, Gansu, Hebei, Jiangsu, Ningxia, Xinjiang, Zhejiang |
| Mode 4 | >0 | <0 | |GCE| < |GCT| | CIT “↓” EIT “↓↓” EC “↑↑” | N/A |
| Mode 5 | >0 | >0 | |GCE| > |GCT| | CIT “↓↓” EIT “↓↓” EC “↓” | Guangdong, Henan, Jiangxi, Liaoning, Shanghai, Tianjin |
| Mode 6 | >0 | >0 | |GCE| < |GCT| | CIT “↓” EIT “↑↑” EC “↓↓” | N/A |
| Mode 7 | <0 | >0 | |GCE| > |GCT| | CIT “↑↑” EIT “↑↑” EC “↓” | Guangxi, Jilin, Inner Mongolia, Shandong, Yunnan |
| Mode 8 | <0 | >0 | |GCE| < |GCT| | CIT “↑” EIT “↑↑” EC “↓↓” | N/A |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, C.; Wu, D.; Liu, H. Using Grey Relational Analysis to Evaluate Energy Consumption, CO2 Emissions and Growth Patterns in China’s Provincial Transportation Sectors. Int. J. Environ. Res. Public Health 2017, 14, 1536. https://doi.org/10.3390/ijerph14121536
Yuan C, Wu D, Liu H. Using Grey Relational Analysis to Evaluate Energy Consumption, CO2 Emissions and Growth Patterns in China’s Provincial Transportation Sectors. International Journal of Environmental Research and Public Health. 2017; 14(12):1536. https://doi.org/10.3390/ijerph14121536
Chicago/Turabian StyleYuan, Changwei, Dayong Wu, and Hongchao Liu. 2017. "Using Grey Relational Analysis to Evaluate Energy Consumption, CO2 Emissions and Growth Patterns in China’s Provincial Transportation Sectors" International Journal of Environmental Research and Public Health 14, no. 12: 1536. https://doi.org/10.3390/ijerph14121536
APA StyleYuan, C., Wu, D., & Liu, H. (2017). Using Grey Relational Analysis to Evaluate Energy Consumption, CO2 Emissions and Growth Patterns in China’s Provincial Transportation Sectors. International Journal of Environmental Research and Public Health, 14(12), 1536. https://doi.org/10.3390/ijerph14121536






