DengueME: A Tool for the Modeling and Simulation of Dengue Spatiotemporal Dynamics †
Abstract
:1. Introduction
2. Related Work
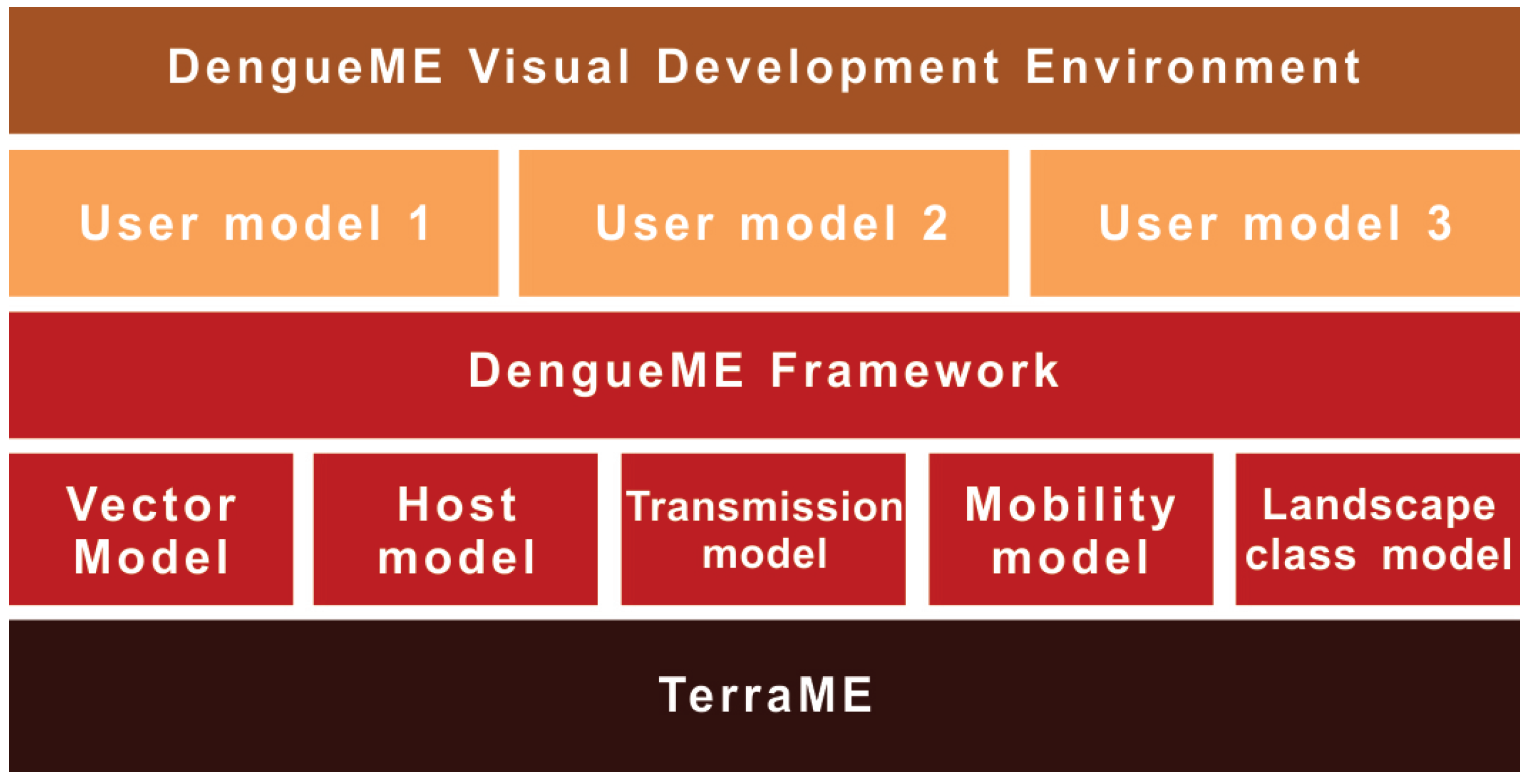
3. DengueME Framework Overview
3.1. Framework Requirements and Design
3.2. Models
3.2.1. Vector Models
3.2.2. Host Models
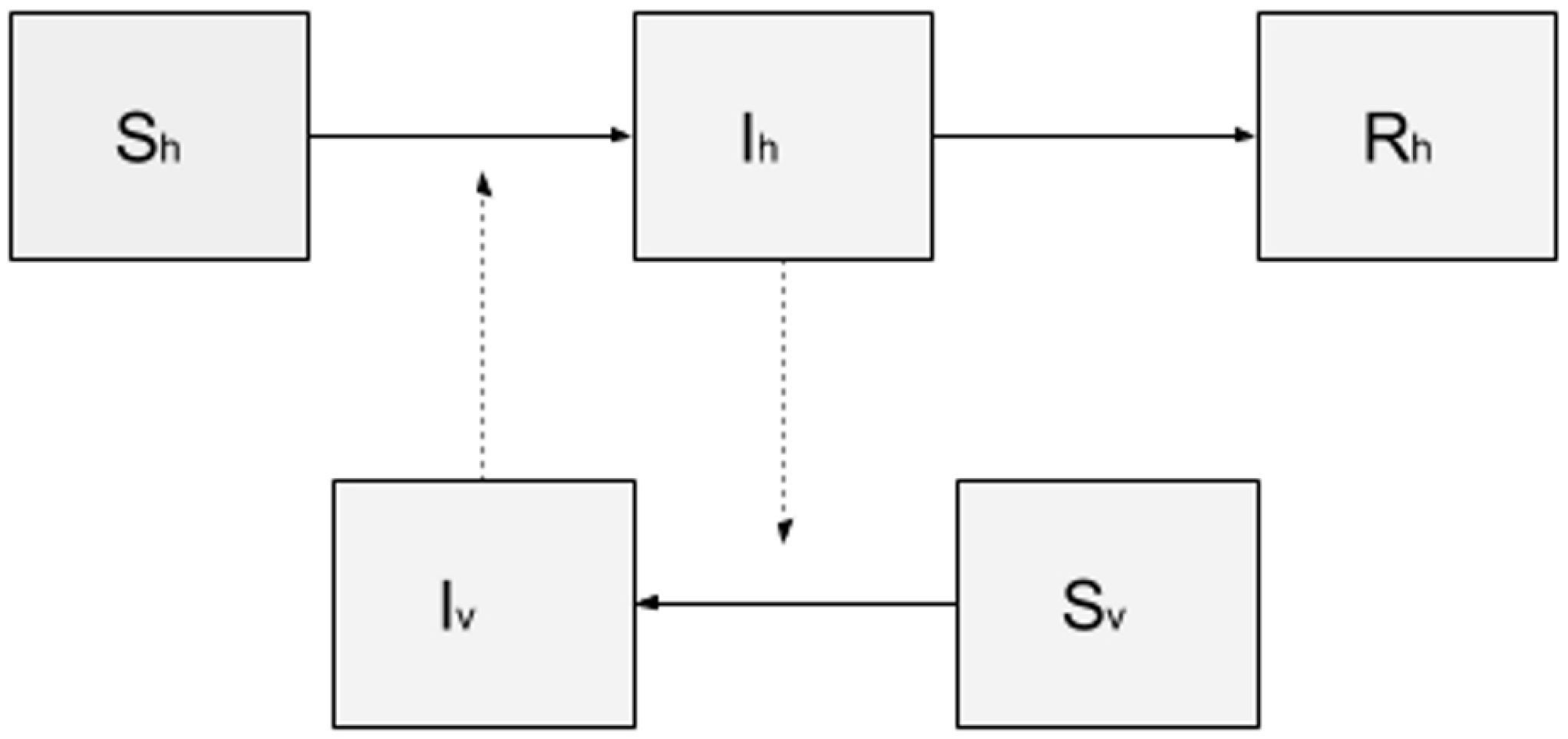
3.2.3. Transmission Models
3.2.4. Mobility Models
3.2.5. Landscape Class Models
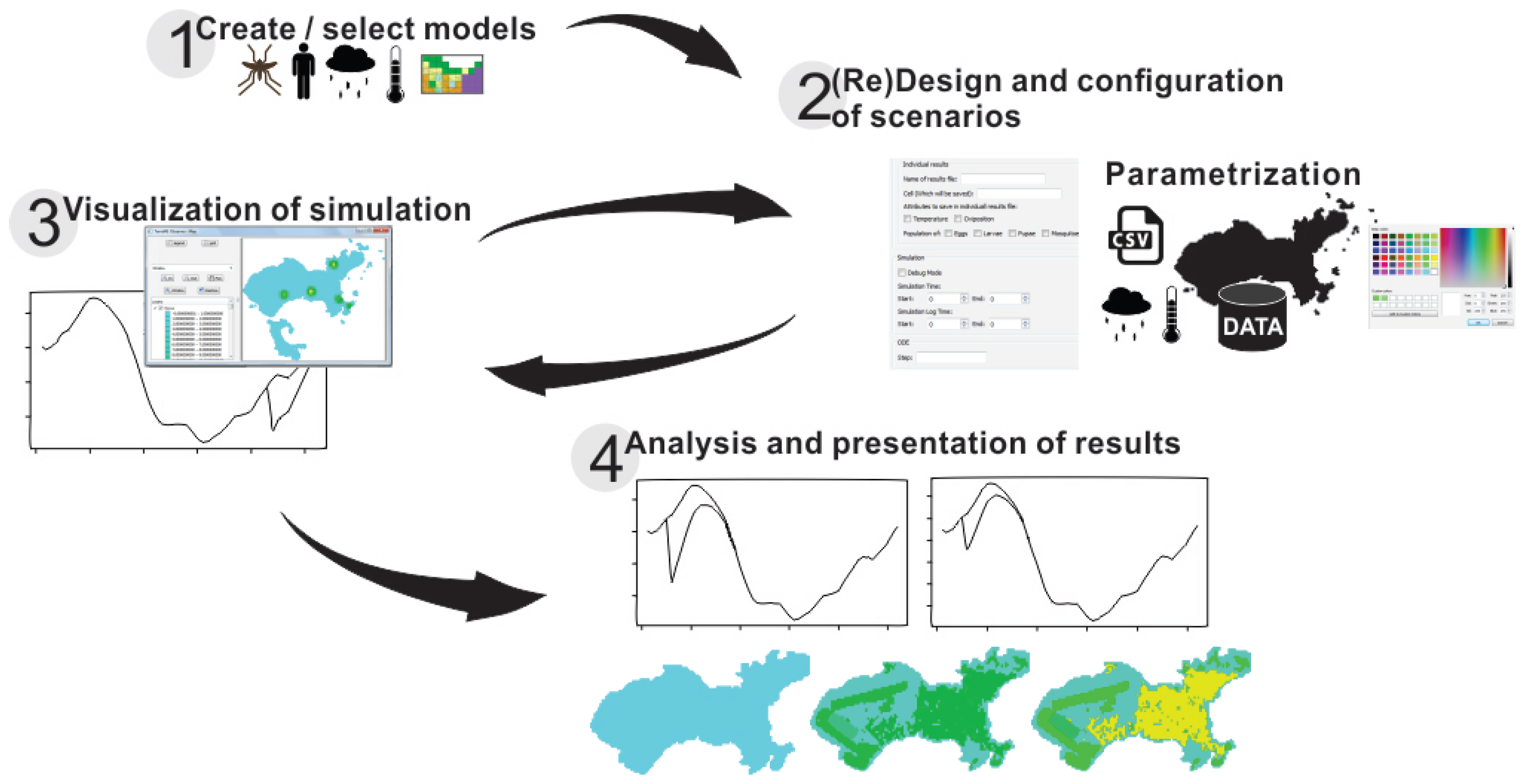
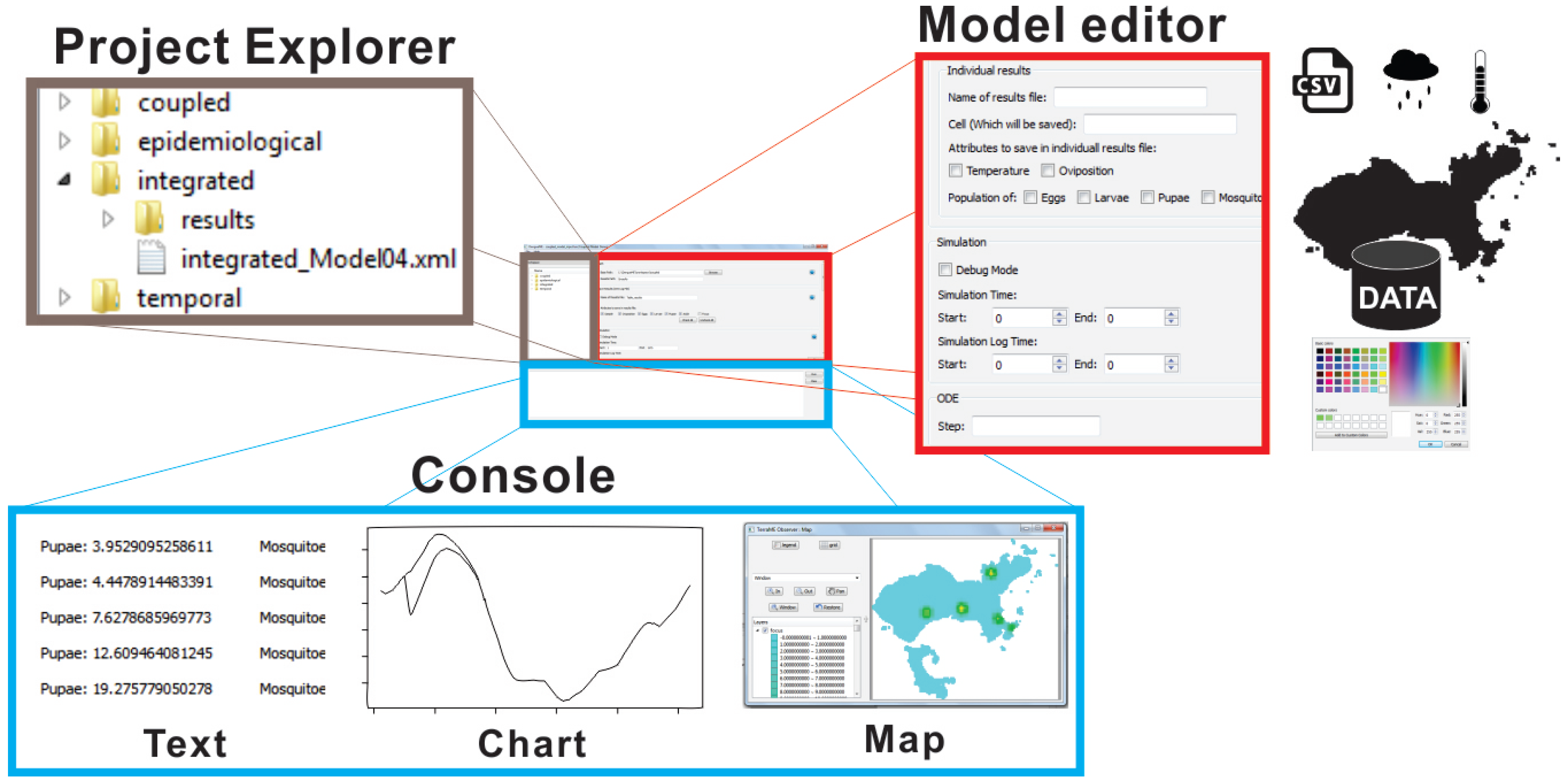
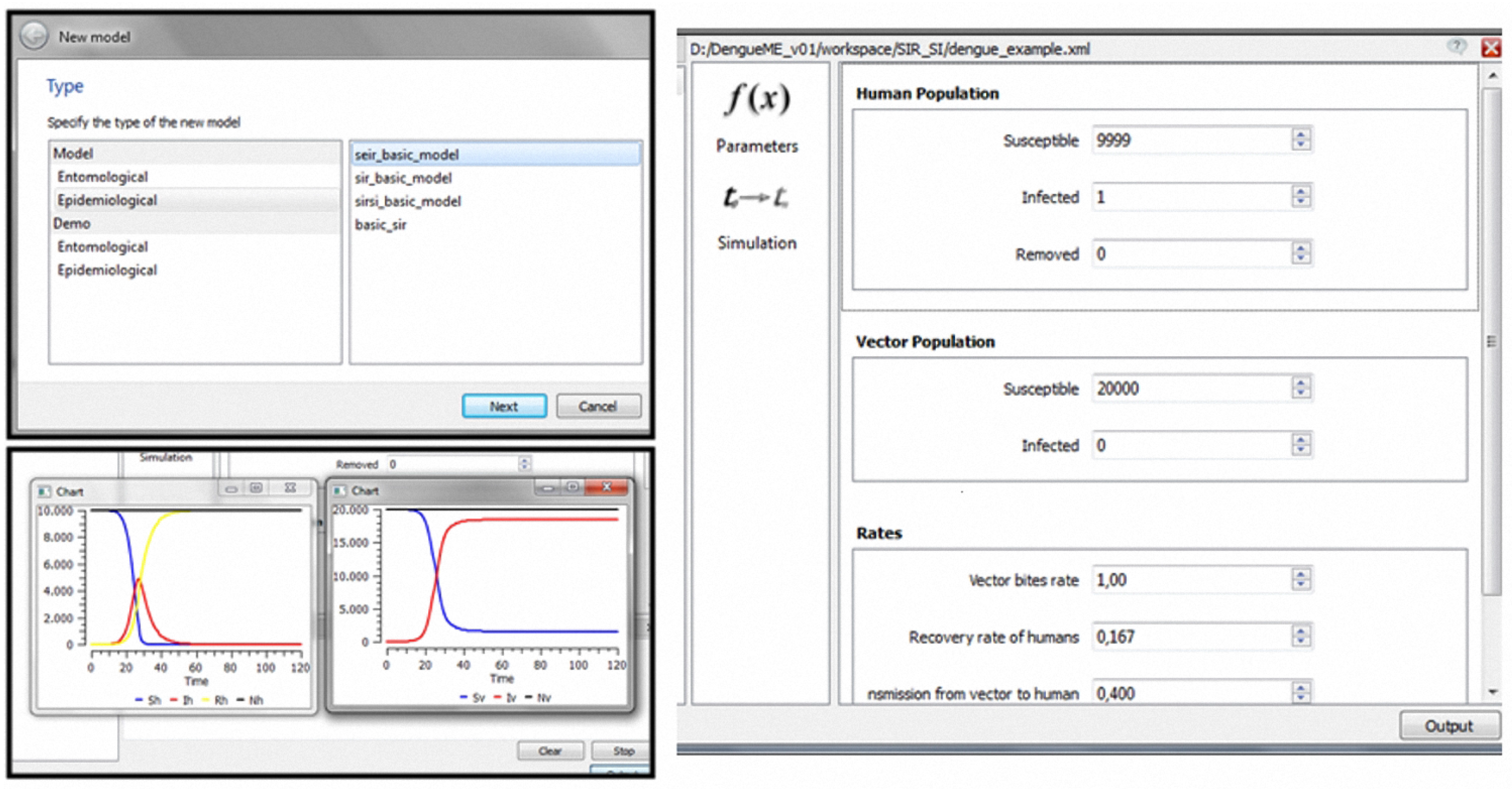
3.2.6. DengueME Visual Development Environment
4. DengueME Application
4.1. A Basic SIR-SI Transmission Model
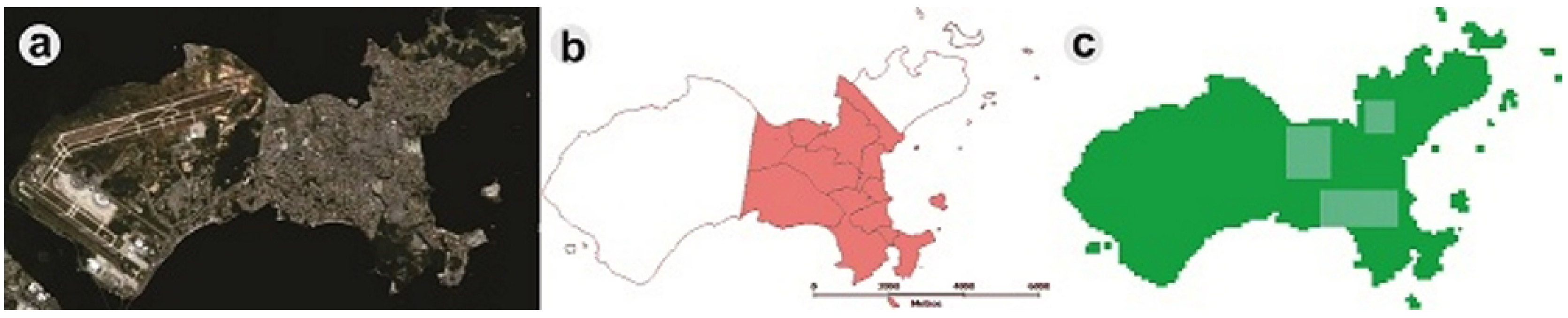
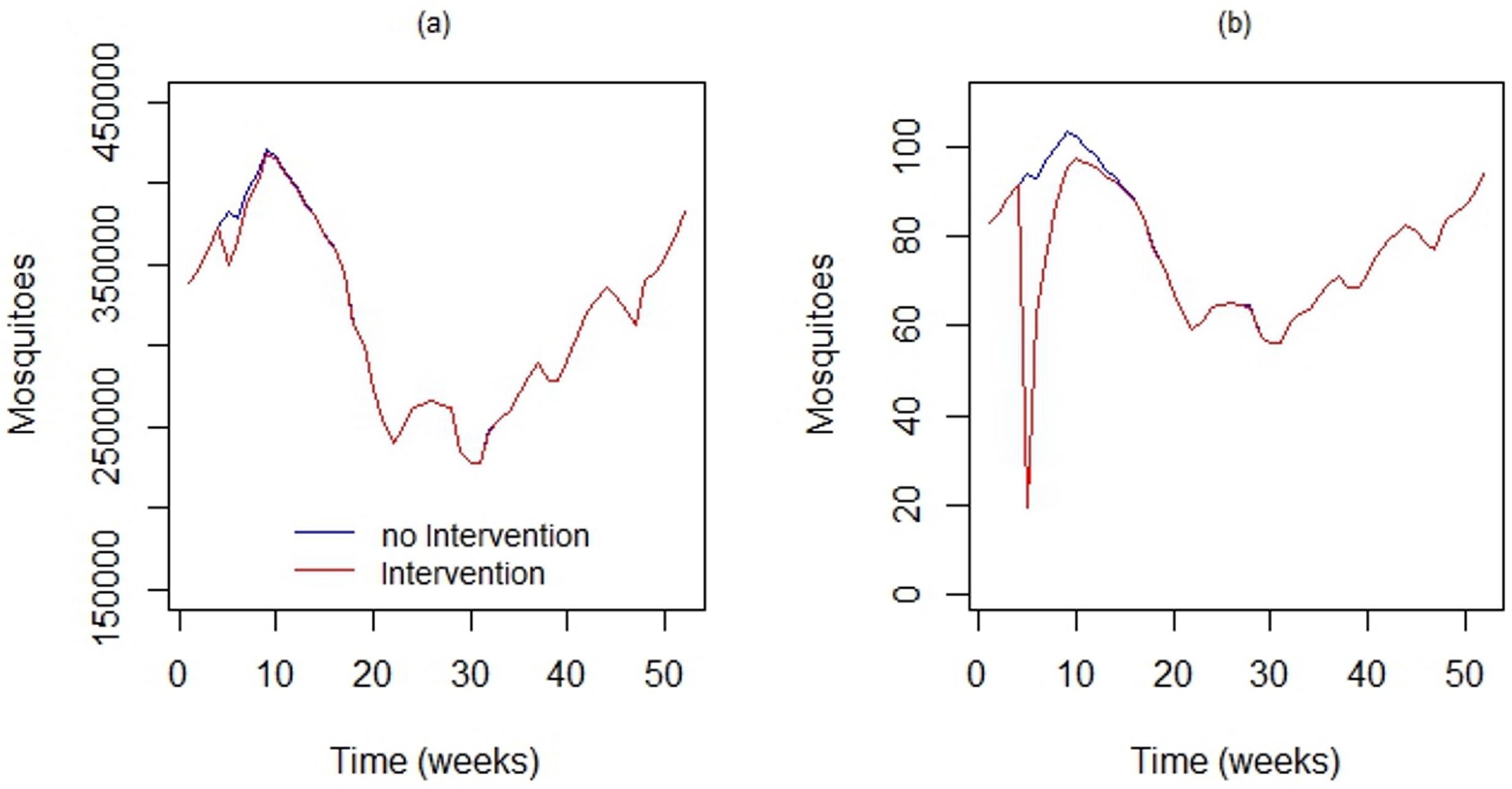
4.2. Simulating the Impact of Local Interventions on Vector Density
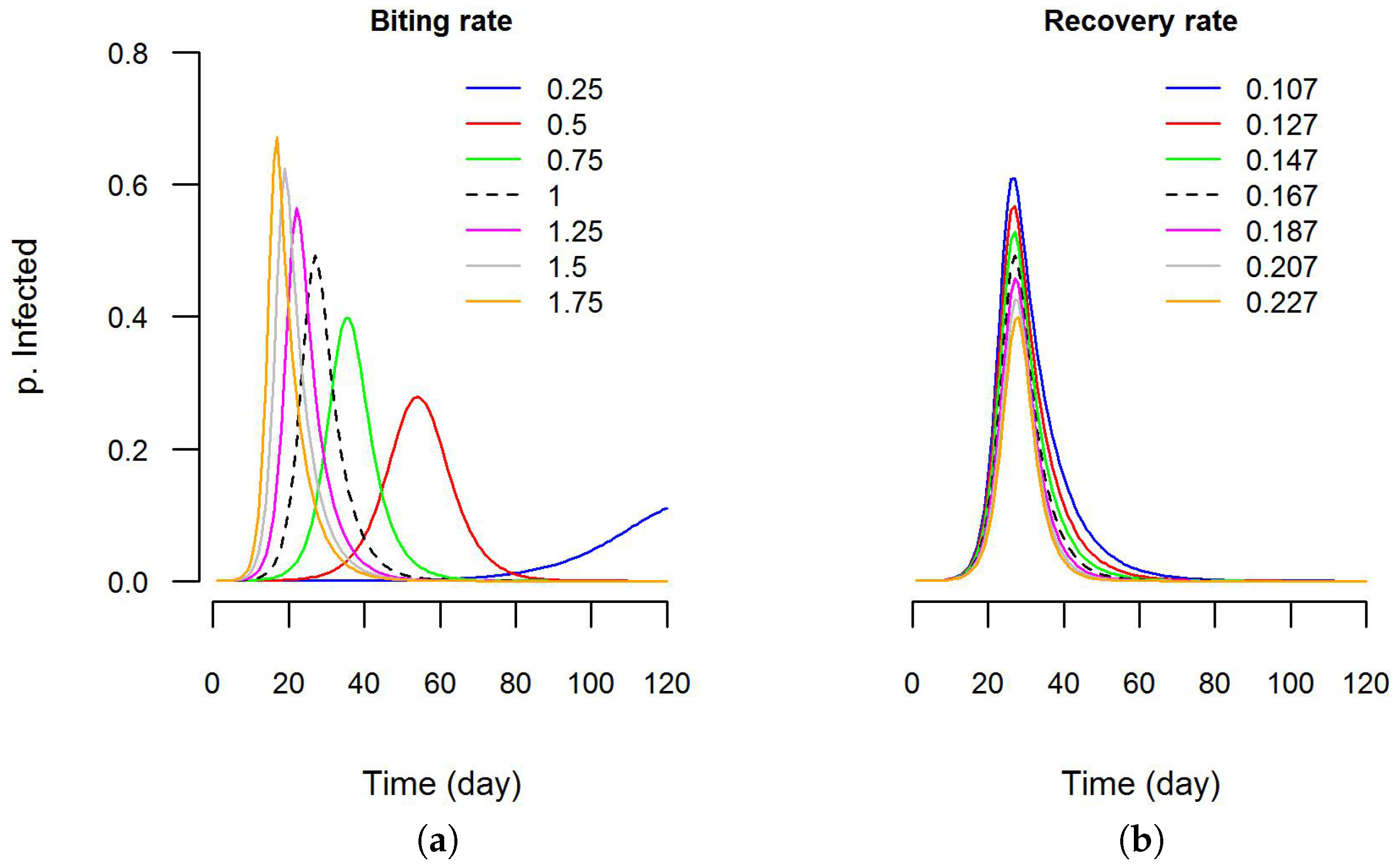
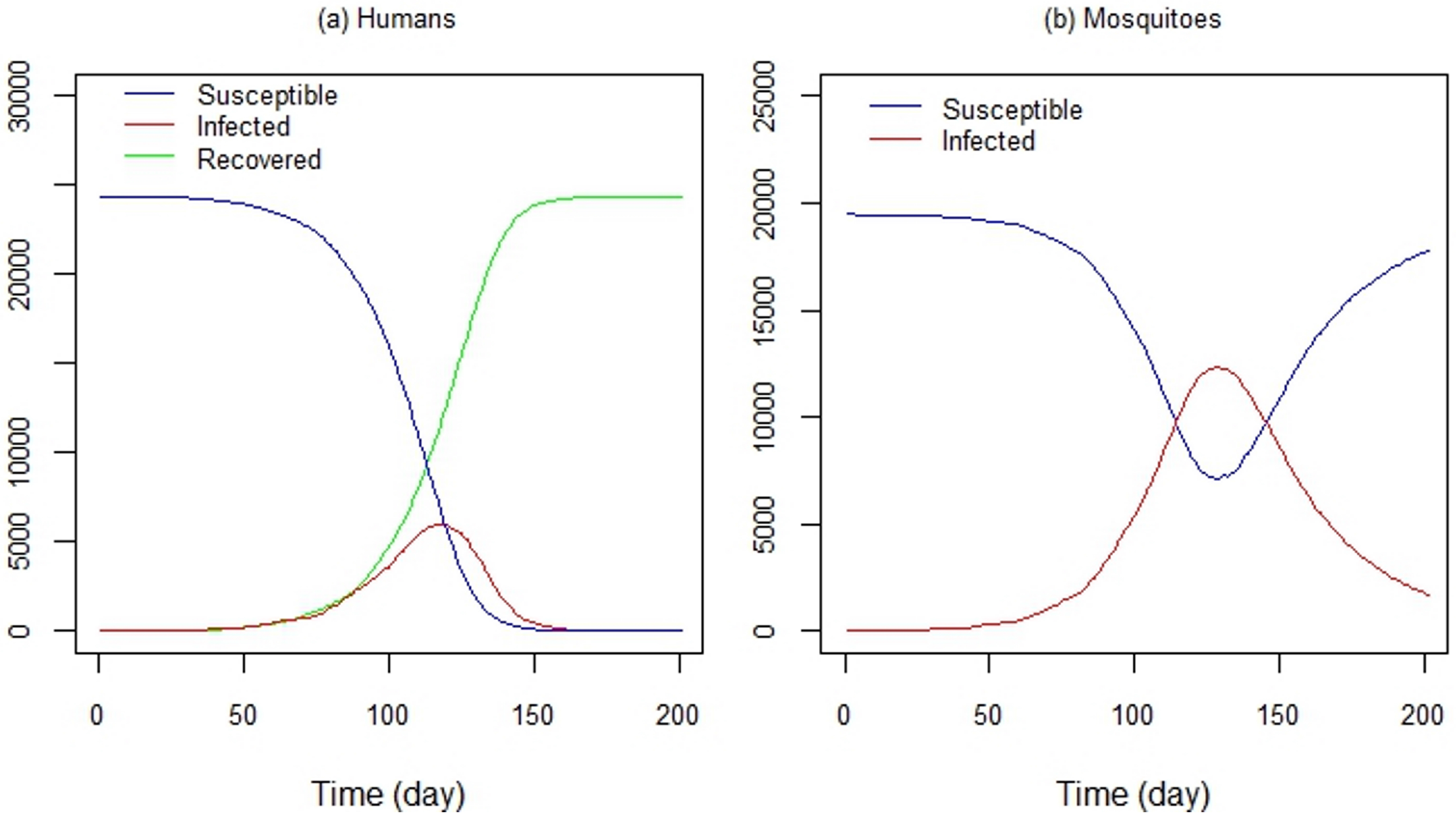
4.3. Simulating an Epidemic Scenario
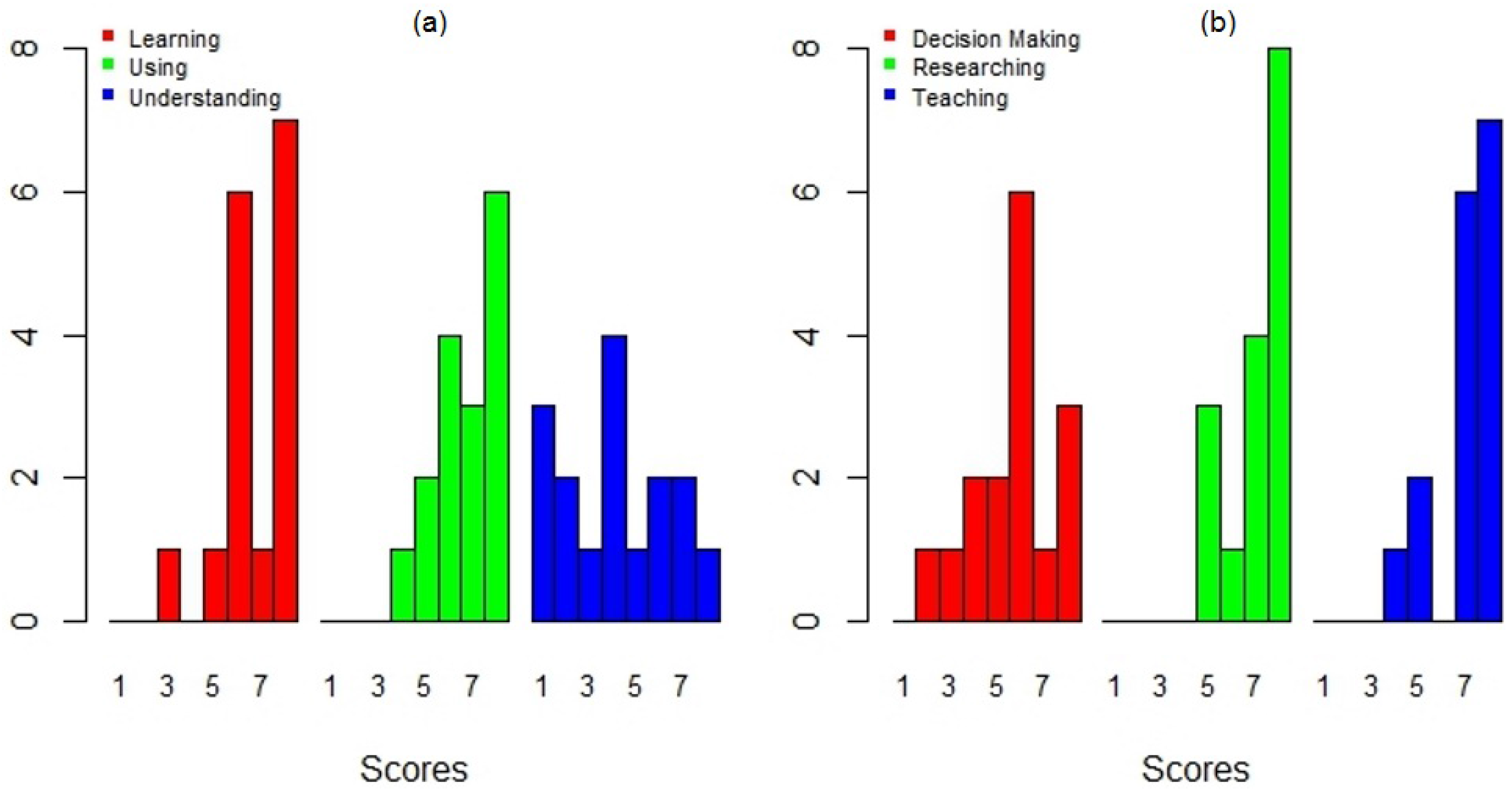
5. DengueME Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CSV | Comma-Separated Values |
| DengueME | Dengue Modeling Environment |
| DengueME VDE | DengueME Visual Development Environment |
| GUI | Graphical User Interface |
| TerraME | Terra Modeling Environment |
| TerraML | Terra Modeling Language |
| XML | eXtensible Markup Language |
References
- Guzman, A.; Isturiz, R.E. Update on the global spread of dengue. Int. J. Antimicrob. Agents 2010, 36, S40–S42. [Google Scholar] [CrossRef] [PubMed]
- Brady, O.J.; Gething, P.W.; Bhatt, S.; Messina, J.P.; Brownstein, J.S.; Hoen, A.G.; Moyes, C.L.; Farlow, A.W.; Scott, T.W.; Hay, S.I. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl. Trop. Dis. 2012, 6, e1760. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Simmons, C.P.; Farrar, J.J.; van Vinh, N.C.; Wills, B.; Nguyen, V.V.C. Dengue. N. Eng. J. Med. 2012, 366, 1423–1432. [Google Scholar] [CrossRef] [PubMed]
- Chikungunya. Available online: http://www.who.int/mediacentre/factsheets/fs327/en/ (accessed on 11 May 2016).
- One Year into the Zika Outbreak: How an Obscure Disease Became a Global Health Emergency. Available online: http://www.who.int/emergencies/zika-virus/articles/one-year-outbreak/en/ (accessed on 11 May 2016).
- Christophers, S.R. Aedes aegypti (L.) The Yellow Fever Mosquito: Its Lfe History, Bionomics, and Structure; Cambridge University Press: Cambridge, UK, 1960; p. 750. [Google Scholar]
- Kraemer, M.U.; Sinka, M.E.; Duda, K.A.; Mylne, A.Q.; Shearer, F.M.; Barker, C.M.; Moore, C.G.; Carvalho, R.G.; Coelho, G.E.; Van Bortel, W.; et al. The global distribution of the arbovirus vectors Aedes aegypti and Ae. albopictus. eLife 2015, 4, e08347. [Google Scholar] [CrossRef] [PubMed]
- Lambrechts, L.; Thomas, S.W.; Gubler, D.J. Consequences of the expanding global distribution of Aedes albopictus for dengue virus transmission. PLoS Negl. Trop. Dis. 2010, 4, e646. [Google Scholar] [CrossRef] [PubMed]
- Guzman, M.G.; Harris, E. Dengue. Lancet 2015, 385, 453–465. [Google Scholar] [CrossRef]
- Schaffner, F.; Mathis, A. Dengue and dengue vectors in the WHO European region: Past, present, and scenarios for the future. Lancet Infect. Dis. 2014, 14, 1271–1280. [Google Scholar] [CrossRef]
- Bouri, N.; Sell, T.K.; Franco, C.; Adalja, A.A. Return of epidemic dengue in the United States: Implications for the public health practitioner. Public Health Rep. 2012, 127, 259–266. [Google Scholar] [PubMed]
- Tatem, A.J.; Hay, S.I.; Rogers, D.J. Global traffic and disease vector dispersal. Proc. Natl. Acad. Sci. USA 2006, 103, 6242–6247. [Google Scholar] [CrossRef] [PubMed]
- Stoddard, S.T.; Forshey, B.M.; Morrison, A.; Paz-Soldan, V.A.; Vazquez-Prokopec, G.M.; Astete, H.; Reiner, R.C.; Vilcarromero, S.; Elder, J.P.; Halsey, E.S.; et al. House-to-house human movement drives dengue virus transmission. Proc. Natl. Acad. Sci. USA 2013, 110, 994–999. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.; Kapan, D.D. Man bites mosquito: Understanding the contribution of human movement to vector-borne disease dynamics. PLoS ONE 2009, 4, e6763. [Google Scholar] [CrossRef] [PubMed]
- Codeco, C.T.; Lima, A.W.S.; Araujo, S.C.; Lima, J.B.P.; Maciel-de Freitas, R.; Honorio, N.A.; Galardo, A.K.R.; Braga, I.A.; Coelho, G.E.; Valle, D. Surveillance of Aedes aegypti: Comparison of house index with four alternative traps. PLoS Negl. Trop. Dis. 2015, 9, e0003475. [Google Scholar] [CrossRef] [PubMed]
- Beatty, M.E.; William, G.L.; Margolis, H.S. Estimating the global burden of dengue. Am. J. Trop. Med. Hyg. 2009, 81, 231. [Google Scholar]
- Van Kleef, E.; Bambrick, H.; Hales, S. The Geographic Distribution of Dengue Fever and the Potential Influence of Global Climate Change. Available online: http://journal.tropika.net/scielo.php?script=sciarttextpid=S2078-86062010005000001 (accessed on 6 September 2016).
- Hales, S.; de Wet, N.; Maindonald, J.; Woodward, A. Potential effect of population and climate changes on global distribution of dengue fever: An empirical model. Lancet 2002, 360, 830–834. [Google Scholar] [CrossRef]
- Rogers, D.J.; Wilson, A.J.; Hay, S.I.; Graham, A.J. The global distribution of yellow fever and dengue. Adv. Parasitol. 2006, 62, 181–220. [Google Scholar] [PubMed]
- Maciel-de Freitas, R.; Codeço, C.T.; Lourenço-de Oliveira, R. Daily survival rates and dispersal of Aedes aegypti females in Rio de Janeiro, Brazil. Am. J. Trop. Med. Hyg. 2007, 76, 659–665. [Google Scholar] [PubMed]
- Mohammed, A.; Chadee, D.D. Effects of different temperature regimens on the development of Aedes aegypti (L.) (Diptera: Culicidae) mosquitoes. Acta Trop. 2011, 119, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Livdahl, T.P.; Edgerly, J.S. Egg hatching inhibition: Field evidence for population regulation in a tree hole mosquito. Ecol. Entomol. 1987, 12, 395–399. [Google Scholar] [CrossRef]
- Grech, M.G.; Sartor, P.D.; Almirón, W.R. Effects of different temperature regimens on the development of Aedes aegypti (L.) (Diptera: Culicidae) mosquitoes. Acta Trop. 2015, 146, 1–6. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Atlas of Health and Climate; World Health Organization: Geneva, Switzerland, 2012; p. 68. [Google Scholar]
- Gubler, D.J. Dengue, urbanization and globalization: The unholy trinity of the 21(st) century. Trop. Med. Health 2011, 39, S3–S11. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J. The many projected futures of dengue. Nat. Rev. Microbiol. 2015, 13, 230–239. [Google Scholar]
- Vong, S.; Khieu, V.; Glass, O.; Ly, S.; Duong, V.; Huy, R.; Ngan, C.; Wichmann, O.; Letson, G.W.; Margolis, H.S.; et al. Dengue incidence in urban and rural Cambodia: Results from population-based active fever surveillance, 2006–2008. PLoS Negl. Trop. Dis. 2010, 4, e903. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J. Dengue and dengue hemorrhagic fever; its history and resurgence as a global public health problem. In Dengue and Dengue Hemorrhagic Fever; CAB International Press: Wallingford, UK, 1997; pp. 1–22. [Google Scholar]
- Sutherst, R.W. Global change and human vulnerability to vector-borne diseases. Clin. Microbiol. Rev. 2004, 17, 136–173. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, T.R.; Medronho Rde, A. Socio-demographic factors and the dengue fever epidemic in 2002 in the State of Rio de Janeiro, Brazil. Cad. Saude Publica 2008, 24, 2160–2170. [Google Scholar] [CrossRef] [PubMed]
- Carbajo, A.E.; Cuto, S.I.; Schweigmann, N.J. Spatial distribution pattern of oviposition in the mosquito Aedes aegypti in relation to urbanization in Buenos Aires: Southern fringe bionomics of an introducted vector. Med. Vet. Entomol. 2006, 20, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Lazcano, J.A.B.; Marquetti, M.C.; Portillo, R.; Rodríguez, M.M.; Suárez, S. Factores ecológicos asociados con la presencia de larvas de Aedes aegypti en zonas de alta infestación del municipio Playa, Ciudad de La Habana, Cuba. Rev. Panam. Salud Pública 2006, 19, 379–384. [Google Scholar] [CrossRef]
- Trpis, M.; Hausermann, W. Dispersal and other population parameters of Aedes aegypti in an African village and their possible significance in epidemiology of vector-borne diseases. Am. J. Trop. Med. Hyg. 1986, 35, 1263–1279. [Google Scholar] [PubMed]
- Harrington, L.C.; Scott, T.W.; Lerdthusnee, K.; Coleman, R.C.; Costero, A.; Clark, G.G.; Jones, J.J.; Kitthawee, S.; Kittayapong, P.; Sithiprasasna, R.; et al. Dispersal of the dengue vector Aedes aegypti within and between rural communities. Am. J. Trop. Med. Hyg. 2005, 72, 209–220. [Google Scholar] [PubMed]
- Smith, A.; Carter, I.D. International transportation of mosquitoes of public health importance. In Commerce and the Spread of Pests and Disease Vectors; Praeger Publishers Inc.: Santa Barbara, CA, USA, 1984; pp. 1–21. [Google Scholar]
- Murrell, S.; Wu, S.C.; Butler, M. Review of dengue virus and the development of a vaccine. Biotechnol. Adv. 2011, 29, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Lin, C.; Wang, S.; Chen, Y.; Yeh, T.; Liu, H.; Anderson, R.; Lin, Y. Current progress in dengue vaccines. J. Biomed. Sci. 2013, 20, 37. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, A.; Malabadi, R.B.; Loebenberg, R.; Suresh, M.R.; Sunwoo, H.H. A mini-review of dengue vaccine development. Res. Pharm. 2015, 3, 18–25. [Google Scholar]
- Dengue Vaccine Research. Available online: http://www.who.int/immunization/research/development/denguevaccines/en/ (accessed on 8 July 2016).
- Vannice, K.; Durbin, A.; Hombach, J. Status of vaccine research and development of vaccines for dengue. Vaccine 2016, 34, 2934–2938. [Google Scholar] [CrossRef] [PubMed]
- Regis, L.N.; Acioli, R.V.; Silveira, J.C.J.; Melo-Santos, M.A.V.; Souza, W.V. Sustained reduction of the dengue vector population resulting from an integrated control strategy applied in two Brazilian cities. PLoS ONE 2013, 8, e67682. [Google Scholar] [CrossRef] [PubMed]
- Wise de Valdez, M.R.; Nimmo, D.; Betz, J.; Gong, H.F.; James, A.A.; Alphey, L.; Black, W.C. Genetic elimination of dengue vector mosquitoes. Proc. Natl. Acad. Sci. USA 2011, 108, 4772–4775. [Google Scholar] [CrossRef] [PubMed]
- Moreira, L.A.; Iturbe-Ormaetxe, I.; Jeffery, J.A.; Lu, G.; Pyke, A.T.; Hedges, L.M.; Rocha, B.C.; Hall-Mendelin, S.; Day, A.; Riegler, M.; et al. A Wolbachia symbiont in Aedes aegypti limits infection with dengue, Chikungunya, and Plasmodium. Cell 2009, 139, 1268–1278. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.A.; Montgomery, B.L.; Popovici, J.; Iturbe-Ormaetxe, I.; Johnson, P.H.; Muzzi, F.; Greenfield, M.; Durkan, M.; Leong, Y.S.; Dong, Y.; et al. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature 2011, 476, 454–457. [Google Scholar] [CrossRef] [PubMed]
- Cook, P.E.; McMeniman, C.J.; O’Neill, S.L. Modifying insect population age structure to control vector-borne disease. In Transgenesis and the Management of Vector-Borne Disease; Springer: Berlin, Germany, 2008; pp. 126–140. [Google Scholar]
- Walker, T.; Johnson, P.H.; Moreira, L.A.; Iturbe-Ormaetxe, I.; Frentiu, F.D.; McMeniman, C.J.; Leong, Y.S.; Dong, Y.; Axford, J.; Kriesner, P.; et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 2011, 476, 450–453. [Google Scholar] [CrossRef] [PubMed]
- Eisen, L.; Beaty, B.J.; Morrison, A.C.; Scott, T.W. ProactiveVector control strategies and improved monitoring and evaluation practices for dengue prevention. J. Med. Entomol. 2009, 46, 1245–1255. [Google Scholar] [CrossRef] [PubMed]
- Santos, L.B.L.; Costa, M.C.; Pinho, S.T.R.; Andrade, R.F.S.; Barreto, F.R.; Teixeira, M.G.; Barreto, M.L. Periodic forcing in a three-level cellular automata model for a vector-transmitted disease. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 016102. [Google Scholar] [CrossRef] [PubMed]
- Pinho, S.T.R.; Ferreira, C.P.; Esteva, L.; Barreto, F.R.; Morato, V.C.S.; Teixeira, M.G.L. Modelling the dynamics of dengue real epidemics. Philos. Trans. A. Math. Phys. Eng. Sci. 2010, 368, 5679–5693. [Google Scholar] [CrossRef] [PubMed]
- de Castro Medeiros, L.C.; Castilho, C.A.R.; Braga, C.; de Souza, W.V.; Regis, L.; Monteiro, A.M.V. Modeling the dynamic transmission of dengue fever: Investigating disease persistence. PLoS Negl. Trop. Dis. 2011, 5, e942. [Google Scholar]
- Chen, S.C.; Hsieh, M.H. Modeling the transmission dynamics of dengue fever: Implications of temperature effects. Sci. Total Environ. 2012, 431, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.M.; Ferreira, C.P. Assessing the effects of vector control on dengue transmission. Appl. Math. Comput. 2008, 198, 401–413. [Google Scholar] [CrossRef]
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes aegypti: Formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68, 1945–1974. [Google Scholar] [CrossRef] [PubMed]
- Otero, M.; Schweigmann, N.; Solari, H. A stochastic spatial dynamical model for Aedes aegypti. Bull. Math. Biol. 2008, 70, 1297–1325. [Google Scholar] [CrossRef] [PubMed]
- Lana, R.M.; Carneiro, T.G.S.; Honorio, N.A.; Codeco, C.T. Seasonal and nonseasonal dynamics of Aedes aegypti in Rio de Janeiro, Brazil: Fitting mathematical models to trap data. Acta Trop. 2014, 129, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Ezanno, P.; Aubry-Kientz, M.; Arnoux, S.; Cailly, P.; L’Ambert, G.; Tran, A. A generic weather-driven model to predict mosquito population dynamics applied to species of Anopheles, Culex and Aedes genera of southern France. Prev. Vet. Med. 2015, 120, 39–50. [Google Scholar] [CrossRef] [PubMed]
- Campbell, L.P.; Luther, C.; Moo-Llanes, D.; Ramsey, J.M.; Danis-Lozano, R.; Peterson, A.T. Climate change influences on global distributions of dengue and chikungunya virus vectors. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2015, 370, 20140135. [Google Scholar] [CrossRef] [PubMed]
- Simoy, M.I.; Simoy, M.V.; Canziani, G.A. The effect of temperature on the population dynamics of Aedes aegypti. Ecol. Model. 2015, 314, 100–110. [Google Scholar] [CrossRef]
- Focks, D.A.; Haile, D.G.; Daniels, E.; Mount, G.A. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): Simulation results and validation. J. Med. Entomol. 1993, 30, 1018–1028. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.L.; Battle, K.E.; Hay, S.I.; Barkr, C.M.; Scott, T.W.; McKenzie, F.E. Ross, macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012, 129, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Reiner, R.C.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; Buckee, C.; George, D.B.; Le Menach, A.; Pulliam, J.R.C.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. R. Soc. Interface 2013, 10, 20120921. [Google Scholar] [CrossRef] [PubMed]
- Lima, T.; Carneiro, T.; Silva, L.; Lana, R.; Codeco, C.; Reis, I.; Maretto, R.; Santos, L.; Monteiro, A.; Medeiros, L.; et al. A framework for modeling and simulating Aedes aegypti and dengue fever dynamics. In Proceedings of the 2014 Winter Simulation Conference, Savannah, GA, USA, 7–10 December 2014; pp. 1481–1492.
- Padmanabha, H.; Correa, F.; Legros, M.; Nijhout, H.F.; Lord, C.; Lounibos, L.P. An eco-physiological model of the impact of temperature on Aedes aegypti life history traits. J. Insect. Physiol. 2012, 58, 1597–1608. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.L.; Perkins, T.A.; Reiner, R.C.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.C.; et al. Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans. R. Soc. Trop. Med. Hyg. 2014, 108, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Epstein, J.M. Why model? J. Artif. Soc. Soc. Simul. 2008, 11, 12. [Google Scholar]
- Homer, J.B.; Hirsch, G.B. System dynamics modeling for public health: background and opportunities. Am. J. Public Health 2006, 96, 452–458. [Google Scholar] [CrossRef] [PubMed]
- Auchincloss, A.H.; Roux, A.V.D. A new tool for epidemiology: The usefulness of dynamic-agent models in understanding place effects on health. Am. J. Epidemiol. 2008, 168, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Eames, K.T. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Luke, D.A.; Harris, J.K. Network analysis in public health: History, methods, and applications. Annu. Rev. Public Health 2007, 28, 69–93. [Google Scholar] [CrossRef] [PubMed]
- Massad, E.; Ma, S.; Chen, M.; Struchiner, C.J.; Stollenwerk, N.; Aguiar, M. Scale-free network of a dengue epidemic. Appl. Math. Comput. 2008, 195, 376–381. [Google Scholar] [CrossRef]
- Villabona-Arenas, C.J.; de Andrade Zanotto, P.M. Worldwide spread of Dengue virus type 1. PLoS ONE 2013, 8, e62649. [Google Scholar] [CrossRef] [PubMed]
- Knight, G.M.; Dharan, N.J.; Fox, G.J.; Stennis, N.; Zwerling, A.; Khurana, R.; Dowdy, D.W. Bridging the gap between evidence and policy for infectious diseases: How models can aid public health decision-making. Int. J. Infect. Dis. 2016, 42, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Luke, D.A.; Stamatakis, K.A. Systems science methods in public health: Dynamics, networks, and agents. Annu. Rev. Public Health 2012, 33, 357–376. [Google Scholar] [CrossRef] [PubMed]
- Maglio, P.P.; Sepulveda, M.J.; Mabry, P.L. Mainstreaming modeling and simulation to accelerate public health innovation. Am. J. Public Health 2014, 104, 1181–1186. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.M.; Abernethy, D.R.; Wang, Y.; Zhao, P.; Zineh, I. The utility of modeling and simulation in drug development and regulatory review. J. Pharm. Sci. 2013, 102, 2912–2923. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Andrews, J. Complexity in mathematical models of public health policies: A guide for consumers of models. PLoS Med. 2013, 10, e1001540. [Google Scholar] [CrossRef] [PubMed]
- North, M.J.; Howe, T.R.; Collier, N.T.; Vos, J.R. The repast simphony development environment. In Proceedings of the Agent 2005 Conference on Generative Social Processes, Models, and Mechanisms, Chicago, IL, USA, October 2005; pp. 159–166.
- Lima, T.; Carneiro, T.; Faria, S.; Silva, P.; Pessoa, M. TerraME GIMS: An eclipse plug-in for environmental modeling. In Proceedings of the 3rd International Workshop on Developing Tools as Plug-Ins, San Francisco, CA, USA, 21 May 2013; pp. 37–42.
- Tisue, S.; Wilensky, U. Netlogo: A simple environment for modeling complexity. In Proceedings of the International Conference on Complex Systems, Boston, MA, USA, 16–21 May 2004; pp. 16–21.
- Muetzelfeldt, R.; Massheder, J. The Simile visual modelling environment. Eur. J. Agron. 2003, 18, 345–358. [Google Scholar] [CrossRef]
- Ford, D.A.; Kaufman, J.H.; Eiron, I. An extensible spatial and temporal epidemiological modelling system. Int. J. Health Geogr. 2006, 5, 4. [Google Scholar] [CrossRef] [PubMed]
- Balcan, D.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Colizza, V.; Vespignani, A. Modeling the spatial spread of infectious diseases: The GLobal Epidemic and Mobility computational model. Nat. Rev. Microbiol. 2010, 1, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Hladish, T.; Melamud, E.; Barrera, L.A.; Galvani, A.; Meyers, L.A. EpiFire: An open source C++ library and application for contact network epidemiology. BMC Bioinform. 2012, 13, 76. [Google Scholar] [CrossRef] [PubMed]
- Malaria Tools. Available online: https://www1.imperial.ac.uk/malariamodelling/toolsdata/tools/ (accessed on 10 May 2016).
- Lana, R.M.; Carneiro, T.G.S.; Honório, N.A.; Codeço, C.T. Multiscale analysis and modelling of Aedes aegyti population spatial dynamics. J. Inf. Data Manag. 2011, 2, 211. [Google Scholar]
- Carneiro, T.G.S.; Andrade, P.R.; Câmara, G.; Monteiro, A.M.V.; Pereira, R.R. An extensible toolbox for modeling nature—Society interactions. Environ. Model. Softw. 2013, 46, 104–117. [Google Scholar] [CrossRef]
- Wainwright, J.; Mulligan, M. Modelling and model building. In Environmental Modelling: Finding Simplicity in Complexity; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 7–73. [Google Scholar]
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Voinov, A.; Bousquet, F. Modelling with stakeholders. Environ. Model. Softw. 2010, 25, 1268–1281. [Google Scholar] [CrossRef]
- Krueger, T.; Page, T.; Hubacek, K.; Smith, L.; Hiscock, K. The role of expert opinion in environmental modelling. Environ. Model. Softw. 2012, 36, 4–18. [Google Scholar] [CrossRef]
- Crout, N.; Kokkonen, T.; Jakeman, A.; Norton, J.; Newham, L.; Anderson, R.; Assaf, H.; Croke, B.; Gaber, N.; Gibbons, J.; et al. Chapter two good modelling practice. Dev. Integr. Environ. Assess. 2008, 3, 15–31. [Google Scholar]
- Holzworth, D.P.; Huth, N.I.; de Voil, P.G. Simple software processes and tests improve the reliability and usefulness of a model. Environ. Model. Softw. 2011, 26, 510–516. [Google Scholar] [CrossRef]
- Turner, M.G.; Gardner, R.H. Introduction to models. In Landscape Ecology in Theory and Practice; Springer: Berlin, Germany, 2001; Volume 401, pp. 47–69. [Google Scholar]
- Lima, T.; Faria, S.; Carneiro, T. Development of a didactic model of the hydrologic cycle using the terrame graphical interface for modeling and simulation. In Computational Science and Its Applications—ICCSA; Springer: Berlin, Germany, 2011; pp. 75–90. [Google Scholar]
- Reich, N.G.; Shrestha, S.; King, A.A.; Rohani, P.; Lessler, J.; Kalayanarooj, S.; Yoon, I.K.; Gibbons, R.V.; Burke, D.S.; Cummings, D.A. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J. R. Soc. Interface 2013, 10, 20130414. [Google Scholar] [CrossRef] [PubMed]
- Chikaki, E.; Ishikawa, H. A dengue transmission model in Thailand considering sequential infections with all four serotypes. J. Infect. Dev. Cories. 2009, 3, 711–722. [Google Scholar] [CrossRef]
- Coudeville, L.; Garnett, G.P. Transmission dynamics of the four dengue serotypes in southern Vietnam and the potential impact of vaccination. PLoS ONE 2012, 7, e51244. [Google Scholar] [CrossRef] [PubMed]
- Wearing, H.J.; Rohani, P. Ecological and immunological determinants of dengue epidemics. Proc. Natl. Acad. Sci. USA 2006, 103, 11802–11807. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.; Boots, M. Modelling the relationship between antibody-dependent enhancement and immunological distance with application to dengue. J. Theor. Biol. 2006, 242, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, J.; Recker, M. Natural, persistent oscillations in a spatial multi-strain disease system with application to dengue. PLoS Comput. Biol. 2013, 9, e1003308. [Google Scholar]
- Lourenço, J.; Recker, M. Dengue serotype immune-interactions and their consequences for vaccine impact predictions. Epidemics 2016, 16, 40–48. [Google Scholar] [CrossRef]
- Chao, D.L.; Longini, I.M., Jr.; Halloran, M.E. The effects of vector movement and distribution in a mathematical model of dengue transmission. PLoS ONE 2013, 8, e76044. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, A.; Qureshi, T.; Boni, M.F.; Sundsøy, P.R.; Johansson, M.A.; Rasheed, S.B.; Engø-Monsen, K.; Buckee, C.O. Impact of human mobility on the emergence of dengue epidemics in Pakistan. Proc. Natl. Acad. Sci. USA 2015, 112, 11887–11892. [Google Scholar] [CrossRef] [PubMed]
- dos Reis, I.C. Caracterização de Paisagens Urbanas Heterogêneas de Interesse Para a Vigilância e Controle da Dengue Com o Uso de Sensoriamento Remoto e Mineração de Padrões Espaciais: Um Estudo Para o Rio de Janeiro; Instituto Nacional de Pesquisas Espaciais: São José dos Campos, Brazil, 2010. [Google Scholar]
- Nishiura, H. Mathematical and statistical analyses of the spread of dengue. Dengue Bull. 2006, 30, 51–67. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Morin, C.W.; Monaghan, A.J.; Hayden, M.H.; Barrera, R.; Ernst, K. Meteorologically driven simulations of dengue epidemics in San Juan, PR. PLoS Negl. Trop. Dis. 2015, 9, e0004002. [Google Scholar] [CrossRef] [PubMed]
- Erickson, R.A.; Presley, S.M.; Allen, L.J.; Long, K.R.; Cox, S.B. A dengue model with a dynamic Aedes albopictus vector population. Ecol. Model. 2010, 221, 2899–2908. [Google Scholar] [CrossRef]
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7, e49085. [Google Scholar] [CrossRef] [PubMed]
- Luz, P.M.; Codeço, C.T.; Medlock, J.; Struchiner, C.J.; Valle, D.; Galvani, A.P. Impact of insecticide interventions on the abundance and resistance profile of Aedes aegypti. Epidemiol. Infect. 2009, 137, 1203. [Google Scholar] [CrossRef] [PubMed]
- Rico-Hesse, R. Dengue virus virulence and transmission determinants. In Dengue Virus; Springer: Berlin, Germany, 2010; pp. 45–55. [Google Scholar]
- Johansson, M.A.; Hombach, J.; Cummings, D.A.T. Models of the impact of dengue vaccines: A review of current research and potential approaches. Vaccine 2011, 29, 5860–5868. [Google Scholar] [CrossRef] [PubMed]
- Stephens, D.S.; Ahmed, R.; Orenstein, W.A. Vaccines at what price? Vaccine 2014, 32, 1029–1030. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Barraquer, I.; Mier-y Teran-Romero, L.; Schwartz, I.B.; Burke, D.S.; Cummings, D.A.T. Potential opportunities and perils of imperfect dengue vaccines. Vaccine 2014, 32, 514–520. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, S.A.; da Silva, S.O.; Charret, I.D.C. Mathematical Modeling of Dengue Epidemic: Control Methods and Vaccination Strategies, 2015. Available online: https://arxiv.org/abs/1508.00961 (accessed on 10 May 2016).
- Godfrey-Smith, P. The strategy of model-based science. Biol. Philos. 2006, 21, 725–740. [Google Scholar] [CrossRef]
- Levins, R. The strategy of model building in population biology. Am. Sci. 1966, 54, 421–431. [Google Scholar]
- Odenbaugh, J. Complex systems, trade-offs, and theoretical population biology: Richard Levin’s “Strategy of model building in population biology” revisited. Philos. Sci. 2003, 70, 1496–1507. [Google Scholar] [CrossRef]
- Weisberg, M. Forty years of ‘‘The strategy’’: Levins on model building and idealization. Biol. Philos. 2006, 21, 623–645. [Google Scholar] [CrossRef]
- Orzack, S.H. Discussion: What, if anything, is “the strategy of model building in population biology?” A comment on Levins (1966) and Odenbaugh (2003). Philos. Sci. 2005, 72, 479–485. [Google Scholar] [CrossRef]
- Odenbaugh, J. The strategy of “The strategy of model building in population biology”. Biol. Philos. 2006, 21, 607–621. [Google Scholar] [CrossRef]
- Coelho, F.C.; Codeço, C.T.; Cruz, O.G.; Camargo, S.; Bliman, P.A. Epidemiological data accessibility in Brazil. Lancet Infect. Dis. 2016, 16, 524525. [Google Scholar] [CrossRef]
- Gomide, J.; Veloso, A.; Meira, W., Jr.; Almeida, V.; Benevenuto, F.; Ferraz, F.; Teixeira, M. Dengue surveillance based on a computational model of spatio-temporal locality of Twitter. In Proceedings of the ACM 3rd International Web Science Conference, Koblenz, Germany, 15–17 June 2011; p. 3.
- Ginsberg, J.; Mohebbi, M.H.; Patel, R.S.; Brammer, L.; Smolinski, M.S.; Brilliant, L. Detecting influenza epidemics using search engine query data. Nature 2009, 457, 1012–1014. [Google Scholar] [CrossRef] [PubMed]
- Chan, E.H.; Sahai, V.; Conrad, C.; Brownstein, J.S. Using web search query data to monitor dengue epidemics: A new model for neglected tropical disease surveillance. PLoS Negl. Trop. Dis. 2011, 5, e1206. [Google Scholar] [CrossRef] [PubMed]
- Althouse, B.M.; Ng, Y.Y.; Cummings, D. Prediction of dengue incidence using search query surveillance. PLoS Negl. Trop. Dis. 2011, 5, e1258. [Google Scholar] [CrossRef] [PubMed]
- Madoff, L.C.; Fisman, D.N.; Kass-Hout, T. A new approach to monitoring dengue activity. PLoS Negl. Trop. Dis. 2011, 5, e1215. [Google Scholar] [CrossRef] [PubMed]
- Gluskin, R.T.; Johansson, M.A.; Santillana, M.; Brownstein, J.S. Evaluation of Internet-based dengue query data: Google Dengue Trends. PLoS Negl. Trop. Dis. 2014, 8, e2713. [Google Scholar] [CrossRef] [PubMed]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Codeco, C.; Cruz, O.; Riback, T.I.; Degener, C.M.; Gomes, M.F.; Villela, D.; Bastos, L.; Camargo, S.; Saraceni, V.; Lemos, M.C.F.; et al. InfoDengue: A Nowcasting System for the Surveillance of Dengue Fever Transmission, 2016. Available online: http://biorxiv.org/content/early/2016/03/29/046193 (accessed on 11 May 2016).


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Lima, T.F.M.; Lana, R.M.; De Senna Carneiro, T.G.; Codeço, C.T.; Machado, G.S.; Ferreira, L.S.; De Castro Medeiros, L.C.; Davis Junior, C.A. DengueME: A Tool for the Modeling and Simulation of Dengue Spatiotemporal Dynamics. Int. J. Environ. Res. Public Health 2016, 13, 920. https://doi.org/10.3390/ijerph13090920
De Lima TFM, Lana RM, De Senna Carneiro TG, Codeço CT, Machado GS, Ferreira LS, De Castro Medeiros LC, Davis Junior CA. DengueME: A Tool for the Modeling and Simulation of Dengue Spatiotemporal Dynamics. International Journal of Environmental Research and Public Health. 2016; 13(9):920. https://doi.org/10.3390/ijerph13090920
Chicago/Turabian StyleDe Lima, Tiago França Melo, Raquel Martins Lana, Tiago Garcia De Senna Carneiro, Cláudia Torres Codeço, Gabriel Souza Machado, Lucas Saraiva Ferreira, Líliam César De Castro Medeiros, and Clodoveu Augusto Davis Junior. 2016. "DengueME: A Tool for the Modeling and Simulation of Dengue Spatiotemporal Dynamics" International Journal of Environmental Research and Public Health 13, no. 9: 920. https://doi.org/10.3390/ijerph13090920
APA StyleDe Lima, T. F. M., Lana, R. M., De Senna Carneiro, T. G., Codeço, C. T., Machado, G. S., Ferreira, L. S., De Castro Medeiros, L. C., & Davis Junior, C. A. (2016). DengueME: A Tool for the Modeling and Simulation of Dengue Spatiotemporal Dynamics. International Journal of Environmental Research and Public Health, 13(9), 920. https://doi.org/10.3390/ijerph13090920





