Spatio-Temporal Distribution Characteristics and Trajectory Similarity Analysis of Tuberculosis in Beijing, China
Abstract
:1. Introduction
2. Materials and Methods
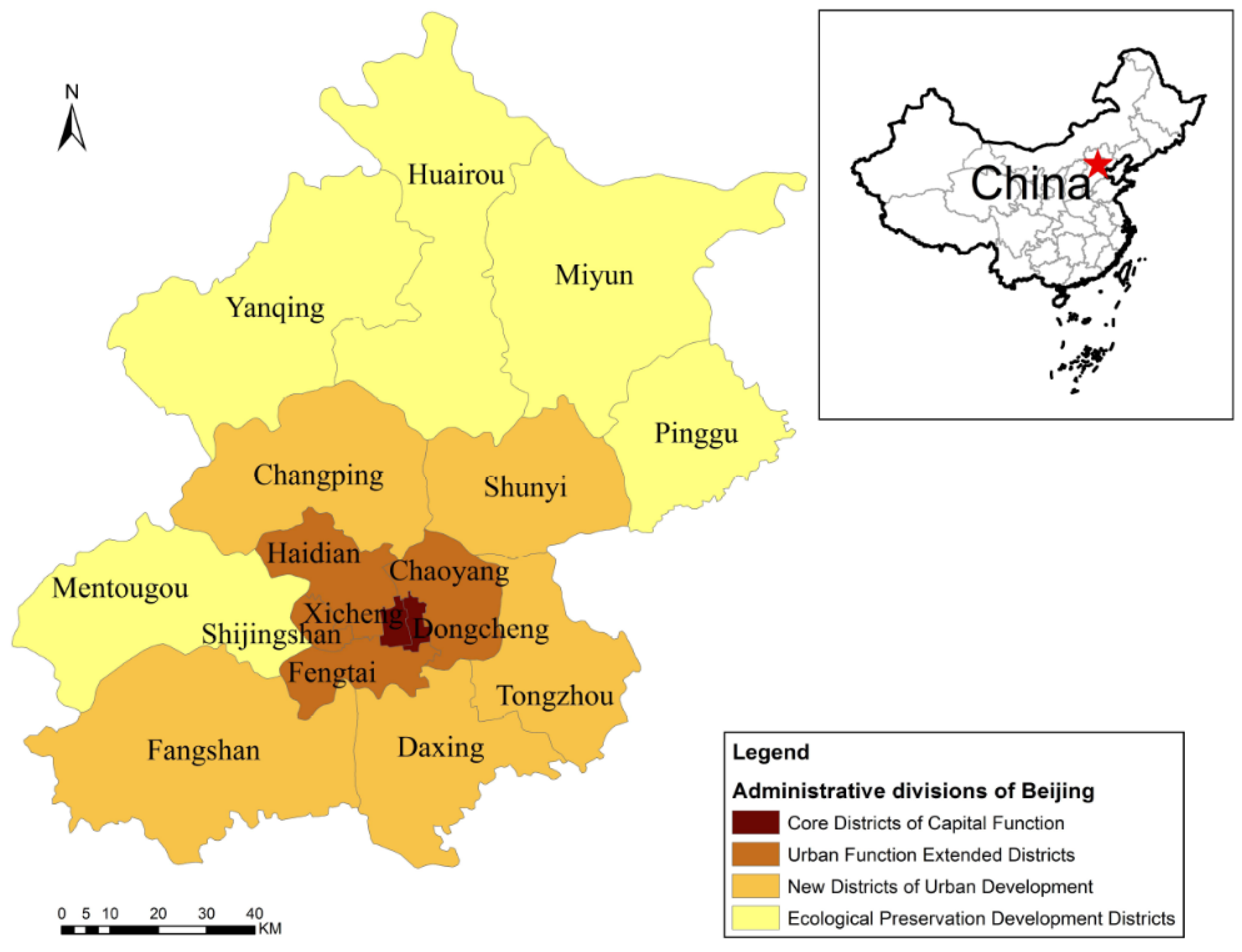
2.1. Study Area
2.2. Data Description
2.2.1. TB Data
2.2.2. Population Data
2.2.3. Spatial District Data
2.3. Methodology
2.3.1. Registration Rate and Incidence Rate Calculations
2.3.2. Spatial Autocorrelation Analysis
2.3.3. Scan Statistics Analysis
2.3.4. Trajectory Similarity Analysis
3. Results and Discussion
3.1. Spatio-Temporal Distribution
3.2. Spatial Autocorrelation Analysis
3.3. Scan Statistics Analysis
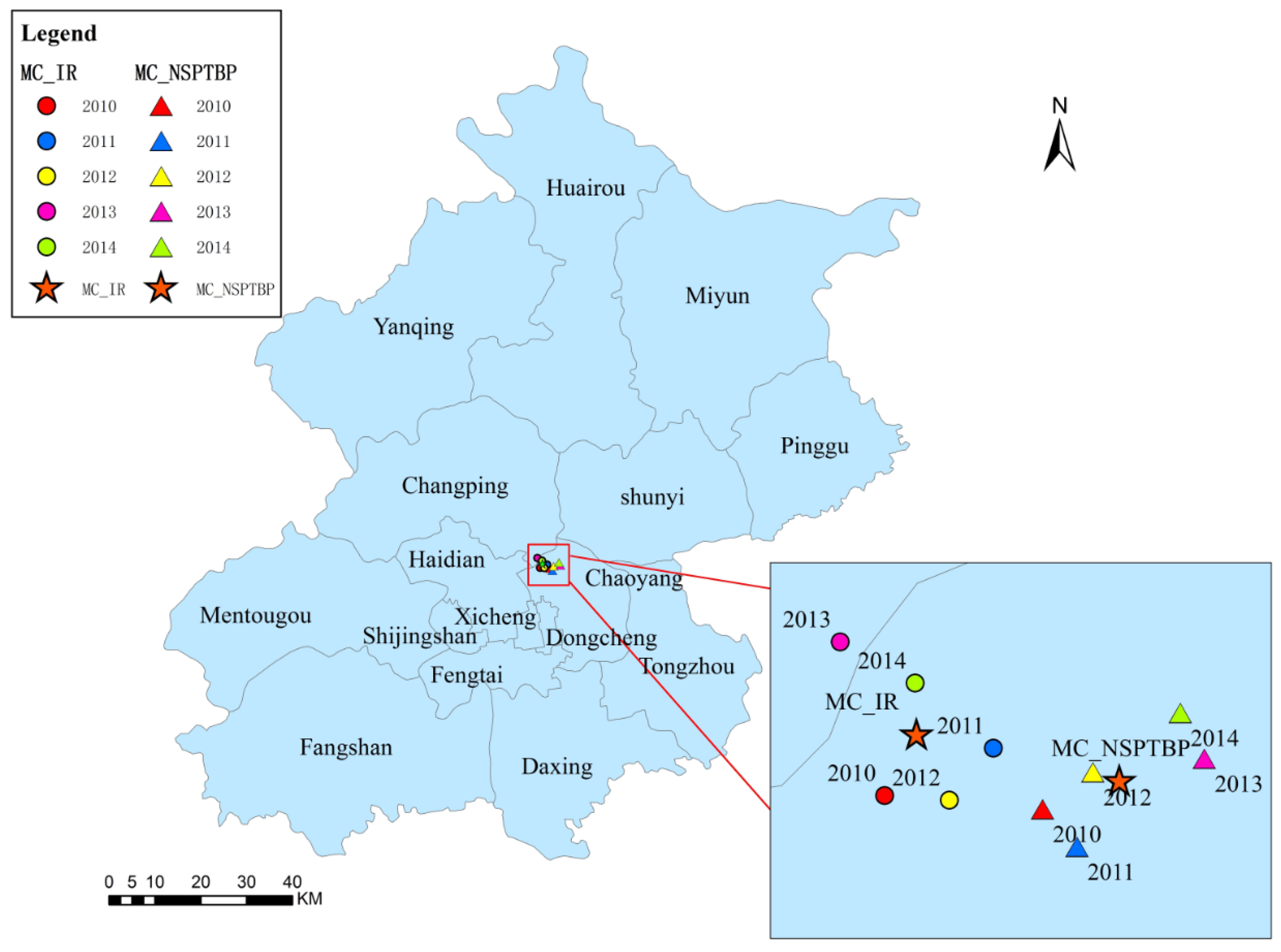
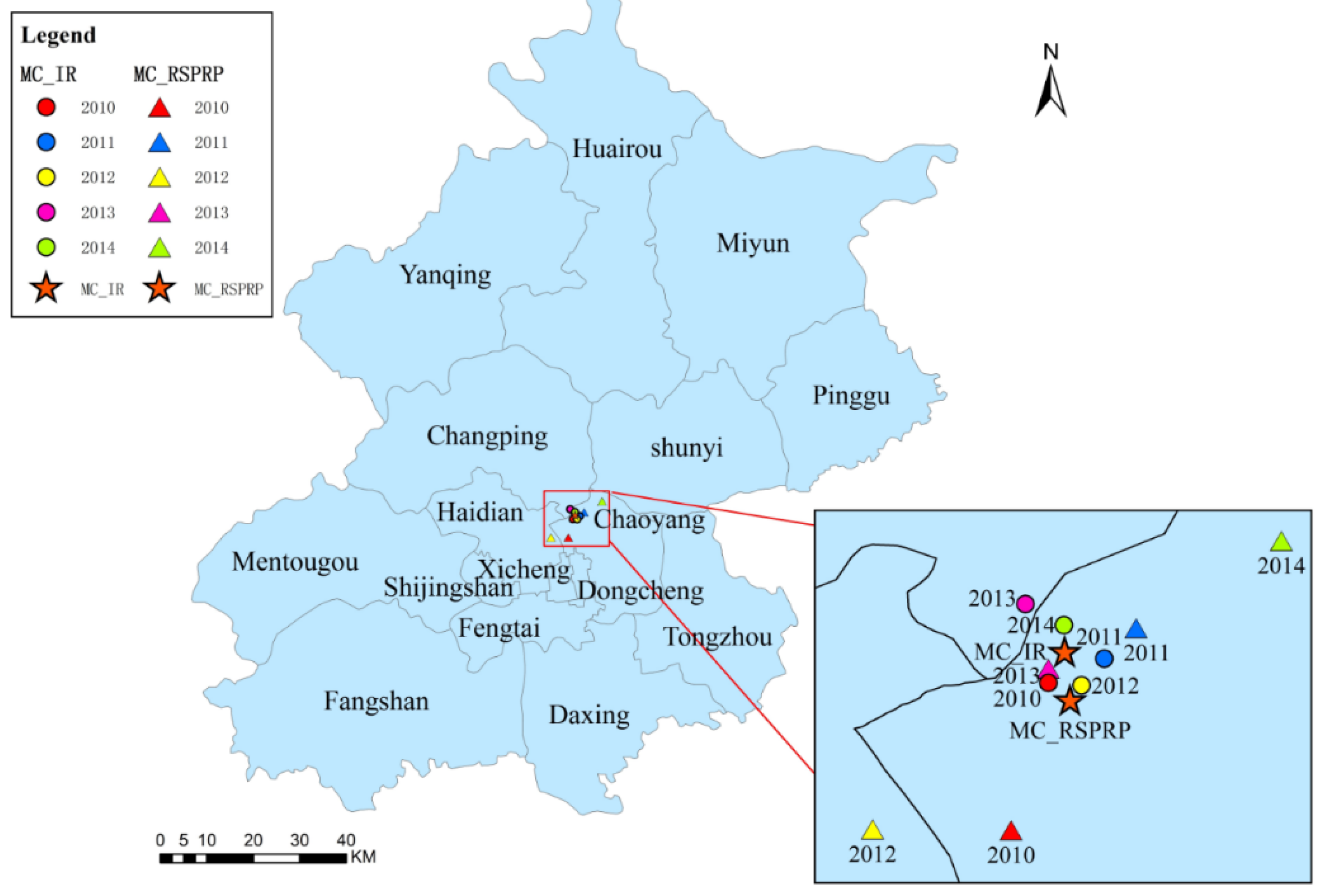
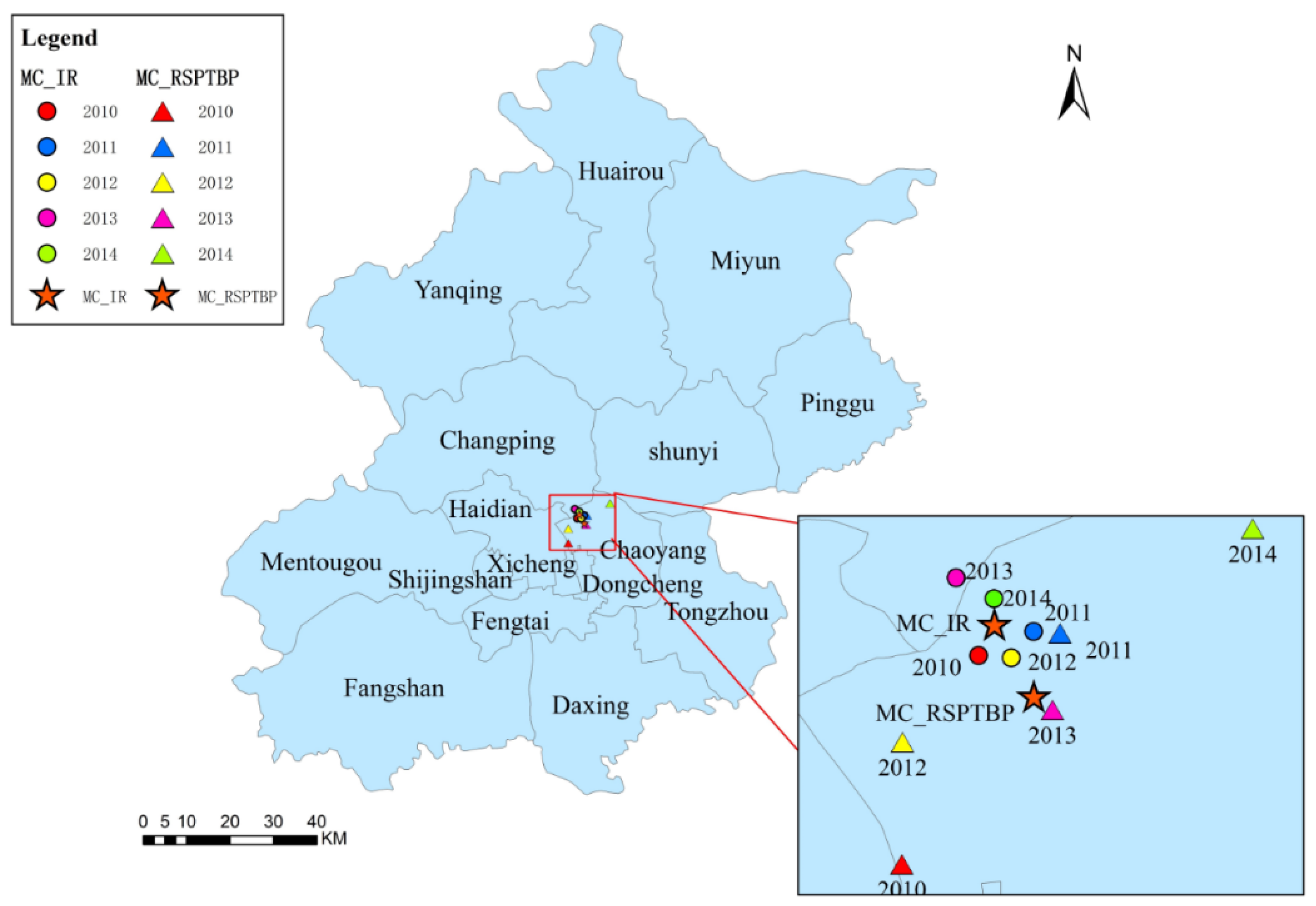
3.4. Trajectory Similarity Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, W.; Gong, J.; Zhou, J.; Zhao, Y.; Tan, J.; Ibrahim, A.N.; Zhou, Y. A spatial, social and environmental study of tuberculosis in China using statistical and GIS technology. Int. J. Environ. Res. Public Health 2015, 12, 1425–1488. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. World Health Statistics 2007; WHO: Geneva, Switzerland, 2011. [Google Scholar]
- Disease Control Bureau of the Ministry of Health. Report on the 5th National Tuberculosis Epidemiological Survey in China; Military Medical Science Press: Beijing, China, 2010; pp. 30–37. [Google Scholar]
- Izumi, K.; Ohkado, A.; Uchimura, K.; Murase, Y.; Tatsumi, Y.; Kayebeta, A.; Watanabe, Y.; Ishikawa, N. Detection of tuberculosis infection hotspots using activity spaces based spatial approach in an urban Tokyo, from 2003 to 2011. PLoS ONE 2015, 10, e0138831. [Google Scholar]
- Pfeiffer, D.U.; Robinson, T.P.; Stevens, K.B.; Rogers, D.J.; Clements, A.C.A. Spatial clustering of disease and global estimates of spatial clustering. In Spatial Analysis in Epidemiology, 1st ed.; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Onozuka, D.; Hagihara, A. Geographic prediction of tuberculosis clusters in Fukuoka, Japan, using the space-time scan statistic. BMC Infect. Dis. 2007, 7. [Google Scholar] [CrossRef] [PubMed]
- Souza, W.V.; Carvalho, M.S.; Albuquerque Mde, F.; Barcellos, C.C.; Ximenes, R.A. Tuberculosis in intra-urban settings: A Bayesian approach. Trop. Med. Int. Health 2007, 12, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Hernández, G.; Lara-Valencia, F.; Reyes-Castro, P.A.; Rascón-Pacheco, R.A. An analysis of spatial and socio-economic determinants of tuberculosis in Hermosillo, Mexico, 2000–2006. Int. J. Tuberc. Lung Dis. 2010, 14, 708–713. [Google Scholar] [PubMed]
- Ng, I.C.; Wen, T.H.; Wang, J.Y.; Fang, C.T. Spatial dependency of tuberculosis incidence in Taiwan. PLoS ONE 2012, 7, e50740. [Google Scholar] [CrossRef] [PubMed]
- Barr, R.G.; Diez-Roux, A.V.; Knirsch, C.A.; Pablos-méndez, A. Neighborhood poverty and the resurgence of tuberculosis in New York City, 1984–1992. Am. J. Public Health 2001, 91, 1487–1493. [Google Scholar] [CrossRef] [PubMed]
- Chan-yeung, M.; Yeh-a, G.O.; Tam, C.M.; Kam, K.M.; Leung, C.C.; Yew, W.W.; Lam, C.W. Socio-demographic and geographic indicators and distribution of tuberculosis in Hong Kong: A spatial analysis. Int. J. Tuberc. Lung Dis. 2005, 9, 1320–1326. [Google Scholar] [PubMed]
- Jafari-Koshki, T.; Arsang-Jang, S.; Raei, M. Applying spatiotemporal models to study risk of smear-positive tuberculosis in Iran, 2001–2012. Int. J. Tuberc. Lung Dis. 2015, 19, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Li, X.X.; Wang, L.X.; Zhang, J.; Liu, Y.X.; Zhang, H.; Jiang, S.W.; Chen, J.X.; Zhou, X.N. Exploration of ecological factors related to the spatial heterogeneity of tuberculosis prevalence in P.R. China. Glob. Health Action 2010, 7, 23620. [Google Scholar]
- Brooks-Pollock, E.; Roberts, G.O.; Keeling, M.J. A dynamic model of bovine tuberculosis spread and control in Great Britain. Nature 2014, 511, 228–231. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.N. Spatial Epidemiology; Science Press: Beijing, China, 2009. [Google Scholar]
- Kulldorff, M.; Nagarwalla, N. Spatial disease clusters: Detection and inference. Stat. Med. 1995, 14, 799–810. [Google Scholar] [CrossRef] [PubMed]
- Kulldorff, M. A spatial scan statistic. Commun. Stat. Theory Methods 1997, 26, 1481–1496. [Google Scholar] [CrossRef]
- Li, X.Z.; Wang, J.F. A fast method for making candidate clusters in spatial scan statistic method. J. Geoinf. Sci. 2013, 15, 505–511. [Google Scholar] [CrossRef]
- Areias, C.; Briz, T.; Nunes, C. Pulmonary tuberculosis space-time clustering and spatial variation in temporal trends in Portugal, 2000–2010: An updated analysis. Epidemiol. Infect. 2015, 143, 3211–3219. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Zheng, K.; Huang, J.; Wang, H.; Zhou, X. Calibrating trajectory data for spatio-temporal similarity analysis. VLDB J. 2015, 24, 93–116. [Google Scholar] [CrossRef]
- Gong, X.; Pei, T.; Sun, J.; Luo, M. Research review of spatio-temporal trajectory clustering methods. Prog. Geogr. 2011, 30, 522–534. [Google Scholar]
- Wang, J.F.; Ge, Y.; Li, L.F.; Meng, B.; Wu, J.L.; Bai, Y.C.; Du, S.H.; Liao, Y.L.; Hu, M.G.; Xu, C.D. Analytical methods of geographical spatio-temporal data. J. Geogr. Sci. 2014, 69, 1326–1345. [Google Scholar]
- Joseph, N.; Nagaraj, K.; Bhat, J.; Babu, R.; Kotian, S.; Ranganatha, Y.; Hocksan, A.; Shetty, V.; Zaki, N.; Swasthik, K.; et al. Treatment outcomes among new smear positive and retreatment cases of tuberculosis in Mangalore, South India—A descriptive study. Australas. Med. J. 2011, 4, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2010), 1st ed.The People’s Medical Publishing House: Beijing, China, 2011; p. 72. [Google Scholar]
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2011), 1st ed.The People’s Medical Publishing House: Beijing, China, 2012; p. 82. [Google Scholar]
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2012), 1st ed.The People’s Medical Publishing House: Beijing, China, 2013; p. 97. [Google Scholar]
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2013), 1st ed.The People’s Medical Publishing House: Beijing, China, 2014; p. 103. [Google Scholar]
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2014), 1st ed.The People’s Medical Publishing House: Beijing, China, 2015; p. 122. [Google Scholar]
- Beijing Statistical Information Net. Available online: http://www.bjstats.gov.cn/ (accessed on 7 March 2015).
- National Geomatics Center of China. Available online: http://ngcc.sbsm.gov.cn/ (accessed on 7 March 2011).
- Latitude and Longitude of Districts in Beijing. Available online: http://wenku.baidu.com/link?url=eIHOPf5jhq00G7grqRXrXZno0pm1Uu8S8GtH_mKRUvxcGqZ2JngoGz7O6fpsyk0wjDckNTv-XvJZVMeJJhQwbYIVS4j5ujJI4s69kDXEcQ_ (accessed on 3 February 2016).
- Beijing Municipal People’s Government. Idexes in each county and district. In Beijing Health and Population Health Status Report (2010), 1st ed.The People’s Medical Publishing House: Beijing, China, 2011; p. 29. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Dolan, C.; O’Halloran, A.; Bradley, D.G.; Croke, D.T.; Evans, A.; O’Brien, J.K.; Shields, D.C. Genetic stratification of pathogen-response-related and other variants within a homogeneous Caucasian Irish population. Eur. J. Hum. Genet. 2005, 13, 798–806. [Google Scholar] [CrossRef] [PubMed]
- Tsai, P.J.; Lin, M.L.; Chu, C.M.; Perng, C.H. Spatial autocorrelation analysis of health care hotspots in Taiwan in 2006. BMC Public Health 2009, 9, 464. [Google Scholar] [CrossRef] [PubMed]
- Kulldorff, M.; Feuer, E.J.; Miller, B.A.; Freedma, L.S. Breast cancer clusters in the northeast United States: A geographic analysis. Am. J. Epidemiol. 1997, 146, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.A.; Gotway, C.A. Spatial clusters of health events: Point data for casesand controls. In Applied Spatial Statistics for Public Health Data, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 219–220. [Google Scholar]
- Hu, T.; Sun, W. Tuberculosis in China. J. Tuberc. Res. 2013, 1, 9–10. [Google Scholar] [CrossRef]
- Central People’s Government of the People’s Republic of China. Available online: http://www.gov.cn/ (accessed on 16 April 2011).
- Behzadifar, M.; Mirzaei, M.; Behzadifar, M.; Keshavarzi, A.; Behzadifar, M.; Saran, M. Patients’ experience of tuberculosis treatment using directly observed treatment, Short-Course (DOTS): A qualitative study. Iran. Red Crescent Med. J. 2015, 17, e20277. [Google Scholar] [CrossRef] [Green Version]
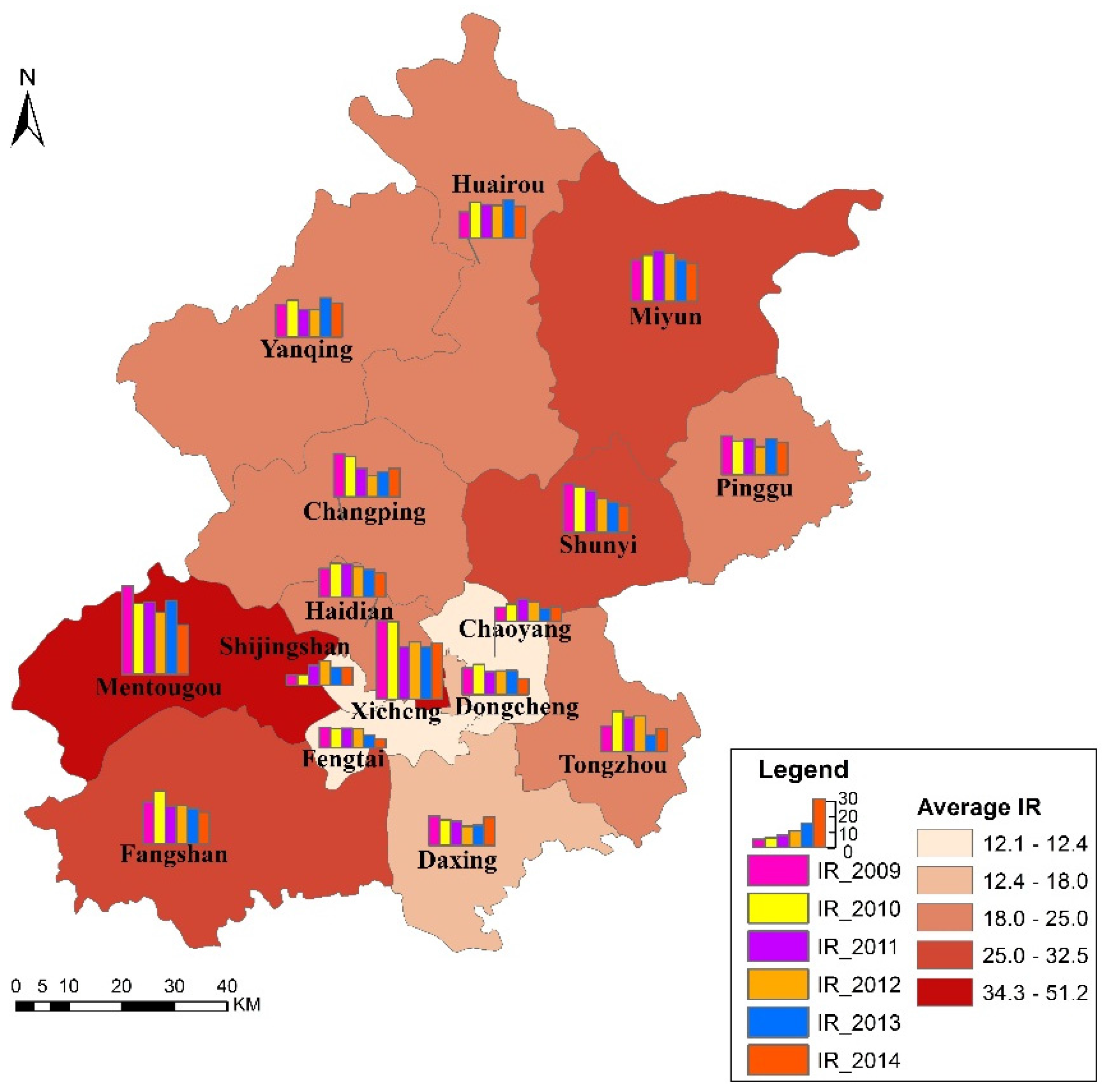
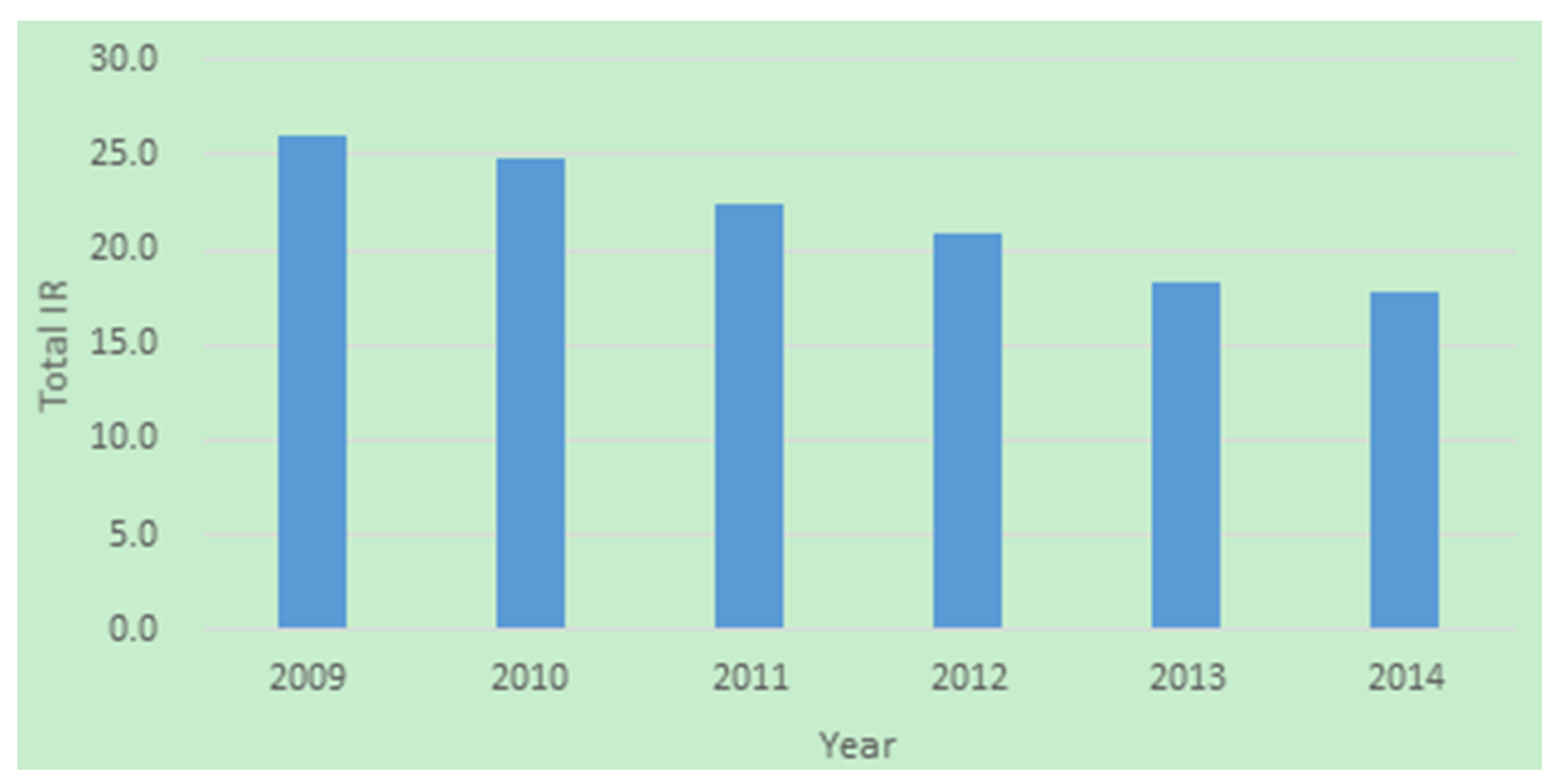
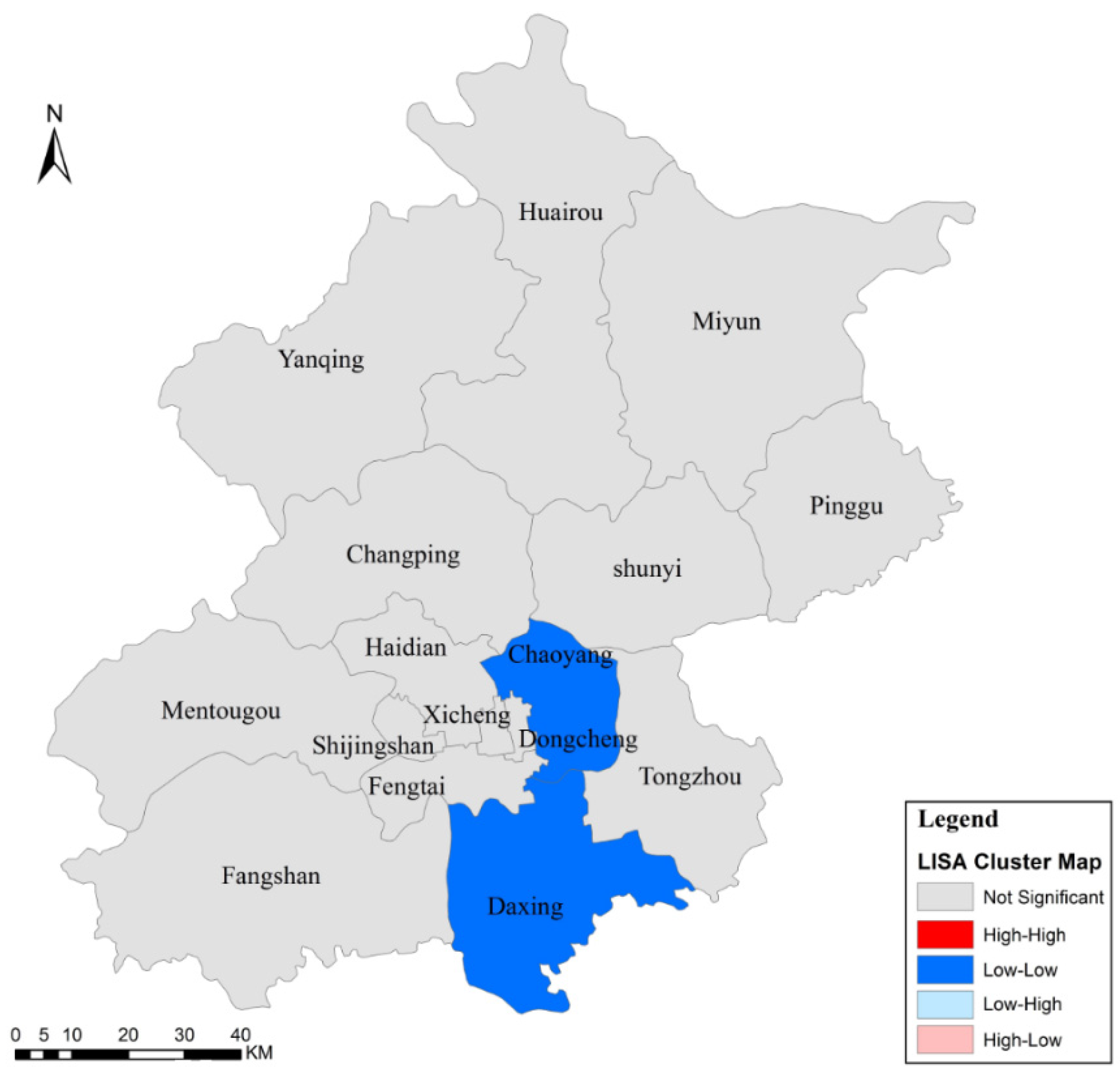
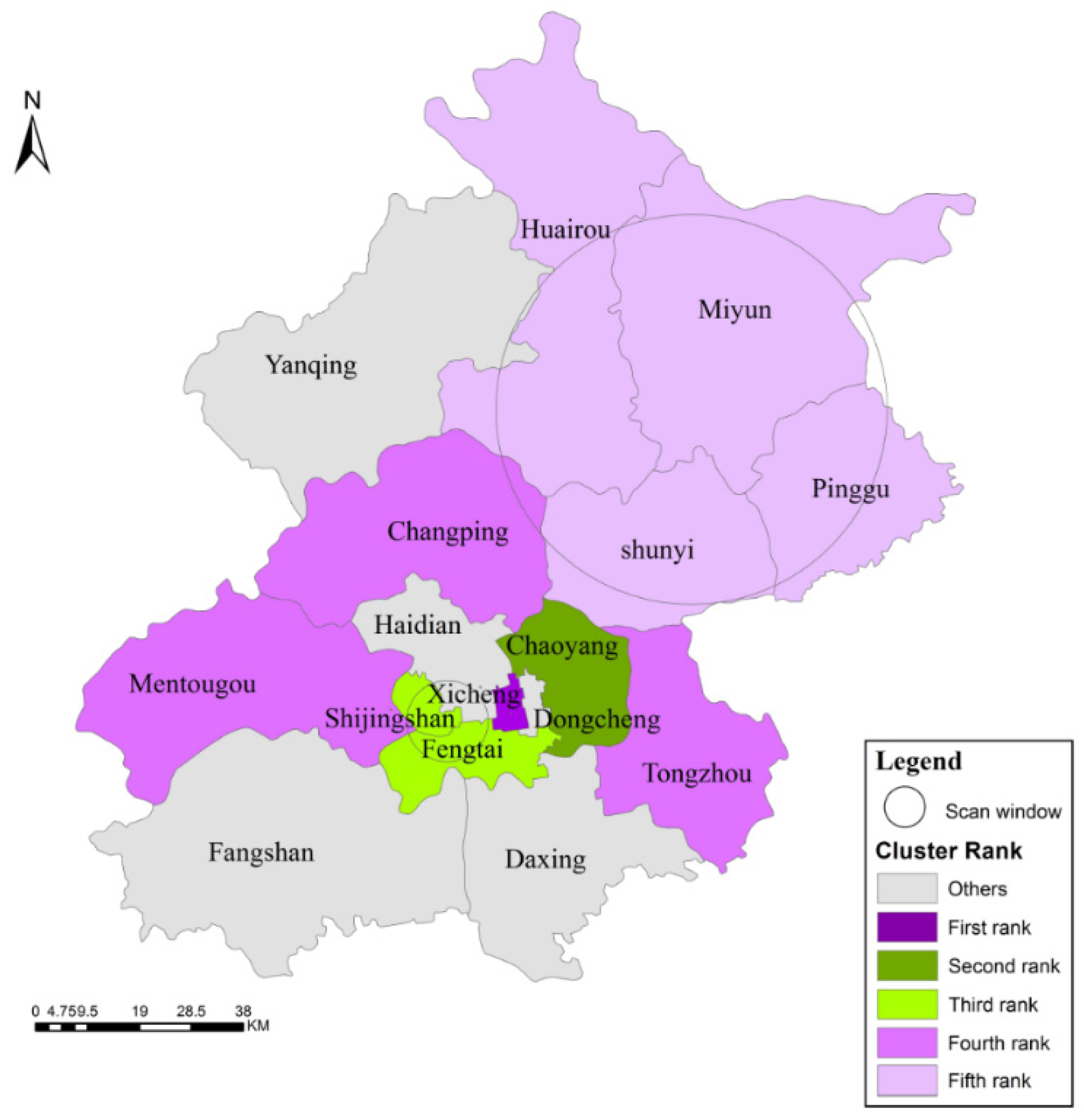


| Cluster Rank | IR | Number of Districts | Districts | Number of Cases | Expected Cases | LLR | RR | p |
|---|---|---|---|---|---|---|---|---|
| First | High | 1 | Xicheng | 3458 | 1638.88 | 832.68 | 2.28 | <0.001 |
| Second | Low | 1 | Chaoyang | 2685 | 4707.95 | 609.13 | 0.52 | <0.001 |
| Third | Low | 2 | Shijingshan, Fengtai | 2078 | 3584.80 | 423.30 | 0.54 | <0.001 |
| Fourth | High | 1 | Mentougou | 906 | 380.86 | 265.43 | 2.43 | <0.001 |
| Fifth | High | 4 | Miyun, Huairou, Shunyi, Pinggu | 3640 | 2812.79 | 126.16 | 1.34 | <0.001 |
| Year | Cluster Rank | IR | Number of Districts | Districts | Number of Cases | Expected Cases | LLR | RR | p |
|---|---|---|---|---|---|---|---|---|---|
| 2009–2011 | First | High | 16 | All districts | 13,950 | 12,342.71 | 199.20 | 1.28 | 0.001 |
| Year | Cluster Rank | IR | Number of Districts | Districts | Number of Cases | Expected Cases | LLR | RR | p |
|---|---|---|---|---|---|---|---|---|---|
| 2009–2011 | First | High | 1 | Xicheng | 1892 | 802.80 | 556.71 | 2.46 | <0.001 |
| 2012–2014 | Second | Low | 2 | Dongcheng, Chaoyang | 1714 | 3062.29 | 392.54 | 0.53 | <0.001 |
| 2012–2014 | Third | Low | 2 | Shijingshan, Fengtai | 960 | 1872.19 | 288.03 | 0.49 | <0.001 |
| 2009–2010 | Fourth | High | 4 | Huairou, Miyun, Shunyi, Changping | 2093 | 1287.08 | 225.05 | 1.68 | <0.001 |
| Dist | a = 0.55 | a = 0.65 | a = 0.75 | a = 0.85 | a = 0.95 | Average |
|---|---|---|---|---|---|---|
| dist_IR&NSPRP | 3.07 | 2.87 | 2.68 | 2.50 | 2.35 | 2.70 |
| dist_IR&NSPTBP | 3.71 | 3.57 | 3.41 | 3.26 | 3.11 | 3.41 |
| dist_IR&RSPRP | 4.78 | 4.60 | 4.43 | 4.29 | 4.17 | 4.46 |
| dist_IR&RSPTBP | 5.59 | 5.28 | 5.02 | 4.80 | 4.63 | 5.06 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xi, Y.; Ren, F. Spatio-Temporal Distribution Characteristics and Trajectory Similarity Analysis of Tuberculosis in Beijing, China. Int. J. Environ. Res. Public Health 2016, 13, 291. https://doi.org/10.3390/ijerph13030291
Li L, Xi Y, Ren F. Spatio-Temporal Distribution Characteristics and Trajectory Similarity Analysis of Tuberculosis in Beijing, China. International Journal of Environmental Research and Public Health. 2016; 13(3):291. https://doi.org/10.3390/ijerph13030291
Chicago/Turabian StyleLi, Lan, Yuliang Xi, and Fu Ren. 2016. "Spatio-Temporal Distribution Characteristics and Trajectory Similarity Analysis of Tuberculosis in Beijing, China" International Journal of Environmental Research and Public Health 13, no. 3: 291. https://doi.org/10.3390/ijerph13030291
APA StyleLi, L., Xi, Y., & Ren, F. (2016). Spatio-Temporal Distribution Characteristics and Trajectory Similarity Analysis of Tuberculosis in Beijing, China. International Journal of Environmental Research and Public Health, 13(3), 291. https://doi.org/10.3390/ijerph13030291





