Dynamic Mathematical Modelling of the Removal of Hydrophilic VOCs by Biotrickling Filters
Abstract
:1. Introduction
2. Experimental Section
2.1. Experimental Set-Up and BTF Operational Conditions for the Experiments at Laboratory Scale
| Inlet load a (g–C·m−3·h−1) | EBRT (s) | Spraying Pattern | Elimination Capacity a (g–C·m−3·h−1) | Removal Efficiency a (%) | |
|---|---|---|---|---|---|
| Run 1 | 32.6 | 60 | 1 h every 4 h | 29.8 | 91 |
| Run 2 | 32.0 | 60 | 30 min every 4 h | 29.7 | 93 |
| Run 3 | 59.6 | 60 | 1 h every 4 h | 53.6 | 90 |
2.2. Experimental Set-Up and BTF Operational Conditions for the Field Scale
| Date | Inlet Load a (g–C·m−3·h−1) | Gas Flow Rate a (m−3·h−1) | Spraying Pattern | Elimination Capacity a (g–C·m−3·h−1) | Removal Efficiency a (%) | ||
|---|---|---|---|---|---|---|---|
| 0–6 am | 6 am–12 pm | ||||||
| Run 4 | October 2009 | 27.5 | 1675 | 6 min every 21 min | 6 min every 21 min | 17.9 | 65 |
| Run 5 | January 2011 | 46.5 | 2717 | 6 min every 1 h | 6 min every 3 h | 29.1 | 63 |
2.3. Analytical Methods
2.4. Model Development
- (1)
- The gas phase flows in a plug flow regime along the filter bed.
- (2)
- Axial dispersion is neglected.
- (3)
- The adsorption of pollutant in the packing material is negligible.
- (4)
- The active biofilm is formed on the external surface of the packing material, and no reaction occurs in the pores. The biofilm covers the surface of the packing material, and its thickness (δ) is much smaller than the size of the solid particles, so a planar geometry is assumed.
- (5)
- The packing material is completely covered by the biofilm.
- (6)
- The biodegradation kinetics are described by a Monod expression, indicating the oxygen limitation.
- (7)
- The diffusion inside of the biofilm is described by Fick’s second law.
- (8)
- A mobile liquid phase is assumed during the spraying period, and a stagnant liquid phase is considered during the non-spraying period.
- (9)
- The gas-liquid interface is in equilibrium according to Henry’s law.
- (10)
- The mass flux at the gas-liquid and the liquid-biofilm interfaces can be expressed by mass transfer coefficients.
- (11)
- The presence of biomass in the bioreactor increases resistance to the mass transfer between the gas and the liquid phase. Thus, the overall mass transfer coefficients experimentally determined in abiotic conditions are corrected by a factor (α1) varying between 0 and 1.
- (12)
- There is no reaction in the liquid phase.
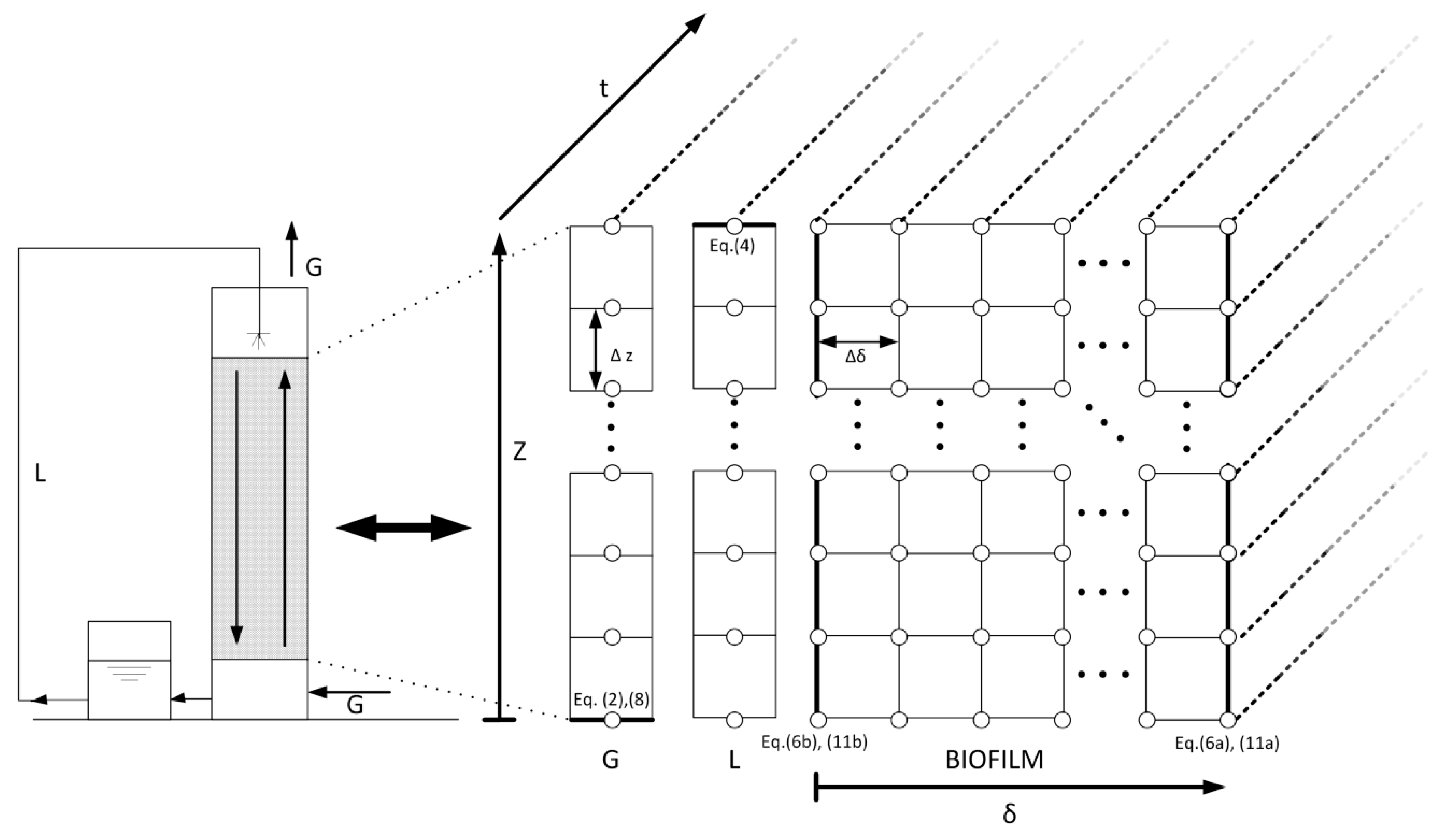
2.4.1. Mass Balances during the Spraying Period
2.4.2. Mass Balances during the Non-Spraying Periods
2.4.3. Numerical Solution
3. Results and Discussion
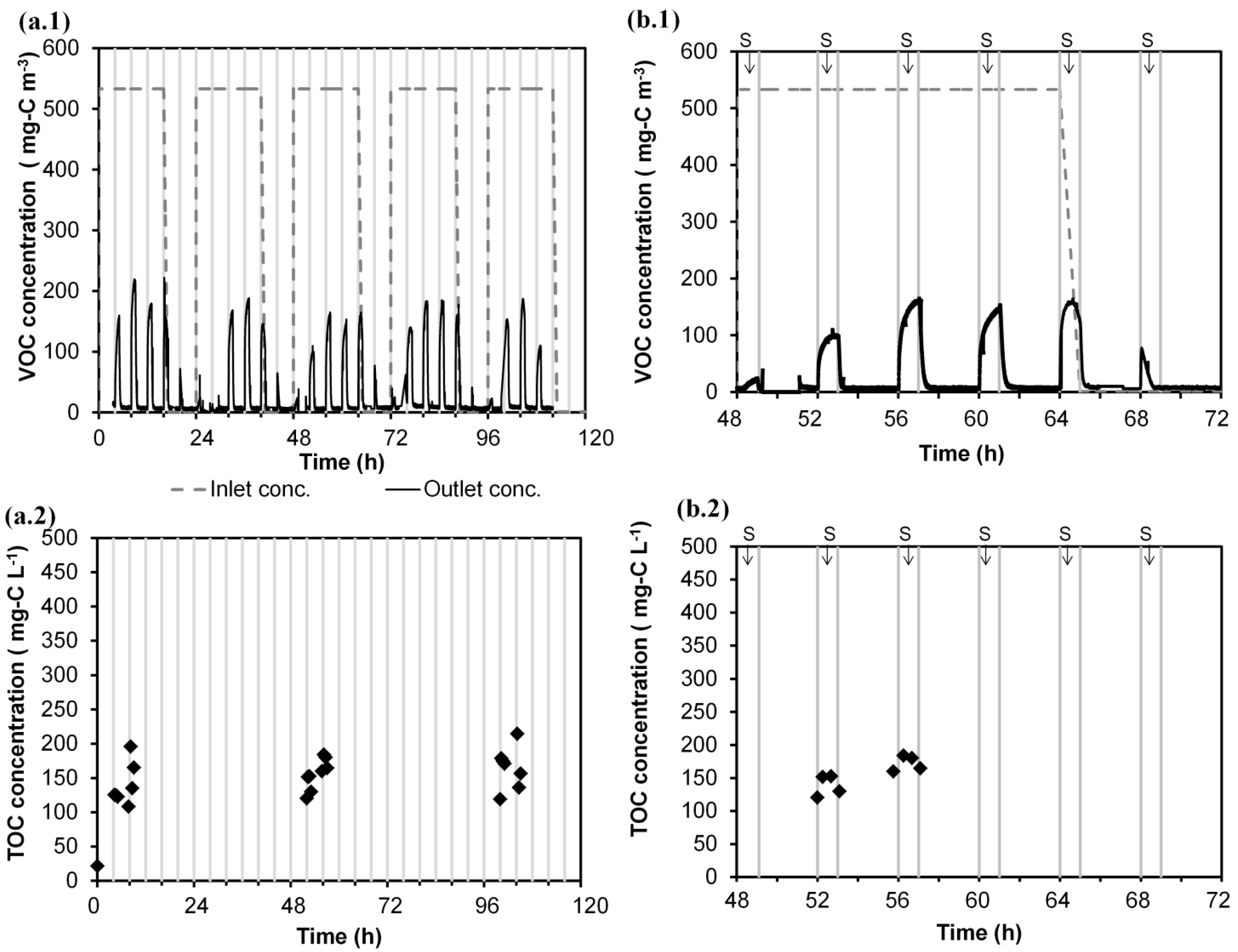
3.1. Model Calibration
| Parameters | Specific Value | Reference |
|---|---|---|
| Physical properties | ||
| DP (m2·s−1) | 1.13 × 10−9 | [25] |
| DO (m2·s−1) | 2.0 × 10−9 | [26] |
| HP | 2.8 × 10−4 | [24] |
| HO | 31.4 | [27] |
| KLaP (s−1) | 2.98 × 10−5 | Using correlation in [24] |
| KLaO (s−1) | 0.0126 | Using correlation in [24] |
| Biofilm properties | ||
| δ (m) | 60 × 10−6 | This work |
| β (m) | 3.8 × 10−6 | This work |
| Kinetic data | ||
| f(Xv) | 0.3495 | [23] |
| Ko | 0.26 | [12] |
| YP | 0.48 | [11] |
| Yo | 0.14 | Stoichiometric balance |
| µmax (s−1) | 2 × 10−5 | This work |
| KsP (g–C·m−3) | 350 | This work |
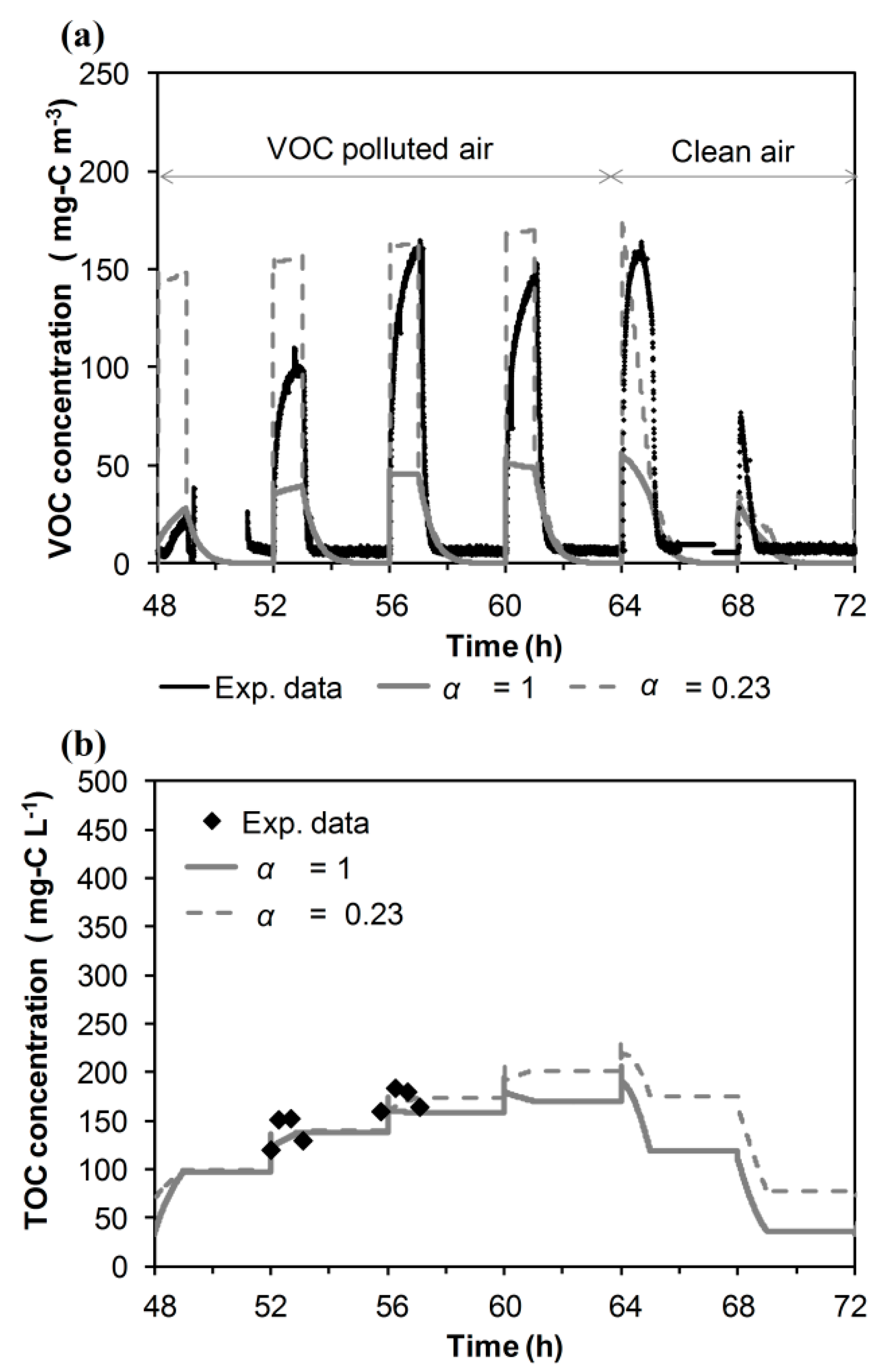
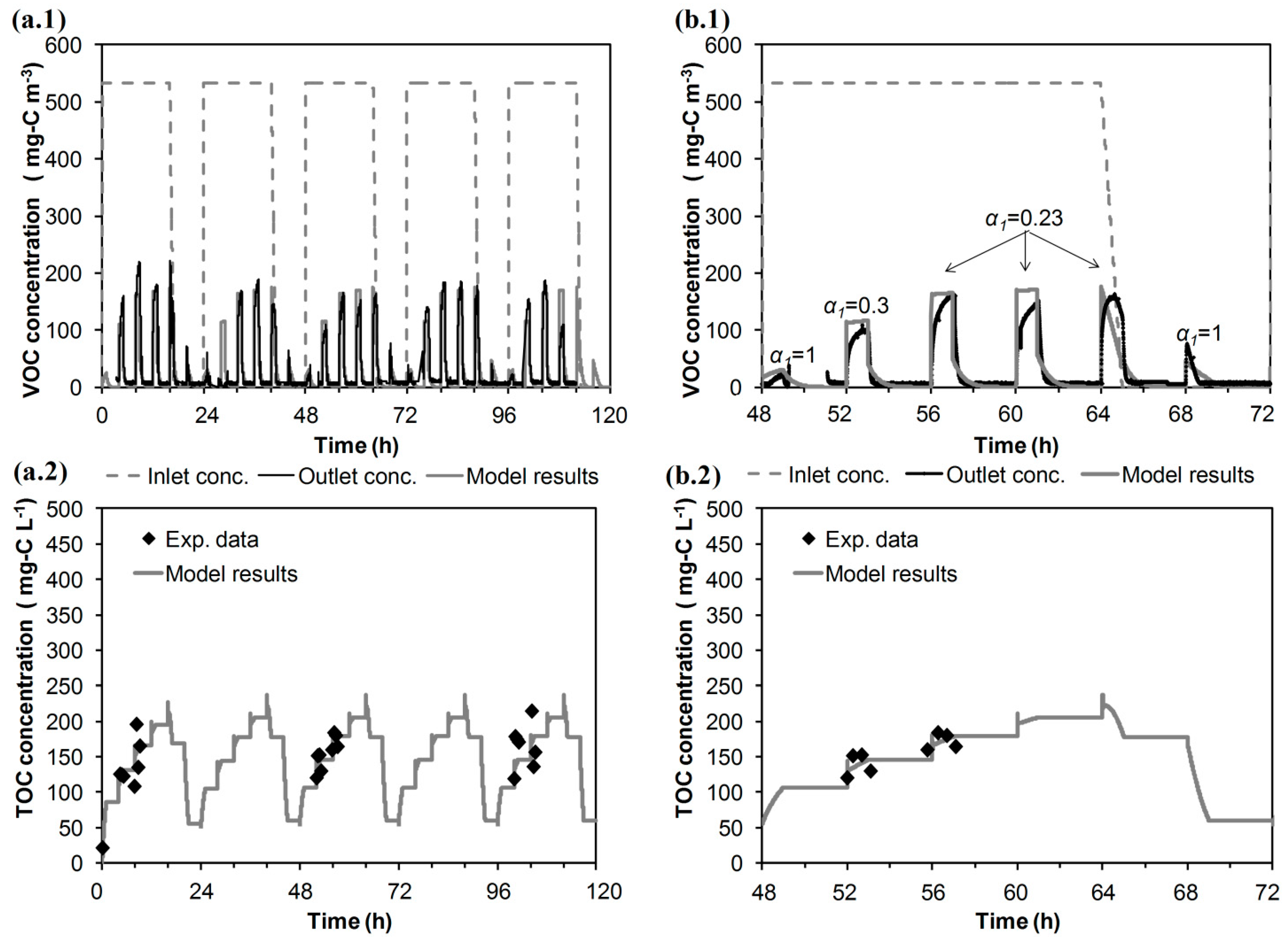
3.2. Model Validation

3.3. Model Simulations
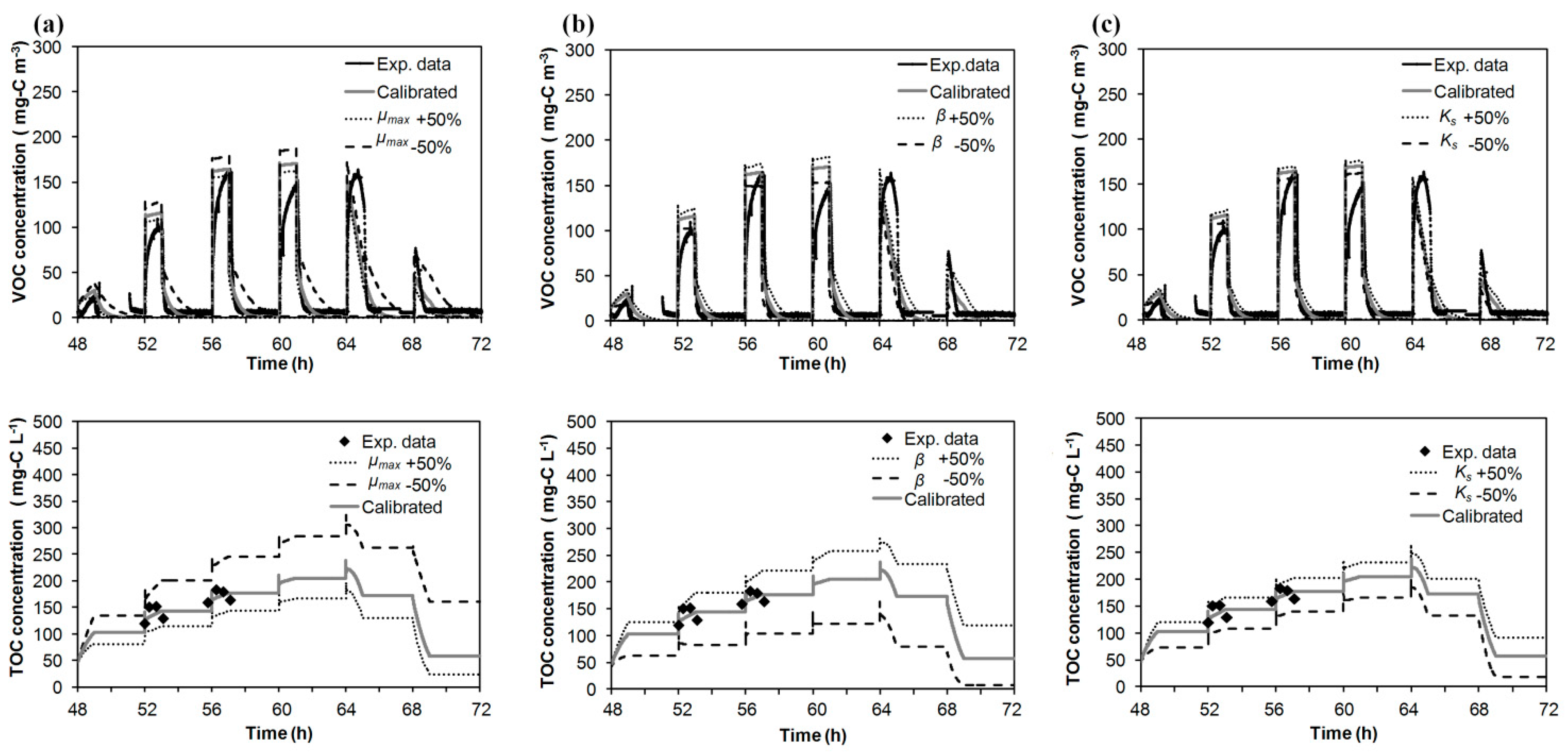
3.4. Model Application to Industrial Unit Processes
| Compounds | Composition (%) | DP (m2·s−1) [25] | HP [27] |
|---|---|---|---|
| Ethanol | 63 | 1.48 × 10−9 | 2.30 × 10−4 |
| Ethyl acetate | 22 | 9.57 × 10−1° | 6.40 × 10−3 |
| 1-Ethoxy-2-propanol | 13 | 8.49 × 10−1° | 1.00 × 10−6 * |

4. Conclusions
Nomenclature
| a | Specific surface area of the packing material (m−1) |
| C | Concentration (g·m−3) |
| D | Diffusion coefficient of substrates (m2·s−1) |
| f(Xv) | Correction factor of diffusivity in biofilm according to Fan’s equation |
| H | Henry’s law constant |
| Ks | Half saturation rate constants of the substrate (g–C·m−3) |
| KLa | Overall mass transfer coefficients of the substrates (s−1) |
| M | Number of divisions along the biofilm |
| N | Number of divisions along the column |
| Q | Flow rate (m3·s−1) |
| S | Concentration in the biofilm (g·m−3) |
| t | Time (s) |
| v | Superficial velocity calculated as a fraction of Q and S (m·s−1) |
| V | Volume (m3) |
| x | Coordinate for the depth in the biofilm, perpendicular to the biofilm surface |
| Xv | Biomass concentration in the biofilm (g·m−3) |
| Y | Yield coefficient (g of dry biomass synthesized per g consumed) |
| z | Axial coordinate in the reactor |
| Z | Height of the reactor (m) |
Greek letters
| α1 | Correction of the mass transfer coefficient between biotic and abiotic systems |
| α2 | Switch parameter of the model |
| β | Thickness of the liquid-biofilm interface (m) |
| δ | Thickness of the biofilm (m) |
| θB | Volume fraction of the biofilm (–) |
| θG | Porosity of the bioreactor (–) |
| θL | Volume fraction of the liquid phase (–) |
| θPM | Porosity of the packing material (–) |
| µmax | Maximum specific growth rate of the substratum (s−1) |
Subscripts
| i | Substance (pollutant and oxygen) |
| G | Gas |
| L | Liquid |
| B | Biofilm |
| P | Pollutant |
| O | Oxygen |
| R | Reactor |
| T | Tank |
Acknowledgements
Author Contributions
Conflicts of Interest
References
- European Environment Agency (EEA). European Environment Agency (EEA). European Union Emission Inventory Report 1990–2012 under the UNECE Convention on Long-Range Transboundary Air Pollution (LRTAP) (Technical Report N° 12/2014); Publications Office of the European Union: Luxembourg city, Luxembourg, 2014. [Google Scholar]
- Kennes, C.; Rene, E.R.; Veiga, M.C. Bioprocesses for air pollution control. J. Chem. Technol. Biotechnol. 2009, 84, 1419–1436. [Google Scholar] [CrossRef]
- Kennes, C.; Thalasso, F. Review: Waste gas biotreatment technology. J. Chem. Technol. Biotechnol. 1998, 72, 303–319. [Google Scholar] [CrossRef]
- Webster, T.S.; Cox, H.H.J.; Deshusses, M.A. Resolving operational and performance problems encountered in the use of a pilot/full-scale biotrickling fiber reactor. Environ. Prog. 1999, 18, 162–172. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Alonso, C.; Suidan, M.T.; Cao, H.W.; Kim, B.J.; Kim, B.R. The effect of liquid phase on VOC removal in trickle-bed biofilters. Water Sci. Technol. 1998, 38, 315–322. [Google Scholar] [CrossRef]
- Sempere, F.; Gabaldón, C.; Martínez-Soria, V.; Marzal, P.; Penya-roja, J.M.; Alvarez-Hornos, F.J. Performance evaluation of a biotrickling filter treating a mixture of oxygenated VOCs during intermittent loading. Chemosphere 2008, 73, 1533–1539. [Google Scholar] [CrossRef]
- Kennes, C.; Veiga, M.C. Biotrickling filters. In Air pollution prevention and control. Bioreactors and Bioenergy; Kennes, C., Veiga, M.C., Eds.; John Wiley & Sons, Ltd.: Oxford, UK, 2013; pp. 121–138. [Google Scholar]
- San-Valero, P.; Penya-Roja, J.M.; Sempere, F.; Gabaldon, C. Biotrickling filtration of isopropanol under intermittent loading conditions. Bioprocess Biosyst. Eng. 2013, 36, 975–984. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.Y.; Chang, K.; Hsu, S. A model for treating isopropyl alcohol and acetone mixtures in a trickle-bed air biofilter. Process Biochem. 2004, 39, 1849–1858. [Google Scholar]
- Ottengraf, S.P.; Van Den Oever, A.H. Kinetics of organic-compound removal from waste gases with a biological filter. Biotechnol. Bioeng. 1983, 25, 3089–3102. [Google Scholar]
- Rene, E.R.; Veiga, M.C.; Kennes, C. Biofilters. In Air Pollution Prevention and Control: Bioreactors and Bioenergy; Kennes, C., Veiga, M.C, Eds.; John Wiley & Sons, Ltd.: Oxford, UK, 2013; pp. 59–120. [Google Scholar]
- Shareefdeen, Z.; Baltzis, B.C.; Oh, Y.S.; Bartha, R. Biofiltration of methanol vapor. Biotechnol. Bioeng. 1993, 41, 512–524. [Google Scholar]
- Shareefdeen, Z.; Baltzis, B.C. Biofiltration of toluene vapor under steady-state and transient conditions—Theory and experimental results. Chem. Eng. Sci. 1994, 49, 4347–4360. [Google Scholar] [CrossRef]
- Mpanias, C.J.; Baltzis, B.C. An experimental and modeling study on the removal of mono-chlorobenzene vapor in biotrickling filters. Biotechnol. Bioeng. 1998, 59, 328–343. [Google Scholar] [PubMed]
- Baltzis, B.C.; Mpanias, C.J.; Bhattacharya, S. Modeling the removal of VOC mixtures in biotrickling filters. Biotechnol. Bioeng. 2001, 72, 389–401. [Google Scholar] [PubMed]
- Okkerse, W.J.H.; Ottengraf, S.P.P.; Osinga-Kuipers, B.; Okkerse, M. Biomass accumulation and clogging in biotrickling filters for waste gas treatment. Evaluation of a dynamic model using dichloromethane as a model pollutant. Biotechnol. Bioeng. 1999, 63, 418–430. [Google Scholar]
- Kim, S.; Deshusses, M.A. Development and experimental validation of a conceptual model for biotrickling filtration of H2S. Environ. Prog. 2003, 22, 119–128. [Google Scholar] [CrossRef]
- Almenglo, F.; Ramírez, M.; Gómez, J.M.; Cantero, D.; Gamisans, X.; Dorado, A.D. Modeling and control strategies development for anoxic biotrickling filtration. In Biotechniques for Air Pollution Control and Bioenergy; Malhautier, L., Ed.; Presses de Mines: Paris, France, 2013; pp. 123–131. [Google Scholar]
- Lee, S.H.; Heber, A.J. Ethylene removal using biotrickling filters: Part II. Parameter estimation and mathematical simulation. Chem. Eng. J. 2010, 158, 89–99. [Google Scholar]
- Alonso, C.; Suidan, M.T.; Kim, B.R.; Kim, B.J. Dynamic mathematical model for the biodegradation of VOCs in a biofilter: Biomass accumulation study. Environ. Sci. Technol. 1998, 32, 3118–3123. [Google Scholar] [CrossRef] [PubMed]
- Iliuta, I.; Iliuta, M.C.; Larachi, F. Hydrodynamics modeling of bioclogging in waste gas treating trickle-bed bioreactors. Ind. Eng. Chem. Res. 2005, 44, 5044–5052. [Google Scholar] [CrossRef]
- Devinny, J.S.; Ramesh, J. A phenomenological review of biofilter models. Chem. Eng. J. 2005, 113, 187–196. [Google Scholar] [CrossRef]
- Fan, L.S.; Leyva-Ramos, R.; Wisecarver, K.D.; Zehner, B.J. Diffusion of phenol through a biofilm grown on activated carbon particles in a draft-tube three-phase fluidized-bed bioreactor. Biotechnol. Bioeng. 1990, 35, 279–286. [Google Scholar]
- San-Valero, P.; Penya-Roja, J.M.; Álvarez-Hornos, F.J.; Gabaldón, C. Modelling mass transfer properties in a biotrickling filter for the removal of isopropanol. Chem. Eng. Sci. 2014, 108, 47–56. [Google Scholar] [CrossRef]
- Tucker, W.A.; Nelken, L.H. Diffusion coefficients in air and water. In Handbook of Chemical Property Estimation Methods; Lyman, W.J., Reehl, W.F., Rosenblatt, D.H., Eds.; American Chemical Society: New York, NY, USA, 1982. [Google Scholar]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw-Hill Book Company: New York, NY, USA, 1987. [Google Scholar]
- Sander, R. Henry’s law constants. In NIST Chemistry Webbook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005. [Google Scholar]
- Bustard, M.T.; Meeyoo, V.; Wright, P.C. Kinetic analysis of high-concentration isopropanol biodegradation by a solvent-tolerant mixed microbial culture. Biotechnol. Bioeng. 2002, 78, 708–713. [Google Scholar] [PubMed]
- Zhang, X.Q.; Bishop, P.L. Biodegradability of biofilm extracellular polymeric substances. Chemosphere 2003, 50, 63–69. [Google Scholar]
- US EPA. Estimation Programs Interface SuiteTM for Microsoft® Windows, V 4.11; United States Environmental Protection Agency: Washington, DC, USA, 2013. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
San-Valero, P.; Penya-roja, J.M.; Alvarez-Hornos, F.J.; Marzal, P.; Gabaldón, C. Dynamic Mathematical Modelling of the Removal of Hydrophilic VOCs by Biotrickling Filters. Int. J. Environ. Res. Public Health 2015, 12, 746-766. https://doi.org/10.3390/ijerph120100746
San-Valero P, Penya-roja JM, Alvarez-Hornos FJ, Marzal P, Gabaldón C. Dynamic Mathematical Modelling of the Removal of Hydrophilic VOCs by Biotrickling Filters. International Journal of Environmental Research and Public Health. 2015; 12(1):746-766. https://doi.org/10.3390/ijerph120100746
Chicago/Turabian StyleSan-Valero, Pau, Josep M. Penya-roja, F. Javier Alvarez-Hornos, Paula Marzal, and Carmen Gabaldón. 2015. "Dynamic Mathematical Modelling of the Removal of Hydrophilic VOCs by Biotrickling Filters" International Journal of Environmental Research and Public Health 12, no. 1: 746-766. https://doi.org/10.3390/ijerph120100746
APA StyleSan-Valero, P., Penya-roja, J. M., Alvarez-Hornos, F. J., Marzal, P., & Gabaldón, C. (2015). Dynamic Mathematical Modelling of the Removal of Hydrophilic VOCs by Biotrickling Filters. International Journal of Environmental Research and Public Health, 12(1), 746-766. https://doi.org/10.3390/ijerph120100746





