Relative Deprivation and Sickness Absence in Sweden
Abstract
:1. Introduction
The Swedish Context
2. Background
3. Data, Variables and Econometric Method
3.1. Data and Sample
3.2. Dependent Variable
3.3. Independent Variables
3.3.1. Relative Income
3.3.2. Other Variables
3.4. Econometric Method
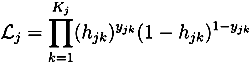
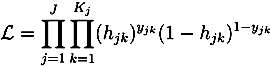
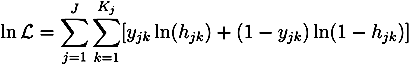
4. Empirical Analysis: The Duration until Sickness Absence
4.1. Descriptive Statistics
| Full sample | Primary education | Secondary education | University education | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | |
| Relative income | 0.964 | 0.001 | 4.597 | 0.975 | 0.047 | 4.597 | 0.972 | 0.006 | 4.591 | 0.939 | 0.001 | 4.597 |
| Absolute income | 4.911 | 3 | 76 | 4.450 | 3 | 28 | 4.643 | 3 | 49 | 5.803 | 3 | 76 |
| Education: | ||||||||||||
| Primary | 0.250 | 0 | 1 | 1.000 | 0 | 1 | 0.000 | 0 | 1 | 0.000 | 0 | 1 |
| Secondary | 0.477 | 0 | 1 | 0.000 | 0 | 1 | 1.000 | 0 | 1 | 0.000 | 0 | 1 |
| University | 0.273 | 0 | 1 | 0.000 | 0 | 1 | 0.000 | 0 | 1 | 1.000 | 0 | 1 |
| Gender (female = 1) | 0.487 | 0 | 1 | 0.439 | 0 | 1 | 0.477 | 0 | 1 | 0.549 | 0 | 1 |
| Civil status (1 = married) | 0.480 | 0 | 1 | 0.515 | 0 | 1 | 0.439 | 0 | 1 | 0.520 | 0 | 1 |
| Age | 38.07 | 18 | 65 | 40.10 | 18 | 65 | 36.64 | 18 | 65 | 38.70 | 18 | 65 |
| Age squared | 1,564 | 324 | 4,225 | 1,733 | 324 | 4,225 | 1,457 | 324 | 4,225 | 1,595 | 324 | 4,225 |
| Years since migration | 6.121 | 0 | 65 | 7.372 | 0 | 65 | 5.780 | 0 | 61 | 5.569 | 0 | 63 |
| Years since migration squared | 121.1 | 0 | 4,225 | 144.3 | 0 | 4,225 | 116.3 | 0 | 3,721 | 108.1 | 0 | 3,969 |
| Metropol.residence | 0.485 | 0 | 1 | 0.465 | 0 | 1 | 0.457 | 0 | 1 | 0.553 | 0 | 1 |
| Local unemployment rate | 6.100 | 0.160 | 24.02 | 5.748 | 0.160 | 24.02 | 6.212 | 0.160 | 24.02 | 6.227 | 0.160 | 24.02 |
| Year | 1993 | 1982 | 2001 | 1992 | 1982 | 2001 | 1993 | 1982 | 2001 | 1994 | 1982 | 2001 |
| Duration | 2.494 | 1 | 20 | 2.063 | 1 | 20 | 2.464 | 1 | 20 | 3.168 | 1 | 20 |
| Lag duration | 1.369 | 0 | 19 | 1.279 | 0 | 19 | 1.384 | 0 | 19 | 1.459 | 0 | 19 |
| Number of spells | 2.953 | 1 | 6 | 3.183 | 1 | 6 | 3.043 | 1 | 6 | 2.543 | 1 | 6 |
| Spell duration conditional on the spells ending in sickness absence: | ||||||||||||
| 1st spell | 2.551 | 1 | 20 | 2.165 | 1 | 20 | 2.543 | 1 | 20 | 3.200 | 1 | 20 |
| 2nd spell | 1.986 | 1 | 19 | 1.747 | 1 | 19 | 1.993 | 1 | 19 | 2.375 | 1 | 18 |
| 3rd spell | 1.756 | 1 | 18 | 1.589 | 1 | 17 | 1.774 | 1 | 18 | 2.016 | 1 | 18 |
| Observations | 1,525,310 | 381,839 | 727,438 | 416,033 | ||||||||
| Spells | 611,599 | 185,094 | 295,180 | 131,325 | ||||||||
| Individuals | 184,494 | 50,854 | 85,952 | 47,688 | ||||||||
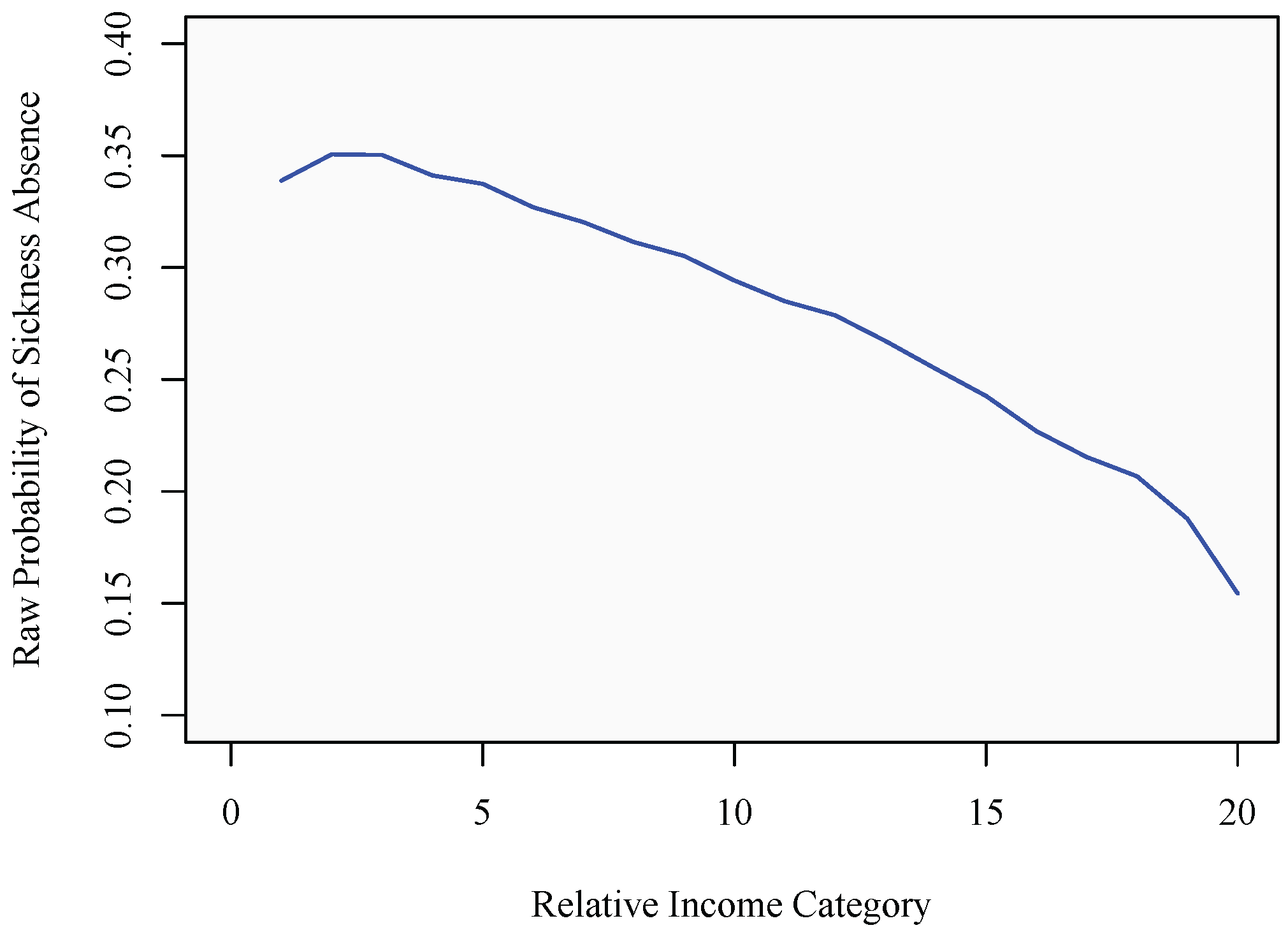
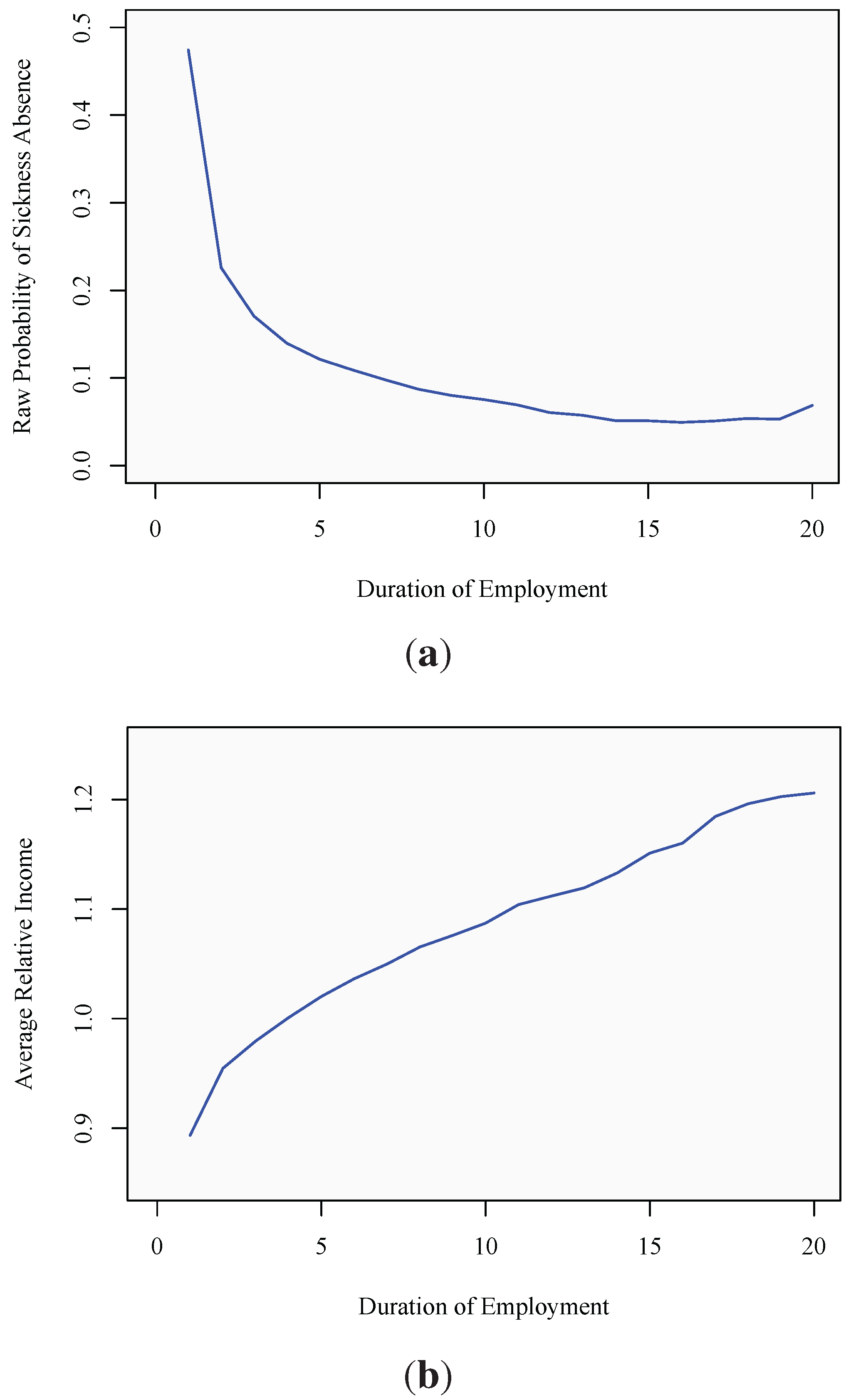
4.2. Regression Analysis
| Baseline analysis | Robustness analysis | |||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | |
| Secondary education | −0.4787 | −0.4146 | −0.3852 | −0.3357 | −0.2964 | −0.4690 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| University education | −1.5668 | −1.3951 | −1.2115 | −0.9829 | −0.8198 | −1.2607 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Gender | 1.0991 | 0.9924 | 0.9164 | 0.9380 | 0.7972 | 0.8653 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Metropolitan dummy | 0.1042 | 0.0958 | 0.0657 | 0.0650 | 0.0789 | 0.1177 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Unemployment rate | 0.0088 | 0.0088 | 0.0095 | 0.0095 | 0.0076 | 0.0078 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.006)} | |
| Age | −0.1235 | −0.0888 | −0.1259 | −0.1299 | −0.0928 | −0.0899 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Age squared | 0.0019 | 0.0015 | 0.0017 | 0.0018 | 0.0012 | 0.0012 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Years since migration | 0.0108 | 0.0184 | −0.0144 | −0.0149 | −0.0200 | 0.0042 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.113) | |
| Years since migration squared | −0.0003 | −0.0004 | 0.0001 | 0.0001 | 0.0003 | −0.0002 |
| (0.000) | (0.000) | (0.001) | (0.001) | (0.000) | (0.008) | |
| Civil status | 0.0263 | 0.0199 | 0.0044 | 0.0064 | 0.0098 | 0.0738 |
| (0.000) | (0.003) | (0.479) | (0.299) | (0.134) | (0.000) | |
| Relative income categories (13 = reference category) | ||||||
| Category 1 | 1.2968 | 1.1267 | 1.1422 | 1.4450 | 1.4082 | 1.1718 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 2 | 0.9920 | 0.8611 | 0.8673 | 1.1585 | 1.0513 | 0.8999 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 3 | 0.8535 | 0.7486 | 0.7498 | 0.9686 | 0.8633 | 0.7360 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 4 | 0.7109 | 0.6226 | 0.6224 | 0.7760 | 0.6723 | 0.5486 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 5 | 0.6218 | 0.5506 | 0.5476 | 0.6791 | 0.5613 | 0.4436 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 6 | 0.5280 | 0.4721 | 0.4679 | 0.5991 | 0.4882 | 0.4504 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 7 | 0.4614 | 0.4143 | 0.4080 | 0.5505 | 0.4736 | 0.4484 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 8 | 0.3873 | 0.3521 | 0.3473 | 0.4523 | 0.3729 | 0.4181 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 9 | 0.3289 | 0.2997 | 0.2961 | 0.3957 | 0.3202 | 0.4052 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 10 | 0.2353 | 0.2171 | 0.2131 | 0.2634 | 0.2128 | 0.2106 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 11 | 0.1498 | 0.1371 | 0.1345 | 0.2227 | 0.1716 | 0.2237 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 12 | 0.0864 | 0.0820 | 0.0814 | 0.1122 | 0.0868 | 0.0749 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.004) | (0.142) | |
| Category 14 | −0.1020 | −0.0949 | −0.0898 | −0.0872 | −0.0837 | −0.0961 |
| (0.000) | (0.000) | (0.000) | (0.001) | (0.006) | (0.066) | |
| Category 15 | −0.1792 | −0.1639 | −0.1584 | −0.1487 | −0.1455 | −0.2091 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 16 | −0.2785 | −0.2560 | −0.2472 | −0.2653 | −0.2264 | −0.2207 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 17 | −0.3620 | −0.3302 | −0.3183 | −0.3536 | −0.3141 | −0.3479 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 18 | −0.4196 | −0.3830 | −0.3701 | −0.4468 | −0.3829 | −0.3854 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 19 | −0.5529 | −0.5018 | −0.4877 | −0.6670 | −0.5504 | −0.5450 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Category 20 | −0.6201 | −0.5687 | −0.5530 | −0.8326 | −0.7442 | −0.8147 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Absolute income in base amounts (1 and 2 are excluded from the sample; 4 = reference category) | ||||||
| 3 | −0.3631 | −0.4259 | −0.3846 | −0.4907 | −0.1780 | −0.4296 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| 5 | 0.1604 | 0.1951 | 0.1773 | 0.2614 | 0.1339 | 0.1750 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| 6 | 0.2579 | 0.3134 | 0.2916 | 0.4569 | 0.2632 | 0.2423 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| 7 | 0.3425 | 0.4035 | 0.3846 | 0.5946 | 0.3487 | 0.2715 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| 8–9 | 0.3655 | 0.4260 | 0.4194 | 0.6975 | 0.4543 | 0.3922 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| ≥10 | 0.2122 | 0.2673 | 0.3017 | 0.4653 | 0.1717 | −0.3442 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.043) | (0.043) | |
| Country dummies | yes | yes | yes | yes | yes | yes |
| Year dummies | yes | yes | yes | yes | yes | yes |
| Duration dummies | no | yes | yes | yes | yes | yes |
| Spell dummies | no | no | yes | yes | yes | no |
| Lagged duration | no | no | yes | yes | yes | no |
| Income-education interactions | no | no | no | yes | yes | yes |
| ρ | 0.4240 | 0.3377 | 0.2425 | 0.2420 | 0.1622 | 0.3360 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Observations | 1,525,310 | 1,525,310 | 1,525,310 | 1,525,310 | 1,322,498 | 592,405 |
| Spells | 611,599 | 611,599 | 611,599 | 611,599 | 408,787 | 184,494 |
| Individuals | 184,494 | 184,494 | 184,494 | 184,494 | 184,494 | 184,494 |
| Log likelihood | −719,085 | −708,801 | −702,840 | −702,317 | −545,275 | −240,238 |
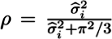 , where
, where 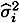 the estimated variance of the individual-specific random intercepts and π2/3 is the variance of the logistic distribution. In Models 1–3, the reported coefficients on the relative and absolute income categories are averages over the complete sample, whereas the respective coefficients in Models 4–6 are averages over the baseline category of individuals with primary education only.
the estimated variance of the individual-specific random intercepts and π2/3 is the variance of the logistic distribution. In Models 1–3, the reported coefficients on the relative and absolute income categories are averages over the complete sample, whereas the respective coefficients in Models 4–6 are averages over the baseline category of individuals with primary education only.
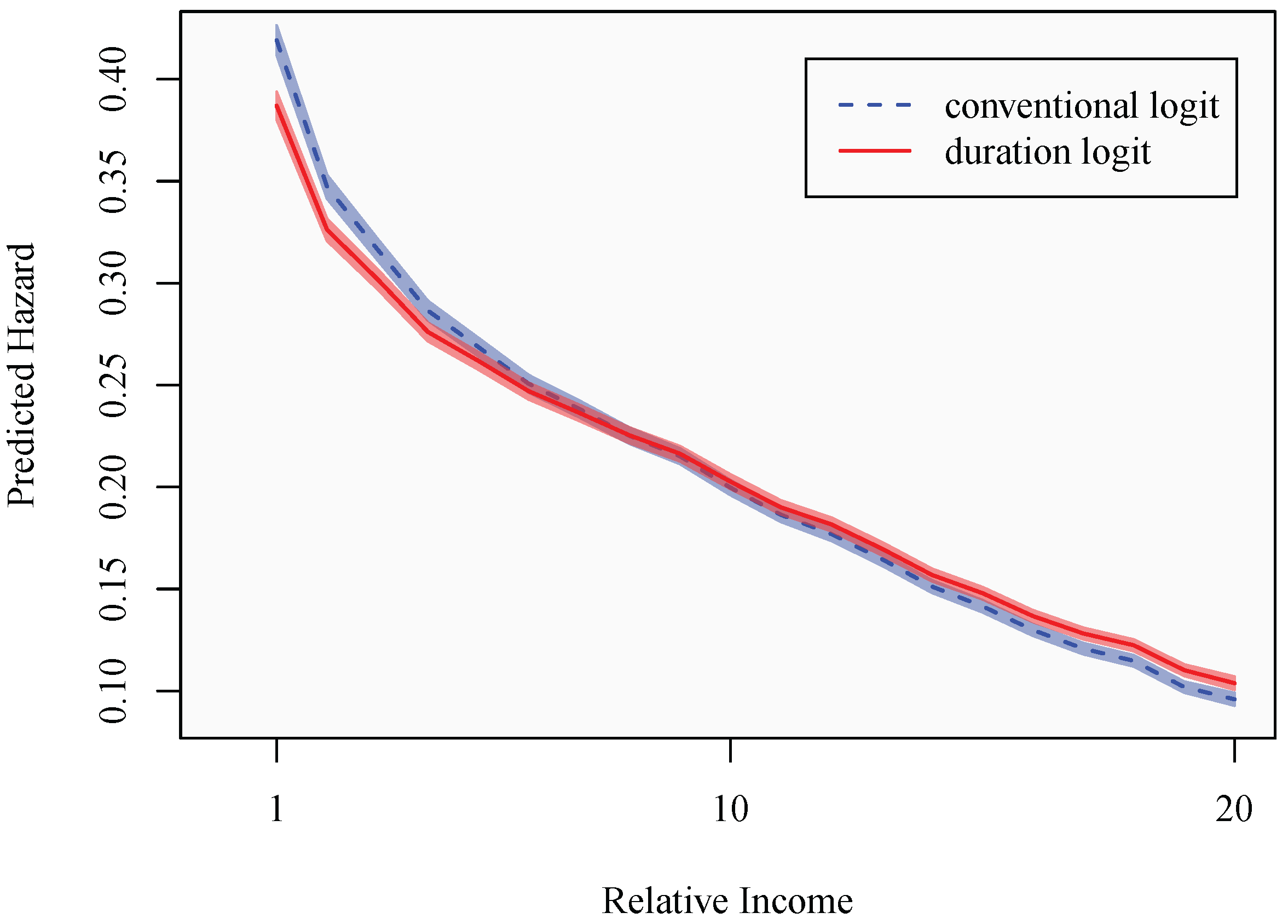
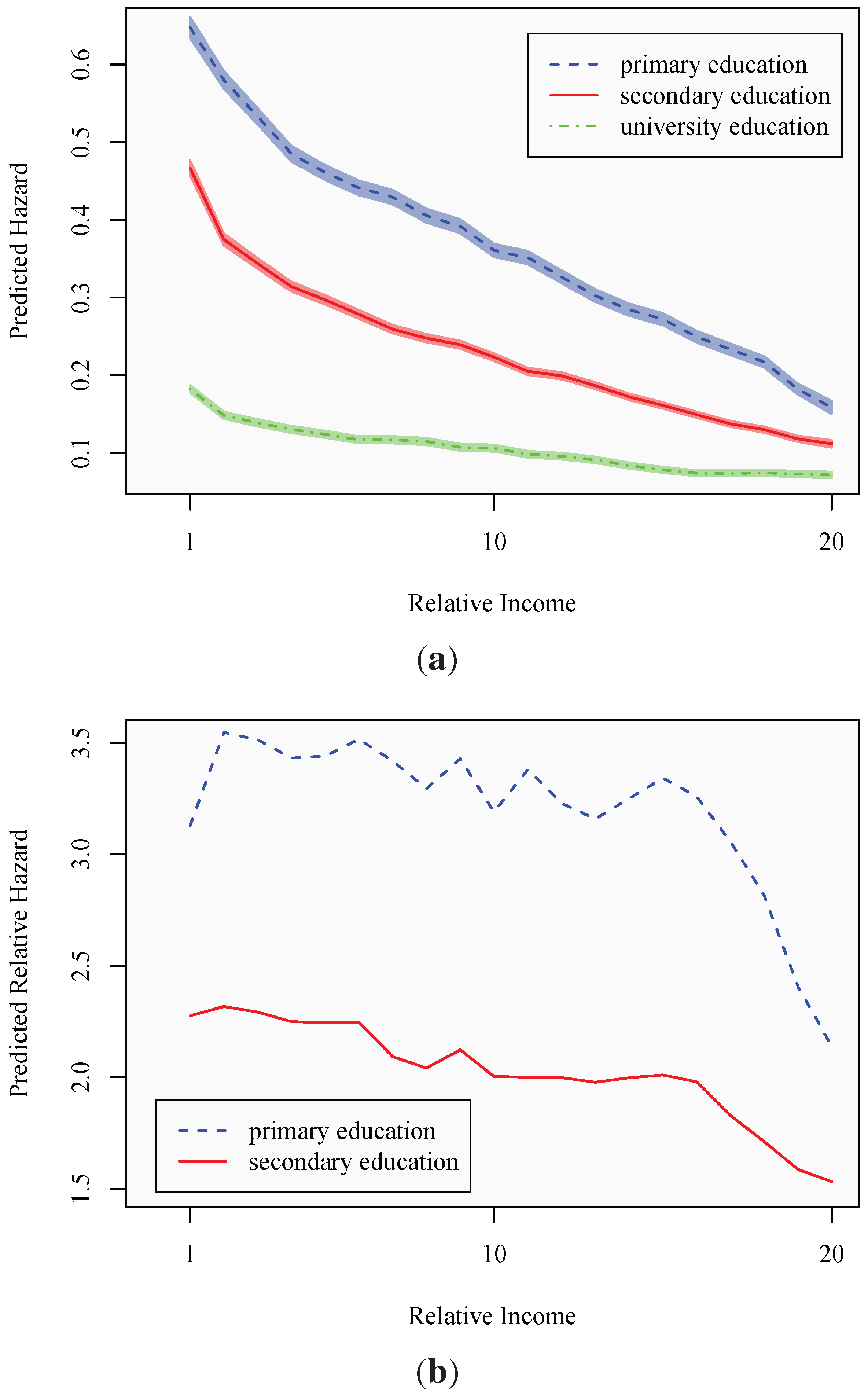
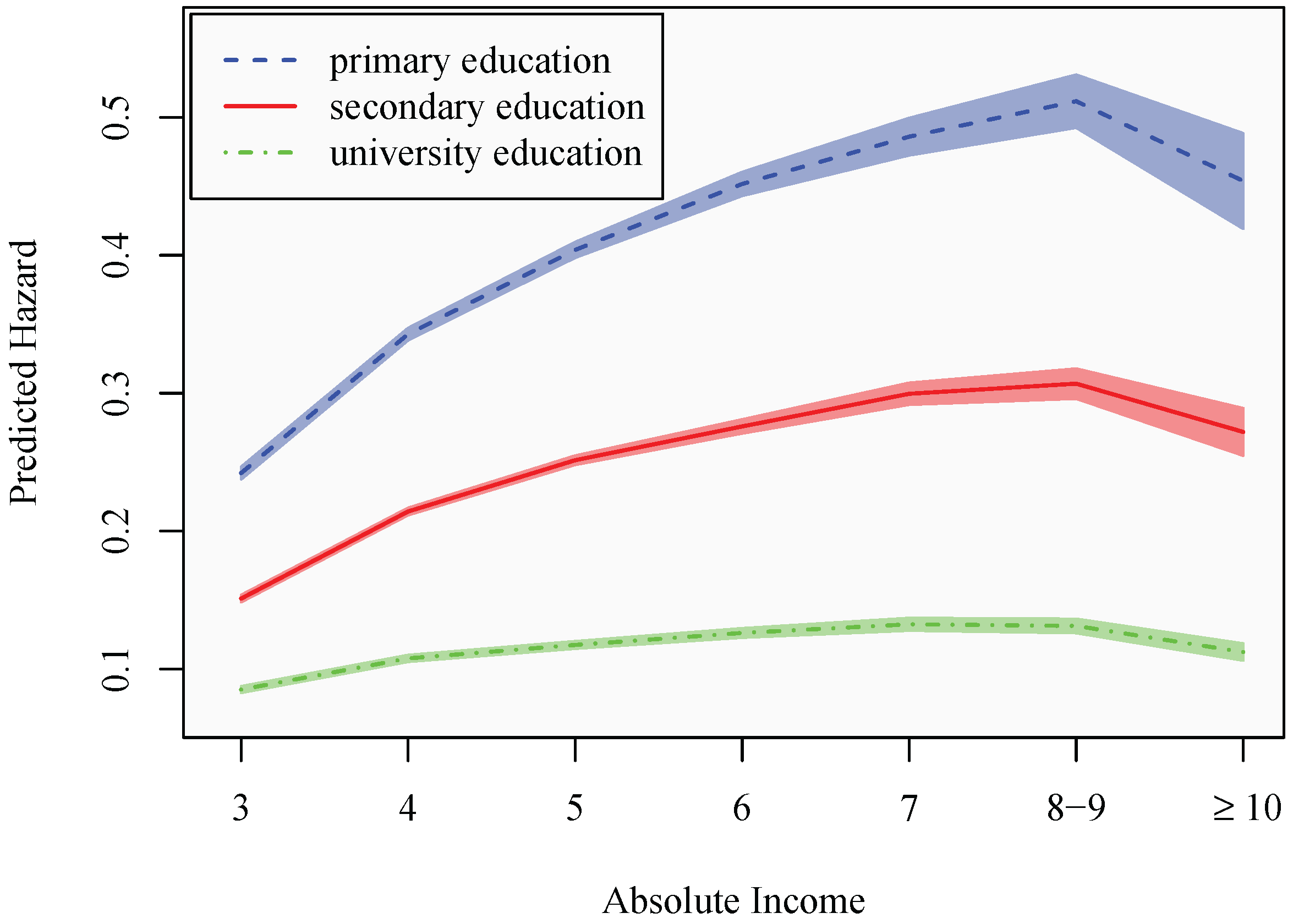
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Friel, S.; Marmot, M.G. Action on the social determinants of health and health inequities goes global. Ann. Rev. Public Health 2011, 32, 225–236. [Google Scholar] [CrossRef]
- Aldabe, B.; Anderson, R.; Lyly-Yrjänäinen, M.; Parent-Thirion, A.; Vermeylen, G.; Kelleher, C.C.; Niedhammer, I. Contribution of material, occupational, and psychosocial factors in the explanation of social inequalities in health in 28 countries in Europe. J. Epidemiol. Commun. Health 2011, 65, 1123–1131. [Google Scholar] [CrossRef]
- Adjaye-Gbewonyo, K.; Kawachi, I. Use of the Yitzhaki Index as a test of relative deprivation for health outcomes: A review of recent literature. Soc. Sci. Med. 2012, 75, 129–137. [Google Scholar] [CrossRef]
- Åberg Yngwe, M.; Kondo, N.; Hagg, S.; Kawachi, I. Relative deprivation and mortality— A longitudinal study in a Swedish population of 4,7 million, 1990–2006. BMC Public Health 2012, 12, 664. [Google Scholar] [CrossRef]
- Swedish Social Insurance Agency. Available online: http://www.forsakringskassan.se (accessed on 11 January 2013).
- Vahtera, J.; Pentti, J.; Kivimaki, M. Sickness absence as a predictor of mortality among male and female employees. J. Epidemiol. Commun. Health 2004, 58, 321–326. [Google Scholar] [CrossRef]
- Voss, M.; Stark, S.; Alfredsson, L.; Vingård, E.; Josephson, M. Comparisons of self-reported and register data on sickness absence among public employees in Sweden. Occup. Environ. Med. 2008, 65, 61–67. [Google Scholar] [CrossRef]
- Hansen, C.D.; Andersen, J.H. Sick at work—A risk factor for long-term sickness absence at a later date? J. Epidemiol. Commun. Health 2009, 63, 397–402. [Google Scholar] [CrossRef]
- Aronsson, G.; Gustafsson, K.; Mellner, C. Sickness presence, sickness absence, and self-reported health and symptoms. Int. J. Workplace Health Manag. 2011, 4, 228–243. [Google Scholar] [CrossRef]
- Mackenbach, J.; Bos, V.; Kunst, A.; Andersen, O.; Cardano, M.; Costa, G.; Harding, S.; Reid, A.; Hemström, O.; Valkonen, T. Widening socioeconomic inequalities in mortality in six Western European countries. Int. J. Epidemiol. 2003, 32, 830–837. [Google Scholar] [CrossRef]
- Meara, E.; Richards, S.; Cutler, D. The gap gets bigger: Changes in mortality and life expectancy, by education, 1981–2000. Health Aff. 2008, 27, 350–360. [Google Scholar] [CrossRef]
- Stringhini, S.; Sabia, S.; Shipley, M.; Brunner, E.; Nabi, H.; Kivimaki, M.; Singh-Manoux, A. Association of socioeconomic position with health behaviors and mortality. J. Am. Med. Assoc. 2010, 303, 1159–1166. [Google Scholar] [CrossRef]
- Winkelmann, R. Markov chain Monte Carlo analysis of underreported count data with an application to worker absenteeism. Empir. Econ. 1996, 21, 575–587. [Google Scholar] [CrossRef]
- Dunn, L.F.; Youngblood, S.A. Absenteeism as a mechanism for approaching an optimal labor market equilibrium: An empirical study. Rev. Econ. Stat. 1986, 68, 668–674. [Google Scholar] [CrossRef]
- Bradley, S.; Green, C.; Leeves, G. Worker absence and shirking: Evidence from matched teacher-school data. Labour Econ. 2007, 14, 319–334. [Google Scholar] [CrossRef]
- Wilkinson, R.G. Unhealthy Societies: The Afflictions of Inequality; Routledge: London, UK, 1996. [Google Scholar]
- Wagstaff, A.; van Doorslaer, E. Duration Models: Specification, Identification, and Multiple Durations. In Handbook of Health Economics; Culyer, A.J., Newhouse, J.P., Eds.; North-Holland: Amsterdam, The Netherlands; Volume 1, pp. 1803–1862.
- Hey, J.D.; Lambert, P.J. Relative deprivation and the Gini coefficient: Comment. Q. J. Econ. 1980, 95, 567–573. [Google Scholar] [CrossRef]
- Deaton, A. Relative Deprivation, Inequality and Mortality. Available online: http://www.nber.org/ papers/w8099 (accessed on 21 August 2013).
- Bygren, M. Pay reference standards and pay satisfaction: What do workers evaluate their pay against? Soc. Sci. Res. 2004, 33, 206–224. [Google Scholar] [CrossRef]
- Gerdtham, U.G.; Johannesson, M. Absolute income, relative income, income inequality, and mortality. J. Hum. Resour. 2004, 39, 228–247. [Google Scholar] [CrossRef]
- Droomers, M.; Schrijvers, C.; Stronks, K.; van de Mheen, D.; Mackenbach, J.P. Educational differences in excessive alcohol consumption: The role of psychosocial and material stressors. Prev. Med. 1999, 29, 1–10. [Google Scholar] [CrossRef]
- Siegrist, J. Adverse health effects of high-effort/low-reward conditions. J. Occup. Health Psychol. 1996, 1, 27–41. [Google Scholar] [CrossRef]
- Steptoe, A.; Siegrist, J.; Kirschbaum, C.; Marmot, M. Effort-reward imbalance, overcommitment, and measures of cortisol and blood pressure over the working day. Psychosom. Med. 2004, 66, 323–329. [Google Scholar] [CrossRef]
- Snyder, S.E.; Evans, W.N. The Impact of Income on Mortality: Evidence from the Social Security Notch. Available online: http://www.nber.org/papers/w9197 (accessed on 21 August 2013).
- Ruhm, C.J. Are recessions good for your health? Q. J. Econ. 2000, 115, 617–650. [Google Scholar] [CrossRef]
- Christopher, J.R. Healthy living in hard times. J. Health Econ. 2005, 24, 341–363. [Google Scholar] [CrossRef]
- Eibner, C.; Evans, W. Relative deprivation, poor health habits and mortality. J. Hum. Resour. 2005, 40, 591–620. [Google Scholar]
- Reagan, P.B.; Salsberry, P.J.; Olsen, R.J. Does the measure of economic disadvantage matter? Exploring the effect of individual and relative deprivation on intrauterine growth restriction. Soc. Sci. Med. 2007, 64, 2016–2029. [Google Scholar] [CrossRef]
- Aberg Yngwe, M.; Fritzell, J.; Lundberg, O.; Diderichsen, F.; Burström, B. Exploring relative deprivation: Is social comparison a mechanism in the relation between income and health? Soc. Sci. Med. 2003, 57, 1463–1473. [Google Scholar] [CrossRef]
- Bengtsson, T.; Scott, K. Immigrant consumption of sickness benefits in Sweden, 1982–1991. J. Socio. Econ. 2006, 35, 440–457. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables (with discussion). J. R. Stat. Soc. 1972, 34, 187–220. [Google Scholar]
- Kalbfleisch, J.D.; Prentice, R.L. Marginal likelihoods based on Cox’s regression and life model. Biometrika 1973, 60, 267–278. [Google Scholar] [CrossRef]
- Prentice, R.L.; Gloeckler, L.A. Regression analysis of grouped survival data with application to breast cancer data. Biometrics 1978, 34, 57–67. [Google Scholar] [CrossRef]
- Allison, P.D. Discrete-time methods for the analysis of event histories. Sociol. Methodol. 1982, 13, 61–98. [Google Scholar] [CrossRef]
- Singer, J.D.; Willett, J.B. It’s about time: Using discrete-time survival analysis to study duration and the timing of events. J. Educ. Stat. 1993, 18, 155–195. [Google Scholar] [CrossRef]
- Jenkins, S.P. Easy estimation methods for discrete-time duration models. Oxford Bull. Econ. Stat. 1995, 57, 129–137. [Google Scholar] [CrossRef]
- Salant, S.W. Search theory and duration data: A theory of sorts. Q. J. Econ. 1977, 91, 39–57. [Google Scholar] [CrossRef]
- Vaupel, J.W.; Manton, K.G.; Stallard, E. The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography 1979, 16, 439–454. [Google Scholar] [CrossRef]
- Vaupel, J.W.; Yashin, A.I. Heterogeneity’s ruses: Some surprising effects of selection on population dynamics. Am. Stat. 1985, 39, 176–185. [Google Scholar]
- Nicoletti, C.; Rondinelli, C. The (mis)specification of discrete duration models with unobserved heterogeneity: A Monte Carlo study. J. Econ. 2010, 159, 1–13. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Helgertz, J.; Hess, W.; Scott, K. Relative Deprivation and Sickness Absence in Sweden. Int. J. Environ. Res. Public Health 2013, 10, 3930-3953. https://doi.org/10.3390/ijerph10093930
Helgertz J, Hess W, Scott K. Relative Deprivation and Sickness Absence in Sweden. International Journal of Environmental Research and Public Health. 2013; 10(9):3930-3953. https://doi.org/10.3390/ijerph10093930
Chicago/Turabian StyleHelgertz, Jonas, Wolfgang Hess, and Kirk Scott. 2013. "Relative Deprivation and Sickness Absence in Sweden" International Journal of Environmental Research and Public Health 10, no. 9: 3930-3953. https://doi.org/10.3390/ijerph10093930
APA StyleHelgertz, J., Hess, W., & Scott, K. (2013). Relative Deprivation and Sickness Absence in Sweden. International Journal of Environmental Research and Public Health, 10(9), 3930-3953. https://doi.org/10.3390/ijerph10093930




