Application of Computational Chemical Shift Prediction Techniques to the Cereoanhydride Structure Problem—Carboxylate Complications
Abstract
:1. Introduction
2. Results and Discussion
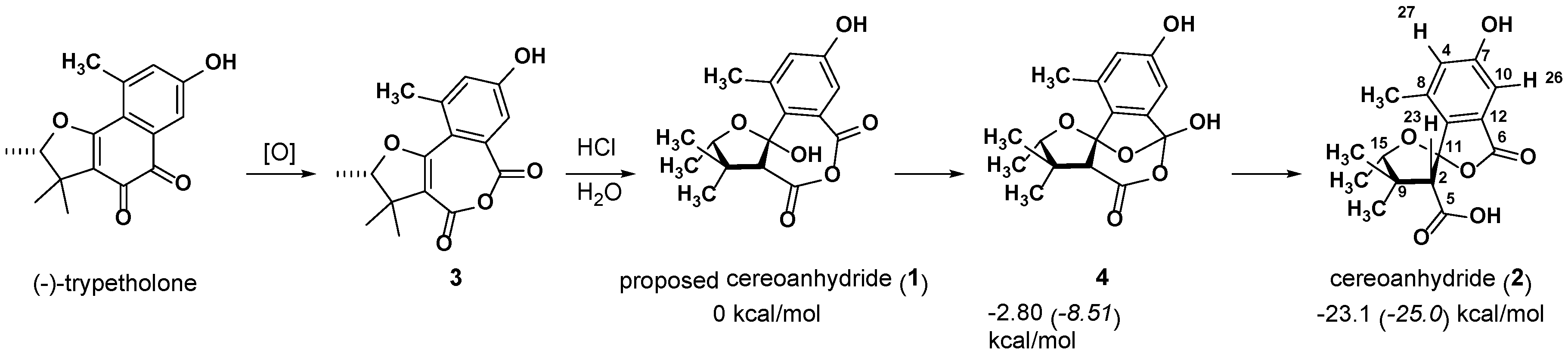
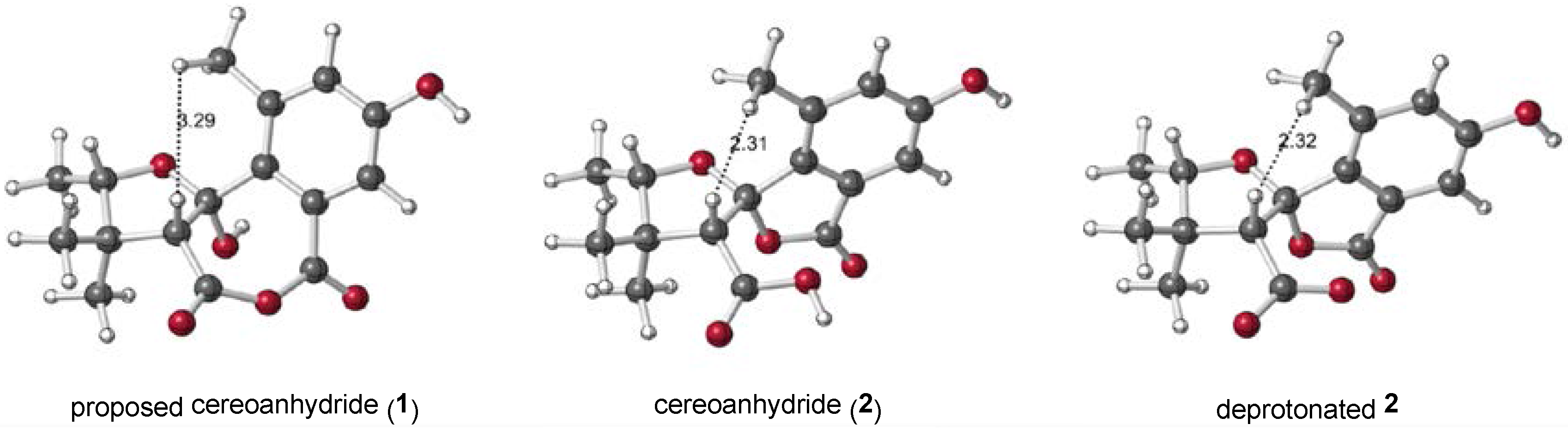
2.1. 1 as a Precursor to 2
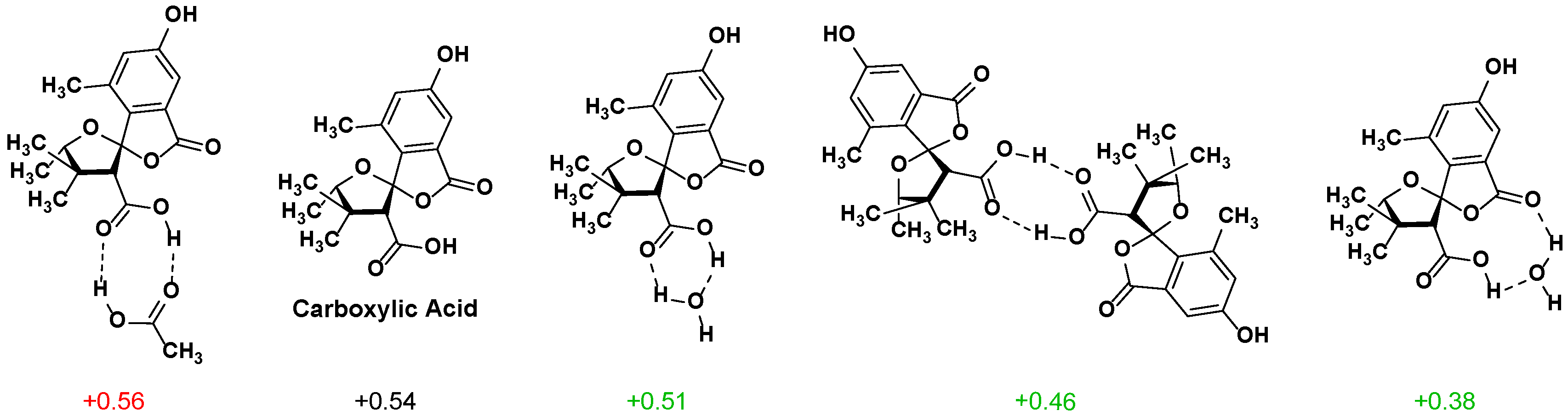
2.2. NMR Chemical Shifts of 1 vs. 2
3. Conclusions
4. Methods
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jin, L.; Quan, C.; Hou, X.; Fan, S. Potential Pharmacological Resources: Natural Bioactive Compounds from Marine-Derived Fungi. Mar. Drugs 2016, 14, 76. [Google Scholar] [CrossRef] [PubMed]
- Nazir, M.; El Maddah, F.; Kehraus, S.; Egereva, E.; Piel, J.; Brachmann, A.O.; König, G.M. Phenalenones: Insight into the biosynthesis of polyketides from the marine alga-derived fungus Coniothyrium cereale. Org. Biomol. Chem. 2015, 13, 8071–8079. [Google Scholar] [CrossRef] [PubMed]
- Rateb, M.E.; Ebel, R. Secondary metabolites of fungi from marine habitats. Nat. Prod. Rep. 2011, 28, 290–344. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, K.C.; Snyder, S.A. Chasing Molecules That Were Never There: Misassigned Natural Products and the Role of Chemical Synthesis in Modern Structure Elucidation. Angew. Chem. Int. Ed. 2005, 44, 1012–1044. [Google Scholar] [CrossRef] [PubMed]
- Yoo, H.D.; Nam, S.J.; Chin, Y.W.; Kim, M.S. Misassigned natural products and their revised structures. Arch. Pharm. Res. 2016, 39, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry. Chem. Rev. 2012, 112, 1839–1862. [Google Scholar] [CrossRef] [PubMed]
- Tantillo, D.J. Walking in the woods with quantum chemistry—Applications of quantum chemical calculations in natural products research. Nat. Prod. Rep. 2013, 30, 1079–1086. [Google Scholar] [CrossRef] [PubMed]
- Di Micco, S.; Chini, M.G.; Riccio, R.; Bifulco, G. Quantum Mechanical Calculation of NMR Parameters in the Stereostructural Determination of Natural Products. Eur. J. Org. Chem. 2010, 2010, 1411–1434. [Google Scholar] [CrossRef]
- Grimblat, N.; Sarotti, A.M. Computational Chemistry to the Rescue: Modern Toolboxes for the Assignment of Complex Molecules by GIAO NMR Calculations. Chem. Eur. J. 2016, 22, 12246–12261. [Google Scholar] [CrossRef] [PubMed]
- Willoughby, P.H.; Jansma, M.J.; Hoye, T.R. A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts. Nat. Protoc. 2014, 9, 643–660. [Google Scholar] [CrossRef] [PubMed]
- Lebold, T.P.; Wood, J.L.; Deitch, J.; Lodewyk, M.W.; Tantillo, D.J.; Sarpong, R. A divergent approach to the synthesis of the yohimbinoid alkaloids venenatine and alstovenine. Nat. Chem. 2013, 5, 126–131. [Google Scholar] [CrossRef] [PubMed]
- Forsyth, D.A.; Sebag, A.B. Computed 13C NMR Chemical Shifts via Empirically Scaled GIAO Shieldings and Molecular Mechanics Geometries. Conformation and Configuration from 13C Shifts. J. Am. Chem. Soc. 1997, 119, 9483–9494. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Seitz, T.; Fu, P.; Haut, F.L.; Adam, L.; Habicht, M.; Lentz, D.; MacMillan, J.B.; Christmann, M. One-Pot Synthesis of 5-Hydroxy-4H-1,3-thiazin-4-ones: Structure Revision, Synthesis, and NMR Shift Dependence of Thiasporine A. Org. Lett. 2016, 18, 3070–3073. [Google Scholar] [CrossRef] [PubMed]
- Elsebai, M.F.; Nazir, M.; Kehraus, S.; Egereva, E.; Ioset, K.N.; Marcourt, L.; Jeannerat, D.; Gütschow, M.; Wolfender, J.-L.; König, G.M. Polyketide Skeletons from the Marine Alga-Derived Fungus Coniothyrium cereale. Eur. J. Org. Chem. 2012, 2012, 6197–6203. [Google Scholar] [CrossRef]
- Powers, J.C.; Asgian, J.L.; Ekici, Ö.D.; James, K.E. Irreversible Inhibitors of Serine, Cysteine, and Threonine Proteases. Chem. Rev. 2002, 102, 4639–4750. [Google Scholar] [CrossRef] [PubMed]
- Skiles, J.W.; Jeng, A.Y. Therapeutic promises of leukocyte elastase and macrophage metalloelastase inhibitors for the treatment of pulmonary emphysema. Expert Opin. Ther. Pat. 1999, 9, 869–895. [Google Scholar] [CrossRef]
- Carreira, E.M.; Wolleb, H. Synthesis of (±)-Cereoanhydride. Synfacts 2016, 12, 1232. [Google Scholar]
- Ren, Z.; Hao, Y.; Hu, X. Total Synthesis and Structural Reassignment of (±)-Cereoanhydride. Org. Lett. 2016, 18, 4958–4961. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Liptrot, D.J.; Power, P.P. London dispersion forces in sterically crowded inorganic and organometallic molecules. Nat. Rev. Chem. 2017, 1, 0004. [Google Scholar] [CrossRef]
- Smith, S.G.; Goodman, J.M. Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability. J. Am. Chem. Soc. 2010, 132, 12946–12959. [Google Scholar] [CrossRef] [PubMed]
- Briggs, J.M.; Nguyen, T.B.; Jorgensen, W.L. Monte Carlo simulations of liquid acetic acid and methyl acetate with the OPLS potential functions. J. Phys. Chem. 1991, 95, 3315–3322. [Google Scholar] [CrossRef]
- Hagen, R.; Roberts, J.D. Nuclear magnetic resonance spectroscopy. Carbon-13 spectra of aliphatic carboxylic acids and carboxylate anions. J. Am. Chem. Soc. 1969, 91, 4504–4506. [Google Scholar] [CrossRef]
- Schah-Mohammedi, P.; Shenderovich, I.G.; Detering, C.; Limbach, H.-H.; Tolstoy, P.M.; Smirnov, S.N.; Denisov, G.S.; Golubev, N.S. Hydrogen/Deuterium-Isotope Effects on NMR Chemical Shifts and Symmetry of Homoconjugated Hydrogen-Bonded Ions in Polar Solution. J. Am. Chem. Soc. 2000, 122, 12878–12879. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision B. 01, Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D. 01, Gaussian, Inc.: Wallingford, CT, USA, 2010.
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Bagno, A.; Saielli, G. Addressing the stereochemistry of complex organic molecules by density functional theory-NMR. Wiley Interdiscip. Rev. 2015, 5, 228–240. [Google Scholar] [CrossRef]
- de Albuquerque, A.C.; Ribeiro, D.J.; de Amorim, M.B. Structural determination of complex natural products by quantum mechanical calculations of 13C NMR chemical shifts: Development of a parameterized protocol for terpenes. J. Mol. Model. 2016, 22, 1–7. [Google Scholar] [CrossRef] [PubMed]
- McWeeny, R. Perturbation Theory for the Fock-Dirac Density Matrix. Phys. Rev. 1962, 126, 1028–1034. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- London, F. Théorie quantique des courants interatomiques dans les combinaisons aromatiques. J. Phys. Radium. 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Jain, R.; Bally, T.; Rablen, P.R. Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets. J. Org. Chem. 2009, 74, 4017–4023. [Google Scholar] [CrossRef] [PubMed]
- CHESHIRE. CHEmical SHift REpository with Coupling Constants Added Too. Available online: http://cheshirenmr.info (accessed on 10 June 2017).
- SPARTAN, Version 10, Wavefunction, Inc.: Irvine, CA, USA, 2010.
- Tantillo, D.J. Biosynthesis via carbocations: Theoretical studies on terpene formation. Nat. Prod. Rep. 2011, 28, 1035–1053. [Google Scholar] [CrossRef] [PubMed]
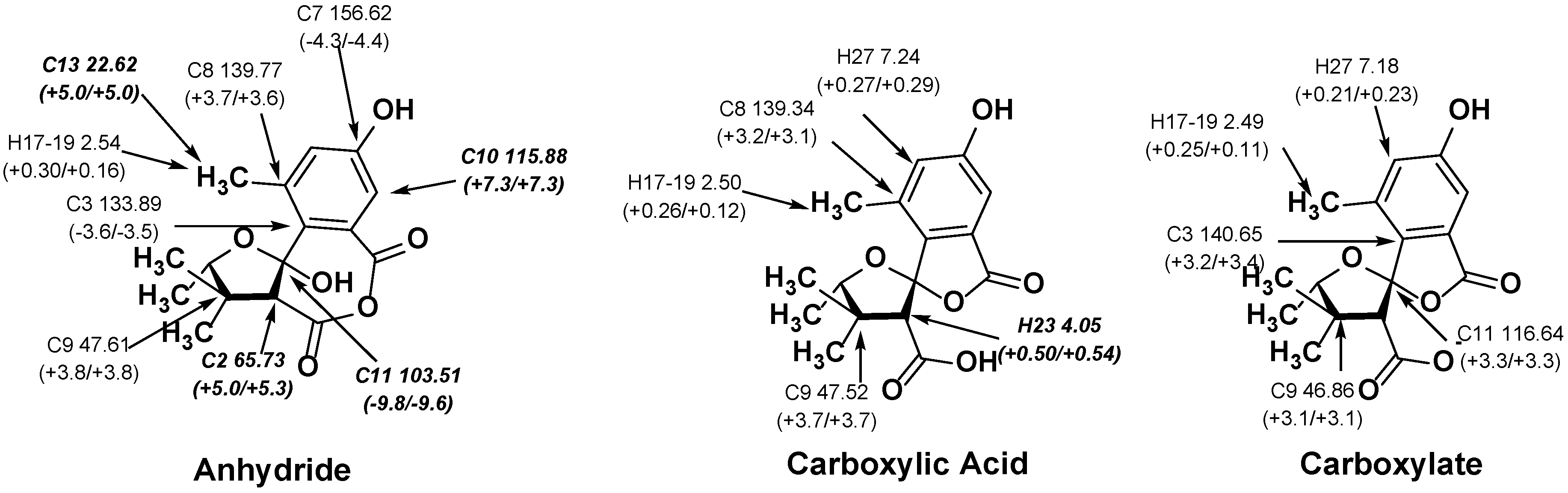

| Atom Label | Exp. δ | Anhydride (1) δ | Abs. Dev. | Acid (2) δ | Abs. Dev. | Carboxylate δ | Abs. Dev. |
|---|---|---|---|---|---|---|---|
| C6 | 170.7 | 168.7 | 2.0 | 171.4 | 0.7 | 172.2 | 1.5 |
| C5 | 170.4 | 168.9 | 1.5 | 172.5 | 2.1 | 172.4 | 2.0 |
| C7 | 161.0 | 156.6 | 4.4 | 159.1 | 1.9 | 158.4 | 2.6 |
| C3 | 137.4 | 133.9 | 3.5 | 138.2 | 0.8 | 140.7 | 3.3 |
| C8 | 136.2 | 139.8 | 3.6 | 139.4 | 3.2 | 138.2 | 2.0 |
| C12 | 131.0 | 132.7 | 1.7 | 129.8 | 1.2 | 131.2 | 0.2 |
| C4 | 124.7 | 123.5 | 1.2 | 124.6 | 0.1 | 123.3 | 1.4 |
| C11 | 113.1 | 103.5 | 9.6 | 112.0 | 1.1 | 116.6 | 3.5 |
| C10 | 108.6 | 115.9 | 7.3 | 108.1 | 0.5 | 107.6 | 1.0 |
| C15 | 87.4 | 85.6 | 1.8 | 86.6 | 0.8 | 85.9 | 1.5 |
| C2 | 60.4 | 65.7 | 5.3 | 59.0 | 1.4 | 61.6 | 1.2 |
| C9 | 43.8 | 47.6 | 3.8 | 47.6 | 3.8 | 46.9 | 3.1 |
| C16 | 26.1 | 24.8 | 1.3 | 24.4 | 1.7 | 26.0 | 0.1 |
| C13 | 17.6 | 22.6 | 5.0 | 17.9 | 0.3 | 17.8 | 0.2 |
| C1 | 17.2 | 16.0 | 1.2 | 16.1 | 1.1 | 16.7 | 0.5 |
| C14 | 14.9 | 14.6 | 0.3 | 14.0 | 0.9 | 15.1 | 0.2 |
| MAD 2 | 3.3 | 1.3 | 1.5 | ||||
| MAX 3 | 9.6 | 3.8 | 3.5 | ||||
| H27 | 6.95 | 7.11 | 0.16 | 7.24 | 0.29 | 7.18 | 0.23 |
| H26 | 6.93 | 7.10 | 0.17 | 7.11 | 0.19 | 7.05 | 0.12 |
| H29 | 4.21 | 4.17 | 0.04 | 4.38 | 0.17 | 4.23 | 0.02 |
| H23 | 3.51 | 3.58 | 0.07 | 4.05 | 0.54 | 3.66 | 0.15 |
| H17-19 | 2.28 | 2.54 | 0.16 | 2.64 | 0.26 | 2.49 | 0.11 |
| H28,31,33 | 1.36 | 1.31 | 0.05 | 1.38 | 0.02 | 1.47 | 0.11 |
| H25,30,32 | 1.28 | 1.31 | 0.03 | 1.31 | 0.03 | 1.29 | 0.01 |
| H20-22 | 1.28 | 1.37 | 0.09 | 1.40 | 0.12 | 1.42 | 0.14 |
| MAD 2 | 0.10 | 0.20 | 0.11 | ||||
| MAX 3 | 0.17 | 0.54 | 0.23 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saunders, C.M.; Tantillo, D.J. Application of Computational Chemical Shift Prediction Techniques to the Cereoanhydride Structure Problem—Carboxylate Complications. Mar. Drugs 2017, 15, 171. https://doi.org/10.3390/md15060171
Saunders CM, Tantillo DJ. Application of Computational Chemical Shift Prediction Techniques to the Cereoanhydride Structure Problem—Carboxylate Complications. Marine Drugs. 2017; 15(6):171. https://doi.org/10.3390/md15060171
Chicago/Turabian StyleSaunders, Carla M., and Dean J. Tantillo. 2017. "Application of Computational Chemical Shift Prediction Techniques to the Cereoanhydride Structure Problem—Carboxylate Complications" Marine Drugs 15, no. 6: 171. https://doi.org/10.3390/md15060171
APA StyleSaunders, C. M., & Tantillo, D. J. (2017). Application of Computational Chemical Shift Prediction Techniques to the Cereoanhydride Structure Problem—Carboxylate Complications. Marine Drugs, 15(6), 171. https://doi.org/10.3390/md15060171





