On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives
Abstract
:1. Introduction
2. Overview on Local Fractional Differential and Integral Calculus
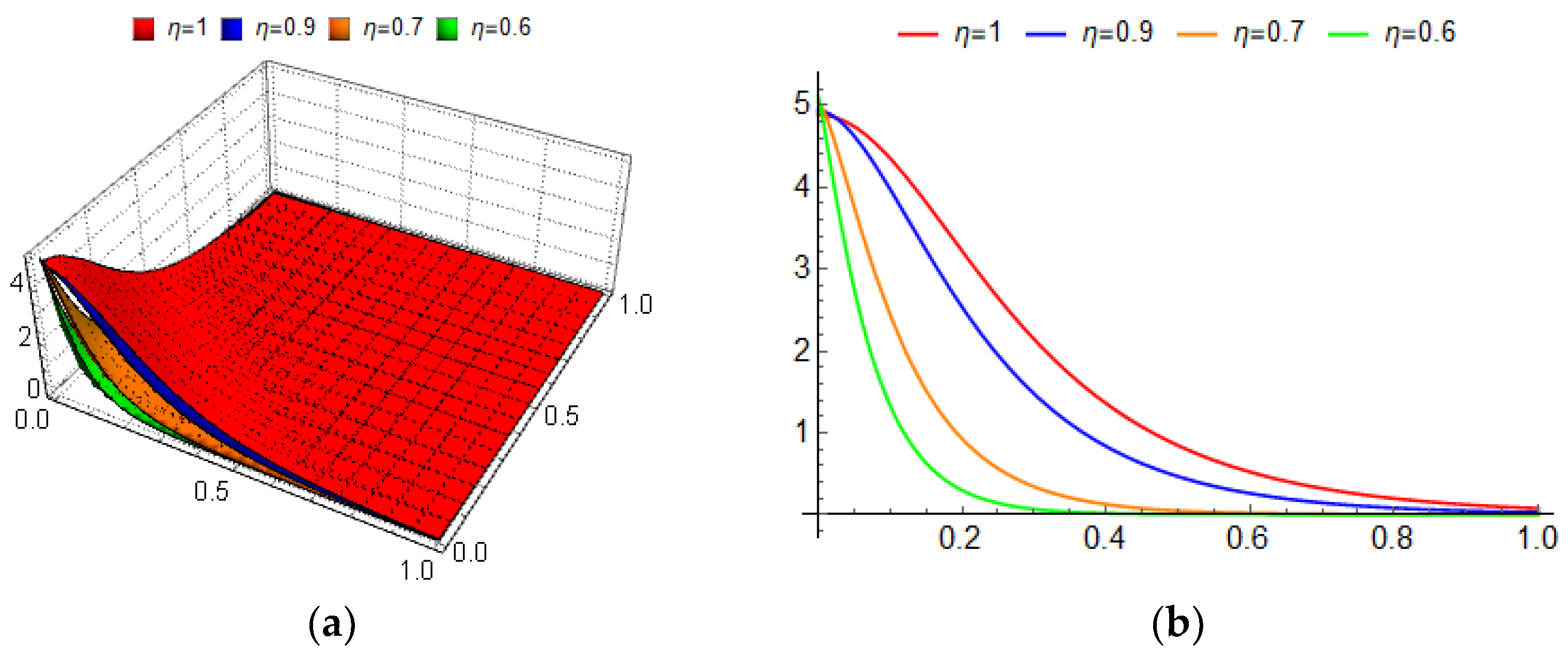
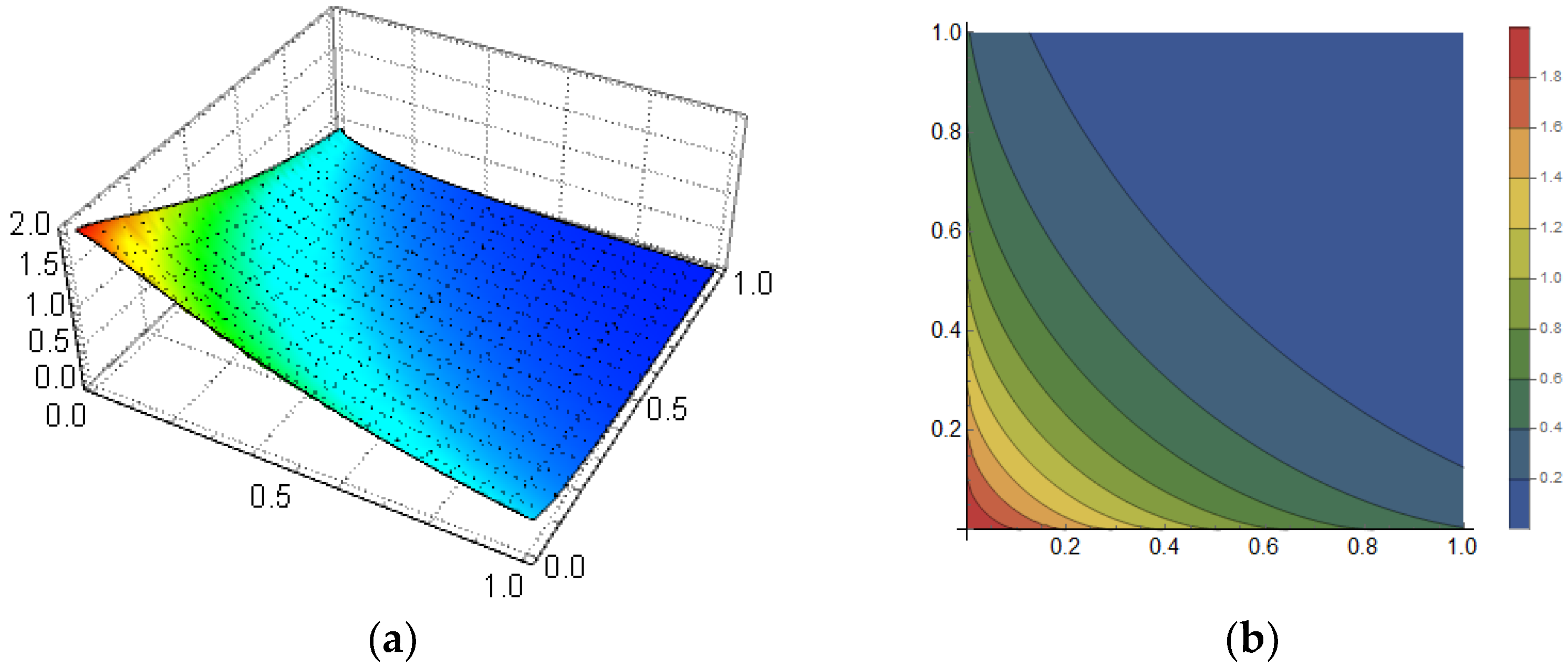
3. Nondifferentiable Solutions for LFKPE
3.1. Nondifferentiable Solution-Type I
3.2. Nondifferentiable Solution-Type II
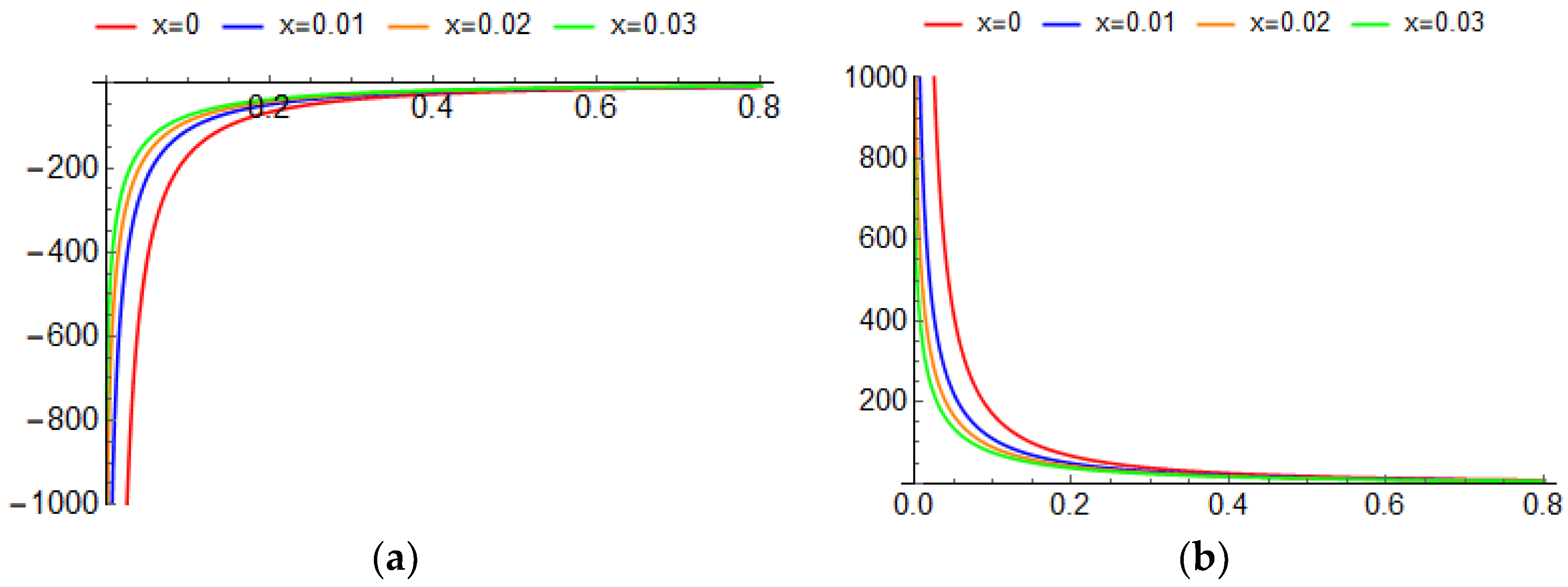
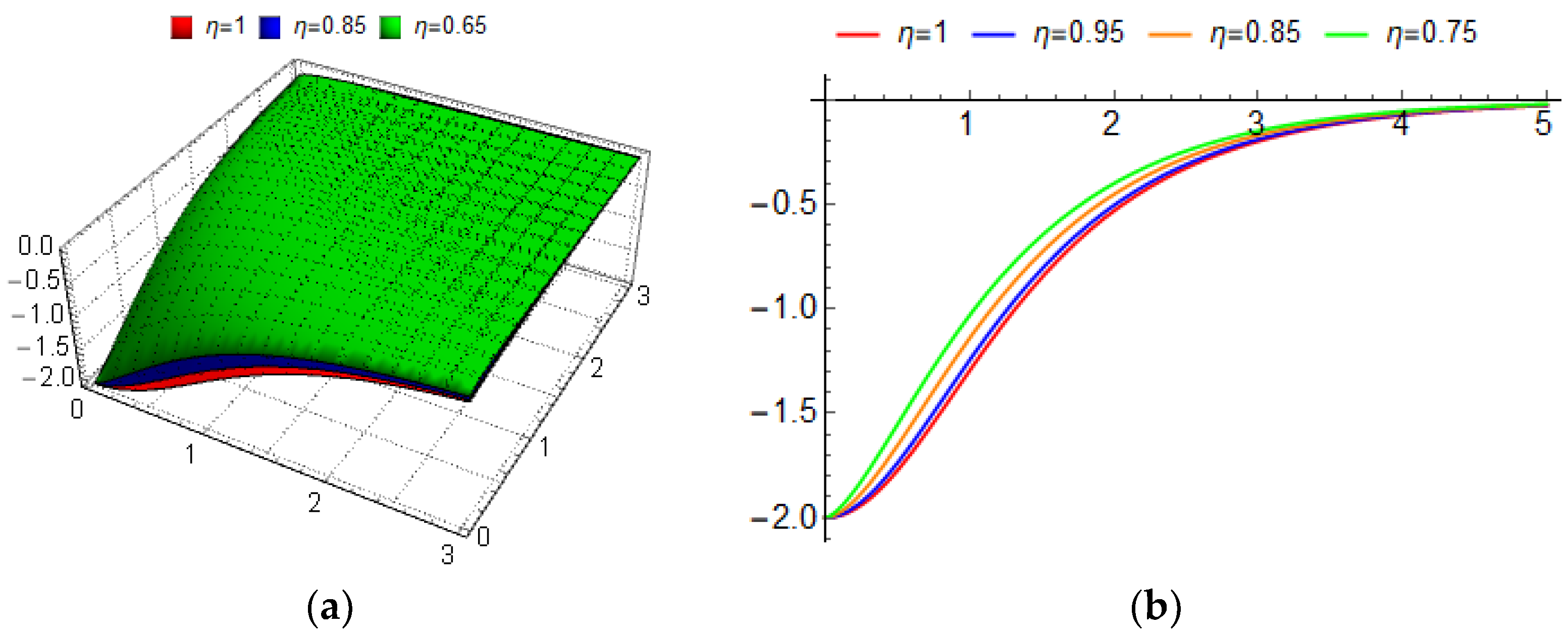
4. Nondifferentiable Solutions for LFKP-MEWE
4.1. Nondifferentiable Exact Solution-Type I
4.2. Nondifferentiable Exact Solution-Type II
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications, 1st ed.; Academic Press: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Al-Smadi, M.; Abu Arqub, O. Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Momani, S. Numerical computations of coupled fractional resonant Schrödinger equations arising in quantum mechanics under conformable fractional derivative sense. Phys. Scr. 2020, 95, 075218. [Google Scholar] [CrossRef]
- Hasan, S.; Al-Smadi, M.; Freihet, A.; Momani, S. Two computational approaches for solving a fractional obstacle system in Hilbert space. Adv. Differ. Equ. 2019, 2019, 55. [Google Scholar] [CrossRef] [Green Version]
- Freihet, A.; Hasan, S.; Al-Smadi, M.; Gaith, M.; Momani, S. Construction of fractional power series solutions to fractional stiff system using residual functions algorithm. Adv. Differ. Equ. 2019, 2019, 95. [Google Scholar] [CrossRef] [Green Version]
- Baillie, R.T. Long memory processes and fractional integration in econometrics. J. Econ. 1996, 73, 5–59. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Hadid, S. An attractive analytical technique for coupled system of fractional partial differential equations in shallow water waves with conformable derivative. Commun. Theor. Phys. 2020, 72, 085001. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Zeidan, D. Fuzzy fractional differential equations under the Mittag-Leffler kernel differential operator of the ABC approach: Theorems and applications. Chaos Solitons Fractals 2021, 146, 110891. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Dutta, H.; Hasan, S.; Momani, S. On numerical approximation of Atangana-Baleanu-Caputo fractional integro-differential equations under uncertainty in Hilbert Space. Math. Model. Nat. Phenom. 2021, 16, 41. [Google Scholar] [CrossRef]
- Günerhan, H.; Dutta, H.; Dokuyucu, M.A.; Adel, W. Analysis of a fractional HIV model with Caputo and constant proportional Caputo operators. Chaos Soliton Fractals 2020, 139, 110053. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Djeddi, N.; Momani, S.; Al-Omari, S.; Araci, S. An attractive numerical algorithm for solving nonlinear Caputo–Fabrizio fractional Abel differential equation in a Hilbert space. Adv. Differ. Equ. 2021, 2021, 271. [Google Scholar] [CrossRef]
- Altawallbeh, Z.; Al-Smadi, M.; Komashynska, I.; Ateiwi, A. Numerical Solutions of Fractional Systems of Two-Point BVPs by Using the Iterative Reproducing Kernel Algorithm. Ukr. Math. J. 2018, 70, 687–701. [Google Scholar] [CrossRef]
- Momani, S.; Freihat, A.; Al-Smadi, M. Analytical study of fractional-order multiple chaotic Fitzhugh-Nagumo neurons model using multistep generalized differential transform method. Abstr. Appl. Anal. 2014, 2014, 276279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Smadi, M.; Freihat, A.; Arqub, O.A.; Shawagfeh, N. A novel multistep generalized differential transform method for solving fractional-order Lü chaotic and hyperchaotic systems. J. Comput. Anal. Appl. 2015, 19, 713–724. [Google Scholar]
- Al-Smadi, M.; Arqub, O.A.; Hadid, S. Approximate solutions of nonlinear fractional Kundu-Eckhaus and coupled fractional massive Thirring equations emerging in quantum field theory using conformable residual power series method. Phys. Scr. 2020, 95, 105205. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Smadi, M.; Al-Omari, S.; Baleanu, D.; Momani, S. Structure of optical soliton solution for nonliear resonant space-time Schrödinger equation in conformable sense with full nonlinearity term. Phys. Scr. 2020, 95, 105215. [Google Scholar] [CrossRef]
- Osman, M.S.; Korkmaz, A.; Rezazadeh, H.; Mirzazadeh, M.; Eslami, M.; Zhou, Q. The unified method for conformable time fractional Schro¨ dinger equation with perturbation terms. Chin. J. Phys. 2018, 56, 2500–2506. [Google Scholar] [CrossRef]
- Islam, M.N.; Akbar, M.A. Closed form exact solutions to the higher dimensional fractional Schrodinger equation via the modified simple equation method. J. Appl. Math. Phys. 2018, 6, 90–102. [Google Scholar] [CrossRef] [Green Version]
- Al-Smadi, M.; Arqub, O.A.; Gaith, M. Numerical simulation of telegraph and Cattaneo fractional-type models using adaptive reproducing kernel framework. Math. Methods Appl. Sci. 2021, 44, 8472–8489. [Google Scholar] [CrossRef]
- Hasan, S.; Al-Smadi, M.; El-Ajou, A.; Momani, S.; Hadid, S.; Al-Zhour, Z. Numerical approach in the Hilbert space to solve a fuzzy Atangana-Baleanu fractional hybrid system. Chaos Solitons Fractals 2021, 143, 110506. [Google Scholar] [CrossRef]
- Momani, S.; Djeddi, N.; Al-Smadi, M.; Al-Omari, S. Numerical investigation for Caputo-Fabrizio fractional Riccati and Bernoulli equations using iterative reproducing kernel method. Appl. Numer. Math. 2021, 170, 418–434. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D.; Cattani, C. On exact traveling-wave solutions for local fractional Korteweg-de Vries equation. Chaos 2016, 26, 084312. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.J.; Machado, J.T.; Cattani, C.; Gao, F. On a fractal LC-electric circuit modeled by local fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 200–206. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.; Nieto, J.J. A new family of the local fractional PDEs. Fundam. Inform. 2017, 151, 63–75. [Google Scholar] [CrossRef]
- Babakhani, A.; Daftardar-Gejji, V. On calculus of local fractional derivatives. J. Math. Anal. Appl. 2002, 270, 66–79. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, J.; Mohyud-Din, S.T. Solving wave and diffusion equations on Cantor sets. Proc. Pak. Acad. Sci. 2015, 52, 81–87. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A hybrid computational approach for Klein–Gordon equations on Cantor sets. Nonlinear Dyn. 2017, 87, 511–517. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. A reliable algorithm for a local fractional Tricomi equation arising in fractal transonic flow. Entropy 2016, 18, 206. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Machado, J.T.; Srivastava, H.M. A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput. 2016, 274, 143–151. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]
- Seadawy, A.R.; El-Rashidy, K. Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 2018, 8, 1216–1222. [Google Scholar] [CrossRef]
- De Bouard, A.; Saut, J.C. Solitary waves of generalized Kadomtsev-Petviashvili equations. In Annales de l’Institut Henri Poincaré C, Analyse Non Linéaire; Elsevier Masson: Paris, France, 1997; Volume 14, pp. 211–236. [Google Scholar]
- Groves, M.D.; Sun, S.M. Fully localised solitary-wave solutions of the three-dimensional gravity–capillary water-wave problem. Arch. Ration. Mech. Anal. 2008, 188, 1–91. [Google Scholar] [CrossRef] [Green Version]
- Rao, J.; He, J.; Mihalache, D.; Cheng, Y. Dynamics and interaction scenarios of localized wave structures in the Kadomtsev–Petviashvili-based system. Appl. Math. Lett. 2019, 94, 166–173. [Google Scholar] [CrossRef]
- Hao, X.; Liu, Y.; Li, Z.; Ma, W.X. Painlevé analysis, soliton solutions and lump-type solutions of the (3 + 1)-dimensional generalized KP equation. Comput. Math. Appl. 2019, 77, 724–730. [Google Scholar] [CrossRef]
- Verma, P.; Kaur, L. Integrability, bilinearization and analytic study of new form of (3 + 1)-dimensional B-type Kadomstev–Petviashvili (BKP)-Boussinesq equation. Appl. Math. Comput. 2019, 346, 879–886. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, H.; Zhou, Q.; Biswas, A.; Alzahrani, A.K.; Liu, W. The mixed interaction of localized, breather, exploding and solitary wave for the (3 + 1)-dimensional Kadomtsev–Petviashvili equation in fluid dynamics. Nonlinear Dyn. 2020, 100, 1611–1619. [Google Scholar] [CrossRef]
- Saha, A. Bifurcation of travelling wave solutions for the generalized KP-MEW equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3539–3551. [Google Scholar] [CrossRef]
- Gao, F.; Yang, X.J.; Ju, Y. Exact Traveling-Wave Solutions for One-Dimensional Modified Korteweg-De Vries Equation Defined on Cantor Sets. Fractal 2019, 27, 1940010. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelhadi, M.; Alhazmi, S.E.; Al-Omari, S. On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives. Fractal Fract. 2022, 6, 210. https://doi.org/10.3390/fractalfract6040210
Abdelhadi M, Alhazmi SE, Al-Omari S. On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives. Fractal and Fractional. 2022; 6(4):210. https://doi.org/10.3390/fractalfract6040210
Chicago/Turabian StyleAbdelhadi, Mohammad, Sharifah E. Alhazmi, and Shrideh Al-Omari. 2022. "On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives" Fractal and Fractional 6, no. 4: 210. https://doi.org/10.3390/fractalfract6040210
APA StyleAbdelhadi, M., Alhazmi, S. E., & Al-Omari, S. (2022). On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives. Fractal and Fractional, 6(4), 210. https://doi.org/10.3390/fractalfract6040210




