A Stochastic Optimization Model for Sustainable Multimodal Transportation for Bioenergy Production
Abstract
:1. Introduction
2. Materials and Methods
2.1. Step 1: Define a Deterministic Formulation of Sustainable Transportation Model
2.2. Step 2: Modification to Stochastic Problem with Vectorization
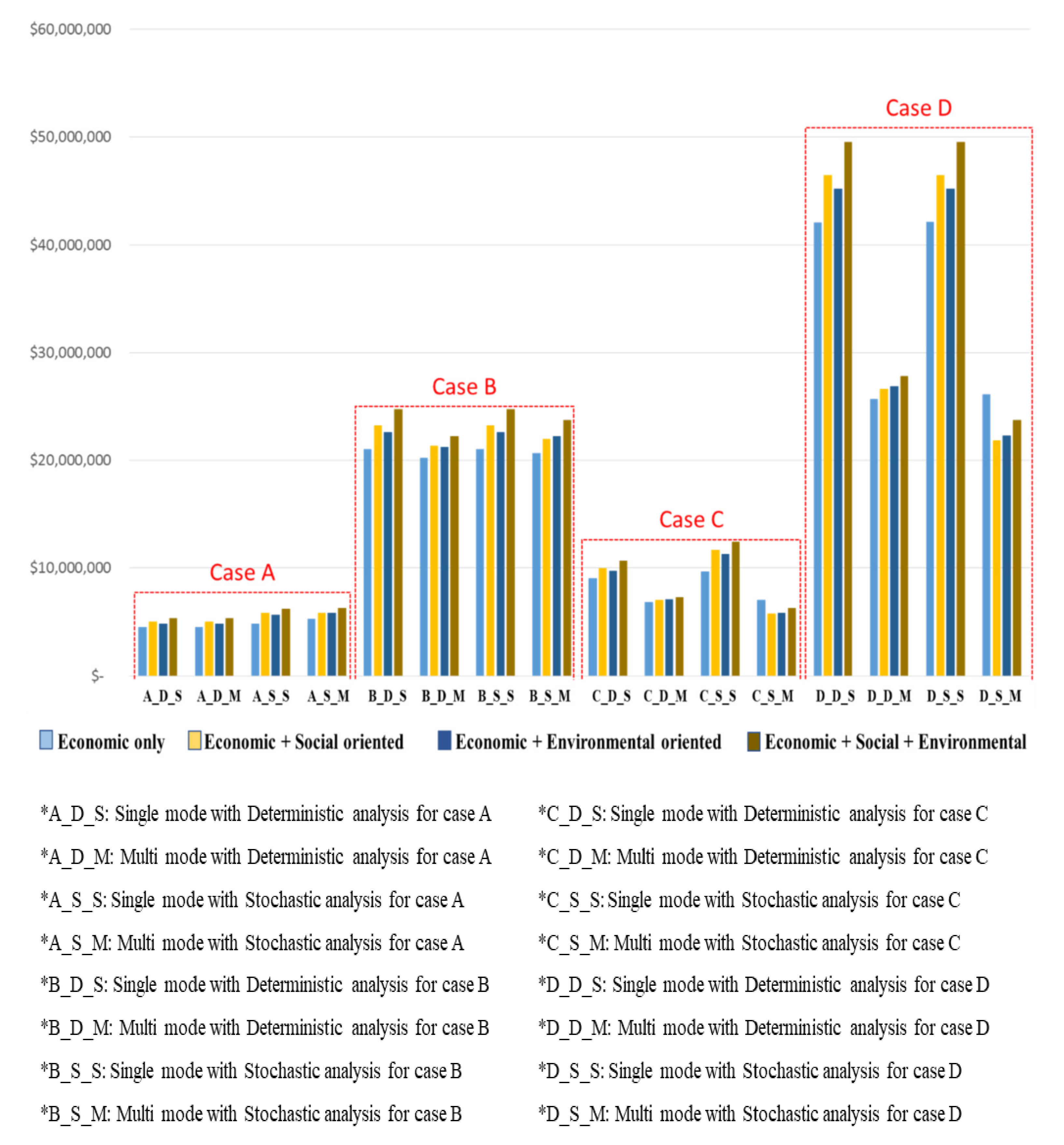
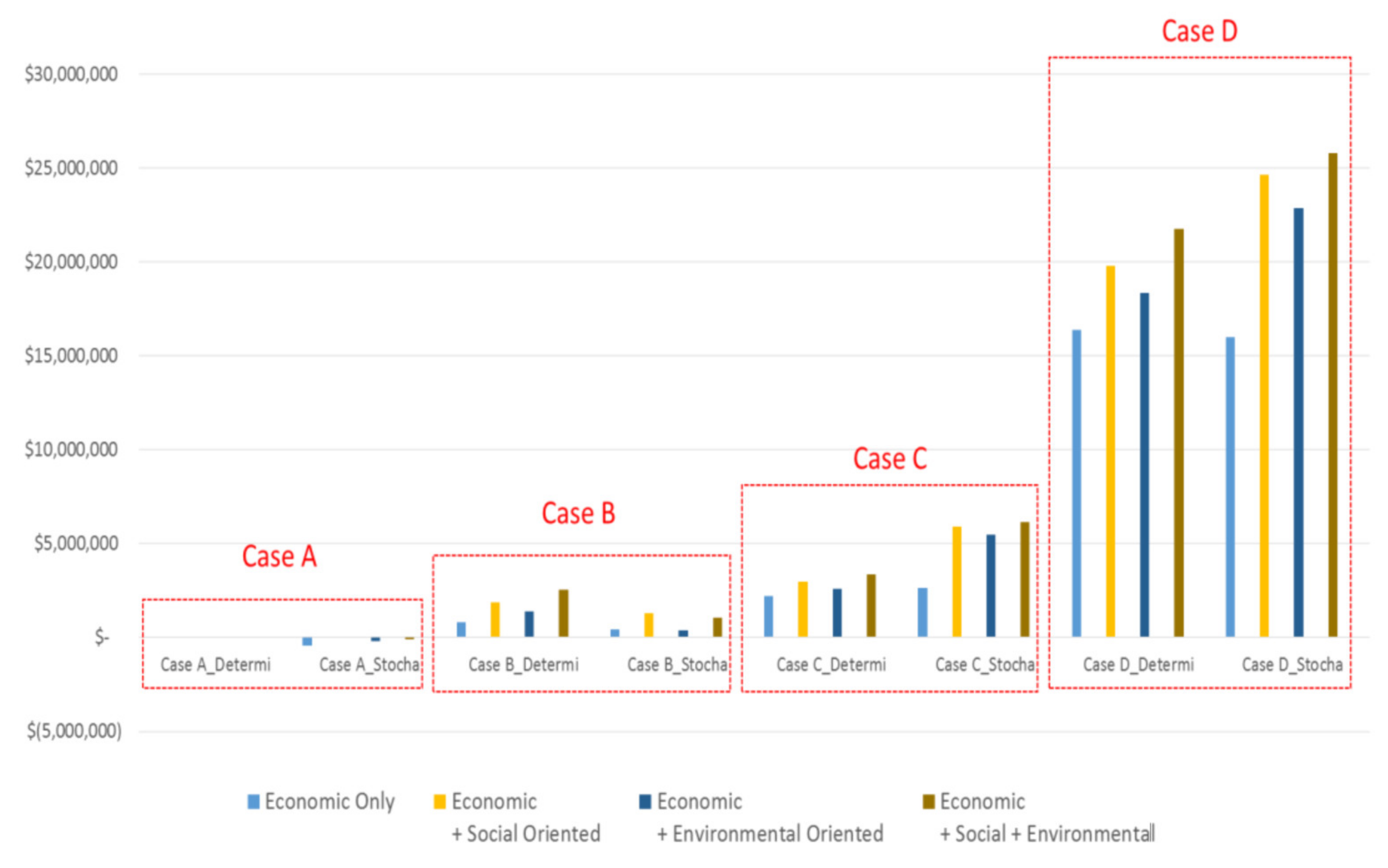
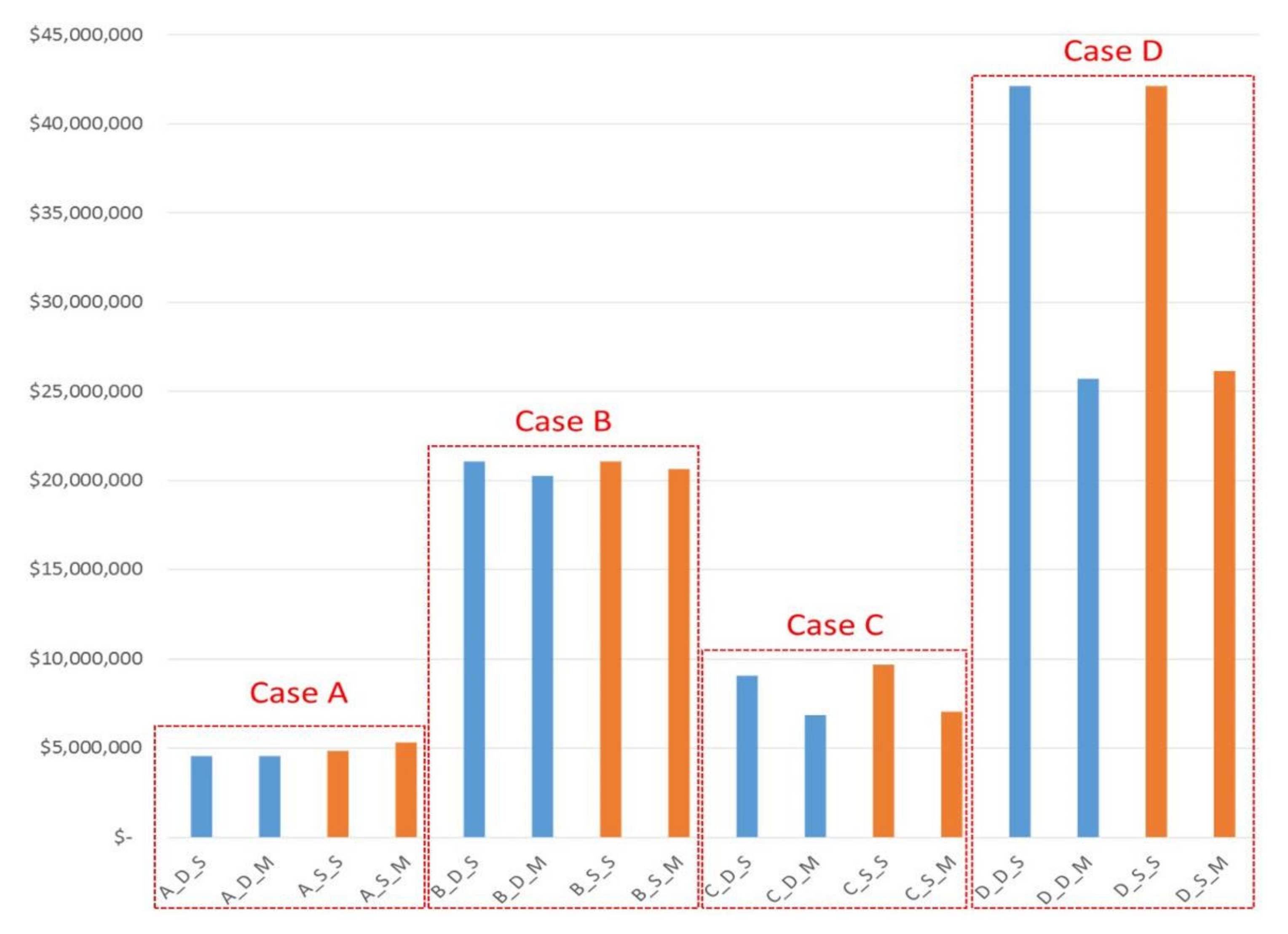
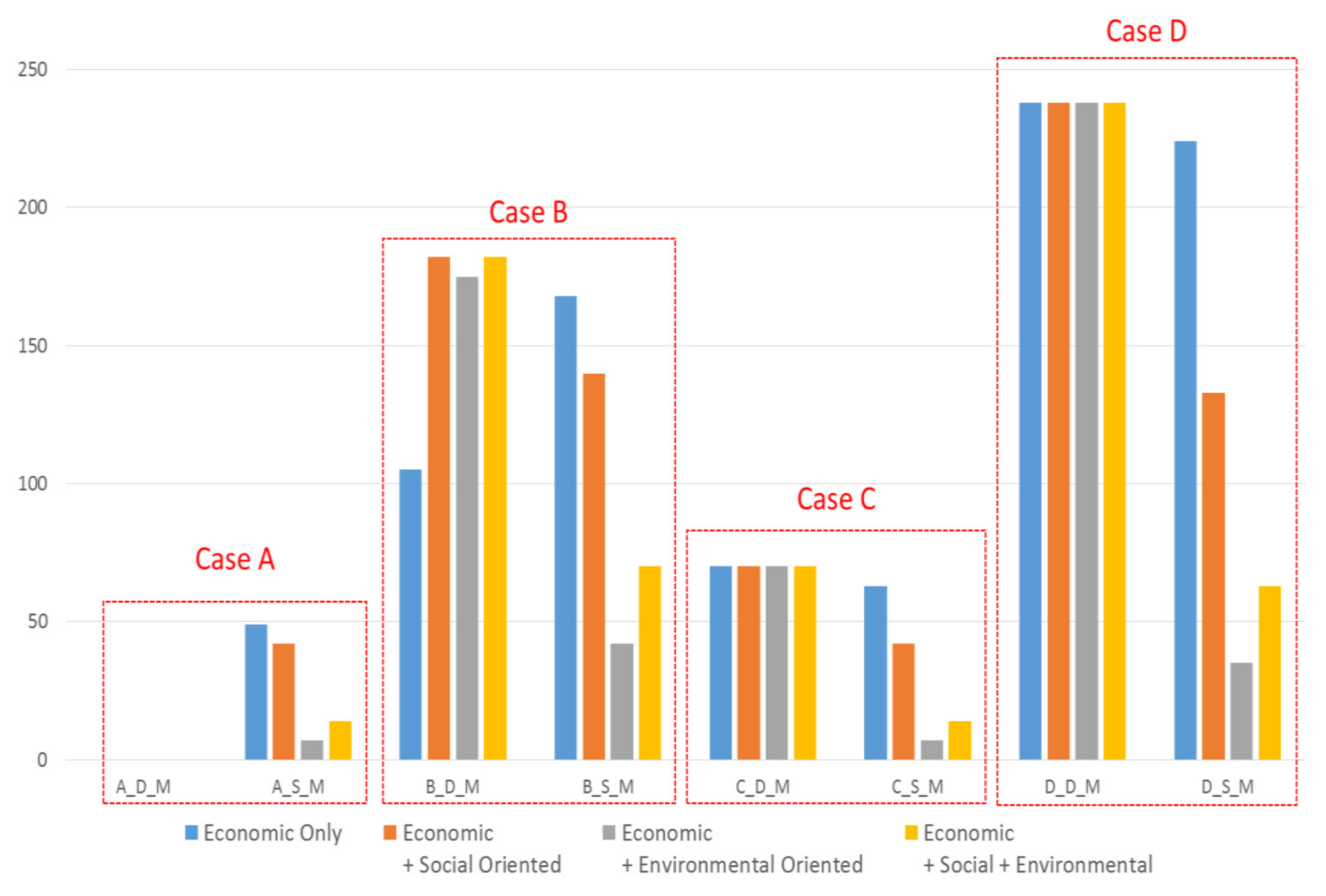
2.3. Numerical Example: 4 Cases
- Case A: Low annual capacity and Short procurement distance for feedstock;
- Case B: High annual capacity and Short procurement distance for feedstock;
- Case C: Low annual capacity and Long procurement distance for feedstock;
- Case D: High annual capacity and Long procurement distance for feedstock.
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
References
- Cundiff, J.S.; Dias, N.; Sherali, H.D. A linear programming approach for designing a herbaceous biomass delivery system. Bioresour. Technol. 1997, 59, 47–55. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Li, X.; Yao, Q.; Chen, Y. Challenges and models in supporting logistics system design for dedicated-biomass-based bioenergy industry. Bioresour. Technol. 2011, 102, 1344–1351. [Google Scholar] [CrossRef] [PubMed]
- Devlin, G.; Talbot, B. Deriving cooperative biomass resource transport supply strategies in meeting co-firing energy regulations: A case for peat and wood fibre in Ireland. Appl. Energy 2014, 113, 1700–1709. [Google Scholar] [CrossRef] [Green Version]
- Sosa, A.; Acuna, M.; McDonnell, K.; Devlin, G. Managing the moisture content of wood biomass for the optimisation of Ireland’s transport supply strategy to bioenergy markets and competing industries. Energy 2015, 86, 354–368. [Google Scholar] [CrossRef]
- Osmani, A.; Zhang, J. Optimal grid design and logistic planning for wind and biomass based renewable electricity supply chains under uncertainties. Energy 2014, 70, 514–528. [Google Scholar] [CrossRef]
- Cucek, L.; Martin, M.; Grossmann, I.E.; Kravanja, Z. Multi-period synthesis of optimally integrated biomass and bioenergy supply network. Comput. Chem. Eng. 2014, 66, 57–70. [Google Scholar] [CrossRef]
- Poudel, S.R.; Marufuzzaman, M.; Bian, L. A hybrid decomposition algorithm for designing a multi-modal transportation network under biomass supply uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 1–25. [Google Scholar] [CrossRef]
- Dal Mas, M.; Giarola, S.; Zamboni, A.; Bezzo, F. Capacity planning and financial optimization of the bioethanol supply chain under price uncertainty. Comput. Aided Chem. Eng. 2010, 28, 97–102. [Google Scholar]
- You, F.; Grossmann, I.E. Design of responsive supply chains under demand uncertainty. Comput. Chem. Eng. 2008, 32, 3090–3111. [Google Scholar] [CrossRef]
- Kim, J.; Realff, M.J.; Lee, J.H.; Whittaker, C.; Furtner, L. Design of biomass processing network for biofuel production using an MILP model. Biomass Bioenergy 2011, 35, 853–871. [Google Scholar] [CrossRef]
- Ravula, P.P.; Grisso, R.D.; Cundiff, J.S. Comparison between two policy strategies for scheduling trucks in a biomass logistic system. Bioresour. Technol. 2008, 99, 5710–5721. [Google Scholar] [CrossRef] [PubMed]
- Simwanda, M.; Wing, M.G.; Sessions, J. Evaluating global positioning system accuracy for forest biomass transportation tracking within varying forest canopy. West. J. Appl. For. 2011, 26, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Han, S.K.; Murphy, G.E. Solving a woody biomass truck scheduling problem for a transport company in Western Oregon, USA. Biomass Bioenergy 2012, 44, 47–55. [Google Scholar] [CrossRef]
- Jones, G.; Loeffler, D.; Butler, E.; Hummel, S.; Chung, W. The financial feasibility of delivering forest treatment residues to bioenergy facilities over a range of diesel fuel and delivered biomass prices. Biomass Bioenergy 2013, 48, 171–180. [Google Scholar] [CrossRef]
- Abbas, D.; Arnosti, D. Economics and Logistics of Biomass Utilization in the Superior National Forest. J. Sustain. For. 2013, 32, 41–57. [Google Scholar] [CrossRef]
- Ko, S.; Lautala, P.; Fan, J.; Shonnard, D.R. Economic, social, and environmental cost optimization of biomass transportation: A regional model for transportation analysis in plant location process. Biofuel Bioprod. Biorefin. 2019, 13, 582–598. [Google Scholar] [CrossRef]
- Kumar, A.; Sokhansanj, S.; Flynn, P.C. Development of a multicriteria assessment model for ranking biomass feedstock collection and transportation systems. Appl. Biochem. Biotechnol. 2006, 129, 71–87. [Google Scholar] [CrossRef]
- Tita, B. Railcar Shortage in US Pushes Up Lease Rates. The Wall Street Journal. 2014. Available online: https://www.wsj.com/articles/railcar-shortage-in-u-s-pushes-up-lease-rates-1401393331 (accessed on 1 September 2020).
- GAO. Transportation Surface Freight: A comparison of the Costs of Road, Rail, and Waterways Freight Shipments That Are Not Passed on to Consumers. 2011, GAO-11-134. Available online: https://www.gao.gov/assets/gao-11-134.pdf (accessed on 15 November 2020).
- Kampempe, J.D.B.; Luhandjula, M.K. Chance-constrained approaches for multiobjective stochastic linear programming problems. Am. J. Oper. Res. 2012, 2, 519–526. [Google Scholar] [CrossRef] [Green Version]
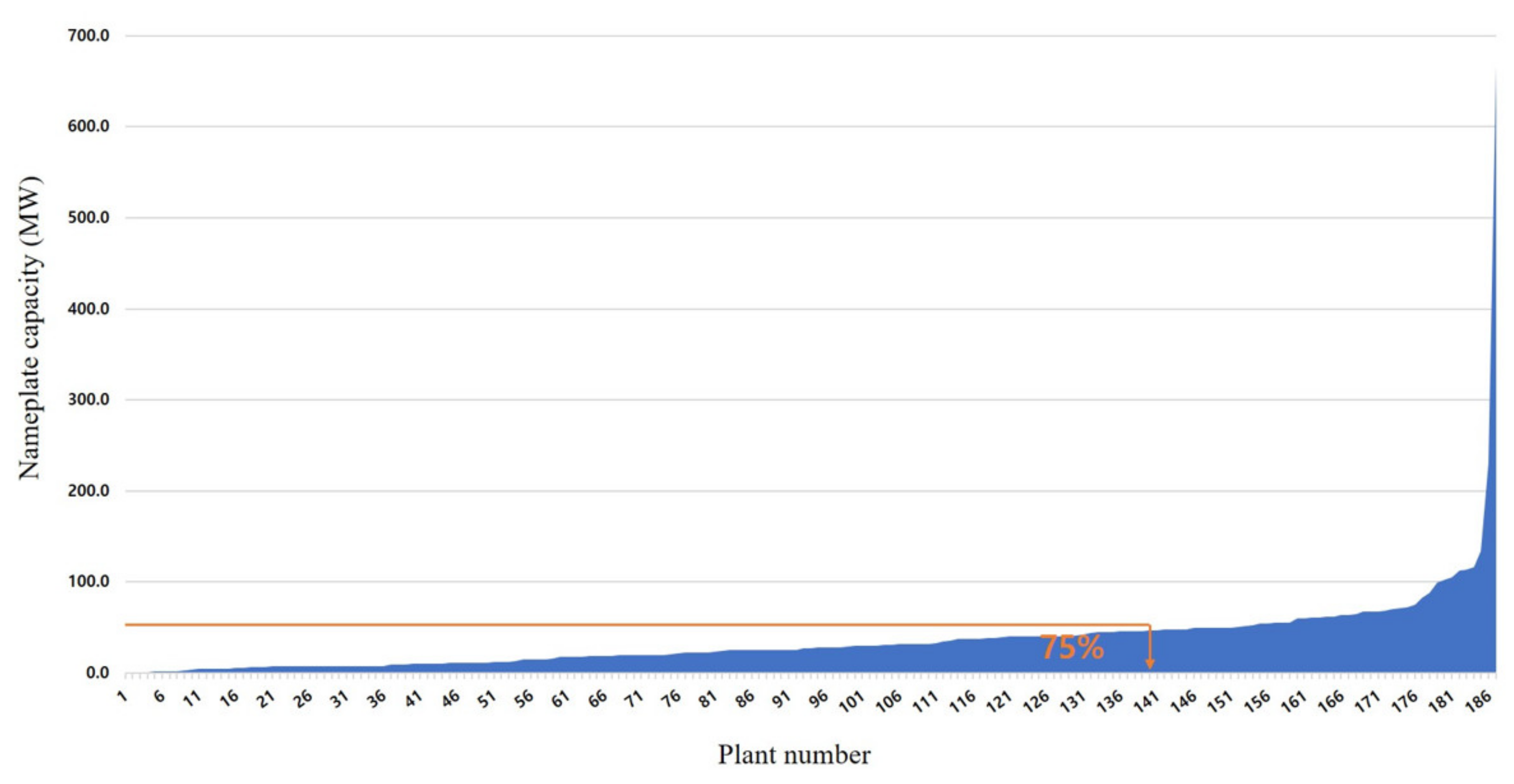
- US EIA. Form EIA-860 Detailed Data with Previous form Data: Year 2020. 2021, Washington, DC. Available online: https://www.eia.gov/electricity/data/eia860/ (accessed on 1 September 2021).
- Hamelinck, C.N.; Suurs, R.A.A.; Faaij, A.P.C. International bioenergy transport costs and energy balance. Biomass Bioenergy 2005, 29, 114–134. [Google Scholar] [CrossRef]
- Ruiz, J.A.; Juarez, M.C.; Morales, M.P.; Munoz, P.; Mendivil, M.A. Biomass logistics: Financial & environmental costs. Case study: 2 MW electrical power plants. Biomass Bioenergy 2013, 56, 260–267. [Google Scholar]
- Mahmudi, H.; Flynn, P.C. Rail vs truck transport of biomass. Appl. Biochem. Biotechnol. 2006, 129, 88–103. [Google Scholar] [CrossRef]
- Gonzales, D.; Searcy, E.M.; Eksioglu, S.D. Cost analysis for high-volume and long-haul transportation of densified biomass feedstock. Transp. Res. 2013, 49, 48–61. [Google Scholar] [CrossRef]
- Searcy, E.; Flynn, P.; Ghafoori, E.; Kumar, A. The relative cost of biomass energy transport. Appl. Biochem. Biotechnol. 2007, 137, 639–652. [Google Scholar] [PubMed]
| I = total number of collecting points (supply areas), |
| = number of trucks shipped between supply area “i” to the conversion plant, |
| = number of trucks shipped short distances between supply area “i” to the rail siding, |
| = number of unit train from rail siding to the conversion plant, |
| = economic transportation costs by mode X, Y at “i”, and Z, respectively, |
| = social transportation costs by mode X, Y at “i”, and Z, respectively, |
| = environmental transportation costs by mode X, Y at “i”, and Z, respectively, |
| = tonnage shipped by mode X, Y, and Z at one time, respectively, |
| P = number of demand points (Conversion Plants), |
| = required demand orders that are transported to conversion plant p, |
| K = dummy variable which value is 0 if the value of Z is 0, 1 otherwise. |
| = daily quantitative limitation in a supply area “i”, |
| = distance between supply area “i” and the conversion plant (long distance), |
| = distance between supply area “i” and the rail siding (short distance), |
| = distance between rail siding and the conversion plant (railroad), |
| = unit costs of economic transport by mode X, Y at “i”, and Z, respectively, |
| = unit costs of unloading work in a rail siding from truck to storage facility, |
| = unit costs of loading work in a rail siding from storage facility to rail cars, |
| = unit costs of leasing a railcar for annual contract, |
| = unit costs of traffic congestions by mode X, Y at “i”, and Z, respectively, |
| = unit costs of accident risks by mode X, Y at “i”, and Z, respectively, |
| = unit costs of CO2 emissions by mode X, Y at “i”, and Z, respectively, |
| = unit costs of PM emissions by mode X, Y at “i”, and Z, respectively, |
| = unit costs of NOx emissions by mode X, Y at “i”, and Z, respectively, |
| = weight factors for economic, social and environmental transportation |
| Feedstock | Truck | Rail | Ship | Region | Reference |
|---|---|---|---|---|---|
| Forest | ~100 km< | <100 km~ | Natherland | [22] | |
| Forest | ~50 km< | <50~200 km< | <200~1200 km< | Spain | [23] |
| Woodchip | ~145 km< | <145 km~ | Canada (Unit Train) | [24] | |
| Woodchip | ~386 km< | <386 km~ | US (Unit Train) | [25] | |
| Woodchip | ~500 km< | <500 km~ | <800 km~ | Canada (Unit Train) | [26] |
| straw | ~170 km< | <170 km~ | Canada (Unit Train) | [24] | |
| straw | ~500 km< | <500 km~ | <1500 km~ | Canada (Unit Train) | [26] |
| corn stover | ~500 km< | <500 km~ | <1500 km~ | US (Unit Train) | [26] |
| corn stover | ~170 km< | <170 km~ | Canada (Unit Train) | [24] | |
| Grain | ~161 km< | <161 km~ | US (Unit Train) | [25] | |
| Grain | ~338 km< | <338 km~ | US (Unit Train) | [25] |
| Annual Capacity | 350,000 Tons | 1,200,000 Tons |
|---|---|---|
| Avg. Distance | ||
| 75 miles | Case: A | Case: B |
| 150 miles | Case: C | Case: D |
| Input Category | Values of Each Case | ||||
|---|---|---|---|---|---|
| Case A | Case B | Case C | Case D | ||
| Conditions | Possible Mode types | Truck | Truck, | Truck, | Truck, |
| Rail | Rail | Rail | Rail | ||
| Number of collecting areas | 3 | 3 | 3 | 3 | |
| Annual capacity of each collecting areas (Tons) | N~(300,000, 10,000) | N~(300,000, 10,000) | N~(300,000, 10,000) | N~(300,000, 10,000) | |
| N~(400,000, 50,000) | N~(400,000, 50,000) | N~(400,000, 50,000) | N~(400,000, 50,000) | ||
| N~(500,000, 200,000) | N~(500,000, 200,000) | N~(500,000, 200,000) | N~(500,000, 200,000) | ||
| Number of | 1 | 1 | 1 | 1 | |
| conversion plants | |||||
| Distance (Mile) from collecting area and plant | Avg. 75 | Avg. 75 | Avg. 150 | Avg. 150 | |
| Distance (Mile) from collecting area rail siding | Avg. 20 | Avg. 20 | Avg. 40 | Avg. 40 | |
| Distance (Mile) from rail siding and plant | Avg. 60 | Avg. 60 | Avg. 120 | Avg. 120 | |
| Economic cost | Demand quantities | N~(350,000, 1000) | N~(1,200,000, 5000) | N~(350,000, 1000) | N~(1,200,000, 5000) |
| (Tons) | |||||
| Supply quantities | N~(350,000, 1000) | N~(1,200,000, 5000) | N~(350,000, 1000) | N~(1,200,000, 5000) | |
| (Tons) | |||||
| Unit costs per tonnage for hauling | Truck: N~(0.14, 0.01) | Truck: N~(0.14, 0.01) | Truck: N~(0.14, 0.01) | Truck: N~(0.14, 0.01) | |
| factors | (US $/Dry ton/km, [17]) | Rail: | Rail: | Rail: | Rail: |
| N~(0.03, 0.001) | N~(0.03, 0.001) | N~(0.03, 0.001) | N~(0.03, 0.001) | ||
| Unit costs of loading/unloading for rail | N~(4.8, 0.4) | N~(4.8, 0.4) | N~(4.8, 0.4) | N~(4.8, 0.4) | |
| (US $/Dry ton, [16]) | |||||
| unit costs of | N~(400, 100) | N~(400, 100) | N~(400, 100) | N~(400, 100) | |
| leasing a railcar | |||||
| (US $/month, [18]) | |||||
| Social cost | Traffic Congestion | Truck: N~(0.66, 0.2) | Truck: N~(0.66, 0.2) | Truck: N~(0.66, 0.2) | Truck: N~(0.66, 0.2) |
| Rail: | Rail: | Rail: | Rail: | ||
| (US cent/ton-mile, [19]) | N~(0.015, 0.1) | N~(0.015, 0.1) | N~(0.015, 0.1) | N~(0.015, 0.1) | |
| factors | Accident Risk | Truck: N~(1.66, 2) | Truck: N~(1.66, 2) | Truck: N~(1.66, 2) | Truck: N~(1.66, 2) |
| Rail: | Rail: | Rail: | Rail: | ||
| (US cent/ton-mile, [19]) | N~(0.018, 0.5) | N~(0.018, 0.5) | N~(0.018, 0.5) | N~(0.018, 0.5) | |
| Environmental cost | Costs of Emissions | Truck: N~(0.71, 0.5) | Truck: N~(0.71, 0.5) | Truck: N~(0.71, 0.5) | Truck: N~(0.71, 0.5) |
| : PM and NOx | Rail: | Rail: | Rail: | Rail: | |
| (US cent/ton-mile, [16]) | N~(0.19, 2) | N~(0.19, 2) | N~(0.19, 2) | N~(0.19, 2) | |
| factors | Costs of Emissions | Truck: N~(0.22, 0.5) | Truck: N~(0.22, 0.5) | Truck: N~(0.22, 0.5) | Truck: N~(0.22, 0.5) |
| : CO2 | Rail: | Rail: | Rail: | Rail: | |
| (US cent/ton-mile, [16]) | N~(0.05, 1) | N~(0.05, 1) | N~(0.05, 1) | N~(0.05, 1) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, S.; Choi, K.; Yu, S.; Lee, J. A Stochastic Optimization Model for Sustainable Multimodal Transportation for Bioenergy Production. Sustainability 2022, 14, 1889. https://doi.org/10.3390/su14031889
Ko S, Choi K, Yu S, Lee J. A Stochastic Optimization Model for Sustainable Multimodal Transportation for Bioenergy Production. Sustainability. 2022; 14(3):1889. https://doi.org/10.3390/su14031889
Chicago/Turabian StyleKo, Sangpil, Kyoungjoon Choi, Seungmin Yu, and Jun Lee. 2022. "A Stochastic Optimization Model for Sustainable Multimodal Transportation for Bioenergy Production" Sustainability 14, no. 3: 1889. https://doi.org/10.3390/su14031889
APA StyleKo, S., Choi, K., Yu, S., & Lee, J. (2022). A Stochastic Optimization Model for Sustainable Multimodal Transportation for Bioenergy Production. Sustainability, 14(3), 1889. https://doi.org/10.3390/su14031889





