Conformational Analysis, Molecular Structure and Solid State Simulation of the Antiviral Drug Acyclovir (Zovirax) Using Density Functional Theory Methods
Abstract
:1. Introduction
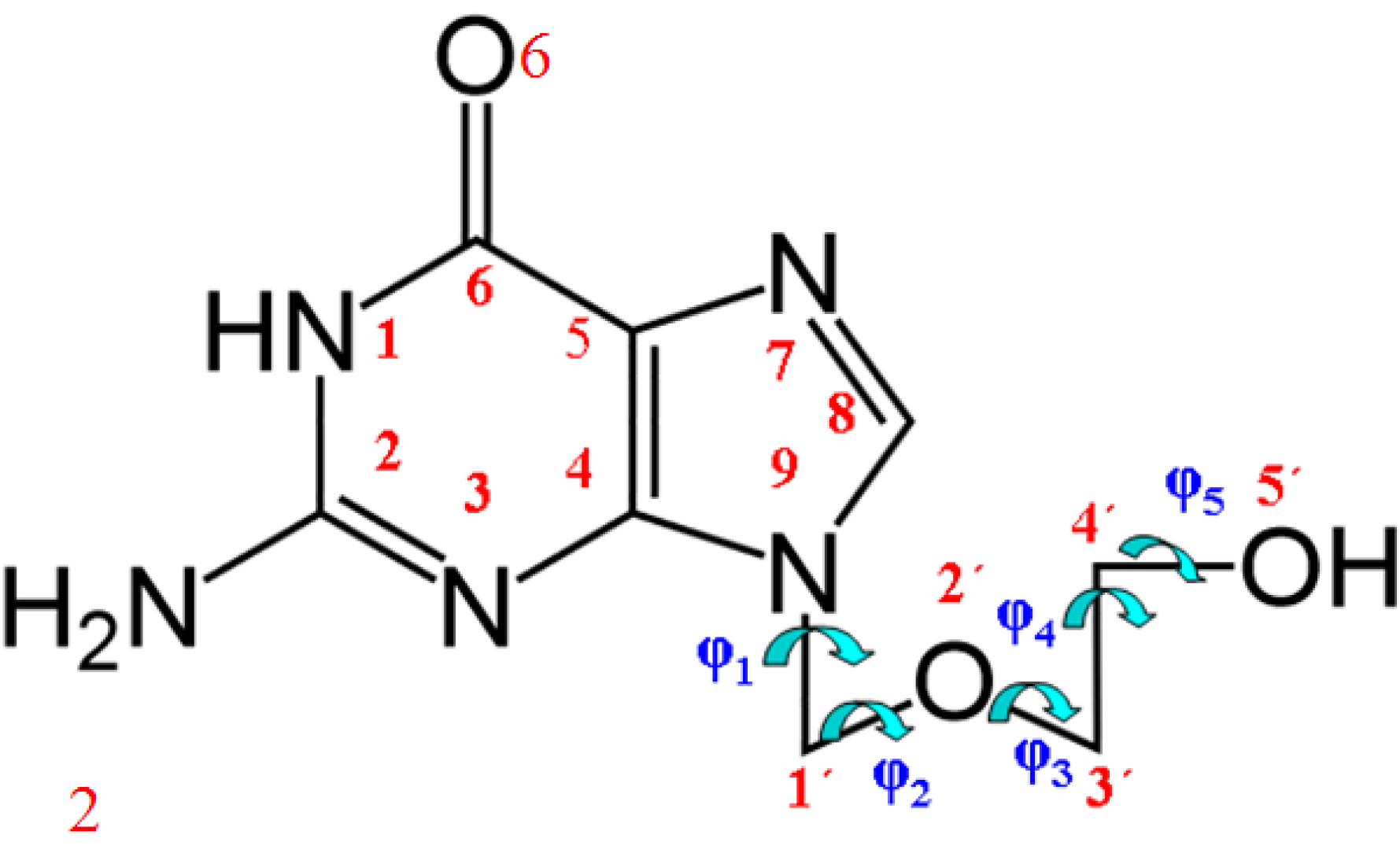
2. Computational Details
3. Results and Discussion

| Tautomers | R | β | Φ | φ1 | φ2 | φ3 | φ4 | φ5 | μ | ΔE | ΔG | P298.15 | P273.15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N1 | 3.963 | 72.5 | 54.3 | −75.3 | 146.4 | −88.5 | 69.8 | −69.3 | 5.739 | 0 a | |||
| N3 | {3.672} | {77.0} | {53.5} | {−45.9} | {149.1} | {−92.5} | {60.2} | {−92.6} | {12.220} | {25.457} | |||
| N7 | {3.741} | {73.0} | {52.0} | {−76.4} | {140.5} | {−80.8} | {72.4} | {−92.7} | {9.841} | {19.302} | |||
| OHC | {3.826} | {73.5} | {51.7} | {−72.3} | {146.5} | {−89.2} | {70.4} | {−82.6} | {2.471} | {0.603} | |||
| OHT | {3.792} | {73.5} | {52.0} | {−72.4} | {145.0} | {−87.2} | {70.6} | {−86.1} | {3.437} | {1.131} |

3.1. Definition of the Conformational Angles
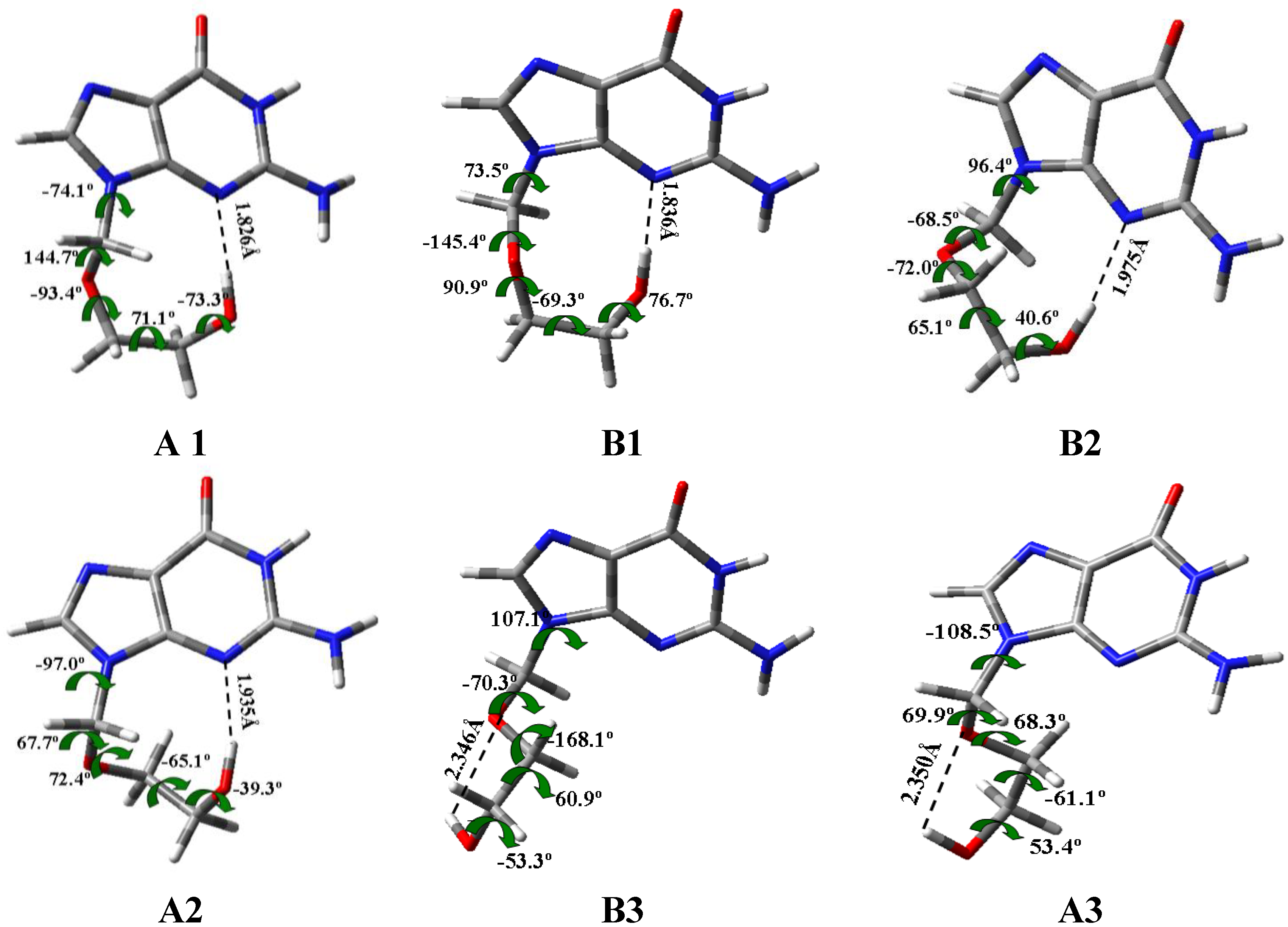
3.2. Conformers and Energetics
| Conformers | R | β a | Φ a | φ1 | φ2 | φ3 | φ4 | φ5 | μ | ΔE | ΔG |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 3.963 | 72.5 | 54.3 | −75.3 | 146.4 | −88.5 | 69.8 | −69.3 | 5.739 | 0 b | |
| A2 | 3.774 | 76.8 | 52.5 | −97.7 | 65.9 | 74.6 | −67.0 | −34.1 | 5.367 | 1.258 | |
| A3 | 5.155 | 118.5 | 37.5 | −107.7 | 71.0 | 171.1 | −63.7 | 57.6 | 5.762 | 1.202 | |
| A4 | 4.592 | 116.2 | 64.7 | −106.0 | 73.2 | 178.6 | 65.0 | −56.8 | 7.630 | 1.726 | |
| A5 | 5.119 | 123.3 | 36.2 | −81.4 | −71.2 | −170.1 | 60.7 | −53.6 | 5.166 | 2.952 | 1.976 |
| A6 | 4.839 | 130.3 | 50.2 | −93.9 | −178.3 | 174.3 | −60.6 | 54.4 | 7.387 | 3.870 | 2.472 |
| A7 | 4.342 | 110.7 | 69.0 | −100.5 | 73.3 | −114.2 | −57.0 | 53.3 | 4.342 | 4.088 | 2.821 |
| A8 | 5.314 | 99.1 | 61.8 | −108.8 | 70.2 | 174.4 | 179.8 | 123.1 | 5.490 | 4.529 | 3.020 |
| A9 | 4.316 | 72.3 | 29.9 | −100.9 | 86.9 | 94.8 | −69.7 | 165.3 | 8.401 | 4.540 | 3.284 |
| A10 | 4.317 | 98.8 | 29.8 | −100.4 | 87.1 | 62.4 | 118.4 | −119.6 | 8.402 | 4.541 | 3.295 |
| A11 | 4.316 | 98.8 | 29.8 | −100.5 | 87.1 | 94.7 | −69.8 | 165.6 | 8.403 | 4.541 | 3.293 |
| A12 | 5.248 | 97.3 | 61.6 | −107.1 | 71.8 | 176.2 | −179.4 | 177.3 | 6.700 | 4.778 | 3.132 |
| A13 | 5.137 | 115.6 | 37.5 | −109.6 | 69.9 | 168.6 | −72.0 | 169.7 | 6.500 | 4.912 | 3.329 |
| A14 | 3.804 | 130.6 | 83.0 | −137.1 | 68.2 | −147.3 | 63.6 | 64.2 | 7.916 | 4.944 | 4.017 |
| A15 | 3.851 | 140.4 | 75.7 | −114.8 | −115.6 | 140.7 | −61.6 | 63.4 | 7.669 | 5.082 | 3.917 |
| A16 | 4.561 | 120.1 | 66.8 | −112.4 | 70.5 | −178.3 | 63.9 | 60.5 | 7.527 | 5.103 | 3.411 |
| A17 | 4.400 | 99.7 | 34.4 | −112.0 | 67.2 | 57.8 | 44.9 | 48.3 | 6.225 | 5.139 | 4.217 |
| A18 | 5.204 | 119.3 | 39.3 | −110.7 | 69.8 | 173.8 | −64.3 | −63.3 | 7.512 | 5.216 | 3.730 |
| A19 | 3.411 | 68.6 | 64.3 | −92.1 | 98.3 | −114.1 | 64.4 | 39.1 | 7.760 | 5.354 | 4.890 |
| A20 | 4.387 | 136.6 | 10.3 | −88.2 | 158.8 | 79.4 | −71.0 | 172.6 | 8.042 | 5.378 | 3.969 |
| A21 | 3.562 | 167.7 | 60.8 | −94.2 | −126.1 | 83.2 | −74.5 | 178.0 | 6.300 | 5.384 | 4.494 |
| A22 | 4.486 | 118.5 | 67.8 | −112.8 | 70.8 | −179.7 | 71.7 | −171.9 | 8.081 | 5.432 | 3.764 |
| A23 | 5.209 | 88.5 | 51.3 | −104.5 | 77.3 | 91.3 | 180.0 | −69.9 | 6.218 | 5.476 | 3.817 |
| A24 | 4.381 | 115.3 | 11.5 | −102.7 | −162.7 | −77.3 | 73.0 | −170.7 | 8.685 | 5.514 | 4.179 |
| A25 | 4.948 | 80.5 | 59.5 | −102.5 | 67.2 | 74.6 | 176.3 | −68.2 | 6.425 | 5.588 | 4.277 |
| A26 | 4.655 | 80.0 | 78.1 | −99.5 | 74.6 | −104.0 | −175.2 | 72.4 | 7.000 | 5.633 | 4.093 |
| A27 | 4.609 | 83.1 | 78.2 | −102.2 | 71.5 | −107.6 | −174.8 | 179.6 | 5.473 | 5.662 | 4.371 |
| A28 | 5.146 | 128.0 | 36.4 | −81.4 | −70.5 | −167.5 | 71.8 | −170.7 | 6.229 | 5.675 | 4.396 |
| A29 | 4.653 | 84.8 | 51.8 | −103.7 | 70.9 | −109.1 | −174.5 | −74.1 | 6.731 | 5.845 | 4.325 |
| A30 | 5.235 | 90.1 | 49.7 | −102.9 | 80.0 | 96.4 | 179.4 | −173.8 | 7.848 | 5.850 | 4.085 |
| A31 | 4.400 | 99.7 | 34.4 | −112.0 | 67.2 | 57.8 | 44.9 | 48.3 | 6.225 | 5.890 | 4.508 |
| A32 | 5.220 | 123.3 | 38.2 | −81.4 | −70.2 | −172.6 | 64.6 | 64.8 | 4.345 | 5.909 | 4.708 |
| A33 | 4.415 | 114.1 | 12.6 | −104.1 | −163.1 | −74.6 | 69.3 | 69.4 | 7.384 | 5.917 | 4.782 |
| A34 | 5.955 | 104.4 | 31.3 | −95.4 | 179.0 | −178.1 | 179.2 | 72.9 | 6.080 | 6.174 | 4.503 |
| A35 | 5.898 | 124.0 | 30.3 | −96.6 | 179.3 | 179.3 | 179.9 | 179.6 | 6.676 | 6.195 | 4.544 |
| A36 | 5.956 | 124.3 | 31.3 | −96.4 | 179.5 | 178.1 | −179.0 | −72.9 | 7.716 | 6.254 | 4.762 |
| A37 | 4.565 | 102.4 | 34.8 | −112.6 | 66.4 | 60.5 | 56.3 | −178.8 | 7.684 | 6.290 | 5.085 |
| A38 | 4.273 | 110.2 | 72.9 | −105.8 | 71.1 | −103.2 | −66.6 | 167.8 | 6.458 | 6.432 | 4.855 |
| A39 | 4.970 | 138.6 | 46.2 | −100.0 | −179.8 | 172.1 | −72.6 | 166.4 | 8.071 | 6.610 | 4.755 |
| A40 | 5.011 | 104.7 | 46.2 | −97.2 | −179.7 | −176.1 | 72.9 | −166.1 | 7.023 | 6.779 | 5.097 |
| A41 | 5.030 | 104.4 | 48.4 | −95.2 | 179.6 | −177.9 | 64.3 | 61.5 | 8.220 | 7.100 | 5.519 |
| A42 | 5.722 | 115.4 | 19.7 | −99.3 | −176.9 | −84.1 | −179.2 | 70.4 | 6.405 | 7.372 | 5.289 |
| A43 | 5.350 | 87.6 | 45.5 | −90.3 | 138.5 | −88.9 | −177.6 | −70.3 | 7.007 | 7.483 | 7.510 |
| A44 | 5.386 | 92.4 | 40.2 | −91.6 | 146.1 | −91.1 | 178.5 | 173.8 | 7.133 | 7.627 | 5.567 |
| A45 | 5.699 | 118.8 | 18.3 | −101.1 | −173.8 | −84.4 | −178.6 | 176.1 | 7.994 | 7.665 | 5.672 |
| A46 | 5.765 | 120.0 | 17.5 | −101.1 | −170.2 | −80.2 | −173.9 | −69.9 | 6.680 | 7.684 | 5.636 |
| A47 | 4.832 | 106.9 | 33.0 | −107.0 | −164.9 | −72.0 | −62.7 | 178.1 | 8.554 | 8.451 | 6.636 |
| B1 | 3.928 | 73.4 | 53.4 | 75.1 | −146.7 | 95.5 | −68.8 | 72.8 | 5.812 | 0.072 | |
| B2 | 3.770 | 77.2 | 52.0 | 97.0 | −66.7 | −74.1 | 66.6 | 36.1 | 5.348 | 1.216 | |
| B3 | 5.157 | 117.3 | 37.3 | 106.1 | −71.7 | −171.1 | 63.5 | −57.6 | 5.951 | 1.157 | |
| B4 | 4.529 | 95.5 | 65.4 | 78.3 | 70.8 | −178.7 | 63.6 | −54.4 | 6.470 | 2.031 | |
| B5 | 4.598 | 115.9 | 64.6 | 105.4 | −72.8 | −178.2 | −64.9 | 56.7 | 7.911 | 1.693 | |
| B6 | 5.119 | 123.1 | 36.3 | 81.0 | 70.9 | 170.1 | −60.7 | 54.1 | 5.460 | 2.993 | 2.035 |
| B7 | 4.991 | 113.3 | 29.3 | 107.2 | −74.7 | −87.7 | −56.9 | 46.5 | 6.027 | 3.636 | 2.427 |
| B8 | 3.582 | 165.9 | 56.3 | 82.7 | 65.4 | 73.0 | −75.2 | 178.4 | 6.463 | 4.240 | 3.708 |
| B9 | 3.793 | 70.4 | 79.1 | 57.2 | 68.0 | −93.9 | −49.8 | 60.8 | 5.069 | 4.263 | 3.900 |
| B10 | 4.325 | 99.2 | 29.1 | 98.3 | −88.0 | −94.7 | 69.5 | −166.2 | 8.268 | 4.496 | 3.334 |
| B11 | 5.318 | 99.2 | 61.7 | 108.3 | −70.8 | −175.3 | 179.6 | 71.1 | 5.640 | 4.508 | 3.006 |
| B12 | 5.002 | 132.0 | 29.1 | 77.5 | 74.7 | 88.4 | 57.0 | −46.2 | 5.222 | 4.791 | 3.824 |
| B13 | 5.138 | 115.0 | 37.3 | 108.2 | −70.2 | −168.4 | 71.8 | −170.5 | 6.133 | 4.845 | 3.212 |
| B14 | 5.246 | 98.4 | 61.7 | 108.6 | −71.5 | −176.6 | 179.2 | 177.1 | 6.553 | 4.852 | 3.244 |
| B15 | 5.312 | 99.2 | 62.1 | 108.6 | −70.7 | −175.8 | −178.5 | −70.6 | 7.964 | 4.893 | 3.413 |
| B16 | 4.407 | 99.6 | 33.7 | 110.2 | −68.1 | −57.9 | −44.6 | −48.7 | 5.939 | 5.042 | 4.065 |
| B17 | 5.205 | 118.2 | 39.0 | 109.3 | −69.6 | −172.9 | 64.6 | 63.9 | 7.429 | 5.101 | 3.551 |
| B18 | 3.562 | 167.3 | 60.9 | 93.8 | 125.8 | −83.0 | 74.6 | −178.0 | 6.069 | 5.456 | 4.582 |
| B19 | 5.277 | 89.9 | 49.5 | 103.3 | −79.4 | −94.8 | −179.7 | 69.2 | 6.054 | 5.577 | 3.960 |
| B20 | 4.876 | 78.3 | 61.1 | 101.0 | −65.9 | −75.2 | 179.3 | −69.0 | 6.102 | 5.694 | 4.494 |
| B21 | 5.253 | 91.0 | 49.4 | 103.8 | −80.2 | −97.6 | −178.6 | 174.8 | 8.034 | 5.950 | 3.922 |
| B22 | 4.534 | 101.8 | 35.0 | 112.6 | −66.2 | −59.3 | −55.7 | 179.6 | 7.559 | 6.169 | 5.032 |
| B23 | 3.146 | 83.0 | 95.1 | 73.1 | 67.3 | −116.9 | 63.5 | 64.3 | 5.334 | 6.305 | 6.199 |
| B24 | 4.610 | 77.9 | 77.5 | 79.0 | 72.8 | −102.2 | −173.9 | −175.2 | 5.317 | 6.617 | 5.315 |
| B25 | 4.365 | 150.0 | 33.5 | 76.4 | 67.0 | 59.5 | 40.5 | 41.6 | 5.882 | 6.677 | 5.427 |
| B26 | 4.618 | 108.0 | 52.5 | 77.2 | 68.5 | −105.1 | −173.1 | −79.3 | 5.308 | 6.689 | 5.500 |
| B27 | 5.184 | 143.6 | 51.8 | 78.9 | 76.5 | 89.5 | −178.9 | −69.4 | 6.563 | 6.718 | 5.374 |
| B28 | 4.635 | 114.4 | 78.3 | 79.8 | 73.8 | −101.1 | −174.8 | 72.3 | 7.031 | 6.831 | 5.483 |
| B29 | 5.194 | 141.1 | 52.7 | 77.5 | 74.5 | 87.3 | 175.3 | 68.0 | 5.203 | 6.997 | 5.596 |
| B30 | 5.129 | 142.9 | 52.3 | 79.1 | 76.5 | 90.0 | −179.5 | −175.2 | 7.031 | 7.015 | 5.609 |
| B31 | 4.964 | 136.4 | 32.2 | 77.2 | 71.0 | 78.8 | 64.1 | −178.9 | 5.033 | 7.508 | 6.051 |
| Conformer | ΔE/kcal·mol−1 |
|---|---|
| A1 | 0.143 |
| A2 | 0.082 |
| A3 | 2.553 |
| A4 | 3.112 |
| B1 | 0.122 |
| B2 | 0 |
| B3 | 2.491 |
| B4 | 1.962 |
| B5 | 3.071 |

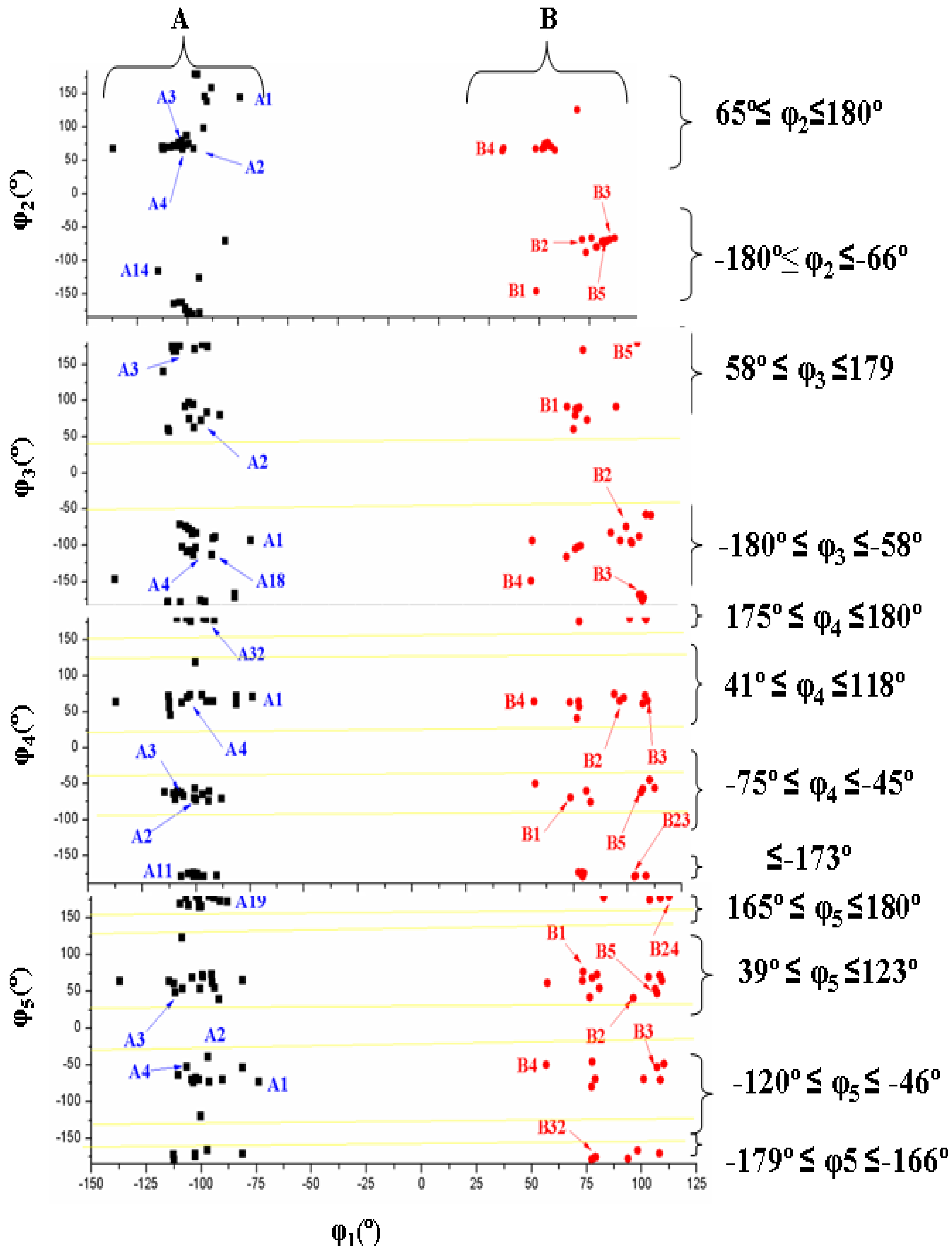
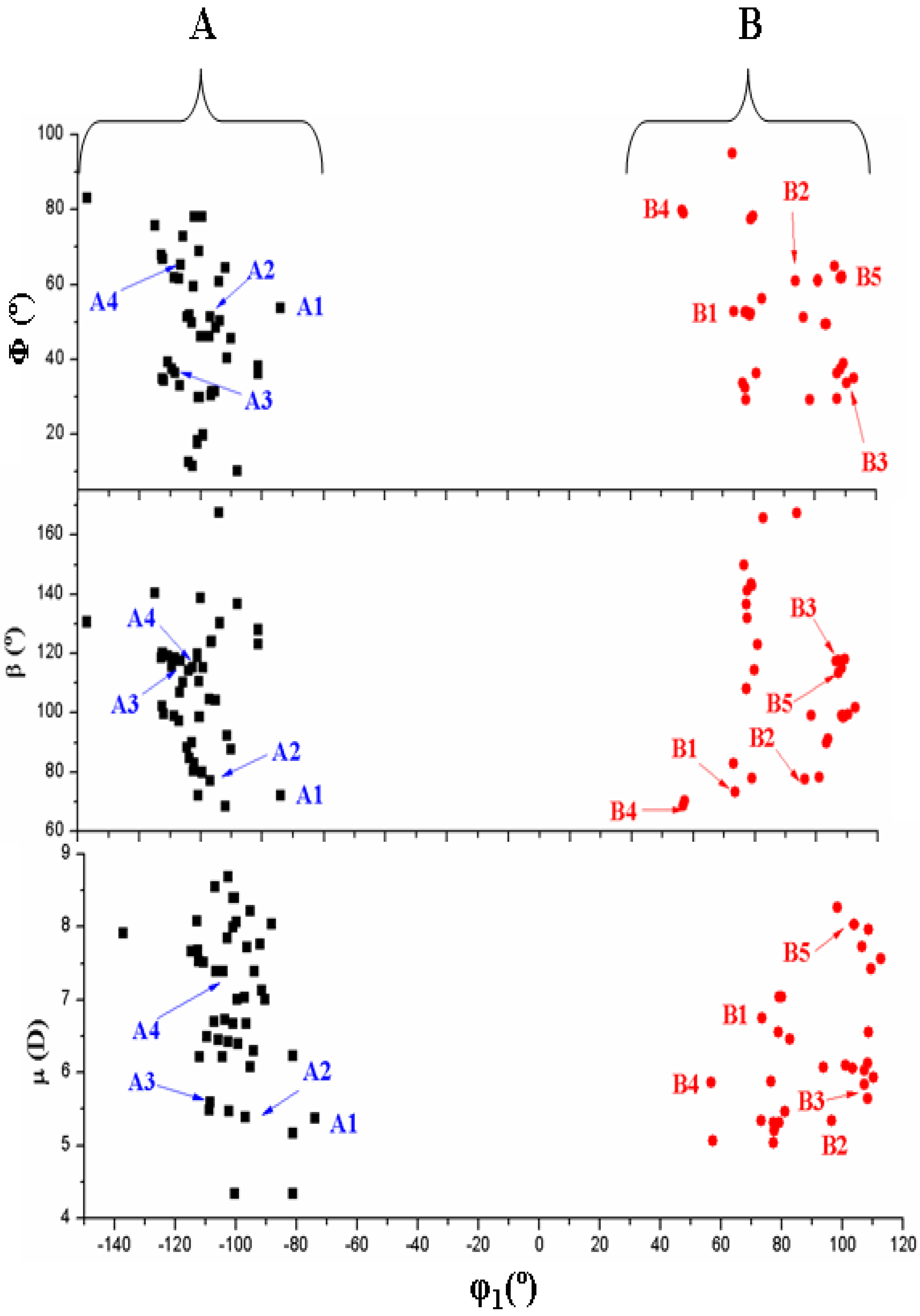

3.3. Conformational Angle Analysis
- (i)
- The dihedral angle φ1 presents a bimodal distribution: (−137° ≤ −74°) 47 conformers A (anti) and (57° ≤ 113°) 31 conformers B (syn). Anti forms prevail in number over syn ones and cover a slight wider range of φ1 values. This anti orientation has been found in the crystal of several nucleosides [51,52,53], and it is the form for biological activity [54]. Although, in many nucleoside analogues syn and anti forms have similar energy, however, the global minimum corresponds in general to the syn form, as in AZT [35]. In purine nucleosides there is relatively little restraint to rotation about the N9-C1' bond [55]. In ACV the high population of the anti forms and the wider range of φ1 values are factors that facilitate its antiviral activity. The sugar ring of the natural nucleoside dG can be mimics by the similar exocyclic angles of ACV
- (ii)
- The torsional φ2 angle has a clear bimodal distribution: 65° ≤ φ2 ≤ 180° (49 conformers, 34 are A and 15 are B) and –180° ≤ φ2 ≤ −66° (29 conformers, 13 are A and 16 are B), Figure 7
- (iii)
- The φ3 angle also has a bimodal conformation: 58° ≤ φ3 ≤ 180° (32 conformers, 22 are A and 10 are B) and −180° ≤ φ3 ≤ −58° (46 conformers, 25 are A and 21 are B)
- (iv)
- The φ4 angle has a trimodal distribution: −173° ≤ φ4 ≤ 175° (28 conformers, 16 are A and 12 are B), 41° ≤ φ4 ≤ 118° (28 conformers, 17 are A and 11 are B), and −75° ≤ φ4 ≤ −45° (22 conformers, 14 are A and 8 are B)
- (v)
- The torsional φ5 angle also has a trimodal distribution: −166° ≤ φ5 ≤ 165° (29 conformers, 19 A and 10 B), 39° ≤ φ5 ≤ 123° range (29 conformers, 16 A and 13 B), and −120° ≤ φ5 ≤ −46° (20 conformers, 12 A and 8 B)
- (vi)
- In the bond angle β has been observed a regular distribution in the 69° ≤ β ≤ 168° range, Figure 8. This large range indicates the high flexibility of the chain with multiple O5'H orientations. The most stable conformers with ΔE < 1 kcal·mol−1 have the β angle with values between 72° and 78°, while the conformers with higher ΔE have some values larger than 140°.
- (vii)
- The bond Φ angle also shows a regular distribution in the 10° ≤ Φ ≤ 83° range for conformers A, and 29° ≤ Φ ≤ 95° for conformers B. The value of this angle appears between 51° and 54° for the four best conformers with ΔE < 1 kcal/mol−1. In general, the most stable conformers do not have large values of Φ, neither low values.
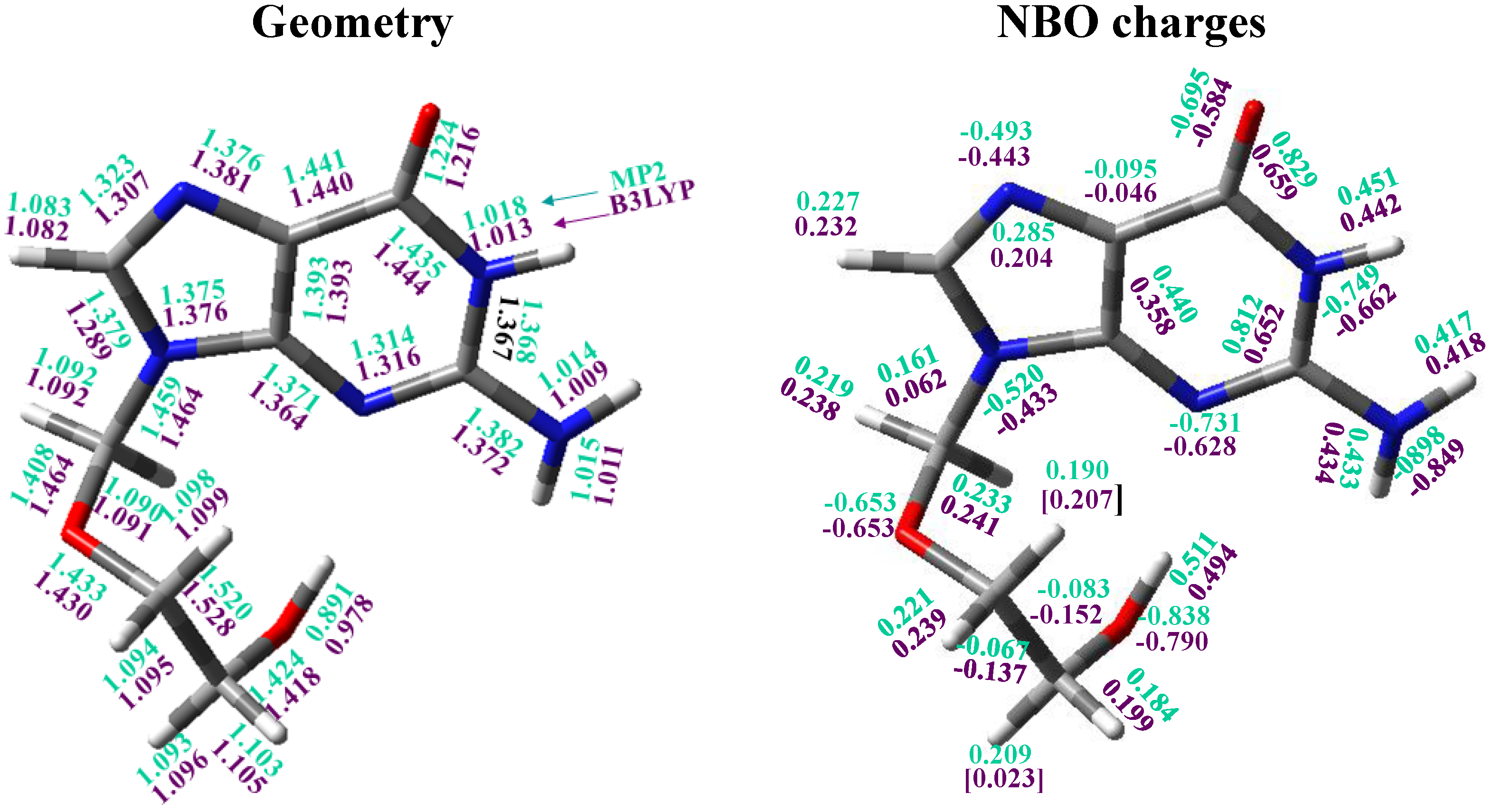
3.4. Guanine Moiety
3.5. The Side Chain
3.6. Intramolecular H-Bonds
3.7. Natural NBO Atomic Charges
3.8. Solid State Simulation
| Solid form | R | β | Φ | φ1 | φ2 | φ3 | φ4 | φ5 |
|---|---|---|---|---|---|---|---|---|
| Dimer | ||||||||
| Molecule A | 5.150 | 127.9 | −82.1 | −82.1 | −70.4 | −168.4 | 71.9 | −168.8 |
| Molecule B | 5.148 | 127.9 | −88.8 | −88.8 | −70.3 | −168.1 | 71.8 | −168.9 |
| Tetramer | ||||||||
| Molecule A | 5.148 | 128.6 | −82.3 | −82.3 | −70.4 | −167.3 | 72.5 | −167.4 |
| Molecule B | 5.212 | 117.2 | −80.1 | −80.1 | −76.3 | 176.8 | 64.2 | −90.8 |
| Molecule C | 5.110 | 122.0 | 158.6 | 158.6 | −71.7 | −50.5 | 60.1 | −53.8 |
| Molecule D | 4.313 | 150.6 | −95.3 | −95.3 | −93.1 | −100.2 | 70.6 | −160.4 |
| X-Ray [62] | ||||||||
| Molecule A0 | −76.5 | −76.9 | 173.2 | 60.6 | ||||
| Molecule B | −74.4 | −66.3 | −176.2 | 73.5 | ||||
| Molecule C | −90.5 | −173.3 | −171.9 | −174.4 |
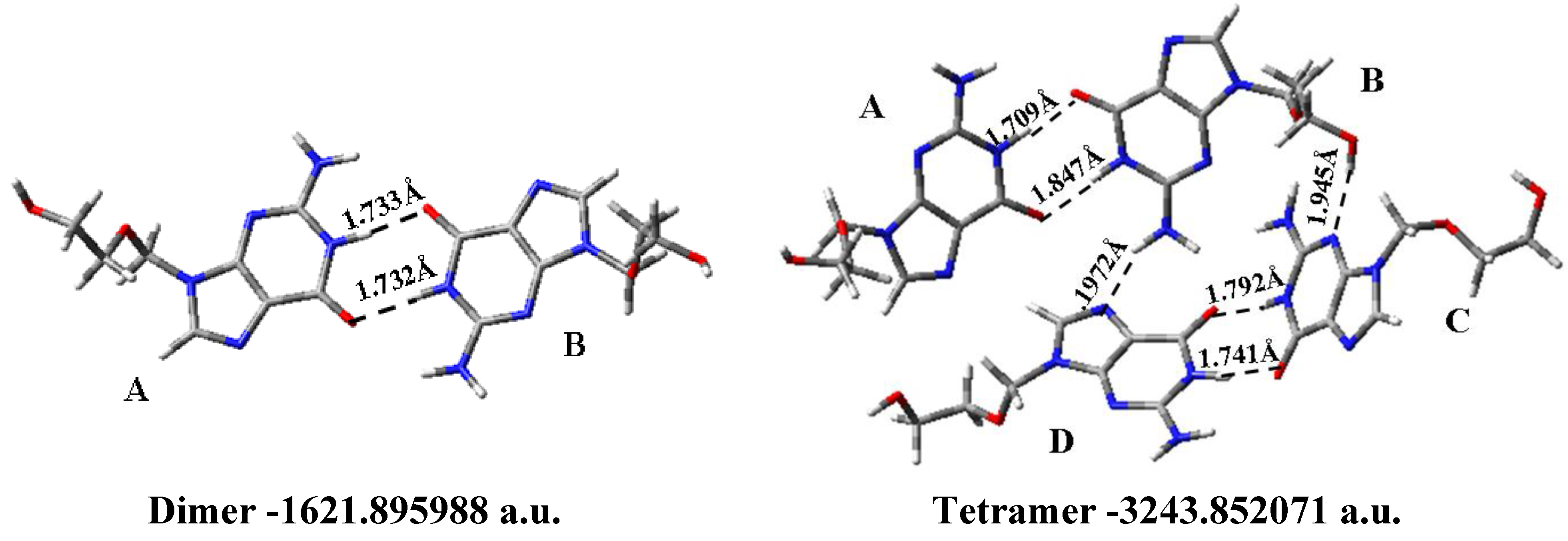
4. Conclusions
- (1)
- Five tautomers of ACV were identified and fully optimized. At room temperature only tautomer N1 (48.1%), OHC (37.7%) and OHT (14.3%) have a noticeable population. It is very small in tautomers N3 and N7, less than 0.05%.
- (2)
- The relative energies of the five tautomers appear related to the dipole moment and to the torsional angle φ1. The least stable tautomer N3 in the isolated state has the highest μ and thus, it is the most favoured in a polarisable environment with water.
- (3)
- In the isolated state the most stable tautomer is N1 by both B3LYP and MP2 methods. In this tautomer, and through a rotation of φ1, φ2, φ3, φ4 and φ5 exocyclic torsional angles, 78 optimized stable conformers were identified, two syn and two anti failing into the 0–1 kcal·mol−1 ΔE + ZPE energy range.
- (4)
- The calculated most stable conformer by all DFT levels corresponds to A1, while by MP2 is B2. In the nitrogen atoms and in the O2' and O5' oxygen atoms of conformer A1 appear a higher reactivity than in the corresponding natural nucleoside deoxyguanosine.
- (5)
- The distribution of all the conformers according to the ranges of stability of the characteristic torsional angles was established. The values obtained indicate the flexible nature of ACV, which is higher than dG. An increase of the stability appears when the side chain is near to the purine base, with a value of R that fails into 3.925–2.892 Å range, and an angle Φ close to 54°.
- (6)
- Only two intramolecular H-bonds may be observed in the main conformers of ACV, in contrast to the six H-bond types calculated in dG. It leads to a flexibility higher in ACV than in dG.
- (7)
- The solid state was simulated through a dimer and tetramer forms. An excellent agreement with the X-ray crystal data was obtained, which indicates the good accuracy of the theoretical methods used.
Supplementary Files
Author Contributions
Conflicts of Interest
References
- Schloemer, G.C.; Han, Y.-K.; Harrington, P.J. Preparation of acyclovir using 1,3-dioxolane. U.S. Patent 5567816, 22 October 1996. [Google Scholar]
- Lazrek, H.B.; Baddi, L.; Smietana, M.; Vasseur, J.-J.; Sebti, S.; Zahouily, M. One-pot synthesis of antiviral acyclovir and other nucleosides derivatives using doped natural phosphate as Lewis acid catalyst. Nucleos. Nucleot. Nucleic Acids 2008, 27, 1107–1112. [Google Scholar] [CrossRef]
- Gao, H.; Mitra, A.K. Synthesis of acyclovir, ganciclovir and their prodrugs: A review. Synthesis 2000, 3, 329–351. [Google Scholar]
- De Clercq, E. Antiviral drugs: Current state of the art. J. Clinical Virol. 2001, 22, 73–89. [Google Scholar] [CrossRef]
- Emmert, D.H.; Lancaster, M.D. Treatment of common cutaneous herpes simplex virus infections. Am. Fam. Physician. 2000, 61, 1697–1607. [Google Scholar]
- Fuchs, J.; Celum, C.; Wang, J.; Hughes, J.; Sánchez, J.; Cowan, F.; Reid, S.; Delany-Moretlwe, S.; Corey, L.; Wald, A. Clinical and virologic efficacy of herpes simplex virus type 2 suppression by acyclovir in a multicontinent clinical trial. J. Infect Dis. 2010, 201, 1164–1168. [Google Scholar] [CrossRef]
- Piret, J.; Boivin, G. Resistance of herpes simplex viruses to nucleoside analogues: Mechanisms, prevalence, and management. Antimicrob. Agents Chemother. 2011, 55, 459–472. [Google Scholar] [CrossRef]
- Harnden, M.R.; Wyatt, P.G.; Boyd, M.R.; Sutton, D. Synthesis and antiviral activity of 9-alcoxypurines. 1.9-(3-hydroxypropoxy)- and 9-[3-hydroxy-2-(hydroxymethyl)propoxy]purines. J. Med. Chem. 1990, 33, 187–196. [Google Scholar] [CrossRef]
- Golankiewicz, B.; Ostrowski, T.; Goslinski, T.; Januszczyk, P.; Zeidler, J.; Baranowski, D.; de Clercq, E. Fluorescent tricyclic analogues of acyclovir and ganciclovir. A structure-antiviral activity study. J. Med. Chem. 2001, 44, 4284–4287. [Google Scholar] [CrossRef]
- Lisco, A.; Vanpouille, C.; Tchesnokov, E.P.; Grivel, J.C.; Biancotto, A.; Brichacek, B.; Elliott, J.; Fromentin, E.; Shattock, R.; Anton, P.; et al. Acyclovir is activated into a HIV-1 reverse transcriptase inhibitor in herpes virus-infected human tissues. Cell Host Microbe. 2008, 4, 260–270. [Google Scholar] [CrossRef]
- Vanpouille, C.; Lisco, A.; Derudas, M.; Saba, E.; Grive, J.-C.; Brichacek, B.; Scrimieri, F.; Schinazi, R.; Schols, D.; McGuigan, C.; et al. A new class of dual-targeted antivirals: Monophosphorylated acyclovir prodrug derivatives suppress both human immunodeficiency virus type 1 and herpes simplex virus type 2. J. Infect Dis. 2010, 201, 635–643. [Google Scholar] [CrossRef]
- Tanton, C.; Weiss, H.A.; LeGoff, J.; Changalucha, J.; Clayton, T.C.; Ross, D.A.; Belec, L.; Hayes, R.J.; Watson-Jones, D. Patterns of herpes simplex virus shedding over 1 month and the impact of acyclovir and HIV in HSV-2-seropositive women in Tanzania. Sex Transmit. Infect. 2011, 87, 406–411. [Google Scholar] [CrossRef]
- Delany, S.; Mlaba, N.; Clayton, T.; Akpomiemie, G.; Capovilla, A.; Legoff, J.; Belec, L.; Stevens, W.; Rees, H.; Mayaud, P. Impact of acyclovir on genital and plasma HIV-1 RNA in HSV-2/HIV-1 co-infected women: a randomized placebo-controlled trial in South Africa. AIDS. 2009, 23, 461–469. [Google Scholar] [CrossRef]
- Prichard, M.N.; Kern, E.R.; Hartline, C.B.; Lanier, E.R.; Quenelle, D.C. CMX001 Potentiates the efficacy of acyclovir in herpes simplex virus infections. Antimicrob. Agents Chemother. 2011, 55, 4728–4734. [Google Scholar]
- Kalachandra, S.; Takamata, T.; Lin, D.M.; Snyder, E.A.; Webster-Cyriaque, J. Stability and release of antiviral drugs from ethylene vinyl acetate (EVA) copolymer. J. Mater. Sci: Mater. Med. 2006, 17, 1227–1236. [Google Scholar] [CrossRef]
- Gavira, J.M.; de la Fuente, M.; Navarro, R.; Hernanz, A. Normal coordinate analysis of acycloguanosine. J. Molec. Struct. 1997, 410–411, 425–429. [Google Scholar]
- Birnbaum, G.I.; Johansson, N.G.; Shugar, D. Conformations of acyclonucleosides: Crystal structure of 9-(4-hydroxybutyl)guanine, an analogue of acyclovir. Nucleos. Nucleot. Nucleic Acids 1987, 6, 775–783. [Google Scholar] [CrossRef]
- Brandi-Blanco, M.P.; Choquesillo-Lazarte, D.; Domínguez-Martín, A.; González-Pérez, J.M.; Castiñeiras, A.; Niclós-Gutiérrez, J. Metal ion binding patterns of acyclovir: Molecular recognition between this antiviral agent and copper(II) chelates with iminodiacetate or glycylglycinate. J. Inorg. Biochem. 2011, 105, 616–623. [Google Scholar] [CrossRef]
- Barceló-Oliver, M.; Terrón, A.; García-Raso, A.; Fiol, J.J.; Molins, E.; Miravitlles, C. Ternary complexes metal [Co(II), Ni(II), Cu(II) and Zn(II)]–ortho-iodohippurate (I-hip)–acyclovir. X-ray characterization of isostructural [(Co, Ni or Zn)(I-hip)2(ACV)(H2O)3] with stacking as a recognition factor. J. Inorg. Biochem. 2004, 98, 1703–1711. [Google Scholar] [CrossRef]
- Brovarets, O.O.; Yurenko, Y.P.; Dubey, I.Y.; Hovorun, D.M. Can DNA-binding proteins of replisome tautomerize nucleotide bases? Ab initio model study. J. Biomol. Struct. Dyn. 2012, 29, 1101–1109. [Google Scholar] [CrossRef]
- Brovarets, O.O.; Hovorun, D.M. Prototropic tautomerism and basic molecular principles of hypoxanthine mutagenicity: An exhaustive quantum-chemical analysis. J. Biomol. Struct. Dyn. 2013, 31, 913–936. [Google Scholar] [CrossRef]
- Plass, M.; Kristl, A.; Abraham, M.H. Spectroscopic investigation of tautomeric equilibria in the guanine derivatives of acyclovir. J. Chem. Soc. Perkin Trans II 1999, 264, 26–41. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Hoe, W.-M.; Cohen, A.J.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Q.; Muller, R.P.; Goddard III, W.A. An extended hybrid density functional (X3LYP) with improved descriptions of nonbond interactions and thermodynamic properties of molecular systems. J. Chem. Phys. 2005, 122, 14105–14114. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. 1988, B37, 785–789. [Google Scholar]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of electron-gas correlation energy. Phys. Rev. 1992, B45, 13244–13249. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision B.04; Gaussian Inc.: Pittsburgh, PA, USA, 2003.
- Yurenko, Y.P.; Zhurakivsky, R.O.; Ghomi, M.; Samijlenko, S.P.; Hovorun, D.M. Ab Initio comprehensive conformational analysis of 2′-deoxyuridine, the biologically significant DNA minor nucleoside, and reconstruction of its low- temperature matrix Infrared spectrum. J. Phys. Chem. B 2008, 112, 1240–1250. [Google Scholar] [CrossRef]
- Yurenko, Y.P.; Zhurakivsky, R.O.; Ghomi, M.; Samijlenko, S.P.; Hovorun, D.M. Comprehensive conformational analysis of the nucleoside analogue 2′-β-deoxy-6-azacytidine by DFT and MP2 calculations. J. Phys. Chem. B 2007, 111, 6263–6271. [Google Scholar]
- Alcolea Palafox, M.; Iza, N.; de la Fuente, M.; Navarro, R. Simulation of the first hydration shell of nucleosides D4T and Thymidine: structures obtained using MP2 and DFT methods. J. Phys. Chem. B 2009, 113, 2458–2476. [Google Scholar] [CrossRef]
- Alcolea Palafox, M.; Iza, N. Structure of the antiviral stavudine using quantum chemical methods: complete conformational space analysis, 3D potential energy surfaces and solid state simulation. J. Molec. Struct. 2012, 1028, 181–195. [Google Scholar]
- Alcolea Palafox, M.; Talaya, J. Hydration analysis of antiviral agent AZT by means of DFT and MP2 calculations. J. Phys. Chem. B 2010, 114, 15199–15211. [Google Scholar] [CrossRef]
- Alcolea Palafox, M.; Posada-Moreno, P.; Villarino-Marín, A.L.; Martinez-Rincon, C.; Ortuño-Soriano, I.; Zaragoza-García, I. DFT Calculation of four new potential agents muscarinic of bispyridinium type: structure, synthesis, biological activity, hydration, and relations with the potents W84 and DUO-3O. J. Comput. Aided Molec. Des. 2011, 25, 145–161. [Google Scholar] [CrossRef]
- Alcolea Palafox, M. Anticancer drug IUdR and other 5-halogen derivatives of 2′-deoxyuridine: conformers, hydrates and structure-activity relationships. Struct. Chem. 2014, 25, 53–69. [Google Scholar] [CrossRef]
- Alcolea Palafox, M.; Nielsen, O.F.; Lang, K.; Garg, P.; Rastogi, V.K. Geometry and vibrational spectra of 5-substituted uracils. Asian Chem. Letts. 2004, 8, 81–93. [Google Scholar]
- Alcolea Palafox, M.; Rastogi, V.K. Quantum Chemical predictions of the vibrational spectra of polyatomic molecules. The uracil molecule and two derivatives. Spectrochim. Acta. 2002, 58, 411–440. [Google Scholar] [CrossRef]
- Alcolea Palafox, M. The Prediction of Vibrational Spectra: The Use of Scale Factors. In Recent Research Developments in Physical Chemistry; Transworld Research Network: Trivandrum, India, 1998; Volume 2. [Google Scholar]
- Alcolea Palafox, M. Scaling factors for the prediction of vibrational spectra. I. Benzene molecule. Int. J. Quantum Chem. 2000, 77, 661–684. [Google Scholar] [CrossRef]
- Alcolea Palafox, M.; Iza, N.; Gil, M. The hydration effect on the uracil frequencies: an experimental and quantum chemical study. J. Molec. Struct. 2002, 585, 69–92. [Google Scholar] [CrossRef]
- Saenger, W. Principles in Nucleic Acid Structure; Springer Verlag: New York, NY, USA, 1984. [Google Scholar]
- Carpenter, J.E.; Weinhold, F. Analysis of the geometry of the hydroxymethyl radical by the “different hybrids for different spins” natural bond orbital procedure. J. Molec. Struct. 1988, 169, 41–62. [Google Scholar] [CrossRef]
- Wesolowski, T.A.; Godzik, A.; Geller, M. Calculations of the conformational properties of Acyclonucleosides. Part I. Stable conformations of acyclovir. Acta Biochim. Polonica. 1987, 34, 111–122. [Google Scholar]
- Tamara Molina, A.; Alcolea Palafox, M. Structure and conformational analysis of the anti-HIV AZT 5′-aminocarbonylphosphonate prodrug using DFT methods. Chem. Phys. 2011, 387, 11–24. [Google Scholar] [CrossRef]
- Alcolea Palafox, M. Molecular structure differences between the antiviral Nucleoside Analogue 5-iodo-2′-deoxyuridine and the natural nucleoside 2′-deoxythymidine using MP2 and DFT methods: Conformational analysis, crystal simulations, DNA pairs and possible behaviour. J. Biomol. Struct. Dyn. 2014, 32, 831–851. [Google Scholar] [CrossRef]
- Alcolea Palafox, M.; Iza, N. Tautomerism of the Natural Thymidine Nucleoside and in the Antiviral Analogue D4T. Structure and influence of an Aqueous Environment Using MP2 and DFT Methods. Phys. Chem. Chem. Phys. 2010, 12, 881–893. [Google Scholar] [CrossRef]
- Birnbaum, G.I.; Cygler, M.; Kusmierek, J.T.; Shugar, D. Structure and conformation of the potent antiherpes 9-(2-hydroxyethoxymethyl)guanine (acycloguanosine). Biochem. Biophys. Res. Comm. 1981, 103, 968–974. [Google Scholar] [CrossRef]
- Yurenko, Y.P.; Zhurakivsky, R.O.; Ghomi, M.; Samijlenko, S.P.; Hovorun, D.M. How many conformers determine the thymidine low-temperature matrix infrared spectrum? DFT and MP2 quantum chemical study. J. Phys. Chem. B. 2007, 111, 9655–9663. [Google Scholar] [CrossRef]
- Parthasarathy, R.; Kim, H. Conformation and sandwiching of bases by azido groups in the crystal structure of 3′-azido-3′-deoxy-thymidine (AZT), an antiviral agent that inhibits HIV reverse transcriptase. Biochem. Biophys. Res. Comm. 1988, 152, 351–358. [Google Scholar] [CrossRef]
- Camerman, A.; Mastropaolo, D.; Camerman, N. Azidothymidine: crystal structure and possible functional role of the azido group. Proc. Natl. Acad. Sci. USA 1987, 84, 8239–8242. [Google Scholar] [CrossRef]
- Dyer, I.; Low, J.N.; Tollin, P.; Wilson, H.R.; Howie, R.A. Structure of 3′-deoxythymidine, AZT. Acta Crystallog. 1988, C44, 767–769. [Google Scholar]
- Painter, G.R.; Andrews, C.W.; Furman, P.A. Conformation and local environment of nucleotides bound to HIV type 1 reverse transcriptase (HIV-1 RT) in the ground state. Nucleos. Nucleot. Nucleic Acids. 2000, 19, 13–29. [Google Scholar] [CrossRef]
- Thewalt, U.; Bugg, C.E.; Marsh, R.E. The crystal structure of guanosine dihydrate and inosine dihydrate. Acta Cryst. 1970, B26, 1089–1101. [Google Scholar] [CrossRef]
- Kazimierczuk, Z.; Stolarski, R.; Shugar, D. Acyclonucleosides: acyclobenzimidazole nucleoside and nucleotide analogues and conformations of the acyclic chains by means of NMR spectroscopy. Acta Biochim. Polonica. 1984, 31, 33–48. [Google Scholar]
- Birnbaum, G.I.; Stolarski, R.; Kazimierczuk, Z.; Shugar, D. Solid state and solution conformations of 1-(β-d-2′-3′-secoribofuranosyl)-5,6-dichlorobenzimidazole, an acyclonucleoside analogue. Can. J. Chem. 1985, 63, 1215–1221. [Google Scholar] [CrossRef]
- Fidanza, N.G.; Sosa, G.L.; Lobayan, R.M.; Peruchena, N.M. Topological analysis of the electronic charge density in nucleoside analogues derivatives of the AZT. Effects of X–H⋯O and X–H⋯F intramolecular H-bonds. J. Molec. Struct. 2005, 722, 65–78. [Google Scholar] [CrossRef]
- Yurenko, Y.P.; Zhurakivsky, R.O.; Samijlenko, S.P.; Hovorun, D.M. Intramolecular CH...O hydrogen bonds in the A1 and B1 DNA-like conformers of canonical nucleosides and their Watson-Crick pairs. Quantum chemical and AIM analysis. J. Biomol. Struct. Dyn. 2011, 29, 51–65. [Google Scholar] [CrossRef]
- Klüfers, P.; Mayer, P. The sodium salt of N1-deprotonated inosine, Na+.C10H11N4O5−.2.5H2O. Acta Crystallogr. 1996, C52, 2970–2972. [Google Scholar]
- Medeiros, G.C.; Thomas, G.-J., Jr. Raman studies of nucleic acids IV. Vibrational spectra and associative interactions of aqueos inosine derivatives. Biochim. Biophys. Acta 1971, 247, 449–462. [Google Scholar] [CrossRef]
- Birnbaum, G.I.; Cygler, M.; Shugar, D. Conformational features of acyclonucleosides: structure of acyclovir, an antiherpes agent. Can. J. Chem. 1984, 62, 2646–2652. [Google Scholar] [CrossRef]
- Lutker, K.M.; Quiñones, R.; Xu, J.; Ramamoorthy, A.; Matzger, A.J. Polymorphs and hydrates of acyclovir. J. Pharm. Sci. 2011, 100, 949–963. [Google Scholar] [CrossRef]
- Sohn, Y.T.; Kim, S.H. Polymorphism and pseudopolymorphism of acyclovir. Arch. Pharm. Res. 2008, 31, 231–234. [Google Scholar] [CrossRef]
- Barboza, F.; Vecchia, D.D.; Tagliari, M.P.; Silva, M.A.S.; Stulzer, H.K. Differential scanning calorimetry as a screening technique in compatibility studies of acyclovir extended release formulations. Pharm. Chem. J. 2009, 43, 363–368. [Google Scholar] [CrossRef]
- Kristl, A.; Srčič, S.; Vrečer, F.; Šuštar, B.; Vojnovic, D. Polymorphism and pseudopolymorphism: Influencing the dissolution properties of the guanine derivative acyclovir. Int. J. Pharm. 1996, 139, 231–235. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alvarez-Ros, M.C.; Palafox, M.A. Conformational Analysis, Molecular Structure and Solid State Simulation of the Antiviral Drug Acyclovir (Zovirax) Using Density Functional Theory Methods. Pharmaceuticals 2014, 7, 695-722. https://doi.org/10.3390/ph7060695
Alvarez-Ros MC, Palafox MA. Conformational Analysis, Molecular Structure and Solid State Simulation of the Antiviral Drug Acyclovir (Zovirax) Using Density Functional Theory Methods. Pharmaceuticals. 2014; 7(6):695-722. https://doi.org/10.3390/ph7060695
Chicago/Turabian StyleAlvarez-Ros, Margarita Clara, and Mauricio Alcolea Palafox. 2014. "Conformational Analysis, Molecular Structure and Solid State Simulation of the Antiviral Drug Acyclovir (Zovirax) Using Density Functional Theory Methods" Pharmaceuticals 7, no. 6: 695-722. https://doi.org/10.3390/ph7060695
APA StyleAlvarez-Ros, M. C., & Palafox, M. A. (2014). Conformational Analysis, Molecular Structure and Solid State Simulation of the Antiviral Drug Acyclovir (Zovirax) Using Density Functional Theory Methods. Pharmaceuticals, 7(6), 695-722. https://doi.org/10.3390/ph7060695





