Evaluation of Docking Machine Learning and Molecular Dynamics Methodologies for DNA-Ligand Systems
Abstract
1. Introduction
2. Results
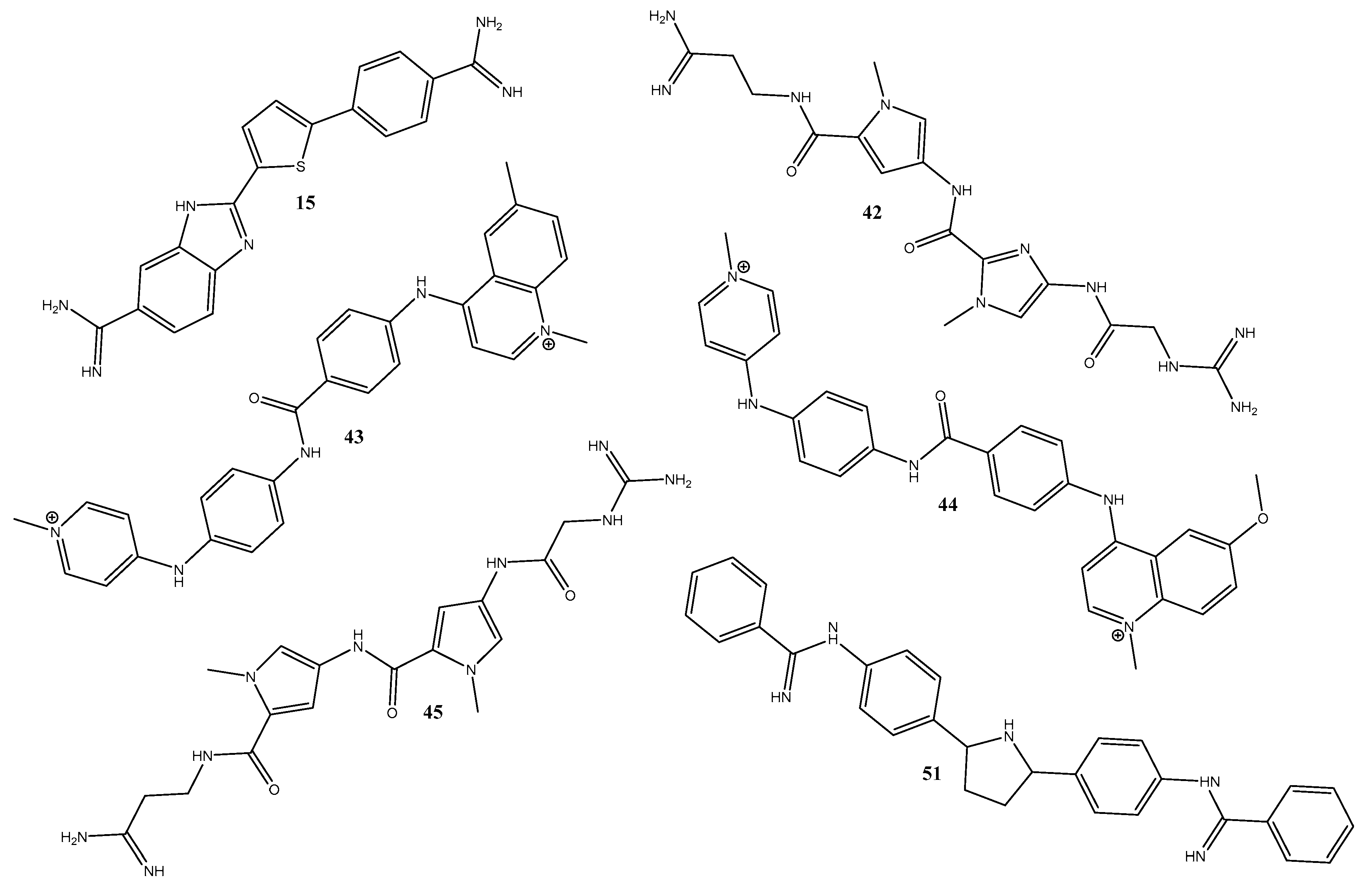
2.1. Molecular Docking
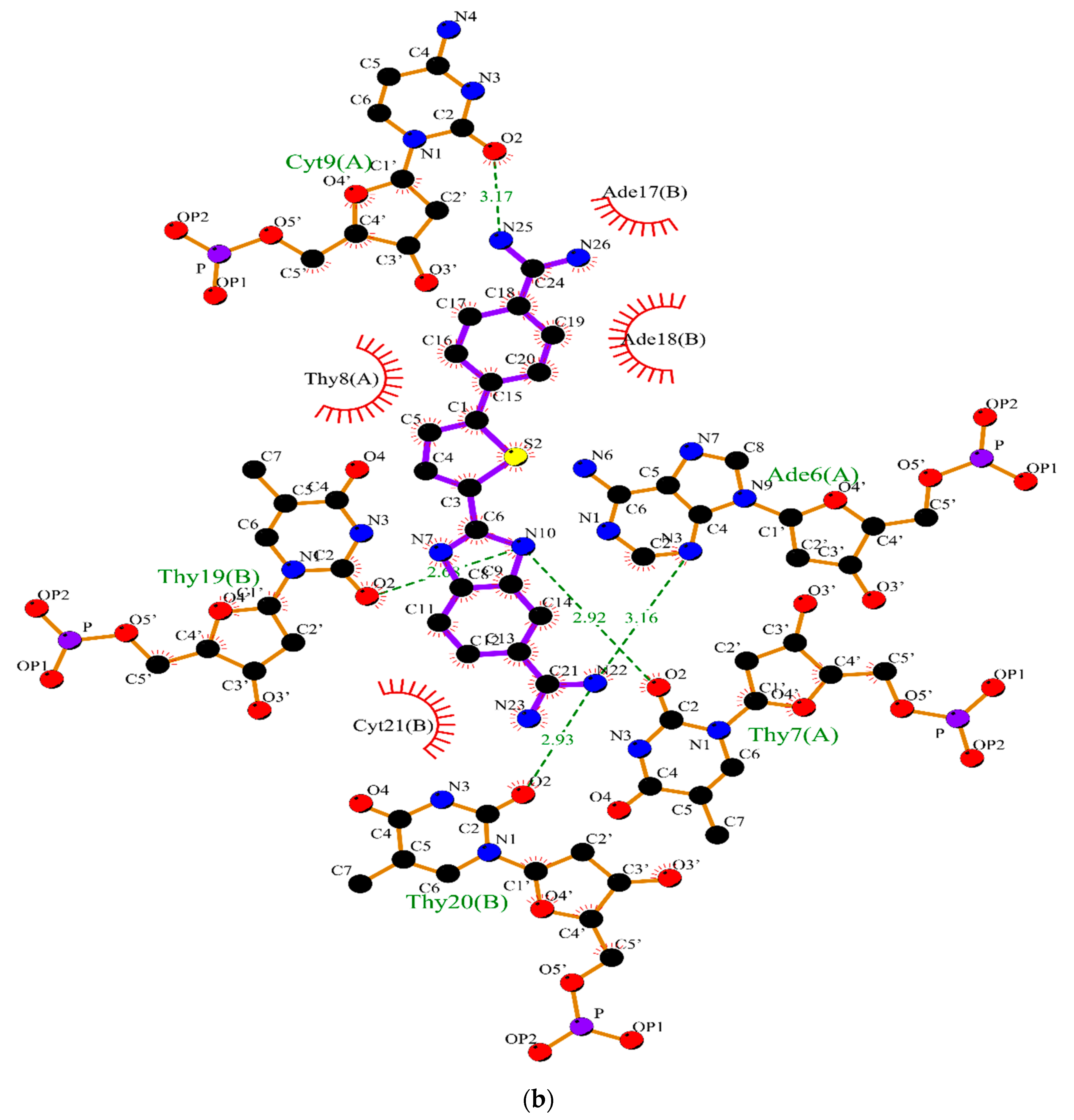
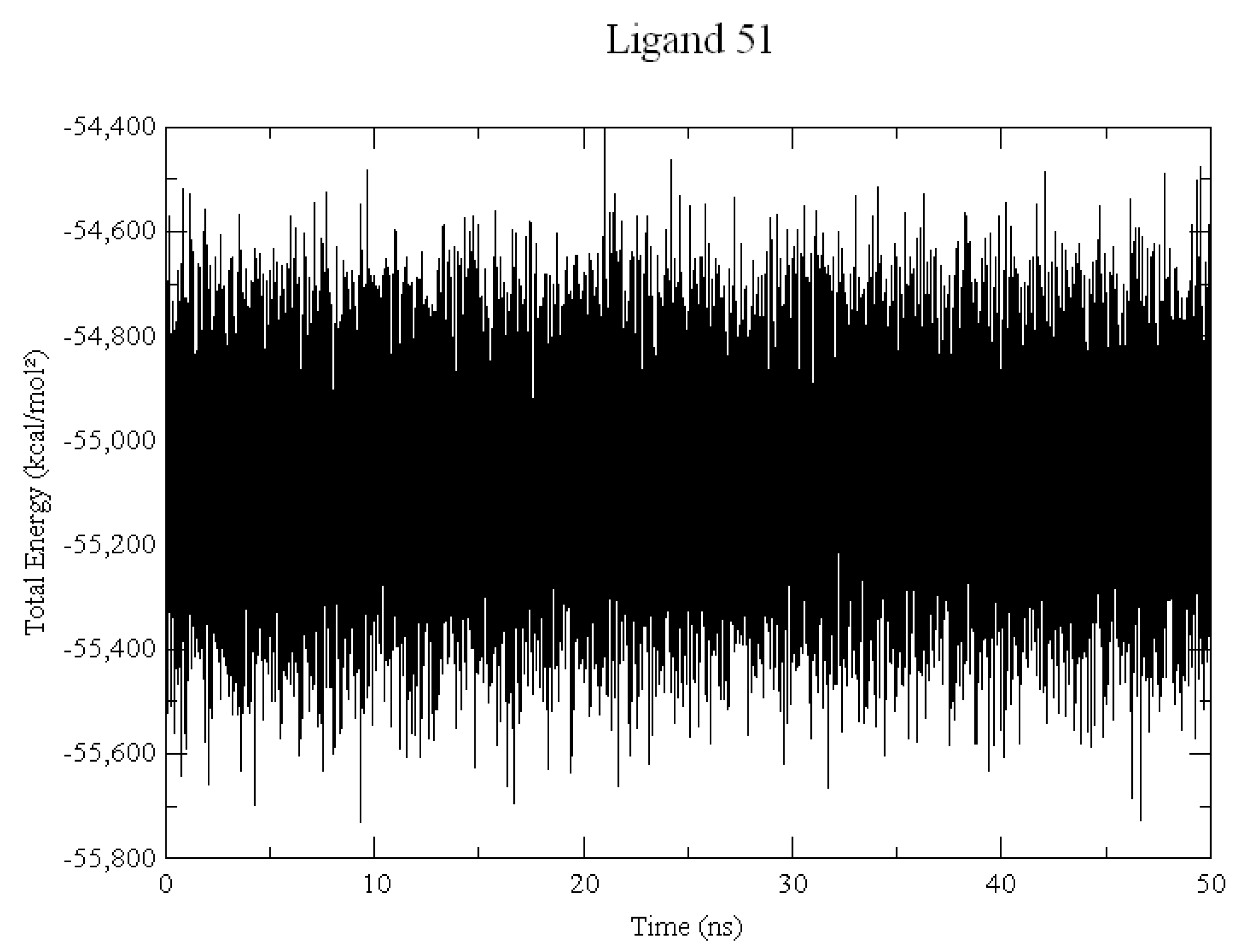
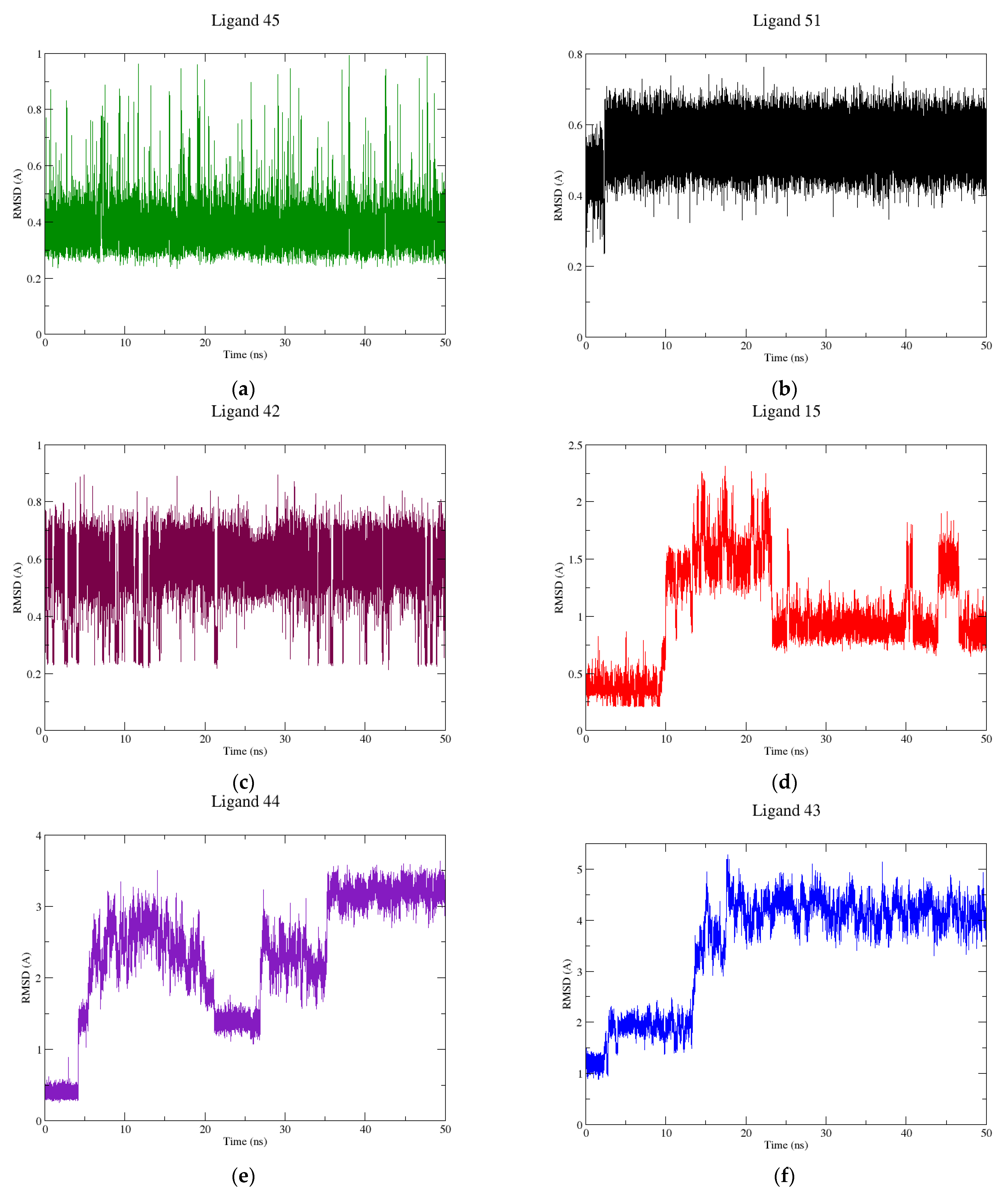
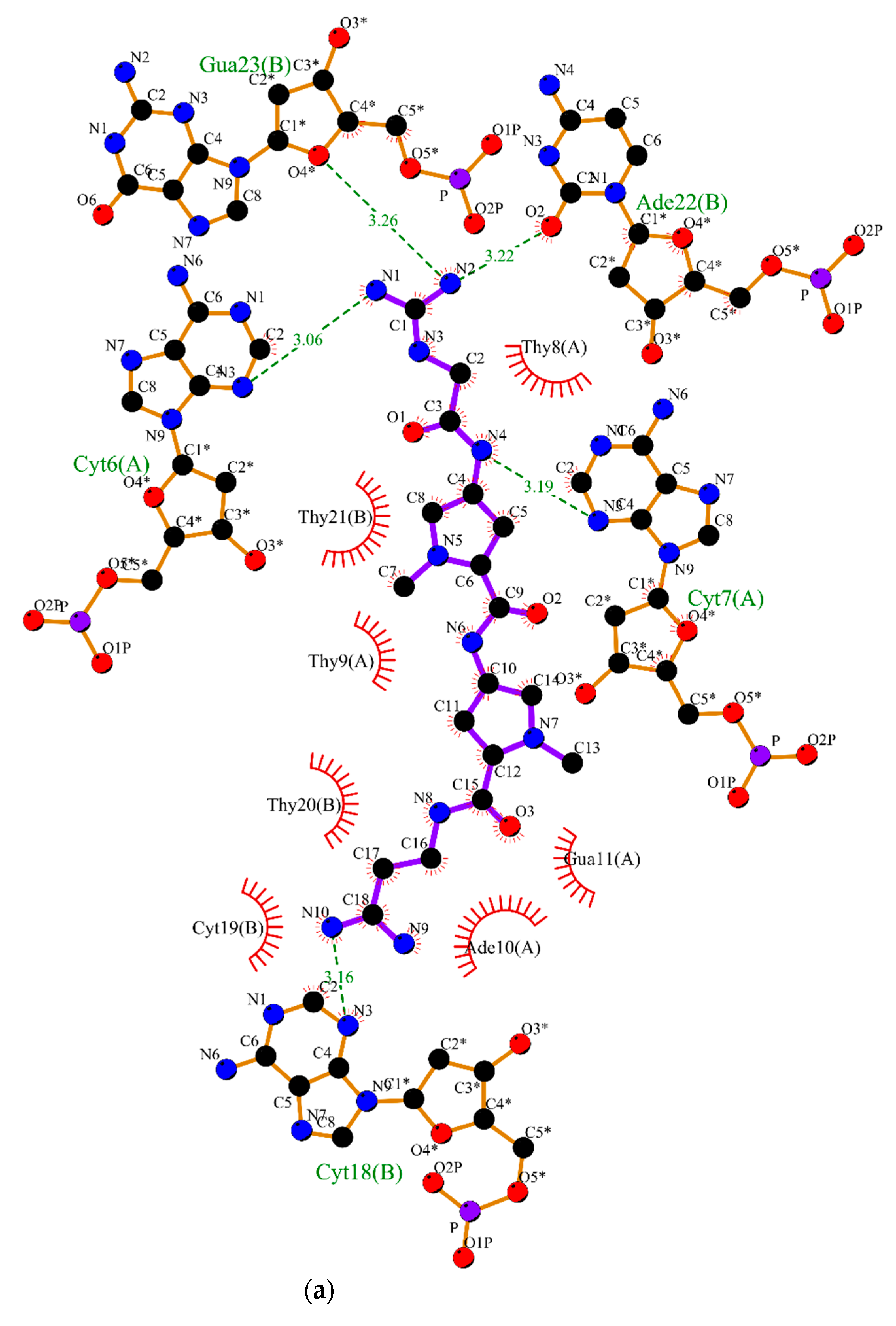
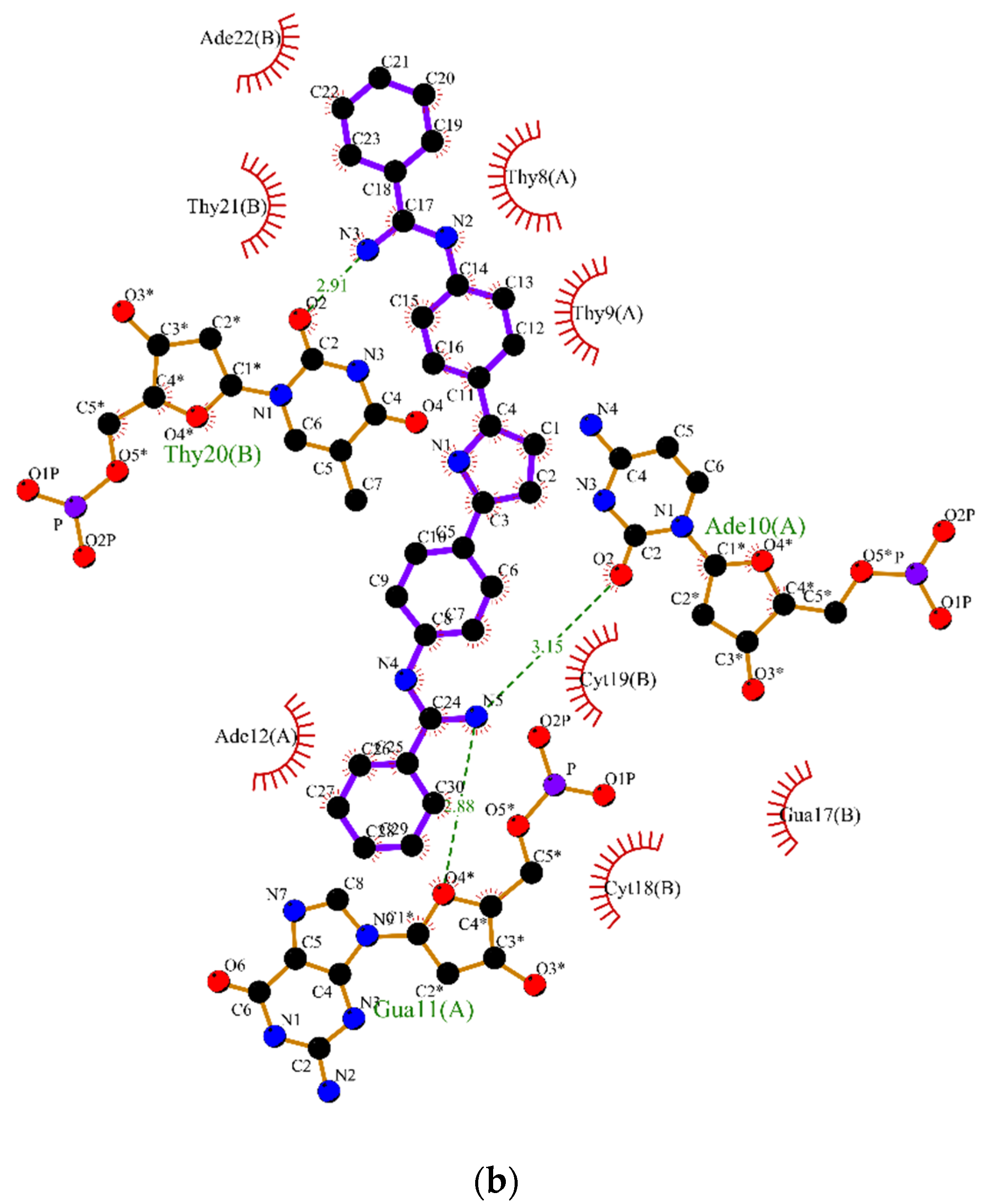
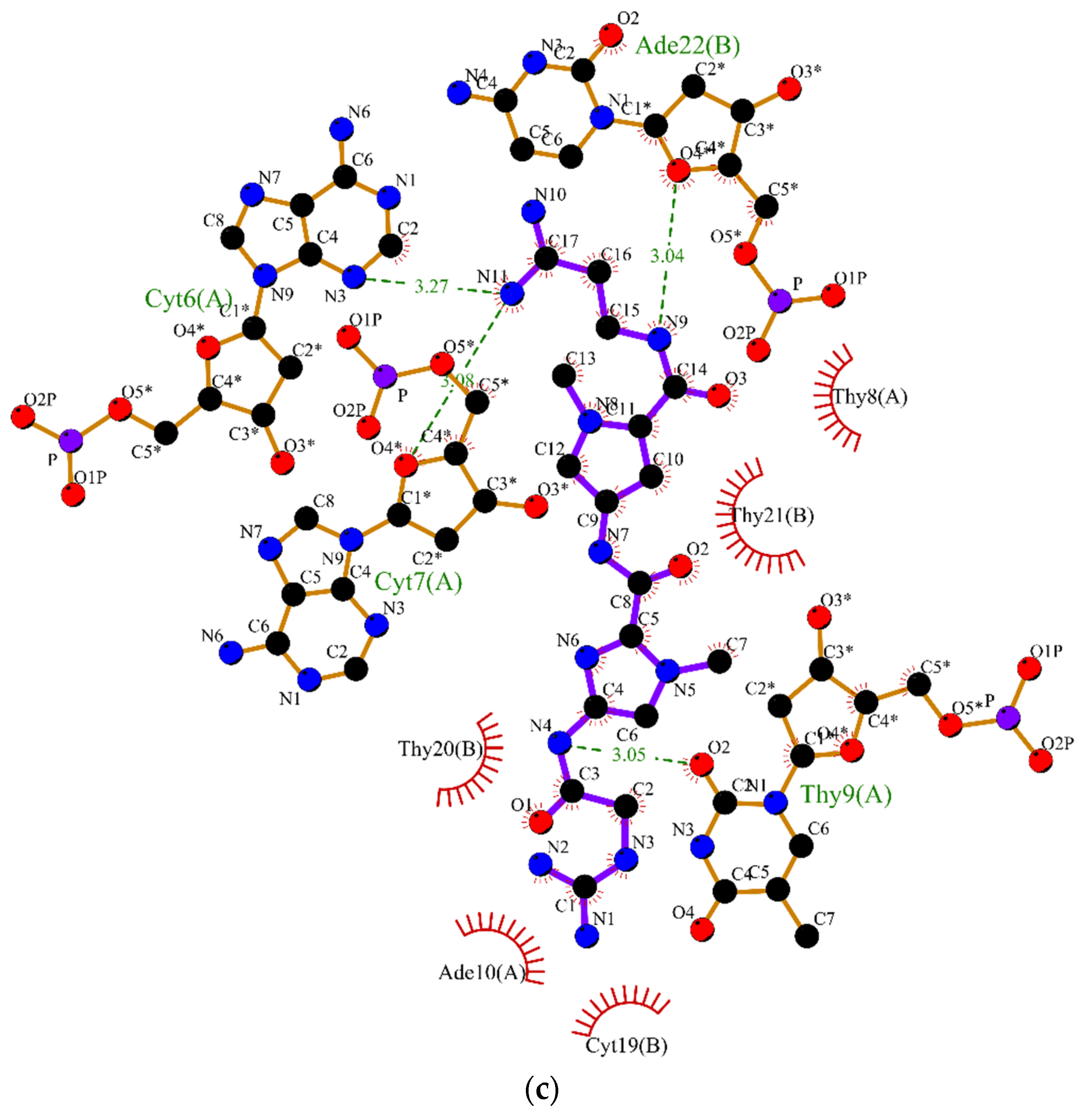
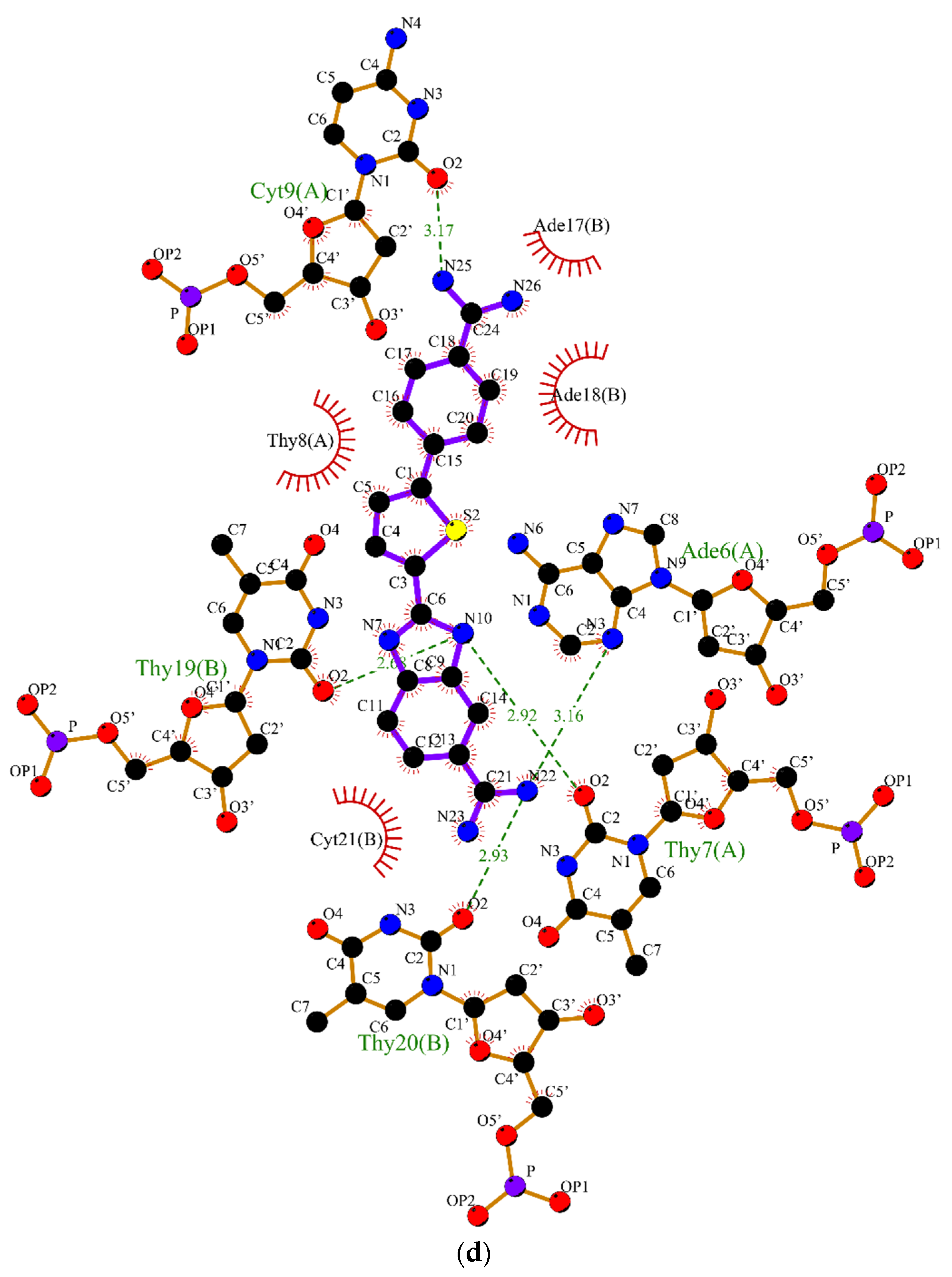
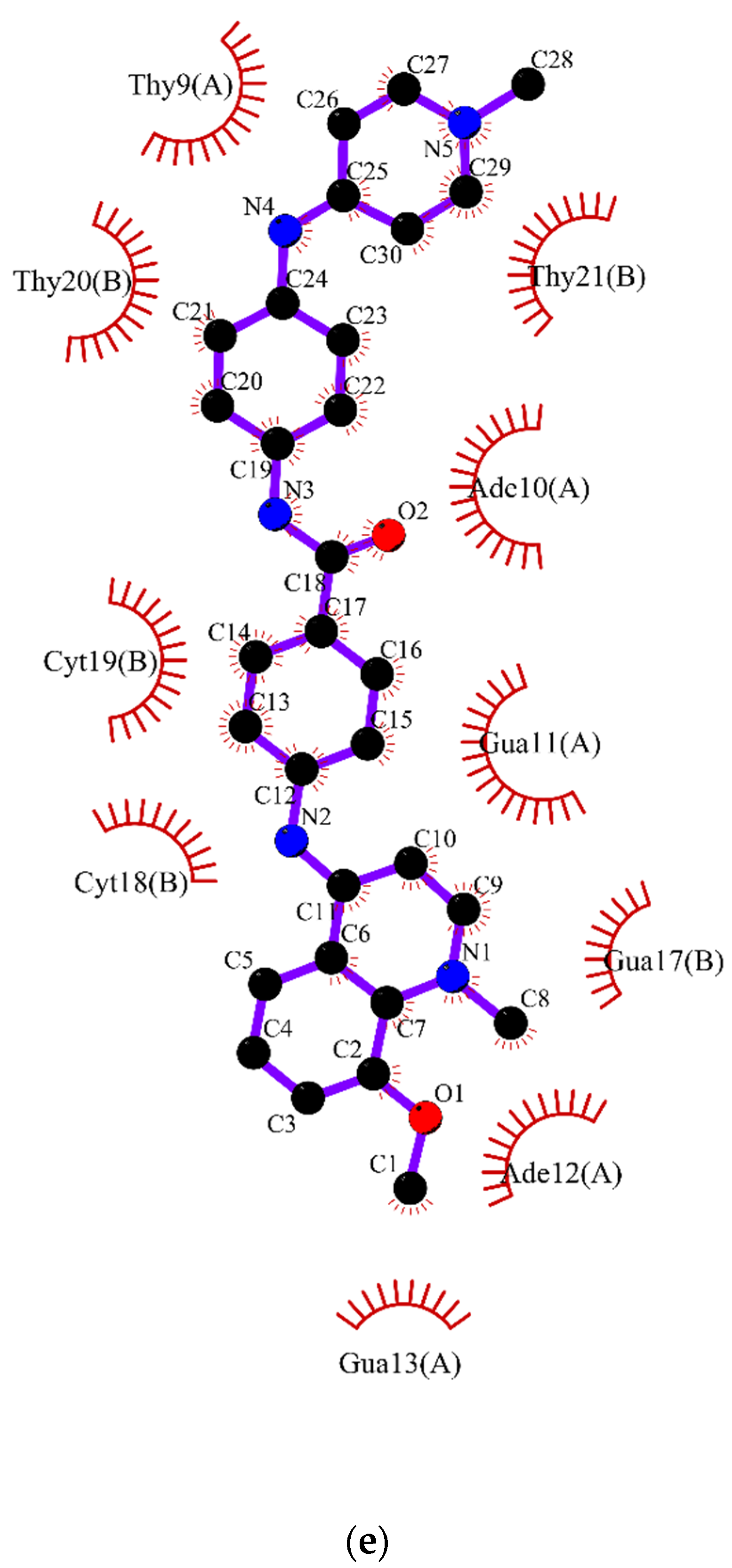
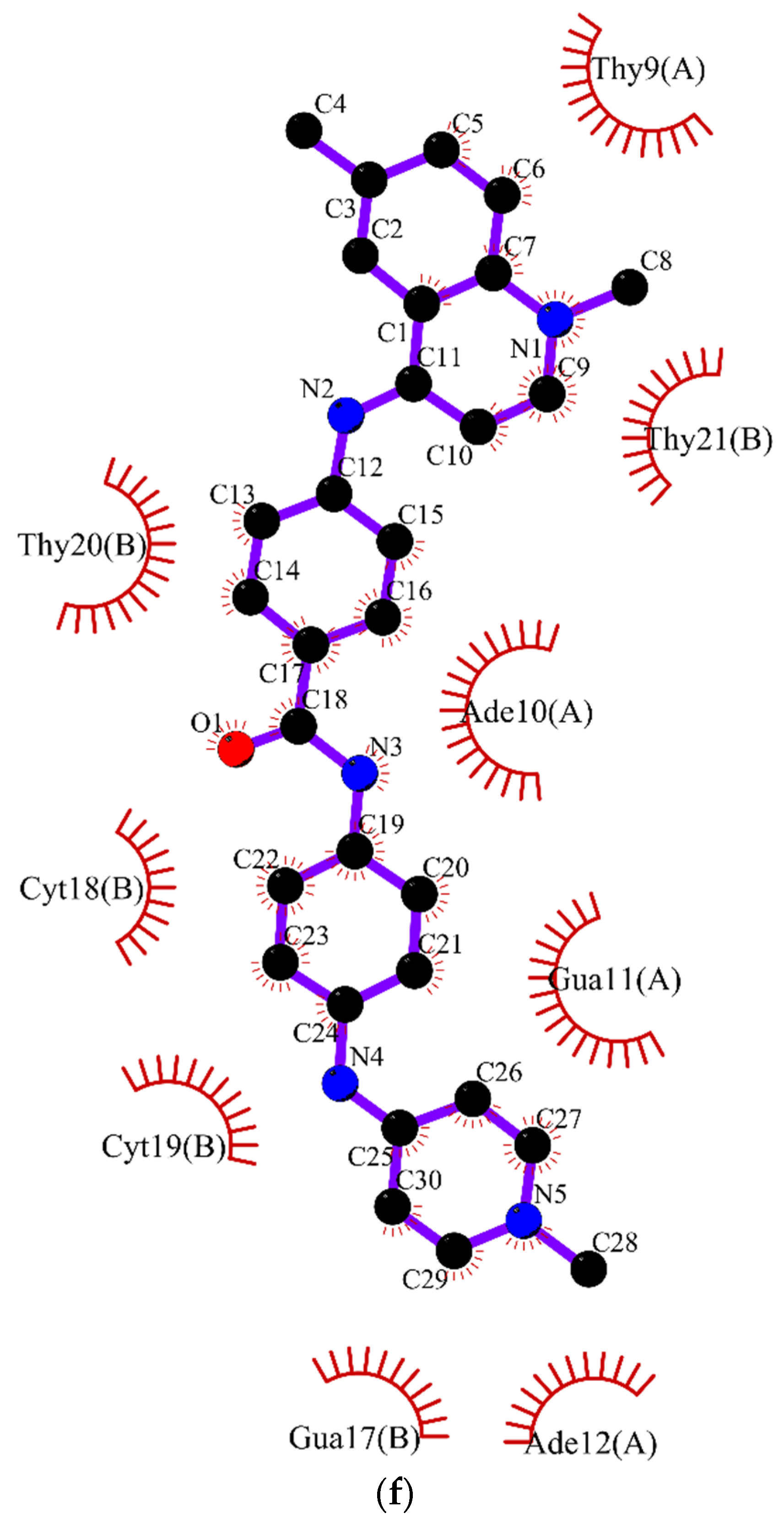
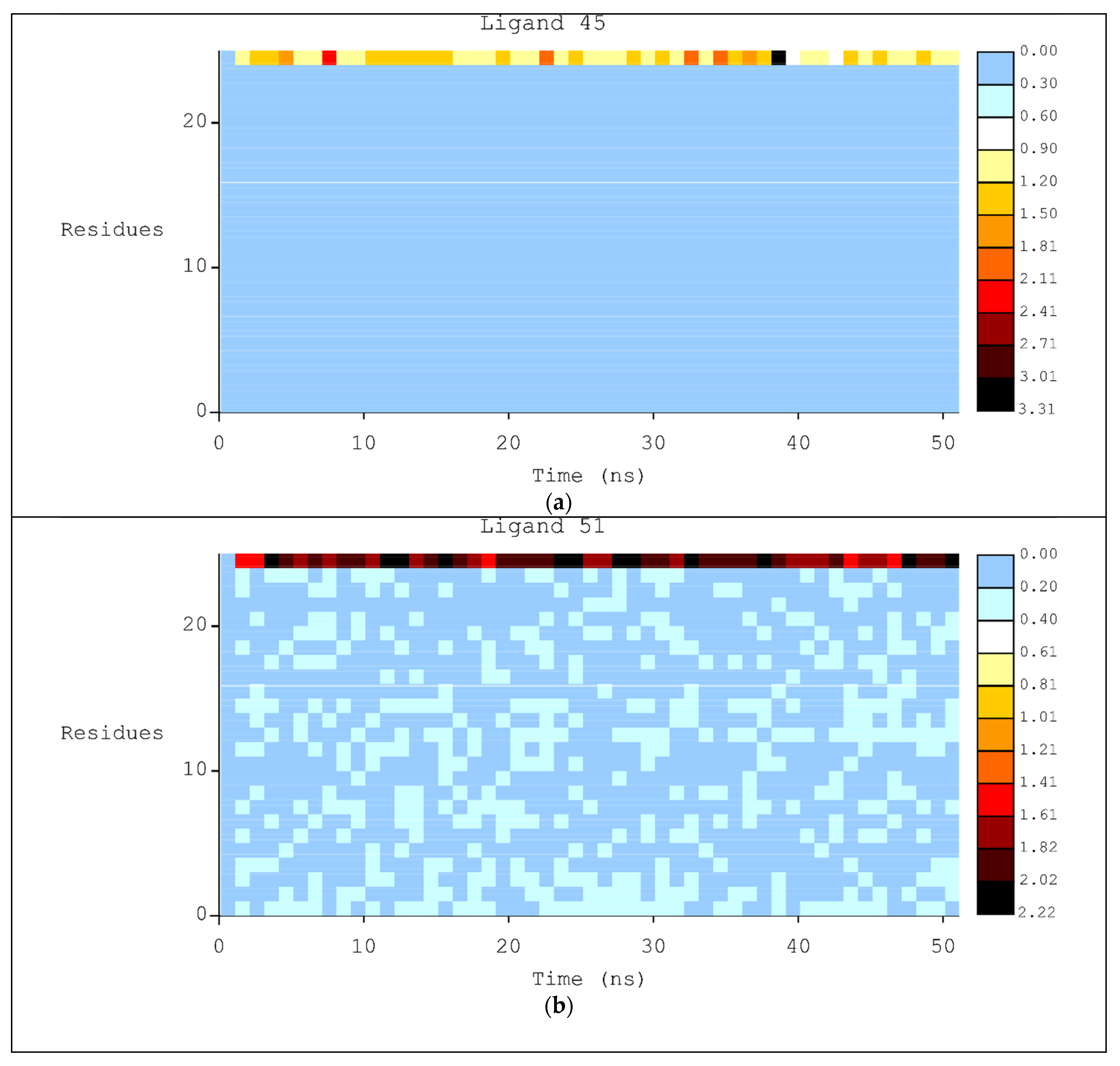
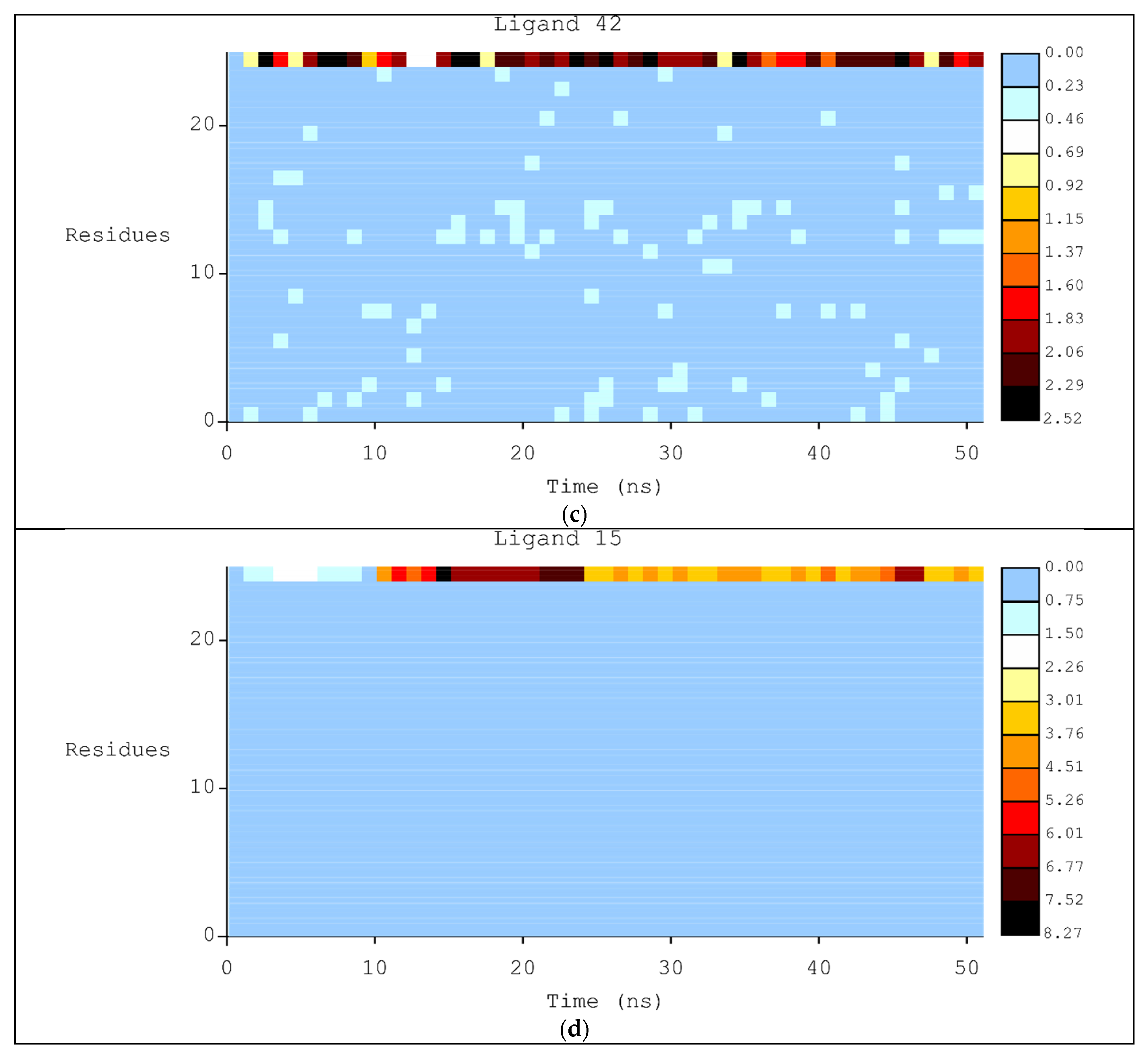
2.2. Molecular Dynamics
3. Discussion
3.1. The Best Docking Methodologies to Study the DNA System
3.2. Molecular Dynamics Simulations
4. Materials and Methods
4.1. Molecular Docking
- removing water molecules and magnesium ions;
- adjusting the protonation state at pH 7.4;
- assigning charges using AMBERff14SB and AM1-BBC;
- minimizing the structure using 100 steps for steepest descent and 10 steps for conjugate gradient, each step measuring 0.02 Å.
4.2. Molecular Dynamics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilad, Y.; Senderowitz, H. Docking Studies on DNA Intercalators. J. Chem. Inf. Modeling 2014, 54, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Silverman, R.B. The Organic Chemistry of Drug Design and Drug Action, 2nd ed.; Elsevier: Evanston, IL, USA, 2004; ISBN 9780080513379. [Google Scholar]
- Plewczynski, D.; Philips, A.; von Grotthuss, M.; Rychlewski, L.; Ginalski, K. HarmonyDOCK: The Structural Analysis of Poses in Protein-Ligand Docking. J. Comput. Biol. 2014, 21, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Bielska, E.; Lucas, X.; Czerwoniec, A.; Kasprzak, J.M.; Kaminska, K.H.; Bujnicki, J.M.; Biology, C.; Bielska, E.; Lucas, X.; Czerwoniec, A.; et al. Virtual Screening Strategies in Drug Design—Methods and Applications. Biotechnologia 2011, 92, 249–264. [Google Scholar] [CrossRef]
- Chen, Y.-C. Beware of Docking! Trends Pharmacol. Sci. 2015, 36, 78–95. [Google Scholar] [CrossRef] [PubMed]
- Mitra, A.; Saikh, F.; Das, J.; Ghosh, S.; Ghosh, R. Studies on the Interaction of a Synthetic Nitro-Flavone Derivative with DNA: A Multi-Spectroscopic and Molecular Docking Approach. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 203, 357–369. [Google Scholar] [CrossRef]
- Lebedeva, A.Y.; Fedorova, O.A.; Tsvetkov, V.B.; Grinberg, V.Y.; Grinberg, N.; Burova, T.; Dubovik, A.S.; Babievsky, K.K.; Fedorov, Y. Novel 18-Crown-6-Ether Containing Mono- and Bisstyryl Dyes Derived from Pyridine Moiety as Fluorescent Dyes for Non-Covalent Interaction with DNA. Dye. Pigment. 2018, 157, 80–92. [Google Scholar] [CrossRef]
- Althaga, I.; Elghalban, M.G.; Saad, F.; Al-fahemi, J.H.; El-metwaly, N.M.; Bondock, S.; Almazroai, L.; Saleh, K.A.; Al-hazmi, G.A. Spectral Characterization, CT-DNA Binding, DFT/B3LYP, Molecular Docking and Antitumor Studies for New Nano-Sized VO (II)-Hydrazonoyl Complexes. J. Mol. Liq. 2017, 242, 662–677. [Google Scholar] [CrossRef]
- Ricci, C.G.; Netz, P.A. Docking Studies on DNA-Ligand Interactions: Building and Application of a Protocol to Identify the Binding Mode. J. Chem. Inf. Modeling 2009, 49, 1925–1935. [Google Scholar] [CrossRef] [PubMed]
- Österberg, F.; Morris, G.M.; Sanner, M.F.; Olson, A.J.; Goodsell, D.S. Automated Docking to Multiple Target Structures: Incorporation of Protein Mobility and Structural Water Heterogeneity in AutoDock. Proteins Struct. Funct. Bioinform. 2002, 46, 34–40. [Google Scholar] [CrossRef]
- Srivastava, H.K.; Chourasia, M.; Kumar, D.; Sastry, G.N. Comparison of Computational Methods to Model DNA Minor Groove Binders. J. Chem. Inf. Modeling 2011, 51, 558–571. [Google Scholar] [CrossRef]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and Validation of a Genetic Algorithm for Flexible Docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K.; et al. Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Robertson, D.H.; Brooks, C.L.; Vieth, M. Detailed Analysis of Grid-Based Molecular Docking: A Case Study of CDOCKER—A CHARMm-Based MD Docking Algorithm. J. Comput. Chem. 2003, 24, 1549–1562. [Google Scholar] [CrossRef]
- Fong, P.; Wong, H.-K. Evaluation of Scoring Function Performance on DNA-Ligand Complexes. Open Med. Chem. J. 2019, 13, 40–49. [Google Scholar] [CrossRef]
- Mooij, W.T.M.; Verdonk, M.L. General and Targeted Statistical Potentials for Protein-Ligand Interactions. Proteins Struct. Funct. Genet. 2005, 61, 272–287. [Google Scholar] [CrossRef] [PubMed]
- Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.v.; Mee, R.P. Empirical Scoring Functions: I. The Development of a Fast Empirical Scoring Function to Estimate the Binding Affinity of Ligands in Receptor Complexes. J. Comput. Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef] [PubMed]
- Maia, E.H.B.; Medaglia, L.R.; da Silva, A.M.; Taranto, A.G. Molecular Architect: A User-Friendly Workflow for Virtual Screening. ACS Omega 2020, 5, 6628–6640. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of New Features and Current Docking Performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef] [PubMed]
- Hamza, A.; Wei, N.-N.; Zhan, C.-G. Ligand-Based Virtual Screening Approach Using a New Scoring Function. J. Chem. Inf. Modeling 2012, 52, 963–974. [Google Scholar] [CrossRef]
- Lätti, S.; Niinivehmas, S.; Pentikäinen, O.T. Rocker: Open Source, Easy-to-Use Tool for AUC and Enrichment Calculations and ROC Visualization. J. Cheminform. 2016, 8, 45. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Hevener, K.E.; White, S.W.; Lee, R.E.; Boyett, J.M. A Statistical Framework to Evaluate Virtual Screening. BMC Bioinform. 2009, 10, 225. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and Simple Linear Regression. Radiology 2003, 227, 617–622. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Stacked Regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- Kwon, S.; Han, S.; Lee, S. A Small Review and Further Studies on the LASSO. J. Korean Data Inf. Sci. Soc. 2013, 24, 1077–1088. [Google Scholar] [CrossRef][Green Version]
- Liu, W.; Li, Q. An Efficient Elastic Net with Regression Coefficients Method for Variable Selection of Spectrum Data. PLoS ONE 2017, 12, e0171122. [Google Scholar] [CrossRef] [PubMed]
- ChemAxon Marvin Version 21.17.0. Available online: https://chemaxon.com/products/marvin (accessed on 27 December 2021).
- Mysinger, M.M.; Carchia, M.; Irwin, J.J.; Shoichet, B.K. Directory of Useful Decoys, Enhanced (DUD-E): Better Ligands and Decoys for Better Benchmarking. J. Med. Chem. 2012, 55, 6582–6594. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. MOPAC2016TM. Available online: http://openmopac.net/MOPAC2016.html (accessed on 14 October 2016).
- Stewart, J.J.P. Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-Optimization of Parameters. J. Mol. Modeling 2013, 19, 1–32. [Google Scholar] [CrossRef]
- Baker, J. An Algorithm for the Location of Transition States. J. Comput. Chem. 1986, 7, 385–395. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Moriwaki, H.; Tian, Y.S.; Kawashita, N.; Takagi, T. Mordred: A Molecular Descriptor Calculator. J. Cheminform. 2018, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Kumar, S.; Huang, C.; Zheng, G.; Bohm, E.; Bhatele, A.; Phillips, J.C.; Yu, H.; Kale, L.V. Scalable Molecular Dynamics with NAMD on the IBM Blue Gene/L System. IBM J. Res. Dev. 2008, 52, 177–188. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hart, K.; Foloppe, N.; Baker, C.M.; Denning, E.J.; Nilsson, L.; MacKerell, A.D. Optimization of the CHARMM Additive Force Field for DNA: Improved Treatment of the BI/BII Conformational Equilibrium. J. Chem. Theory Comput. 2012, 8, 348–362. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Banavali, N.K. All-Atom Empirical Force Field for Nucleic Acids: II. Application to Molecular Dynamics Simulations of DNA and RNA in Solution. J. Comput. Chem. 2000, 21, 105–120. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Feig, M.; Brooks, C.L. Improved Treatment of the Protein Backbone in Empirical Force Fields. J. Am. Chem. Soc. 2004, 126, 698–699. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]

| Algorithm | MSE | R2 Score |
|---|---|---|
| Gradient Boosting Regressor | 3.06 | 0.84 |
| Random Forest Regressor | 13.05 | 0.33 |
| Linear Regressor | 6.18 | 0.68 |
| Voting Regressor | 4.48 | 0.77 |
| Lasso | 7.88 | 0.59 |
| Elastic Net | 7.18 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, T.A.; Medaglia, L.R.; Maia, E.H.B.; Assis, L.C.; de Carvalho, P.B.; da Silva, A.M.; Taranto, A.G. Evaluation of Docking Machine Learning and Molecular Dynamics Methodologies for DNA-Ligand Systems. Pharmaceuticals 2022, 15, 132. https://doi.org/10.3390/ph15020132
de Oliveira TA, Medaglia LR, Maia EHB, Assis LC, de Carvalho PB, da Silva AM, Taranto AG. Evaluation of Docking Machine Learning and Molecular Dynamics Methodologies for DNA-Ligand Systems. Pharmaceuticals. 2022; 15(2):132. https://doi.org/10.3390/ph15020132
Chicago/Turabian Stylede Oliveira, Tiago Alves, Lucas Rolim Medaglia, Eduardo Habib Bechelane Maia, Letícia Cristina Assis, Paulo Batista de Carvalho, Alisson Marques da Silva, and Alex Gutterres Taranto. 2022. "Evaluation of Docking Machine Learning and Molecular Dynamics Methodologies for DNA-Ligand Systems" Pharmaceuticals 15, no. 2: 132. https://doi.org/10.3390/ph15020132
APA Stylede Oliveira, T. A., Medaglia, L. R., Maia, E. H. B., Assis, L. C., de Carvalho, P. B., da Silva, A. M., & Taranto, A. G. (2022). Evaluation of Docking Machine Learning and Molecular Dynamics Methodologies for DNA-Ligand Systems. Pharmaceuticals, 15(2), 132. https://doi.org/10.3390/ph15020132








