Should We Embed in Chemistry? A Comparison of Unsupervised Transfer Learning with PCA, UMAP, and VAE on Molecular Fingerprints
Abstract
:1. Introduction
2. Results and Discussion
2.1. Setting the Baseline
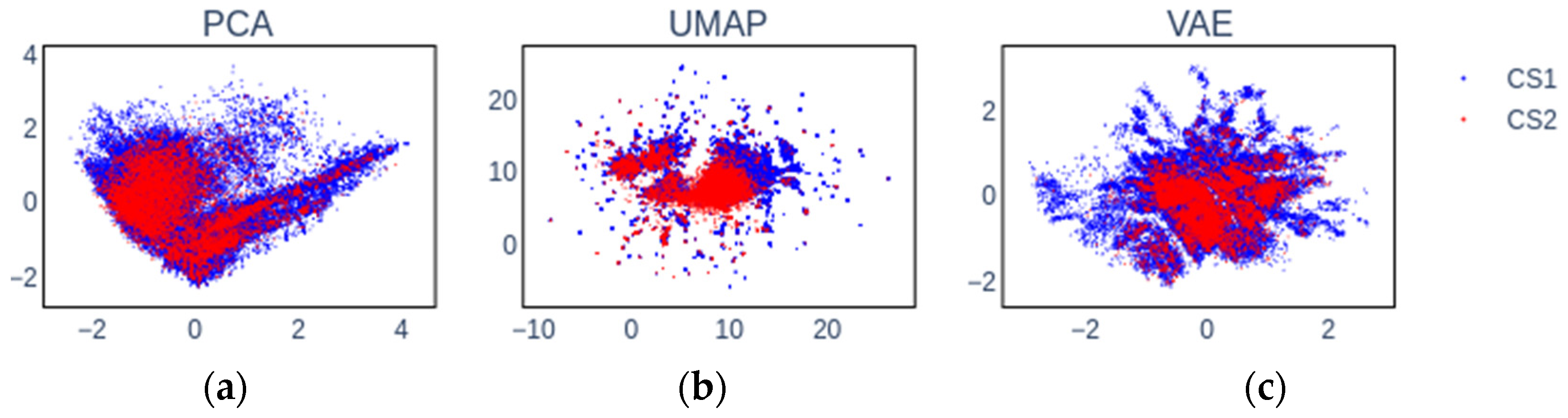
2.2. Embedding Chemical Spaces
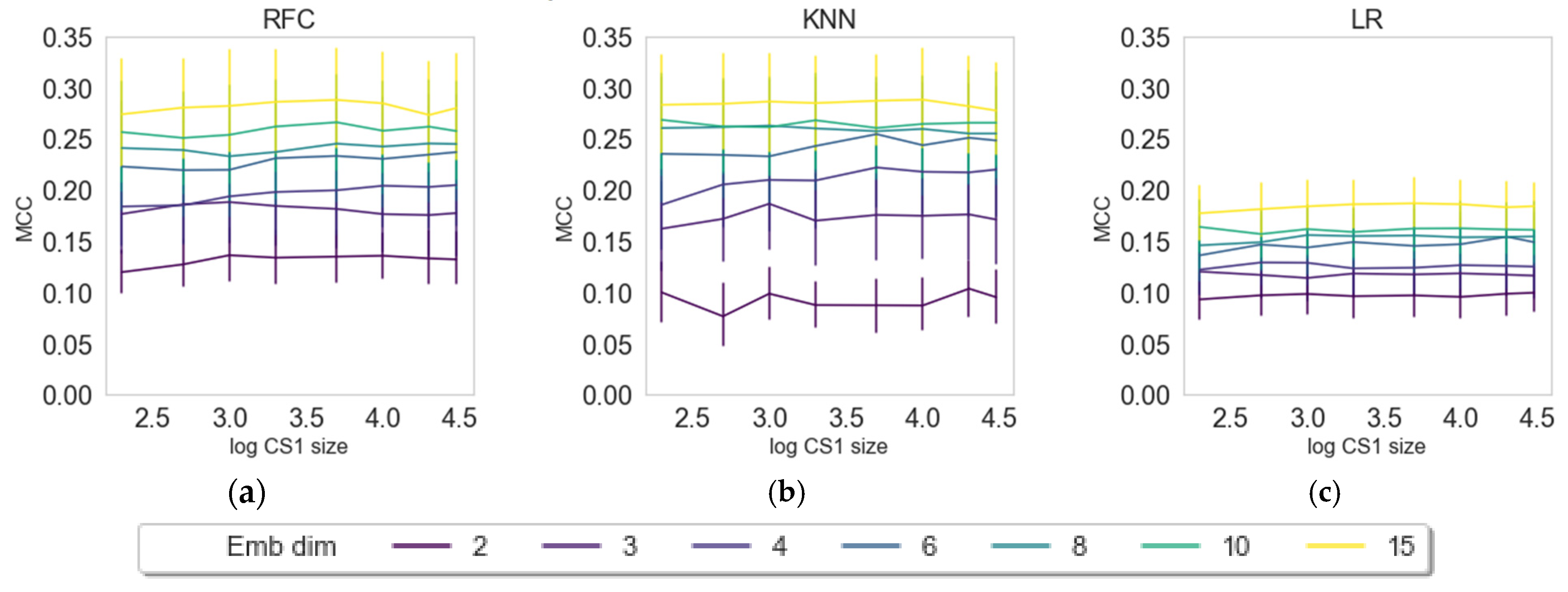
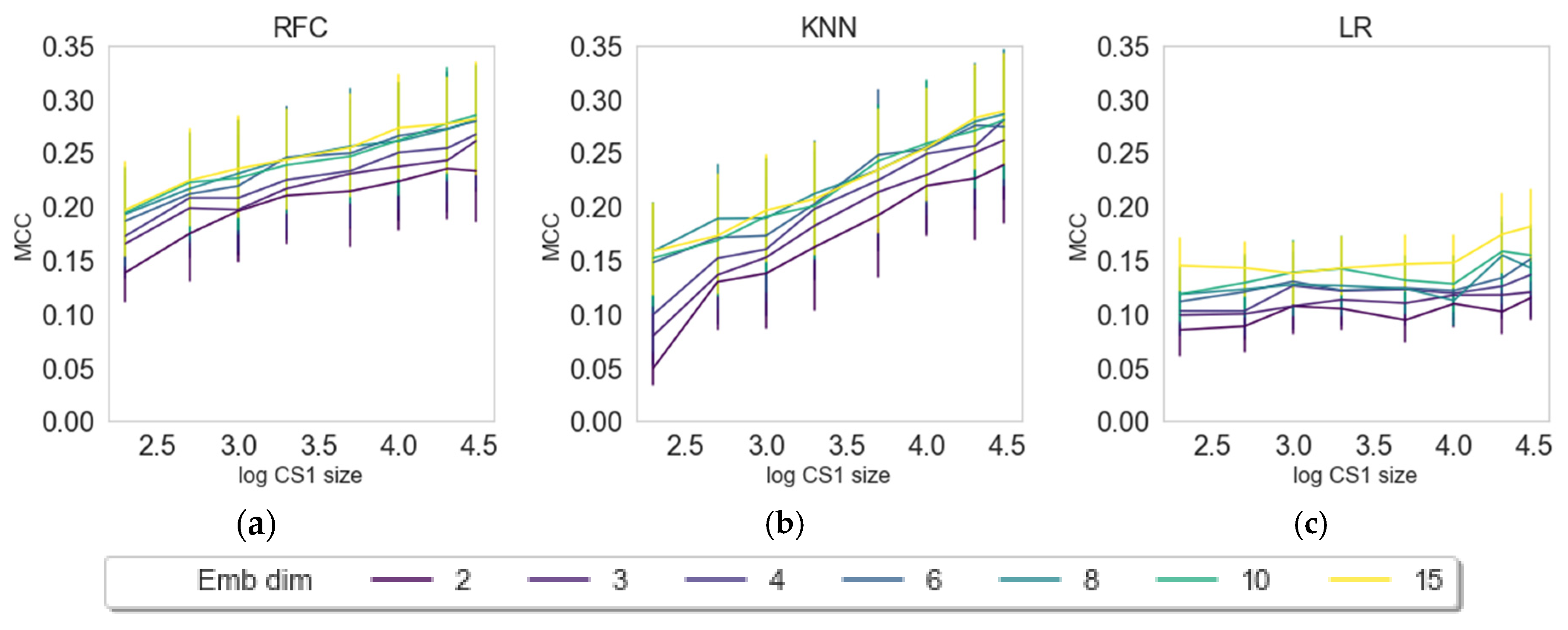
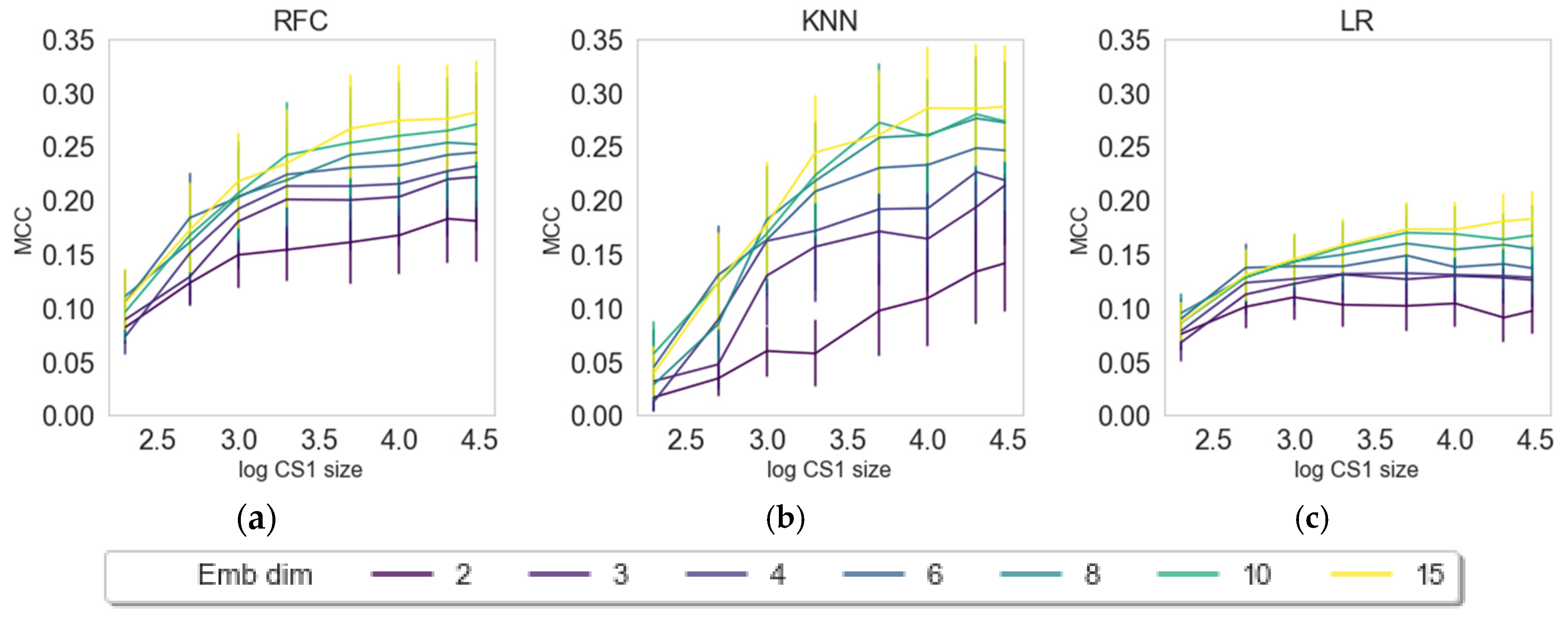
2.3. Impact of Embedding Size and Information Content
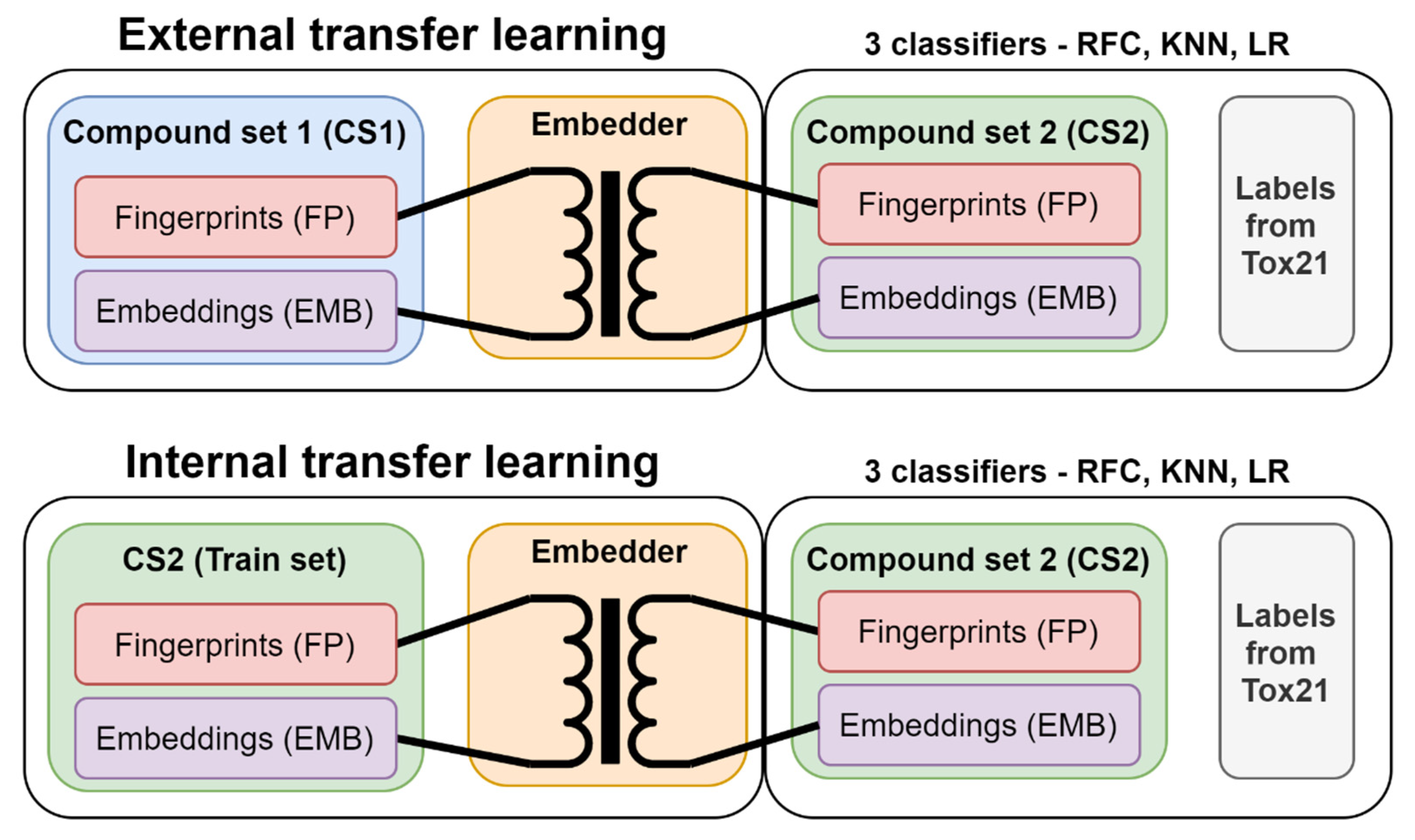
2.4. Internal versus External Knowledge
2.5. Should We Embed? Does Embedding Win over Baseline?
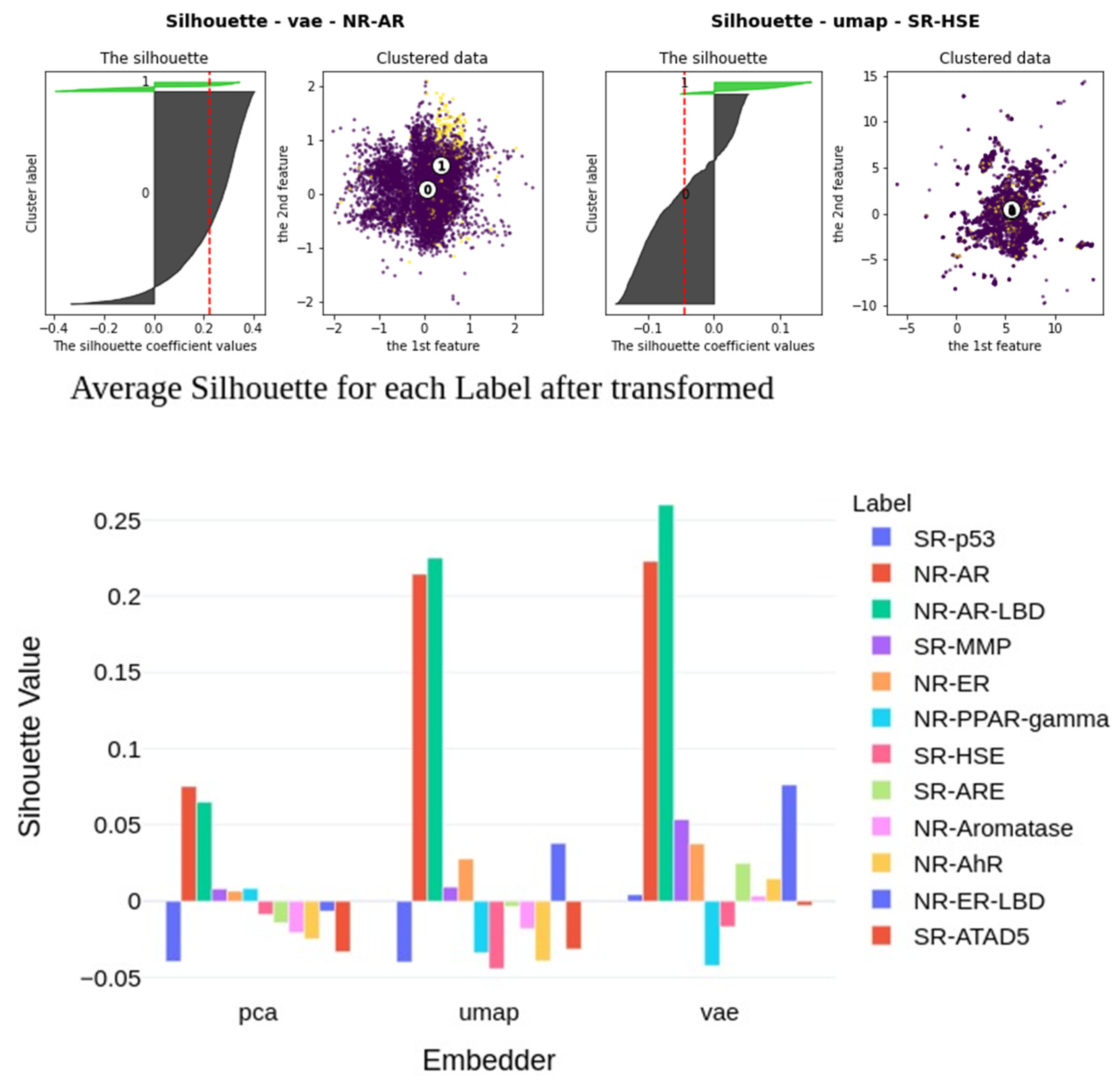
2.6. Insights into Latent Representations
3. Materials and Methods
3.1. Data
3.2. Machine Learning Methods
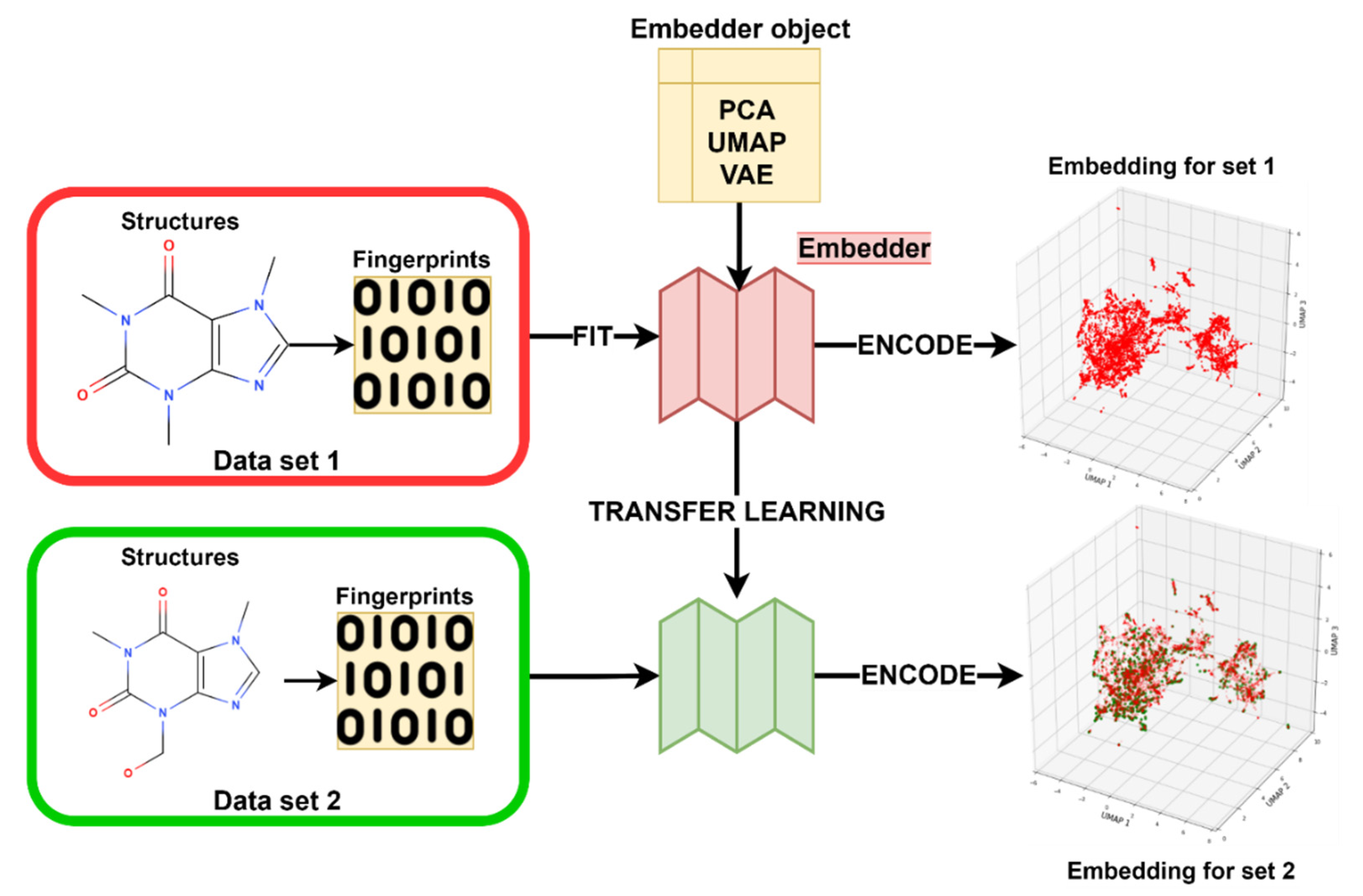
3.3. Transfer Learning with Embeddings
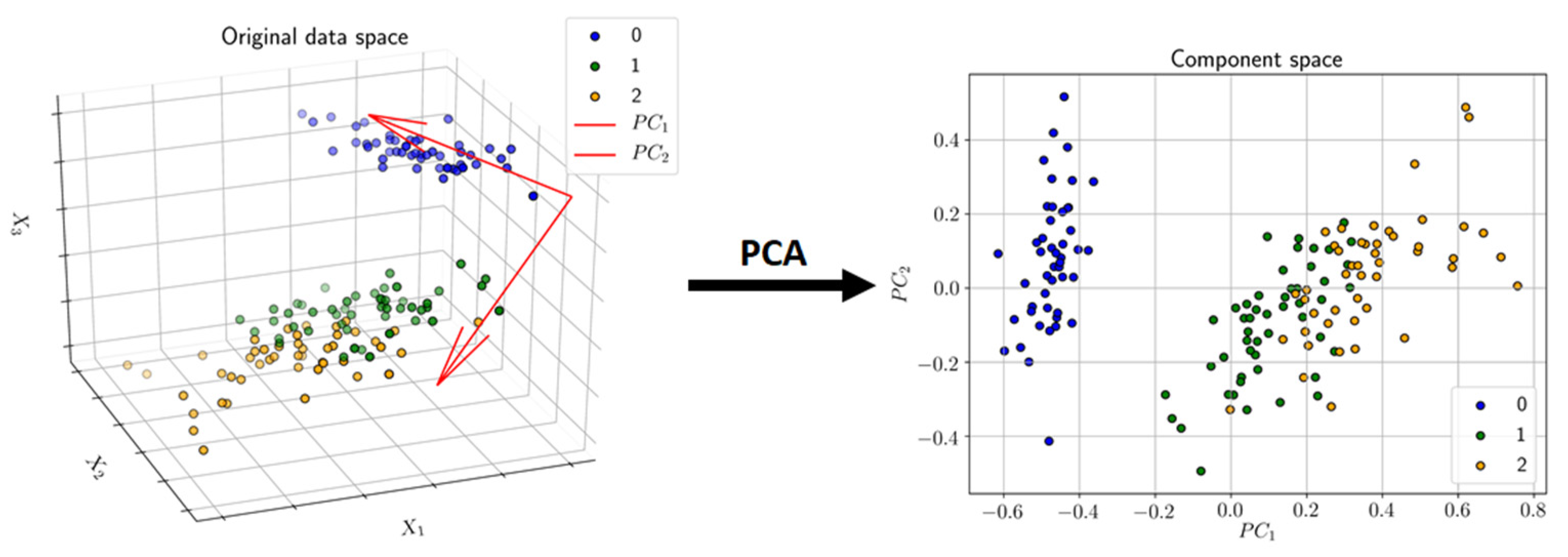
3.3.1. Principal Component Analysis (PCA)
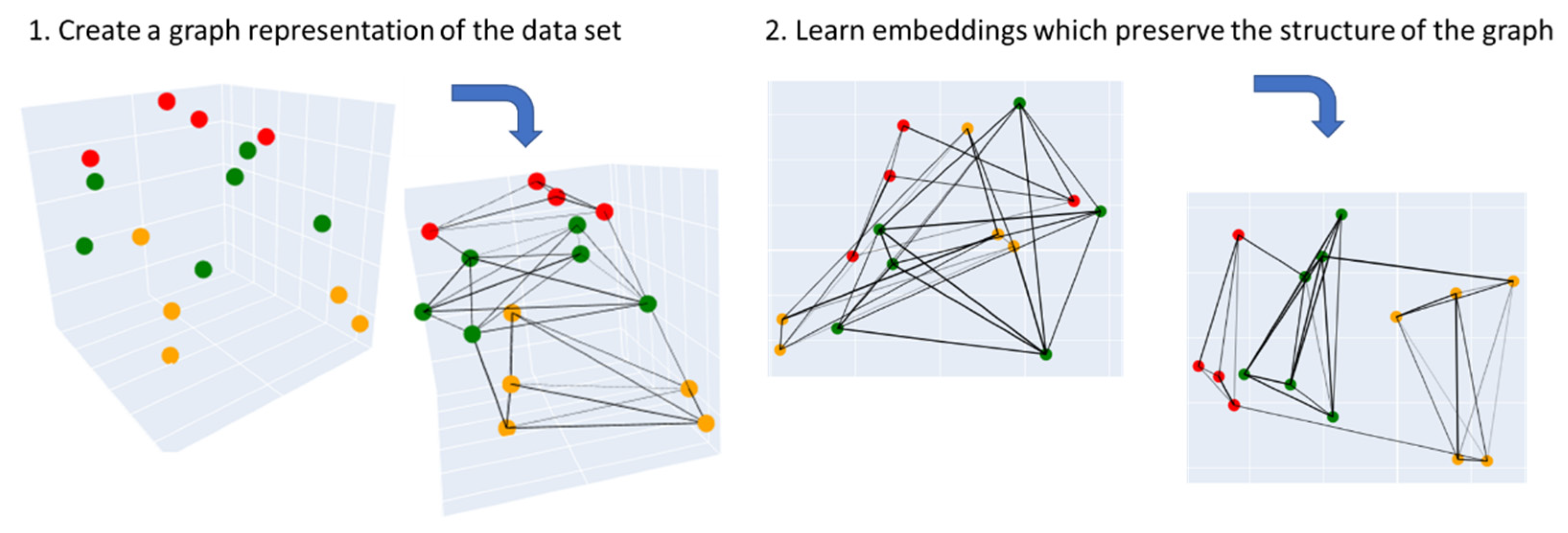
3.3.2. Uniform Manifold Approximation and Projection (UMAP)
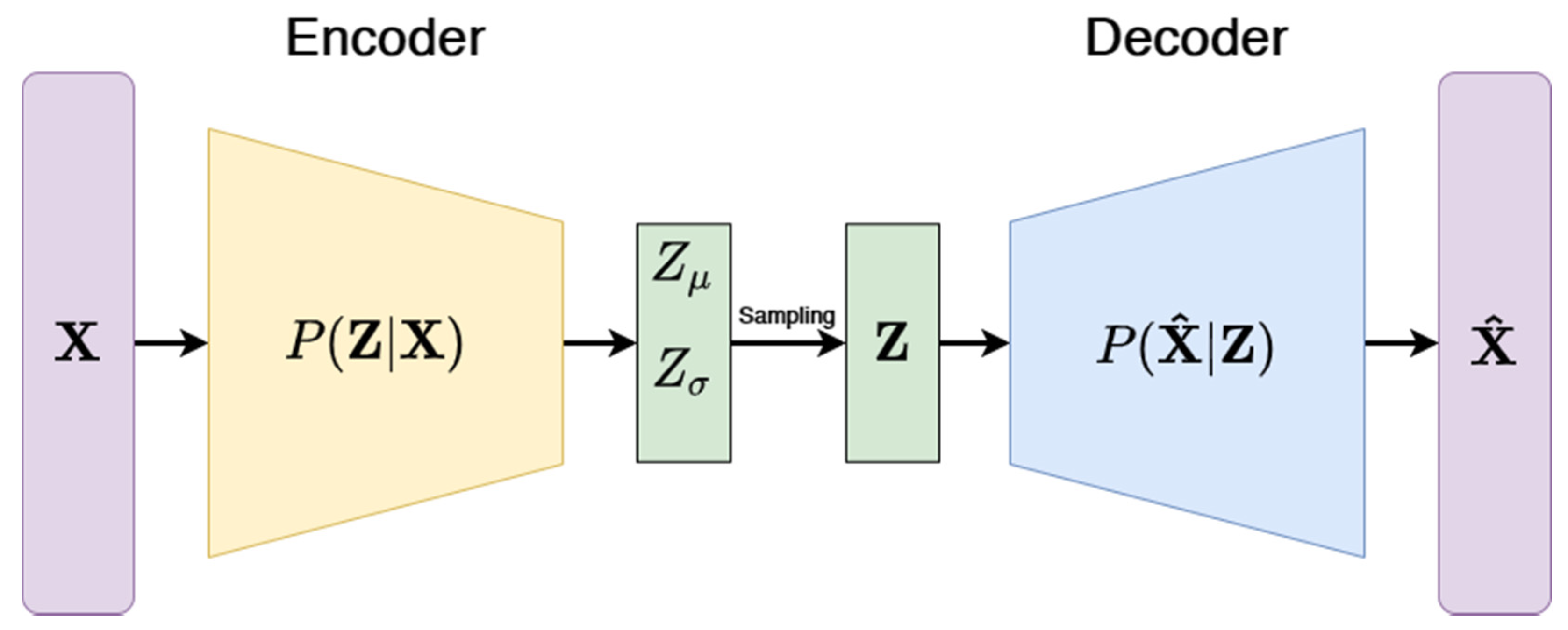
3.3.3. Variational Autoencoders (VAE)
3.3.4. Embedder Training
3.3.5. Modeling
4. Limitations and Future Outlook
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- David, L.; Thakkar, A.; Mercado, R.; Engkvist, O. Molecular representations in AI-driven drug discovery: A review and practical guide. J. Cheminform. 2020, 12, 56. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, F.; Mehridehnavi, A.; Pérez-Garrido, A.; Pérez-Sánchez, H. Neural network and deep-learning algorithms used in QSAR studies: Merits and drawbacks. Drug Discov. Today 2018, 23, 1784–1790. [Google Scholar] [CrossRef] [PubMed]
- Mayr, A.; Klambauer, G.; Unterthiner, T.; Hochreiter, S. DeepTox: Toxicity prediction using deep learning. Front. Environ. Sci. 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- Prykhodko, O.; Johansson, S.V.; Kotsias, P.-C.; Arús-Pous, J.; Bjerrum, E.J.; Engkvist, O.; Chen, H. A de novo molecular generation method using latent vector based generative adversarial network. J. Cheminform. 2019, 11, 74. [Google Scholar] [CrossRef] [Green Version]
- Lusci, A.; Pollastri, G.; Baldi, P. Deep architectures and deep learning in chemoinformatics: The prediction of aqueous solubility for drug-like molecules. J. Chem. Inf. Model. 2013, 53, 1563–1575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capuccini, M.; Ahmed, L.; Schaal, W.; Laure, E.; Spjuth, O. Large-scale virtual screening on public cloud resources with Apache Spark. J. Cheminformatics 2017, 9, 15. [Google Scholar] [CrossRef] [Green Version]
- Lovrić, M.; Molero, J.M.; Kern, R. PySpark and RDKit: Moving towards big data in cheminformatics. Mol. Inform. 2019, 38, e1800082. [Google Scholar] [CrossRef]
- Tetko, I.V.; Engkvist, O.; Chen, H. Does “Big Data” exist in medicinal chemistry, and if so, how can it be harnessed? Future Med. Chem. 2016, 8, 1801–1806. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Kogej, T.; Engkvist, O. Cheminformatics in drug discovery, an industrial perspective. Mol. Inform. 2018, 37. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Jaeger, S.; Fulle, S.; Turk, S. Mol2vec: Unsupervised machine learning approach with chemical intuition. J. Chem. Inf. Model. 2018, 58, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Wu, Z.; Hsieh, C.-Y.; Chen, G.; Liao, B.; Wang, Z.; Shen, C.; Cao, D.; Wu, J.; Hou, T. Could graph neural networks learn better molecular representation for drug discovery? A comparison study of descriptor-based and graph-based models. J. Cheminform. 2021, 13, 12. [Google Scholar] [CrossRef] [PubMed]
- Lovrić, M.; Malev, O.; Klobučar, G.; Kern, R.; Liu, J.; Lučić, B. Predictive capability of QSAR models based on the CompTox zebrafish embryo assays: An imbalanced classification problem. Molecules 2021, 26, 1617. [Google Scholar] [CrossRef] [PubMed]
- Abdelaziz, A.; Spahn-Langguth, H.; Schramm, K.-W.; Tetko, I.V. Consensus modeling for HTS assays using in silico descriptors calculates the best balanced accuracy in Tox21 challenge. Front. Environ. Sci. 2016, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Idakwo, G.; Thangapandian, S.; Luttrell, J.; Li, Y.; Wang, N.; Zhou, Z.; Hong, H.; Yang, B.; Zhang, C.; Gong, P. Structure–Activity relationship-based chemical classification of highly imbalanced Tox21 datasets. J. Cheminform. 2020, 12, 66. [Google Scholar] [CrossRef] [PubMed]
- Lovrić, M.; Pavlović, K.; Žuvela, P.; Spataru, A.; Lučić, B.; Kern, R.; Wong, M.W. Machine learning in prediction of intrinsic aqueous solubility of drug-like compounds: Generalization, complexity, or predictive ability? J. Chemom. 2021, e3349. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In Database Theory—ICDT 2001. Lecture Notes in Computer Science; van den Bussche, J., Vianu, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1973. [Google Scholar] [CrossRef] [Green Version]
- Geng, X.; Zhan, D.-C.; Zhou, Z.-H. Supervised nonlinear dimensionality reduction for visualization and classification. IEEE Trans. Syst. Man Cybern. Part B 2005, 35, 1098–1107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis—MLSDA’14, Gold Coast, QLD, Australia, 2 December 2014; p. 4. [Google Scholar]
- Duricic, T.; Hussain, H.; Lacic, E.; Kowald, D.; Helic, D.; Lex, E. Empirical comparison of graph embeddings for trust-based collaborative filtering. In Proceedings of the 25th International Symposium on Methodologies for Intelligent Systems, Graz, Austria, 23–25 September 2020. [Google Scholar]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet allocation. J. Mach. Learn. Res 2003, 3, 993–1022. [Google Scholar]
- Choi, S. Algorithms for orthogonal nonnegative matrix factorization. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1828–1832. [Google Scholar]
- Sampson, G.; Rumelhart, D.E.; McClelland, J.L. The PDP research group parallel distributed processing: Explorations in the microstructures of cognition. Language 1987, 63, 871. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Van der Maaten, L. Hinton G visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for dimension reduction. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Shrivastava, A.; Kell, D. FragNet, a contrastive learning-based transformer model for clustering, interpreting, visualizing, and navigating chemical space. Molecules 2021, 26, 2065. [Google Scholar] [CrossRef]
- Probst, D.; Reymond, J.-L. Visualization of very large high-dimensional data sets as minimum spanning trees. J. Cheminformatics 2020, 12, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.-A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Obermeier, M.M.; Wicaksono, W.A.; Taffner, J.; Bergna, A.; Poehlein, A.; Cernava, T.; Lindstaedt, S.; Lovric, M.; Bogotá, C.A.M.; Be1rg, G. Plant resistome profiling in evolutionary old bog vegetation provides new clues to understand emergence of multi-resistance. ISME J. 2021, 15, 921–937. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. Adv. Neural. Inf. Process. Syst. 2007, 153–160. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Kwon, Y.; Yoo, J.; Choi, Y.-S.; Son, W.-J.; Lee, D.; Kang, S. Efficient learning of non-autoregressive graph variational autoencoders for molecular graph generation. J. Cheminformatics 2019, 11, 70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bjerrum, E.J.; Sattarov, B. Improving chemical autoencoder latent space and molecular de novo generation diversity with heteroencoders. Biomolecules 2018, 8, 131. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Mucs, D.; Norinder, U.; Svensson, F. LightGBM: An effective and scalable algorithm for prediction of chemical toxicity–application to the Tox21 and mutagenicity data sets. J. Chem. Inf. Model. 2019, 59, 4150–4158. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Li, X.; Gudivada, V.N. Augmentation and evaluation of training data for deep learning. In Proceedings of the 2017 IEEE International Conference on Big Data (IEEE Big Data 2017), Boston, MA, USA, 11–14 December 2017; pp. 2603–2611. [Google Scholar]
- Ehuang, R.; Exia, M.; Nguyen, D.-T.; Ezhao, T.; Esakamuru, S.; Ezhao, J.; Shahane, S.A.; Erossoshek, A.; Esimeonov, A. Tox21Challenge to build predictive models of nuclear receptor and stress response pathways as mediated by exposure to environmental chemicals and drugs. Front. Environ. Sci. 2016, 3, 85. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, M.; Ban, F.; Woo, G.; Hsing, M.; Yamazaki, T.; Leblanc, E.; Rennie, P.S.; Welch, W.J.; Cherkasov, A. Toxic colors: The use of deep learning for predicting toxicity of compounds merely from their graphic images. J. Chem. Inf. Model. 2018, 58, 1533–1543. [Google Scholar] [CrossRef] [PubMed]
- Hemmerich, J.; Asilar, E.; Ecker, G. Conformational oversampling as data augmentation for molecules. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2019; pp. 788–792. [Google Scholar]
- Klimenko, K.; Rosenberg, S.A.; Dybdahl, M.; Wedebye, E.B.; Nikolov, N.G. QSAR modelling of a large imbalanced aryl hydrocarbon activation dataset by rational and random sampling and screening of 80,086 REACH pre-registered and/or registered substances. PLoS ONE 2019, 14, e0213848. [Google Scholar] [CrossRef] [PubMed]
- Fourches, D.; Muratov, E.; Tropsha, A. Trust, but verify: On the importance of chemical structure curation in cheminformatics and QSAR modeling research. J. Chem. Inf. Model. 2010, 50, 1189–1204. [Google Scholar] [CrossRef]
- Greg Landrum, RDKit. Available online: http://rdkit.org (accessed on 21 May 2020).
- Gütlein, M.; Kramer, S. Filtered circular fingerprints improve either prediction or runtime performance while retaining interpretability. J. Cheminform. 2016, 8, 60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landrum G RDKit: Colliding Bits III. Available online: http://rdkit.blogspot.com/2016/02/colliding-bits-iii.html (accessed on 23 December 2019).
- Alygizakis, N.; Slobodnik, J. S32 | REACH2017 | >68,600 REACH Chemicals. 2018. Available online: https://zenodo.org/record/4248826 (accessed on 23 December 2020).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classfication. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Lučić, B.; Batista, J.; Bojović, V.; Lovrić, M.; Kržić, A.S.; Bešlo, D.; Nadramija, D.; Vikić-Topić, D. Estimation of random accuracy and its use in validation of predictive quality of classification models within predictive challenges. Croat. Chem. Acta 2019, 92, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Boughorbel, S.; Jarray, F.; El Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef]
- Žuvela, P.; Lovrić, M.; Yousefian-Jazi, A.; Liu, J.J. Ensemble learning approaches to data imbalance and competing objectives in design of an industrial machine vision system. Ind. Eng. Chem. Res. 2020, 59, 4636–4645. [Google Scholar] [CrossRef]
- Lerman, P.M. Fitting segmented regression models by Grid Search. J. R. Stat. Soc. Ser. C Appl. Stat. 1980, 29, 77. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Deisenroth, M.P.; Faisal, A.A.; Ong, C.S. Mathematics for Machine Learning; Cambridge University Press: Cambridge, UK, 2020; p. 391. [Google Scholar]
- Sainburg, T.; McInnes, L.; Gentner, T.Q. Parametric UMAP embeddings for representation and semi-supervised learning. arXiv 2020, arXiv:2009.12981. [Google Scholar]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Jordan, M.I.; Ghahramani, Z.; Jaakkola, T.S.; Saul, L.K. An introduction to variational methods for graphical models. Mach. Learn. 1999, 37, 183–233. [Google Scholar] [CrossRef]
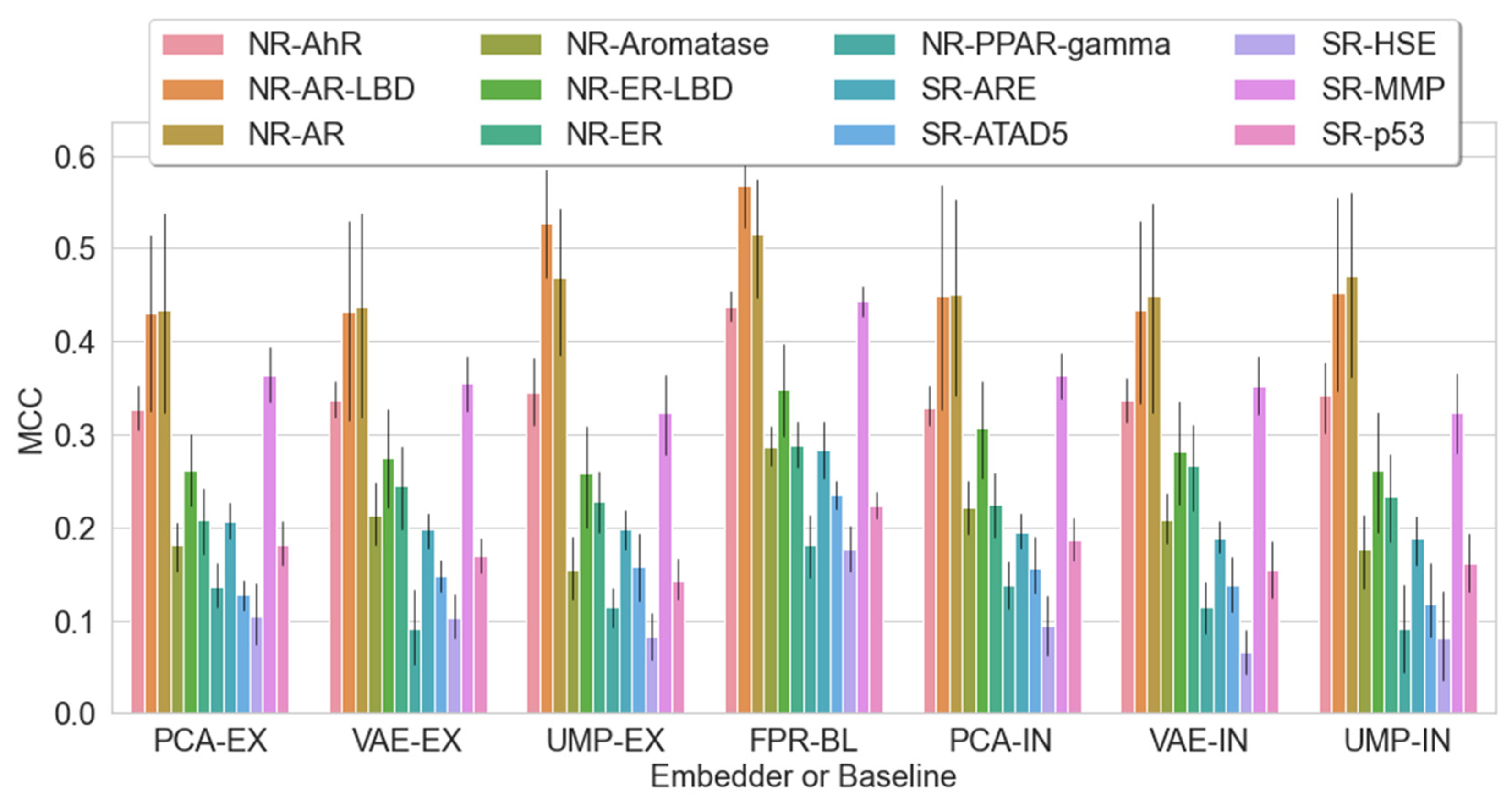
| Label (endpoint) | Mean (all) | Max (all) | KNN | LR | RFC | Z-L | Z-R | Z-S | Z-X | Z-D |
|---|---|---|---|---|---|---|---|---|---|---|
| NR-AR | 0.52 | 0.62 | a0.59 | 0.4 | 0.56 | 0.50 | 0.62 | 0.43 | 0.60 | b0.68 |
| NR-AR-LBD | 0.57 | 0.63 | 0.61 | 0.48 | a0.62 | 0.60 | 0.71 | 0.60 | b0.73 | 0.72 |
| NR-AhR | 0.44 | 0.47 | a0.45 | 0.44 | 0.43 | 0.52 | b0.61 | 0.47 | 0.54 | 0.59 |
| NR-Aromatase | 0.29 | 0.35 | a0.32 | 0.25 | 0.29 | 0.28 | b0.52 | 0.32 | 0.50 | 0.48 |
| NR-ER | 0.29 | 0.34 | a0.33 | 0.24 | 0.29 | 0.37 | 0.42 | 0.32 | 0.40 | b0.44 |
| NR-ER-LBD | 0.35 | 0.47 | 0.37 | 0.26 | a0.42 | 0.45 | 0.56 | 0.36 | b0.59 | 0.58 |
| NR-PPAR-gamma | 0.18 | 0.26 | 0.14 | 0.18 | a0.22 | 0.32 | 0.50 | 0.30 | b0.52 | 0.47 |
| SR-ARE | 0.28 | 0.36 | 0.25 | a0.31 | 0.29 | 0.46 | 0.49 | 0.36 | 0.46 | 0.48 |
| SR-ATAD5 | 0.24 | 0.26 | a0.25 | 0.22 | 0.24 | 0.37 | b0.59 | 0.36 | 0.53 | 0.55 |
| SR-HSE | 0.18 | 0.25 | 0.15 | 0.18 | a0.20 | 0.31 | b0.37 | 0.21 | 0.40 | b0.37 |
| SR-MMP | 0.44 | 0.47 | 0.44 | a0.47 | 0.43 | 0.63 | b0.65 | 0.54 | 0.64 | 0.63 |
| SR-p53 | 0.22 | 0.26 | 0.21 | a0.24 | 0.23 | 0.42 | b0.57 | 0.37 | 0.52 | 0.55 |
| Label | PCA | UMAP | VAE | |||
|---|---|---|---|---|---|---|
| IN | EX | IN | EX | IN | EX | |
| NR-AR | 0.45 | 0.43 | ‘ 0.47 | ‘ 0.47 | 0.45 | 0.44 |
| NR-AR-LBD | 0.45 | 0.43 | * 0.45 | * 0.53 | ‘ 0.43 | ‘ 0.43 |
| NR-AhR | ‘ 0.33 | ‘ 0.33 | * 0.34 | * 0.35 | ‘ 0.34 | ‘ 0.34 |
| NR-Aromatase | 0.22 | 0.18 | 0.18 | 0.15 | ‘ 0.21 | ‘ 0.21 |
| NR-ER | 0.22 | 0.21 | ‘ 0.23 | ‘ 0.23 | ‘ 0.27 | 0.24 |
| NR-ER-LBD | 0.31 | 0.26 | ‘ 0.26 | ‘ 0.26 | ‘ 0.28 | ‘ 0.28 |
| NR-PPAR-gamma | ‘ 0.14 | ‘ 0.14 | * 0.09 | * 0.11 | 0.11 | 0.09 |
| SR-ARE | * 0.19 | * 0.21 | * 0.19 | * 0.2 | * 0.19 | * 0.2 |
| SR-ATAD5 | 0.16 | 0.13 | * 0.12 | * 0.16 | * 0.14 | * 0.15 |
| SR-HSE | * 0.09 | * 0.11 | ‘ 0.08 | ‘ 0.08 | * 0.07 | * 0.1 |
| SR-MMP | ‘ 0.36 | ‘ 0.36 | ‘ 0.32 | ‘ 0.32 | * 0.35 | * 0.36 |
| SR-p53 | 0.19 | 0.18 | 0.16 | 0.14 | * 0.15 | * 0.17 |
| Label (endpoint) | FPR-BL | PCA-EX | PCA-IN | UMAP-EX | UMAP-IN | VAE-EX | VAE-IN |
|---|---|---|---|---|---|---|---|
| NR-AR | 100 | 95 | 99 | 96 | 96 | 97 | * 100 |
| NR-AR-LBD | 100 | 92 | 98 | * 100 | 97 | 98 | * 102 |
| NR-AhR | 100 | 84 | 85 | 90 | 86 | 83 | 85 |
| NR-Aromatase | 100 | 65 | 82 | 75 | 74 | 84 | 75 |
| NR-ER | 100 | 83 | 85 | 86 | 95 | * 103 | * 101 |
| NR-ER-LBD | 100 | 70 | 90 | 79 | 88 | 90 | 83 |
| NR-PPAR-gamma | 100 | 81 | 82 | 68 | 81 | 78 | 75 |
| SR-ARE | 100 | 74 | 69 | 70 | 69 | 63 | 63 |
| SR-ATAD5 | 100 | 63 | 99 | 92 | 84 | 75 | 88 |
| SR-HSE | 100 | 82 | 77 | 56 | 90 | 65 | 55 |
| SR-MMP | 100 | 92 | 87 | 83 | 83 | 93 | 89 |
| SR-p53 | 100 | 99 | 95 | 79 | 87 | 85 | 93 |
| PCA-EX | UMAP-EX | VAE-EX | |
|---|---|---|---|
| s(PCA) | 0.74 | ||
| s(UMAP) | 0.86 | ||
| s(VAE) | 0.85 | ||
| Pos class % | 0.11 | 0.02 | 0.13 |
| FPR-BL | 0.98 | 0.98 | 0.99 |
| Experimental/Model | Positive (Model) (1) | Negative (Model) (0) |
|---|---|---|
| Positive (Experimental) (1) | TP (experimentally active and predicted active) | FN (experimentally active, but predicted as inactive) |
| Negative (Experimental) (0) | FP (experimentally inactive, but predicted as active) | TN (inactive experimentally and predicted) |
| Predictive Variables | Classifier | Seed | Embedder | Emb. Dim. | CS1 Data Size | N Models |
|---|---|---|---|---|---|---|
| Fingerprints (raw data) | RFC, KNN, LR | 1–3 | N/A | N/A | N/A | 144 |
| Internal emb. | RFC, KNN, LR | 1–3 | PCA, UMAP, VAE | 2–15 | N/A | 9072 |
| External emb. | RFC, KNN, LR | 1–3 | PCA, UMAP, VAE | 2–15 | 200–30,000 | 9072 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovrić, M.; Đuričić, T.; Tran, H.T.N.; Hussain, H.; Lacić, E.; Rasmussen, M.A.; Kern, R. Should We Embed in Chemistry? A Comparison of Unsupervised Transfer Learning with PCA, UMAP, and VAE on Molecular Fingerprints. Pharmaceuticals 2021, 14, 758. https://doi.org/10.3390/ph14080758
Lovrić M, Đuričić T, Tran HTN, Hussain H, Lacić E, Rasmussen MA, Kern R. Should We Embed in Chemistry? A Comparison of Unsupervised Transfer Learning with PCA, UMAP, and VAE on Molecular Fingerprints. Pharmaceuticals. 2021; 14(8):758. https://doi.org/10.3390/ph14080758
Chicago/Turabian StyleLovrić, Mario, Tomislav Đuričić, Han T. N. Tran, Hussain Hussain, Emanuel Lacić, Morten A. Rasmussen, and Roman Kern. 2021. "Should We Embed in Chemistry? A Comparison of Unsupervised Transfer Learning with PCA, UMAP, and VAE on Molecular Fingerprints" Pharmaceuticals 14, no. 8: 758. https://doi.org/10.3390/ph14080758
APA StyleLovrić, M., Đuričić, T., Tran, H. T. N., Hussain, H., Lacić, E., Rasmussen, M. A., & Kern, R. (2021). Should We Embed in Chemistry? A Comparison of Unsupervised Transfer Learning with PCA, UMAP, and VAE on Molecular Fingerprints. Pharmaceuticals, 14(8), 758. https://doi.org/10.3390/ph14080758








