Abstract
This review describes different trials to model and predict drug payload in lipid and polymeric nanocarriers. It traces the evolution of the field from the earliest attempts when numerous solubility and Flory-Huggins models were applied, to the emergence of molecular dynamic simulations and docking studies, until the exciting practically successful era of artificial intelligence and machine learning. Going through matching and poorly matching studies with the wet lab-dry lab results, many key aspects were reviewed and addressed in the form of sequential examples that highlighted both cases.
1. Introduction
Nowadays, many efforts are exerted in the pharmaceutical field regarding the development of different types of drug delivery systems (DDS). This aims to keep the therapeutic efficacy of the active pharmaceutical ingredient (API), and successfully deliver the proper dose to the physiological target site. Among different types of existing DDS, nanocarriers have gained great interest due to their ultra-small size that controls the pharmacokinetics and pharmacodynamics of the drug [1,2]. Nanocarriers made specifically of lipids and polymers are extensively investigated in the literature, and the number of papers dealing with them is dramatically increasing over time [3,4,5,6]. A core feature for a successful lipid/polymeric formulation is the capacity of the carrier to retain its cargo, i.e., the drug payload [7,8,9]. Selecting the optimum carrier for this purpose is an issue of time, cost and effort if the design is solely built on the basis of wet-lab methods. In silico pharmaceutical formulation design now constitutes a key part of contemporary drug delivery research. It is gaining popularity because it offers the experimentalists a highly pixilated picture of their target based on molecular details of both the drug and the carrier. With this knowledge, designing nanocarriers with optimized properties is much faster with minimal laboratory effort and cost concerns. The scope of the current review is to illustrate the different reported techniques to model and predict he drug payload in the lipid and the polymeric nanocarriers. Evaluation of the consistency of these models with respect to their experimental validation results is another perspective. Given the diversity of APIs and the heterogeneity of lipids and polymeris that are used in nanocarriers preparation, many modelling techniques are described in literature to explain the complex relationship of drug-carrier systems. Some groups emphasized the use of the Flory-Huggins theory and the different solubility models for drug loading prediction. Similarly, increased understanding of the drug-carrier interaction process began reaching its full potential upon reviews discussing molecular dynamics simulations and docking applications in this area. Furthermore, recent related research reports that deal with larger number of parameters tend to apply novel concepts of prediction such as the smart artificial intelligence-based models. Thereby, the aim of this review is to cover all these techniques from naïve primitive approaches to the most innovative ones. The investigated studies include the polymeric and the lipid nanocarriers along with hybrids of them. Each section of the review addresses one modelling area from the perspective of its implications for DL prediction, to the scientific and technical challenges associated with its development. Important literature examples demonstrating these aspects are highlighted. Such a work, appeals to researchers who are interested in the intervention between computer and formulation science to reach state-of-the-art solutions for DL in lipid and polymeric nanocarriers.
Along with the review, the reader can find brief definitions and explanations of the mentioned tools. Furthermore, some hints are provided that may help future tuning of technique selection. Figure 1 depicts the scope of this review.
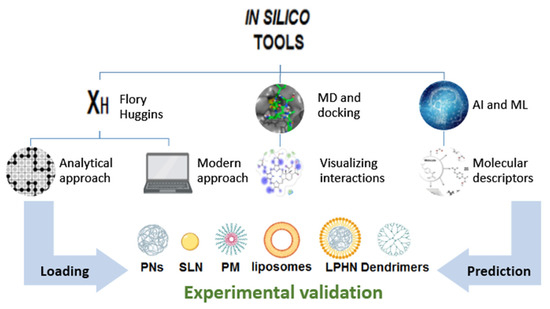
Figure 1.
Contribution of different analytical and in silico tools to the drug loading optimization in different classes of nanocarriers.
2. Solubility Parameters and Flory-Huggins Theory
The essence of DL optimization is to predict molecules’ preferences in excipients depending on their physicochemical properties [10,11]. These are empirical mathematical equations parameterized to wrap the physical details and some structural integration of the involved molecules [11]. The most frequently noticed one is the Flory-Huggins theory (FH). It is a thermodynamic model first introduced in the world of polymers to explain their behavior in solutions [12], and this is well documented in polymers literature [13,14,15]. Recently, this technique was used to extract valuable information regarding the plausible loading of many drugs in polymeric [16,17,18,19] and even lipid [20]—carriers via predicting their mutual solubility/miscibility. It is well known that one of the most important factors that determine the loading capacity of a carrier is the solubility of the drug in this carrier [10,21,22]. Thus, this model depends on estimating specific solubility parameters (SP), usually Hildebrand and Hansen SP, to calculate the final FH interaction parameter (XH) as follows:
where δ is the solubility parameter, Vd is the molar volume of the drug, R is the gas constant and T is the temperature in kelvin [12].
Assuming constant T and R, the equation clearly stated that the difference in solubility parameters between the drug and the carrier (Δδ) constitutes the driving force of the model. In other words, components with nearly the same solubility parameters are potential companions and vice versa. Actually, the threshold of Δδ below which components are considered soluble slightly differs among published papers. For uniformity, a difference of fewer than 4 MPa1/2 was commonly considered as the best approximation that represents all the studied cases. Because of the extensive investigation of this old model, examples are limited to the most recent applications and do not cover all similar cases (Table 1).

Table 1.
Recent classical applications of solubility parameters and Flory-Huggins interaction theory for different lipid and polymeric nanocarriers and their main outcomes.
2.1. Classical Approach
2.1.1. Analytical Procedure
Both solubility parameters (Hansen and Hildebrand) have been used in FH models as they are closely related [23,24]. It is worth mentioning that the group contribution method (GCM) reported by Fedros [25] and Hoftyzer/Van Krevelen [12] is the most common method used for the analytical estimation of SP. It is based on determining the cohesive energy density (CED) in the form of polar, dispersion and hydrogen bond (HB) contributions of various chemical groups -so the name of the method- within a molecule. As shown in Table 1, the first three examples used GCM-based SP along with XH to predict several drugs payload in different nano-formulations using different carriers. In Ghitman et al. work [17], reasonable exponential correlation coefficients between entrapment efficiency (%EE) and XH were obtained with better outcome in case of LPHN (R2 of 0.86) c.f. PLGA nanoparticles (R2 of 0.61). In contrast, Δδ values obtained by Sun et al. [18] did not distinguish between high and low DL in the PLA core of the prepared PEG-PLA micells. Similarly, their XH values did not provide a well-defined miscibility region and therefore could not predict well the DL capability of these micelles (Table 1). But for Raveendran et al. [19], values of Δδ and XH served well in predicting the polymer core with the highest curcumin payload among four synthesized polymers (Table 1).
2.1.2. Software
Currently, different computer software packages are accommodating computational modules for easier, more interactive and more user-friendly estimation of these contributions. Examples include Hansen Solubility Parameters in Practice (HSPiP) package, Molecular Modeling Pro and Maple software. It is important to mention that using these programs do not contribute in enhancing the performance of the model itself, and the same limitations -like handling very polar and large molecules- still exist. For example, Makoni et al. [20] used HSPiP software to calculate Hansen SP of different drugs and lipid carriers prior to optimization of SLN. Some values were consistent with the experimental results (like Geleol for efavirenz), while others were inconsistent (Table 1). Authors concluded that simple SP predictions could not be used alone to identify the lipid with the best solubilizing potential for a specific drug.
2.2. Computational (Modern) Approach
To this end, the classical representation of these solubility models needs upgrading to more explicit versions by incorporating precise modeling techniques. Molecular dynamics simulations (MD) and molecular docking calculations could enhance the performance of solubility models towards complex systems [26]. That is because, MD treats both entities of the model (carrier and drug) in a dynamic manner over time, which means calculating the fine movements of atoms in addition to the rotation, stretching and bending of the flexible bonds [27,28]. Also, instead of representing the carrier in the form of a single unit, MD simulations allow repeating this unit (many chains of building units) to form a 3D structure of interacting, energy minimized carrier molecules that resemble the actual case in the prepared nanoparticle. This tuning of volume difference along with mobility considerations allows catching interactions equally between neighbors. Now, docking is able to provide the binding energy (∆G) between the drug and its carrier based on the whole space and geometry of the carrier, all possible orientations of the drug inside the carrier, and of course accurate physical interactions.
On this basis, an early comparative study was designed by Patel et al. [29] using two approaches for calculating the FH interaction parameter between two drugs and a series of different molecular weights of PEO-PCL copolymer. The first approach was the traditional GCM, and the second was MD simulation. Using Materials Studio (MS) software, MD simulation was applied to the polymer and both API in their pure component form. The output trajectory files were used for extracting CED for all structures and subsequent calculation of FH interaction parameter according to Equation (1). Compared to the analytical GCM which was reported to give paradoxical results to the observed solubility of fenofibrate and nimodipine in liquid caprolactone, MD simulation results were consistent with the experimental validation (Table 2). These findings confirmed the superiority of modern approaches in the correct prediction of solubility and FH interaction parameters.

Table 2.
Simulations-derived solubility parameters and Flory-Huggins interaction theory for different nanocarriers and their outcomes.
By the exact same computational protocol, Meunire et al. [30] predicted the loading of six anticancer drugs inside the PLA core of PLA-PEG nanoparticles using the FH interaction parameter. A relatively reasonable exponential correlation between theoretical and experimental data was obtained despite being not completely satisfying for the author (Table 2). The reason was that the author noticed more dispersion in the correlation at low loading hydrophilic compounds especially SAR molecule (outlier) which scored higher than expected XH value. (Table 2). He suggested alternative techniques implementing more relevant algorithms that consider the potential energy of the entire drug-carrier complex besides its pure components such as the mixing energy (Emix), for better results. Figure 2 demonstrates in a schematic way the contrast between the classical drug-carrier interaction (solubility parameters) with the modern 3D representation (molecular dynamics and molecular docking).
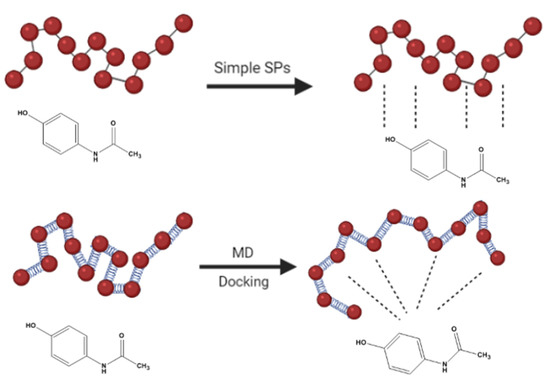
Figure 2.
Schematic presentation to contrast classical drug-carrier interaction (solubility parameters) with the modern 3D representation (molecular dynamics and molecular docking).
In testing this hypothesis, it was noticed that Machacˇkova et al. [31] used this modelling algorithm (Emix) to evaluate cyclosporine-A miscibility with six virtually built polymers. Using Blends module in MS software, a docking method based on the generalization of the FH theory was applied. The energy obtained after calculations is so called the mixing energy (Emix) and leads to XH by replacing the numerator of Equation (1) to be Emix. The values of XH revealed that both cellulose and chitosan seem to be the best carriers for the modeled drug c.f. other polymers (Table 2). These results were in accordance with previous experimental reports cited by the author, but it is always recommended to consider differences in laboratory protocols while citing experimental validation. The experimental tests remain an essential tool that is usually used to validate the simulation results (should not be thought of as an alternative to experiments), but the two approaches should be seen as complementary.
3. MD Simulations and Docking
Simulations and docking obviously add merits of power and accuracy to the prediction models. Recently, these techniques have come into play and show up in published papers as shifting paradigms in modelling nanocarriers. This new concept significantly aids the pre-formulation stage utilizing knowledge-based procedures and hence reaching better formulation targets.
3.1. Screening
Many reports confirmed the profound role of MD simulations and docking in the pre-formulation screening of carriers and in identifying candidate drugs expected to have high loading capacity towards specific carrier. This approach makes the whole formulation process extremely time and cost-effective with accurate prediction results that compare fairly well with experimental data.
3.1.1. Carriers-Oriented Screening
For instance, Yadav et al. [32] screened curcumin against five polymers using MD sim ulation and docking. Observations indicated that chitosan outperformed other tested polymers with an excellent ∆G pattern (Table 3). Chitosan was therefore selected for the experimental design of that study. Such a finding was not surprising as Dhanasekaran et al. [33] previously experienced the same results. Curcumin docking results showed a lower ∆G in chitosan c.f. chitin (Table 3). This was in good agreement with the experimental findings, which interestingly offered the maximum capacity of a carrier that can be experienced with any drug, i.e., about 100%.

Table 3.
Applications of molecular dynamic simulations coupled with docking techniques for modeling drug payload in different lipid and polymeric nanocarriers and their outcomes.
Similarly, Aparna et al. [34] have picked gelatin as a polymeric carrier for the delivery of amphotericin B based on an in silico outcome. Among eight different evaluated amino-functionalized polymers, gelatin showed the highest docking score for amphotericin B (Table 3). The experimental EE and loading of amphotericin B in gelatin nanoparticles were found to be highly accepted.
Ahmed et al. [35] also screened fluticasone against different polymers prior to the production of stable fluticasone nanoparticles. MD simulation and docking were performed. PVP stabilized HPMC and PVP stabilized Eudragit complexes scored the best ∆G results (−35.22 kcal/mol and −25.17 kcal/mol respectively) c.f. other simulated polymeric structures. After preparation of these nanoparticles, EE percentage was >90% confirming the in silico optimization.
Furthermore, a certain E-coli endotoxin structure was in silico screened by Altintas et al. [36] against twenty-one monomer building blocks commonly used for the preparation of molecularly imprinted polymeric nanoparticles (nanoMIPs). According to the results, itaconic acid, methacrylic acid and acrylamide with ∆G values of −52.24 kcal/mol, −41.43 kcal/mol and −39.87 kcal/mol, respectively, were selected. Experimentally, surface plasmon resonance (SPR) signaling revealed an affinity pattern of 99.5 RU, 66.4 RU and 35.6 RU for itaconic acid, methacrylic acid and acrylamide respectively. The experimental analysis of nanoMIPs for endotoxin detection by SPR sensor yielded results of similar pattern and conforming well to the computational modelling experiments (Table 3).
3.1.2. Drugs-Oriented Screening
A combination of MD simulations and docking calculations was also used to test the stable incorporation of curcumin, paclitaxel and vitamin D3 in PEG-Tyrosine derived polyarylates-PEG carrier. [37]. For the three drugs used, ΔG results that were computationally obtained, were correlated with the maximum drug loading as measured experimentally (Table 3), and a strong linear correlation (R2 = 0.93) was observed.
In other similar paper works, Gayathri et al. [38] and Geetha et al. [39] investigated the loading of three antibacterial drugs and three anticancer drugs, respectively, inside chitin nanocarriers. The antibacterial drugs and anticancer drugs were subjected to docking using the same modeled chitin nanocarriers. In both papers, the DL values of the three antibacterial drugs (8.9%, 5.6% and 3.5%) and the three anticancer drugs (3%, 2% and 1%) followed a similar trend with respect to ΔG data (−8.1, −7.3, −5.1 and −6.9, −6.5, −5.4 kcal/mol respectively). Excellent correlations between computational and experimental data were obtained with R2 of 0.85 for the antibacterial drugs and 0.93 for the anticancer drugs.
In the same context, Nosrat M. Mahani [40] tested the ability of PLGA to accommodate nine potent, but unstable, thiazoline derivatives with different alkyl and aryl substitutions. Using the hybrid ONIOM calculation reported before [41], all derivatives exhibited negative binding energies indicating good interaction with PLGA. Substitution with R = CH3 and Ar = 1-Methyl-1H-tetrazol-5-yl or 1-Phenyl-1H-tetrazol-5-yl in derivatives 3 and 7 respectively caused more potent binding interactions between the drug and the polymer (best ΔG results) (Table 3). This led to the final selection of these moieties for the successful preparation of stable, biologically active antimicrobial/anticancer formulations.
Talking about stability, Tais et al. applied MD simulations and docking studies to predict the most stable stoichiometric inclusion complex of naringenin with cyclodextrin (CD) [42]. Their main goal was to enhance the solubility of this poorly water soluble drug -and hence its dissolution rate- by high encapsulation inside CD with minimum dissociation rate. Three stoichiometric ratios of naringenin to CD (1:1, 1:2 and 2:1) were then in silico tested. Naringenin was docked on the energy minimized (MM+ FF) CD structure using Polak-Ribiere algorithm in HyperChem® software. Results showed that the 1:1 stoichiometry produced the most stable complex with stabilization energy of 150 and 165 kcal/mol (for hydroxyphenyl ring and chromanone ring orientations of naringenin respectively) c.f. 280 kcal/mol for the 1:2 stoichiometry. The 2:1 stoichiometry was not stabilized due to steric hinderance. Further MD simulations of the most stable complex, i.e., 1:1 stoichiometry, demonstrated conformation change of the chromanone ring orientation to the more stable hydroxyphenyl ring orientation with little or no mobility of the hydroxyphenyl ring orientation at the end of the simulation run. These data confirm the docking results obtained above.
With the same modeling package regarding structure optimization, docking algorithm and MD simulations mentioned previously, Thaiene et al. predicted the stability of Aluminium-chloride-phathalocyanine (AlCIPc) inclusion complex with βCD and its derivative hydroxypropyl-βCD [43]. In general, the 1:1 stoichiometry produced more stable complexes in both AlCIPc-βCD and AlCIPc-hydroxypropyl βCD c.f. stoichiometries 1:2 and 2:1. More specifically, there was no significant difference between stabilization energies of both complexes in 1:1 stoichiometric ratio especially in aqueous medium (−1064 to −1047 kcal/mol and −959 to −944 kcal/mol). Hydroxypropyl βCD was selected for the experimental study.
The ability of a closely related polymer to PLGA, PLA, to interact with another group of drugs was demonstrated in the aforementioned report by Meunire et al. [30]. Being unsatisfied with the results of SP/FH modelling utilizing the solubility parameters described earlier (Table 2), the authors remodeled the same six investigated API using a full Monte Carlo algorithm. This time, they found a strong linear correlation (R2 = 0.82) between the obtained ΔG data and the experimental drug loading (Table 3).
Another example of multidrug modelling was introduced by Hathout et al. [44] using gelatin as a principle matrix. Ten API were docked on the gelatin matrix simulated by MD, and the obtained ΔG data were correlated with the experimental masses of the loaded drugs. This model was highly fitting associated with an R2 approaching 1 (Table 3).
On a larger dataset comprising a lipid carrier, Metwally and Hathout modelled the loading of twenty-one API in tripalmitin and PLGA 50:50 based nanocarriers simulated by MD [45]. Ten drugs were assigned for the PLGA system and eleven for tripalmitin. Obvious correlations between docking ΔG data of the tripalmitin and PLGA loaded drugs and their corresponding reported drug loading were obtained (Table 3). Furthermore, the authors validated the predictability of the constructed models using a model drug, curcumin. The calculated percentage bias between the actual and the predicted loading values were 12% and 2.03% for tripalmitin SLN and PLGA nanoparticles, respectively.
A similar study was reported by the same authors using the same group of drugs in the tripalmitin based system but with a different docking protocol [46]. The new protocol applied ASE scoring function implemented in Molecular Operating Environment (MOE) software. This score is quietly different from the Ascore implemented in ArgusLab as it considers the distances between the ligand atom-carrier atom pairs in the form of a Gaussian function [46]. Accordingly, a comparable R2 for the constructed ΔG-loading correlation (0.86) was found with lower bias percentage (7.71%). This data furnished evidence for the effect of different docking protocols (scoring functions equations) on the accuracy of modelling nanocarriers.
Different simulation protocols also strongly affect the success of modelling. A systematic study of twenty-one approved drugs was carried out by Sizochenko, and Leszczynski, [47] using again PLGA 50:50 as a carrier and AutoDock Vina for docking. A correlation of R2 = 0.36 (R = 0.6) was obtained between the literature gathered drug loading data and the resulted ∆G data. Compared to the correlation coefficient value in Metwally and Hathout report (0.9) [45] where the same carrier type and docking algorithm but different simulation force field were used- this recorded value was much lower. A force field (FF) is what defines the fundamental physics of the simulated system, i.e., determining the default values for physical interactions, bond lengths, partial charges and any force acting on/between atoms [48]. So, the quality of the FF will affect the accuracy and reliability of the simulated systems [28]. These approaches were summarized in Figure 3.
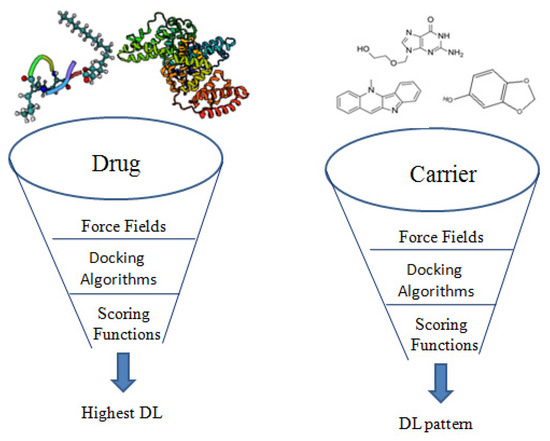
Figure 3.
Screening role of different in silico parameters in the drug loading optimization of nanocarriers.
3.2. Visualizing Interactions
In addition to the screening and the carriers-selection tasks, simulations and docking are further used to gain insights into the mechanism by which binding processes occur. More specifically, the typical atomic/molecular level interactions between the drug and the carrier can be visualized and analyzed given the microscopic potential of these techniques [49]. From the following examples, it will be demonstrated how ΔG was related to different interactions in several studies, and how this relationship may contribute to the interpretation of unexpected loading cases of some compounds in different carriers.
In an important study, Brunacci et al. [50] conducted MD simulation to visualize possible interactions of dexamethasone in two polymers, PLGA 50:50 and oligobutylmorpholinediol (OBMD). They found that the amide group in OBMD acts as a hydrogen donor that supports the other hydrogen acceptor groups. Accordingly, a single OBMD unit was able to form three HB with a single dexamethasone molecule. In contrast, a PLGA unit that contains only hydrogen acceptors accompanied by its ester groups forms two HB with dexamethasone. Subsequent molecular docking analysis showed better ΔG of dexamethasone with OBMD compared to PLGA (Table 4). The experimental validation results, represented by EE and DL, ascertained the superiority of OBMD over PLGA to form dexamethasone-loaded polymeric nanoparticles (Table 4).

Table 4.
Cases of binding site analysis in simulated lipid and polymeric nanocarriers and their observations.
Also, Sonawane et al. [51] offered an excellent explanation of vancomycin loading pattern in compritol SLN, compritol-Eudragit RS 100 hybrid nanoparticles (LPHN) and compritol-PAMAM hybrid nanoparticles (LDHN). Simulations suggested that the only possible interaction between vancomycin and compritol was the weak hydrophobic interaction of vancomycin isopropyl moiety with compritol carbon chain backbone. In contrast, the highly branched PAMAM dendrimer was able to accommodate vancomycin molecules in its void spaces and back foldings. Analysis of the dendrimer-drug complex revealed that each dendrimer molecule was able to bind four vancomycin molecules by means of multiple HB (multivalent binding capacity). In the Eudragit core, vancomycin was not/barely able to form interactions despite the presence of active groups (alkyl groups and hydrogen acceptors (C=O)) in the Eudragit structure. In fact, the alkyl and hydrogen acceptor moieties of Eudragit were not practically available for interaction due to the steric hindrance effect (aligned chains/architecture of polymer with minimum void space c.f. dendrimer) especially with a bulky molecule like vancomycin. These findings were in line with the experimental results (Table 4).
Apart from physical interactions, other structural contributions like bulkiness, flexibility/rigidity and even isomerism of API can share in the final computation of ΔG. Costache et al.’s [37] previous perfect ranking (Table 3) was due to not only the binding interactions but also the drug bulkiness and flexibility. The size and flexibility of the three model drugs controlled their orientation and hence the inside tight binding in the nanocarrier core. Paclitaxel was theoretically able to form eighteen HB and many π-π interactions, but most of them were of intramolecular type due to its large size. This lead to a more rigid conformation of paclitaxel that mainly allowed of surface binding and therefore lower DL. The small rather flexible vitamin D3 then showed the best ΔG and DL (Table 4). Accordingly, it is evident that physical interactions solely are not sufficient to understand the binding affinity in nanosystems.
With more complex structural features, the affinity prediction job of binding energies becomes more difficult or even disabled, and counterintuitive experimental loading results can be observed. This can be clearly seen with Sánchez et al. [52] during the study of morphine and tramadol loading in PAMAM dendrimer. The experimental results showed a higher encapsulation proportion for morphine c.f. tramadol, while ΔG results exhibited more negative values for tramadol c.f. morphine (Table 5). This discrepancy was due to the possible drug-drug interactions of the racemic tramadol molecules. Based on this fact, an enantiomeric pair of tramadol can block the entranceway to the dendrimer cavity leading to the escape of molecules to the surrounding media despite the higher affinity of tramadol towards the dendrimer system as shown by ΔG values (Table 5).

Table 5.
Cases of contradictory wet lab-dry lab results explained only by binding site analysis.
A similar issue was encountered by Costache et al. [37] upon studying camptothecin docking on the PEG-tyrosine derived polyryltes-PEG carrier. The experimental results showed that camptothecin (small polycyclic and highly rigid drug) owned the lowest drug loading (Table 5) among the other three drugs (curcumin, paclitaxel and vitamin D3) (Table 4). Interestingly, camptothecin scored high ΔG (−9.27 kcal/mol) comparable to that of vitamin D3. Visualizing the atomic-level interactions revealed that for all docking replicates, camptothecin was preferably aligned in a specific spot of the carrier. About 70% of camptothecin hits accumulated in that “hot spot” with the remaining flew away the search space leading to false high scores. Translating this fact experimentally, nanoparticles would accommodate only few molecules of the drug and leak the rest to the surrounding media. The authors end with recommendations of searching and scoring refinement algorithms that consider not only the thermodynamic binding of molecules but also the kinetic view of binding [37].
Furthermore, melittin, a bee venom peptide, scored a higher ΔG upon docking on the simulated lecithin system c.f. a polymeric system (Table 5) [53]. However, the biophysical approach for drug loading measurement indicated lower drug loading in the case of lecithin c.f. the polymer. Upon visualizing molecular details of these interactions, the authors found that melittin interacts with the carriers by only certain residues critical for binding. Thus, there was an unnecessary overestimation of the contribution of bulkiness and flexibility of melittin molecules which lead to false better results with lecithin. These residues paralleled well with the polymer chain forming many interactions, but were loose with far intermolecular distances and only a few interactions in the case of lecithin. For further confirmation of these findings, the authors re-docked that specific residue of melittin sequence on lecithin and polymer systems. The obtained ΔG data flipped this time and matched the actual loading results (Table 5).
Dhanasekaran et al. [33] further went from modeling peptides to modeling the bulkiest, most complex pharmaceutical API, proteins. In their study, they applied MD simulation and docking calculations to predict insulin loading in both chitin and chitosan nanoparticles. They used HEX software for this purpose. Experimental loading results declared that chitosan was a better carrier for insulin c.f. chitin. Unfortunately, docking results failed to predict this finding. The obtained ΔG data was in contrast to the experimental loading results (Table 5). It seems that even the specialized protein docking servers were unable to account for the complexity of protein-polymer systems. A solution like that proposed by Misra et al. [53] may help.
Between success and failure stories of simulations and docking, the key strength and weaknesses at the same time of these techniques lie in their versatility. In docking, this can be best understood from the multiple engines available for conformations sampling (searching algorithms) and poses ranking (scoring functions) [54,55,56,57,58]. Similarly, diverse collection of force fields in the molecular simulation are also available besides different levels of resolution [28,46,59,60]. It is not so easy to predict the exact simulation-docking protocol suitable for a proposed situation, and many trials are sometimes needed for such a choice leading to high consumption of computational power and long timescales.
4. Artificial Intelligence and Machine Learning
Artificial intelligence (AI) is another field of problem solving used for complex multivariable data. The term originates from the fact it is a kind of simulation of human brain intelligence in machines that are programmed to think and act like humans. One great advance in this field is machine learning (ML), both supervised and unsupervised. Focusing on the first type, supervised ML is an area in AI which has the ability to learn and model the relationship between a set of independent variables and an outcome (response) [45]. The net result is a feature mapping equation that can predict outcomes for new observations [61,62,63,64]. In the world of drugs and carriers, supervised ML model inputs (independent variables) could be molecular descriptors and/or formulation parameters. Molecular descriptors are cheminformatics-based comprehensive numbers that abstract hundreds of structural characteristics of a compound [65]. It is ranging from simple bulk 1D features (molecular weight, polarizability, partition coefficient, etc) to the 2D features (number of atoms and bonds) and 3D features (pharmacophoric points and molecular fingerprints) [66].Generally, ML models are less computationally expensive compared to the combined MD and docking approach. In this context, ML techniques can provide results that are either complementary-to or comparable-with the MD and docking approach (Figure 4).
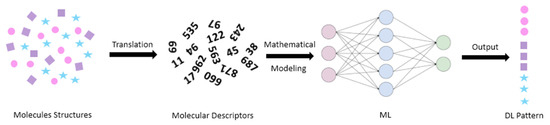
Figure 4.
Molecular descriptors and machine learning in drug loading prediction.
Hathout and Metwally experienced this concept in their previous work [45,46]. The authors represented the previously obtained ∆G by molecular descriptors of API and relate them using two supervised ML algorithms, an artificial neural network (ANN) algorithm [45] and a gaussian process (GP) algorithm [46]. Model inputs were the molecular weight, xlogP, topological polar surface area and fragment complexity of the literature gathered API, whereas model output was set as the obtained binding energies. This led to robust (Table 6) and fast estimation of ∆G without the need to encounter software limitations and high CPU computations cost during simulations and docking studies. Each descriptor was assessed for its significance to the differences in ΔG data. Subsequent loading prediction of API in the corresponding nanoparticles was encouraging (Table 3).

Table 6.
Different applications of machine learning techniques for modelling lipid and polymeric nanocarriers.
Also, Sizochenko, and Leszczynski [47] used molecular descriptors of their API as inputs in another supervised ML model against experimental DL as output. Briefly, they reflected API Van der Waals interaction potential by hydrophobicity (log P), miscibility and hydrogen bonds by lipophilicity (SIRMS-lip), electrostatic interactions by electronegativity (SIRMS-EO) and finally, they added a chirality representative of the studied compounds (Continuous Chirality Measure or CCM) as half of the used dataset were chiral drugs. They referred to the modeling algorithm as M5P. This algorithm combines a classification technique and a linear regression function at the nodes. This time, an excellent correlation between predicted and observed DL was obtained with R2 of >0.9 (Table 6). A Pearson evaluation of the effect of all descriptors on drug payload showed correlations of R > 0.9 indicating their great significance.
Actually, direct prediction of drug payload in nanoparticles from molecular descriptors of API is not a brand new idea. It was previously reported by Das et al. [67] on a dataset of twenty-two compounds using three different sets of molecular descriptors generated from three different software packages (Table 6). DRAGON descriptors were combination of 1D, 2D and 3D classes, while MOE generated 2D and 3D descriptors, and 2D descriptors only from VolSurf+. Each descriptors set was fitted in multiple linear regression model against the logarithmic form of the maximum attainable DL. After several permutations to exclude inter-correlations, each descriptors set was reduced to few non-correlated variables of primary significance on nanoparticles payload (Table 6). The success of the generated models was marked by R2 of >0.8 especially with the most inclusive set, DRAGON set (Table 6). This suggests that as more data from API becomes available, machine learning would become more powerful in the loading prediction job. Experimental validation was carried out using two drugs (silibin and andrographolide) and the observations correlated well with in silico predictive mass loading inside PLGA 50:50 nanoparticles.
Combining computed descriptors with experimental conditions, Cern et al. [68] developed two ML models to assess drug candidates that are able to achieve high remote (trans-membrane) loading in liposomes. A total of sixty drugs in three hundred sixty-six loading experiments were used to assemble a hybrid features model. Thus, molecular descriptors were combined with the experimental conditions for the entry in the dataset. Model output was set as the drug to lipid ratio (D/L) which is representative of the loading efficiency percentage. Determination coefficient (R2) and determination coefficient of the regression line forced to come through the origin (R20) tested the predictive power of the model and retained a good fit between the predicted and observed target properties (Table 6).
Overall, these results are encouraging regarding payload prediction. Also, configuring the most important descriptors may be a mirror image to the possible interaction mechanism responsible for affinity during MD simulations and docking calculations [69,70,71,72,73,74].
5. Conclusions
In this review, an overview of the evolution of in silico formulation design technology in the investigation and prediction of drug payload in lipid and polymeric nanocarriers was presented. As illustrated, this technology is close to becoming routine add-ins for formulation scientists even for non-informatics specialists. They represent the next industrial revolution and deserve many other reviews to describe. Going from simple thermodynamic models to the 3D MD-docking approaches and AI-oriented algorithms, the extent to which a specific technique can guide the process of drug loading and formulation development have been explored. The researcher applying the idea has the welling to choose the most favorite/suitable technique from the above discussed ones or even merge between them.
Author Contributions
Conceptualization, H.M.A.-B., A.A.M. and R.M.H.; methodology, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; validation, H.M.A.-B., A.A.M. and R.M.H.; investigation, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; resources, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; data curation, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; writing—original draft preparation, S.A.A., H.M.A.-B. and A.A.M.; writing—review and editing, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; visualization, S.A.A., H.M.A.-B., A.A.M. and R.M.H.; supervision, S.A.A., H.M.A.-B., A.A.M. and R.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| (%)DL | drug loading (percentage) |
| (%)EE | entrapment efficiency (percentage) |
| AI | artificial intelligence |
| AlCIPc | Aluminium-chloride-phathalocyanine |
| Amber FF | assisted model building with energy refinement force field |
| ANN | artificial neural network |
| API | active pharmaceutical ingredient |
| CCM | continuous chirality measure |
| CD | cyclodextrin |
| CED | cohesive energy density |
| CGen FF | CHARMM general force field |
| CHARMM FF | chemistry at Harvard macromolecular mechanics force field |
| DDS | drug delivery system |
| DFT | density function theory |
| EC | ethylcellulose |
| Emix | mixing energy |
| FF | force field |
| FFT | fast fourier transform algorithm |
| FH | Flory-Huggins theory |
| GCM | group contribution method |
| GP | Gaussian process |
| HB | hydrogen bond |
| HPMC | hydroxypropylmethyl cellulose |
| HSPiP | Hansen solubility parameter in practice |
| KNN | k-nearest neighbor |
| LDHN | lipid-dendrimer hybrid nanoparticles |
| LGA | Lamarckian genetic algorithm |
| LPHN | lipid-polymer hybrid nanoparticles |
| MD | molecular dynamics |
| ML | machine learning |
| MLR | multiple linear regression |
| MMFF | Merck molecular force field |
| MOE | molecular operating environment |
| MS | materials studio |
| Mwt | molecular weight |
| NanoMIPs | molecularly imprinted polymeric nanopartices |
| NIPAAm | N-isopropylacrylamide |
| OBMD | oligobutylmorpholinediol |
| ONIOM | our N-layered integrated molecular orbital+molecular mechanics |
| OPLS FF | optimized potentials for liquid simulations force field |
| PAA | Polyallylamine |
| PAMAM | polyamidoamine |
| PAS | Polyaminostyrene |
| PCFF | polymer consistent force filed |
| PCL | polycaprolactone |
| PDLA | poly-D-lactic acid |
| PEA | Polyethyleneamine |
| PEG | polyethylene glycol |
| PEO | polyethylene oxide |
| PGA | polyglycolic acid |
| PLGA | polylactic-co-glycolic acid |
| PLL | poly-L-lysine |
| PLLA | poly-L-lactic acid |
| PM | polymeric micelles |
| PN | polymeric nanoparticles |
| PS-PAA | polystyrene-polyacrylic acid |
| PVA1 | polyvinyl alcohol |
| PVA2 | polyvinyl amine |
| QM/MM | quantum mechanics/molecular mechanics |
| QSPR | quantitative structure-property relationship |
| R/R2 | correlation/determination coefficients |
| SF | scoring function |
| SLN | solid lipid nanoparticles |
| SP/δ | solubility parameter |
| SPF | spherical polar fourier algorithm |
| SPR | surface plasmon resonance |
| SVR | support vector regression |
| TPSA | topological polar surface area |
| UFF | universal force field |
| XH | Flory-Huggins interaction parameter |
| xLog P | partition coefficient |
| Δδ | difference in solubility parameters (drug and carrier) |
| ΔG | binding energy |
References
- Rawat, M.; Singh, D.; Saraf, S. Nanocarriers: Promising Vehicle for Bioactive Drugs. Biol. Pharm. Bull. 2006, 29, 1790–1798. [Google Scholar] [CrossRef]
- Torchilin, V.P. Multifunctional nanocarriers. Adv. Drug Deliv. Rev. 2012, 64, 302–315. [Google Scholar] [CrossRef]
- Mishra, D.K.; Shandilya, R.; Mishra, P.K. Lipid based nanocarriers: A translational perspective. Nanomed. Nanotechnol. Biol. Med. 2018, 14, 2023–2050. [Google Scholar] [CrossRef] [PubMed]
- Kumari, A.; Yadav, S.K.; Yadav, S.C. Biodegradable polymeric nanoparticles based drug delivery systems. Colloids Surf. B Biointerfaces 2010, 75, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, H.; Bala, R.; Arora, S. Lipid-Based Drug Delivery Systems. J. Pharm. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Siepmann, J.; Faham, A.; Clas, S.-D.; Boyd, B.J.; Jannin, V.; Bernkop-Schnürch, A.; Zhao, H.; Lecommandoux, S.; Evans, J.C.; Allen, C.; et al. Lipids and polymers in pharmaceutical technology: Lifelong companions. Int. J. Pharm. 2019, 558, 128–142. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Wu, Y.; Liu, Y.; Wu, D. High drug-loading nanomedicines: Progress, current status, and prospects. Int. J. Nanomed. 2017, 12, 4085–4109. [Google Scholar] [CrossRef] [PubMed]
- Palanikumar, L.; Choi, E.S.; Oh, J.Y.; Park, S.A.; Choi, H.; Kim, K.; Kim, C.; Ryu, J.-H. Importance of Encapsulation Stability of Nanocarriers with High Drug Loading Capacity for Increasing in Vivo Therapeutic Efficacy. Biomacromolecules 2018, 19, 3030–3039. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Zhao, J.; Lu, M.; Garvey, C.J.; Stenzel, M.H. Correlation between Drug Loading Content and Biological Activity: The Complexity Demonstrated in Paclitaxel-Loaded Glycopolymer Micelle System. Biomacromolecules 2019, 20, 1545–1554. [Google Scholar] [CrossRef]
- Li, Y.; Yang, L. Driving forces for drug loading in drug carriers. J. Microencapsul. 2015, 32, 1–18. [Google Scholar] [CrossRef]
- Huynh, L.; Neale, C.; Pomès, R.; Allen, C. Computational approaches to the rational design of nanoemulsions, polymeric micelles, and dendrimers for drug delivery. Nanomed. Nanotechnol. Biol. Med. 2012, 8, 20–36. [Google Scholar] [CrossRef] [PubMed]
- Van Krevelen, D.; Nijenhuis, K.T. Cohesive Properties and Solubility. In Properties of Polymers; Elsevier: Amsterdam, The Netherlands, 2009; pp. 189–227. [Google Scholar]
- Paik, J.S.; Writer, M.S. Prediction of Flavor Sorption Using the Flory-Huggins Equation. J. Agric. Food Chem. 1995, 43, 175–178. [Google Scholar] [CrossRef]
- Kamal, M.R.; Demarquette, N.R.; Lai-Fook, R.A.; Price, T.A. Evaluation of thermodynamic theories to predict interfacial tension between polystyrene and polypropylene melts. Polym. Eng. Sci. 1997, 37, 813–825. [Google Scholar] [CrossRef]
- Lindvig, T.; Michelsen, M.L.; Kontogeorgis, G. A Flory–Huggins model based on the Hansen solubility parameters. Fluid Phase Equilibria 2002, 203, 247–260. [Google Scholar] [CrossRef]
- Mahmud, A.; Patel, S.; Molavi, O.; Choi, P.; Samuel, J.; Lavasanifar, A. Self-Associating Poly(ethylene oxide)-b-poly(r-cholesterylcarboxylate-ε-caprolactone) Block Copolymer for the Solubilization of STAT-3 Inhibitor Cucurbitacin I. Biomacromolecules 2009, 10, 471–478. [Google Scholar] [CrossRef] [PubMed]
- Ghitman, J.; Stan, R.; Vlasceanu, G.; Vasile, E.; Iovu, H. Predicting the drug loading efficiency into hybrid nanocarriers based on PLGA-vegetable oil using molecular dynamic simulation approach and Flory-Huggins theory. J. Drug Deliv. Sci. Technol. 2019, 53, 101203. [Google Scholar] [CrossRef]
- Sun, J.; Wei, Q.; Shen, N.; Tang, Z.; Chen, X. Predicting the Loading Capability of mPEG-PDLLA to Hydrophobic Drugs Using Solubility Parameters. Chin. J. Chem. 2020, 38, 690–696. [Google Scholar] [CrossRef]
- Raveendran, R.; Mullen, K.M.; Wellard, R.M.; Sharma, C.P.; Hoogenboom, R.; Dargaville, T. Poly(2-oxazoline) block copolymer nanoparticles for curcumin loading and delivery to cancer cells. Eur. Polym. J. 2017, 93, 682–694. [Google Scholar] [CrossRef]
- Makoni, P.A.; Ranchhod, J.; Kasongo, K.W.; Khamanga, S.M.; Walker, R.B. The use of quantitative analysis and Hansen solubility parameter predictions for the selection of excipients for lipid nanocarriers to be loaded with water soluble and insoluble compounds. Saudi Pharm. J. 2020, 28, 308–315. [Google Scholar] [CrossRef]
- Rane, S.S.; Anderson, B.D. What determines drug solubility in lipid vehicles: Is it predictable? Adv. Drug Deliv. Rev. 2008, 60, 638–656. [Google Scholar] [CrossRef]
- Qian, F.; Huang, J.; Hussain, M.A. Drug–Polymer Solubility and Miscibility: Stability Consideration and Practical Challenges in Amorphous Solid Dispersion Development. J. Pharm. Sci. 2010, 99, 2941–2947. [Google Scholar] [CrossRef]
- Venkatram, S.; Kim, C.; Chandrasekaran, A.; Ramprasad, R. Critical Assessment of the Hildebrand and Hansen Solubility Parameters for Polymers. J. Chem. Inf. Model. 2019, 59, 4188–4194. [Google Scholar] [CrossRef] [PubMed]
- Kitak, T.; Dumičić, A.; Planinšek, O.; Šibanc, R.; Srčič, S. Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate. Molecules 2015, 20, 21549–21568. [Google Scholar] [CrossRef] [PubMed]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Gupta, J.; Nunes, C.; Vyas, S.; Jonnalagadda, S. Prediction of Solubility Parameters and Miscibility of Pharmaceutical Compounds by Molecular Dynamics Simulations. J. Phys. Chem. B 2011, 115, 2014–2023. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1134. [Google Scholar] [CrossRef]
- González, M. Force fields and molecular dynamics simulations. JDN 2011, 12, 169–200. [Google Scholar] [CrossRef]
- Patel, S.; Lavasanifar, A.; Choi, P. Application of Molecular Dynamics Simulation To Predict the Compatability between Water-Insoluble Drugs and Self-Associating Poly(ethylene oxide)-b-poly(ε-caprolactone) Block Copolymers. Biomacromolecules 2008, 9, 3014–3023. [Google Scholar] [CrossRef] [PubMed]
- Meunier, M.; Goupil, A.; Lienard, P. Predicting drug loading in PLA-PEG nanoparticles. Int. J. Pharm. 2017, 526, 157–166. [Google Scholar] [CrossRef]
- Macháčková, M.; Tokarský, J.; Čapková, P. A simple molecular modeling method for the characterization of polymeric drug carriers. Eur. J. Pharm. Sci. 2013, 48, 316–322. [Google Scholar] [CrossRef]
- Yadav, P.; Bandyopadhyay, A.; Chakraborty, A.; Sarkar, K. Enhancement of anticancer activity and drug delivery of chitosan-curcumin nanoparticle via molecular docking and simulation analysis. Carbohydr. Polym. 2018, 182, 188–198. [Google Scholar] [CrossRef]
- Dhanasekaran, S.; Rameshthangam, P.; Venkatesan, S.; Singh, S.K.; Vijayan, S.R. In Vitro and In Silico Studies of Chitin and Chitosan Based Nanocarriers for Curcumin and Insulin Delivery. J. Polym. Environ. 2018, 26, 4095–4113. [Google Scholar] [CrossRef]
- Aparna, V.; Melge, A.R.; Rajan, V.K.; Biswas, R.; Jayakumar, R.; Mohan, C.G. Carboxymethylated L-carrageenan conjugated amphotericin B loadedgelatin nanoparticles for treating intracellular Candida glabratainfections. Int. J. Biol. Macromol. 2018, 110, 140–149. [Google Scholar] [CrossRef]
- Ahmed, S.; Govender, T.; Khan, I.; Rehman, N.U.; Ali, W.; Shah, S.M.H.; Khan, S.; Hussain, Z.; Ullah, R.; Alsaid, M.S. Experimental and molecular modeling approach to optimize suitable polymers for fabrication of stable fluticasone nanoparticles with enhanced dissolution and antimicrobial activity. Drug Des. Dev. Ther. 2018, 12, 255–269. [Google Scholar] [CrossRef] [PubMed]
- Altintas, Z.; Abdin, M.J.; Tothill, A.M.; Karim, K.; Tothill, I.E. Ultrasensitive detection of endotoxins using computationally designed nanoMIPs. Anal. Chim. Acta 2016, 935, 239–248. [Google Scholar] [CrossRef]
- Costache, A.D.; Sheihet, L.; Zaveri, K.; Knight, D.D.; Kohn, J. Polymer−Drug Interactions in Tyrosine-Derived Triblock Copolymer Nanospheres: A Computational Modeling Approach. Mol. Pharm. 2009, 6, 1620–1627. [Google Scholar] [CrossRef] [PubMed]
- Gayathri, N.K.; Aparna, V.; Maya, S.; Biswas, R.; Jayakumar, R.; Mohan, C.G. Preparation, characterization, drug release and computational modelling studies of antibiotics loaded amorphous chitin nanoparticles. Carbohydr. Polym. 2017, 177, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Geetha, P.; Sivaram, A.J.; Jayakumar, R.; Mohan, C.G. Integration of in silico modeling, prediction by binding energy and experimental approach to study the amorphous chitin nanocarriers for cancer drug delivery. Carbohydr. Polym. 2016, 142, 240–249. [Google Scholar] [CrossRef]
- Mahani, N.M. Quantum Chemical Study of Interaction of PLGA Polymeric Nanoparticles as Drug Delivery with Anti-Cancer Agents of Thiazoline. Int. J. New Chem. 2019, 6, 34–42. [Google Scholar]
- Morokuma, K. ONIOM and Its Applications to Material Chemistry and Catalyses. Bull. Korean Chem. Soc. 2003, 24, 797–801. [Google Scholar] [CrossRef]
- Gratieri, T.; Pinho, L.A.G.; Oliveira, M.A.; Barreto, L.S.; Marreto, R.N.; Silva, I.C.; Gelfuso, G.M.; Quintans, J.D.S.S.; Quintans-Junior, L.J.; Cunha-Filho, M. Hydroxypropyl-β-cyclodextrin-complexed naringenin by solvent change precipitation for improving anti-inflammatory effect in vivo. Carbohydr. Polym. 2020, 231, 115769. [Google Scholar] [CrossRef] [PubMed]
- Reis, T.A.; Jaculi, A.E.; Ramos, K.L.V.; Souza, P.E.N.; Veiga-Souza, F.H.; Joanitti, G.A.; Azevedo, R.B.; Gratieri, T.; Cunha-Filho, M.; Gelfuso, G.M. Cobination of cyclodextrin complexation and iontiphoresis as a promising strategy for the cutaneous delivery of aluminium-chloride-phthalocyanine in photodynamic therapy. Eur. J. Pharm. Sci. 2019, 139, 105056. [Google Scholar] [CrossRef] [PubMed]
- Hathout, R.M.; Metwally, A.; Woodman, T.J.; Hardy, J.G. Prediction of Drug Loading in the Gelatin Matrix Using Computational Methods. ACS Omega 2020, 5, 1549–1556. [Google Scholar] [CrossRef]
- Metwally, A.A.; Hathout, R.M. Computer-Assisted Drug Formulation Design: Novel Approach in Drug Delivery. Mol. Pharm. 2015, 12, 2800–2810. [Google Scholar] [CrossRef] [PubMed]
- Hathout, R.M.; Metwally, A.A. Towards better modelling of drug-loading in solid lipid nanoparticles: Molecular dynamics, docking experiments and Gaussian Processes machine learning. Eur. J. Pharm. Biopharm. 2016, 108, 262–268. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Leszczynski, J. Drug-Nanoparticle Composites: A Predictive Model for Mass Loading. J. Nanotoxicol. Nanomed. 2017, 2, 1–10. [Google Scholar] [CrossRef]
- Hossain, S.; Kabedev, A.; Parrow, A.; Bergström, C.A.; Larsson, P. Molecular simulation as a computational pharmaceutics tool to predict drug solubility, solubilization processes and partitioning. Eur. J. Pharm. Biopharm. 2019, 137, 46–55. [Google Scholar] [CrossRef]
- Seeliger, D.; de Groot, B.L. Ligand docking and binding site analysis with PyMOL and Autodock/Vina. J. Comput. Aided Mol. Des. 2010, 24, 417–422. [Google Scholar] [CrossRef]
- Brunacci, N.; Neffe, A.T.; Wischke, C.; Naolou, T.; Nöchel, U.; Lendlein, A. Oligodepsipeptide (nano)carriers: Computational design and analysis of enhanced drug loading. J. Control. Release 2019, 301, 146–156. [Google Scholar] [CrossRef]
- Sonawane, S.J.; Kalhapure, R.S.; Rambharose, S.; Mocktar, C.; Vepuri, S.B.; Soliman, M.; Govender, T. Ultra-small lipid-dendrimer hybrid nanoparticles as a promising strategy for antibiotic delivery: In vitro and in silico studies. Int. J. Pharm. 2016, 504, 1–10. [Google Scholar] [CrossRef]
- Carrasco-Sanchez, V.; Vergara-Jaque, A.; Zuñiga, M.; Comer, J.; John, A.; Nachtigall, F.M.; Valdés, O.; Duran-Lara, E.F.; Sandoval, C.; Santos, L.S. In situ and in silico evaluation of amine- and folate-terminated dendrimers as nanocarriers of anesthetics. Eur. J. Med. Chem. 2014, 73, 250–257. [Google Scholar] [CrossRef]
- Misra, S.K.; Ye, M.; Kim, S.; Pan, D. Defined Nanoscale Chemistry Influences Delivery of Peptido-Toxins for Cancer Therapy. PLoS ONE 2015, 10, e0125908. [Google Scholar] [CrossRef] [PubMed]
- Dias, R.; Azevedo, J.D.; Walter, F. Molecular Docking Algorithms. Curr. Drug Targets 2008, 9, 1040–1047. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Grinter, S.Z.; Zou, X. Scoring functions and their evaluation methods for protein–ligand docking: Recent advances and future directions. Phys. Chem. Chem. Phys. 2010, 12, 12899–12908. [Google Scholar] [CrossRef]
- Yu, M.X.; Xing, Z.H.; Mihaly, M.; Meng, C. Molecular Docking: A powerful approach for structure-based drug discovery. Curr. Comput. Aided Drug Des. 2011, 7, 146–157. [Google Scholar]
- Pagadala, N.S.; Syed, K.; Tuszynski, J. Software for molecular docking: A review. Biophys. Rev. 2017, 9, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Martinez, F.D.P.; Arciniega, M.; Franco, J.L.M. Molecular docking: Current advances and challenges. Cienc. Químico-Biológicas 2018, 21, 65–87. [Google Scholar]
- Ramezanpour, M.; Leung, S.; Delgado-Magnero, K.; Bashe, B.; Thewalt, J.; Tieleman, D. Computational and experimental approaches for investigating nanoparticle-based drug delivery systems. Biochim. Biophys. Acta 2016, 1858, 1688–1709. [Google Scholar] [CrossRef]
- Guvench, O.; Mackerell, A.D. Comparison of Protein Force Fields for Molecular Dynamics Simulations. Mol. Modeling Proteins 2008, 443, 63–88. [Google Scholar]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Akinjobi, J. Supervised Machine Learning Algorithms: Classification and Comparison. Int. J. Comput. Trends Technol. 2017, 48, 128–138. [Google Scholar]
- Praveena, M.; Jaiganesh, V. A Literature Review on Supervised Machine Learning Algorithms and Boosting Process. Int. J. Comput. Appl. 2017, 169, 32–35. [Google Scholar] [CrossRef]
- Muhammad, I.; Yan, Z. Supervised Machine Learning Approaches: A Survey. ICTACT J. Soft Comput. 2015, 5, 946–952. [Google Scholar] [CrossRef]
- Jiang, T.; Gradus, J.L.; Rosellini, A.J. Supervised Machine Learning: A Brief Primer. Behav. Ther. 2020, 51, 675–687. [Google Scholar] [CrossRef]
- Moriwaki, H.; Tian, Y.-S.; Kawashita, N.; Takagi, T. Mordred: A molecular descriptor calculator. J. Cheminf. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Xue, L.; Bajorath, J. Molecular Descriptors in Chemoinformatics, Computational Combinatorial Chemistry, and Virtual Screening. Comb. Chem. High Throughput Screen. 2000, 3, 363–372. [Google Scholar] [CrossRef]
- Das, S.; Roy, P.; Islam, A.; Saha, A.; Mukherjee, A. Poly(DL-lactide-co-glycolic acid) Nanoparticle Design and Payload Prediction: A Molecular Descriptor Based Study. Chem. Pharm. Bull. 2013, 61, 125–133. [Google Scholar] [CrossRef][Green Version]
- Cern, A.; Golbraikh, A.; Sedykh, A.; Tropsha, A.; Barenholz, Y.; Goldblum, A. Quantitative structure - property relationship modeling of remote liposome loading of drugs. J. Control. Release 2012, 160, 147–157. [Google Scholar] [CrossRef]
- Ossama, M.; Hathout, R.M.; Attia, D.A.; Mortada, N.D. Enhanced Allicin Cytotoxicity on HEPG-2 Cells Using Glycyrrhetinic Acid Surface-Decorated Gelatin Nanoparticles. ACS Omega 2019, 4, 11293–11300. [Google Scholar] [CrossRef] [PubMed]
- Hathout, R.M.; Abdelhamid, S.G.; Metwally, A.A. Chloroquine and hydroxychloroquine for combating COVID-19: Inves-tigating efficacy and hypothesizing new formulations using Bio/chemoinformatics tools. Inform. Med. Unlocked 2020, 21, 100446. [Google Scholar] [CrossRef]
- Hathout, R.M.; Abdelhamid, S.G.; El-Housseiny, G.S.; Metwally, A.A. Comparing cefotaxime and ceftriaxone in combating meningitis through nose-to-brain delivery using bio/cheminformatics tools. Sci. Rep. 2020, 10, 21250. [Google Scholar] [CrossRef]
- Hathout, R.M.; El-Ahmady, S.H.; Metwally, A.A. Curcumin or besdemethoxycurcumin for nose-to-brain treatment of Alzhiemer disease? A bio/chemo-informatics case study. Nat. Prod. Res. 2018, 32, 2873–2881. [Google Scholar] [CrossRef]
- Metwally, A.A.; El-Ahmady, S.H.; Hathout, R.M. Selecting optimum protein nano-carriers for natural polyphenols using chemoinformatics tools. Phytomedicine 2016, 23, 1764–1770. [Google Scholar] [CrossRef] [PubMed]
- Metwally, A.A.; Hathout, R.M. Replacing microemulsion formulations experimental solubility studies with in-silico methods comprising molecular dynamics and docking experiments. Chem. Eng. Res. Des. 2015, 104, 453–456. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).