A New Computer Model for Evaluating the Selective Binding Affinity of Phenylalkylamines to T-Type Ca2+ Channels
Abstract
1. Introduction
2. Results
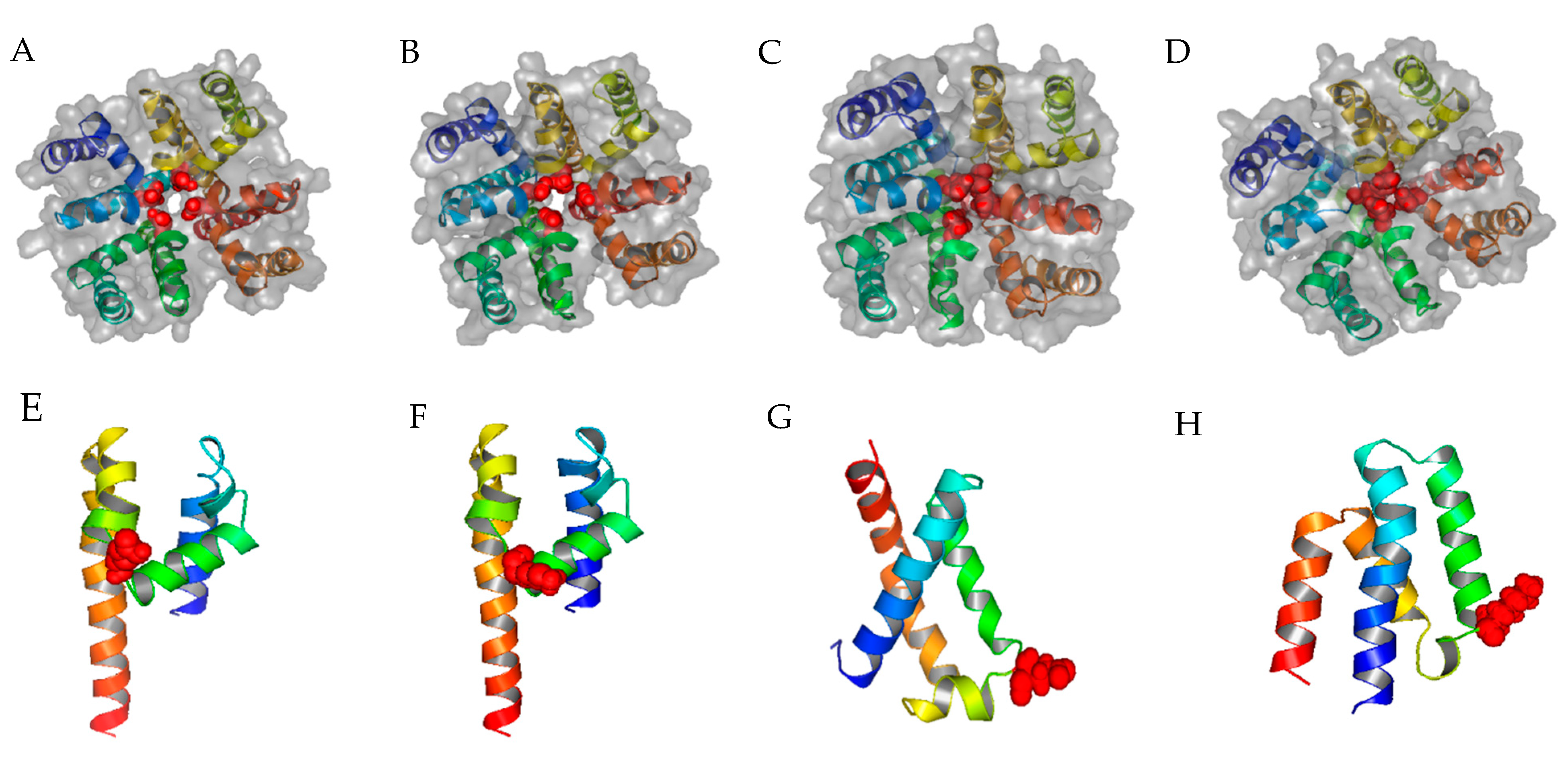
2.1. Homology Modeling of TCCs and α1C LCC
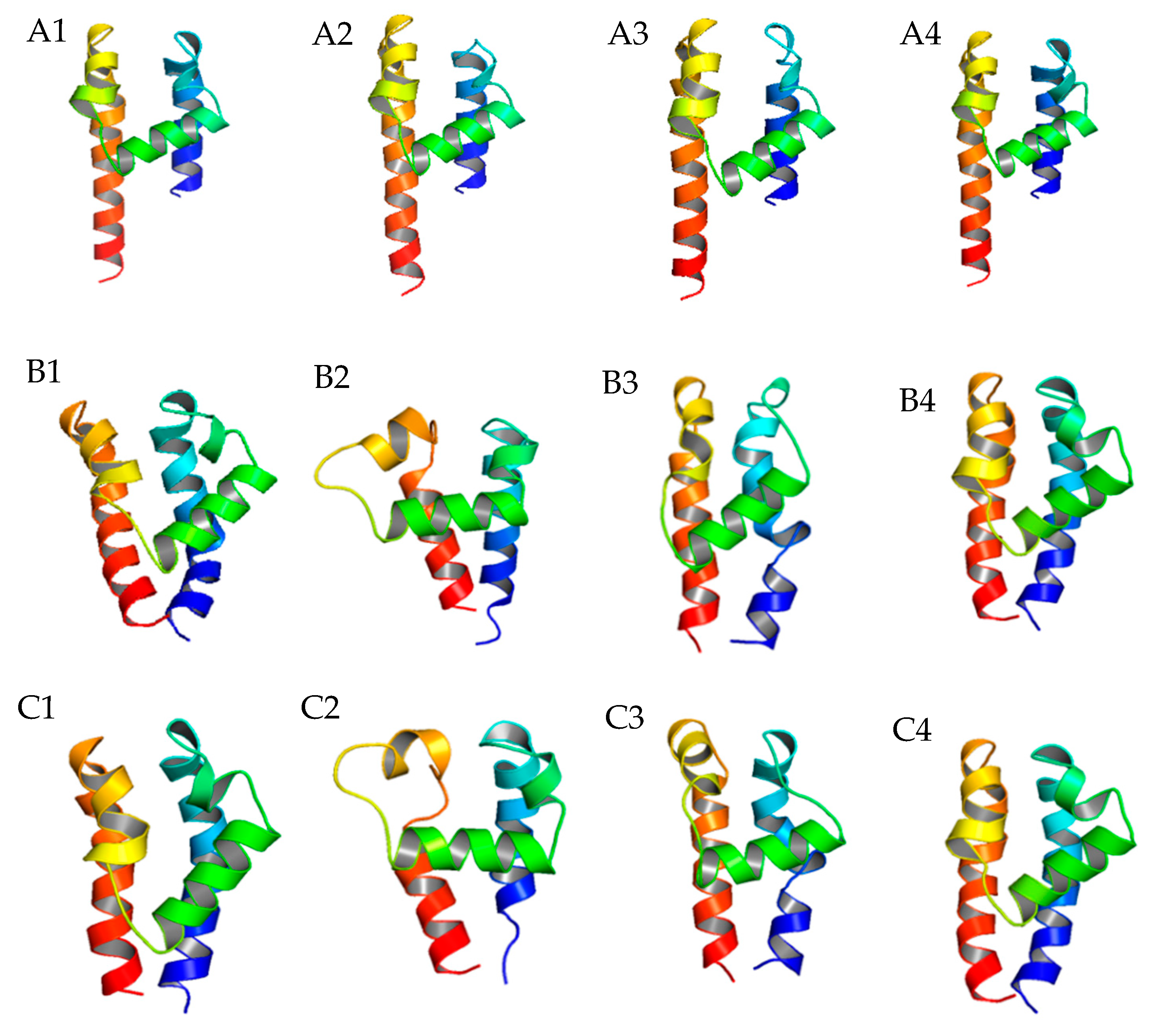
2.2. Further P-Loop Remodeling of TCCs
2.3. Local Electrostatic Potentials of the Selective P-Loop of TCC Domains and the Impact of K3p49
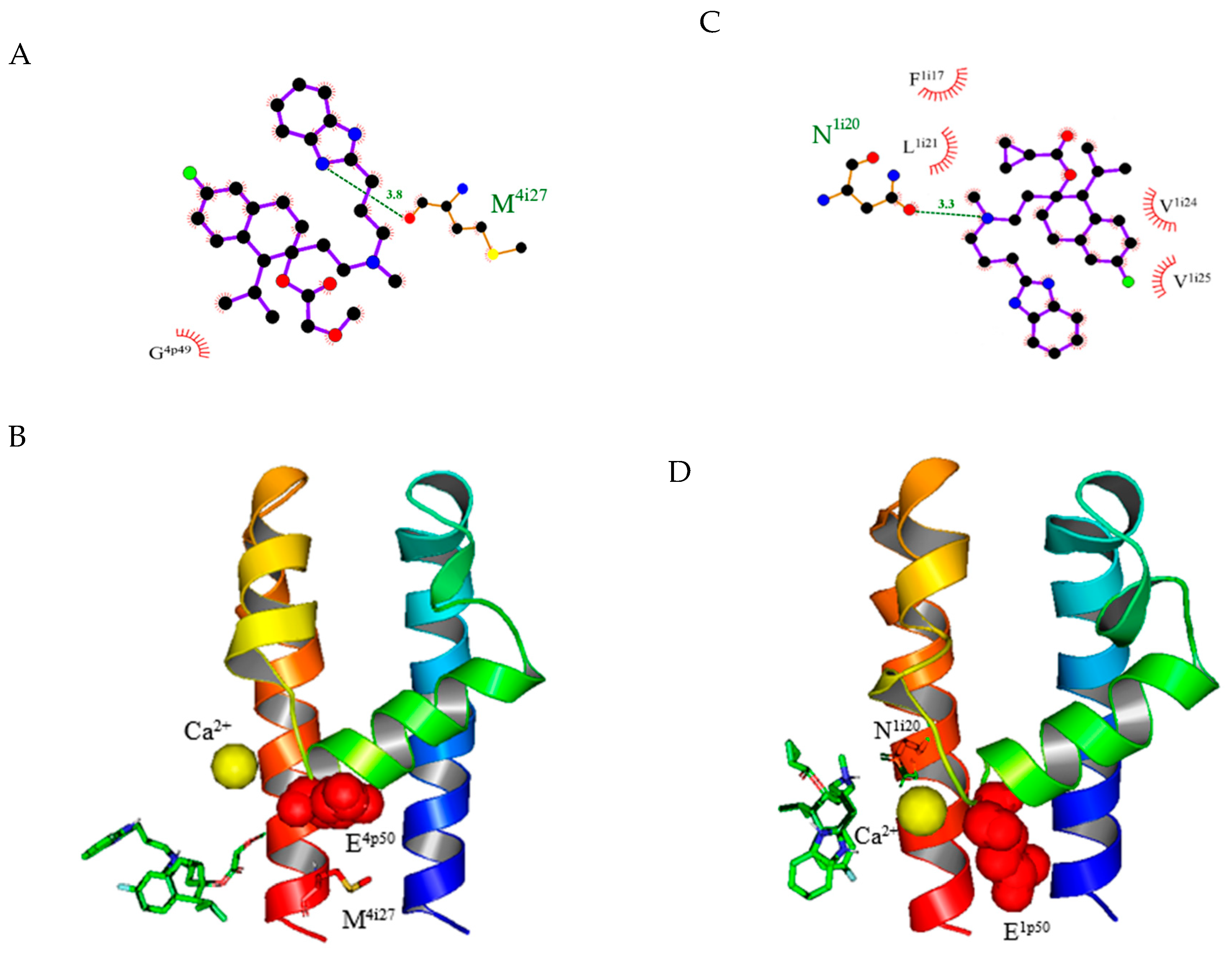
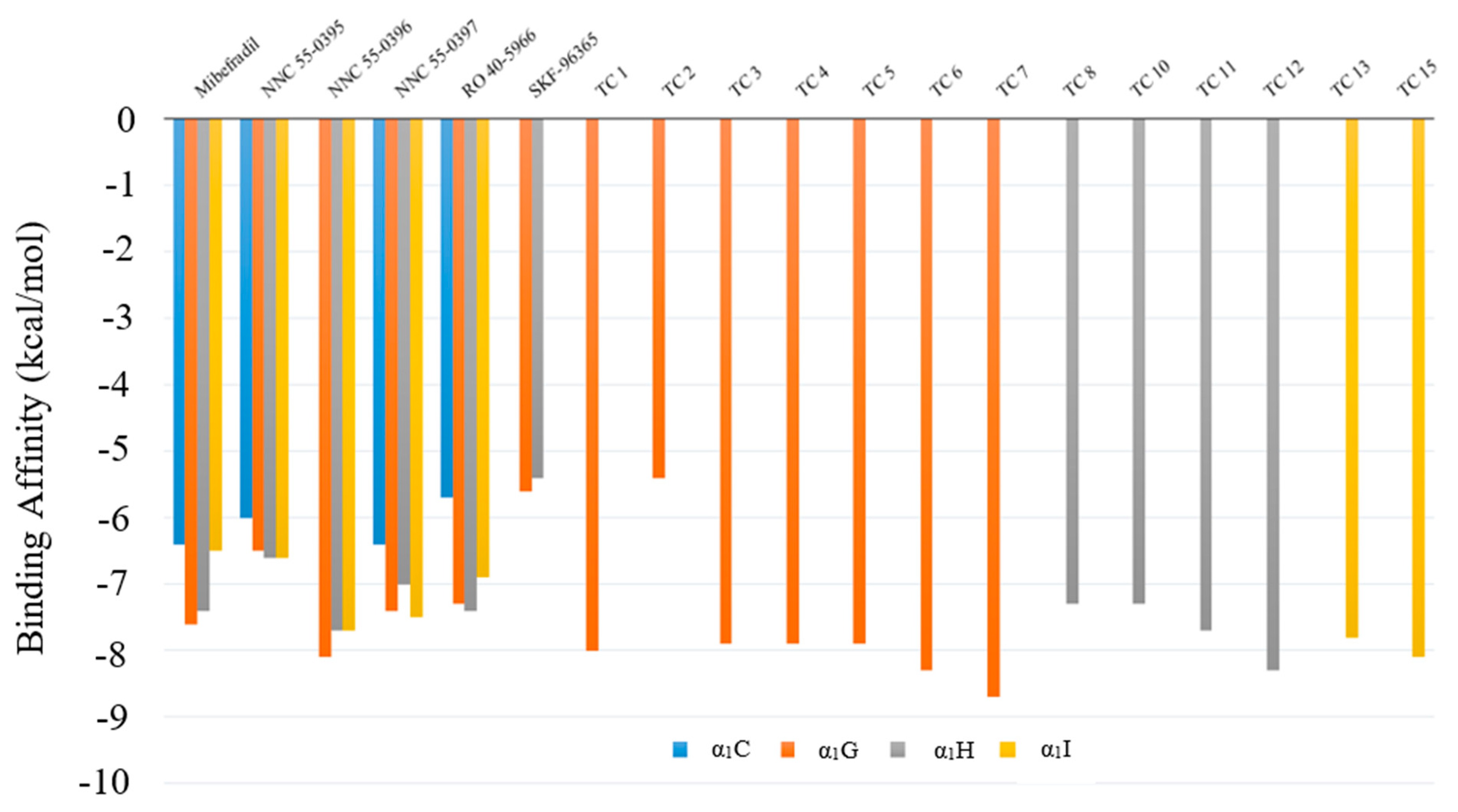
2.4. Model Predictions and Vina Screening Output of Some Current T-Type Ca2+ Channel Blockers
2.5. Evaluation of New Compounds
3. Discussion
4. Materials and Methods
4.1. Homology Modeling of the α1 Subunit
4.2. Local Electrostatic Potential Calculation
4.3. Ab Initio Modeling
4.4. P-Loop Remodeling
4.5. Compound Generation
4.6. Virtual Drug Screening
4.7. Data Analysis
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, J.T.; Huang, L.; Pottle, J.E.; Liu, K.; Yang, Y.; Zeng, X.; Keyser, B.M.; Agrawal, K.C.; Hansen, J.B.; Li, M. Selective blockade of T-type Ca2+ channels suppresses human breast cancer cell proliferation. Cancer Lett. 2008, 267, 116–124. [Google Scholar] [CrossRef]
- Keyser, B.M.; Taylor, J.T.; Choi, S.K.; Lu, Y.; Bhattacharjee, A. Role of T-type Ca 2+ channels in basal [Ca 2+] i regulation and basal insulin secretion in rat islet cells. Curr. Trend Endocrinol. 2014, 7, 35–44. [Google Scholar]
- Lu, Y.; Long, M.; Zhou, S.; Xu, Z.; Hu, F.; Li, M. Mibefradil reduces blood glucose concentration in db/db mice. Clinics 2014, 69, 61–67. [Google Scholar] [CrossRef]
- Pottle, J.; Sun, C.; Gray, L.; Li, M. Exploiting MCF-7 Cells’ Calcium Dependence with Interlaced Therapy. J. Cancer Ther. 2013, 4, 32–40. [Google Scholar] [CrossRef]
- Dogrul, A.; Gardell, L.R.; Ossipov, M.H.; Tulunay, F.C.; Lai, J.; Porreca, F. Reversal of experimental neuropathic pain by T-type calcium channel blockers. Pain 2003, 105, 159–168. [Google Scholar] [CrossRef]
- Li, M. Role of T-Type Ca2+ Channels in Basal Insulin Release. In T-Type Calcium Channels in Basic and Clinical Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 137–150. [Google Scholar]
- Cribbs, L. T-type calcium channel expression and function in the diseased heart. Channels (Austin) 2010, 4, 447–452. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Huang, G.; Wu, Q.; Wu, K.; Li, R.; Lei, J.; Pan, X.; Yan, N. Cryo-EM structures of apo and antagonist-bound human Ca v 3.1. Nature 2019, 576, 492–497. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; El-Din, T.M.G.; Swanson, T.M.; Pryde, D.C.; Scheuer, T.; Zheng, N.; Catterall, W.A. Structural basis for inhibition of a voltage-gated Ca(2+) channel by Ca(2+) antagonist drugs. Nature 2016, 537, 117–121. [Google Scholar] [CrossRef]
- Li, Z.Q.; Scheraga, H.A. Monte-Carlo-Minimization Approach to the Multiple-Minima Problem in Protein Folding. Prac. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef]
- Zhorov, B.S. Vector Method for Calculating the Derivatives of the Energy of Deformation of the Valence Angles and the Torsional Energy of Complex-Molecules with Respect to Generalized Coordinates. J. Struct. Chem. 1982, 23, 649–655. [Google Scholar] [CrossRef]
- Zhorov, B.S. A Vector Method for Calculating the Derivatives of the Energy of the Atom-Atom Interactions of Complex-Molecules with Respect to Generalized Coordinates. J. Struct. Chem. 1981, 22, 4–8. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. Software News and Update AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [PubMed]
- Li, M.; Hansen, J.B.; Huang, L.; Keyser, B.M.; Taylor, J.T. Towards selective antagonists of T-type calcium channels: Design, characterization and potential applications of NNC 55-0396. Cardiovasc. Drug Rev. 2005, 23, 173–196. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.C.K.; Tikhonov, D.B.; Zhorov, B.S. Structural Model for Phenylalkylamine Binding to L-type Calcium Channels. J. Biol. Chem. 2009, 284, 28332–28342. [Google Scholar] [CrossRef] [PubMed]
- Li, S.C.; Ng, Y.K. Calibur: A tool for clustering large numbers of protein decoys. BMC Bioinform. 2010, 11, 25. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; DiMaio, F.; Wang, R.Y.-R.; Kim, D.; Miles, C.; Brunette, T.; Thompson, J.; Baker, D. High-resolution comparative modeling with RosettaCM. Structure 2013, 21, 1735–1742. [Google Scholar] [CrossRef]
- Hosseinzadeh, P.; Bhardwaj, G.; Mulligan, V.K.; Shortridge, M.D.; Craven, T.W.; Pardo-Avila, F.; Retti, S.A.; Kim, D.E.; Silva, D.A.; Ibrahim, Y.M.; et al. Comprehensive computational design of ordered peptide macrocycles. Science 2017, 358, 1461–1466. [Google Scholar] [CrossRef]
- Cooper, C.D.; Barba, L.A. Poisson–Boltzmann model for protein–surface electrostatic interactions and grid-convergence study using the PyGBe code. Comput. Phys. Commun. 2016, 202, 23–32. [Google Scholar] [CrossRef]
- Wu, S.W.; Zhang, M.; Vest, P.A.; Bhattacharjee, A.; Liu, L.; Li, M. A mibefradil metabolite is a potent intracellular blocker of L-type Ca2+ currents in pancreatic beta-cells. J. Pharmacol. Exp. Ther. 2000, 292, 939–943. [Google Scholar]
- Gomez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernandez-Lobato, J.M.; Sanchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Central Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Tang, L.; Gamal El-Din, T.M.; Payandeh, J.; Martinez, G.Q.; Heard, T.M.; Scheuer, T.; Zheng, N.; Catterall, W.A. Structural basis for Ca2+ selectivity of a voltage-gated calcium channel. Nature 2014, 505, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Hockerman, G.H.; Peterson, B.Z.; Johnson, B.D.; Catterall, W.A. Molecular determinants of drug binding and action on L-type calcium channels. Annu. Rev. Pharmacol. Toxicol. 1997, 37, 361–396. [Google Scholar] [CrossRef]
- Peterson, B.Z.; Tanada, T.N.; Catterall, W.A. Molecular determinants of high affinity dihydropyridine binding in L-type calcium channels. J. Biol. Chem. 1996, 271, 5293–5296. [Google Scholar] [CrossRef] [PubMed]
- Hockerman, G.H.; Johnson, B.D.; Scheuer, T.; Catterall, W.A. Molecular Determinants of High-Affinity Phenylalkylamine Block of L-Type Calcium Channels. J. Biol. Chem. 1995, 270, 22119–22122. [Google Scholar] [CrossRef]
- Catterall, W.A.; Striessnig, J. Receptor-Sites for Ca2+ Channel Antagonists. Trends Pharmacol. Sci. 1992, 13, 256–262. [Google Scholar] [CrossRef]
- Barreiro, G.; Guimarães, C.R.W.; de Alencastro, R.B. A molecular dynamics study of an L-type calcium channel model. Protein Eng. 2002, 15, 109–122. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.H.; Hou, T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Shapovalov, M.V.; Wang, Q.; Xu, Q.F.; Andrake, M.; Dunbrack, R.L. BioAssemblyModeler (BAM): User-Friendly Homology Modeling of Protein Homo- and Heterooligomers. PLoS ONE 2014, 9, e98309. [Google Scholar] [CrossRef]
- Sanner, M.F.; Olson, A.J.; Spehner, J.C. Reduced surface: An efficient way to compute molecular surfaces. Biopolymers 1996, 38, 305–320. [Google Scholar] [CrossRef]
- Kim, D.E.; Chivian, D.; Baker, D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 2004, 32, W526–W531. [Google Scholar] [CrossRef]
- Ertl, P.; Schuffenhauer, A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions. J. Cheminformatics 2009, 1, 8. [Google Scholar] [CrossRef] [PubMed]
- Bickerton, G.R.; Paolini, G.V.; Besnard, J.; Muresan, S.; Hopkins, A.L. Quantifying the chemical beauty of drugs. Nat. Chem. 2012, 4, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Leite, T.B.; Gomes, D.; Miteva, M.A.; Chomilier, J.; Villoutreix, B.O.; Tuffery, P. Frog: A FRee Online druG 3D conformation generator. Nucleic Acids Res. 2007, 35, W568–W572. [Google Scholar] [CrossRef] [PubMed]
- Miteva, M.A.; Guyon, F.; Tuffery, P. Frog2: Efficient 3D conformation ensemble generator for small compounds. Nucleic Acids Res. 2010, 38, W622–W627. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminformatics 2011, 3, 33. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Swindells, M.B. LigPlot+: Multiple Ligand-Protein Interaction Diagrams for Drug Discovery. J. Chem. Inf. Model. 2011, 51, 2778–2786. [Google Scholar] [CrossRef]
| Channel Domain | Channel Type | AA Sequence Alignment | PyGBe [19] (Esol, Ecoul) |
|---|---|---|---|
| α1G | I T L E G W V D | −11, −407 | |
| Domain I | α1H | I T L E G W V D | −110, −408 |
| α1I | I T L E G W V E | −116, −409 | |
| Reduced TCC | T L E G W V | −87, −323 | |
| α1G | L T Q E D W N K | −217, −631 | |
| Domain II | α1H | L T Q E D W N V | −262, −631 |
| α1I | L T Q E D W N V | −487, −633 | |
| Reduced TCC | T Q E D W | −164, −425 | |
| α1G | A S K D G W V D | −107, −392 | |
| Domain III | α1H | S S K D G W V N | −113, −425 |
| α1I | A S K D G W V N | −105, −394 | |
| Reduced TCC | S K D G W | −101, −303 | |
| α1G | S T G D N W N G | −132, −568 | |
| Domain IV | α1H | S T G D N W N G | −164, −574 |
| α1I | S T G D N W N G | −177, −574 | |
| Reduced TCC | T G D N W | −86, −393 |
| Receptor | Drug ID | ΔG (kcal/mol) | Binding Domain |
|---|---|---|---|
| α1C | NNC 55-0395 | −6.0 | IV |
| NNC 55-0396 | N/A | N/A | |
| NNC 55-0397 | −6.4 | IV | |
| Mibefradil | −6.4 | IV | |
| RO 40-5966 | −5.7 | IV | |
| SKF-96365 | N/A | IV | |
| α1G | NNC 55-0395 | −6.5 | I |
| NNC 55-0396 | −8.1 | I | |
| NNC 55-0397 | −7.4 | I | |
| Mibefradil | −6.8 | I | |
| RO 40-5966 | −7.3 | I | |
| SKF-96365 | −5.6 | I | |
| α1H | NNC 55-0395 | −6.6 | I |
| NNC 55-0396 | −7.7 | I | |
| NNC 55-0397 | −7.0 | IV | |
| Mibefradil | −7.4 | I | |
| RO 40-5966 | −7.4 | IV | |
| SKF-96365 | −5.4 | I | |
| α1I | NNC 55-0395 | −6.6 | I |
| NNC 55-0396 | −7.7 | I | |
| NNC 55-0397 | −7.5 | I | |
| Mibefradil | −6.5 | IV | |
| RO 40-5966 | −6.9 | I | |
| SKF-96365 | N/A | N/A |
| Compound Name | logP | SAS | QED |
|---|---|---|---|
| NNC 55-0365 | 6.8147 | 3.678636 | 0.273518 |
| NNC 55-0396 | 6.0345 | 3.716436 | 0.351695 |
| NNC 55-0397 | 6.2805 | 3.718535 | 0.337773 |
| Mibefradil | 5.2709 | 3.71918 | 0.367183 |
| TC 1 | 6.1671 | 4.433975 | 0.402836 |
| TC 2 | 5.3351 | 5.24865 | 0.408449 |
| TC 3 | 4.8963 | 4.777741 | 0.474028 |
| TC 4 | 5.0404 | 4.731275 | 0.441386 |
| TC 5 | 5.5879 | 4.951457 | 0.415026 |
| TC 6 | 4.4585 | 4.79633 | 0.469604 |
| TC 7 | 3.6902 | 4.806084 | 0.63381 |
| TC 8 | 6.2697 | 4.851381 | 0.242332 |
| TC 10 | 4.1891 | 4.542497 | 0.312353 |
| TC 11 | 5.372 | 3.089346 | 0.276759 |
| TC 12 | 4.9472 | 3.971406 | 0.248549 |
| TC 13 | 5.7028 | 4.449589 | 0.406663 |
| TC 15 | 4.73 | 3.921747 | 0.368816 |
| Channel | Domain/Segment | Residue Label Prefix a | Selected Key Amino Acid Sequence b |
|---|---|---|---|
| 1 11 21 | |||
| α1C | 1S5 | 1o | PLLHIALLVL FVIIIYAIIG LELFMGK |
| α1G | 1S5 | 1o | MLGNVLLLCF FVFFIFGIVG VQLWAGL |
| α1C | 2S5 | 2o | SIASLLLLLF LFIIIFSLLG MQLFGGK |
| α1G | 2S5 | 2o | NVATFCMLLM LFIFIFSILG MHLFGCK |
| α1C | 3S5 | 3o | TIGNIVIVTT LLQFMFACIG VALFKGK |
| α1G | 3S5 | 3o | PIGNIVVICC AFFIIFGILG VQLFKGK |
| α1C | 4S5 | 4o | ALPYVALLIV MLFFIYAVII GMQVFGK |
| α1G | 4S5 | 4o | QVGNLGLLFM LLFFIFAALG VELFGDL |
| 33 43 53 | |||
| α1C | 1p | 1p | FDNFAFAMLT VFQCITMEGW TDVLY |
| α1G | 1p | 1p | FDNIGYAWIA IFQVITLEGW VDIMY |
| α1C | 2p | 2p | FDNFPQSLLT VFQILTGEDW NSVMY |
| α1G | 2p | 2p | FDSLLWAIVT VFQILTQEDW NKVLY |
| α1C | 3p | 3p | FDNVLAAMMA LFTVSTFEGW PELLY |
| α1G | 3p | 3p | FDNLGQALMS LFVLASKDGW VDIMY |
| α1C | 4p | 4p | FQTFPQAVLL LFRCATGEAW QDIML |
| α1G | 4p | 4p | FRNFGMAFLT LFRVSTGDNW NGIMK |
| 1 11 21 | |||
| α1C | 1S6 | 1i | ELPWVYFVSL VIFGSFFVLN LVLGVLSGEF |
| α1G | 1S6 | 1i | FYNFIYFILL IIVGSFFMIN LCLVVIATQF |
| α1C | 2S6 | 2i | MLVCIYFIIL FICGNYILLN VFLAIAYDNL |
| α1G | 2S6 | 2i | SWAALYFIAL MTFGNYVLFN LLVAILVEGF |
| α1C | 3S6 | 3i | VEISIFFIIY IIIIAFFMMN IFVGFVIVTF |
| α1G | 3S6 | 3i | PWMLLYFISF LLIVAFFVLN MFVGVVVENF |
| α1C | 4S6 | 4i | SFAVFYFISF YMLCAFLIIN LFVAVIMDNF |
| α1G | 4S6 | 4i | VISPIYFVSF VLTAQFVLVN VVIAVLMKHL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Li, M. A New Computer Model for Evaluating the Selective Binding Affinity of Phenylalkylamines to T-Type Ca2+ Channels. Pharmaceuticals 2021, 14, 141. https://doi.org/10.3390/ph14020141
Lu Y, Li M. A New Computer Model for Evaluating the Selective Binding Affinity of Phenylalkylamines to T-Type Ca2+ Channels. Pharmaceuticals. 2021; 14(2):141. https://doi.org/10.3390/ph14020141
Chicago/Turabian StyleLu, You, and Ming Li. 2021. "A New Computer Model for Evaluating the Selective Binding Affinity of Phenylalkylamines to T-Type Ca2+ Channels" Pharmaceuticals 14, no. 2: 141. https://doi.org/10.3390/ph14020141
APA StyleLu, Y., & Li, M. (2021). A New Computer Model for Evaluating the Selective Binding Affinity of Phenylalkylamines to T-Type Ca2+ Channels. Pharmaceuticals, 14(2), 141. https://doi.org/10.3390/ph14020141





