Full Hierarchic Versus Non-Hierarchic Classification Approaches for Mapping Sealed Surfaces at the Rural-Urban Fringe Using High-Resolution Satellite Data
Abstract
:1. Introduction
1.1 Context-based approaches
1.2 Object-oriented approach
1.3 Non-parametric classification
1.4 Objectives of the study
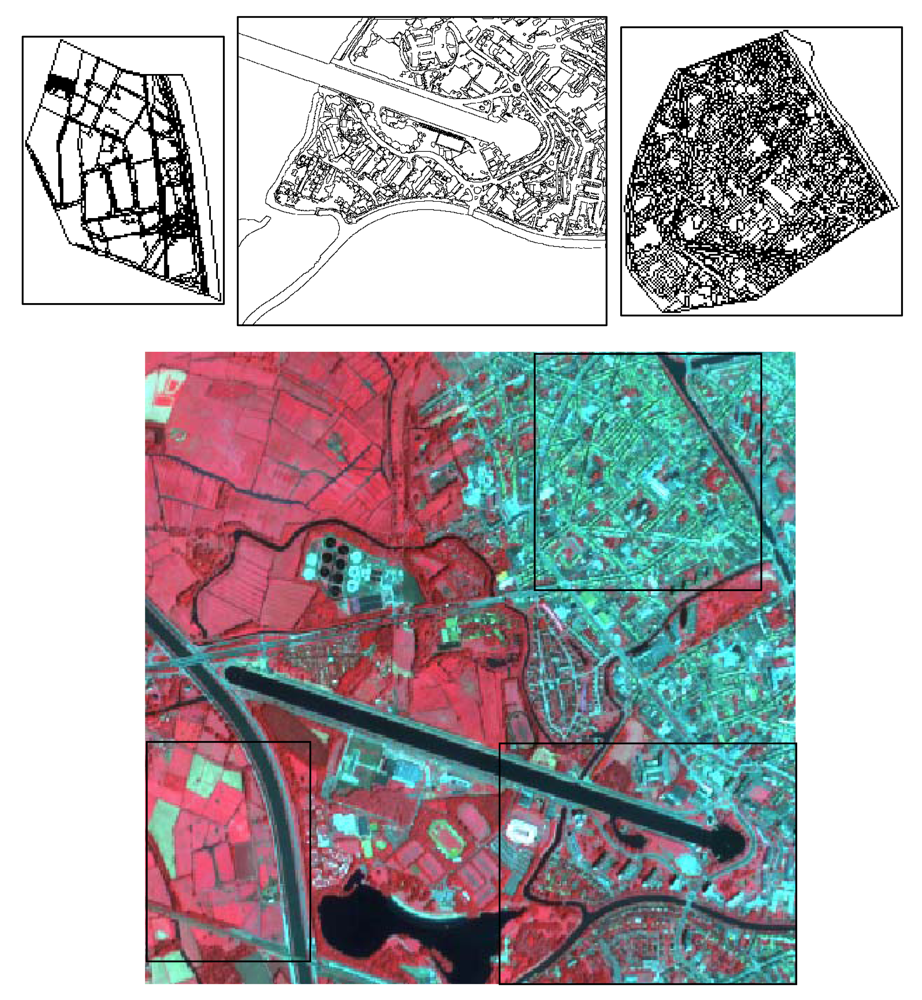
2. Study area and data
3. Methods
3.1. Classification scheme, selection of training data and strategy for accuracy assessment
3.2. Segmentation
3.3. Classification algorithms
3.4. Feature selection
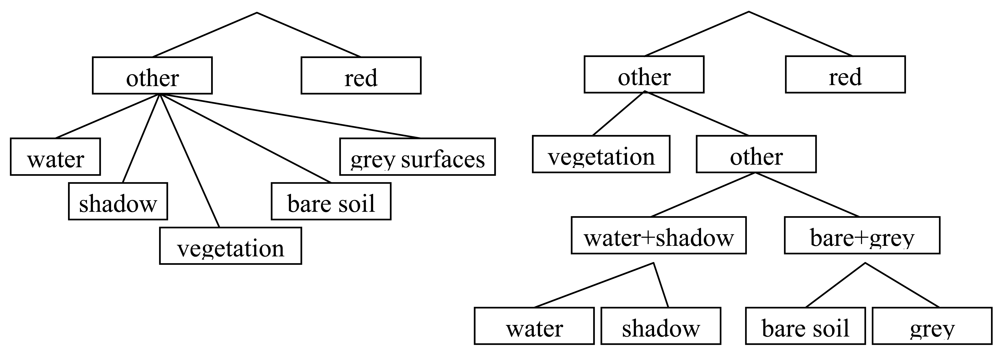
3.5. Classification strategies
3.6. Shadow reclassification
4. Results and Discussion
4.1. Feature selection
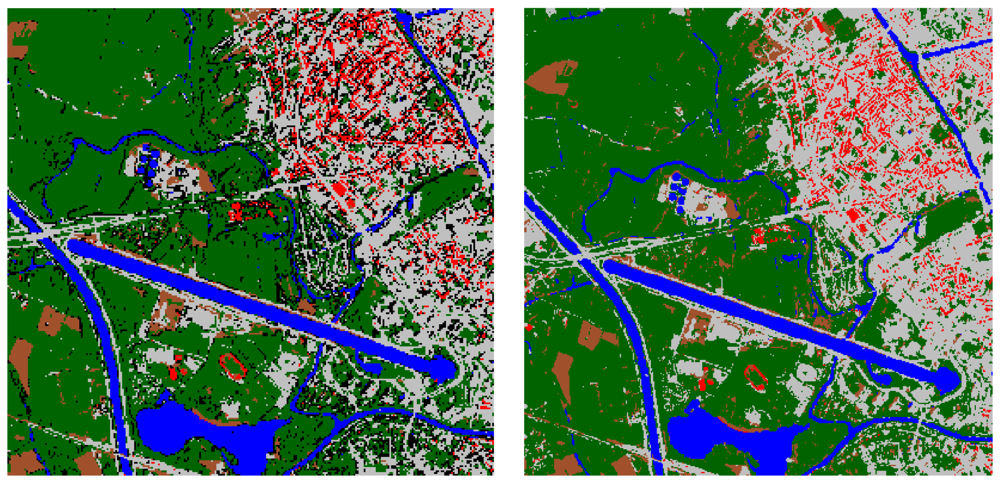
4.2. Classification
4.3. Shadow reclassification
5. Conclusions
Acknowledgments
References
- UNFPA. State of world population 2007 – Unleashing the potential of urban growth; United Nations Population Fund, 2007. http://www.unfpa.org/swp/2007/presskit/pdf/sowp2007_eng.pdf.
- EEA. Urban sprawl in Europe; Briefing 4 of the European Environment Agency, 2006. http://reports.eea.europa.eu/briefing_2006_4/en.
- Jensen, J.R.; Cowen, D.C. Remote sensing of urban suburban infrastructure and socio-economic attributes. Photogramm. Eng. Remote Sens. 1999, 65, 611–622. [Google Scholar]
- Schueler, T.R. The importance of imperviousness. Watersh. Protect. Techn. 1994, 1, 100–111. [Google Scholar]
- Weng, Q. Remote Sensing of Impervious Surfaces; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Thomas, N.; Hendrix, C.; Congalton, R.G. A comparison of urban mapping methods using high-resolution digital imagery. Photogramm. Eng. Remote Sens. 2003, 69, 963–972. [Google Scholar]
- Hodgson, M.E.; Jensen, J.R.; Tullis, J.A.; Riordan, K.D.; Archer, C.M. Synergistic use of lidar and color aerial photography for mapping urban parcel imperviousness. Photogramm. Eng. Remote Sens. 2003, 69, 973–980. [Google Scholar]
- Dare, P.M. Shadow analysis in high-resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar]
- Van de Voorde, T.; De Genst, W.; Canters, F. Improving pixel-based VHR land-cover classifications of urban areas with post-classification techniques. Photogramm. Eng. Remote Sens. 2007, 73, 1017–1027. [Google Scholar]
- Gurney, M.C.; Townshend, J.R.G. The use of contextual information in the classification of remotely sensed data. Photogramm. Eng. Remote Sens. 1983, 49, 55–64. [Google Scholar]
- Barnsley, M.J.; Barr, S.L. Inferring urban land use from satellite sensor images using kernel-based spatial reclassification. Photogramm. Eng. Remote Sens. 1996, 62, 949–958. [Google Scholar]
- Barr, S.; Barnsley, M. Reducing structural clutter in land cover classifications of high spatial resolution remotely-sensed images for urban land use mapping. Comput. Geosci. 2000, 26, 433–449. [Google Scholar]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar]
- He, H.; Collet, C. Combining spectral and textural features for multispectral image classification with artificial neural networks. Int. Arch. Photogramm. Remote Sens. 1999, 32(part 7-4-3), W6. [Google Scholar]
- Gong, P.; Howarth, P.J. The use of structural information for improving land-cover classification accuracies at the rural-urban fringe. Photogramm. Eng. Remote Sens. 1990, 56, 67–73. [Google Scholar]
- Huang, X.; Zhang, L.; Li, P. Classification of very high spatial resolution imagery based on the fusion of edge and multispectral information. Photogramm. Eng. Remote Sens. 2008, 74, 1585–1596. [Google Scholar]
- Xu, B.; Gong, P.; Seto, E.; Spear, R. Comparison of grey-level reduction and different texture spectrum encoding methods for land-use classification using a panchromatic Ikonos image. Photogramm. Eng. Remote Sens. 2003, 69, 529–536. [Google Scholar]
- Laha, A.; Pal, N.R.; Das, J. Land cover classification using fuzzy rules and aggregation of contextual information through evidence theory. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1633–1641. [Google Scholar]
- Chan, J.C.-W.; Bellens, R.; Canters, F.; Gautama, S. An assessment of geometric activity features for classification of urban man-made objects using very-high-resolution imagery. Photogramm. Eng. Remote Sens. In press.
- Ji, C.Y. Land-use classification of remotely sensed data using Kohonen self-organizing feature map neural networks. Photogramm. Eng. Remote Sens. 2000, 66, 1451–1460. [Google Scholar]
- Chen, D.; Stow, D.A.; Gong, P. Examining the effect of spatial resolution and texture window size on classification accuracy: an urban environment case. Int. J. Remote Sens. 2004, 25, 2177–2192. [Google Scholar]
- Myint, S.W.; Lam, N. A study of lacunarity-based texture analysis approaches to improve urban image classification. Comput. Environ. Urban Syst. 2005, 29, 501–523. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: an optimization approach for high quality multi-scale image segmentation. Strobl, Blaschke, Greisebener, Eds.; In Angewandte Geographische Informationsverarbeitung XI. Beiträge zum AGIT-Symposium Salzburg; Herbert Wichmann Verlag; Karlsruhe, 2000. [Google Scholar]
- Schiewe, J. Segmentation of high-resolution remotely sensed data – concepts, applications and problems. Symposium on Geospatial Theory, Processing and Applications, Ottawa. Canada, July 9-12, 2002.
- Lee, D.S.; Shan, J.; Bethel, J.S. Class-guided building extraction from Ikonos imagery. Photogramm. Eng. Remote Sens. 2003, 69, 143–150. [Google Scholar]
- Liu, Z.J.; Wang, J.; Liu, W.P. Building extraction from high resolution imagery based on multi-scale object oriented classification and probabilistic Hough transform. Proceedings of the IGARSS 2005 Symposium, Seoul, South Korea, July 25-29, 2005.
- Flanders, D.; Hall-Beyer, M.; Pereverzoff, J. Preleminary evaluation of eCognition object-based software for cut block delineation and feature extraction. Can. J. Remote Sens. 2003, 29, 441–452. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar]
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar]
- Siachalou, S.; Doxani, G.; Tsakiri-Strati, M. Classification enhancement in urban areas. Proceedings of the 1st Workshop of the EARSeL SIG on Urban Remote Sensing, Berlin, Germany, March 2-3; 2006. [Google Scholar]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar]
- Rangsaneri, Y.; Thitimajshima, P.; Kanotai, S. Multispectral image segmentation using art1/art2 neural networks. Proceedings 22nd Asian Conference on Remote Sensing, Singapore, November 5-9, 2001.
- Guarnieri, A.; Vettore, A. Automated techniques for satellite image segmentation. Proceedings of the Symposium on Geospatial Theory, Processing and Applications, Ottawa, Canada, July 9-12, 2002.
- Chen, Q.; Zhou, C.; Luo, J.; Ming, D. Fast segmentation of high-resolution satellite images using watershed transform combined with an efficient region merging approach. In IWCIA; Auckland, New Zealand, December 1-3 2004. [Google Scholar]
- Esch, T.; Roth, A.; Dech, S. Robust approach towards an automated detection of built-up areas from high resolution radar imagery. Proceedings of the ISPRS WG VII/1 “Human Settlements and Impact Analysis” 3rd International Symposium Remote Sensing and Data Fusion over Urban Areas (URBAN 2005) and 5th International Symposium Remote Sensing of Urban Areas (URS 2005), Tempe, AZ, USA, March 14-16, 2005.
- Meinel, G.; Neubert, M. A comparison of segmentation programs for high resolution remote sensing data. Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, July, 12-23, 2004.
- Carleer, A. Region-based Classification Potential for Land-cover Classification with Very High Spatial Resolution Satellite Data. Ph.D. thesis, ULB, Brussels, Belgium, 2005. [Google Scholar]
- Zhou, Y.; Wang, Y.Q. Extraction of impervious surface area using orthophotos in Rhode Island. Proceedings of ASPRS 2006 Annual Conference, Reno, NV, USA, May, 1-5, 2006.
- Yuan, F.; Bauer, M.E. Mapping impervious surface area using high resolution imagery: a comparison of object-based and per pixel classification. Proceedings of ASPRS 2006 Annual Conference, Reno, NV, USA, May, 1-5, 2006.
- Carleer, A.P.; Debeir, O.; Wolff, E. Assessment of very high spatial resolution satellite image segmentations. Photogramm. Eng. Remote Sens. 2005, 71, 1285–1294. [Google Scholar]
- Diermayer, E.; Hostert, P.; Schiefer, S.; Damm, A. Comparing pixel- and object-based classification of imperviousness with HRSC-AX data. Proceedings of the 1st Workshop of the EARSeL SIG on Urban Remote Sensing, Berlin, Germany, March 2-3, 2006.
- Caprioli, M.; Tarantino, E. Urban features recognition from VHR satellite data with an object-oriented approach. ISPRS Challenges in Geospatial Analysis, Stuttgart, Germany; 2003; pp. 176–180. [Google Scholar]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar]
- Foody, G.M. Hard and soft classifications by a neural network with a non-exhaustively defined set of classes. Int. J. Remote Sens. 2002, 23, 3853–3864. [Google Scholar]
- Cetin, M.; Kavzoglu, T.; Musaoglu, N. Classification of multi-spectral, multi-temporal and multi-sensor images using principal components analysis and artificial neural networks: Beykoz case. Proceedings XXth International Society for Photogrammetry and Remote Sensing-Congress, Istanbul, Turkey, July 12-23, 2004.
- Liu, J.; Shao, G.; Zhu, H.; Liu, S. A neural network approach for information extraction from remotely sensed data. Proceedings 12th International Conference on Geoinformatics – Geospatial Information Research: Bridging the Pacific and Atlantic, Sweden, June 7-9, 2004.
- Running, S.; Loveland, T.R.; Pierce, L.L.; Nemani, R.R.; Hunt, E.R., Jr. A remote sensing based vegetation classification logic for global land cover analysis. Remote Sens. Environ. 1995, 51, 39–48. [Google Scholar]
- Hansen, M.; Dubayah, R.; Defries, R. Classification trees: an alternative to traditional land cover classifiers. Int. J. Remote Sens. 1996, 17, 1075–1081. [Google Scholar]
- Quinlan, R.J. C4.5: Programs for Machine Learning.; Morgan Kaufmann Publishers Inc.: San Mateo, CA, USA, 1993. [Google Scholar]
- Sheeren, D.; Puissant, A.; Weber, C.; Gançarski, P.; Wemmert, C. Deriving classification rules from multiple remotely sensed urban data with data mining. Proceedings of the 1st Workshop of the EARSeL SIG on Urban Remote Sensing, Berlin, Germany, March 2-3, 2006.
- Rollet, R.; Benie, G.B.; Li, W.; Wang, S.; Boucher, J.-M. Image classification algorithm based on the RBF neural network and K-means. Int. J. Remote Sens. 1998, 19, 3003–3009. [Google Scholar]
- Carpenter, G.; Gopal, S.; Macomber, S.A.; Martens, S.; Woodcock, C.; Franklin, J. A neural network method for efficient vegetation mapping. Remote Sens. Environ. 1999, 70, 326–338. [Google Scholar]
- Gopal, S.; Woodcock, C.E.; Strahler, A.H. Fuzzy neural network classification of global land cover from a 1° AVHRR data set. Remote Sens. Environ. 1999, 67, 230–243. [Google Scholar]
- Seto, K.C.; Liu, W. Comparing ARTMAP neural network with the maximum-likelihood classifier for detecting urban change. Photogramm. Eng. Remote Sens. 2003, 69, 981–990. [Google Scholar]
- Ito, Y.; Omatu, S. Extended LVQ neural network approach to land cover mapping. IEEE Trans. Geosci. Remote Sens. 1999, 37, 313–317. [Google Scholar]
- Molinier, M.; Laaksonen, J.; Ahola, J.; Häme, T. Self-organizing map application for retrieval of man-made structures in remote sensing data. IGARSS, Denver, CO, USA, July 31 - August 4, 2006.
- Paola, J.D.; Schowengerdt, R.A. The effect of neural-network structure on a multispectral land-use/land-cover classification. Photogramm. Eng. Remote Sens. 1997, 63, 535–544. [Google Scholar]
- Benediktsson, J.A.; Pesaresi, M.; Arnason, K. Classification and feature extraction for remote sensing images from urban areas based on morphological transformations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1940–1949. [Google Scholar]
- Chormanski, J.; Van de Voorde, T.; De Roeck, T.; Batelaan, O.; Canters, F. Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover. Sensors 2008, 8, 910–932. [Google Scholar]
- Bianchin, A.; Bravin, L. Land use in urban context from IKONOS image: a case study. Proceedings of the 4th International Symposium on Remote Sensing of Urban Areas, Regensburg, Germany, June 27-29, 2003.
- Lu, D.; Weng, Q. Mapping urban impervious surfaces from medium and high spatial resolution multispectral imagery. In Remote Sensing of Impervious Surfaces; Weng, Q., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 59–73. [Google Scholar]
- Yoon, J.J.; Koch, C.; Ellis, T.J. ShadowFlash: an approach for shadow removal in an active illumination environment. Electronic Proceedings of the 13th British Machine Vision Conference, UK, September 2-5, 2002.
- De Genst, W.; Canters, F. Extracting detailed urban land-cover information from hyper-spectral imagery. Proceedings of the 24th Urban Data Management Symposium (UDMS 2004), Chiogga-Venice, Italy, unpaginated CD-ROM. October 27-29, 2004.
- Gigandet, X. Satellite Image Segmentation and Classification.; Diploma project, Signal Processing Institute of the Swiss Federal Institute of Technology: Lausanne, Switzerland, 2004. [Google Scholar]
- Hu, X.; Tao, C.V.; Prenzel, B. Automatic segmentation of high-resolution satellite imagery by integrating texture, intensity and color features. Photogramm. Eng. Remote Sens. 2005, 71, 1399–1406. [Google Scholar]
- Baatz, M.; Benz, U.; Dehghani, S.; Heynen, M.; Höltje, A.; Hofmann, P.; Lingenfelder, I.; Mimler, M.; Sohlbach, M.; Weber, M.; Willhauck, G. eCognition Professional – User Guide 4.; Munich: Definiens-Imaging: Munich, Germany, 2004. [Google Scholar]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: bagging, boosting, and variants. J. Machine Learn. 1999, 36, 105–139. [Google Scholar]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: bagging, boosting and randomization. Machine Learn. 2000, 40, 139–158. [Google Scholar]
- Lawrence, R.L.; Bunn, A.; Powell, S.; Zambon, M. Classification of remotely sensed imagery using stochastic gradient boosting as a refinement of classification tree analysis. Remote Sens. Environ. 2004, 90, 331–336. [Google Scholar]
- Liu, W.; Gopal, S.; Woodcock, C.E. Uncertainty and confidence in land cover classification using a hybrid classifier approach. Photogramm. Eng. Remote Sens. 2004, 70, 963–971. [Google Scholar]
- Misakova, L.; Jacquin, A.; Gay, M. Mapping urban sprawl using VHR-data and object oriented classification. Proceedings of the 1st Workshop of the EARSeL SIG on Urban Remote Sensing, Berlin, Germany, March 2-3, 2006.
- Herold, M.; Gardner, M.; Hadley, B.; Roberts, D. The spectral dimension in urban land cover mapping from high-resolution optical remote sensing data. Proceedings of the 3rd Symposium on Remote Sensing of Urban Areas, Istanbul, Turkey; 2002. [Google Scholar]
- Syed, S.; Dare, P.; Jones, S. Automatic classification of land cover features with high resolution imagery and lidar data: an object-oriented approach. Proceedings of the National Biennial Conference of the Spatial Sciences Institute, Melbourne, Australia; 2005. [Google Scholar]
- Ben-Dor, E. Image spectrometry for urban applications. In Imaging Spectrometry.; Van der Meer, F., De Jong, S., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 2001; pp. 243–281. [Google Scholar]
- Chen, J.; Hepner, G. Investigation of imaging spectrometry for discriminating urban land covers and surface materials. Proceedings of the ASPRS Annual Conference 2001, St Louis, MO, USA; unpaginated CD-ROM. 2001. [Google Scholar]
- Herold, M.; Roberts, D.; Gardner, M.; Dennison, P. Spectrometry for urban area remote sensing – development and analysis of a spectral library from 350 to 2400 nm. Remote Sens. Environ. 2004, 91, 304–319. [Google Scholar]

| red surfaces | vegetation | water | bare soil | grey surfaces | shadow | total | |
|---|---|---|---|---|---|---|---|
| total | 74,868 | 436,972 | 195,490 | 47,842 | 440,182 | 68,436 | 1,263,790 |
| 5.9% | 34.6% | 15.5% | 3.8% | 34.8% | 5.4% | 100% | |
 |  |  |  |  |  |
| mean (x4) | average of the values in the spectral band, taken over all pixels within the segment |
| ratio (x4) | ratio between the mean of the spectral band and the sum of the mean values in every spectral band within the segment |
| stddev (x4) | standard deviation of all pixel values in the spectral band within the segment |
| glcm asm (x4) | angular second moment of the grey-level co-occurrence matrix: reflects the degree of homogeneity present in the spectral band within the segment |
| glcm contrast (x4) | contrast of the grey-level co-occurrence matrix: reflects the contrasts present in the spectral band within the segment |
| glcm entropy (x4) | entropy of the grey-level co-occurrence matrix: reflects the randomness in the spatial arrangement of spectral band values within the segment |
| ratio green-blue | average of the green band divided by average of the blue band |
| ratio red-blue | average of the red band divided by average of the blue band |
| ratio red-green | average of the red band divided by average of the green band |
| brightness | sum of the mean values in every spectral band |
| ndvi | (nir - red) / (nir + red) |
| two-step strategy | ||
|---|---|---|
| DT | MLP | |
| red | mean nir ratio red-green | mean green ratio nir ndvi |
| rest | mean blue stddev blue mean green ratio green stddev green glcm asm green stddev red glcm contrast red mean nir stddev nir asm nir ratio green-blue ratio red-blue ratio red-green brightness ndvi | ratio blue stddev blue glcm asm blue glcm entropy blue mean green ratio green glcm asm green glcm contrast green mean red ratio red stddev red mean nir ratio nir glcm contrast nir ratio green-blue ratio red-blue brightness |
| full hierarchic strategy | ||
|---|---|---|
| DT | MLP | |
| vegetation | mean blue mean red ratio red ratio nir stddev nir ratio red-green | stddev red glcm contrast red ratio nir glcm entropy nir ratio red-blue ratio red-green |
| water+shade <> bare+grey | stddev blue mean green ratio green stddev red mean nir ratio green-blue ratio red-green | mean green ratio green mean red stddev red contrast nir |
| water<>shade | glcm asm green glcm entropy red glcm asm nir ratio green-blue brightness | mean blue ratio blue ratio green-blue |
| bare<>grey | ratio blue stddev blue glcm contrast blue ratio green stddev green ratio red-blue | mean blue mean red stddev red glcm contrast nir glcm entropy nir |
| nearest neighbour | two-steps | hierarchic | ||||
|---|---|---|---|---|---|---|
| DT | MLP | DT | MLP | |||
| user's accuracy | red surfaces | 0.79 | 0.89 | 0.76 | 0.89 | 0.76 |
| vegetation | 0.95 | 0.93 | 0.93 | 0.94 | 0.93 | |
| water | 0.97 | 0.99 | 0.97 | 0.99 | 0.98 | |
| bare soil | 0.46 | 0.60 | 0.65 | 0.70 | 0.83 | |
| grey surfaces | 0.82 | 0.86 | 0.86 | 0.84 | 0.88 | |
| shadow | 0.19 | 0.27 | 0.25 | 0.26 | 0.30 | |
| PCC | 76.2% | 80.4% | 78.2% | 79.3% | 82.5% | |
| kappa | 0.69 | 0.74 | 0.71 | 0.73 | 0.77 | |
| exhaustive validation | sum | user's | |||||||
|---|---|---|---|---|---|---|---|---|---|
| red | veg | water | bare | grey | shadow | accuracy | |||
| classification | red | 64763 | 221 | 464 | 25 | 17985 | 1892 | 85350 | 0.76 |
| veg | 282 | 362442 | 5458 | 2167 | 11834 | 5951 | 388134 | 0.93 | |
| water | 0 | 2539 | 177895 | 0 | 323 | 615 | 181372 | 0.98 | |
| bare | 1375 | 2305 | 757 | 43838 | 4482 | 209 | 52966 | 0.83 | |
| grey | 4386 | 31051 | 1672 | 736 | 343980 | 10114 | 391939 | 0.88 | |
| shadow | 4062 | 38414 | 9244 | 1076 | 61578 | 49655 | 164029 | 0.30 | |
| sum | 74868 | 436972 | 195490 | 47842 | 440182 | 68436 | 1263790 | ||
| producer's accuracy | 0.87 | 0.83 | 0.91 | 0.92 | 0.78 | 0.73 | PCC: 82.5% kappa: 0.77 | ||
| exhaustive validation | sum | user's accuracy | ||||||
|---|---|---|---|---|---|---|---|---|
| red | veg | water | bare | grey | ||||
| classification | red | 64048 | 228 | 482 | 26 | 20343 | 85127 | 0.75 |
| veg | 1520 | 392315 | 7198 | 9655 | 23470 | 434158 | 0.9 | |
| water | 2 | 4388 | 184960 | 1018 | 1287 | 191655 | 0.97 | |
| bare | 1412 | 7597 | 1009 | 51436 | 11826 | 73280 | 0.7 | |
| grey | 7886 | 36571 | 1841 | 7748 | 425524 | 479570 | 0.89 | |
| sum | 74868 | 441099 | 195490 | 69883 | 482450 | 1263790 | ||
| producer's accuracy | 0.86 | 0.89 | 0.95 | 0.74 | 0.88 | PCC: 88.5% kappa: 0.84 | ||
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Roeck, T.; Van de Voorde, T.; Canters, F. Full Hierarchic Versus Non-Hierarchic Classification Approaches for Mapping Sealed Surfaces at the Rural-Urban Fringe Using High-Resolution Satellite Data. Sensors 2009, 9, 22-45. https://doi.org/10.3390/s90100022
De Roeck T, Van de Voorde T, Canters F. Full Hierarchic Versus Non-Hierarchic Classification Approaches for Mapping Sealed Surfaces at the Rural-Urban Fringe Using High-Resolution Satellite Data. Sensors. 2009; 9(1):22-45. https://doi.org/10.3390/s90100022
Chicago/Turabian StyleDe Roeck, Tim, Tim Van de Voorde, and Frank Canters. 2009. "Full Hierarchic Versus Non-Hierarchic Classification Approaches for Mapping Sealed Surfaces at the Rural-Urban Fringe Using High-Resolution Satellite Data" Sensors 9, no. 1: 22-45. https://doi.org/10.3390/s90100022
APA StyleDe Roeck, T., Van de Voorde, T., & Canters, F. (2009). Full Hierarchic Versus Non-Hierarchic Classification Approaches for Mapping Sealed Surfaces at the Rural-Urban Fringe Using High-Resolution Satellite Data. Sensors, 9(1), 22-45. https://doi.org/10.3390/s90100022




