1. Introduction
The urban heat island effect is the temperature increase according to urbanization and has been studied for about four decades. The urban heat island phenomenon occurs as a mixed result of anthropogenic heat discharge, decreased vegetation cover, and increased use of artificial impervious surface materials. These factors modify the heat balance at the land surface and eventually raise the atmospheric temperature. To clarify the contribution of each factor to the urban heat island, it is necessary to evaluate the surface heat balance. Kato and Yamaguchi [
1] estimated surface heat fluxes in an urban area of Nagoya, Japan, by using visible to thermal infrared data observed by Terra ASTER and Landsat ETM+. Modifying the proposed method, The same authors [
2] introduced storage heat flux,
ΔG, in order to evaluate the heat storage and discharge of urban surfaces. Their results of estimated heat fluxes are reasonable compared with previous ground measurement data in other cities [
3-
8]. However, because the highest spatial resolution of ASTER sensors is 15 m for visible and near-infrared radiometer (VNIR), there is a limitation in detecting small objects in urban areas. The limitation of the spatial resolution is one of the major error sources of heat flux estimation because Kato and Yamaguchi [
1,
2] assigned some important parameters according to surface types classified from satellite images. In order to reduce such error induced by mislabeled surface types, the authors used Formosat-2 data in combination with ASTER data in this study. Because of the 8m spatial resolution of Formosat-2 multispectral data, we can identify surface types with a pixel area of 3.5 times higher resolution than that of ASTER VNIR data. Moreover, spectral coverage of the blue band of Formosat-2 data is another advantage in classifying the land surface. These advantages could eliminate misclassifications caused by mixed pixels and similarities of spectral patterns. Since surface heat fluxes are estimated in the 90m spatial resolution of ASTER thermal-infrared radiometer (TIR), we can evaluate intra-pixel heterogeneity of surface coverage more clearly by Formosat-2 than ASTER data. This paper presents a case study of surface heat balance that was estimated based on surface classification maps from ASTER and Formosat-2 data in Tainan City, Taiwan on March 6, 2001. Then, the heat fluxes are compared to evaluate the sensitivity of spatial resolution and accuracy of surface classification maps against our procedure of heat balance estimation. Moreover, we interpret the characteristics of surface heat balance in Tainan City based on heat fluxes estimated from ASTER with Formosat-2 data.
2. Theory and Estimation Methods of Surface Heat Balance in Urban Areas
In this study, based on the same assumption used by Kato and Yamaguchi [
2], who estimated the surface heat balance in an urban area by using ASTER and Formosat-2 data. For an urban surface, the absorbed net radiation and the anthropogenic heat discharge should balance the outgoing fluxes of sensible heat, latent heat and ground heat when advection is negligible,
where
Rn is the net radiation,
A is the anthropogenic heat discharge,
H is the sensible heat flux,
LE is the latent heat flux, and
G is the ground heat flux. The net radiation is the sum of the absorbed shortwave and longwave radiation. The absorbed shortwave radiation is the difference between incident shortwave radiation from the sun and reflected shortwave radiation. The net absorbed longwave radiation is determined from atmospheric emissions absorbed by the surface and emitted longwave radiation. The sensible heat and latent heat fluxes are the energy transported into the atmosphere by turbulent flow. Sensible heat increases the atmospheric temperature, while latent heat is produced by transpiration of vegetation and evaporation of land surface water, contributing to limiting surface and atmospheric temperature increases under a given net radiation. During the day, ground heat is conducted into the ground, because the surface temperature is generally higher than the underground temperature. Heat stored in the ground during the daytime is conducted to the atmosphere at night. The anthropogenic heat discharge increases the heat budget as well as the net radiation. Energy consumption due to human activities generates anthropogenic heat discharge in the form of sensible heat, latent heat, and ground heat. There is no anthropogenic heat discharge from natural land surfaces.
Because
G and
A depend on surface and subsurface materials and human activities, it is difficult to calculate
G and
A separately from satellite data. Therefore, Kato and Yamaguchi [
2] applied
ΔG estimated by merging
G and
A based on the heat balance equation (
Equation (1)), which is often used in tower measurements in urban areas [
3,
8], as follows:
For the case in which the storage heat flux exceeds 0 W m-2, i.e., when a downward heat flux exists, it can be interpreted as net heat storage in the urban canopy. In contrast, when the storage heat flux is negative, there is a net loss of heat from storage and/or anthropogenic heat discharge from urban canopy.
Theories for calculating the net radiation, sensible heat and latent heat fluxes have already been established. These three heat fluxes can be estimated by combining remote sensing and ground meteorological data, because these are the heat exchange between land surface and atmosphere. In the present study, general procedures for the calculation of these heat budgets are applied. Because estimation methods of these heat fluxes are described in Kato and Yamaguchi [
2], the authors have omitted the explanation other than
H and
LE that are critical to the present study.
Sensible heat flux is given by
where
ρ is the air density in kg m
-3,
Cp is the specific heat of air at constant pressure in J kg
-1 K
-1,
T0 is the surface aerodynamic temperature in K,
Ta is the atmospheric temperature in K, and
ra is the aerodynamic resistance in s m
-1. Because
T0 is difficult to obtain by thermal infrared remote sensing, we used surface temperature
Ts instead of
T0. The sensible heat flux might be overestimated when the surface temperature is high. Here,
ra is calculated using the following expression [
9]:
where
zu and
zt are the respective heights at which the wind speed
u (in m s
-1) and atmospheric temperature are measured,
d0 is the displacement height, and
z0M and
z0H are the roughness lengths for momentum and heat transport, respectively. All heights and roughness lengths are in meters.
ΨM and
ΨH are stability correction functions for momentum and heat, which depend on the Monin-Obukhov length [
9], and
k is von Karman's constant (= 0.4).
zu,
zt and
d0 are obtained by the methods described in Kato and Yamaguchi [
1]. Roughness lengths show the height at which the neutral wind profile is extrapolated to a zero wind speed [
10] and depend on obstacle heights and spacing on land surface. Some methods have been offered to estimate surface roughness from obstacle height, area and arrangement [
11-
13]. However, it is quite difficult to obtain requisite parameters to estimate roughness length through a wide area. Although we used ASTER DEM data, about 15 m of vertical accuracy and 15m of spatial resolution are not enough to evaluate obstacle height and arrangement. In this study, typical values of roughness lengths,
z0M and
z0H, are alternatively used for the selected surface types [
9,
14 -
21], as shown in
Table 1. The surface types were obtained from a land cover map, as described in Section 4. We applied a logarithmic averaging procedure [
22] in order to set the roughness length in each resultant pixel, which is 90m resolution according to ASTER TIR data in this particular case. Although spatial resolution of ASTER TIR data is 90m, the roughness length varies with location in this study.
Latent heat flux for evapotranspiration is expressed as
where
es* is the saturation water vapor pressure in hPa at the surface temperature,
ea is the atmospheric water vapor pressure in hPa,
γis the psychrometric constant in hPa K
-1, and
rs is the stomatal resistance in s m
-1. Stomatal resistance is calculated based on the Jarvis-type scheme [
23] simplified by Nishida et al. [
24]:
where
PAR is the photosynthetic active radiation in W m
-2,
rsMIN is the minimum stomatal resistance in s m
-1, and
rcuticle is the canopy resistance related to the diffusion through the cuticle layer of leaves in s m
-1.
f1 and
f2 are estimated by the equations proposed by Jarvis [
23] and Nishida
et al. [
24]. As well as roughness lengths,
rsMIN was alternatively determined for each vegetation type that was decided upon and interpolated via surface classification based on the reference of Kelliher
et al. [
25] and Noilhan and Lacarrère [
22]. The values of
rsMIN used in this particular case are listed in
Table 1. Latent heat flux is calculated in proportion to the fraction of water, vegetation type, and pervious surfaces with each
rsMIN in one pixel.
3. Study Area and Data Used
We selected an area of approximately 280 km
2 covering Tainan City, Taiwan, for our study area, as Lin
et al. [
26] reported 3.4°C of heat island intensity at midnight in this area (
Figure 1). Tainan currently has a population of about 750, 000 and is the fourth largest city of Taiwan. The present study area covers five of six districts in Tainan. The remaining northernmost district, An Nan, was excluded in this study because most of the area is used for agriculture. A large portion of the urban areas are located on the plain at the left side of the study area. The other areas are occupied by agricultural use. In the upper left of the study area, there are maintained fish farms which are widely distributed on the northwestern coast of Tainan City.
3.1. Satellite Data
The Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) is an instrument onboard the Terra satellite. The spatial resolutions of the sensor are 15 m for the VNIR, 30 m for the shortwave infrared radiometer (SWIR), and 90 m for the TIR, respectively. Band numbers of each radiometer are 3 for VNIR, 6 for SWIR and 5 for TIR. The following ASTER data products were used: surface kinetic temperature, surface spectral emissivity, VNIR surface spectral reflectance, SWIR surface spectral reflectance, and the relative digital elevation model (DEM).
Formosat-2 is the Taiwanese satellite launched by the National Space Organization (NSPO), Taiwan, in 2004. Spatial resolution of Formosat-2 data is 8 m for the 4-band multispectral mode and 2 m for the panchromatic mode, respectively. Formosat-2 can revisit the same areas in one-day intervals. The authors used only multispectral data at the 8 m spatial resolution for the purpose of classifying the surface cover types.
We used ASTER data acquired in the daytime of March 6, 2001 and Formosat-2 data acquired on July 12, 2004, respectively, to estimate the heat balance in Tainan City.
3.2. Meteorological Data
The authors used the ground meteorological data acquired at the meteorological station in Tainan City, managed by the Southern Region Weather Center, Central Weather Bureau of Taiwan. The weather station is located in the center of the city, as shown in
Figure 1. Meteorological observations come from a standard site but which is surrounded by dense urbanized surfaces and thus it is expected that the observations are representative of canopy layer conditions in the urban area. In the present study, the data used were solar radiation, wind speed, relative humidity, air-pressure and atmospheric temperature acquired at 1100 TST on March 6, 2001, according to the acquisition date of the ASTER data.
The meteorological data are summarized in
Table 2. The interpolation method is basically the same as that of Kato and Yamaguchi [
2]. Because there is only one meteorological observation site and the study area is relatively small, we assumed that atmospheric temperature and air-pressure, at 0m ASL, are the same throughout the study area. Extrapolations of these parameters for each pixel including altitudinal corrections were applied based on the environmental lapse rate with ASTER DEM data. Solar radiation, wind speed and relative humidity were assumed to be constant throughout the study area.
4. Surface Classification
In order to estimate surface heat fluxes, the authors needed to interpolate the roughness length for sensible and latent heat fluxes, and the minimum stomatal resistance for latent heat flux, respectively, based on surface types as mentioned in Section 2. Because of that, we wanted to classify the surfaces according to vegetation types, and density and height of buildings. In the present study, the authors classified surface types from satellite data by the combined methods of the maximum likelihood, decision tree and manual classification in order to separate surface coverage having similar spectral patterns. First, we classify the surface types in more than 30 categories by the maximum likelihood method. The categories are too numerous for the following analysis because they are based on not only surface coverage but also their spectral pattern. Therefore, they are combined into 8 categories: buildings, roads, water, bare soil, short grass (e.g., lawn), tall grass (e.g., paddy field), bushes, and forests. However, in the case of ASTER, bush could not be distinguished from the other vegetation types because of the limitations of band numbers and spatial resolution. In the case of Formosat-2, misclassification often occurred between water, sparse vegetation, dark soil and shadow because of the similarity of their spectral patterns. We extracted areas selected as water, and then classified them by the decision tree method. The decision tree was constructed by the following steps: 1) separate sparse vegetation by NDVI; 2) separate dark soil by NIR spectral pattern (band 4 of Formosat-2); and, 3) separate pavement and water by the sum of the DN values of band 1, 2, 3 and 4 of Formosat-2. We manually determined the thresholds for each step. Step 2 is based on the spectral characteristic of water that is low in the NIR region. Step 3 is based on the fact that reflectance of water is low for all spectral bands. After the decision tree procedure, there were still small areas suffering misclassifications. It is difficult to distinguish between water surfaces and shaded areas from their spectral patterns because the ranges of DN values of each band are extremely small. However, the areas of shadows are usually much smaller than those of water bodies, therefore we could manually distinguish them by comparison with the other maps.
We applied the above mentioned procedures to Formosat-2 multispectral data. On the other hand, for comparison purposes, we used the Maximum Likelihood method for ASTER VNIR data. Since the data acquisition dates of Formosat-2 and ASTER data are different, surface coverage is different in some agricultural areas. In the present study, our primary purpose of surface classification is to obtain a detailed surface coverage to estimate the heat fluxes on March 6, 2001. In order to modify the changed surface coverage between the two dates, we replaced the classification results by Formosat-2 data in some agricultural areas where surface types were different from those on the classification map produced from ASTER data.
5. Comparison of Surface Classification Maps
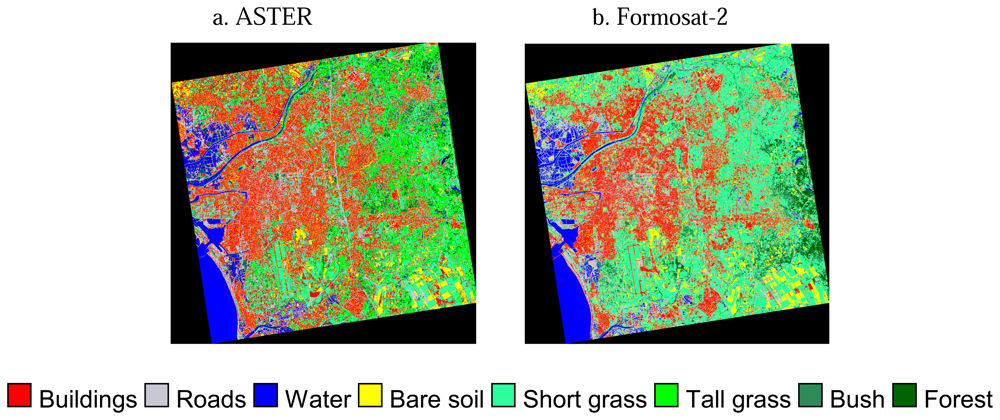
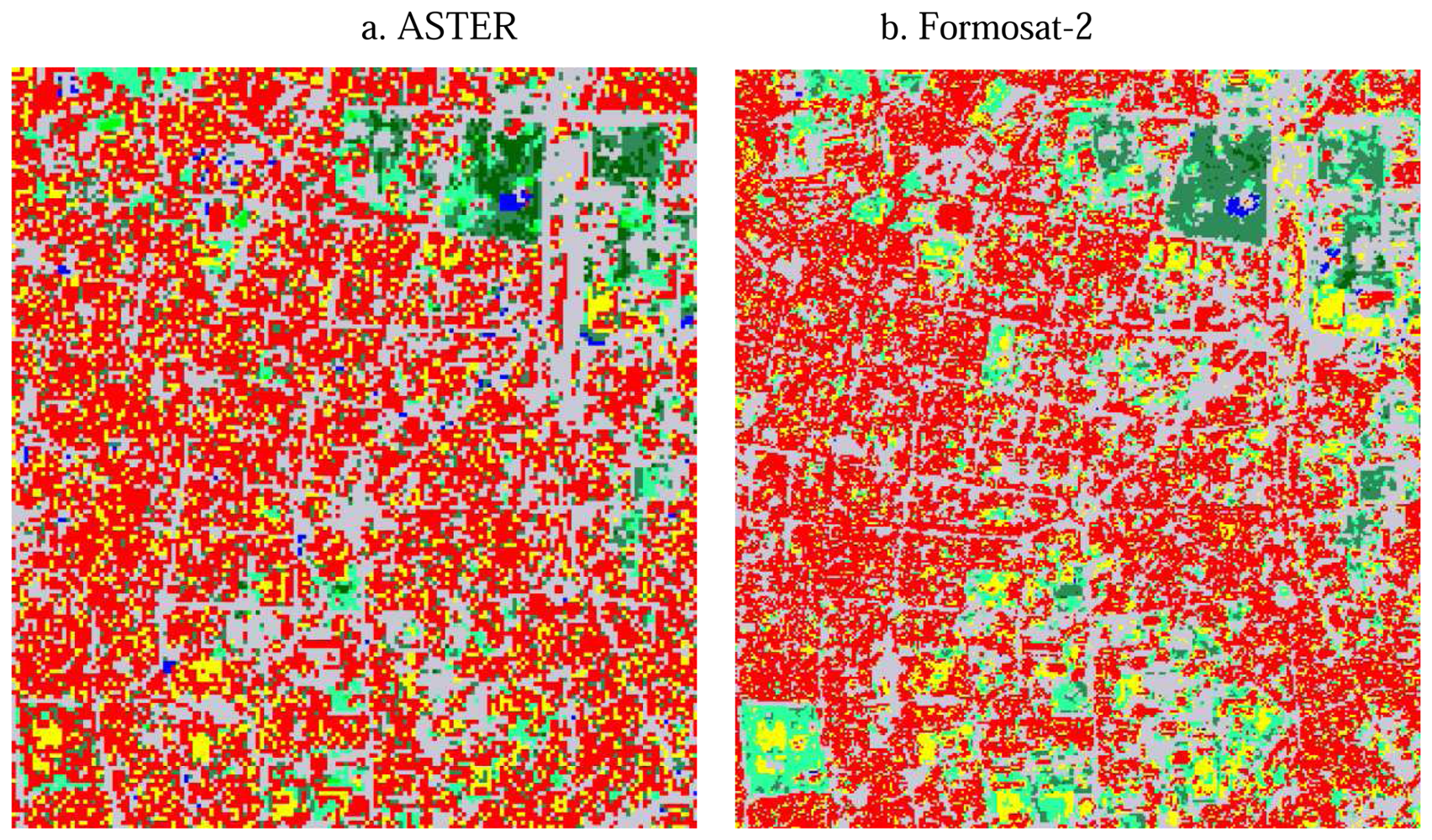
Surface classification maps derived from ASTER and Formosat-2 data are shown in
Figure 2, while the pixel numbers of each surface type are compared in
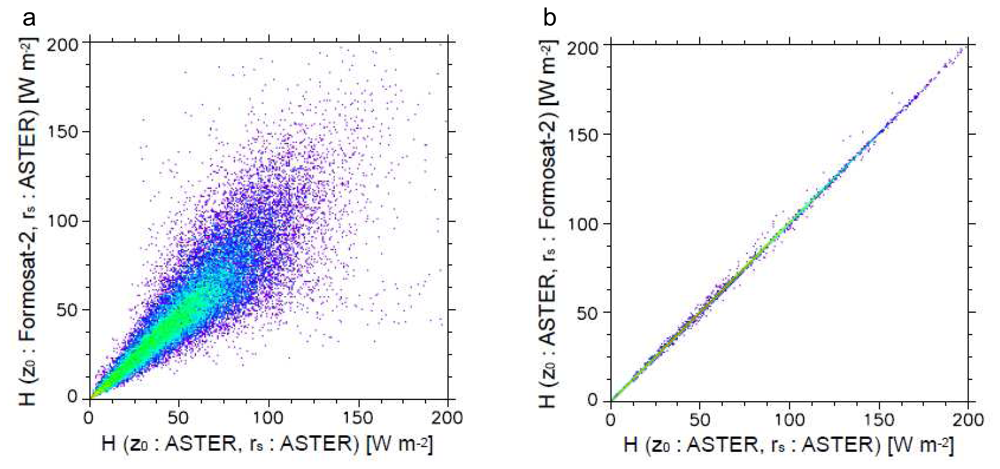
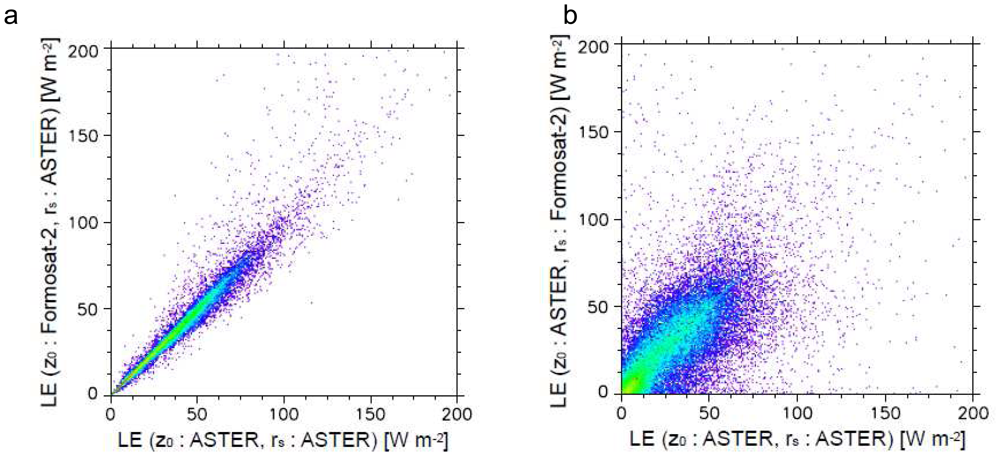
Table 3. In the case of the classified results by ASTER, the buildings category shows the largest area. However, more areas were classified as short grass than urban areas on the Formosat-2 image. The areas classified as tall grass by ASTER changes to short grass in the case of Formosat-2 because of the similar spectral patterns of these two types. Because of the higher spatial resolution and additional blue band of Formosat-2, short grass in the parks in urban areas could be distinguished from building roofs. In fact, when surface types are classified without band 1 of Formosat-2, the areas of short grass were partly classified as buildings. The areas classified as road increased about 39% because of the higher spatial resolution of Formosat-2. Because usually a two-track road is wider than 8m and because of the spatial resolution of Formosat-2, narrow roads are detected relatively well. 49% and 20% of the areas of road were originally classified as road and buildings by ASTER, respectively. These results imply that the surface classification map by Formosat-2 distinguishes roads between buildings more clearly. In the case of ASTER, only some major roads are separated from buildings, but the areas of roads are overestimated because pixels are classified as road even if they contain roads with a width of less than 15m.
Both results show different spatial distributions of vegetation because it is difficult to distinguish vegetation types between grasses, while seasonal differences change the colors of vegetation. Similarly, because the spectral patterns of bare soil and building roofs are similar in this area, considerable areas of bare soil are misclassified as buildings and vice versa in both ASTER and Formosat-2 data.
In addition to misclassification between buildings and bare soil, there are some paved areas misclassified as buildings in both classification maps from ASTER and Formosat-2 because of their similar spectral patterns. For example, the considerable areas of the runways of Tainan airport, which is located in the lower left of the study area, are classified as bare soil and buildings rather than as roads by ASTER and Formosat-2, respectively. Since it is difficult to distinguish these surface types with similar spectral patterns by the supervised classification methods and to correct them manually through the whole area, the authors used these classification results as input data to the heat balance analysis without further correction.
7. Conclusions
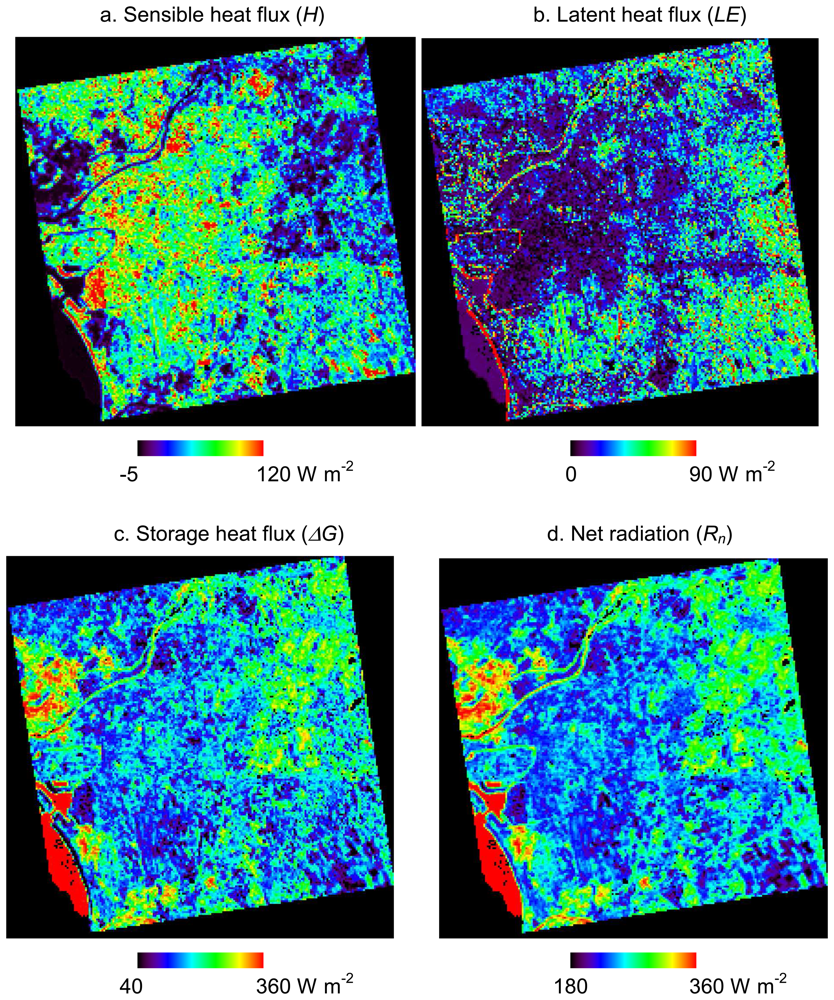
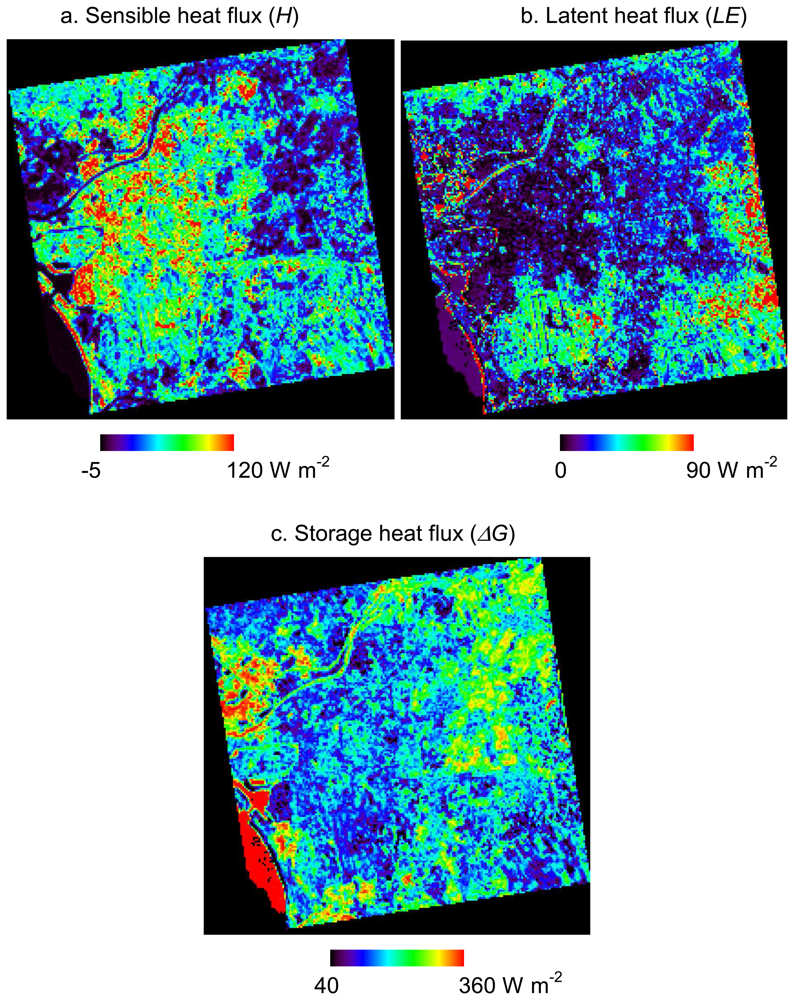
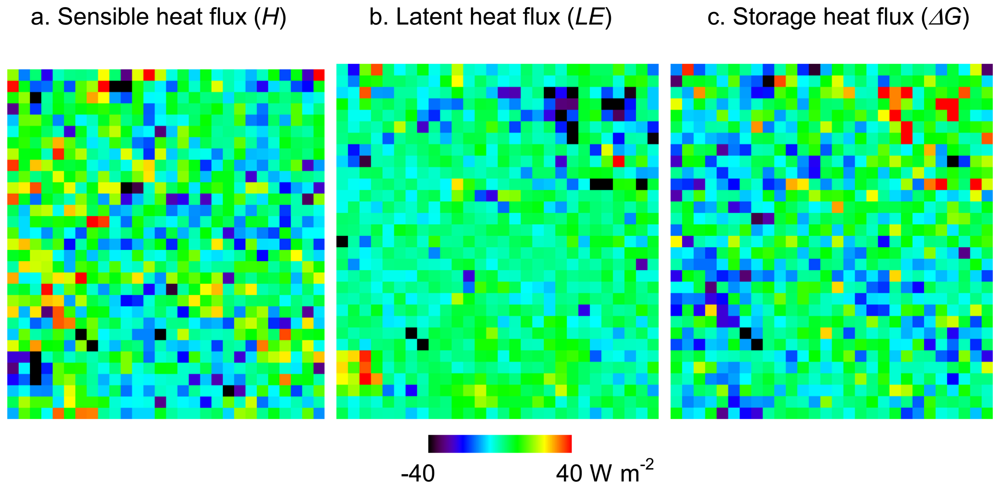
Surface heat balance in Tainan City, Taiwan, on March 6, 2001 was estimated by ASTER and Formosat-2 data. Formosat-2 data were used to overcome the limitation of low spatial resolution of ASTER VNIR data. By using Formosat-2 data, we could reduce misclassifications attributed to mixed pixels and less spectral range. In particular, roads and small vegetation areas are easily distinguished from buildings, so that heat fluxes in urban areas could be estimated more accurately.
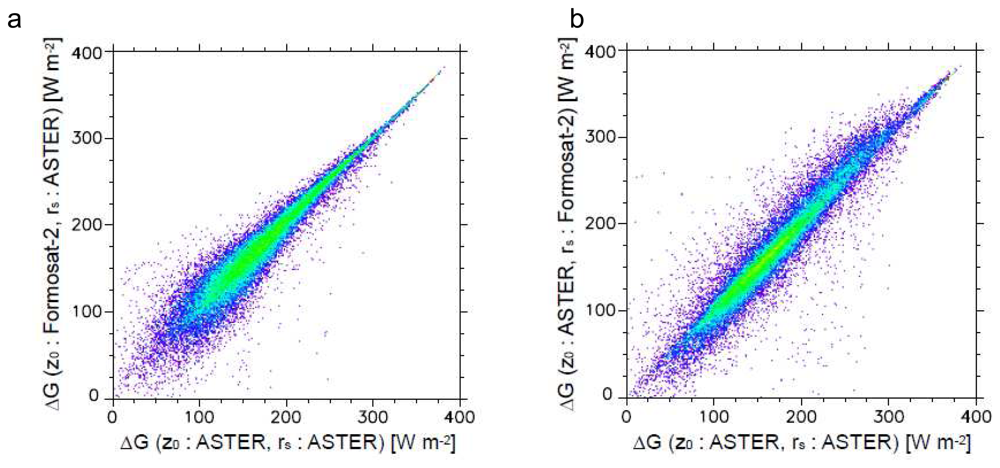
There are small differences between the heat fluxes estimated from the surface classification maps by ASTER and Formosat-2. However, Formosat-2's higher spatial resolution of surface types improves the heat flux estimation in certain areas. Most of the improved results are due to decreases in H and LE and increases in ΔG caused by decreased overestimation of roughness lengths and vegetation areas. There are also increases and decreases of heat fluxes raised from misclassifications by Formosat-2. Such misclassifications were caused by land use changes which occurred in an interval of about three years between the acquisition dates of ASTER and Formosat-2 data. In order to mitigate misclassification, it is desirable to use satellite data taken on the same or closer dates or, at least, in the same season. In addition, the authors concluded that surface classification maps are appropriate qualitatively by the visual comparison and the tendency of results of heat flux analysis. However, it is necessary to verify the accuracy of surface classification with independent data and testing in order to estimate quantitative accuracy.
Heat fluxes estimated in this study are comparable with previous in situ measurement data in other cities. However, ΔG in urban areas has no contrast with ΔG in surrounding residential areas. This result disagrees with the general trend in urban areas with a high heat capacity. We assume this is because of the homogeneity of building materials in both business and residential areas, and the many roofs that are made of steel with zinc plating, which has a small heat capacity in Tainan. It would be interesting to compare heat balances in other cities belonging to different climates and to consider the influence of construction materials.
The present study showed that the 8m spatial resolution and 4 spectral bands of Formosat-2 can improve the classification of surface types for input data to estimate the heat balance in urban areas as compared with the 15m spatial resolution and 3 spectral bands of ASTER VNIR data. As a result of the level of sensitivity in this study, the vegetation types classified in higher spatial resolution and accuracy by Formosat-2 increased the accuracy of latent heat flux estimation. This is one of the future issues to examine -which spatial resolution is the most suitable to, or high enough, for identifying vegetation areas and types for heat balance analysis. Interestingly, there are still higher spatial resolution data from satellite remote sensing; for example, even Formosat-2 has a 2m panchromatic band. On the other hand, all of the sensible, latent and storage heat fluxes are slightly improved by the roughness length in higher spatial resolution. Interpolating the roughness lengths from surface types has a limitation in obtaining accurate values because roughness length is the index of obstacle height and spacing, not land coverage. If the surface elevation can be directly measured via satellite in high resolution, it will be possible to estimate much more accurate roughness lengths and, consequently, heat fluxes.