Structural Simulation of a Bone-Prosthesis System of the Knee Joint
Abstract
:1. Introduction and Motivation
- The final model is represented as a triangle mesh, but the interior density of the bone must be known for stress estimation
- The algorithm to extract and classify bone structures from medical data works on a slice-by-slice basis, rather than using the dataset as a whole; this reduces the chance of detecting long structures spanning over different slices; moreover, it can detect only cortical structures
- The segmentation requires too much human intervention, since the user must set a number of seed points to initialise the algorithm and clean the resulting images from incorrectly assigned pixels
- No error control/estimation is provided by the various sub-units of the tool
2. System Overview
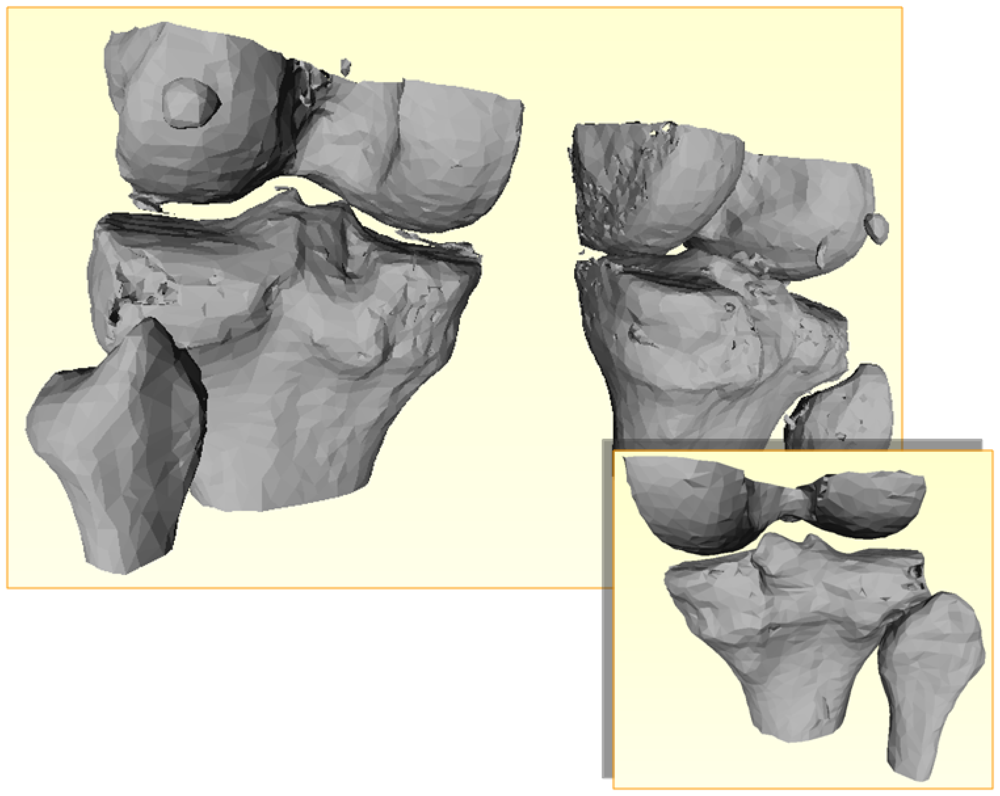
3. Bone Modelling
3.1. CT Data
3.2. Classification and Volume Segmentation
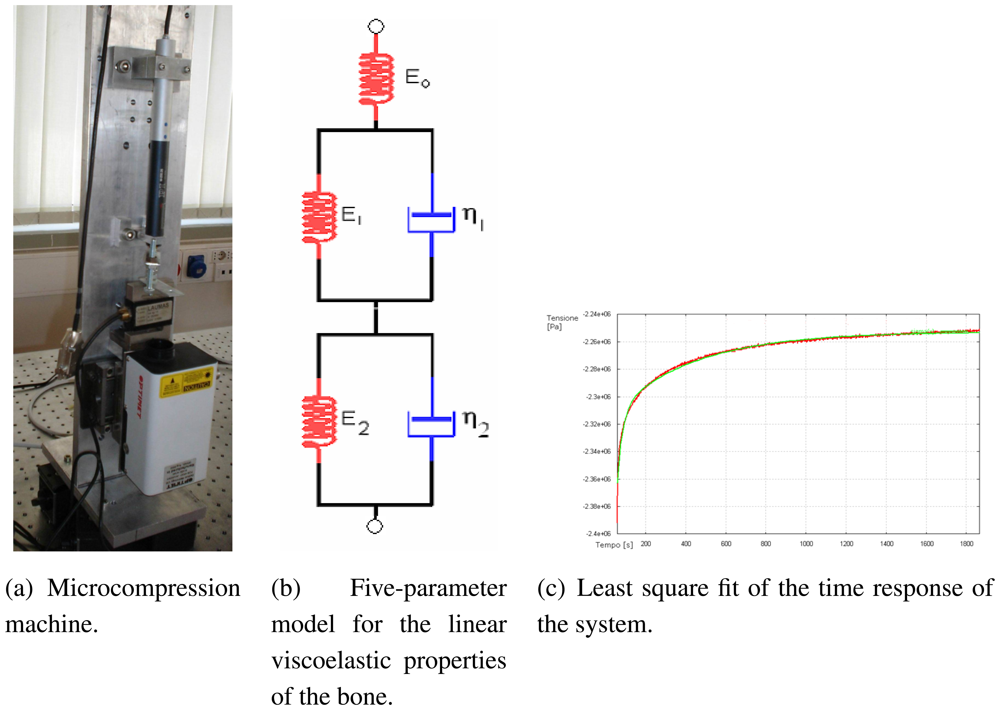
3.3. Bone Mechanical Parameters
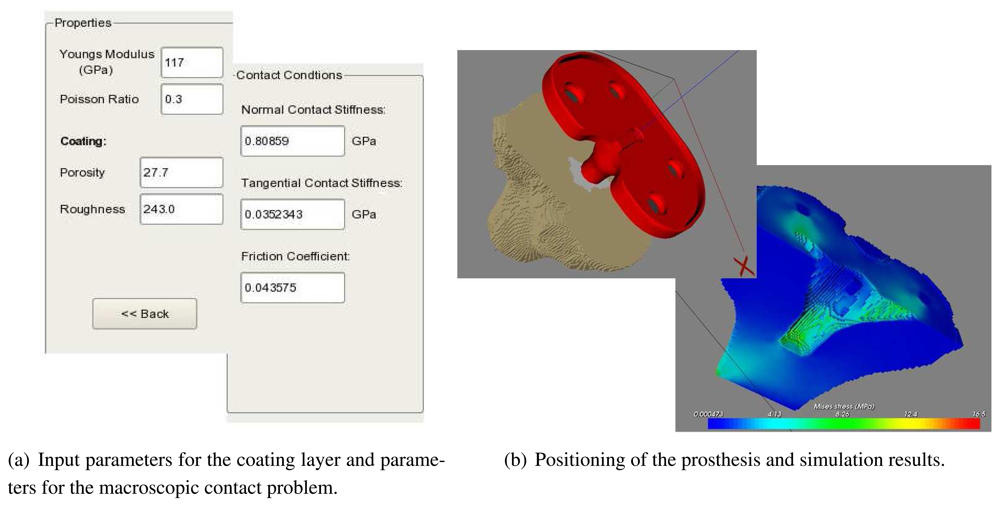
4. Prosthesis Modelling
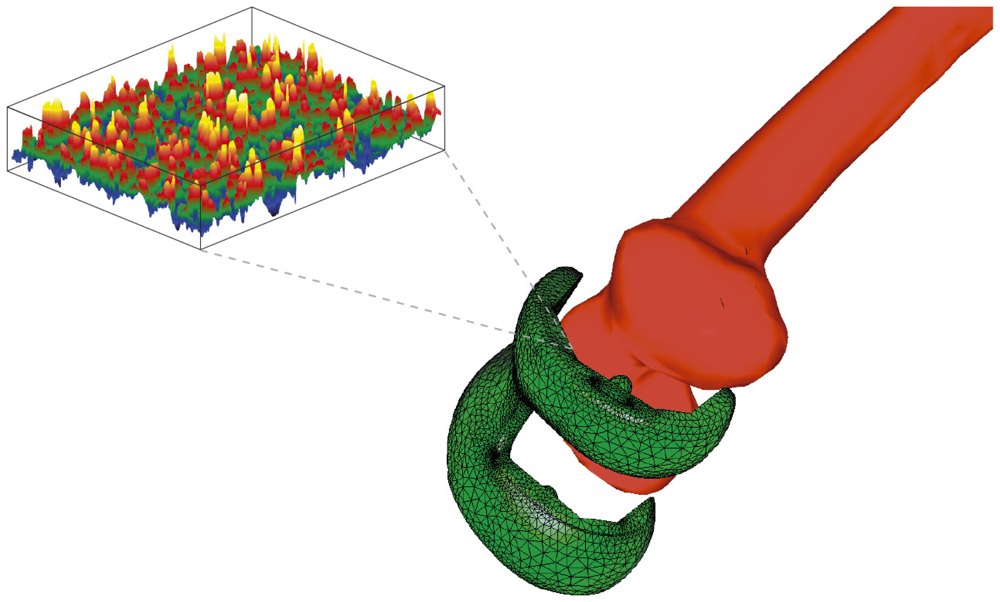
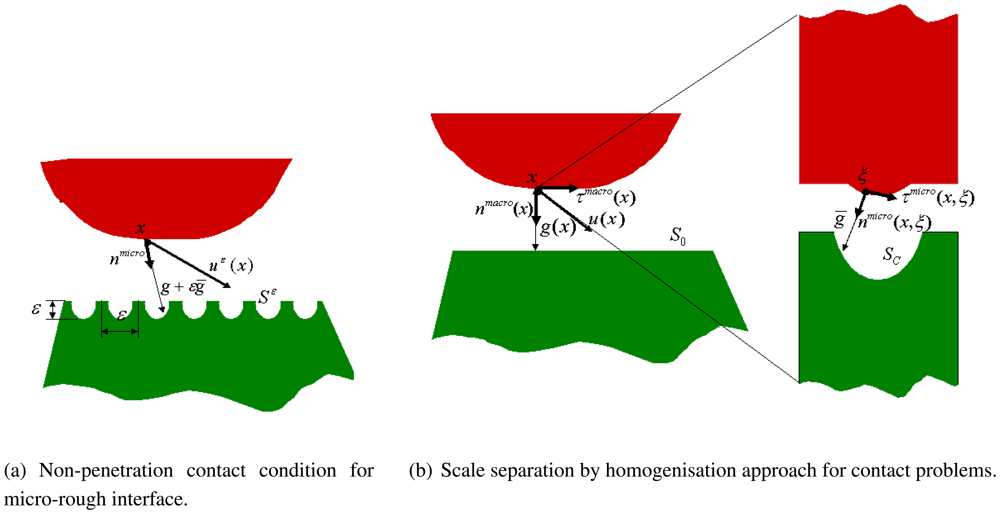
5. Mathematical Description and Multi-Scale Modelling of the Bone-Prosthesis Contact
6. Simulation
6.1. Finite Element Discretisation
 = { υi ∈ H1 (Ω), i = 1,…, N | υi(x) = g0i(x), x ∈ Γu}. The elasticity problem without contact can be rewritten in a weak formulation as follows: find ui ∈
= { υi ∈ H1 (Ω), i = 1,…, N | υi(x) = g0i(x), x ∈ Γu}. The elasticity problem without contact can be rewritten in a weak formulation as follows: find ui ∈
 such that for all υi ∈
such that for all υi ∈

 .
. h, i = 1, ..,N which minimises the functional
h, i = 1, ..,N which minimises the functional
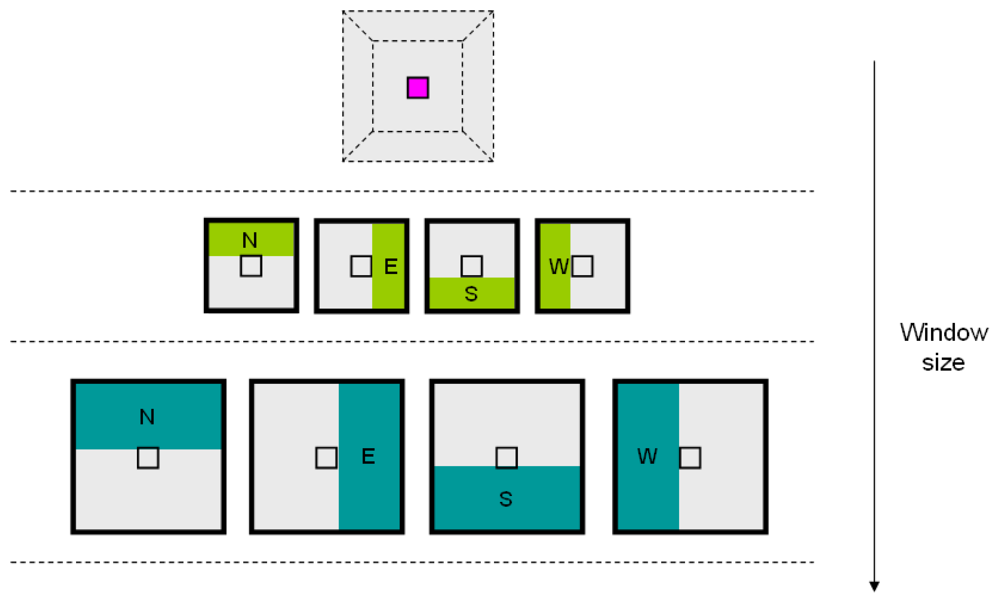
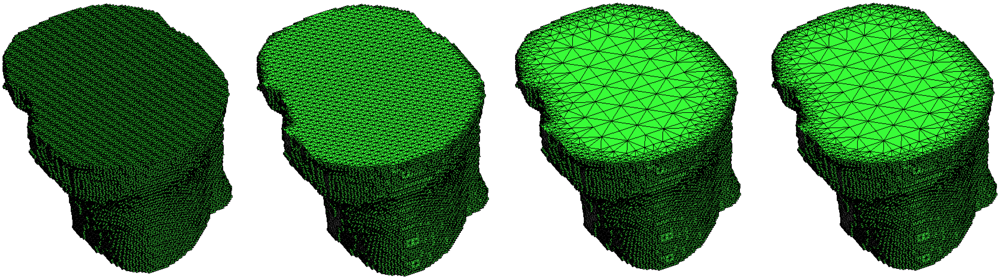
6.2. Hierarchical mesh coarsening
6.3. Dealing with Uncertainties
7. Discussion
Acknowledgments
- ∗Data is usually acquired using spiral scanning. Pixel values are interpolated from spiral data
- †For this reason, hereafter we will use the terms pixel and voxel interchangeably.
References
- Ollé, K.; Erdőhelyi, B.; Halmai, C.; Kuba, A. MedEdit: A computer assisted planning and simulation system for orthopedic-trauma surgery. 8th Central European Seminar on Computer Graphics Conference Proceedings, (19-21 April 2004).
- LIMA spa. http://www.lima.it/.
- Bishop, C. M. Pattern Recognition Machine Learning.; Springer, August 2006. [Google Scholar]
- Rubin, P. J.; Leyvraz, P. F.; Aubaniac, J. M.; Argenson, J. N.; Esteve, P.; de Roguin, B. The morphology of the proximal femur. a three-dimensional radiographic analysi. Journal of Bone and Joint Surgery 1992, 74-B(1), 28–32. [Google Scholar]
- Battiato, S.; Bosco, C.; Farinella, G. M.; Impoco, G. 3D CT segmentation for clinical evaluation of knee prosthesis operations. Proceedings of 4th Eurographics Conference - Italian Chapter, (22–24, Feb. 2006).
- Battiato, S.; Di Blasi, G.; Farinella, G. M.; Gallo, G.; Guarnera, G. C. Adaptive techniques for microarray image analysis with related quality assessment. SPIE Journal of Electronic Imaging 2007, 16(4). [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. International Journal of Computer Vision 1988, 1(4), 321–331. [Google Scholar]
- Osher, S.; Fedkiw, R. P. Level Set Methods and Dynamic Implicit Surfaces.; Springer, October 2002. [Google Scholar]
- Lu, H.; Liang, Z.; Li, B.; Li, X.; Meng, J.; Liu, X. Mixture-based bone segmentation and its application in computer aided diagnosis and treatment planning. Proceedings of the Third International Conference on Image and Graphics (ICIG'04), Washington, DC, USA; 2004; pp. 507–510. [Google Scholar]
- Battiato, S.; Farinella, G. M.; Impoco, G.; Garretto, O.; Privitera, C. Cortical bone classification by local context analysis. Lecture Notes in Computer Science 2007, 4418/2007. [Google Scholar]
- Clienti, C.; Indelicato, C.; Marino, A. Modelli viscoelastici del tessuto osseo mediante prove di rilassamento. Convegno Nazionale AIAS 2007. [Google Scholar]
- Clienti, C.; Corallo, D.; Indelicato, C.; Risitano, A. Caratterizzazione statica e dinamica di ma-teriali e componenti per applicazioni protesiche di ginocchio. Convegno Nazionale AIAS 2007. [Google Scholar]
- Buüchler, P.; Pioletti, D. P.; Rakotomanana, L. R. Biphasic constitutive laws for biological interface evolution. Biomechanical Model Mechanobiology 2003, 1(4), 239–249. [Google Scholar]
- Faust, G. Bone remodelling: An approach of fase transition in saturated porus solids. Proceedings of ECCM'99 1999. [Google Scholar]
- Kuhl, E.; Menzel, A.; Steinmann, P. Computational modeling of growth: A critical review, a classification of concepts and two new consistent approaches. Computational Mechanics 2003, 32, 71–88. [Google Scholar]
- Orlik, J. Homogenization for contact problems with periodically rough surfaces. Berichte des Fraunhofer ITWM 2004, 59. [Google Scholar]
- T., O. J.; Martins, J. A. C. Models and computational methods for dynamic friction phenomena. Computer methods in applied mechanic and engineering 1985, 52, 527–634. [Google Scholar]
- Goryacheva, I. G.; Dobychin, M. N. Contact Problems in Tribology (in Russian).; Mashinostroenie: Moscow, 1988. [Google Scholar]
- Christensen, R. M. Mechanics of Composite Materials.; Wiley-Interscience Publication. John Wiley & Sons: New York, Chichester, Brisbane, Toronto, 1979. [Google Scholar]
- ITWM-Bericht. Kneemech. 2008. http://www.itwm.fhg.de/en/sks__projects__sks_biomech/biomech/.
- Brenner, S.; Scott, L. R. The Mathematical Theory of Finite Element Methods.; Springer: New York, 1994. [Google Scholar]
- Ciarlet, P. The Finite Element Method for Elliptic Problems.; North-Holland Publishing Company: Amsterdam, New York, Oxford, 1978. [Google Scholar]
- Zienkiewicz, O. C.; Taylor, R. The Finite Element Method.; McGraw-Hill, 1991. [Google Scholar]
- Kikuchi, N.; Oden, J. Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods.; SIAM: Philadelphia, 1988. [Google Scholar]
- Alberty, J.; Carstensen, C.; Funken, S. A.; Klose, R. MatLab implementation of the finite element method in elasticity. Computing 2002, 69(3), 239–263. [Google Scholar]
- Golub, G. H.; van Loan, C. F. Matrix Computations.Johns Hopkins University Press, 3rd edition; 1996. [Google Scholar]
- Shirley, P.; Tuchman, A. A polygonal approximation to direct scalar volume rendering. SIGGRAPH Comput. Graph. 1990, 24(5), 63–70. [Google Scholar]
- Schroeder, W. J.; Geveci, B.; Malaterre, M. Compatible triangulations of spatial decompositions. Proceedings of the conference on Visualization; 2004. [Google Scholar]
- Moore, R. E. Interval Analysis.; Automatic Computation. Prentice Hall: Englewood Cliffs, NJ, 1996. [Google Scholar]
- Muhanna, R. L.; Mullen, R. L.; Zhang, H. Interval finite element as a basis for generalized models of uncertainty in engineering mechanics. Reliable Computing Journal 2007, 13(2), 173–194. [Google Scholar]
- Stolfi, J.; H., D. F. L. Self-Validated Numerical Methods and Applications.; Institute for Pure and Applied Mathematics (IMPA): Rio de Janeiro, 1997. [Google Scholar]










| Parameter | Value |
|---|---|
| Exposure | 200 Sv |
| kVp | 140 kiloVolt |
| Slice thickness | 1.3 mm |
| Slice spacing | 0.6 mm |
| Slice resolution | 512 × 512 pixels |
| Number of slices | 70–140 |
| Coating | 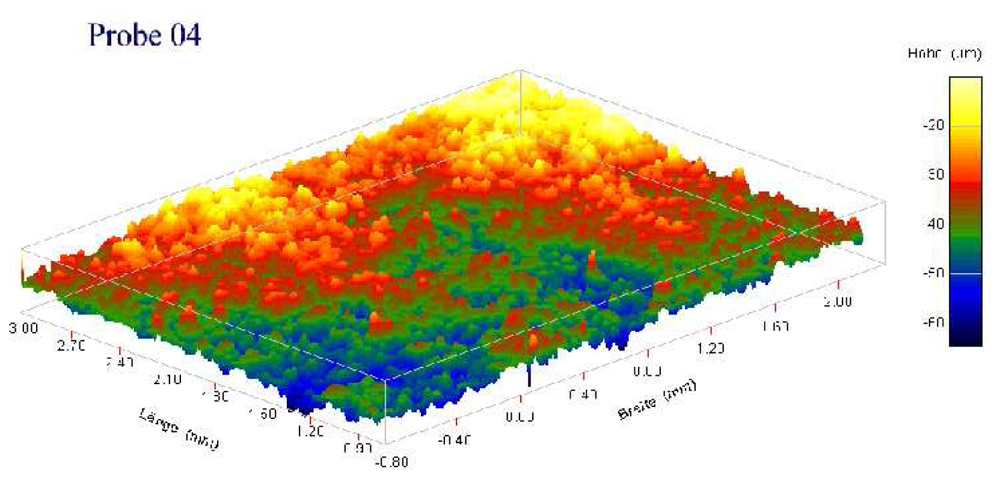 | 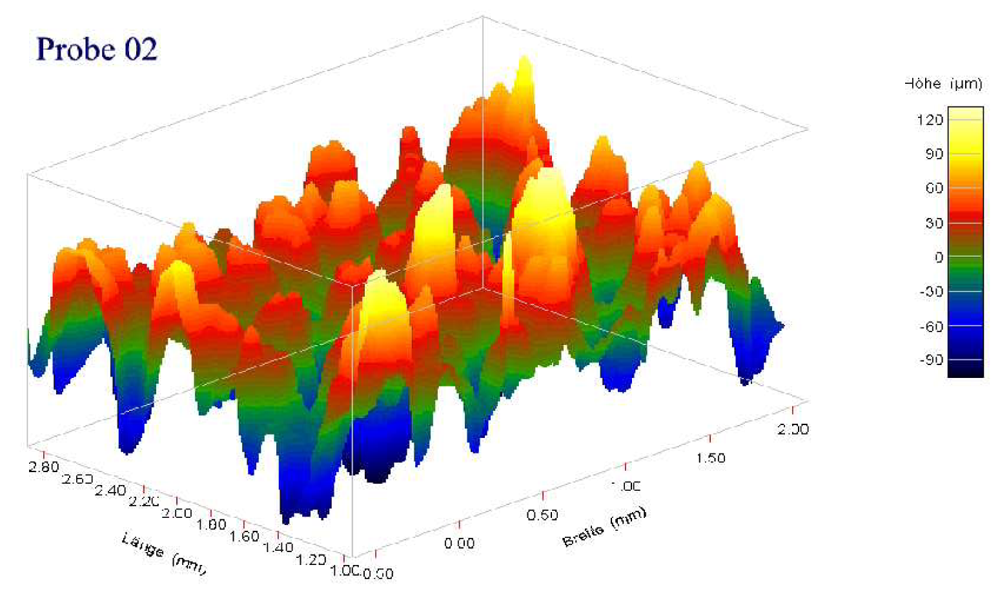 |  |
| Roughness, Rt, µm | 150 ± 50 | 200 ± 100 | 200 ± 100 |
| Porosity, % | 15 ± 10 | 30 ± 10 | 15 ± 10 |
| Normal contact stiffness knn | 0.99 | 0.96 | 0.87 |
| Friction coefficient | 9.78e-04 | 5.45e-02 | 2.21e-01 |
| Contact param. for knn(u) from (7) | |||
| an | 4.933230 | 2.337140 | 1.766300 |
| bn | 0.497877 | 0.382857 | 0.427986 |
| Coarsening Levels | Number of Nodes | Number of Elements | Node reduction | Time (sec.) |
|---|---|---|---|---|
| 0 | 346 783 | 1 636 175 | 1.0 | 135 |
| 1 | 81 816 | 341 152 | 4.2 | 65 |
| 2 | 58 640 | 230 642 | 6.2 | 56 |
| 3 | 57 186 | 223 763 | 6.4 | 56 |
| Position of the prosthesis | 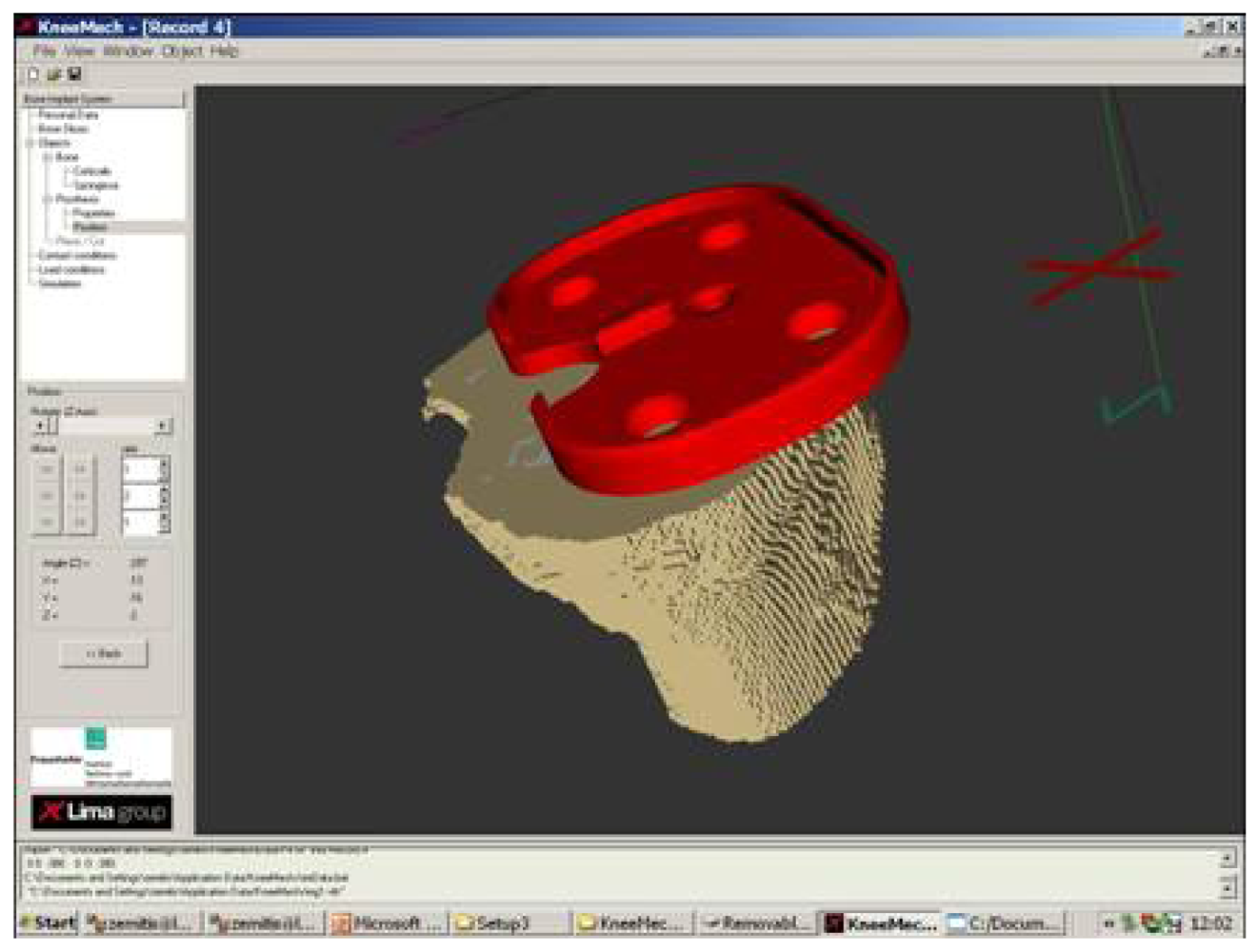 |  |  |
| Equivalent stress (MPa) | 1.25 | 1.1 | 1.18 |
| E (GPa) | Equivalent stress (MPa) | Vertical displacement (mm) |
|---|---|---|
| 5 | 1.18 | 0.0316 |
| 10 | 1.19 | 0.0233 |
| 14.7 | 1.20 | 0.0152 |
| Angle, ° | Equivalent stress (MPa) | Horizontal displacement (mm) |
|---|---|---|
| 0 | 1.1 | 0.0152 |
| 45 | 1.2 | 0.00722 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Andrä, H.; Battiato, S.; Bilotta, G.; Farinella, G.q.M.; Impoco, G.; Orlik, J.; Russo, G.; Zemitis, A. Structural Simulation of a Bone-Prosthesis System of the Knee Joint. Sensors 2008, 8, 5897-5926. https://doi.org/10.3390/s8095897
Andrä H, Battiato S, Bilotta G, Farinella GqM, Impoco G, Orlik J, Russo G, Zemitis A. Structural Simulation of a Bone-Prosthesis System of the Knee Joint. Sensors. 2008; 8(9):5897-5926. https://doi.org/10.3390/s8095897
Chicago/Turabian StyleAndrä, Heiko, Sebastiano Battiato, Giuseppe Bilotta, Giovanni q M. Farinella, Gaetano Impoco, Julia Orlik, Giovanni Russo, and Aivars Zemitis. 2008. "Structural Simulation of a Bone-Prosthesis System of the Knee Joint" Sensors 8, no. 9: 5897-5926. https://doi.org/10.3390/s8095897
APA StyleAndrä, H., Battiato, S., Bilotta, G., Farinella, G. q. M., Impoco, G., Orlik, J., Russo, G., & Zemitis, A. (2008). Structural Simulation of a Bone-Prosthesis System of the Knee Joint. Sensors, 8(9), 5897-5926. https://doi.org/10.3390/s8095897






