Downscaling Thermal Infrared Radiance for Subpixel Land Surface Temperature Retrieval
Abstract
:1. Introduction
2. Downscaling Methods
2.1. Physical downscaling
2.2 Statistical downscaling
3. Validation and Evaluation
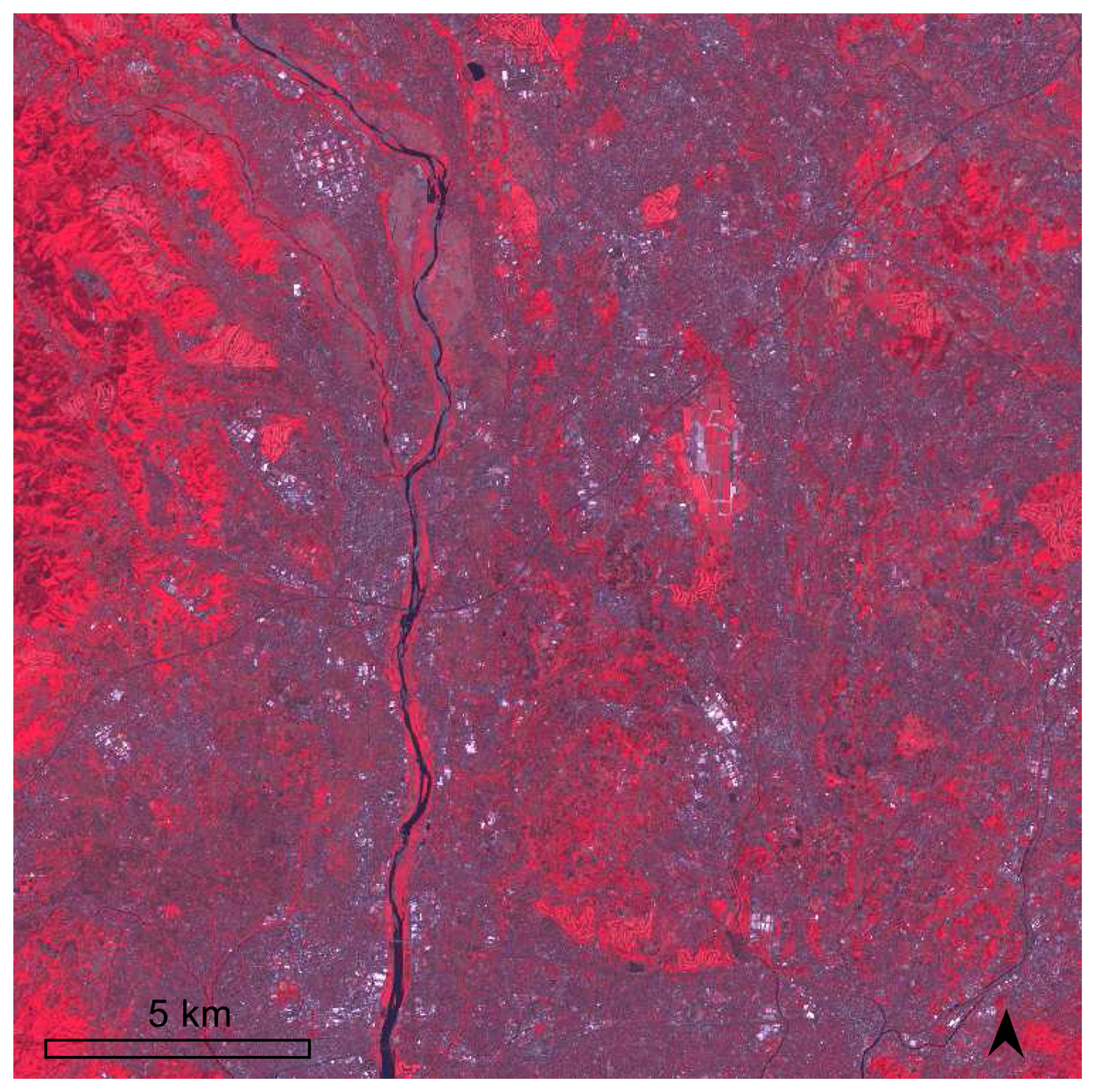
3.1. ASTER data
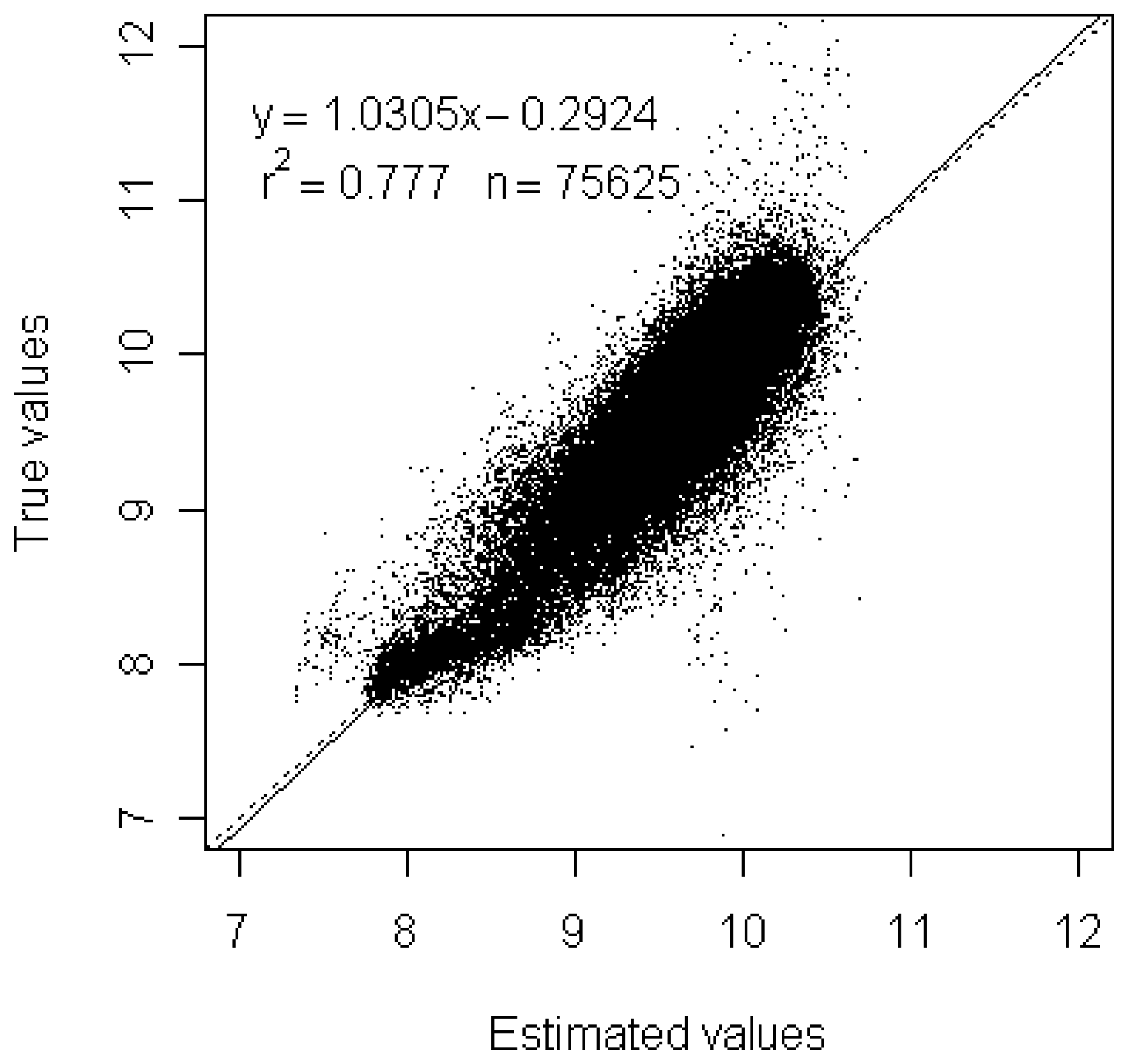
3.2. Physical downscaling results
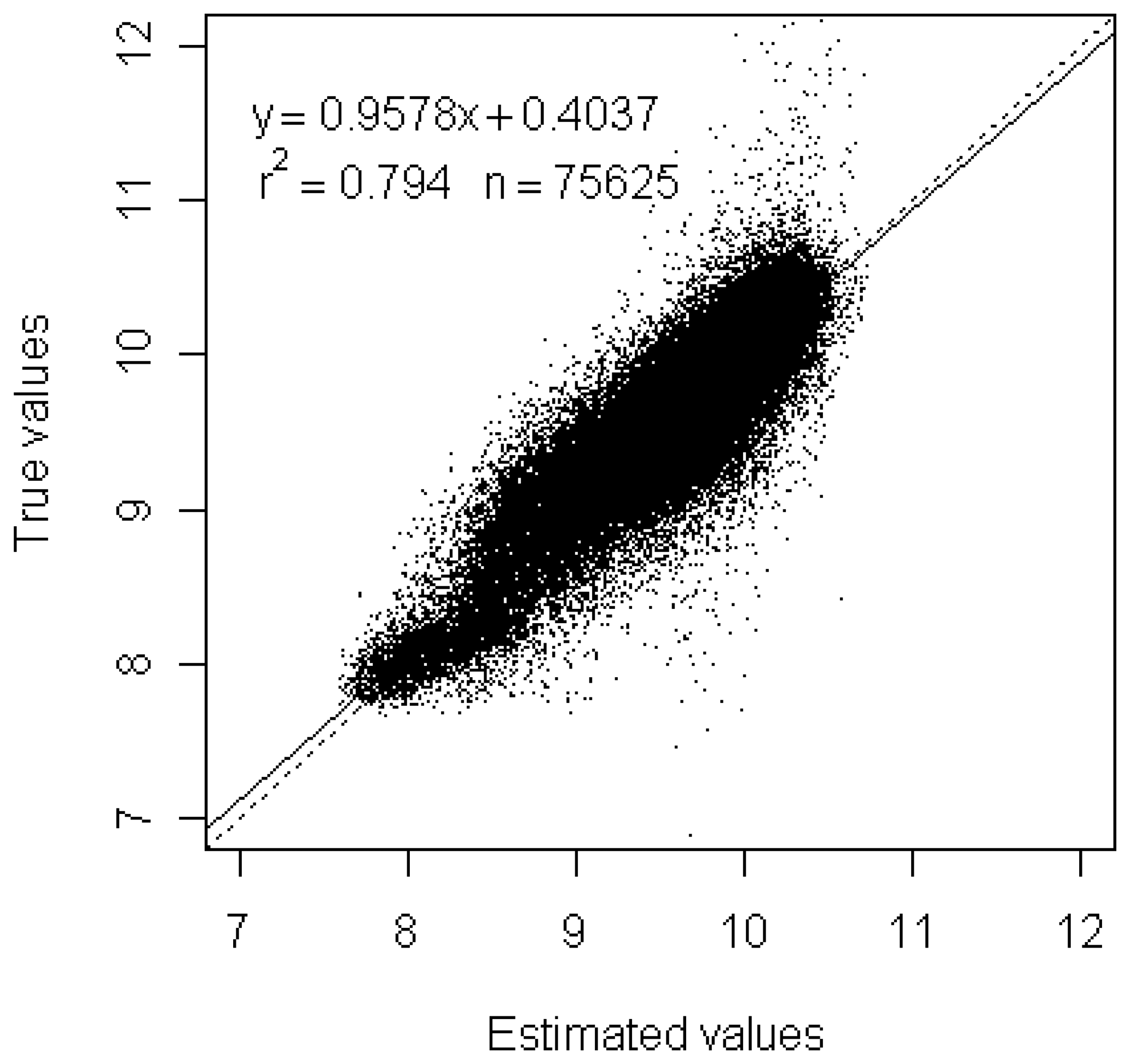
3.3. Statistical downscaling results
4. Conclusions
References
- Price, J.C. On the use of satellite data to infer surface fluxes at meterological scales. Journal of Applied Meteorology 1982, 21, 1111–1122. [Google Scholar]
- Qin, Z.; Karnieli, A. Progress in the remote sensing of land surface temperature and ground emissivity using NOAA-AVHRR data. International Journal of Remote Sensing 1999, 20(12), 2367–2393. [Google Scholar]
- Wilson, J. S.; Clay, M.; Martin, E.; Stuckey, D.; Vedder-Risch, K. Evaluating environmental influences of zoning in urban ecosystems with remote sensing. Remote Sensing of Environment 2003, 86, 303–321. [Google Scholar]
- Lu, D.; Weng, Q. Spectral mixture analysis of ASTER images for examining the relationship between urban thermal features and biophysical descriptors in Indianapolis, Indiana, USA. Remote Sensing of Environment 2006, 104, 157–167. [Google Scholar]
- Gustafson, W.T.; Handcock, R.; Gillespie, A.R.; Tonooka, H. An image-sharpening method to recover stream temperatures from ASTER images. Ehlers, M., Ed.; In Remote Sensing for Environmental Monitoring, GIS Applications and Geology. Proceedings of SPIE; 2003; Volume 4486, pp. 72–83. [Google Scholar]
- Sentlinger, G.I.; Hook, S.J.; Laval, B. Sub-pixel water temperature estimation from thermal-infrared imagery using vectorized lake features. Remote Sensing of Environment. (in press). [CrossRef]
- Liu, Y.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: a case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sensing of Environment 2006, 105, 115–128. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sensing of Environment 1981, 11, 221–229. [Google Scholar]
- Gillespie, A.R. Spectral mixture analysis of Multispectral thermal infrared images. Remote Sensing of Environment 1992, 42, 137–145. [Google Scholar]
- Collins, E.F.; Roberts, D.A.; Borel, C.C. Spectral mixture analysis of simulated thermal infrared spectrometry data: an initial temperature estimate bounded TESSMA search approach. IEEE Transactions on Geoscience and Remote Sensing 2001, 39, 1435–1446. [Google Scholar]
- Song, X.; Zhao, Y. Study on component temperatures inversion using satellite remotely sensed data. International Journal of Remote Sensing 2007, 28, 2567–2579. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Transactions on Geoscience and Remote Sensing 1996, 34, 898–905. [Google Scholar]
- Gillespie, A.R.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Esimssion and Reflection Radiometer (ASTER) images. IEEE Transactions on Geoscience and Remote Sensing 1998, 36, 1113–1126. [Google Scholar]
- Qin, Z.; Olmo, G.D.; Karnieli, A. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data. Journal of Geophysical Research 2001, 106(D19), 22655–22670. [Google Scholar]
- Pu, R.; Gong, P.; Michishita, R.; Sasagawa, T. Assessment of Multi-Resolution and Multi-Sensor Data for Urban Surface Temperature Retrieval. Remote Sensing of Environment 2006, 104, 211–225. [Google Scholar]
- Harvey, J.T. Population estimation models based on individual TM pixels. Photogrammetric Engineering and Remote Sensing 2002, 68(11), 1181–1192. [Google Scholar]
- Wu, C.; Murray, A.T. Population estimation using Landsat enhanced Thematic Mapper imagery. Geographical Analysis 2007, 39, 26–43. [Google Scholar]
- Yamaguchi, Y.; Kahle, A.B.; Tsu, H.; Kawakami, T.; Pniel, M. Overview of Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). IEEE Transactions on Geoscience and Remote Sensing 1998, 36, 1062–1071. [Google Scholar]
- Abrams, M.; Hook, S.; Ramachandran, B. ASTER user handbook, version 2; 1999; Pasadena, CA; Jet Propulsion Laboratory. [Google Scholar]


| Parameters | Estimate | Standard Error | P-value |
|---|---|---|---|
| A | 2.56986 | 0.18414 | <2e-16 |
| 0.49519 | 0.03397 | <2e-16 | |
| 0.70226 | 0.01831 | <2e-16 | |
| 0.71396 | 0.01829 | <2e-16 | |
| 0.74050 | 0.02203 | <2e-16 | |
| 0.69724 | 0.01876 | <2e-16 | |
| 0.63358 | 0.02272 | <2e-16 | |
| 0.64320 | 0.02016 | <2e-16 |
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Liu, D.; Pu, R. Downscaling Thermal Infrared Radiance for Subpixel Land Surface Temperature Retrieval. Sensors 2008, 8, 2695-2706. https://doi.org/10.3390/s8042695
Liu D, Pu R. Downscaling Thermal Infrared Radiance for Subpixel Land Surface Temperature Retrieval. Sensors. 2008; 8(4):2695-2706. https://doi.org/10.3390/s8042695
Chicago/Turabian StyleLiu, Desheng, and Ruiliang Pu. 2008. "Downscaling Thermal Infrared Radiance for Subpixel Land Surface Temperature Retrieval" Sensors 8, no. 4: 2695-2706. https://doi.org/10.3390/s8042695
APA StyleLiu, D., & Pu, R. (2008). Downscaling Thermal Infrared Radiance for Subpixel Land Surface Temperature Retrieval. Sensors, 8(4), 2695-2706. https://doi.org/10.3390/s8042695





