Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape
Abstract
:1. Introduction
2. What VIs Measure
3. VIs as Proxies for Other Canopy Attributes
3.1 VIs and LAI
3.2 VIs and fc
3.3 VIs and Roughness Lengths, Emissivity and Albedo
4. Combining ground data and VIs to scale biophysical processes over large areas
4.1 Flux Towers and Other Methods to Measure Carbon Assimilation and ET at Plot Scales of Measurement
4.2 What Flux Towers Measure and Sources of Error in Flux Towers
4.3 Examples of Combining VIs and Flux Tower Data to Estimate Carbon Fluxes
4.4 Examples of VIs and Flux Tower Data to Estimate ET
5. Reformulating SVAT models to accommodate new data sources
6. Conclusions
References
- Pettorelli, N.; Vik, J.; Mysterud, A.; Gaillard, J.; Tucker, C.; Stenseth, N. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends in Ecology and Evolution 2005, 20, 503–510. [Google Scholar]
- Kerr, J.; Ostrovsky, M. From space to species: ecological applications for remote sensing. Trends in Ecology and Evolution 2003, 18, 299–305. [Google Scholar]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS vegetation indices. Land Remote Sensing and Global Environmental Change: NASA's Earth Observing System and the Science of ASTER and MODIS 2008, in press. [Google Scholar]
- Field, C. Ecological scaling of carbon gain to stress and resource availability. Mooney, H., Winner, W., Pell, E., Eds.; In Response of Plants to Multiple Stresses; 1991; London; Academic Press; pp. 35–66. [Google Scholar]
- Ninemets, U. Photosynthesis and resource distribution through plant canopies. Plant, Cell and Environment 2007, 30, 1052–1071. [Google Scholar]
- Glenn, E.; Huete, A.; Nagler, P.; Hirschboeck, K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. Critical Reviews in Plant Sciences 2007, 26, 139–168. [Google Scholar]
- Jordan, C. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar]
- Rouse, J.; Hass, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. In Third ERTS Symposium; 1973; NASA; SP-351 I; pp. 309–317. [Google Scholar]
- Tucker, C.; Townshend, J.; Goff, T. African land cover classification using satellite data. Science 1985, 227, 229–235. [Google Scholar]
- Tucker, C. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sensing of Environment 1979, 8, 127–150. [Google Scholar]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics, 2nd. Edition ed; 1990; Edward Arnold: London. [Google Scholar]
- Myneni, R.; Hall, F.; Seller, P.; Marshak, A. The interpretation of spectral vegetation indexes. IEEE Transactions on Geoscience and Remote Sensing 1995, 33, 481. [Google Scholar]
- Sellers, P. Canopy reflectance, photosynthesis and transpiration. International Journal of Remote Sensing 1985, 6, 1335–1372. [Google Scholar]
- Hall, F. Satellite remote sensing of surface energy balance: success, failures and unresolved issues in FIEF. Journal of Geophysics Research 1992, 97, 19061–19090. [Google Scholar]
- Jiang, Z.; Huete, A.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sensing of Environment 2006, 101, 366–378. [Google Scholar]
- Beyschlag, W.; Ryel, R. Canopy photosynthesis modeling. In Functional Plant Ecology; Pugnaire, F., Valladares, F., Eds.; Taylor & Francis Group: Boca Raton, FL, 2007; pp. 627–654. [Google Scholar]
- Harper, P. Optimum leaf area index in the potato crop. Nature 1963, 4770, 917–918. [Google Scholar]
- Stern, W.; Donald, C. Relationship of radiation, leaf area index and crop growth rate. Nature 1961, 4764, 597–598. [Google Scholar]
- Pearcy, R.; Schulze, E.; Zimmermann, R. Measurement of transpiration and leaf conductance. In Plant Physiological Ecology; Pearcy, R., Ehleringer, J., Mooney, H., Rundel, P., Eds.; Chapman & Hall: London, 1991; pp. 137–160. [Google Scholar]
- Sellers, P.; Randall, D.; Collatz, G.; Berry, J.; Field, C.; Dazlich, D.; Zhang, C.; Collelo, G.; Bounoua, L. A revised land surface parameterization (SiB2) for atmospheric GCMs. 1. Model formulation. Journal of Climate 1996, 9, 676–705. [Google Scholar]
- Liang, S. Recent developments in estimating land surface biogeophysical variables from optical remote sensing. Progress in Physical Geography 2007, 31, 501–516. [Google Scholar]
- Wang, Y.; Woodcock, C.; Buermann, W.; Stenberg, P.; Voipio, P.; Smolander, H.; Hame, T.; Yuhong, T.; Hu, J.; Knyazikhin, Y.; Myneni, R. Evaluation of the MODIS LAI algorithm at a coniferous forest site in Finland. Remote Sensing of Environment 2004, 91, 114–127. [Google Scholar]
- Roberts, G. A review of the application of BRDF models to infer land cover parameters at regional and global scales. Progress in Physical Geography 2001, 25, 483–511. [Google Scholar]
- Widowski, J.; Pinty, B.; Lavergne, T.; Verstraete, M.; Gobron, N. Using 1-D models to interpret the reflectance anisotropy of 3-D canopy targets: Issues and caveats. IEEE Transactions on Geoscience and Remote Sensing 2005, 43, 2008–2017. [Google Scholar]
- Frank, A.; Karn, J. Vegetation indices, CO2 flux, and biomass for Northern Plains grasslands. Journal of Range Management 2003, 56, 382–387. [Google Scholar]
- Leuning, R.; Cleugh, H.; Zegelin, S.; Hughes, D. Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: measurements and comparison with MODIS remote sensing estimates. Agricultural and Forest Meteorology 2005, 129, 151–173. [Google Scholar]
- Asner, G.; Scurlock, J.; Hicke, J. Global synthesis of leaf area index observations: implications for ecological and remote sensing studies. Global Ecology and Biogeography 2003, 122, 191–205. [Google Scholar]
- Breda, N. Ground-based measurements of leaf area index: a review of methods, instruments and current controversies. Journal of Experimental Botany 2003, 54, 2403–2417. [Google Scholar]
- Chen, J.; Black, T. Defining leaf area index for non-flat leaves. Plant, Cell & Environment 1992, 15, 21–29. [Google Scholar]
- Asrar, G.; Kanemasu, E.; Yoshida, M. Estimates of leaf area index from spectral reflectance of wheat under different cultural practices and solar angles. Remote Sensing of Environment 1985, 17, 1–11. [Google Scholar]
- Nagler, P.; Cleverly, J.; Lampkin, D.; Glenn, E.; Huete, A.; Wan, Z. Predicting riparian evapotranspiration from MODIS vegetation indices and meteorological data. Remote Sensing of Environment 2005, 94, 17–30. [Google Scholar]
- Nagler, P.; Glenn, E.; Huete, A. Assessment of vegetation indices for riparian vegetation in the Colorado River delta, Mexico. Journal of Arid Environments 2001, 49, 91–110. [Google Scholar]
- Nagler, P.; Glenn, E.; Thompson, T.; Huete, A. Leaf area index and Normalized Difference Vegetation Index as predictors of canopy characteristics and light interception by riparian species on the Lower Colorado River. Agricultural and Forest Meteorology 2004, 116, 103–112. [Google Scholar]
- Nagler, P.; Scott, R.; Westenberg, C.; Cleverly, J.; Glenn, E.; Huete, A. Evapotranspiration on western U.S. rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sensing of Environment 2005, 97, 337–351. [Google Scholar]
- Nagler, P.; Glenn, E.; Hursh, K.; Curtis, C.; Huete, A. Vegetation mapping for change detection on an arid-zone river. Environmental Monitoring and Assessment 2005, 109, 255–274. [Google Scholar]
- Nagler, P.; Glenn, E.; Thompson, T. Comparison of transpiration rates among saltcedar, cottonwood and willow trees by sap flow and canopy temperature methods. Agricultural and Forest Meteorology 2003, 116, 73–89. [Google Scholar]
- Gamon, J.; Qui, H. Ecological applications of remote sensing at multiple scales. Pugmaore., F., Valladares, F., Eds.; In Handbook of Function Plant Ecology; 2007; Taylor and Francis Group: Boca Raton, FL; pp. 655–684. [Google Scholar]
- Kustas, W.; Norman, J. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrological Sciences Journal - Journal des Sciences Hydrologiques 1996, 41, 495–516. [Google Scholar]
- Anderson, M. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sensing of Environment 1997, 60, 195–216. [Google Scholar]
- Timmerman, W.; Kustas, W.; Anderson, M.; French, A. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sensing of Environment 2007, 108, 369–384. [Google Scholar]
- Carlson, T.; Ripley, D. On the relationship between fractional vegetation cover, leaf area index, and NDVI. Remote Sensing of Environment 1997, 62, 241–252. [Google Scholar]
- Ormsby, J.; Choudry, B.; Owe, M. Vegetation spatial variability and its effect on vegetation indexes. International Journal of Remote Sensing 1987, 8, 1301–1306. [Google Scholar]
- Li, F.; Kustas, W.; Preuger, J.; Neale, C.; Jackson, T. Utility of remote sensing-based two-source balance model under low- and high-vegetation cover conditions. Journal of Hydrometeorology 2005, 6, 878–891. [Google Scholar]
- Bastiaanssen, W.; Menentia, M.; Feddes, R.; Holstag, A. A remote sensing surface energy balance algorithm for Land (SEBAL), Part I, Formulation. Journal of Hydrology 1998, 212-213, 198–212. [Google Scholar]
- Lagouarde, J.; Jacob, J.; Gu, X.; Olioso, A.; Bonnefond, J.; Kerr, Y.; McAneney, K.; Irvine, M. Spatialization of sensible heat flux over a heterogeneous landscape. Agronomie 2002, 22, 627–633. [Google Scholar]
- Jimenez-Munoz, J.; Sobrino, J.; Gillespie, A.; Sabol, D.; Gustafson, W. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sensing of Environment 2006, 103, 474–487. [Google Scholar]
- Momeni, M.; Saradjian, M. Evaluating NDVI-based emissivities of MODIS bands 31 and 32 using emissivities derived by Day/Night LST algorithm. Remote Sensing of Environment 2007, 106, 190–198. [Google Scholar]
- Wittich, K.; Kraft, M. The normalized difference vegetation index obtained from agrometeorological standard radiation sensors: a comparison with ground-based multiband spectroradiometer measurements during the phenological development of an oat canopy. International Journal of Biometeorology 2008, 52, 167–177. [Google Scholar]
- Shuttleworth, W. Putting the ‘vap’ in evaporation. Hydrology & Earth System Sciences 2007, 11, 210–244. [Google Scholar]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthone, P.; Berhofer, C.; Davis, K.; Evans, R.; Fuentes, J.; Goldstein, A.; Katul, G.; Law, B.; Lee, X.; Malhi, Y.; Meyers, T.; Munger, W.; Oechel, W.; Pilegaard, K.; Schmid, H.; Valentini, R.; Verma, S.; Vesala, T.; Wilson, K.; Wofsy, S. Fluxnet: a new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bulletin of the American Meteorological Society 2001, 82, 2415–2434. [Google Scholar]
- Baldocchi, D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: past, present and future. Global Change Biology 2003, 9, 479–492. [Google Scholar]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: a review. European Journal of Agronomy 2000, 13, 125–153. [Google Scholar]
- Bowen, I. The ratio of heat losses by conduction and by evaporation from any water surface. Physical Review 1926, 27, 779–787. [Google Scholar]
- Twine, T.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Weslely, M. Correcting eddy-covariance flux underestimates over a grassland. Agricultural and Forest Meteorology 2000, 103, 279–300. [Google Scholar]
- Misson, L.; Baldocchi, D.; Black, T.; Banken, P.; Falk, M.; Granier, A.; Irvine, M.; Jarosz, N.; Lamaud, E.; Launiainen, S.; McKay, M.; Paw, K.; Vesala, T.; Vickers, D.; Wilson, K.; Goldstein, A. Partitioning forest carbon fluxes with overstory and understory eddy-covariance measurements: A synthesis based on FLUXNET data. Agricultural and Forest Meteorology 2007, 144, 14–31. [Google Scholar]
- Scott, R.; Huxman, T.; Cable, W.; Emmerich, W. Partitioning of evapotranspiration and its relation to carbon dioxide exchange in a Chihuahuan Desert shrubland. Hydrological Processes 2006, 20, 3227–3243. [Google Scholar]
- Yepez, E.; Williams, D.; Scott, R.; Lin, G. Partitioning overstory and understory evapotranspiration in a semiarid savanna woodland from the isotopic composition of water vapor. Agricultural and Forest Meteorology 2003, 119, 53–68. [Google Scholar]
- Scott, R.; Edwards, E.; Shuttleworth, W.; Huxman, T.; Watts, C.; Goodrich, D. Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agricultural and Forest Meteorology 2004, 122, 65–84. [Google Scholar]
- Running, S.; Nemani, R.; Heinsch, F.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global primary production. Bioscience 2004, 54, 547–560. [Google Scholar]
- Potter, C.; Klooster, S.; Huete, A.; Genovese, V. Terrestrial carbon sinks for the United States predicted from MODIS satellite data and ecosystem modeling. Earth Interactions 2007, 11. Art. No.13. [Google Scholar]
- Zhao, M.; Heinsch, R.; Nemani, R.; Running, W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sensing of Environment 2005, 95, 164–176. [Google Scholar]
- Yuan., W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.; Goulden, M.; Hollinger, D.; Hu, Y.; Law, B.; Stoy, P.; Vesala, T.; Wofsy, S. Deriving a light use efficiency model from eddy covariance flux data for predicting gross primary production across biomes. Agricultural and Forest Meteorology 2007, 143, 189–207. [Google Scholar]
- Owen, K.; Tenhunen, J.; Reichstein, M.; Wang, Q.; Falge, E.; Geyer, R.; Xiao, X.; Stoy, P.; Ammann, C.; Arain, A.; Aubiinet, M.; Aurela, M.; Bernhofer, C.; Chojnicki, B.; Granier, A.; Gruenwald, T.; Hollinger, D.; Knohl, A.; Kutsch, W.; Lohila, A.; Meyers, T.; Moors, E.; Moureaux, C.; Pilegaard, K.; Saigusa, N.; Verma, S.; Vesala, T.; Vogel, C. Linking flux network measurements to continental scale simulations: ecosystem carbon dioxide exchange capacity under non-water-stressed conditions. Global Change Biology 2007, 13, 734–760. [Google Scholar]
- Heinsch, F.; Zhao, M.; Running, S.; Kimball, J.; Nemani, R.; Davis, K.; Ricciuto, D.; Law, B.; Oechel, W.; Kwon, H.; Munger, J.; Baldocchi, D.; Xu, L.; Hollinger, D.; Richardson, A.; Stoy, P.; Siquerira, M.; Monson, R.; Burns, S.; Flanagan, L. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 1908–1925. [Google Scholar]
- Wylie, B.; Johnson, D.; Laca, E.; Saliendra, N.; Gilmanov, T.; Reed, B.; Tieszen, L.; Worstell, B. Calibration of remotely sensed, coarse resolution NDVI to CO2 fluxes in a sagebrush-steppe ecosystem. Remote Sensing of Environment 2003, 85, 243–255. [Google Scholar]
- Huete, A.; Didan, K.; Shimabakuro, Y.; Ratana, P.; Saleska, S.; Hutyra, L.; Yang, W.; Nemani, R.; Myneni, R. Amazon rainforest green-up with sunlight in dry season. Geophysical Research Letters 2006, 33, L06405. [Google Scholar]
- Saleska, S.; Didan, K.; Huete, A.; da Rocha, R. Amazon forests green-up during 2005 drought. Science 2007, 318, 612. [Google Scholar]
- Huete, A.; Restrepo-Coupe, N.; Ratana, P.; Didan, K.; Saleska, S.; Ichii, K.; Panuthai, S.; Gamo, M. Multiple site tower flux and remote sensing comparisons of tropical forest dynamics in monsoon Asia. Agricultural and Forest Meteorology 2008, (in press). [Google Scholar]
- Sims, D.; Rahman, A.; Cordova, V.; El-Masria, B.; Baldocchi, D.; Flanagan, L.; Goldstein, A.; Hollinger, D.; Misson, L.; Schmid, H.; Wofsy, S.; Xu, L. On the use of MODIS EVI to assess gross primary productivity of North American ecosystems. Journal of Geophysical Research – Biogeosciences 2006, 111. Art. No. G04015. [Google Scholar]
- Rahman, A.; Sims, D.; Cordova, V.; El-Masri, B. Potential of MODIS EVI and surface temperature for directly estimating per-pixel ecosystem C fluxes. Geophysical Research Letters 2005, 32. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.Y.; Tieszen, L.; Baldochhi, D.; Bernhofer, C.; Cholz, H.; Godstein, A.; Goulden, M.; Hollinger, D.; Hu, Y.; Law, B.; Stoy, P.; Vesala, T.; Wofsy, S. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agricultural and Forest Metoerology 2007, 143, 189–207. [Google Scholar]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, I.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sensing of Environment 2004, 91, 256–270. [Google Scholar]
- Jenkins, J.; Richardson, A.; Braswell, B.; Ollinger, S.; Hollinger, D.; Smith, M. Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements. Agricultural and Forest Meteorology 2007, 143, 64–79. [Google Scholar]
- Grace, J.; Nichol, C.; Disney, M.; Lewis, P.; Quaife, T.; Bowyer, P. Can we measure terrestrial photosynthesis from space directly, using spectral reflectance and flourescence? Global Change Biology 2007, 13, 1484–1497. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Nagler, P.; Glenn, E.; Kim, H.; Emmerich, W.; Scott, R.; Huxman, T.; Huete, A. Relationship between evapotranspiration and precipitation pulses in a semiarid rangeland estimated by moisture flux towers and MODIS vegetation indices. Journal of Arid Environments 2007, 70, 443–462. [Google Scholar]
- Cleugh, H.; Leuning, R.; Mu, Q.; Running, S. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sensing of Environment 2007, 106, 285–304. [Google Scholar]
- Mu, Q.; Heinsch, F.; Zhao, M.; Running, S. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sensing of Environment 2007, 111, 519–536. [Google Scholar]
- Yang, F.; White, M.; Michaelis, A.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, H.; Nemani, R. Prediction of continental-scale evapotranspiration by combining MODIS and Ameriflux data through support vector machine. IEEE Transactions on Geoscience and Remote Sensing 2006, 44, 3452–3461. [Google Scholar]
- Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. Journal of Geophysical Research – Atmospheres 2007, 12. Art. No. D15107. [Google Scholar]
- Groeneveld, D.; Baugh, W.; Sanderson, J.; Cooper, D. Annual groundwater evapotranspiration mapped from single satellite scenes. Journal of Hydrology 2007, 344, 146–156. [Google Scholar]
- Beven, K. A manifesto for the equifinality thesis. Journal of Hydrology 2006, 320, 18–36. [Google Scholar]
- Swinburne, R. Simplicity as Evidence for Truth; Marquette University Press: Marquette, MI, 1997. [Google Scholar]
- Falge, E.; Reth, S.; Bruggemann, N.; Butterbach-Bahl, K.; Goldberg, V.; Oltchev, A.; Schaaf, S.; Spindler, G.; Spiller, B.; Queck, R.; Kostner, B.; Bernhofer, C. Comparison of surface energy exchange models with eddy flux data in forest and grassland ecosystems of Germany. Ecological Modeling 2005, 188, 174–216. [Google Scholar]

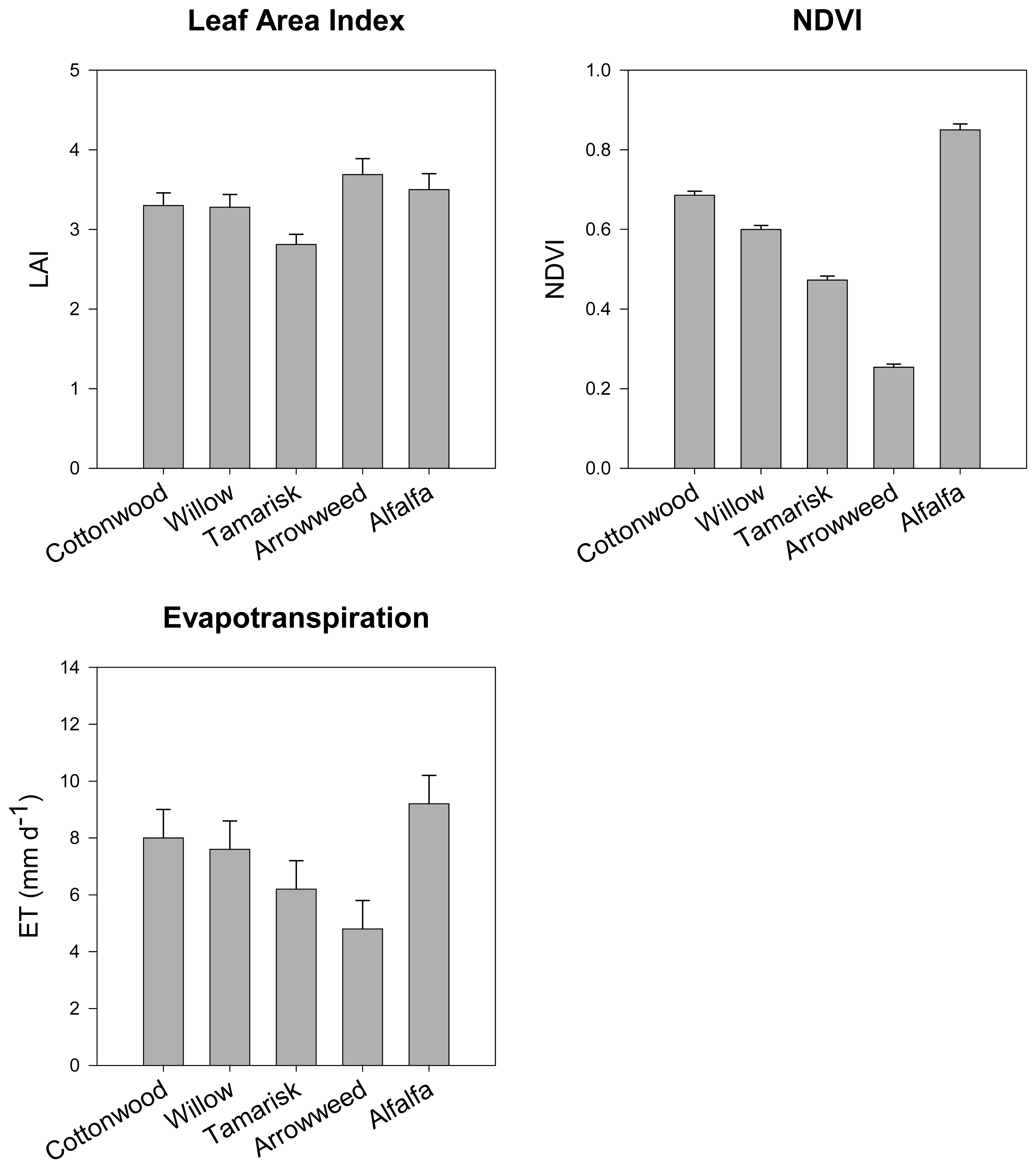

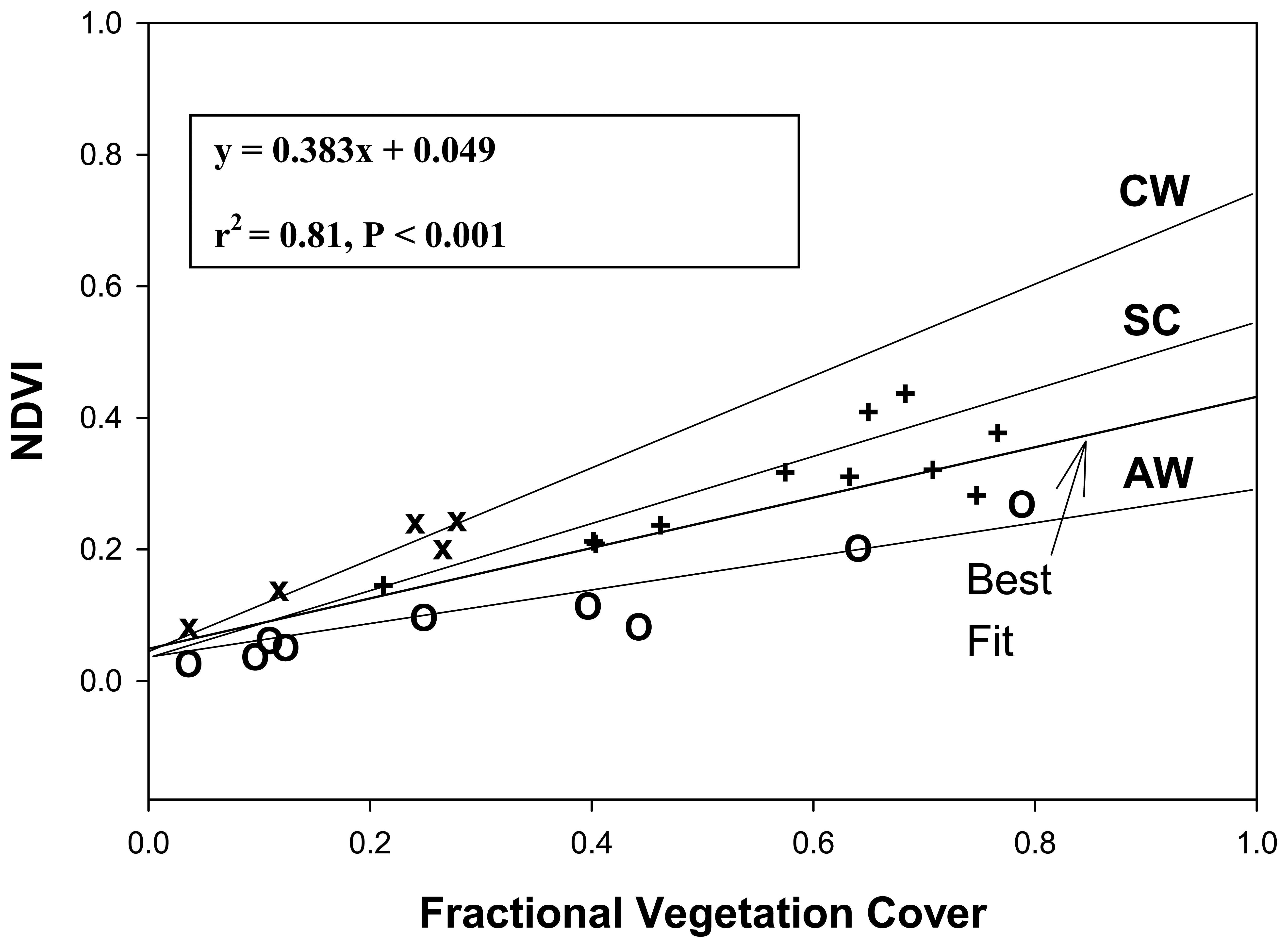
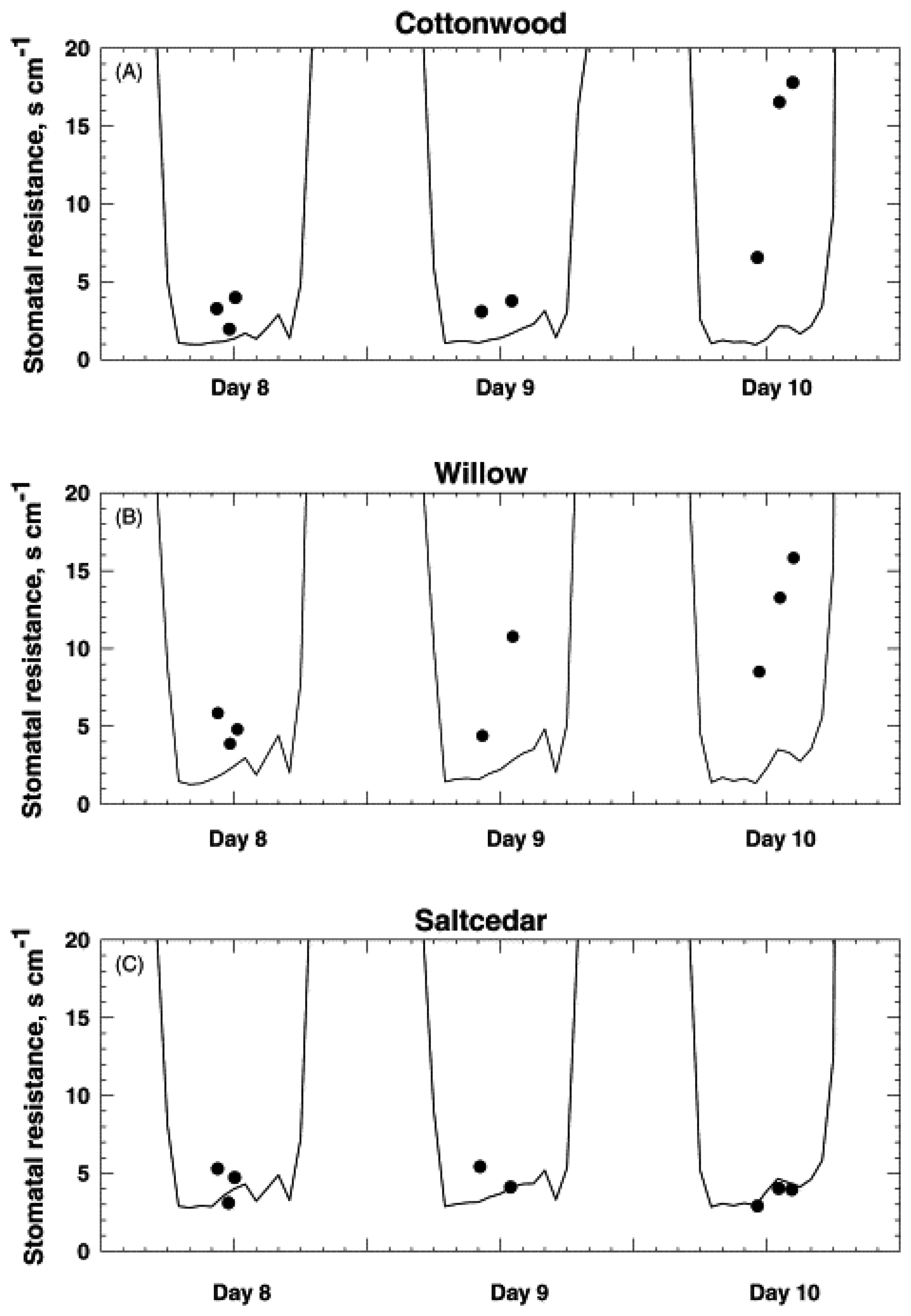
| Tower Site | Vegetation | EVI | NDVI | Ta | P | EVI + Ta | EVI + P |
|---|---|---|---|---|---|---|---|
| Riparian | |||||||
| San Pedro 1 | Mesquite | 0.87 | 0.83 | 0.77 | - | 0.88 | - |
| San Pedro 2 | Mesquite | 0.86 | 0.82 | 0.77 | - | 0.90 | - |
| San Pedro 3 | Sacaton | 0.94 | 0.82 | 0.77 | - | 0.97 | - |
| Rio Grande 1 | Saltcedar | 0.83 | 0.68 | 0.84 | - | 0.88 | - |
| Rio Grande 2 | Saltcedar | 0.84 | 0.52 | 0.82 | - | 0.89 | - |
| Rio Grande 3 | Cottonwood | 0.84 | 0.74 | 0.86 | - | 0.90 | - |
| Rio Grande 4 | Cottonwood | 0.82 | 0.77 | 0.89 | - | 0.89 | - |
| Colorado 1 | Saltcedar | 0.83 | 0.64 | 0.92 | - | 0.92 | - |
| Colorado 2 | Arrowweed | 0.64 | 0.50 | 0.76 | - | 0.79 | - |
| Upland | |||||||
| Grassland | Grama | 0.82 | 0.80 | - | 0.66 | - | 0.84 |
| Shrubland | Mixed | 0.87 | 0.78 | - | 0.72 | - | 0.90 |
| Mean | 0.83 | 0.72 | 0.82 | 0.69 | 0.89 | 0.87 |
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors 2008, 8, 2136-2160. https://doi.org/10.3390/s8042136
Glenn EP, Huete AR, Nagler PL, Nelson SG. Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors. 2008; 8(4):2136-2160. https://doi.org/10.3390/s8042136
Chicago/Turabian StyleGlenn, Edward P., Alfredo R. Huete, Pamela L. Nagler, and Stephen G. Nelson. 2008. "Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape" Sensors 8, no. 4: 2136-2160. https://doi.org/10.3390/s8042136
APA StyleGlenn, E. P., Huete, A. R., Nagler, P. L., & Nelson, S. G. (2008). Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors, 8(4), 2136-2160. https://doi.org/10.3390/s8042136






