1. Introduction
The so called photostriction effect in semiconductors was found in germanium by Figielski in 1961 [
2] and in silicon by Gauster and Habing six years later [
3]. Similar effects were also found in some ceramic materials [
4],and can be used as photostrictive actuators [
5,
6]. Under that effect, the photogeneration of free charge carriers (electrons and holes) in a semiconductor, results in the development of a local mechanical strain [
1,
7,
8]. In the late 1990s, Datskos's team investigated the photostriction effect in a silicon microcantilever structure [
1,
7,
8]. It was also applied in photon detection [
1,
7,
8] and chemical gas sensing [
9]. They constructed a basic theory of the photostriction effect in a semiconductor cantilever structure. Their assumption was that the density of the photoinduced excess carriers was homogeneous in the microcantilever, shown by the average density they used to calculate photoinduced strain in
equations 2 and
3 in reference [
1,
7,
8]. However, their theoretical results were about 25 times larger than the experimental values [
1,
7,
8]. In this study, by considering the spatial distribution and surface recombination of photoinduced carriers in silicon, we have constructed a model for prediction the photoinduced deformation in a microcantilever structure. The calculated results are also compared with Datskos's theoretical and experimental data.
2. Modeling
Under illumination with light with an energy above the band gap of silicon, the lattice in the microcantilever will be strained as the presence of excess electron-hole-pairs. Different from Datskos's assumption of homogeneous excess carriers, we suppose that the light intensity will be reduced along the depth of the cantilever (x direction in
Figure 1), because of the intensive absorption of photons by Si. Therefore, the density gradient of the excess carries causes a strain gradient in the cantilever and thus the bending of the silicon cantilever.
Assuming that the light intensity at the top surface of the microcantilever is a constant,
I0, the light intensity I along the x direction is as expressed by [
10]:
where α is light absorption coefficient of silicon.
Following Datskos's deduction, the density of photoinduced excess carriers is given by [
10]:
where
η is the quantum efficiency and τ is the life time of the excess carriers in silicon.
The photoinduced strain is given by
where β is the photostriction coefficient. [
2]
Derived from equations (
1-
3), the relationship between the light and the photoinduced strain can be written as:
For a cantilever with a rectangular cross section, the deformation curvature of the structure can be given by [
11]
where
W,
H, and
I are the width, thickness and the moment of inertia of the microcantilever, respectively.
E is the elastic modulus of the cantilever, given by
Ey/(1− υ) with the Poisson's ratio of silicon
υ.
M is the bending moment, which is the integral force moment of the forces (against the neutral plane) across the cross section of the structure [
11], given by
The maximum displacement
Zmax due to photoinduced carriers can then be written as [
11]
In order to compare with Datskos's expression in reference [
1,
7,
8], the above equation can be rewritten as
where a = 1 −
e−αH, which is the photo absorptivity of silicon [
10]. Let
Two obvious differences between the two equations can be seen. One is that in our equation, there is
a' but not
a as in Datskos's equation. In
Equation (10), the first item 2-
a indicates the effect of the photo absorptivity
a on the part of the microcantilever above the neutral plane, while the second item
indicates the effect of the photo absorptivity
a on the part below the neutral plane.
a' and
a denote two different strain generation mechanisms, i.e., the density of photoinduced excess carriers in the cantilever is asymmetrical in our theory while homogenous in Datskos's. The other is that in our
Eq. (9), there is no item including the Poisson's ratio as in Datskos's equation. The reason is that because photostriction effect directly results in local mechanical strain. That indicates the photo-induced bending is caused by lattice contraction, not by stress. Therefore, the elastic modulus of the cantilever is eliminated from the deformation equation.
Furthermore, the recombination of the photoinduced excess carriers at the top and bottom surfaces must be considered in the prediction of the deformation, because the thickness of the microcantilever is as thin as some hundreds nanometers (e.g. 500 nm in [
1]). The recombination of the photoinduced excess carriers has a great effect on the carrier density and thereafter the photoinduced strain. In addition, the surface recombination velocity is different at the two surfaces, which also plays an important role in the photoinduced bending. From the viewpoint of fabrication, one of the two surfaces of the microcantilever is formed by etching with rough surface, and the other is formed by the original polished silicon surface. The surface recombination velocity at the rough surface is much faster than that at the polished surface.
Suppose that excess carrier density at the etched surface equals to 0, while the carrier recombination at the polished surface can be omitted. Under this assumption, the bending moment M and deflection Zmax can be approximated as follows.
3. Verification of the model
To verify our model, the calculated results from our model are compared with the theoretical and experimental data in [
1,
8]. The experimental parameters are listed in
Table 1. It should be noted that the photo absorptivity of silicon was set as
a=0.95 in [
1,
8], which is about ten time larger than its real value. From [
12], for λ=780nm,
a can be derived as 0.0952-0.1393 with the light absorption coefficient of silicon in the range of 2×10
3 to 3×10
3cm
-1. In our calculation, we set
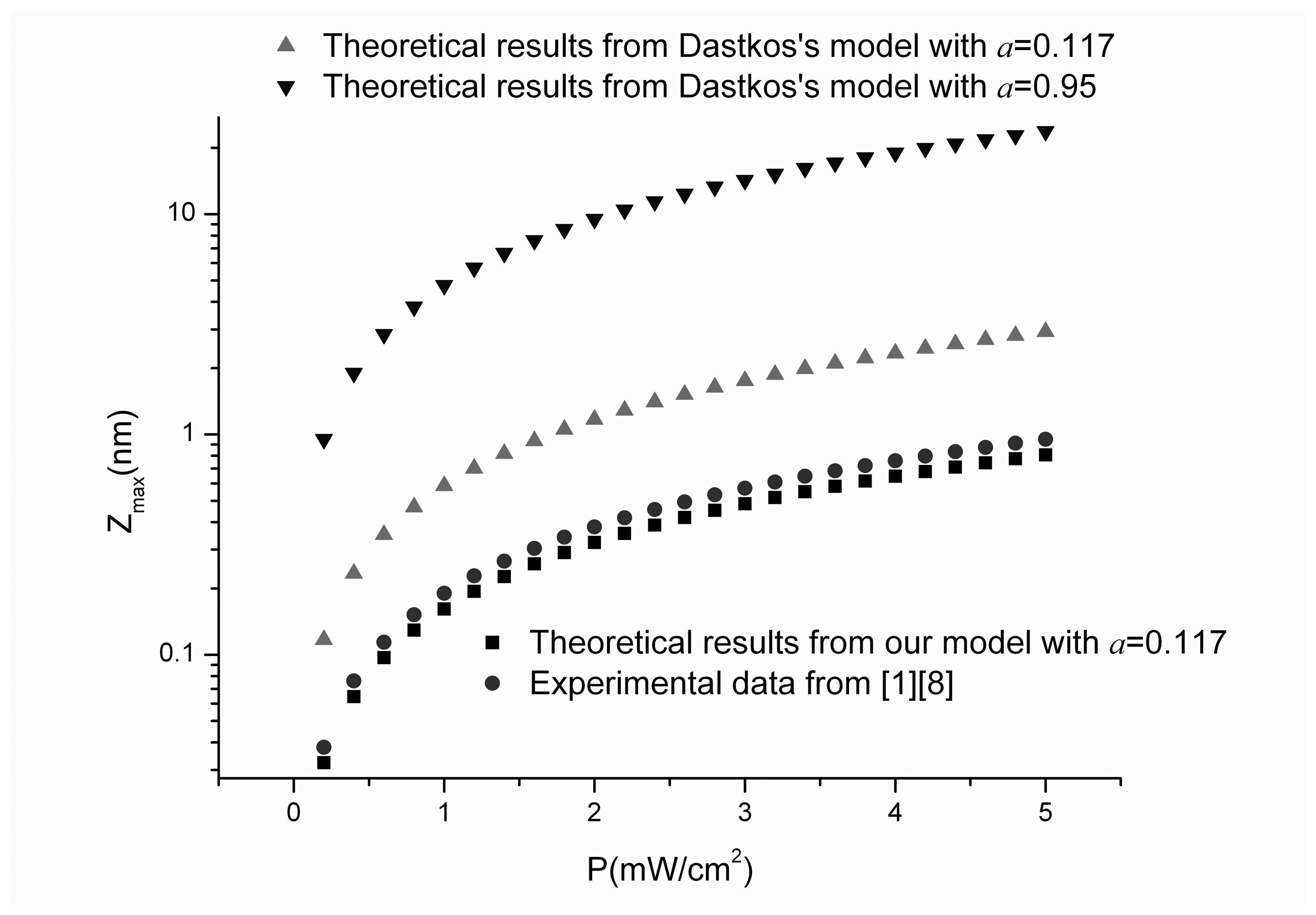
a as the average value of 0.117. The results shown in
Figure 2 are the calculated data by Datskos's model (
Eq. 11) and our model (
Eq. 13), in addition with Datskos's experimental data in [
1,
8]. The experimental data in
Figure 2 is obtained from the fitting line shown in [
1,
8].
The x ordinate of the plot is power density P instead of absorbed power Φ used in [
1,
8] because we have to put theoretical data with
a=0.95 and
a=0.117 both in the plot for comparison. Power density
P is given by
P=
I0hC/
λ, where
h is Planck's constant and
C is the velocity of light. The y ordinate shows the maximum deflection on a logarithmic scale.
From the figure, higher accuracy of our model is obvious. For a=0.117, our theoretical data is 0.85 times the experimental one, while the results from Datskos's model are about 25 times when a=0.95 and 3 times when a=0.117 larger than that they measured. The difference between our calculation and the experimental data most likely comes from the assumption on the carrier recombination velocity of the top and bottom surfaces of the microcantilever.