An Overview of the "Triangle Method" for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery
Abstract
:1. Background
2. A Description of the Triangle Method
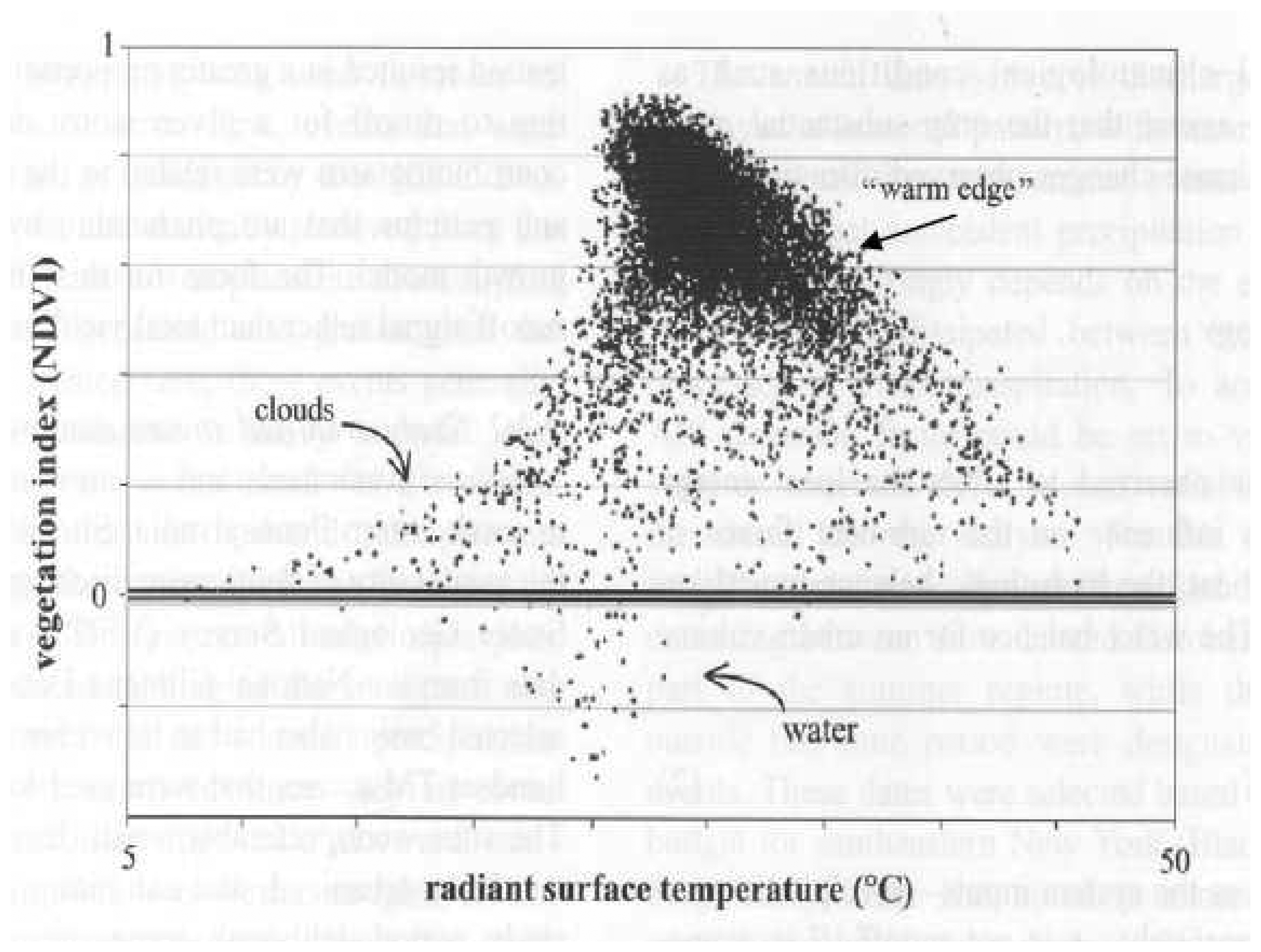
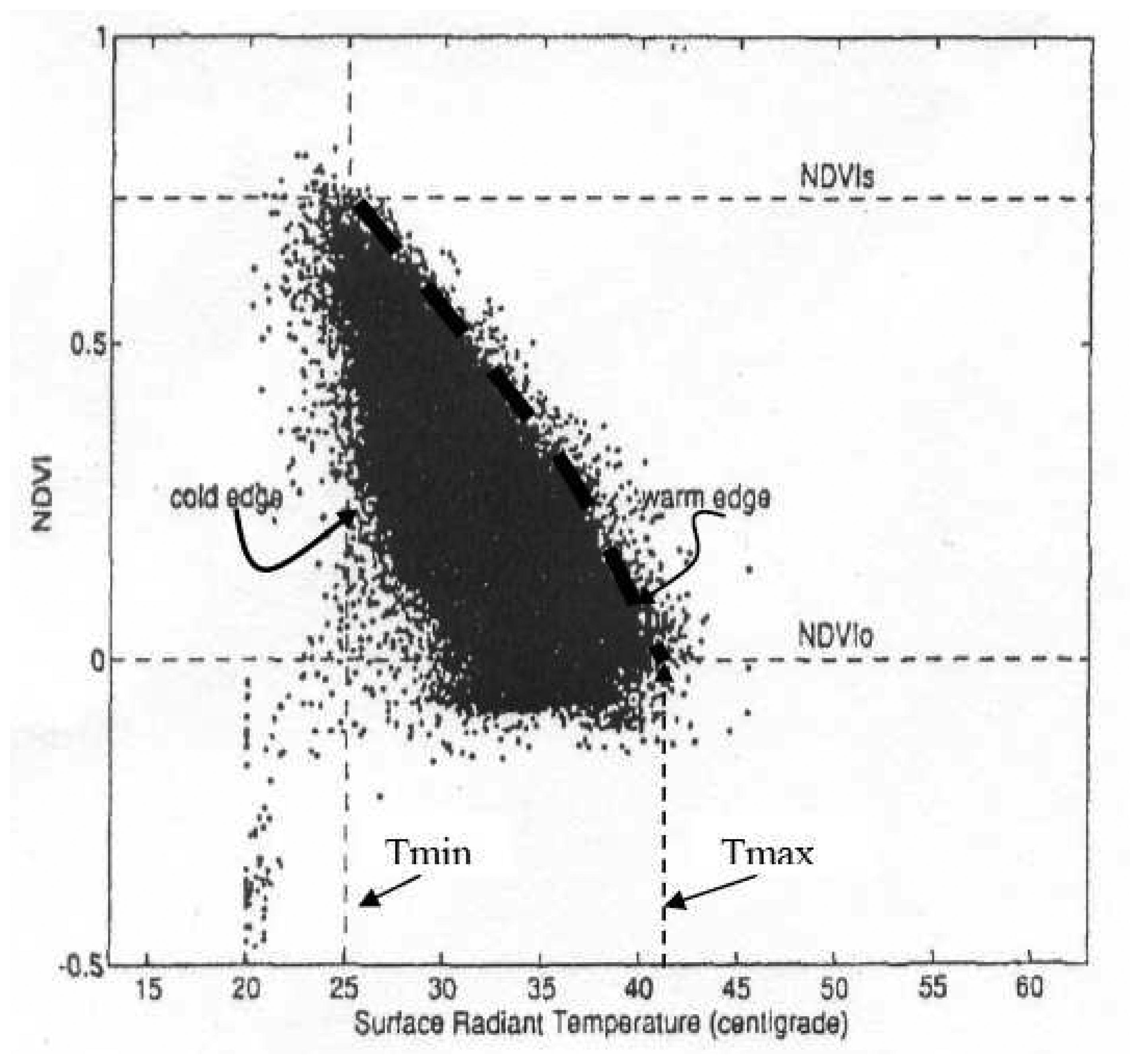
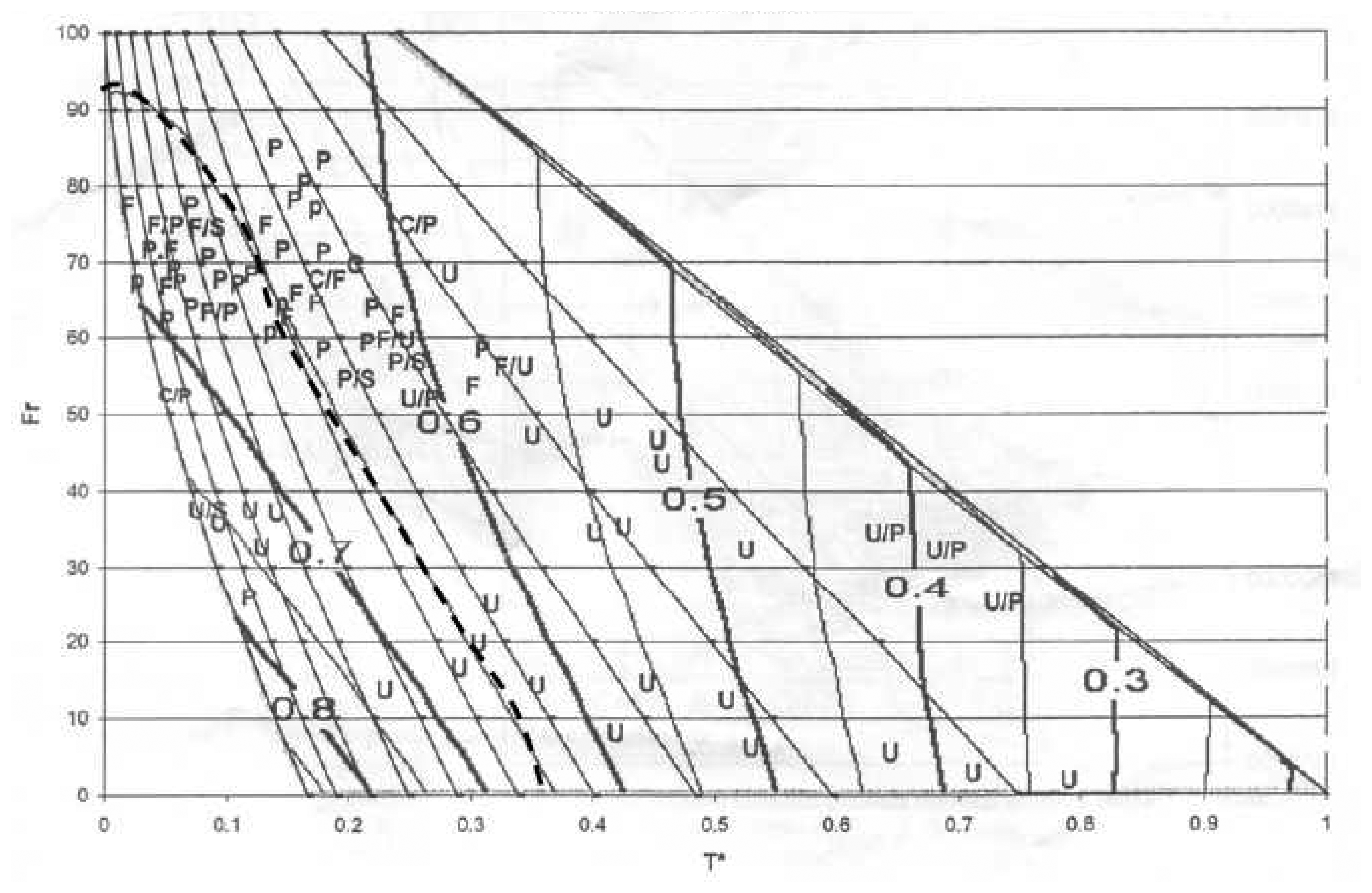
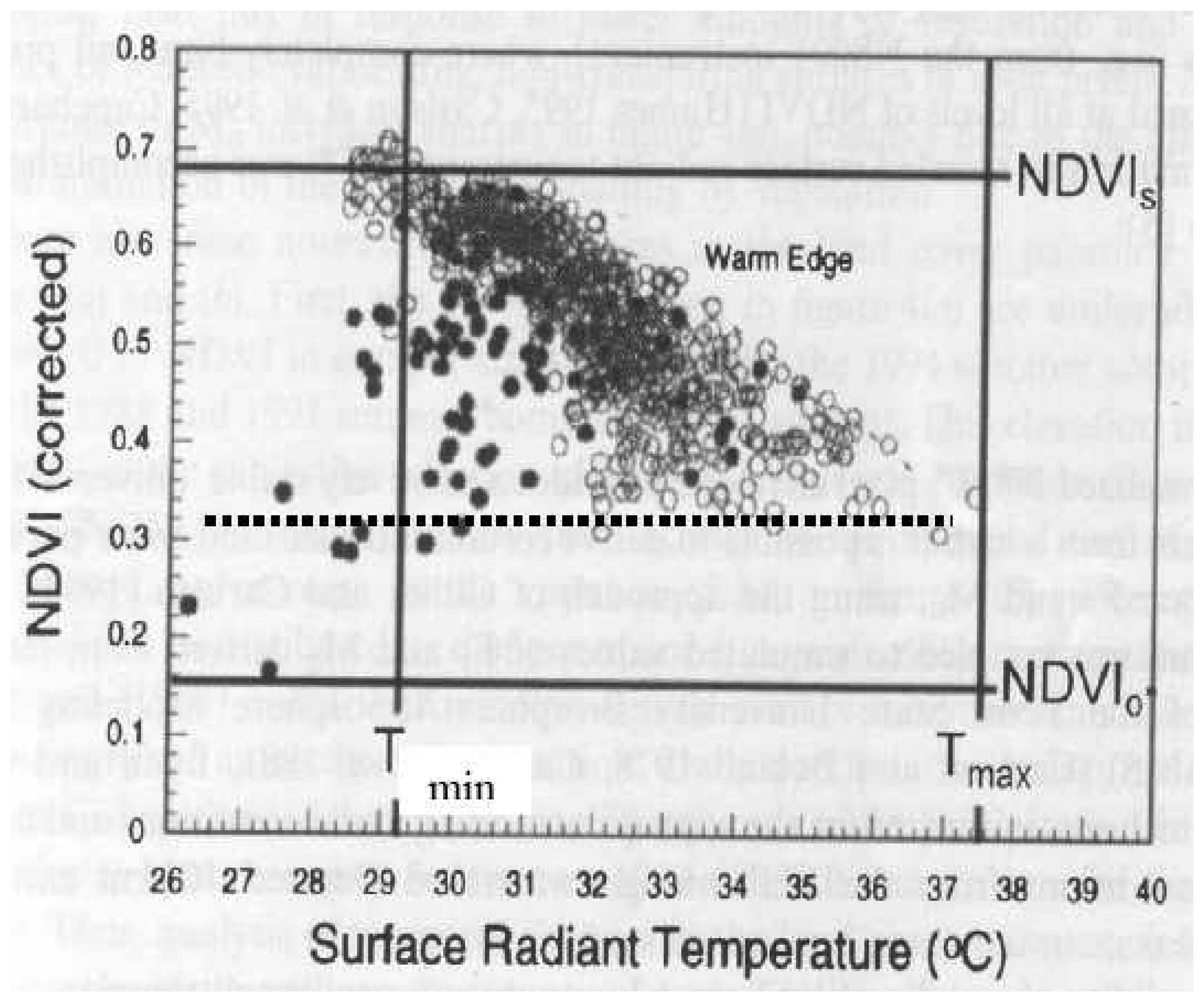
a) Observed properties of the triangle
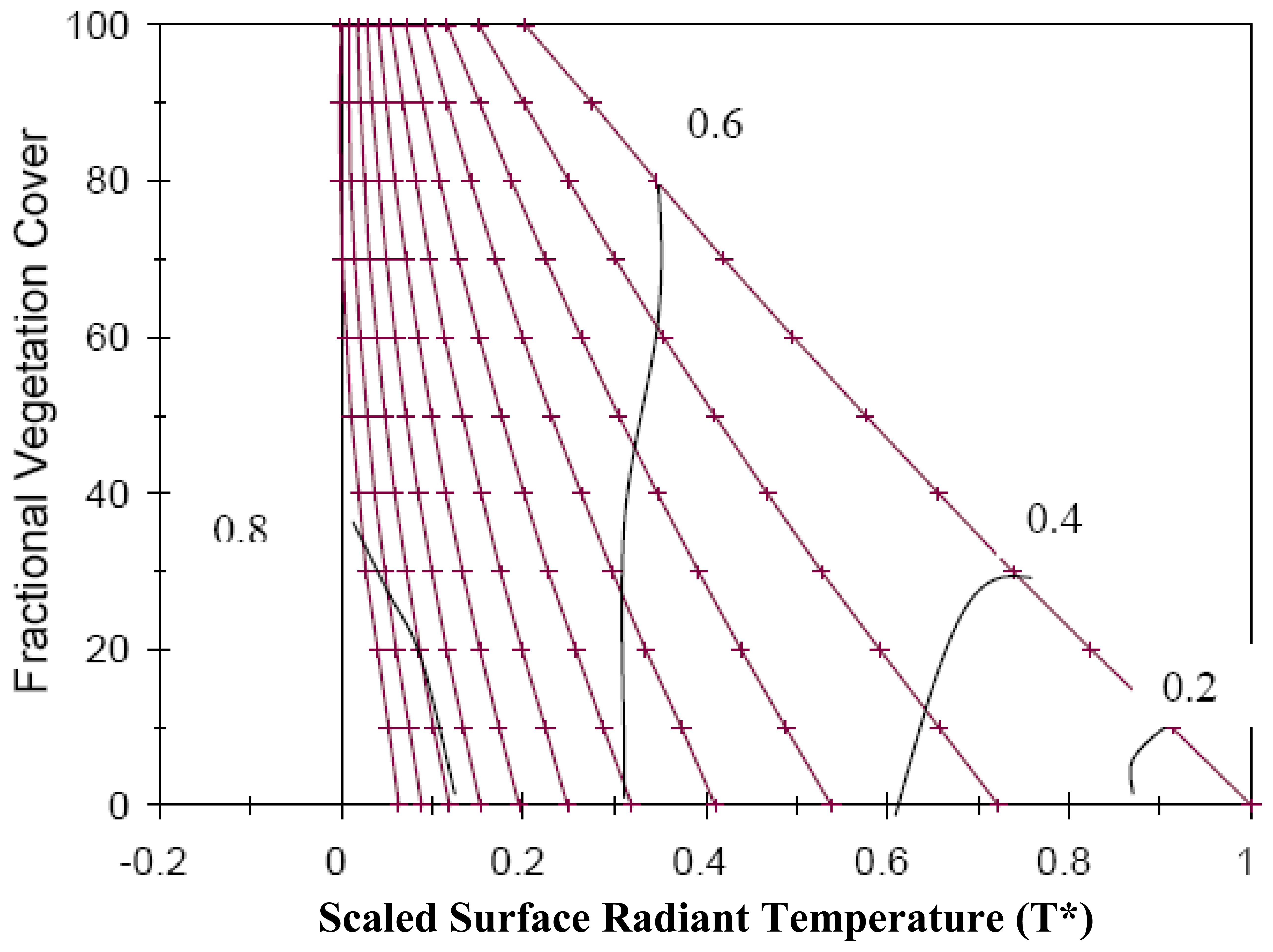
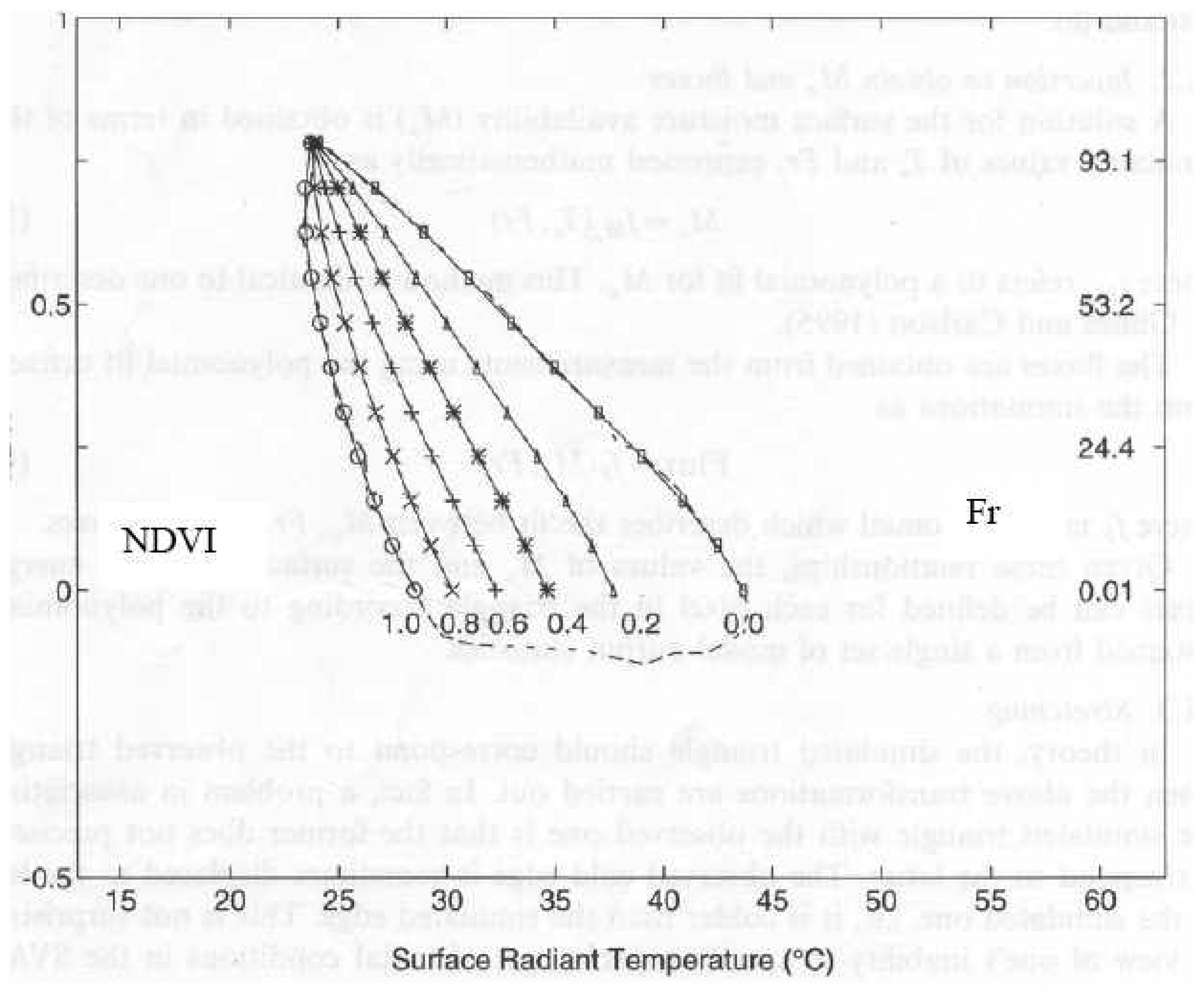
b) Modeling the triangle
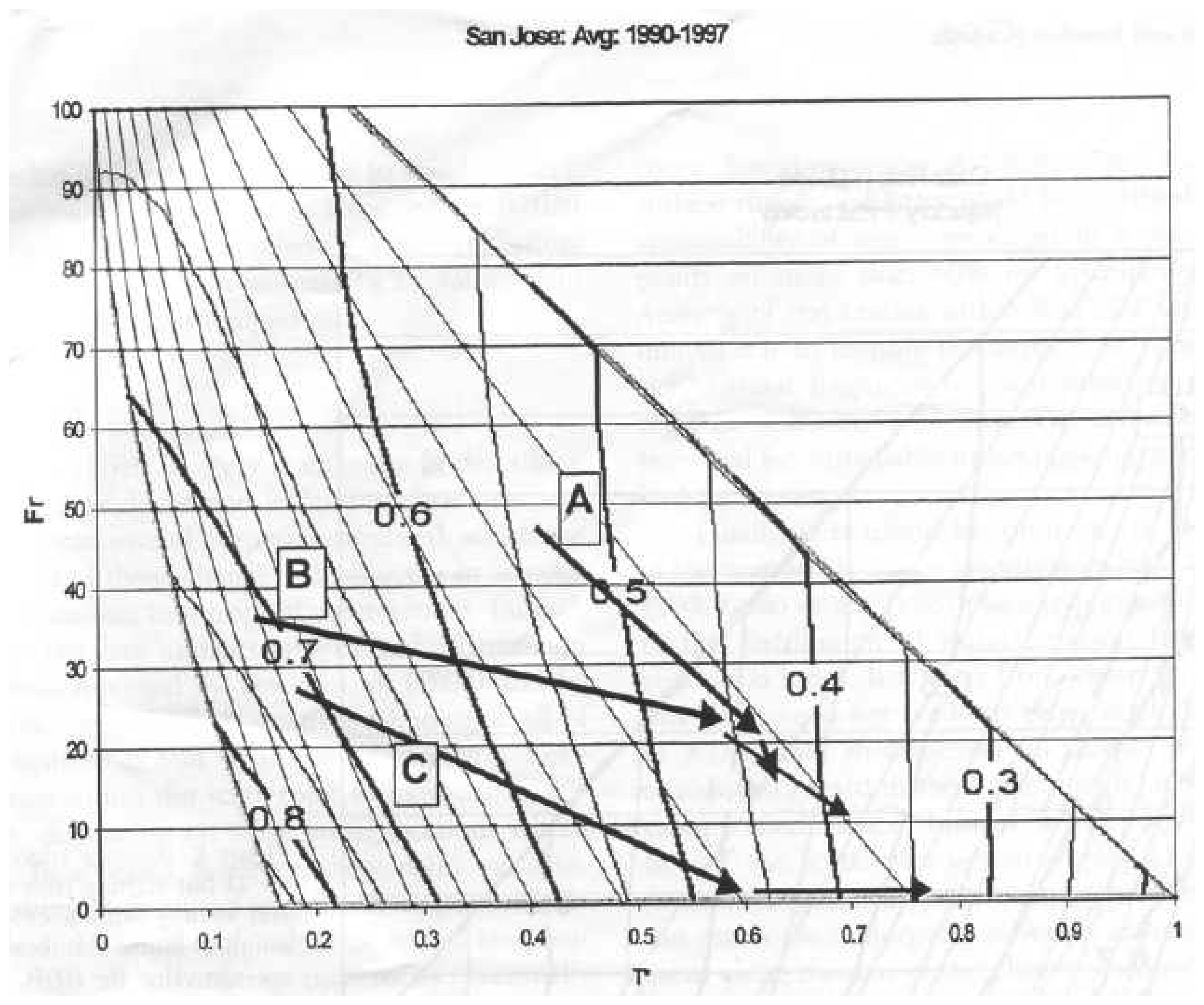
3. Practical applications
4. Qualitative Interpretation of the Triangle
5. Limitations of the Triangle Method Time
6. Summary
References
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) - 2.Validation. Journal of Hydrology 1998, 213, 198–212. [Google Scholar]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Allen, R.G. SEBAL for spatially distributed ET under actual management and growing conditions. ASCE Journal of Irrigation and Drainage Engineering 2005, 131, 85–93. [Google Scholar]
- Carlson, T.N.; Dodd, J.K.; Benjamin, S.G.; Cooper, J.N. Remote Estimation of Surface Energy Balance, Moisture Availability and Thermal Inertia. J. Appl. Meteor. 1981, 20, 67–87. [Google Scholar]
- Carlson, T.N.; Rose, F.G.; Perry, E.M. Regional Scale Estimates of Surface Moisture Availability from GOES Satellite. Agron. J. 1984, 76, 972–979. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A Method to Make Use of Thermal Infrared Temperature and NDVI measurements to Infer Surface Soil Water Content and Fractional Vegetation Cover. Remote Sensing Reviews 1994, 9, 161–173. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An Interpretation of Methodologies for Indirect Measurement of Soil-Water Content. Agricultural and Forest Meteorology 1995, 77, 191–205. [Google Scholar]
- Carlson, T.N.; Ripley, D.A.J. On the Relationship Between NDVI, Fractional Vegetation Cover and Leaf Area Index. Remote Sensing Environment 1997, 62, 241–252. [Google Scholar]
- Carlson, T.N.; Sanchez-Azofeifa, G.A. Satellite remote sensing of land use changes in and around San Jose, Costa Rica. Remote Sensing of Environment 1999, 70, 247–256. [Google Scholar]
- Carlson, T.N.; Arthur, A.T. The Impact of Land Use – Land Cover Changes Due to Urbanization on Surface Microclimate and Hydrology: A Satellite Perspective. Global and Planetary Change 2000, 25, 49–65. [Google Scholar]
- Chauhan, N.; Miller, S.S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: a microwave-optical/IR synergistic approach. International Journal of Remote Sensing 2003, 22, 4599–4622. [Google Scholar]
- Crombie, M.K.; Gillies, R.R.; Avidson, R.E.; Brookmeyer, P.; Weil, G.J.; Sultan, M.; Harb, M. An Application of Remotely Derived Climatological Fields for Risk Assessment of Vector-borne Diseases – A Spatial Study of Filariasis Prevalence in the Nile Delta, Egypt. Photogramm. Eng. Remote Sensing 1999, 65, 1401–1409. [Google Scholar]
- Gillies, R.R.; Carlson, T.N. Thermal Remote Sensing of Surface Soil Water Content with Partial Vegetation Cover for Incorporation into Climate Models. Journal of Applied Meteorology 1995, 34, 745–756. [Google Scholar]
- Gillies, R.R.; Carlson, T.N.; Cui, J.; Kustas, W.P.; Humes, K.S. A verification of the ‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface radiant temperature. International Journal of Remote Sensing 1997, 18, 3145–3166. [Google Scholar]
- Gillies, R.R.; Temesgen, B. Coupling Thermal Infrared and Visible Satellite Measurements to Infer Biophysical Variables at the Land Surface. In Thermal Remote Sensing in Land Surface Processes; Quattrochi, Luval, Eds.; CRC Press, 2004. [Google Scholar]
- Gutman, G.; Ignatov, A. The Derivation of the Green Vegetation Fraction from NOAA/AVHRR Data for Use in Numerical Weather Prediction Models. Int. J. of Remote Sensing 1998, 8, 1533–1543. [Google Scholar]
- Jiang, L.; Islam, S. A Methodology for Estimation of Surface Evapotranspiration over Large Areas using Remote Sensing Observations. Geophysical Research Letters 1999, 26, 2773–2776. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of Surface Evaporation Map over Southern Great Plains Using Remote Sensing Data. Water Resources Research 2001, 37, 329–340. [Google Scholar]
- Jiang, L.; Islam, S. An Intercomparison of Regional Latent Heat Flux Estimation using Remote Sensing Data. International Journal of Remote Sensing 2003, 24, 2221–2236. [Google Scholar]
- Jiang, L.; Islam, S.; Carlson, T.N. Uncertainties in latent heat flux measurement and estimation: implications for using a simplified approach with remote sensing data. Canadian Journal of Remote Sensing 2004, 30, 769–787. [Google Scholar]
- Kustas, W.P. Estimates of Evapotranspiration with a One- and Two-layer Model of Heat Transfer Over Partial Canopy Cover. J. Appl., Meteor. 1990, 29, 205–223. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Use of Remote Sensing for Evapotranspiration Monitoring Over Land Surfaces. Hydrological Sciences Journal 1996, 41, 495–516. [Google Scholar]
- Lambin, E.G.; Ehrlich, D. The Surface Temperature-vegetation Index Space for Land Cover and Land-cover Change Analysis. Int. J. Remote Sensing 1996, 17, 463–487. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces.; Wiley Series on Remote Sensing; 2004; p. 536 pp. [Google Scholar]
- Margulis, S.A.; Kim, J.; Hogue, T. A Comparison of the Triangle Retrieval and Variational Data Assimilation Methods for Surface Turbulent Flux Estimation. J. Hydromet. 2005, 6, 1063–1072. [Google Scholar]
- Mecikalski, J.R.; Diak, G.R.; Anderson, M.C.; Norman, J.M. Estimating Fluxes on Continental Scales using Remotely Sensed Data in an Atmospheric-land Exchange Model. J. Appl. Meteor. 1999, 38, 1352–1369. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Kustas, W.P.; Weltz, M.; Amer, S.A. Evaluation of Hydrologic Parameters in A Semiarid Rangeland Using Remotely-Sensed Spectral Data. Water Resources Research 1994, 30, 1287–1297. [Google Scholar]
- Nemani, R.R.; Running, S.W. Estimation of Regional Surface-Resistance to Evapotranspiration from NDVI and Thermal-IR AVHRR Data. Journal of Applied Meteorology 1989, 28, 276–284. [Google Scholar]
- Owen, T.W.; Carlson, T.N.; Gillies, R.R. An Assessment of satellite Remotely-sensed Land Cover Parameters in Quantitatively Describing the Climatic Effect of Urbanization. Int. J. Remote Sensing 1998, 19, 1663–1681. [Google Scholar]
- Petropoulis, G.P.; Wooster, M.J.; Drake, N.J. Investigating the Performance of a Coupled SVAT/Model Remote Sensing Method to Derive Spatially Explicit Maps of Land Atmosphere Energy Fluxes; Geophysical Research Abstracts, 0634, European Geosciences Union, 2006; ISBN: SRef ID: 1607-7962. [Google Scholar]
- Price, J.C. The Potential of Remotely Sensed Thermal Infrared Data to Infer Surface Soil Moisture and Evaporation. Water Resources Research 1980, 16, 787–795. [Google Scholar]
- Price, J.C. Estimation of Regional Scale Evapotranspiration through Analysis of Satellite thermal-infrared Data. IEEE Transactions on Geoscience and Remote Sensing 1982, GE-20, 286–292. [Google Scholar]
- Price, J.C. Using Spatial Context in Satellite Data to Infer Regional Scale Evapotranspiration. IEEE Transactions on Geoscience and Remote Sensing 1990, 28, 940–948. [Google Scholar]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sensing of Environment 1997, 60, 335–346. [Google Scholar]
- Ray, D.K.; Nair, U.S.; Welch, R.M.; Su, W.; Kikutchi, T. Influence of land use on the regional climate of southwest Australia. 13th Symposium on Global Change and Climate Variations and 16th Conference on Hydrology, Australia, Jan, 17, 2002; 2002. Available on http://ams.confex.com/ams/annual2002/techprogram/paper_29880.htm.
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sensing of Environment 2002, 79, 213–224. [Google Scholar]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Jensen, K.H. Combining the Triangle Methodl with Thermal Inertia to Estimate Regional Evapotanspiration – Applied to MSG-SEVIRI Data in the Senegal River Basin. Remote Sensing Environment 2007, in press. [Google Scholar]
- Seguin, B.; Itier, B. Using Midday Surface-Temperature to Estimate Daily Evaporation from Satellite Thermal Ir Data. International Journal of Remote Sensing 1983, 4, 371–383. [Google Scholar]
- Soer, G.J.R. Estimation of Regional Evapotranspiration and Soil Moisture Conditions using Remotely Sensed Crop Surface Temperatures. Remote Sensing Environment 1980, 9, 27–45. [Google Scholar]
- Stewart., J.B.; Kustas, W.P.; Humes, K.S.; Nichols, W.D.; Moran, M.S.; De Bruin, H.A.R. Sensible Heat Flux-Radiant Surface Temperature Relationship for Semiarid Areas. J. Appl. Meteor. 1994, 33, 1110–1117. [Google Scholar]
- Watson, K. Applications of Thermal Modeling in the Geological Interpretation of IR Images. Proceedings of the Seventh Int. Symposium of Remote Sensing of Environment. ERIM., Ann Arbor, MI. 1971; pp. 2017–2041. [Google Scholar]
- Wetzel, P.; Atlas, D.; Woodward, R. Determining Soil Moisture from Study. J. Climate and Applied Meteor. 1983, 23, 375–391. [Google Scholar]
| aij | j=0 | j=1 | j=2 | j=3 |
|---|---|---|---|---|
| i=0 | 2.058 | -1.644 | 0.850 | -0.313 |
| i=1 | -6.490 | 1.112 | -3.420 | -0.062 |
| i=2 | 7.618 | 3.494 | 10.869 | 4.831 |
| i=3 | -3.190 | -3.871 | -6.974 | -16.902 |
| aij | j=0 | j=1 | j=2 | j=3 |
| i=0 | 0.8106 | -0.5967 | 0.4049 | -0.0740 |
| i=1 | -0.8029 | 0.7537 | 0.0681 | 0.2302 |
| i=2 | 0.4866 | 1.2402 | -0.9489 | -0.8676 |
| i=3 | -0.3702 | -1.3943 | -0.7359 | 0.3860 |
| Edge | b | a1 | a2 | r2 | RMSE |
|---|---|---|---|---|---|
| (Warm Edge)Mo=0 | 1.001 | -0.892 | 0.075 | 1 | 0.0009 |
| (Cold Edge)Mo=1 | 0.216 | -0.366 | 0.149 | 1 | 0.0005 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Carlson, T. An Overview of the "Triangle Method" for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612-1629. https://doi.org/10.3390/s7081612
Carlson T. An Overview of the "Triangle Method" for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors. 2007; 7(8):1612-1629. https://doi.org/10.3390/s7081612
Chicago/Turabian StyleCarlson, Toby. 2007. "An Overview of the "Triangle Method" for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery" Sensors 7, no. 8: 1612-1629. https://doi.org/10.3390/s7081612
APA StyleCarlson, T. (2007). An Overview of the "Triangle Method" for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors, 7(8), 1612-1629. https://doi.org/10.3390/s7081612




