Magnetostrictive Microcantilever as an Advanced Transducer for Biosensors
Abstract
:1. Introduction
2. Experimental Details
2.1 Cantilever fabrication
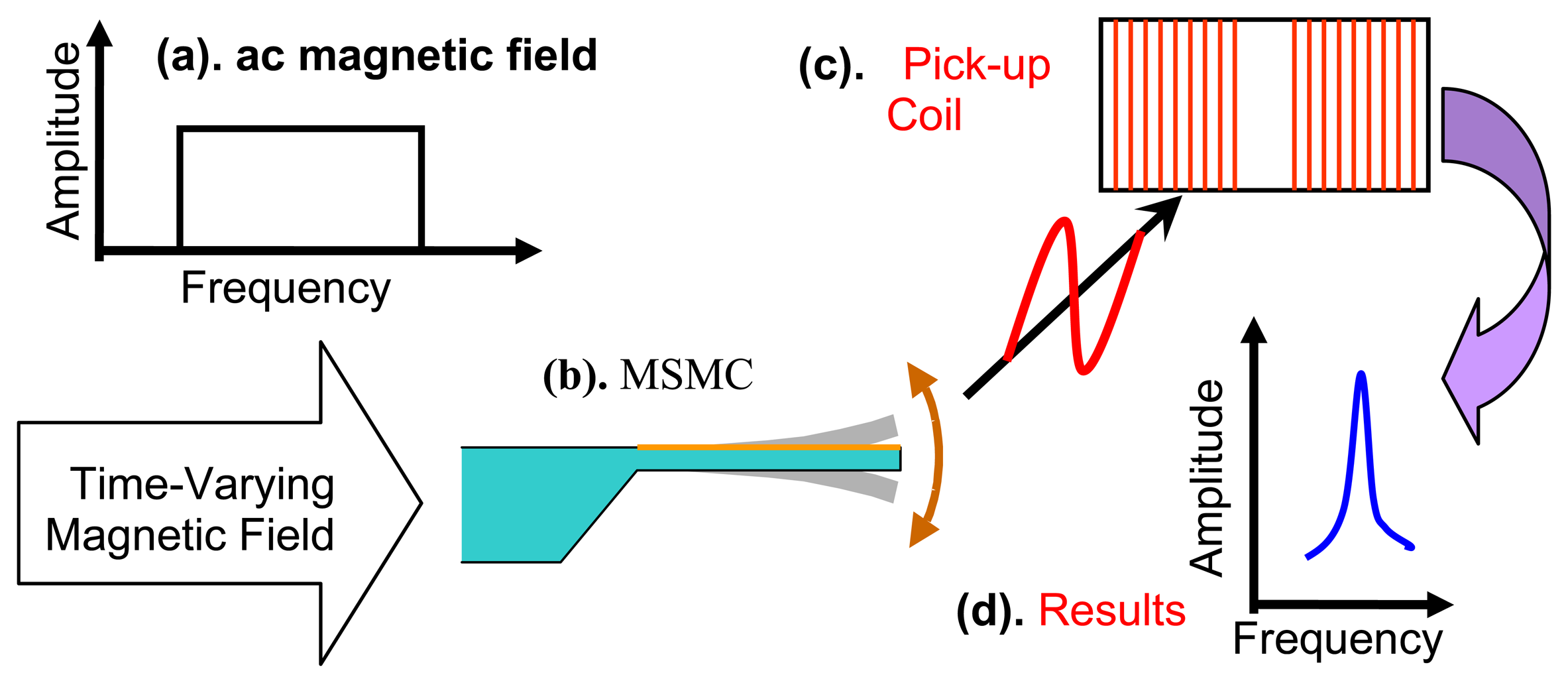
2.2 Operation principle
2.3 Set-up for measurement
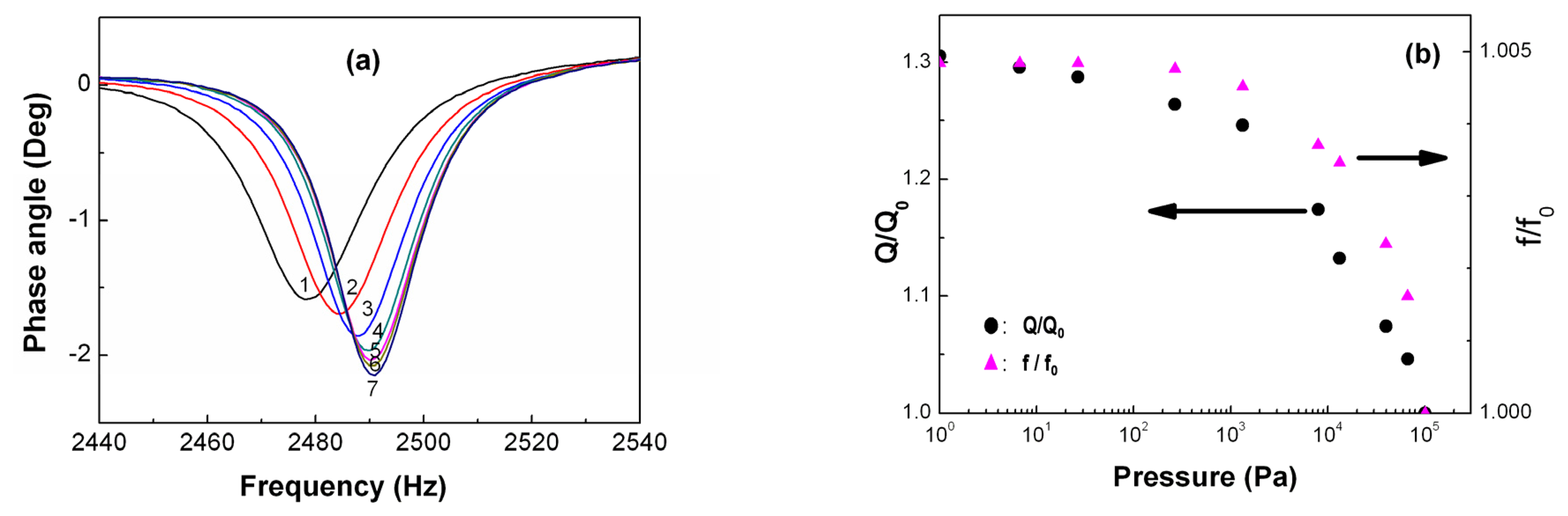
2.4 MSMC operated in different media
2.5 Phage and its immobilization
2.6 Real time detection of S. typhimurium cells in water
3. Results and Discussion
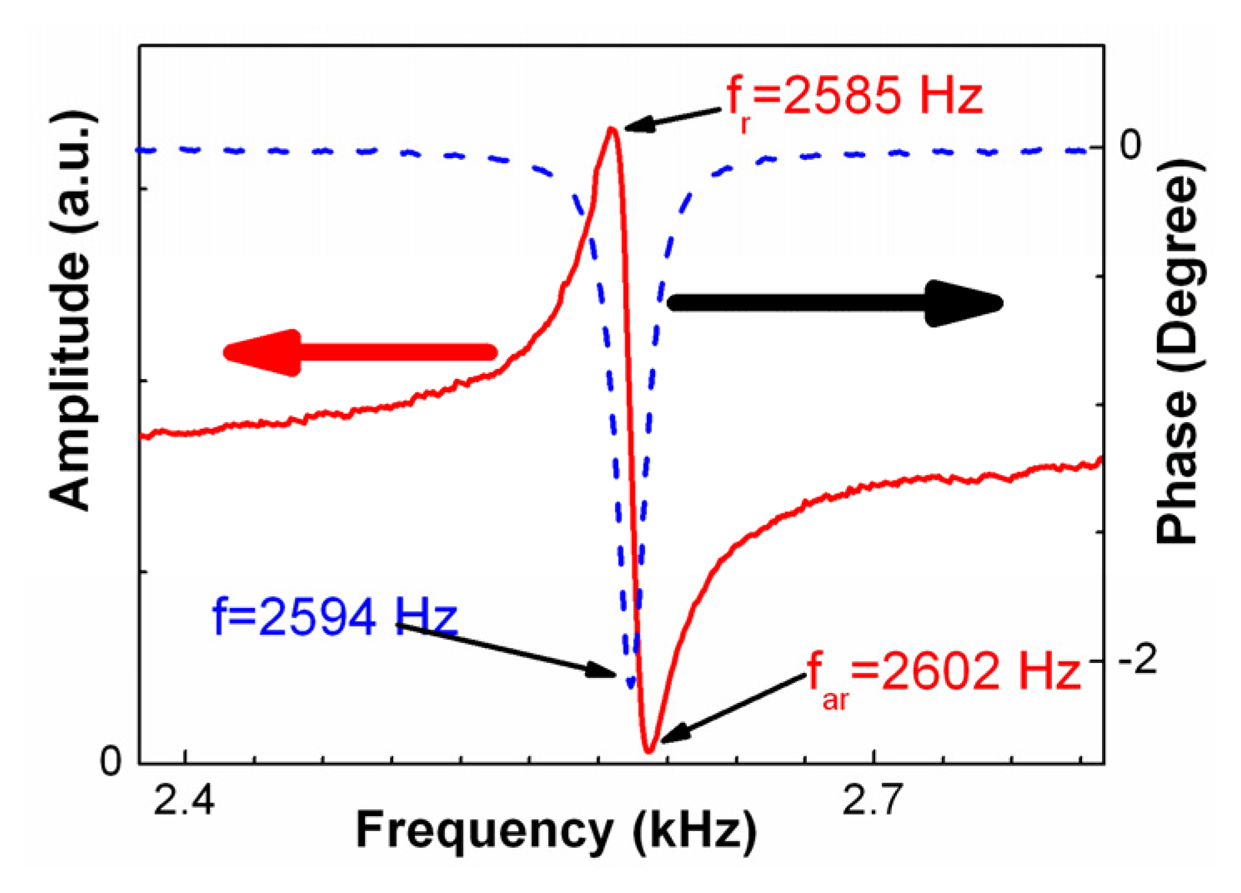
3.1 Resonance behavior of MSMCs operated in different media
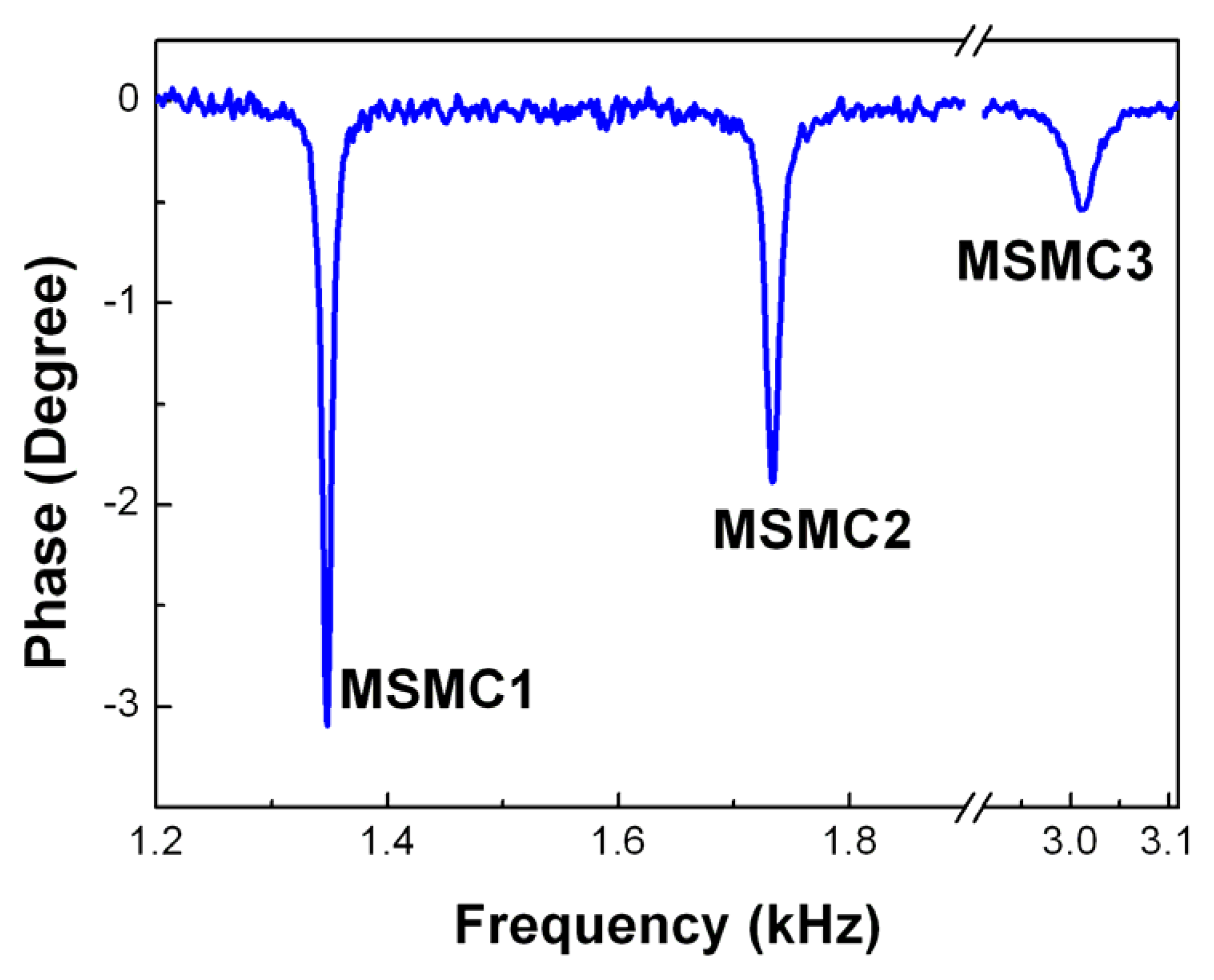
3.2 MSMC Array
3.3 Detection of S. typhimurium in water
Conclusions
Acknowledgments
References
- He, F. J.; Geng, Q.; Zhu, W.; Nie, L. H.; Yao, S. Z.; Meifeng, C. Rapid detection for E. coli using a separated electrode piezoelectric crystal sensor. Anal. Chim. Acta 1994, 289, 313–319. [Google Scholar]
- Dhayal, B.; Henne, W. A.; Doorneweerd, D. D.; Reifenberger, R. G.; Low, P. S. Detection of Bacillus subtilis spores using peptide-functionalized cantilever arrays. Journal of the American Chemical Society 2006, 128(11), 3716–3721. [Google Scholar]
- Kim, R.; Mulchandani, A. Affinity biosensors: techniques and protocols; Humana Press: Totowa, NJ, 1998. [Google Scholar]
- Petrenko, V.A.; Vodyanoy, V.J. Phage display for detection of biological threat agents. The Journal of Microbiological Methods 2003, 53(2), 243–252. [Google Scholar]
- Ballantine, D. S.; White, R. M.; Martin, S. J.; Ricco, A. J.; Frye, G. C.; Zellers, E. T.; Wohltjen, H. Acoustic wave sensors: theory, design and physico-chemical applications; Academic Press: Boston, 1997. [Google Scholar]
- Yang, X.; Li, Z. M.; Odum, L.; Cheng, Z.-Y.; Xu, Z. Piezoelectric diaphragm as a high performance biosensor platform. Applied Physics Letters 2006, 89(22), 223508. [Google Scholar]
- Grate, J. W.; Martin, S. J.; White, R. M. Acoustic wave microsensors. Analytical Chemistry 1993, 65(21), 940A–948A. [Google Scholar]
- Ali, Z. Acoustic wave mass sensors. Journal of Thermal Analysis and Calorimetry 1999, 55(2), 397–412. [Google Scholar]
- Li, S. Q.; Orona, L.; Li, Z. M.; Cheng, Z.-Y. Biosensor based on magnetostrictive microcantilever. Applied Physics Letters 2006, 88(7), 073507. [Google Scholar]
- Tamarin, O.; Dejous, C.; Rebiere, D.; Pistre, J.; Comeau, S.; Moynet, D.; Bezian, J. Study of acoustic Love wave devices for real time bacteriophage detection. Sensors and Actuators B-Chemical 2003, 91, 275–284. [Google Scholar]
- Su, X. D.; Low, S.; Kwang, J.; Chew, V. H. T.; Li, S. F. Y. Piezoelectric quartz crystal based veterinary diagnosis for Salmonella enteritidis infection in chicken and egg. Sensors and Actuators B-Chemical 2001, 75, 29–35. [Google Scholar]
- Lavrik, N. V.; Sepaniak, M. J.; Datskos, P. G. Cantilever transducers as a platform for chemical and biological sensors. Review of Scientific Instruments 2004, 75(7), 2229–2253. [Google Scholar]
- Hierlemann, A.; Baltes, H. CMOS-based chemical microsensors. Analyst 2003, 128, 15–28. [Google Scholar]
- Ziegler, C. Cantilever-based biosensors. Analytical and Bioanalytical Chemistry 2004, 379(7-8), 946–959. [Google Scholar]
- Yi, J. W.; Shih, W. Y.; Shih, W. H. Effect of length, width, and mode on the mass detection sensitivity of piezoelectric unimorph cantilevers. Journal of Applied Physics 2002, 91, 1680–1686. [Google Scholar]
- Lavrik, N. V.; Datskos, P. G. Femtogram mass detection using photothermally actuated nanomechanical resonator. Applied Physics Letters 2003, 82(16), 2697–2699. [Google Scholar]
- Ilic, B.; Czaplewski, D.; Zalalutdinov, M.; Craighead, H. G.; Neuzil, P.; Campagnolo, C.; Batt, C. Single cell detection with micromechanical oscillators. Journal of Vacuum Science and Technology B: Microelectronics and Nanometer Structures 2001, 19(6), 2825–2828. [Google Scholar]
- Carrascosa, L. G.; Moreno, M.; Alvarez, M.; Lechaga, L. M. Nanomechanical biosensors: A new sensing tool. TrAC - Trends in Analytical Chemistry 2006, 25(3), 196–206. [Google Scholar]
- Raiteri, R.; Grattarola, M.; Butt, H. J.; Skladal, P. Micromechanical cantilever-based biosensors. Sensors and Actuators, B: Chemical 2001, 79(2-3), 115–126. [Google Scholar]
- Burg, T. P.; Godin, M.; Knudsen, S. M.; Shen, W.; Carlson, G.; Foster, J. S.; Babcock, K.; Manalis, S. R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446(7139), 1066–1069. [Google Scholar]
- Moulin, A. M.; O'Shea, S. J.; Welland, M. E. Microcantilever-based biosensors. Ultramicroscopy 2000, 82(1), 23–31. [Google Scholar]
- Bunde, R. L.; Jarvi, E. J.; Rosentreter, J. J. Piezoelectric quartz-crystal biosensors. Talanta 1998, 46(6), 1223–1236. [Google Scholar]
- Merhaut, J. Theory of Electroacoustics; Gerber, R., Ed.; McGRaw-Hill Inc.: New York, 1981. [Google Scholar]
- Petrenko, V. A.; Smith, G. P.; Gong, X.; Quinn, T. A library of organic landscapes on filamentous phage. Protein Eng. 1996, 9, 797–801. [Google Scholar]
- Sorokulova, I.B.; Olsen, E.V.; Chen, I-H.; Fiebor, B.; Barbaree, J.M.; Vodyanoy, V.J.; Chin, B.A.; Petrenko, V.A. Landscape Phage Probes for Salmonella typhimurium. The Journal of Microbiological Methods 2005, 63(1), 55–72. [Google Scholar]
- Olsen, E.V.; Sorokulova, I.B.; Petrenko, V.A.; Chen, I-H.; Barbaree, J.M.; Vodyanoy, V.J. Affinity-selected filamentous bacteriophage as a probe for acoustic wave biodetectors of. Salmonella typhimurium. Biosensors and Bioelectronics 2006, 21, 1434–1442. [Google Scholar]
- Newwell, W.E. Miniaturization of tuning forks. Science 1968, 161, 1320–1326. [Google Scholar]
- Lee, J. H.; Lee, S. T.; Yao, C. M.; Fan, W. L. Comments on the size effect on the microcantilever quality factor in free air space. J. Micromech. Microeng 2007, 17, 139–146. [Google Scholar]
- Benenson, W.; Harris, J.W.; Stocker, H.; Lutz, H. Handbook of Physics; Springer-Verlag: New York, 2002; p. 274. [Google Scholar]
- Chen, G. Y.; Warmack, R. J.; Thundat, T.; Allison, D. P.; Huang, A. Resonance response of scanning force microscopy cantilevers. Review of Scientific Instruments 1994, 65(8), 2532–2537. [Google Scholar]
- Weigert, S.; Dreire, M.; Hegner, M. Frequency shifts of cantilevers vibrating in various media. Applied Physics Letters 1996, 69(19), 2834–2837. [Google Scholar]


| Fundamental Mode (n=0) | First Mode (n=1) | |||||
|---|---|---|---|---|---|---|
| Air | Water | Ethanol | Air | Water | Ethanol | |
| Resonance frequency (Hz) | 1885 | 871 | 907 | 11912 | 6915 | 6182 |
| Q value | 191 | 19 | 9 | 265 | 38 | 27 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Fu, L.; Li, S.; Zhang, K.; Chen, I.-H.; Petrenko, V.A.; Cheng, Z. Magnetostrictive Microcantilever as an Advanced Transducer for Biosensors. Sensors 2007, 7, 2929-2941. https://doi.org/10.3390/S7112929
Fu L, Li S, Zhang K, Chen I-H, Petrenko VA, Cheng Z. Magnetostrictive Microcantilever as an Advanced Transducer for Biosensors. Sensors. 2007; 7(11):2929-2941. https://doi.org/10.3390/S7112929
Chicago/Turabian StyleFu, Liling, Suiqiong Li, Kewei Zhang, I-Hsuan Chen, Valery. A. Petrenko, and Zhongyang Cheng. 2007. "Magnetostrictive Microcantilever as an Advanced Transducer for Biosensors" Sensors 7, no. 11: 2929-2941. https://doi.org/10.3390/S7112929
APA StyleFu, L., Li, S., Zhang, K., Chen, I.-H., Petrenko, V. A., & Cheng, Z. (2007). Magnetostrictive Microcantilever as an Advanced Transducer for Biosensors. Sensors, 7(11), 2929-2941. https://doi.org/10.3390/S7112929




