A MEMS-based Air Flow Sensor with a Free-standing Micro-cantilever Structure
Abstract
:1. Introduction
2. Design
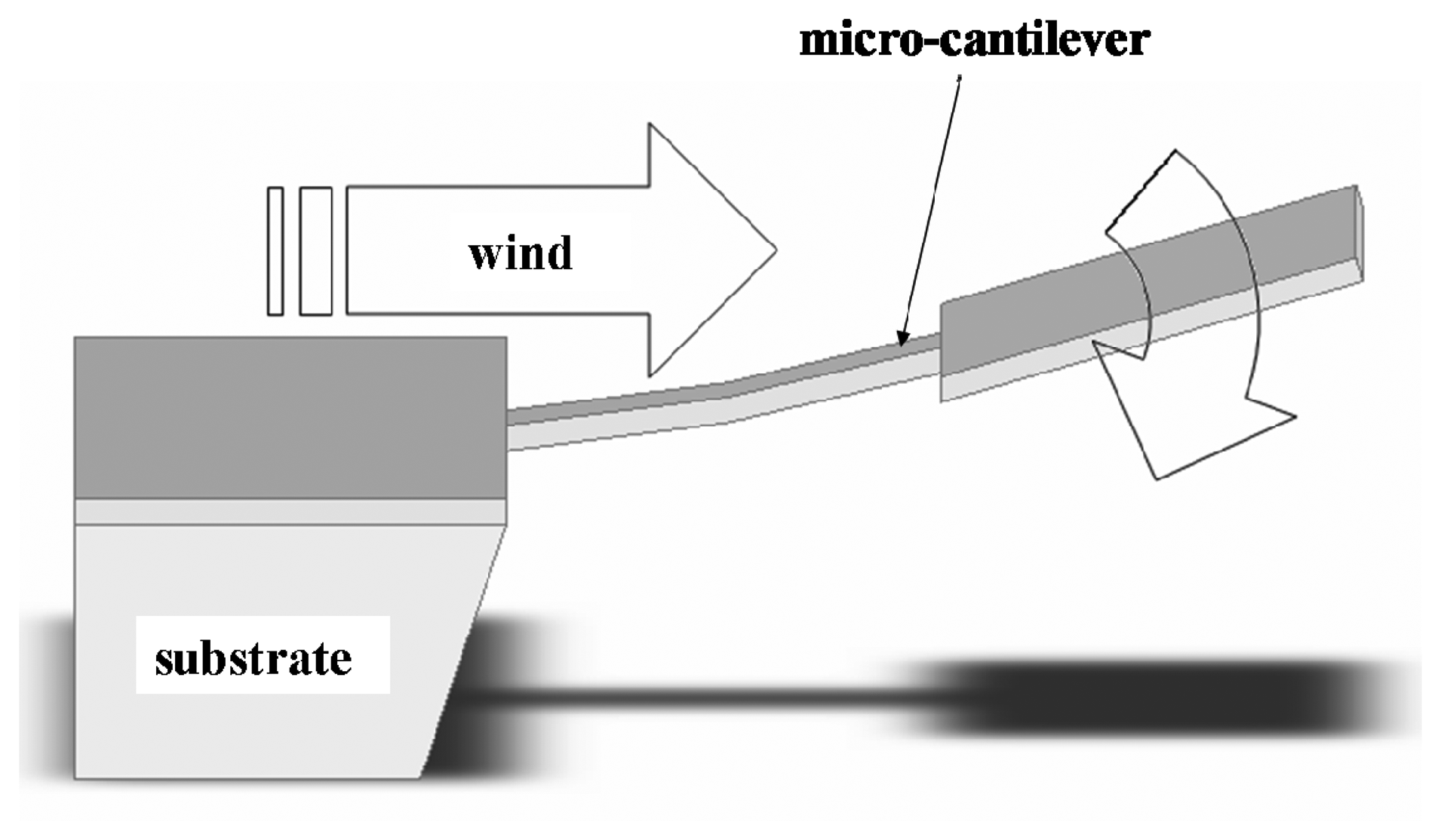
2.1. Sensing principle
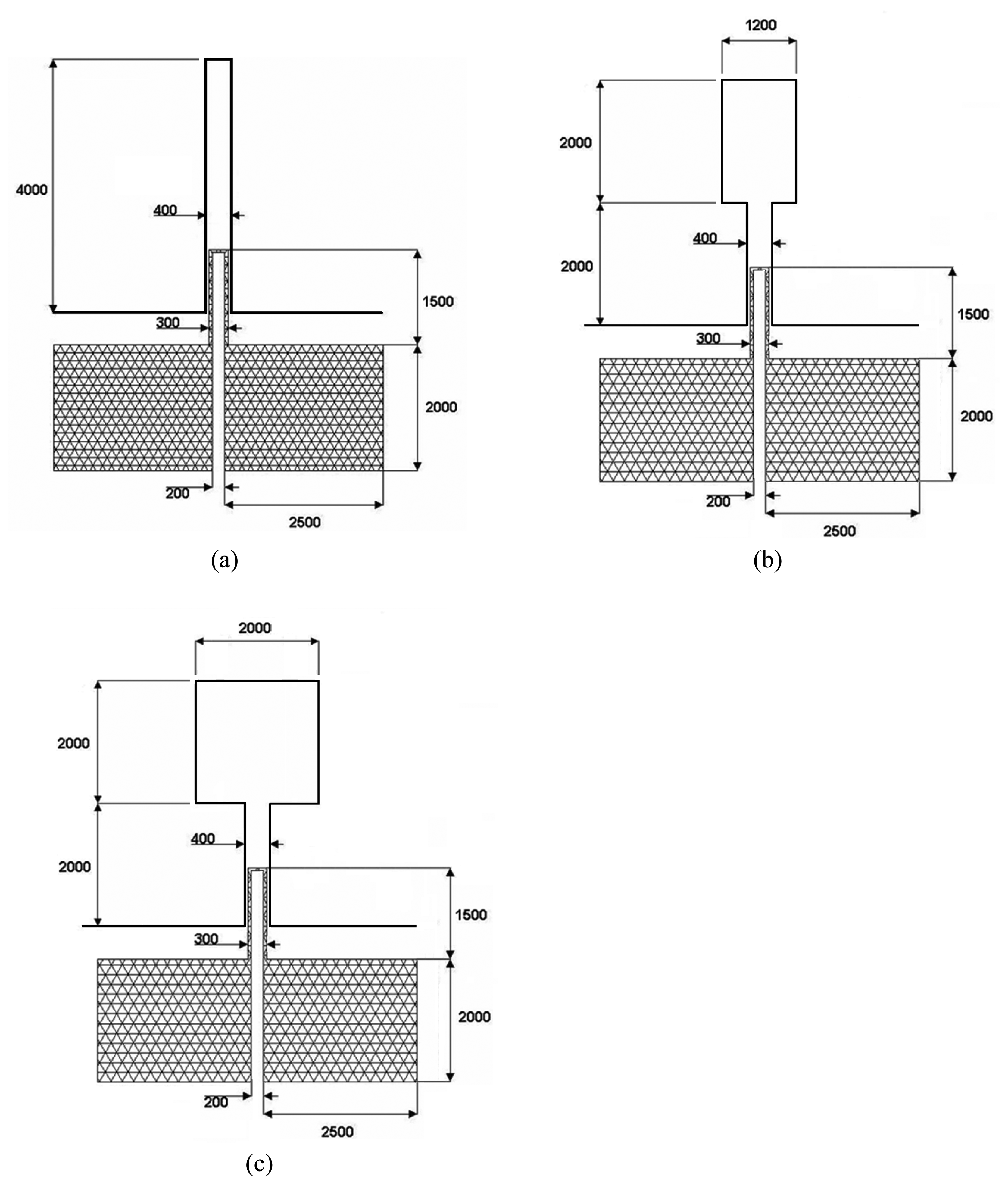
2.2. Cantilever beam dimensions
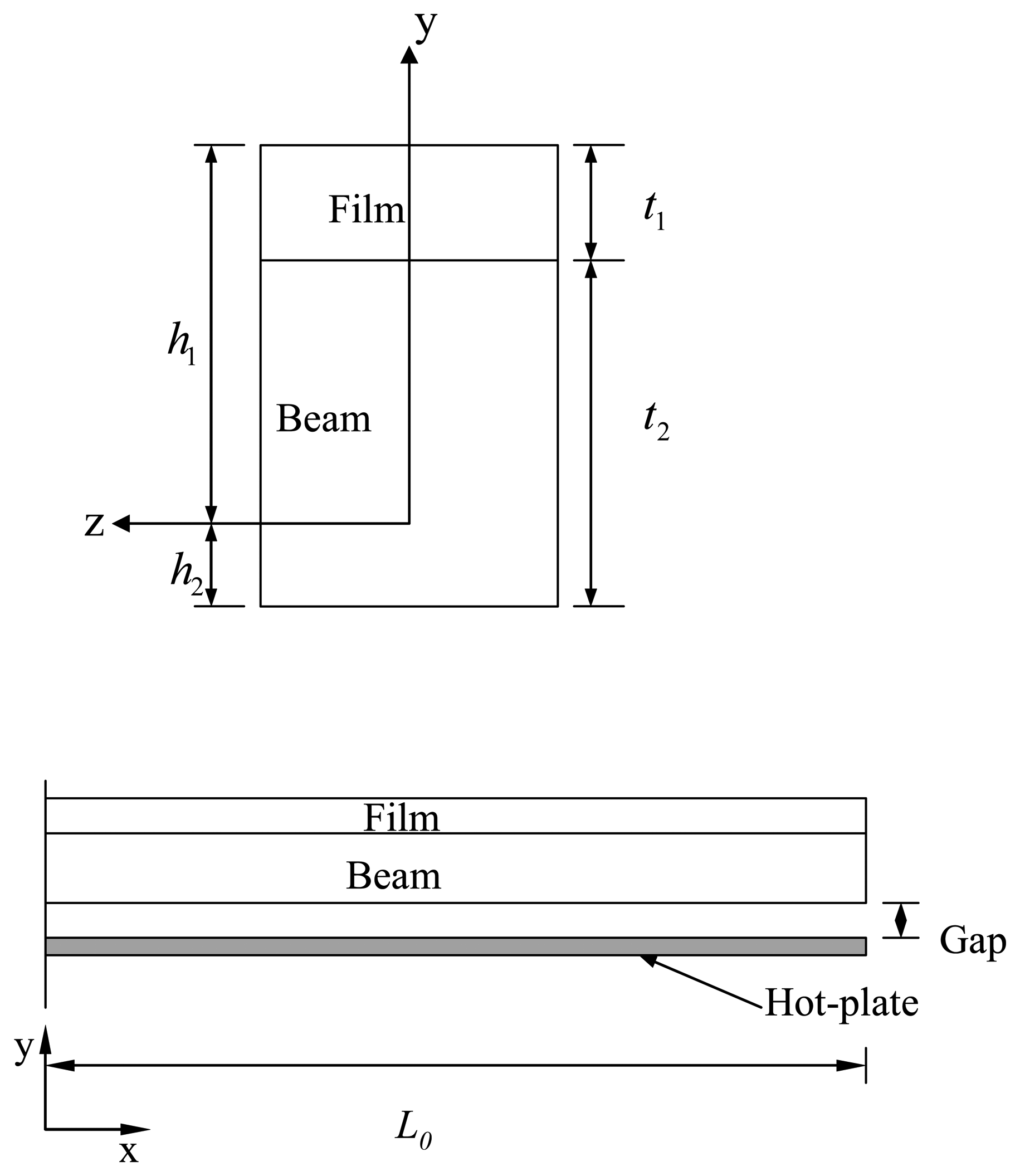
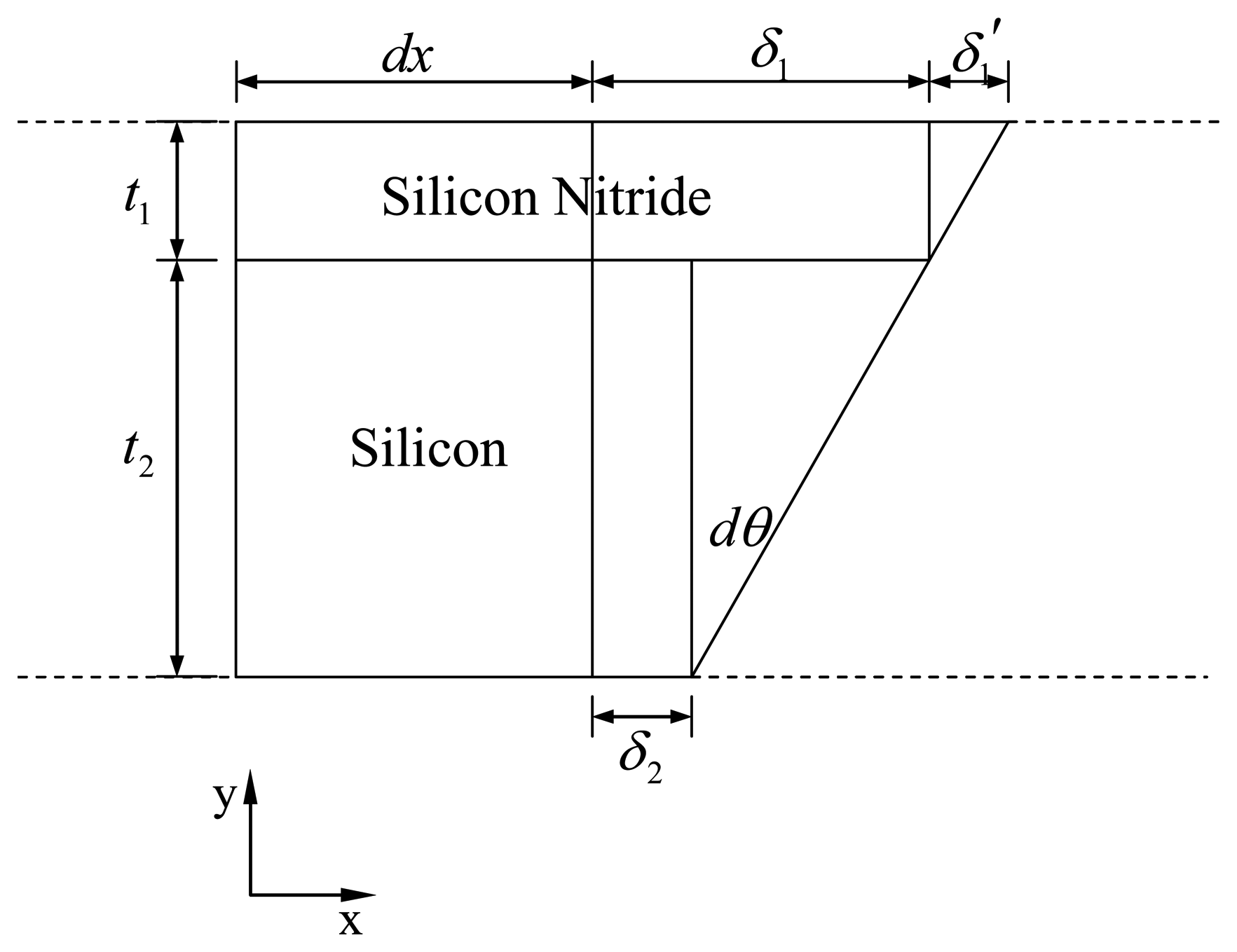
2.3. Cantilever deflection induced by thermal stress
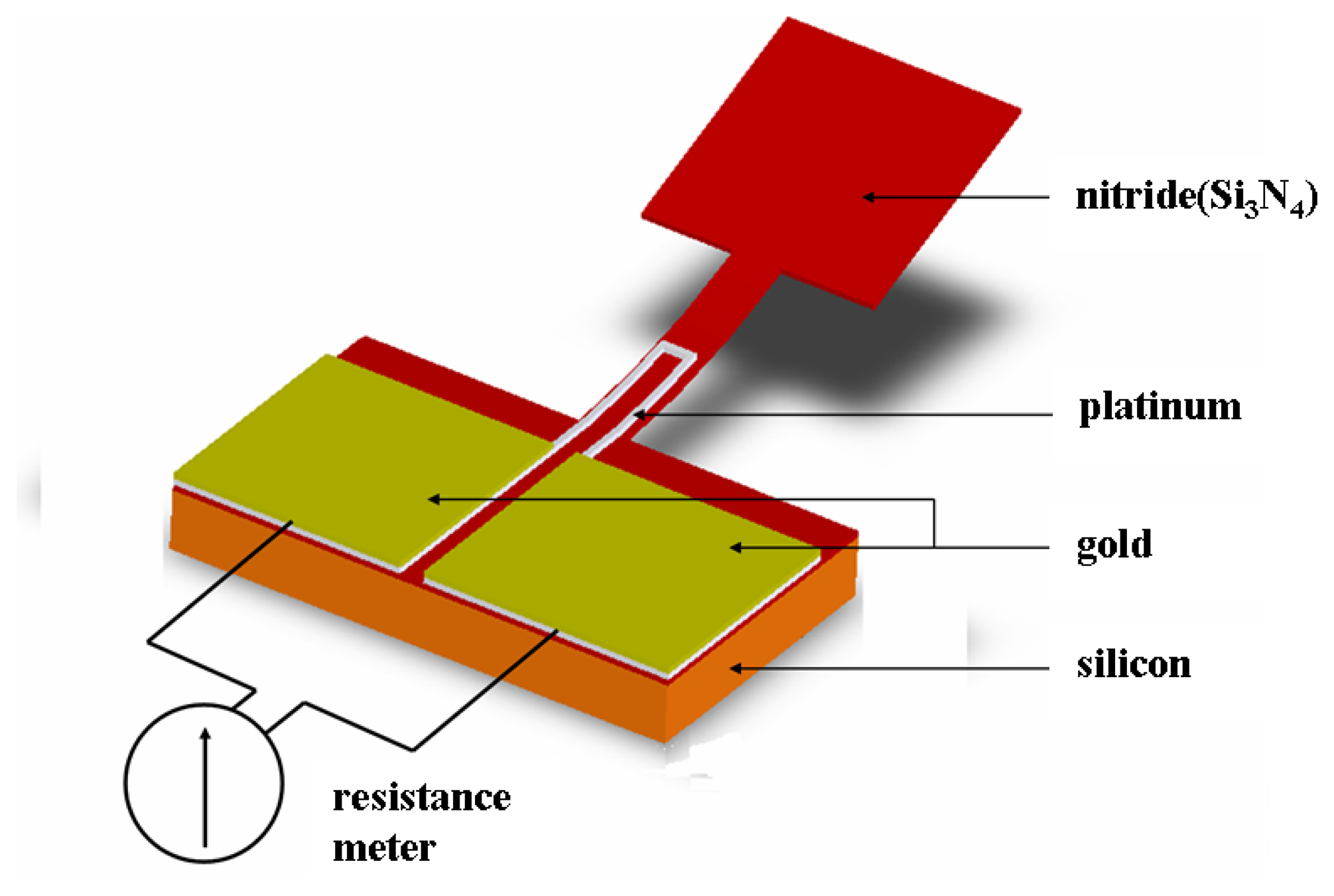
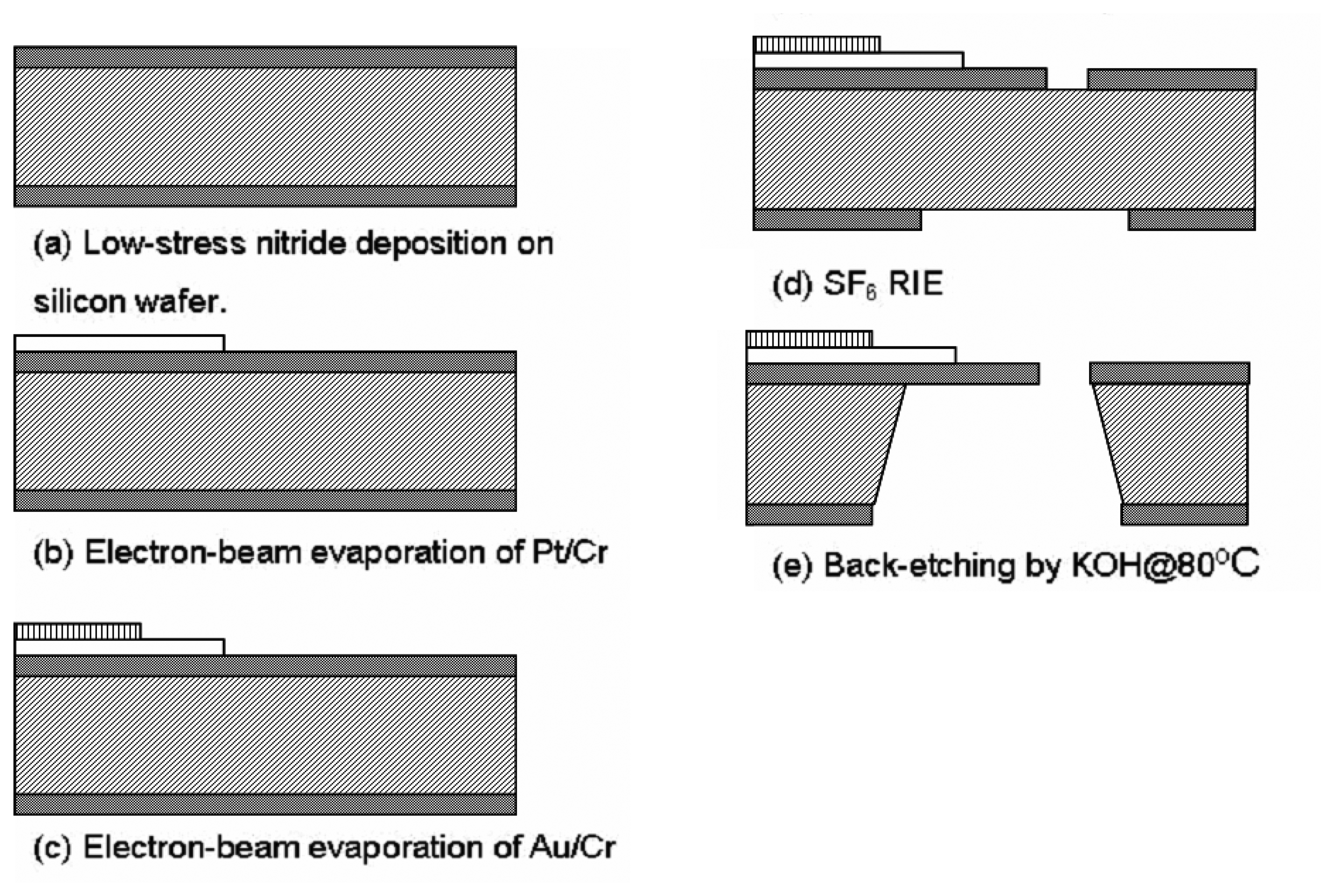
3. Fabrication
4. Results and Discussion
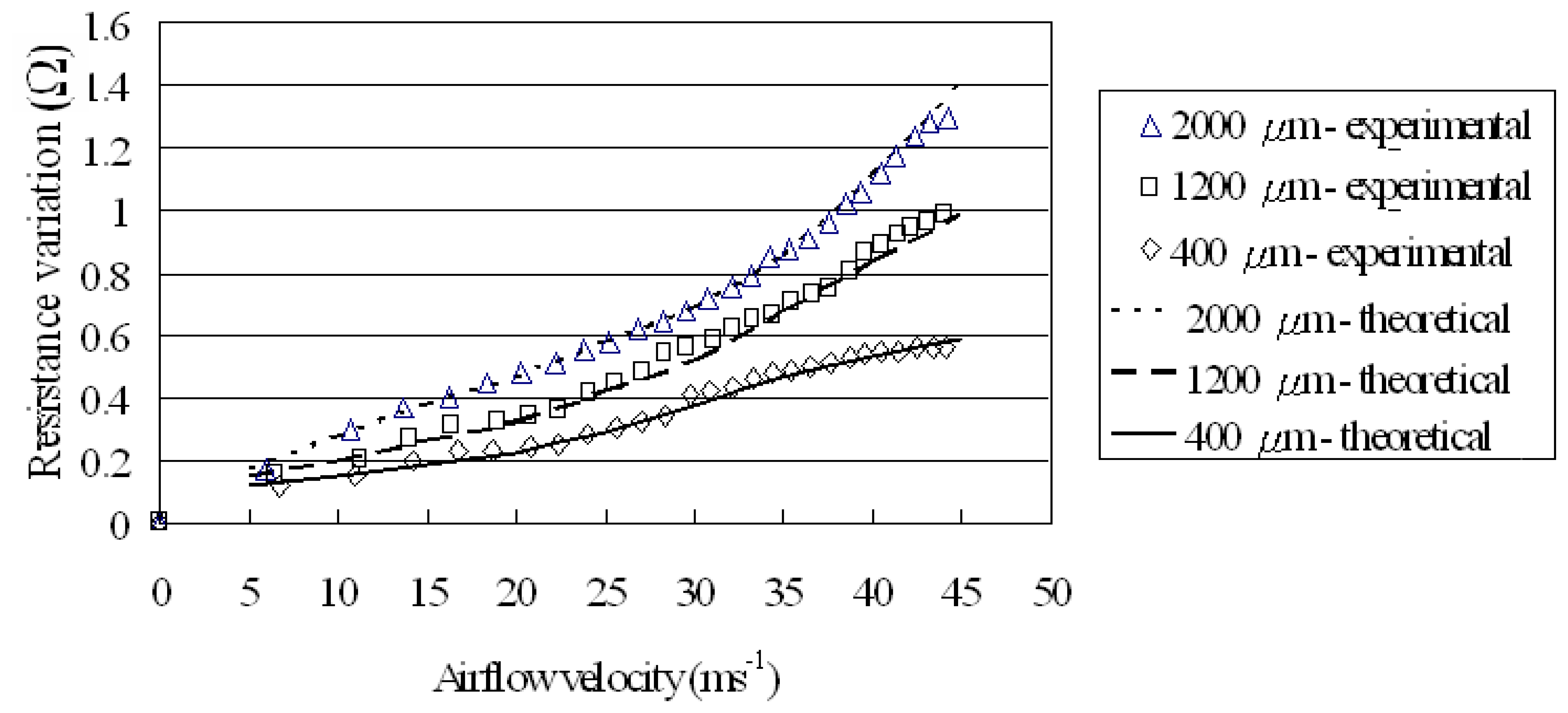
4.1. Sensitivity of gas flow sensors
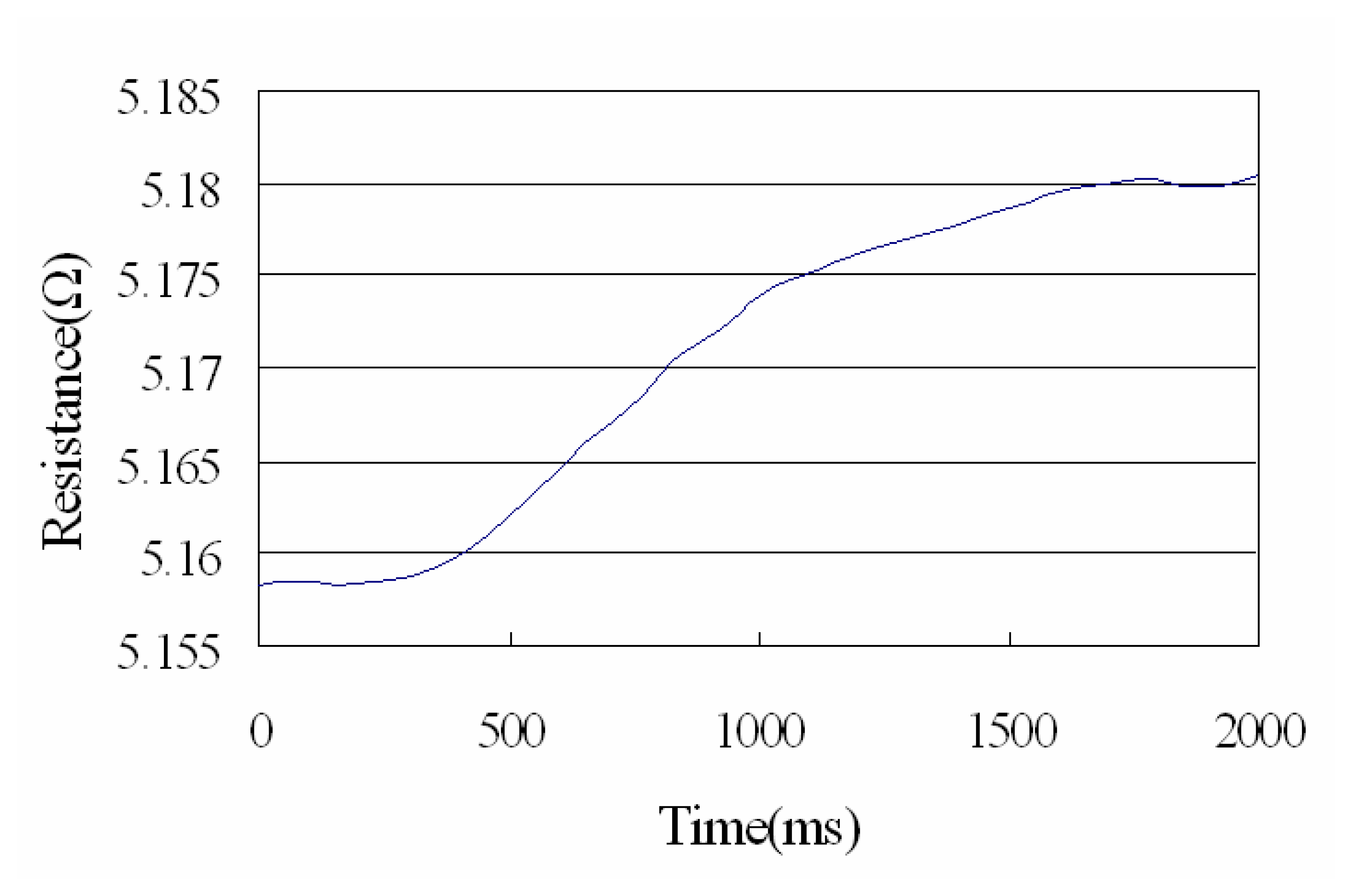
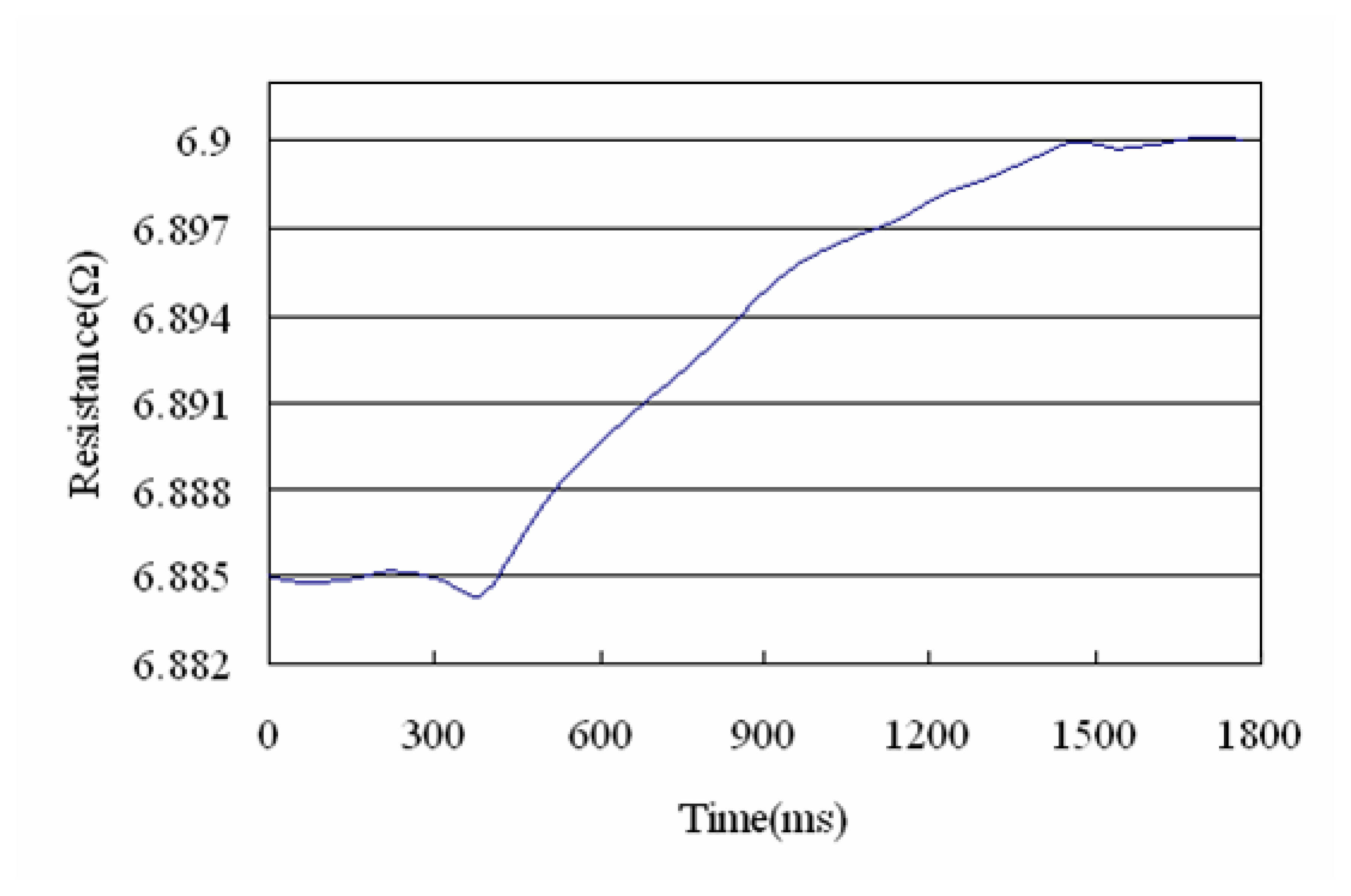
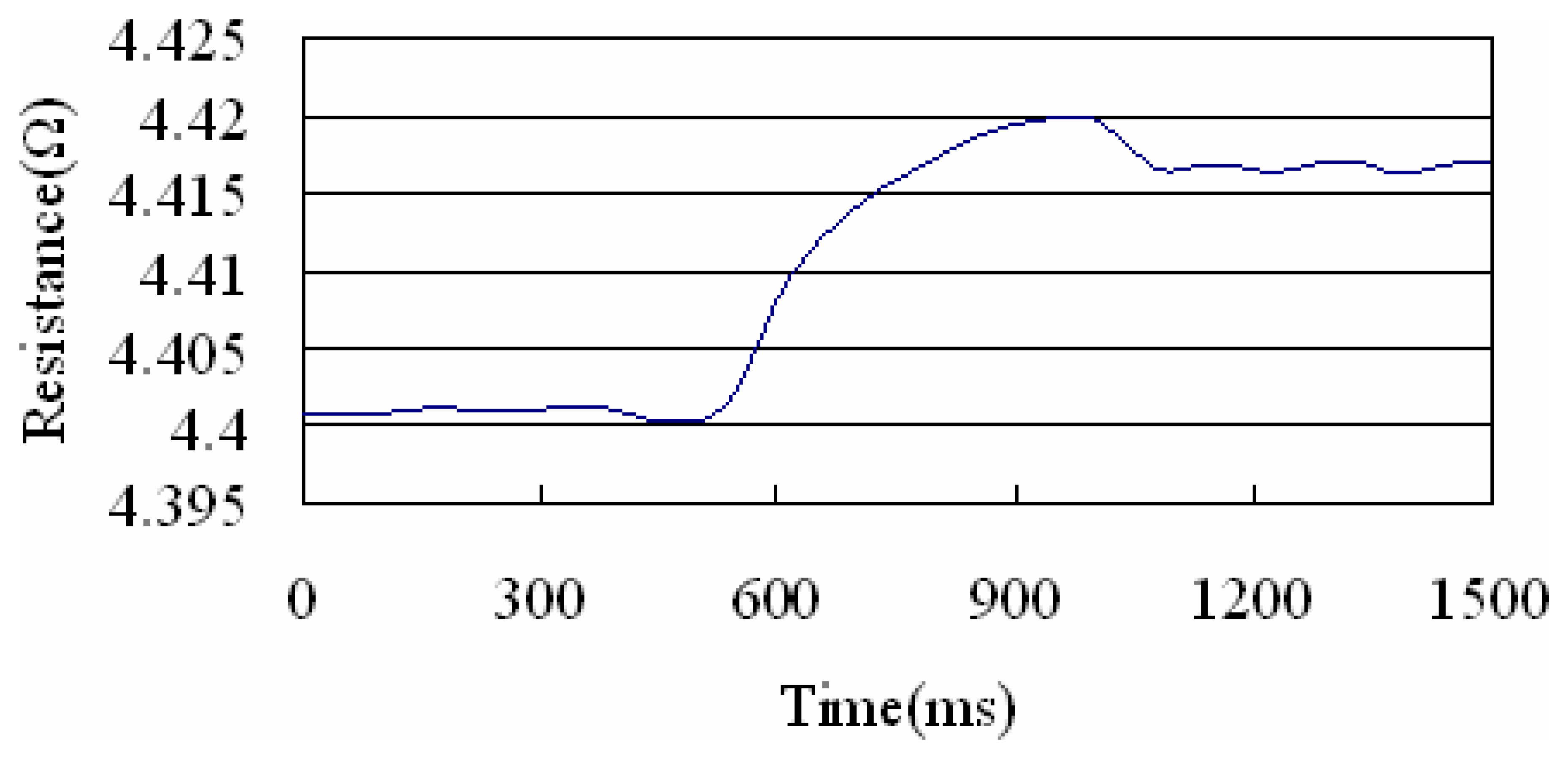
4.2. Time response of flow sensors
4.3. Stability of flow sensors
5. Conclusions
Acknowledgments
References and Notes
- Qiu, L.; Hein, S.; Obermeier, E.; Schubert, A. Micro gas-flow sensor with integrated heat sink and flow guide. Sensors and Actuators A 1996, 54, 547–551. [Google Scholar]
- Neda, T.; Nakmura, K.; Takumi, T. A polysilicon flow sensor for gas flow meters. Sensors and Actuators A 1996, 54, 626–631. [Google Scholar]
- Makinwa, K.A.A.; Huijsing, J.H. A wind-sensor interface using thermal sigma delta modulation techniques. Sensors and Actuators A 2001, 92, 280–285. [Google Scholar]
- Matova, S.P.; Makinwa, K.A.A.; Huijsing, J.H. Compensation of packaging asymmetry in a 2-D wind sensor. IEEE Sensors Journal 2003, 3, 761–765. [Google Scholar]
- Mailly, F.; Giani, A.; Bonnot, R.; Temple-Boyer, P.; Pascal-Delannoy, F.; Foucaran, A.; Boyer, A. Anemometer with hot platinum thin film. Sensors and Actuators A 2001, 94, 32–38. [Google Scholar]
- Kim, S.; Nam, T.; Park, S. Measurement of flow direction and velocity using a micromachined flow sensor. Sensors and Actuators A 2004, 114, 312–318. [Google Scholar]
- Poghossian, A.; Yoshinobu, T.; Schöning, M. J. Flow-velocity microsensors based on semiconductor field-effect structures. Sensors 2003, 3, 202–212. [Google Scholar]
- Svedin, N.; Stemme, E.; Stemme, G. A static turbine flow meter with a micromachined silicon torque sensor. Journal of Microelectromechanical Systems 2003, 12, 937–946. [Google Scholar]
- Su, Y.; Evans, A.G.R.; Brunnschweile, A.; Ensell, G. Characterization of a highly sensitive ultra-thin piezoresistive silicon cantilever probe and its application in gas flow velocity sensing. J. Micromech. Microeng 2002, 12, 780–785. [Google Scholar]
- Wu, J.; Zhou, Q.; Liu, J.; Lou, Z. Simulation study of nano aqueous flow sensor based on amperometric measurement. Sensors 2006, 6, 473–479. [Google Scholar]
- Gundogdu, S.; Sahin, O. E.M.I. effects of cathodic protection on electromagnetic flowmeters. Sensors 2007, 7, 75–83. [Google Scholar]
- Nguyen, N. T. Micromachined flow sensors – a review. Flow Meas. Instrum. 1997, 8, 7–16. [Google Scholar]
- Neuzil, P.; Sridhar, U.; llic, B. Air flow actuation of micromechanical oscillators. Applied Physics Letters 2001, 79, 138–140. [Google Scholar]
- Putten, V.; Middelhoek, S. Integrated silicon anemometer. Electronics Letters 1974, 10, 425–426. [Google Scholar]
- Wang, X.; Qian, J.; Zhang, D. Design, fabrication, testing and mechanical analysis of bulk-micromachined flowmeters. ACTC Mechanica Sinica 2004, 20, 152–158. [Google Scholar]
- Lee, C.Y.; Lee, G.B. Micromachine-based humidity sensors with integrated temperature sensors for signal drift compensation. J. Micromech. Microeng 2003, 13, 620–627. [Google Scholar]
- Gere, J.M. Mechanics of Materials, 5th Ed. ed; Nelson Thornes Ltd: United Kingdom, 2002; pp. 887–888. [Google Scholar]
- Lee, C.Y.; Tsai, C.H.; Chen, L.W.; Fu, L.M.; Chen, Y.C. Elastic-plastic modeling of heat-treated bimorph micro-cantilevers. Microsystem Technologies 2006, 12, 979–986. [Google Scholar]


© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Wang, Y.-H.; Lee, C.-Y.; Chiang, C.-M. A MEMS-based Air Flow Sensor with a Free-standing Micro-cantilever Structure. Sensors 2007, 7, 2389-2401. https://doi.org/10.3390/s7102389
Wang Y-H, Lee C-Y, Chiang C-M. A MEMS-based Air Flow Sensor with a Free-standing Micro-cantilever Structure. Sensors. 2007; 7(10):2389-2401. https://doi.org/10.3390/s7102389
Chicago/Turabian StyleWang, Yu-Hsiang, Chia-Yen Lee, and Che-Ming Chiang. 2007. "A MEMS-based Air Flow Sensor with a Free-standing Micro-cantilever Structure" Sensors 7, no. 10: 2389-2401. https://doi.org/10.3390/s7102389
APA StyleWang, Y.-H., Lee, C.-Y., & Chiang, C.-M. (2007). A MEMS-based Air Flow Sensor with a Free-standing Micro-cantilever Structure. Sensors, 7(10), 2389-2401. https://doi.org/10.3390/s7102389



