Modeling Forest Productivity Using Envisat MERIS Data
Abstract
:1. Introduction
2. Study Area and Data
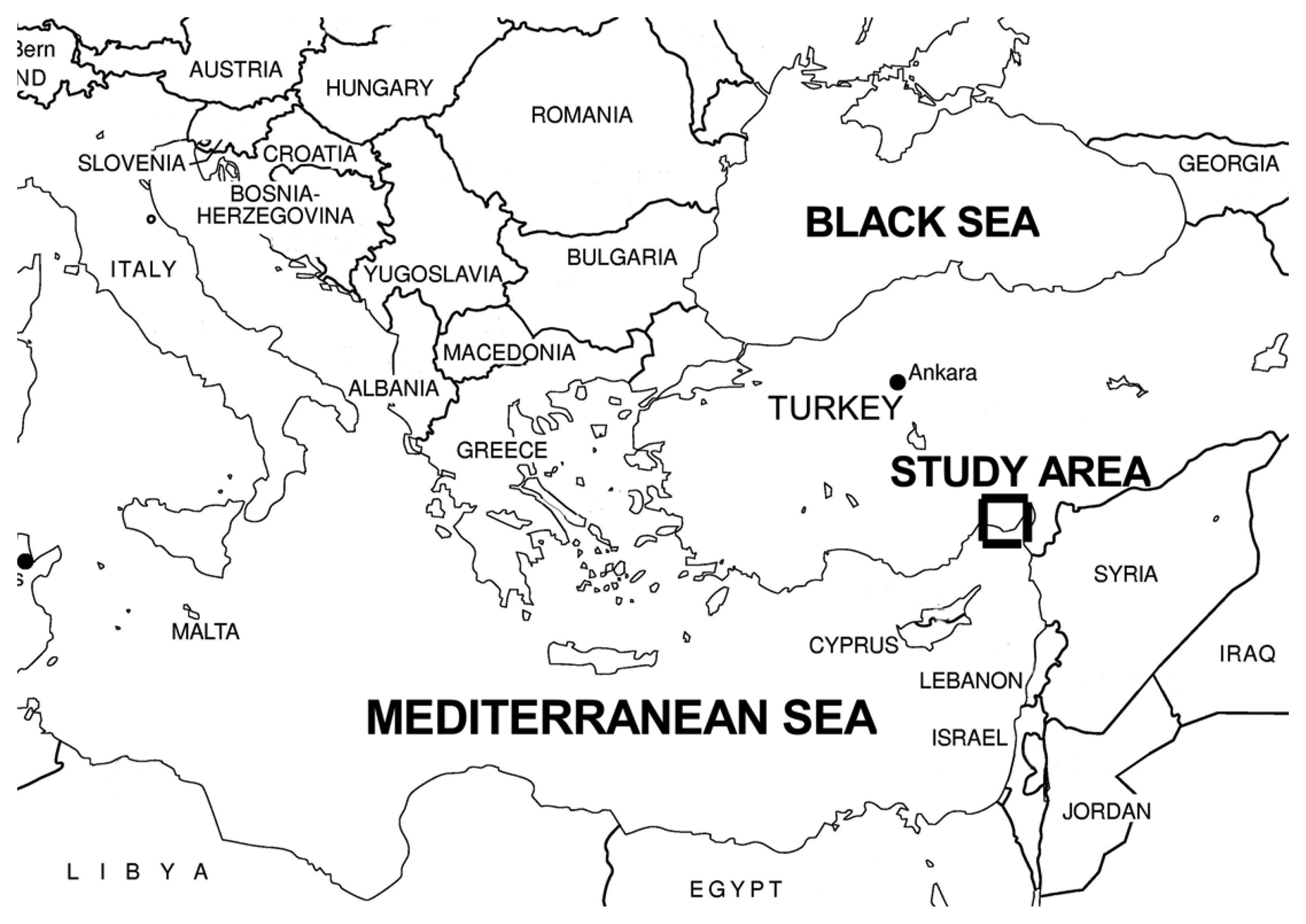
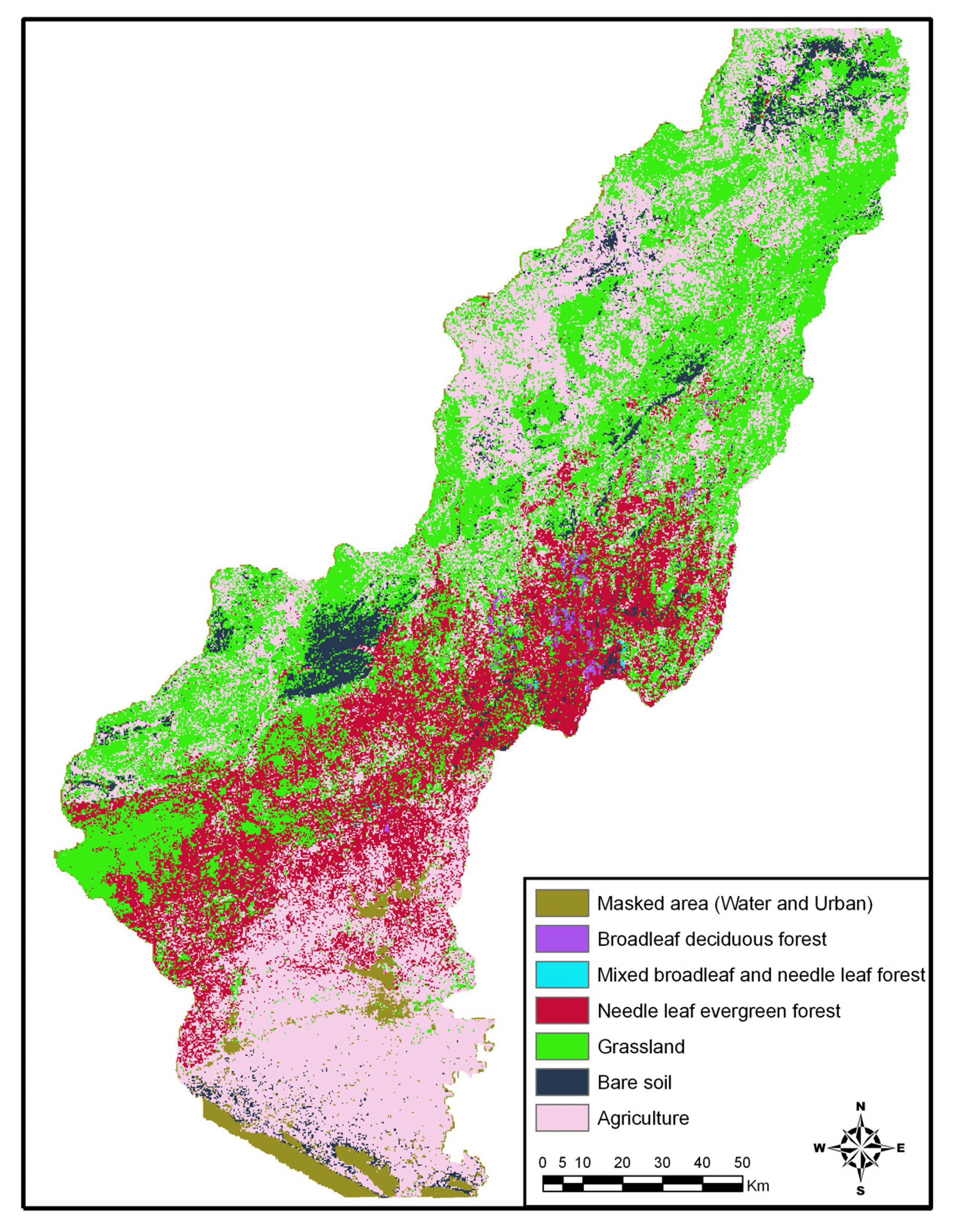
2.1. Study Area
2.2. Envisat MERIS data
2.3. Climate Data
2.4. Soil Texture
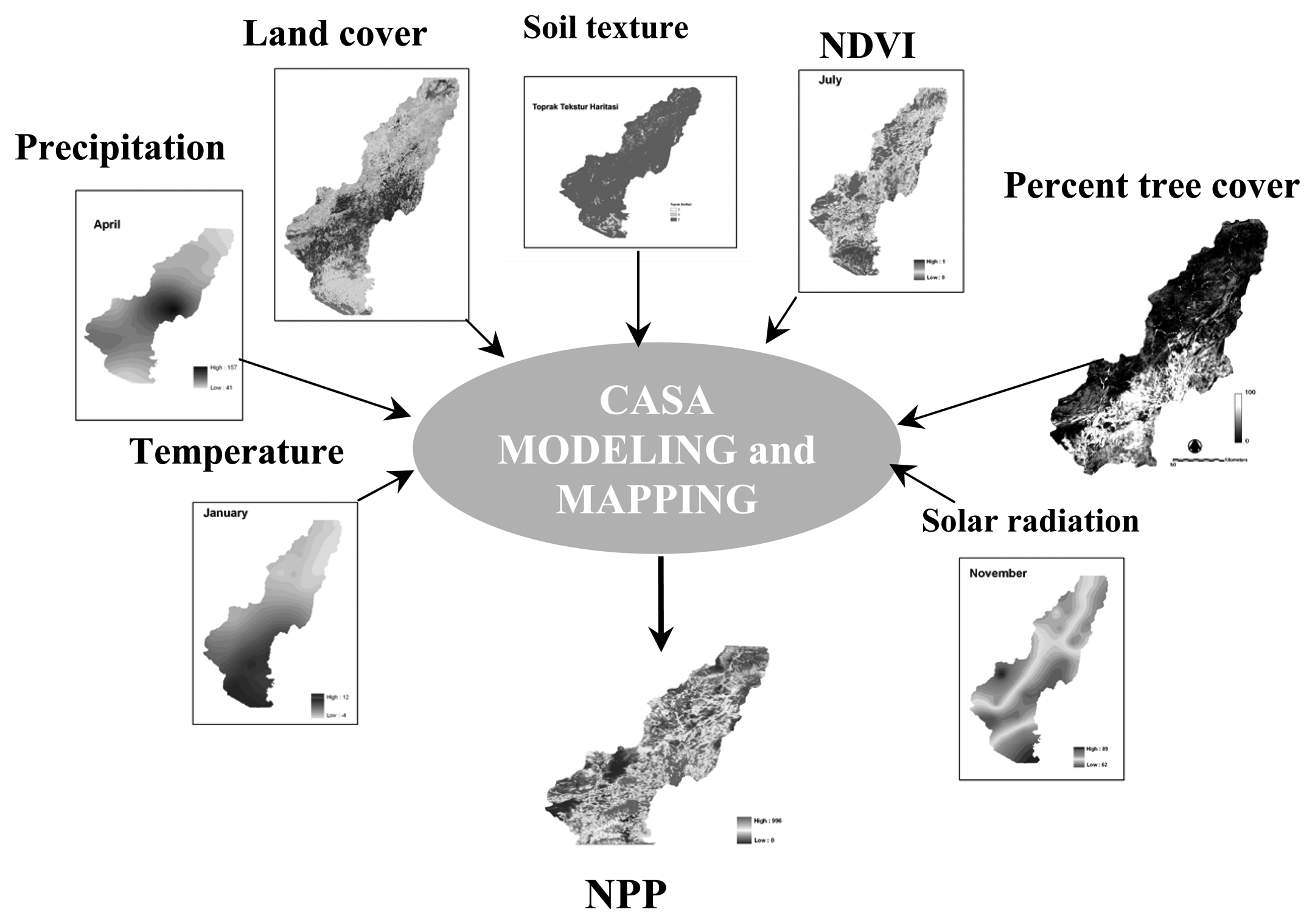
3. Modeling and Mapping NPP
3.1. Modeling Algorithm
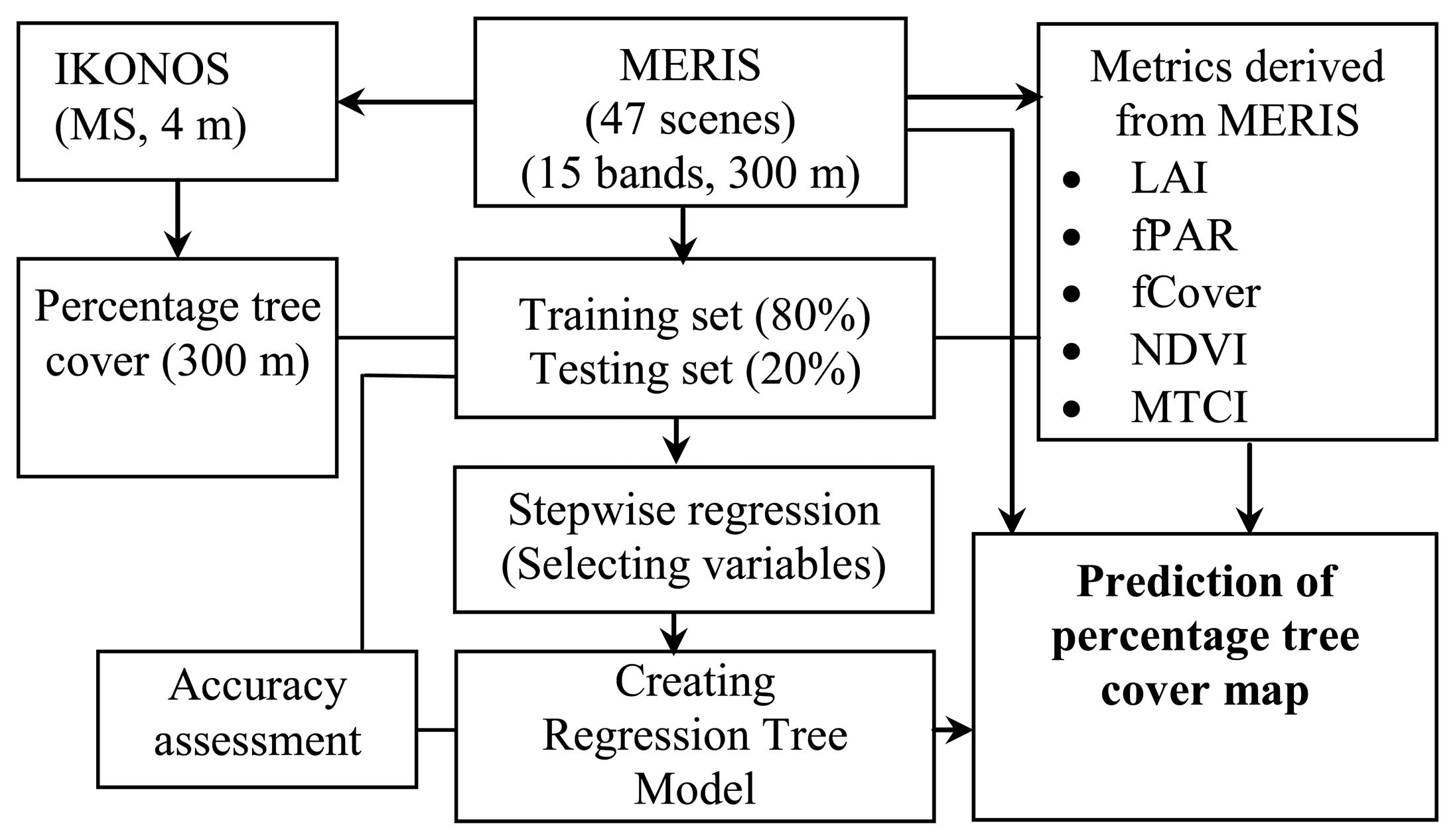
3.2. Estimation of Fractional Tree Cover
3.3. Mapping Land Cover
3.4. NDVI
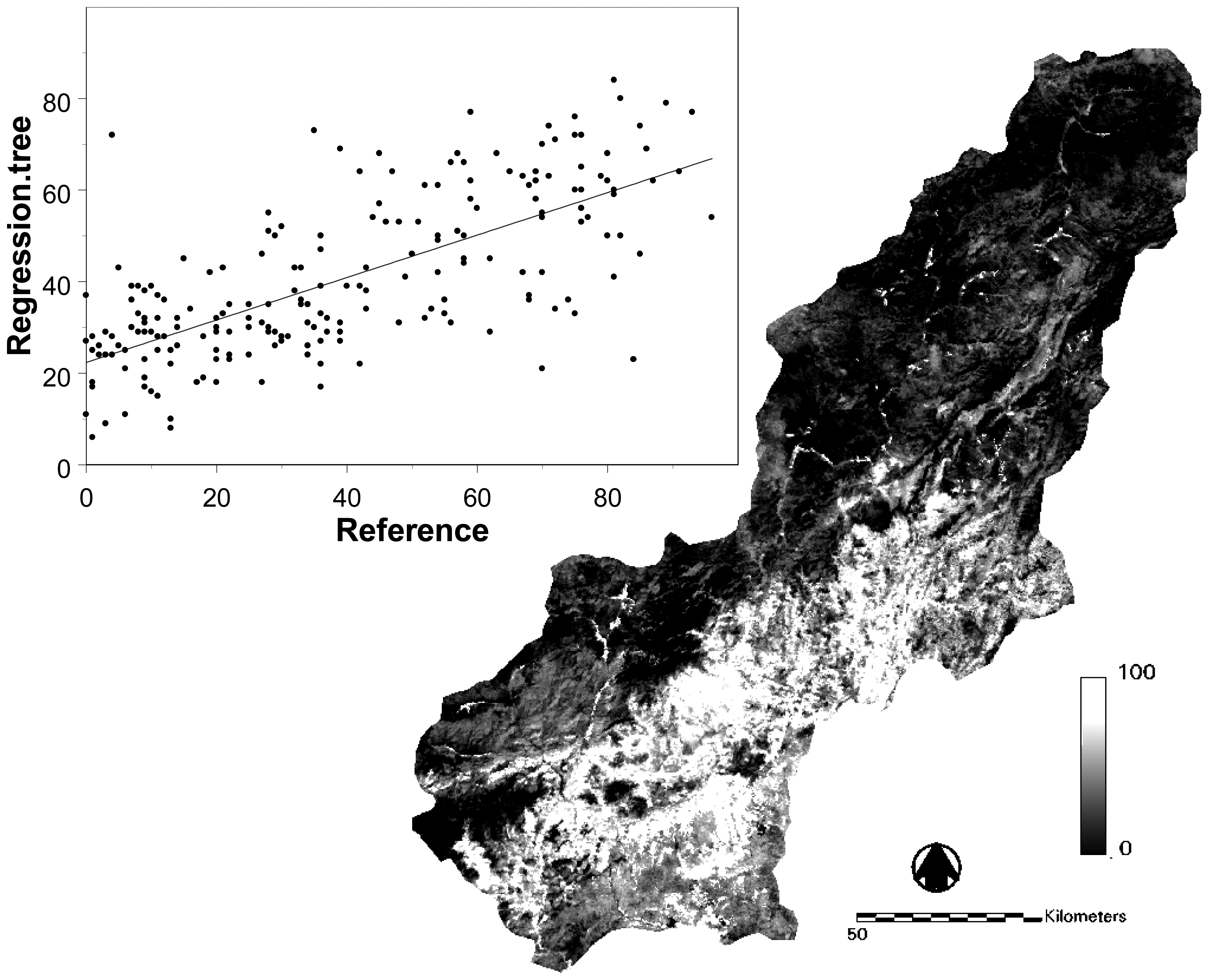
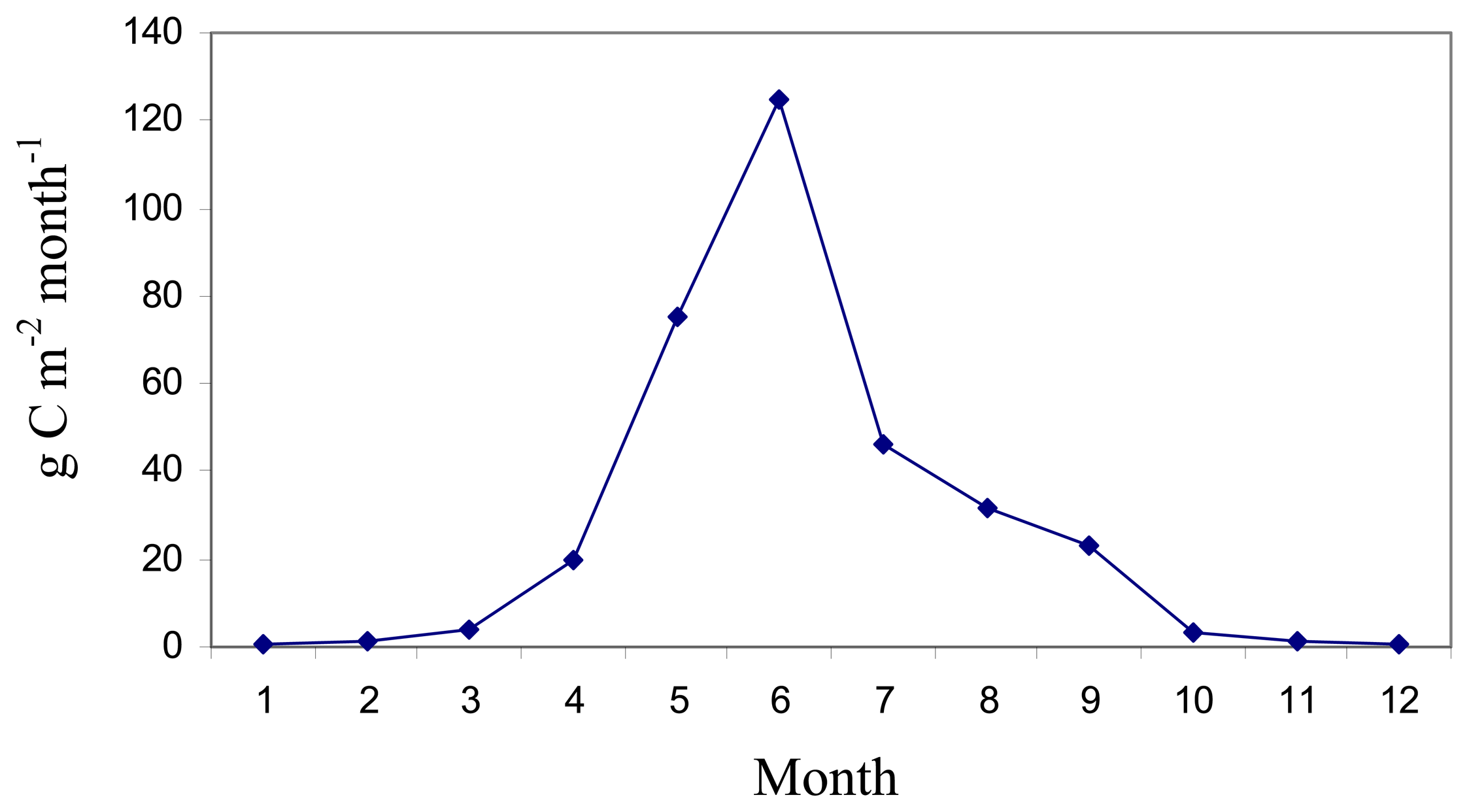
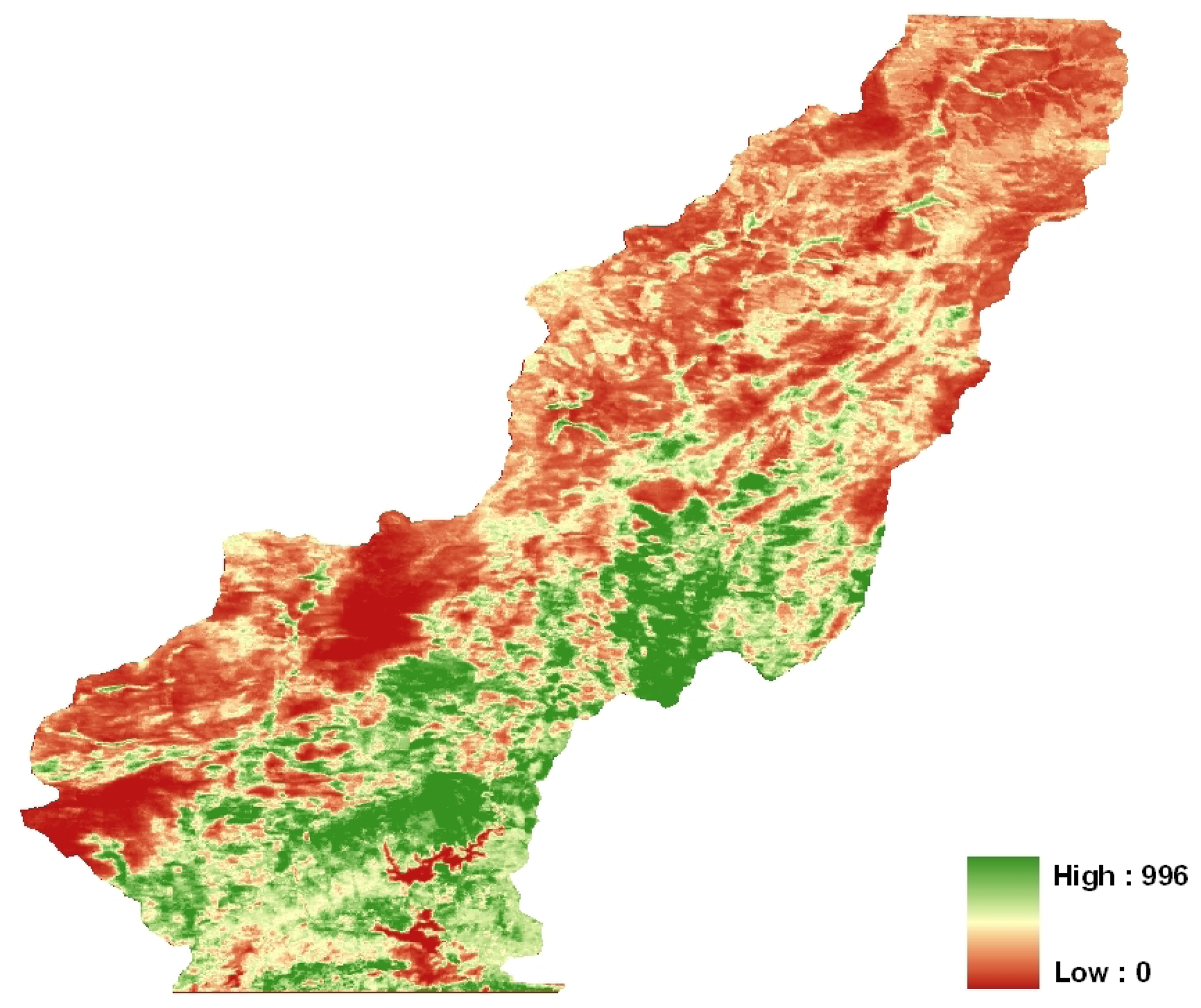
4. Results and Discussion
5. Conclusions
Acknowledgments
References
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite estimates of productivity and light use efficiency in United States agriculture 1982–1998. Global Change Biology 2002, 8(8), 722–735. [Google Scholar]
- Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexler, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystems. Science 1994, 263(5144), 185–190. [Google Scholar]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooser, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Global Biogeochemical Cycles 1993, 7(4), 811–841. [Google Scholar]
- Ruimy, A.; Dedieu, G.; Saugier, B. Methodology for the estimation of terrestrial net primary production from remotely sensed data. Journal of Geophysical Research 1994, 99(D3), 5263–5284. [Google Scholar]
- Prince, S.D.; Goward, S.N. Global primary production: a remote sensing approach. Journal of Biogeography 1995, 22(4-5), 815–835. [Google Scholar]
- Malmstrom, C.M.; Thompson, M.V.; Juday, G.P.; Los, S.O.; Randerson, J.T.; Fıeld, C.B. Interannual variation in global-scale net primary production: testing model estimates. Global Biogeochemical Cycles 1997, 11(3), 367–392. [Google Scholar]
- Running, S.W.; Baldocchi, D.D.; Turner, D.P.; Gower, S.T.; Bakwin, P.S.; Hibbard, K.A. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and EOS satellite data. Remote Sensing of Environment 1999, 70(1), 108–127. [Google Scholar]
- Verstraete, M.M.; Pinty, B.; Curran, P.J. MERIS potential for land applications. International Journal of Remote Sensing 1999, 20(9), 1747–1756. [Google Scholar]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. International Journal of Remote Sensing 2004, 25(23), 5403–5413. [Google Scholar]
- Davis, P.H. Flora of Turkey and the East Aegean Islands.; Edinburgh University Press: Edinburgh, 1965. [Google Scholar]
- Evrendilek, F.; Berberoglu, S.; Taskinsu-Meydan, S.; Yilmaz, E. Quantifying carbon budgets of conifer Mediterranean forest ecosystems, Turkey. Environmental Monitoring and Assessment 2006, 119(1-3), 527–543. [Google Scholar]
- Soil Survey Staff. Keys to soil taxonomy.; USDA-NRCS, US Government Printing Office: Washington, D.C., 1998. [Google Scholar]
- Potter, C.S.; Davidson, E.A.; Klooster, S.A.; Nepstad, D.C.; De Negreiros, G.H.; Brooks, V. Regional application of an ecosystem production model for studies of biogeochemistry in Brazilian Amazonia. Global Change Biology 1998, 4(3), 315–333. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. Journal of Applied Ecology 1972, 9, 747–766. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. Journal of Geophysical Research-Atmospheres 1998, 103(D24), 32257–32275. [Google Scholar]
- Zhu, Z.; Evans, D.L. United States forest types and predicted percent forest cover from AVHRR data. Photogrammetric Engineering and Remote Sensing 1994, 60(5), 525–531. [Google Scholar]
- Defries, R.S.; Hansen, M.C.; Townshend, J.R.G. Global continuous fields of vegetation characteristics: a linear mixture model applied to multi-year 8km AVHRR data. International Journal of Remote Sensing 2000, 21(6-7), 1389–1414. [Google Scholar]
- Iverson, L.R.; Cook, E.A.; Graham, R.L. A technique for extrapolating and validating forest cover across large regions: calibrating AVHRR data with TM data. International Journal of Remote Sensing 1989, 10(11), 1805–1812. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R.A. Global land cover classification at 1km spatial resolution using a classification tree approach. International Journal of Remote Sensing 2000, 21(6-7), 1331–1364. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Carroll, M.; Dimiceli, C.; Sohlberg, R.A. Global percent tree cover at a spatial resolution of 500 metres: First results of the MODIS vegetation continuous fields algorithm. Earth Interactions 2003, 7, 1–15. [Google Scholar]
- Hansen, M.C.; Townshend, J.R.G.; Defries, R.S.; Carroll, M. Estimation of tree cover using MODIS data at global, continental and regional/local scales. International Journal of Remote Sensing 2005, 26(19), 4359–4380. [Google Scholar]
- Baret, F.; Pavageau, K.; Weiss, M.; Moreno, J.; Berthelot, B.; Gonzales, M.C. Report on the validation of MERIS Top of canopy Land Products. (TOA_VEG) land products. Contract ESA AO/1-4233/02/I-LG. 2006.
- Insightful Corp. S-Plus 6.2. Guide to Statistics; Volume 2, Seattle: Washington, 2001. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical methods in water resources; Elsevier Science Publishers: Amsterdam, 1992. [Google Scholar]
- Rokhmatuloh, R.; Al-Bilbisi, H.; Arihara, K.; Kobayashi, T.; Nitto, D.; Erdene, B.; Hirabayashi, K.; Javzandulam, T. A.; Lee, S.A.; Migita, E.; Soliman, N.; Ouma, Y.; Aslam, M.; Tateishi, R. Application of Regression Tree Method for Estimating Percent Tree Cover of Asia with QuickBird Images as Training Data. In The 11th CEReS International Symposium on Remote Sensing; Chiba University: Chiba, Japan, 2005. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malmstrom, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sensing of Environment 1995, 51(1), 74–88. [Google Scholar]
- Goetz, S.J.; Prince, D.S.; Goward, N.S.; Thawley, M.M.; Small, J. Satellite remote sensing of primary production: an improved production efficiency modeling approach. Ecological Modelling 1999, 122, 239–255. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R.A.; Dimiceli, C.; Carroll, M. Towards an operational MODIS continuous field of percent tree cover algorithm: Examples using AVHRR and MODIS data. Remote Sensing of Environment 2002, 83, 303–319. [Google Scholar]
- Wali, M.K.; Evrendilek, F.; West, T.; Watts, S.; Pant, D.; Gibbs, H.; McClead, B. Assessing terrestrial ecosystem sustainability: usefulness of regional carbon and nitrogen models. Nature & Resources 1999, 35(4), 20–33. [Google Scholar]
- Evrendilek, F.; Berberoglu, S. Quantifying spatial patterns of bioclimatic zones and controls in Turkey. Theoretical and Applied Climatology 2007. [Google Scholar] [CrossRef]
- Evrendilek, F.; Wali, M.K. Changing global climate: historical carbon and nitrogen budgets and projected responses of Ohio's cropland ecosystems. Ecosystems 2004, 7(4), 381–392. [Google Scholar]

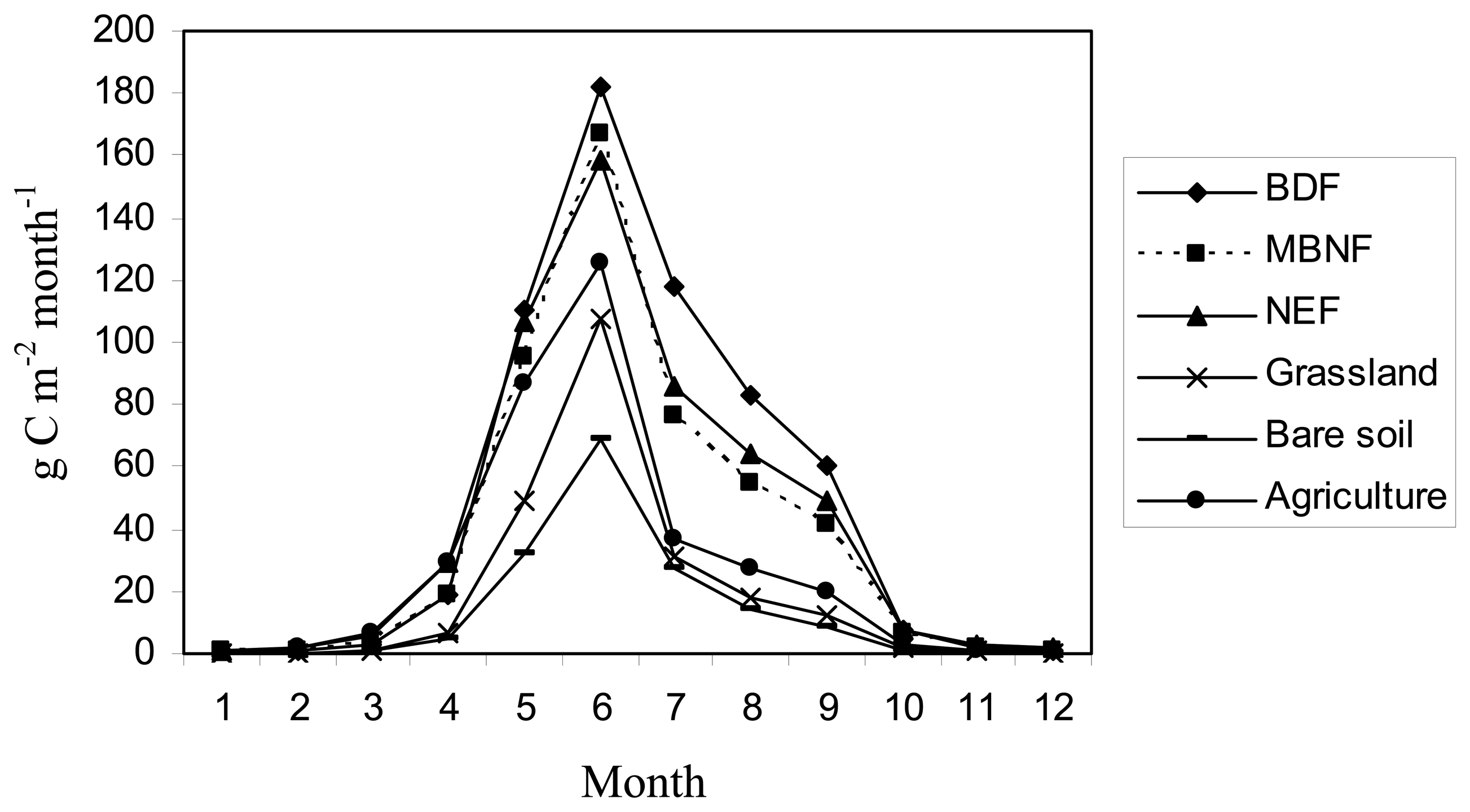
| Land-Use Land-Cover Classes | Mean NPP (g C m-2yr-1) |
|---|---|
| Broadleaf deciduous forest | 588.6 |
| Mixed broadleaf and needleleaf forest | 468.7 |
| Needleleaf evergreen forest | 512.9 |
| Grassland | 227.7 |
| Bare soil | 158.4 |
| Agriculture | 338.7 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Berberoglu, S.; Evrendilek, F.; Ozkan, C.; Donmez, C. Modeling Forest Productivity Using Envisat MERIS Data. Sensors 2007, 7, 2115-2127. https://doi.org/10.3390/S7102115
Berberoglu S, Evrendilek F, Ozkan C, Donmez C. Modeling Forest Productivity Using Envisat MERIS Data. Sensors. 2007; 7(10):2115-2127. https://doi.org/10.3390/S7102115
Chicago/Turabian StyleBerberoglu, Suha, Fatih Evrendilek, Coskun Ozkan, and Cenk Donmez. 2007. "Modeling Forest Productivity Using Envisat MERIS Data" Sensors 7, no. 10: 2115-2127. https://doi.org/10.3390/S7102115
APA StyleBerberoglu, S., Evrendilek, F., Ozkan, C., & Donmez, C. (2007). Modeling Forest Productivity Using Envisat MERIS Data. Sensors, 7(10), 2115-2127. https://doi.org/10.3390/S7102115




