Effects of Acute Altitude, Speed and Surface on Biomechanical Loading in Distance Running
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Study Design
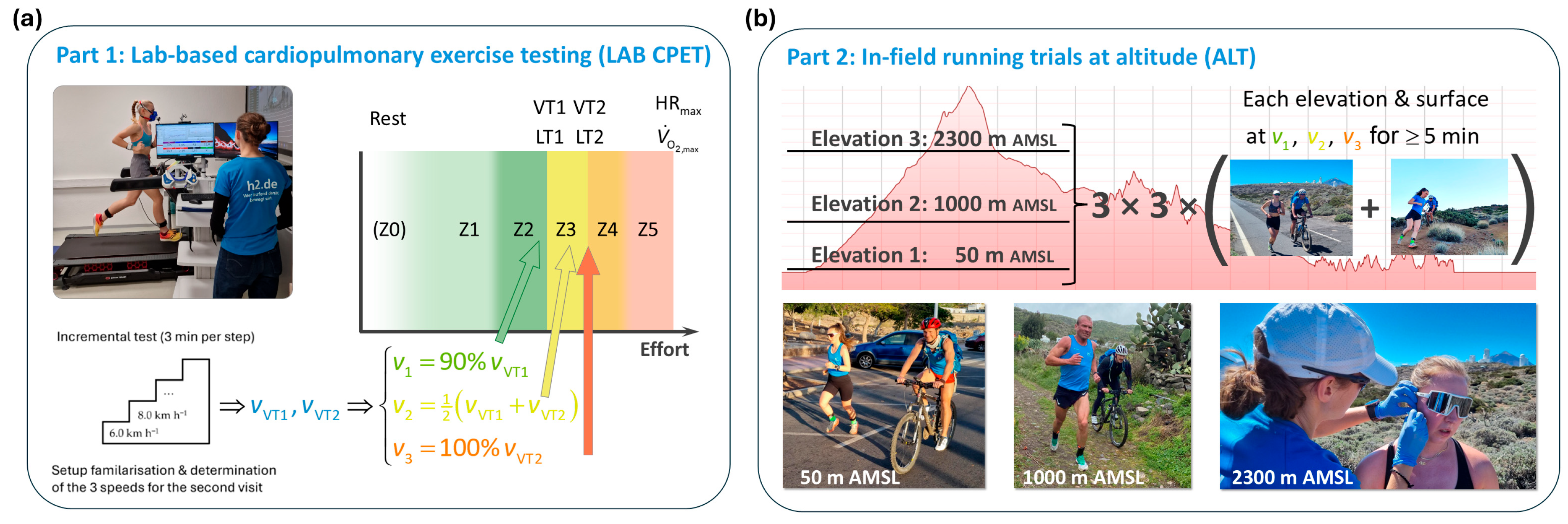
2.2.1. Part 1: Laboratory-Based Cardiopulmonary Exercise Testing (LAB CPET)
2.2.2. Part 2: Altitude Trials (ALTs)
2.3. Biomechanical and Physiological Measurements During ALTs
2.4. Data Post Processing
2.5. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| %HRmax | Percentage of maximum heart rate |
| aLA | Absolute lateral asymmetry index |
| ALT | In-field running trial at altitude |
| AMSL | Above mean sea level |
| bpm | Beats per minute |
| CAD | Cadence (step frequency) |
| HR | Heart rate |
| IMU | Inertial measurement unit |
| LA | Lateral asymmetry index |
| LAB CPET | Laboratory-based cardiopulmonary exercise testing |
| LAC | Blood lactate |
| LACex | Blood lactate at volitional exhaustion |
| PTA | Peak tibial acceleration |
| rmANOVA | Repeated measures analysis of variance |
| ROAD | Road surface |
| RPE | Rating of perceived exertion (RPE) |
| RSh | Residual shock |
| SD | Standard deviation |
| spm | Steps per minute |
| TRAIL | Trail surface |
| VEpeak | Peak ventilation |
| Maximum oxygen uptake per unit time and body mass | |
| Peak oxygen uptake per unit time and body mass | |
| VT1 | Ventilatory threshold 1 |
| VT2 | Ventilatory threshold 2 |
Appendix A
Appendix A.1. Detailed Results Tables
| Load Metric | Elevation AMSL | Speed | Surface | Significance Level p and Effect Size ηp2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ROAD | TRAIL | Elevation | Speed | Surface | Elevation × Surface | Elevation × Speed | Speed × Surface | Elevation × Speed × Surface | |||
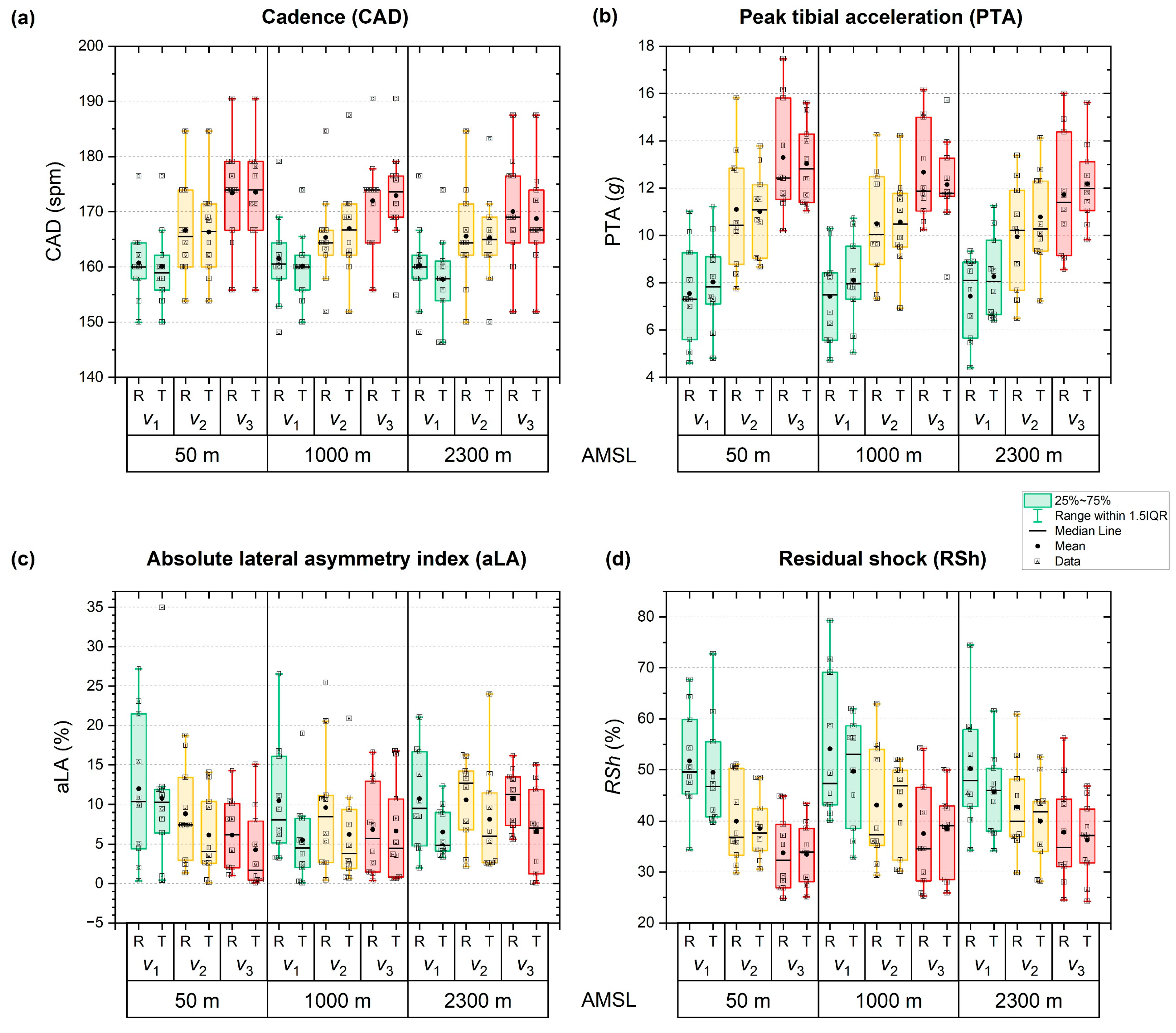
| Cadence (CAD, spm) | 50 m | v1 | 161 ± 7 | 160 ± 7 | p < 0.001 | p < 0.001 | p = 0.610 | p = 0.287 | p < 0.001 | p = 0.003 | p = 0.135 |
| v2 | 167 ± 9 | 166 ± 9 | |||||||||
| v3 | 173 ± 9 | 173 ± 9 | |||||||||
| 1000 m | v1 | 161 ± 8 | 160 ± 7 | ||||||||
| v2 | 165 ± 9 | 167 ± 9 | |||||||||
| v3 | 172 ± 9 | 173 ± 9 | |||||||||
| 2300 m | v1 | 160 ± 8 | 158 ± 8 | ηp2 = 0.659 | ηp2 = 0.894 | ηp2 = 0.030 | ηp2 = 0.130 | ηp2 = 0.487 | ηp2 = 0.481 | ηp2 = 0.173 | |
| v2 | 166 ± 10 | 165 ± 9 | |||||||||
| v3 | 170 ± 10 | 169 ± 9 | |||||||||
| Peak tibial acceleration (PTA, g) | 50 m | v1 | 7.5 ± 2.1 | 8.0 ± 1.9 | p = 0.197 | p < 0.001 | p = 0.614 | p = 0.445 | p < 0.001 | p = 0.003 | p = 0.422 |
| v2 | 11.1 ± 2.6 | 11.0 ± 1.8 | |||||||||
| v3 | 13.3 ± 2.4 | 13.0 ± 1.7 | |||||||||
| 1000 m | v1 | 7.4 ± 1.9 | 8.1 ± 1.8 | ||||||||
| v2 | 10.5 ± 2.3 | 10.6 ± 2.0 | |||||||||
| v3 | 12.7 ± 2.1 | 12.2 ± 2.0 | |||||||||
| 2300 m | v1 | 7.4 ± 1.8 | 8.3 ± 1.8 | ηp2 = 0.165 | ηp2 = 0.926 | ηp2 = 0.029 | ηp2 = 0.086 | ηp2 = 0.503 | ηp2 = 0.477 | ηp2 = 0.100 | |
| v2 | 9.9 ± 2.3 | 10.8 ± 2.1 | |||||||||
| v3 | 11.7 ± 2.6 | 12.2 ± 1.7 | |||||||||
| Lateral asymmetry index (LA, %) | 50 m | v1 | 12.0 ± 9.4 | 10.8 ± 9.6 | p = 0.664 | p = 0.058 | p = 0.150 | p = 0.302 | p = 0.089 | p = 0.743 | p = 0.389 |
| v2 | 8.8 ± 6.1 | 6.1 ± 5.3 | |||||||||
| v3 | 6.1 ± 4.7 | 4.3 ± 5.2 | |||||||||
| 1000 m | v1 | 10.5 ± 7.4 | 5.5 ± 5.6 | ||||||||
| v2 | 9.6 ± 8.1 | 6.2 ± 6.3 | |||||||||
| v3 | 6.8 ± 5.9 | 6.7 ± 6.2 | |||||||||
| 2300 m | v1 | 10.7 ± 6.3 | 6.5 ± 3.2 | ηp2 = 0.045 | ηp2 = 0.317 | ηp2 = 0.215 | ηp2 = 0.033 | ηp2 = 0.228 | ηp2 = 0.032 | ηp2 = 0.106 | |
| v2 | 10.6 ± 5.2 | 8.1 ± 6.9 | |||||||||
| v3 | 10.7 ± 3.7 | 6.6 ± 5.5 | |||||||||
| Residual shock (RSh, %) | 50 m | v1 | 52 ± 10 | 49 ± 11 | p = 0.218 | p < 0.001 | p = 0.416 | p = 0.775 | p < 0.001 | p = 0.181 | p = 0.537 |
| v2 | 40 ± 8 | 39 ± 6 | |||||||||
| v3 | 34 ± 8 | 33 ± 6 | |||||||||
| 1000 m | v1 | 54 ± 14 | 50 ± 11 | ||||||||
| v2 | 43 ± 12 | 43 ± 9 | |||||||||
| v3 | 38 ± 11 | 38 ± 9 | |||||||||
| 2300 m | v1 | 50 ± 11 | 46 ± 8 | ηp2 = 0.156 | ηp2 = 0.897 | ηp2 = 0.075 | ηp2 = 0.028 | ηp2 = 0.425 | ηp2 = 0.185 | ηp2 = 0.068 | |
| v2 | 43 ± 9 | 40 ± 8 | |||||||||
| v3 | 38 ± 10 | 36 ± 8 | |||||||||
| Load Metric | Factor | Post Hoc Testing | Mean Difference (95% CI) | Significance Level |
|---|---|---|---|---|
| Cadence (CAD, spm) | Elevation | 50 vs. 1000 m AMSL | +0.3 (−0.5 to +1.1) | p = 0.849 |
| 50 vs. 2300 m AMSL | +2.2 (+0.7 to +3.7) | p = 0.006 | ||
| 1000 vs. 2300 m AMSL | +1.9 (+0.7 to +3.0) | p = 0.383 | ||
| Speed | v1 vs. v2 | −5.9 (−8.5 to −3.3) | p < 0.001 | |
| v1 vs. v3 | −11.7 (−15 to −8.1) | p < 0.001 | ||
| v2 vs. v3 | −5.7 (−7.7 to −3.8) | p < 0.001 | ||
| Surface | Road vs. Trail | +0.4 (−1.4 to +2.2) | p = 0.610 | |
| Peak tibial acceleration (PTA, g) | Elevation | 50 vs. 1000 m AMSL | +0.43 (−0.46 to +1.32) | p = 0.563 |
| 50 vs. 2300 m AMSL | +0.62 (−0.37 to +1.61) | p = 0.303 | ||
| 1000 vs. 2300 m AMSL | +0.18 (−0.88 to +1.25) | p = 1.000 | ||
| Speed | v1 vs. v2 | −2.85 (−3.49 to −2.20) | p < 0.001 | |
| v1 vs. v3 | −4.71 (−5.96 to −3.46) | p < 0.001 | ||
| v2 vs. v3 | −1.86 (−2.64 to −1.08) | p < 0.001 | ||
| Surface | Road vs. Trail | −0.28 (−1.48 to +0.92) | p = 0.614 | |
| Lateral asymmetry index (LA, %) | Elevation | 50 vs. 1000 m AMSL | +0.5 (−3.2 to +4.2) | p = 1.000 |
| 50 vs. 2300 m AMSL | −0.9 (−5.7 to +4.0) | p = 1.000 | ||
| 1000 vs. 2300 m AMSL | −1.3 (−5.6 to +2.9) | p = 1.000 | ||
| Speed | v1 vs. v2 | +1.1 (−1.2 to +3.4) | p = 0.608 | |
| v1 vs. v3 | +2.5 (−0.8 to +5.7) | p = 0.166 | ||
| v2 vs. v3 | +1.4 (−0.3 to +3.0) | p = 0.106 | ||
| Surface | Road vs. Trail | +2.8 (−1.2 to +6.8) | p = 0.150 | |
| Residual shock (RSh, %) | Elevation | 50 vs. 1000 m AMSL | −3.2 (−8.5 to +2.1) | p = 0.343 |
| 50 vs. 2300 m AMSL | −1.0 (−4.8 to +2.9) | p = 1.000 | ||
| 1000 vs. 2300 m AMSL | +2.2 (−4.0 to +8.4) | p = 0.979 | ||
| Speed | v1 vs. v2 | +8.9 (+6.2 to +11.7) | p < 0.001 | |
| v1 vs. v3 | 13.9 (+9.5 to +18.4) | p < 0.001 | ||
| v2 vs. v3 | +5.0 (+2.6 to +7.4) | p < 0.001 | ||
| Surface | Road vs. Trail | +1.8 (−3.0 to +6.6) | p = 0.416 |
| Load Metric | Factor | Post Hoc Testing | Mean Difference (95% CI) | Significance Level |
|---|---|---|---|---|
| Cadence (CAD, spm) | Elevation × Speed | 50 m × v1 vs. 50 m × v2 | −6.090 | <0.001 |
| 50 m × v1 vs. 50 m × v3 | −13.090 | <0.001 | ||
| 50 m × v1 vs. 1000 m × v1 | −0.430 | 0.317 | ||
| 50 m × v1 vs. 1000 m × v2 | −5.770 | <0.001 | ||
| 50 m × v1 vs. 1000 m × v3 | −12.080 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v1 | 1.380 | 0.036 | ||
| 50 m × v1 vs. 2300 m × v2 | −5.030 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v3 | −9.030 | <0.001 | ||
| 50 m × v2 vs. 50 m × v3 | −7.000 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v1 | 5.660 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v2 | 0.320 | 0.57 | ||
| 50 m × v2 vs. 1000 m × v3 | −5.990 | <0.001 | ||
| 50 m × v2 vs. 2300 m × v1 | 7.470 | <0.001 | ||
| 50 m × v2 vs. 2300 m × v2 | 1.060 | 0.113 | ||
| 50 m × v2 vs. 2300 m × v3 | −2.940 | 0.012 | ||
| 50 m × v3 vs. 1000 m × v1 | 12.660 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v2 | 7.320 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v3 | 1.010 | 0.016 | ||
| 50 m × v3 vs. 2300 m × v1 | 14.470 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v2 | 8.060 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v3 | 4.060 | <0.001 | ||
| 1000 m × v1 vs. 1000 m × v2 | −5.340 | <0.001 | ||
| 1000 m × v1 vs. 1000 m × v3 | −11.650 | <0.001 | ||
| 1000 m × v1 vs. 2300 m × v1 | 1.810 | 0.003 | ||
| 1000 m × v1 vs. 2300 m × v2 | −4.600 | <0.001 | ||
| 1000 m × v1 vs. 2300 m × v3 | −8.600 | <0.001 | ||
| 1000 m × v2 vs. 1000 m × v3 | −6.310 | <0.001 | ||
| 1000 m × v2 vs. 2300 m × v1 | 7.150 | <0.001 | ||
| 1000 m × v2 vs. 2300 m × v2 | 0.740 | 0.089 | ||
| 1000 m × v2 vs. 2300 m × v3 | −3.260 | 0.001 | ||
| 1000 m × v3 vs. 2300 m × v1 | 13.460 | <0.001 | ||
| 1000 m × v3 vs. 2300 m × v2 | 7.050 | <0.001 | ||
| 1000 m × v3 vs. 2300 m × v3 | 3.050 | 0.002 | ||
| 2300 m × v1 vs. 2300 m × v2 | −6.410 | <0.001 | ||
| 2300 m × v1 vs. 2300 m × v3 | −10.410 | <0.001 | ||
| 2300 m × v2 vs. 2300 m × v3 | −4.000 | <0.001 | ||
| Speed × Surface | v1 × Road vs. v1 × Trail | −5.04 | <0.001 | |
| v1 × Road vs. v2 × Road | −11.03 | <0.001 | ||
| v1 × Road vs. v2 × Trail | 1.46 | 0.147 | ||
| v1 × Road vs. v3 × Road | −5.38 | 0.002 | ||
| v1 × Road vs. v3 × Trail | −10.94 | <0.001 | ||
| v1 × Trail vs. v2 × Road | −5.99 | <0.001 | ||
| v1 × Trail vs. v2 × Trail | 6.5 | <0.001 | ||
| v1 × Trail vs. v3 × Road | −0.34 | 0.658 | ||
| v1 × Trail vs. v3 × Trail | −5.9 | <0.001 | ||
| v2 × Road vs. v2 × Trail | 12.49 | <0.001 | ||
| v2 × Road vs. v3 × Road | 5.65 | <0.001 | ||
| v2 × Road vs. v3 × Trail | 0.09 | 0.910 | ||
| v2 × Trail vs. v3 × Road | −6.84 | <0.001 | ||
| v2 × Trail vs. v3 × Trail | −12.4 | <0.001 | ||
| v3 × Road vs. v3 × Trail | −5.56 | <0.001 | ||
| Peak tibial acceleration (PTA, g) | Elevation × Speed | 50 m × v1 vs. 50 m × v2 | −3.290 | <0.001 |
| 50 m × v1 vs. 50 m × v3 | −5.380 | <0.001 | ||
| 50 m × v1 vs. 1000 m × v1 | 0.030 | 0.882 | ||
| 50 m × v1 vs. 1000 m × v2 | −2.740 | <0.001 | ||
| 50 m × v1 vs. 1000 m × v3 | −4.640 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v1 | −0.060 | 0.865 | ||
| 50 m × v1 vs. 2300 m × v2 | −2.580 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v3 | −4.170 | <0.001 | ||
| 50 m × v2 vs. 50 m × v3 | −2.090 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v1 | 3.320 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v2 | 0.550 | 0.111 | ||
| 50 m × v2 vs. 1000 m × v3 | −1.350 | 0.013 | ||
| 50 m × v2 vs. 2300 m × v1 | 3.230 | <0.001 | ||
| 50 m × v2 vs. 2300 m × v2 | 0.710 | 0.095 | ||
| 50 m × v2 vs. 2300 m × v3 | −0.880 | 0.088 | ||
| 50 m × v3 vs. 1000 m × v1 | 5.410 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v2 | 2.640 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v3 | 0.740 | 0.125 | ||
| 50 m × v3 vs. 2300 m × v1 | 5.320 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v2 | 2.800 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v3 | 1.210 | 0.008 | ||
| 1000 m × v1 vs. 1000 m × v2 | −2.770 | <0.001 | ||
| 1000 m × v1 vs. 1000 m × v3 | −4.670 | <0.001 | ||
| 1000 m × v1 vs. 2300 m × v1 | −0.090 | 0.813 | ||
| 1000 m × v1 vs. 2300 m × v2 | −2.610 | <0.001 | ||
| 1000 m × v1 vs. 2300 m × v3 | −4.200 | <0.001 | ||
| 1000 m × v2 vs. 1000 m × v3 | −1.900 | <0.001 | ||
| 1000 m × v2 vs. 2300 m × v1 | 2.680 | <0.001 | ||
| 1000 m × v2 vs. 2300 m × v2 | 0.160 | 0.687 | ||
| 1000 m × v2 vs. 2300 m × v3 | −1.430 | 0.019 | ||
| 1000 m × v3 vs. 2300 m × v1 | 4.580 | <0.001 | ||
| 1000 m × v3 vs. 2300 m × v2 | 2.060 | 0.002 | ||
| 1000 m × v3 vs. 2300 m × v3 | 0.470 | 0.263 | ||
| 2300 m × v1 vs. 2300 m × v2 | −2.520 | <0.001 | ||
| 2300 m × v1 vs. 2300 m × v3 | −4.110 | <0.001 | ||
| 2300 m × v2 vs. 2300 m × v3 | −1.590 | <0.001 | ||
| Speed × Surface | v1 × Road vs. v1 × Trail | −3.06 | <0.001 | |
| v1 × Road vs. v2 × Road | −5.11 | <0.001 | ||
| v1 × Road vs. v2 × Trail | −0.16 | 0.355 | ||
| v1 × Road vs. v3 × Road | −3.03 | <0.001 | ||
| v1 × Road vs. v3 × Trail | −5 | <0.001 | ||
| v1 × Trail vs. v2 × Road | −2.05 | <0.001 | ||
| v1 × Trail vs. v2 × Trail | 2.9 | <0.001 | ||
| v1 × Trail vs. v3 × Road | 0.03 | 0.859 | ||
| v1 × Trail vs. v3 × Trail | −1.94 | <0.001 | ||
| v2 × Road vs. v2 × Trail | 4.95 | <0.001 | ||
| v2 × Road vs. v3 × Road | 2.08 | <0.001 | ||
| v2 × Road vs. v3 × Trail | 0.11 | 0.423 | ||
| v2 × Trail vs. v3 × Road | −2.87 | <0.001 | ||
| v2 × Trail vs. v3 × Trail | −4.84 | <0.001 | ||
| v3 × Road vs. v3 × Trail | −1.97 | <0.001 | ||
| Residual shock (RSh, %) | Elevation × Speed | 50 m × v1 vs. 50 m × v2 | 0.1136000 | <0.001 |
| 50 m × v1 vs. 50 m × v3 | 0.1699800 | <0.001 | ||
| 50 m × v1 vs. 1000 m × v1 | −0.0130300 | 0.599 | ||
| 50 m × v1 vs. 1000 m × v2 | 0.0755100 | 0.007 | ||
| 50 m × v1 vs. 1000 m × v3 | 0.1283200 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v1 | 0.0141900 | 0.496 | ||
| 50 m × v1 vs. 2300 m × v2 | 0.0927500 | <0.001 | ||
| 50 m × v1 vs. 2300 m × v3 | 0.1355700 | <0.001 | ||
| 50 m × v2 vs. 50 m × v3 | 0.0563800 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v1 | −0.1266300 | <0.001 | ||
| 50 m × v2 vs. 1000 m × v2 | −0.0380900 | 0.066 | ||
| 50 m × v2 vs. 1000 m × v3 | 0.0147200 | 0.388 | ||
| 50 m × v2 vs. 2300 m × v1 | −0.0994100 | 0.005 | ||
| 50 m × v2 vs. 2300 m × v2 | −0.0208500 | 0.132 | ||
| 50 m × v2 vs. 2300 m × v3 | 0.0219700 | 0.188 | ||
| 50 m × v3 vs. 1000 m × v1 | −0.1830100 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v2 | −0.0944700 | <0.001 | ||
| 50 m × v3 vs. 1000 m × v3 | −0.0416600 | 0.013 | ||
| 50 m × v3 vs. 2300 m × v1 | −0.1557900 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v2 | −0.0772300 | <0.001 | ||
| 50 m × v3 vs. 2300 m × v3 | −0.0344100 | 0.018 | ||
| 1000 m × v1 vs. 1000 m × v2 | 0.0885400 | <0.001 | ||
| 1000 m × v1 vs. 1000 m × v3 | 0.1413500 | <0.001 | ||
| 1000 m × v1 vs. 2300 m × v1 | 0.0272200 | 0.412 | ||
| 1000 m × v1 vs. 2300 m × v2 | 0.1057800 | 0.002 | ||
| 1000 m × v1 vs. 2300 m × v3 | 0.1486000 | <0.001 | ||
| 1000 m × v2 vs. 1000 m × v3 | 0.0528100 | <0.001 | ||
| 1000 m × v2 vs. 2300 m × v1 | −0.0613200 | 0.079 | ||
| 1000 m × v2 vs. 2300 m × v2 | 0.0172400 | 0.361 | ||
| 1000 m × v2 vs. 2300 m × v3 | 0.0600600 | 0.029 | ||
| 1000 m × v3 vs. 2300 m × v1 | −0.1141300 | 0.010 | ||
| 1000 m × v3 vs. 2300 m × v2 | −0.0355700 | 0.098 | ||
| 1000 m × v3 vs. 2300 m × v3 | 0.0072500 | 0.723 | ||
| 2300 m × v1 vs. 2300 m × v2 | 0.0785600 | 0.004 | ||
| 2300 m × v1 vs. 2300 m × v3 | 0.1213800 | 0.001 | ||
| 2300 m × v2 vs. 2300 m × v3 | 0.0428200 | 0.008 |
Appendix A.2
Appendix A.2.1. Detailed Results on Physiological Control Variables
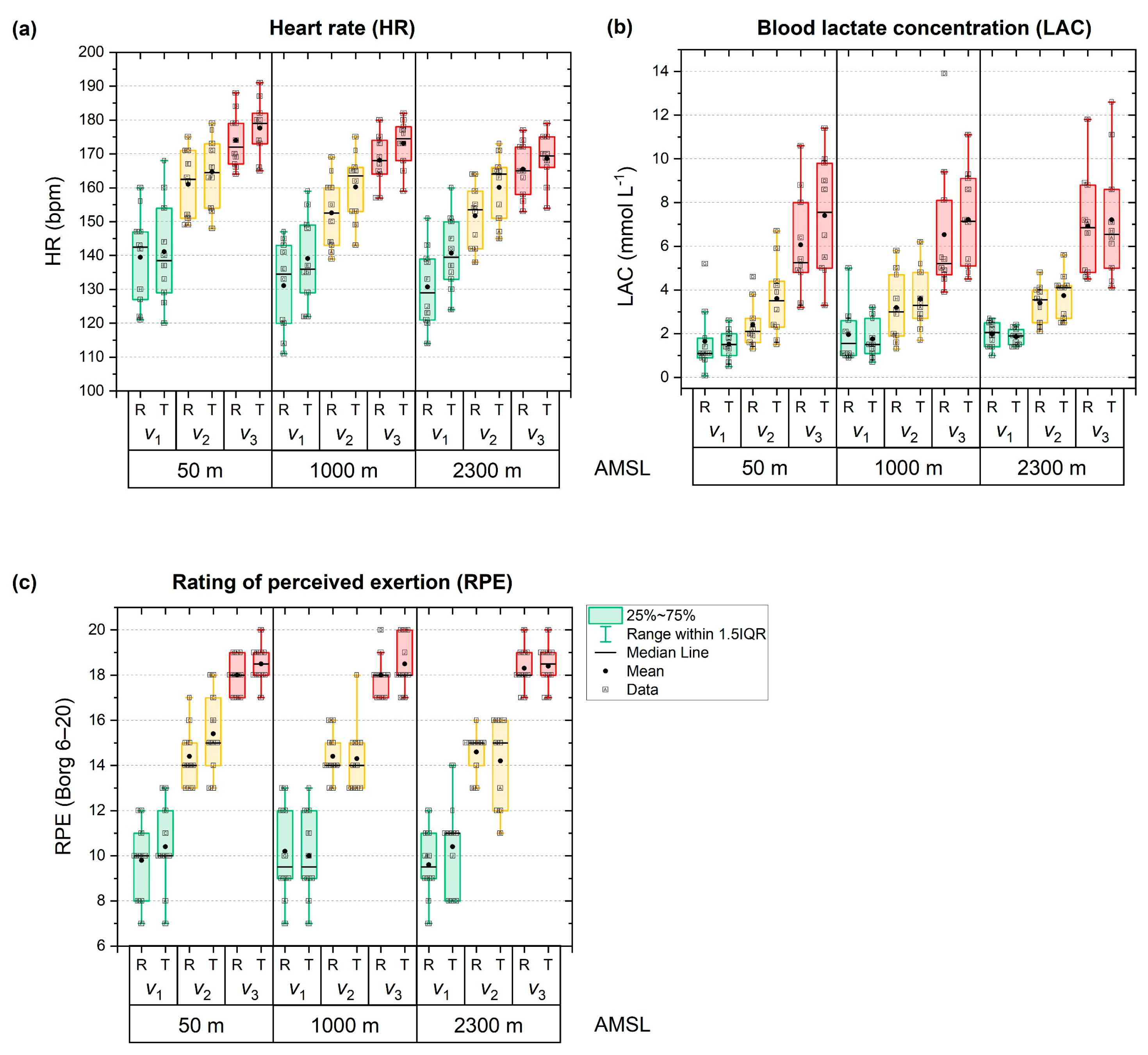
Appendix A.2.2. Detailed Discussion of Physiological Control Variables
| Load Metric | Elevation AMSL | Speed | Surface | Significance Level p and Effect Size ηp2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ROAD | TRAIL | Elevation | Speed | Surface | Elevation × Surface | Elevation × Speed | Speed × Surface | Elevation × Speed × Surface | |||
| Heart rate (HR, bpm) | 50 m | v1 | 140 ± 14 | 141 ± 15 | p < 0.001 | p < 0.001 | p < 0.001 | p = 0.045 | p = 0.011 | p = 0.164 | p = 0.002 |
| v2 | 161 ± 10 | 165 ± 11 | |||||||||
| v3 | 174 ± 8 | 178 ± 8 | |||||||||
| 1000 m | v1 | 131 ± 13 | 139 ± 13 | ||||||||
| v2 | 153 ± 11 | 160 ± 10 | |||||||||
| v3 | 168 ± 8 | 173 ± 7 | |||||||||
| 2300 m | v1 | 131 ± 12 | 141 ± 11 | ηp2 = 0.787 | ηp2 = 0.948 | ηp2 = 0.776 | ηp2 = 0.291 | ηp2 = 0.299 | ηp2 = 0.199 | ηp2 = 0.361 | |
| v2 | 152 ± 9 | 160 ± 10 | |||||||||
| v3 | 166 ± 8 | 169 ± 7 | |||||||||
| Blood lactate concentration (LAC, mmol L−1) | 50 m | v1 | 1.6 ± 1.5 | 1.5 ± 0.7 | p = 0.320 | p < 0.001 | p = 0.013 | p = 0.337 | p = 0.980 | p = 0.165 | p = 0.661 |
| v2 | 2.4 ± 1.1 | 3.6 ± 1.7 | |||||||||
| v3 | 6.1 ± 2.4 | 7.4 ± 2.7 | |||||||||
| 1000 m | v1 | 2.0 ± 1.3 | 1.8 ± 0.9 | ||||||||
| v2 | 3.2 ± 1.6 | 3.6 ± 1.4 | |||||||||
| v3 | 6.5 ± 3.1 | 7.2 ± 2.3 | |||||||||
| 2300 m | v1 | 2.0 ± 0.6 | 1.9 ± 0.4 | ηp2 = 0.119 | ηp2 = 0.862 | ηp2 = 0.514 | ηp2 = 0.114 | ηp2 = 0.011 | ηp2 = 0.181 | ηp2 = 0.039 | |
| v2 | 3.4 ± 0.9 | 3.7 ± 1.0 | |||||||||
| v3 | 6.9 ± 2.4 | 7.2 ± 2.8 | |||||||||
| Rating of perceived exertion (RPE; Borg 6–20) | 50 m | v1 | 9.8 ± 1.7 | 10.4 ± 2.0 | p = 0.812 | p < 0.001 | p = 0.051 | p = 0.525 | p = 0.491 | p = 0.695 | p = 0.043 |
| v2 | 14.4 ± 1.4 | 15.4 ± 1.8 | |||||||||
| v3 | 18.0 ± 0.8 | 18.5 ± 0.8 | |||||||||
| 1000 m | v1 | 10.2 ± 2.2 | 10.0 ± 1.9 | ||||||||
| v2 | 14.4 ± 1.1 | 14.3 ± 1.6 | |||||||||
| v3 | 18.0 ± 0.9 | 18.5 ± 1.2 | |||||||||
| 2300 m | v1 | 9.6 ± 1.5 | 10.4 ± 2.0 | ηp2 = 0.023 | ηp2 = 0.971 | ηp2 = 0.359 | ηp2 = 0.069 | ηp2 = 0.077 | ηp2 = 0.040 | ηp2 = 0.234 | |
| v2 | 14.6 ± 1.0 | 14.2 ± 2.0 | |||||||||
| v3 | 18.3 ± 0.9 | 18.4 ± 1.0 | |||||||||
| Load Metric | Factor | Post Hoc Testing | Mean Difference (95% CI) | Significance Level |
|---|---|---|---|---|
| Heart rate (HR, bpm) | Elevation | 50 vs. 1000 m AMSL | 5.6 (2.4 to 8.8) | p = 0.002 |
| 50 vs. 2300 m AMSL | 6.8 (4.5 to 9.0) | p < 0.001 | ||
| 1000 vs. 2300 m AMSL | 1.2 (−1.1 to 3.8) | p = 0.489 | ||
| Speed | v1 vs. v2 | −21 (−25 to −17) | p < 0.001 | |
| v1 vs. v3 | −34 (−42 to −26) | p < 0.001 | ||
| v2 vs. v3 | −12 (−17 to −9) | p < 0.001 | ||
| Surface | Road vs. Trail | −5.7 (3.4 to 7.9 | p < 0.001 | |
| Blood lactate concentration (LAC, mmol L−1) | Elevation | 50 vs. 1000 m AMSL | −0.3 (−1.0 to 0.4) | p = 0.814 |
| 50 vs. 2300 m AMSL | −0.4 (−1.4 to 0.5) | p = 0.698 | ||
| 1000 vs. 2300 m AMSL | −0.1 (−0.9 to 0.6) | p = 1.000 | ||
| Speed | v1 vs. v2 | −1.5 (−2.4 to −0.7) | p = 0.002 | |
| v1 vs. v3 | −5.1 (−7.0 to −3.2) | p < 0.001 | ||
| v2 vs. v3 | −3.6 (−4.9 to −2.2) | p < 0.001 | ||
| Surface | Road vs. Trail | −0.4 (−0.7 to −0.1) | p = 0.013 | |
| Rating of perceived exertion (RPE, Borg 6–20) | Elevation | 50 vs. 1000 m AMSL | 0.2 (−0.5 to 0.9) | p = 1.000 |
| 50 vs. 2300 m AMSL | 0.2 (−0.9 to 1.2) | p = 1.000 | ||
| 1000 vs. 2300 m AMSL | −0.02 (−1.0 to 1.0) | p = 1.000 | ||
| Speed | v1 vs. v2 | −4.5 (−5.1 to −3.9) | p < 0.001 | |
| v1 vs. v3 | −8.2 (−9.5 to −7.0) | p < 0.001 | ||
| v2 vs. v3 | −3.7 (−4.7 to −2.7) | p < 0.001 | ||
| Surface | Road vs. Trail | −0.3 (−0.6 to 0.002) | p = 0.051 |
References
- Wilber, R.L. Current Trends in Altitude Training. Sports Med. 2001, 31, 249–265. [Google Scholar] [CrossRef]
- Mujika, I.; Sharma, A.P.; Stellingwerff, T. Contemporary Periodization of Altitude Training for Elite Endurance Athletes: A Narrative Review. Sports Med. 2019, 49, 1651–1669. [Google Scholar] [CrossRef]
- Bonetti, D.L.; Hopkins, W.G. Sea-level exercise performance following adaptation to hypoxia: A meta-analysis. Sports Med. 2009, 39, 107–127. [Google Scholar] [CrossRef] [PubMed]
- Chapman, R.F.; Laymon Stickford, A.S.; Lundby, C.; Levine, B.D. Timing of return from altitude training for optimal sea level performance. J. Appl. Physiol. 2014, 116, 837–843. [Google Scholar] [CrossRef] [PubMed]
- Lundby, C.; Millet, G.P.; Calbet, J.A.; Bärtsch, P.; Subudhi, A.W. Does ‘altitude training’ increase exercise performance in elite athletes? Br. J. Sports Med. 2012, 46, 792–795. [Google Scholar] [CrossRef] [PubMed]
- Lundby, C.; Nielsen, T.K.; Dela, F.; Damsgaard, R. The influence of intermittent altitude exposure to 4100 m on exercise capacity and blood variables. Scand. J. Med. Sci. Sports 2005, 15, 182–187. [Google Scholar] [CrossRef]
- Lundby, C.; Araoz, M.; van Hall, G. Peak heart rate decreases with increasing severity of acute hypoxia. High Alt. Med. Biol. 2001, 2, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Lundby, C.; Saltin, B.; van Hall, G. The ‘lactate paradox’, evidence for a transient change in the course of acclimatization to severe hypoxia in lowlanders. Acta Physiol. Scand. 2000, 170, 265–269. [Google Scholar] [CrossRef]
- Levine, B.D.; Stray-Gundersen, J. “Living high-training low”: Effect of moderate-altitude acclimatization with low-altitude training on performance. J. Appl. Physiol. 1997, 83, 102–112. [Google Scholar] [CrossRef]
- Friedmann, B.; Bärtsch, P. High altitude training: Benefits, problems, trends. Der Orthopäde 1997, 26, 987–992. [Google Scholar] [CrossRef]
- Gore, C.J.; Sharpe, K.; Garvican-Lewis, L.A.; Saunders, P.U.; Humberstone, C.E.; Robertson, E.Y.; Wachsmuth, N.B.; Clark, S.A.; McLean, B.D.; Friedmann-Bette, B.; et al. Altitude training and haemoglobin mass from the optimised carbon monoxide rebreathing method determined by a meta-analysis. Br. J. Sports Med. 2013, 47, i31–39. [Google Scholar] [CrossRef]
- Geiser, J.; Vogt, M.; Billeter, R.; Zuleger, C.; Belforti, F.; Hoppeler, H. Training high-living low: Changes of aerobic performance and muscle structure with training at simulated altitude. Int. J. Sports Med. 2001, 22, 579–585. [Google Scholar] [CrossRef]
- Hamlin, M.J.; Lizamore, C.A.; Hopkins, W.G. The Effect of Natural or Simulated Altitude Training on High-Intensity Intermittent Running Performance in Team-Sport Athletes: A Meta-Analysis. Sports Med. 2018, 48, 431–446. [Google Scholar] [CrossRef]
- Treml, B.; Gatterer, H.; Burtscher, J.; Kleinsasser, A.; Burtscher, M. A Focused Review on the Maximal Exercise Responses in Hypo- and Normobaric Hypoxia: Divergent Oxygen Uptake and Ventilation Responses. Int. J. Environ. Res. Public Health 2020, 17, 5239. [Google Scholar] [CrossRef]
- Friedmann, B.; Frese, F.; Menold, E.; Bärtsch, P. Effects of acute moderate hypoxia on anaerobic capacity in endurance-trained runners. Eur. J. Appl. Physiol. 2007, 101, 67–73. [Google Scholar] [CrossRef]
- Midgley, A.W.; McNaughton, L.R.; Jones, A.M. Training to enhance the physiological determinants of long-distance running performance: Can valid recommendations be given to runners and coaches based on current scientific knowledge? Sports Med. 2007, 37, 857–880. [Google Scholar] [CrossRef] [PubMed]
- Fleckenstein, D.; Ueberschär, O.; Wüstenfeld, J.C.; Rüdrich, P.; Wolfarth, B. Effect of Uphill Running on VO2, Heart Rate and Lactate Accumulation on Lower Body Positive Pressure Treadmills. Sports 2021, 9, 51. [Google Scholar] [CrossRef] [PubMed]
- Ueberschär, O.; Fleckenstein, D.; Warschun, F.; Kränzler, S.; Walter, N.; Hoppe, M.W. Measuring biomechanical loads and asymmetries in junior elite long-distance runners through triaxial inertial sensors. Sports Orthop. Traumatol. 2019, 35, 296–308. [Google Scholar] [CrossRef]
- Ueberschär, O.; Fleckenstein, D.; Warschun, F.; Walter, N.; Hoppe, M.W. Case report on lateral asymmetries in two junior elite long-distance runners during a high-altitude training camp. Sports Orthop. Traumatol. 2019, 35, 399–406. [Google Scholar] [CrossRef]
- Miltko, A.; Milner, C.E.; Powell, D.W.; Paquette, M.R. The influence of surface and speed on biomechanical external loads obtained from wearable devices in rearfoot strike runners. Sports Biomech. 2025, 24, 541–555. [Google Scholar] [CrossRef]
- Moon, G.R.; Leary, B.K.; Nguyen, A.-D.; McCrory, J.L. A comparison of running biomechanics on track, asphalt, grass, and treadmill using wearable sensors. Sports Biomech. 2025, 24, 2766–2778. [Google Scholar] [CrossRef]
- Catalá-Vilaplana, I.; Encarnación-Martínez, A.; Camacho-García, A.; Sanchis-Sanchis, R.; Pérez-Soriano, P. Influence of surface condition and prolonged running on impact accelerations. Sports Biomech. 2025, 24, 1064–1078. [Google Scholar] [CrossRef]
- Li Tee, C.C.; Chong, M.C.; Sundar, V.; Chok, C.L.; Md Razali, M.R.; Yeo, W.K.; Girard, O. Influence of exercise intensity and hypoxic exposure on physiological, perceptual and biomechanical responses to treadmill running. Eur. J. Sport Sci. 2023, 23, 1581–1590. [Google Scholar] [CrossRef]
- Riedl, M.; Schwesig, R.; Ueberschär, O. Effect of various carbon plate running shoes on peak tibial accelerations, lateral asymmetry and shock attenuation in running. Sci. Rep. 2025, under review. [Google Scholar]
- Rasmussen, J.; Skejø, S.; Waagepetersen, R.P. Predicting Tissue Loads in Running from Inertial Measurement Units. Sensors 2023, 23, 9836. [Google Scholar] [CrossRef]
- Matijevich, E.S.; Scott, L.R.; Volgyesi, P.; Derry, K.H.; Zelik, K.E. Combining wearable sensor signals, machine learning and biomechanics to estimate tibial bone force and damage during running. Hum. Mov. Sci. 2020, 74, 102690. [Google Scholar] [CrossRef]
- Derie, R.; Robberechts, P.; Van den Berghe, P.; Gerlo, J.; De Clercq, D.; Segers, V.; Davis, J. Tibial acceleration-based prediction of maximal vertical loading rate during overground running: A machine learning approach. Front. Bioeng. Biotechnol. 2020, 8, 33. [Google Scholar] [CrossRef] [PubMed]
- Sheerin, K.R.; Reid, D.; Besier, T.F. The measurement of tibial acceleration in runners—A review of the factors that can affect tibial acceleration during running and evidence-based guidelines for its use. Gait Posture 2019, 67, 12–24. [Google Scholar] [CrossRef] [PubMed]
- Sheerin, K.R.; Besier, T.F.; Reid, D.; Hume, P.A. The one-week and six-month reliability and variability of three-dimensional tibial acceleration in runners. Sports Biomech. 2018, 17, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Sheerin, K.R.; Besier, T.F.; Reid, D. The influence of running velocity on resultant tibial acceleration in runners. Sports Biomech. 2018, 19, 750–760. [Google Scholar] [CrossRef]
- Sheerin, K.; Besier, T.; Reid, D.; Hume, P. The Reliability and variability of three-dimensional tibial Acceleration during running. In Proceedings of the 34th International Conference of Biomechanics in Sport, Tsukuba, Japan, 18–22 July 2016. [Google Scholar]
- Zhang, J.H.; An, W.W.; Au, I.P.H.; Chen, T.L.; Cheung, R.T.H. Comparison of the correlations between impact loading rates and peak accelerations measured at two different body sites: Intra- and inter-subject analysis. Gait Posture 2016, 46, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.; Strout, Z.A.; Shull, P.B. Accurate Impact Loading Rate Estimation During Running via a Subject-Independent Convolutional Neural Network Model and Optimal IMU Placement. IEEE J. Biomed. Health Inform. 2021, 25, 1215–1222. [Google Scholar] [CrossRef]
- Zandbergen, M.A.; Ter Wengel, X.J.; van Middelaar, R.P.; Buurke, J.H.; Veltink, P.H.; Reenalda, J. Peak tibial acceleration should not be used as indicator of tibial bone loading during running. Sports Biomech. 2023, 24, 2953–2970. [Google Scholar] [CrossRef]
- Waite, N.; Goetschius, J.; Lauver, J.D. Effect of grade and surface type on peak tibial acceleration in trained distance runners. J. Appl. Biomech. 2020, 37, 2–5. [Google Scholar] [CrossRef]
- Garcia, M.C.; Gust, G.; Bazett-Jones, D.M. Tibial acceleration and shock attenuation while running over different surfaces in a trail environment. J. Sci. Med. Sport 2021, 24, 1161–1165. [Google Scholar] [CrossRef]
- Zifchock, R.A.; Davis, I.; Hamill, J. Kinetic asymmetry in female runners with and without retrospective tibial stress fractures. J. Biomech. 2006, 39, 2792–2797. [Google Scholar] [CrossRef]
- Zifchock, R.A.; Davis, I.; Higginson, J.; McCaw, S.; Royer, T. Side-to-side differences in overuse running injury susceptibility: A retrospective study. Hum. Mov. Sci. 2008, 27, 888–902. [Google Scholar] [CrossRef]
- Willwacher, S.; Kurz, M.; Robbin, J.; Thelen, M.; Hamill, J.; Kelly, L.; Mai, P. Running-Related Biomechanical Risk Factors for Overuse Injuries in Distance Runners: A Systematic Review Considering Injury Specificity and the Potentials for Future Research. Sports Med. 2022, 52, 1863–1877. [Google Scholar] [CrossRef] [PubMed]
- Alda-Blanco, A.; Rodríguez-Barbero, S.; Rodrigo-Carranza, V.; Valero, F.; Chico, P.; González-Mohíno, F. Influence of Running Surface Using Advanced Footwear Technology Spikes on Middle- and Long-Distance Running Performance Measures. Sports 2024, 12, 329. [Google Scholar] [CrossRef] [PubMed]
- Riedl, M.; von Diecken, C.; Ueberschär, O. One Shoe to Fit Them All? Effect of Various Carbon Plate Running Shoes on Running Economy in Male and Female Amateur Triathletes and Runners at Individual Training and Race Paces. Appl. Sci. 2024, 14, 11535. [Google Scholar] [CrossRef]
- Ueberschär, O.; Fleckenstein, D.; Warschun, F.; Walter, N.; Wüstenfeld, J.C.; Wolfarth, B.; Hoppe, M.W. Energy cost of running under hypogravity in well-trained runners and triathletes: A biomechanical perspective. Int. J. Comput. Sci. Sport 2019, 18, 60–80. [Google Scholar] [CrossRef]
- Jones, A.M.; Doust, J.H. A 1% treadmill grade most accurately reflects the energetic cost of outdoor running. J. Sports Sci. 1996, 14, 321–327. [Google Scholar] [CrossRef]
- Jacko, T.; Bartsch, J.; von Diecken, C.; Ueberschär, O. Validity of Current Smartwatches for Triathlon Training: How Accurate Are Heart Rate, Distance, and Swimming Readings? Sensors 2024, 24, 4675. [Google Scholar] [CrossRef]
- Borg, G.; Ljunggren, G.; Ceci, R. The increase of perceived exertion, aches and pain in the legs, heart rate and blood lactate during exercise on a bicycle ergometer. Eur. J. Appl. Physiol. Occup. Physiol. 1985, 54, 343–349. [Google Scholar] [CrossRef]
- Sitko, S.; Artetxe, X.; Bonnevie-Svendsen, M.; Galán-Rioja, M.Á.; Gallo, G.; Grappe, F.; Leo, P.; Mateo, M.; Mujika, I.; Sanders, D. What Is “Zone 2 Training”?: Experts’ Viewpoint on Definition, Training Methods, and Expected Adaptations. Int. J. Sports Physiol. Perform. 2025, 1, 1614–1617. [Google Scholar] [CrossRef] [PubMed]
- Dill, D.B. Oxygen used in horizontal and grade walking and running on the treadmill. J. Appl. Physiol. 1965, 20, 19–22. [Google Scholar] [CrossRef]
- Chen, M.J.; Fan, X.; Moe, S.T. Criterion-related validity of the Borg ratings of perceived exertion scale in healthy individuals: A meta-analysis. J. Sports Sci. 2002, 20, 873–899. [Google Scholar] [CrossRef]
- Scherr, J.; Wolfarth, B.; Christle, J.W.; Pressler, A.; Wagenpfeil, S.; Halle, M. Associations between Borg’s rating of perceived exertion and physiological measures of exercise intensity. Eur. J. Appl. Physiol. 2013, 113, 147–155. [Google Scholar] [CrossRef]
- Wehrlin, J.P.; Hallén, J. Linear decrease in and performance with increasing altitude in endurance athletes. Eur. J. Appl. Physiol. 2006, 96, 404–412. [Google Scholar] [CrossRef] [PubMed]
- Saunders, P.U.; Pyne, D.B.; Gore, C.J. Endurance training at altitude. High Alt. Med. Biol. 2009, 10, 135–148. [Google Scholar] [CrossRef] [PubMed]
- Fercher, C.; Bartsch, J.; Kluge, S.; Schneider, F.; Liedtke, A.M.; Schleichardt, A.; Ueberschär, O. Applying Multi-Purpose Commercial Inertial Sensors for Monitoring Equine Locomotion in Equestrian Training. Sensors 2024, 24, 8170. [Google Scholar] [CrossRef]
- Lang, C.; Schleichardt, A.; Warschun, F.; Walter, N.; Fleckenstein, D.; Berkel, F.; Ueberschär, O. Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners. Sports 2023, 11, 204. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Leacox, A.; Fashingbauer, L.; Ferguson, T.; Zajakowski, A.; Baum, B.; Reinking, M. The Effect of Running Speed on Cadence and Running Kinetics. Int J Sports Phys Ther 2025, 20, 957–963. [Google Scholar] [CrossRef] [PubMed]
- Lambert, M.I.; Mbambo, Z.H.; Gibson, A.S.C. Heart rate during training and competition for longdistance running. J. Sports Sci. 1998, 16, 85–90. [Google Scholar] [CrossRef]
- Faude, O.; Kindermann, W.; Meyer, T. Lactate threshold concepts: How valid are they? Sports Med. 2009, 39, 469–490. [Google Scholar] [CrossRef] [PubMed]
- Fleckenstein, D.; Seelhöfer, J.; Walter, N.; Ueberschär, O. From Incremental Test to Continuous Running at Fixed Lactate Thresholds: Individual Responses on %VO2max, %HRmax, Lactate Accumulation, and RPE. Sports 2023, 11, 198. [Google Scholar] [CrossRef]
| Characteristic | Mean ± SD | Range |
|---|---|---|
| Age (years) | 28.2 ± 9.2 | 18–44 |
| Stature (cm) | 176.0 ± 7.8 | 162.0–187.0 |
| Body mass (kg) | 68.2 ± 8.1 | 58.0–82.3 |
| BMI (kg m−2) | 22.1 ± 2.4 | 17.8–25.1 |
| Weekly exercise load (hours per week) | 10.7 ± 3.7 | 5.0–16.0 |
| Weekly running mileage (km) | 29.5 ± 13.5 | 10.0–50.0 |
| Personal best 10 km road running (mm:ss) | 42:36 ± 06:12 | 33:26–57:00 |
| Performance Outcome | Mean ± SD | Range | |
|---|---|---|---|
| Achieved maximal running speed (km h−1) | 17.0 ± 1.7 | 14.3–20.0 | 100.0 ± 0.0 |
| HRpeak (bpm) | 190 ± 6.3 | 178–200 | 100.0 ± 0.0 |
| VEpeak (L min−1) | 132 ± 24 | 101.2–177.3 | 100.0 ± 0.0 |
| (mL min−1 kg−1) | 54.9 ± 5.9 | 47–66 | 100.0 ± 0.0 |
| LACex (mmol L−1) | 10.4 ± 3.6 | 6.0–17.3 | – |
| RPE (Borg 20) | 20 ± 0 | 20–20 | 100.0 ± 0.0 |
| vVT1 (km h−1) | 10.4 ± 0.7 | 9.4–12.0 | 69.1 ± 8.9 |
| vVT2 (km h−1) | 15.0 ± 1.6 | 12.3–17.8 | 93.9 ± 3.8 |
| v1 (km h−1) | 9.4 ± 0.8 | 8.5–11.3 | 62.2 ± 8.0 |
| v2 (km h−1) | 12.7 ± 1.2 | 11.3–15.2 | 81.5 ± 6.4 |
| v3 (km h−1) | 14.9 ± 1.9 | 12.2–17.8 | 93.9 ± 3.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Ueberschär, O.; Riedl, M.; Fleckenstein, D.; Falz, R. Effects of Acute Altitude, Speed and Surface on Biomechanical Loading in Distance Running. Sensors 2026, 26, 276. https://doi.org/10.3390/s26010276
Ueberschär O, Riedl M, Fleckenstein D, Falz R. Effects of Acute Altitude, Speed and Surface on Biomechanical Loading in Distance Running. Sensors. 2026; 26(1):276. https://doi.org/10.3390/s26010276
Chicago/Turabian StyleUeberschär, Olaf, Marlene Riedl, Daniel Fleckenstein, and Roberto Falz. 2026. "Effects of Acute Altitude, Speed and Surface on Biomechanical Loading in Distance Running" Sensors 26, no. 1: 276. https://doi.org/10.3390/s26010276
APA StyleUeberschär, O., Riedl, M., Fleckenstein, D., & Falz, R. (2026). Effects of Acute Altitude, Speed and Surface on Biomechanical Loading in Distance Running. Sensors, 26(1), 276. https://doi.org/10.3390/s26010276








