Covert Communication Scheme for OOK in Asymmetric Noise Systems
Abstract
1. Introduction
2. Related Works
- (1)
- This work investigates the covertness performance of an OOK coding scheme in asymmetric Gaussian noise environments, where the “on” and “off” symbols exhibit asymmetry both in geometric structure and probability distribution. This inherent asymmetry distinguishes OOK codebooks fundamentally from centrally symmetric ones such as BPSK and QAM. As a result, conventional analytical methods that rely on uniformly distributed symbols and symmetric constellations are inadequate for accurately analyzing the covertness and transmission performance of an OOK coding scheme in asymmetric Gaussian noise environments. To address this issue, our work overcomes this limitation by providing a more generalized theoretical framework for analyzing OOK-based covert communication in asymmetric noise systems.
- (2)
- Existing studies have demonstrated that the initial phase angle imposed by the transmitter on the transmitted symbols has a negligible effect on the covertness performance of the codebook in asymmetric noise systems. However, our study reveals that in asymmetric noise systems, the phase angle plays a crucial role in covert communication. Specifically, under covertness constraint, the optimal phase angle that maximizes the transmission rate is not fixed but is influenced by the asymmetry of the noise components, tending to align with the direction of the weaker noise component.
3. System Model
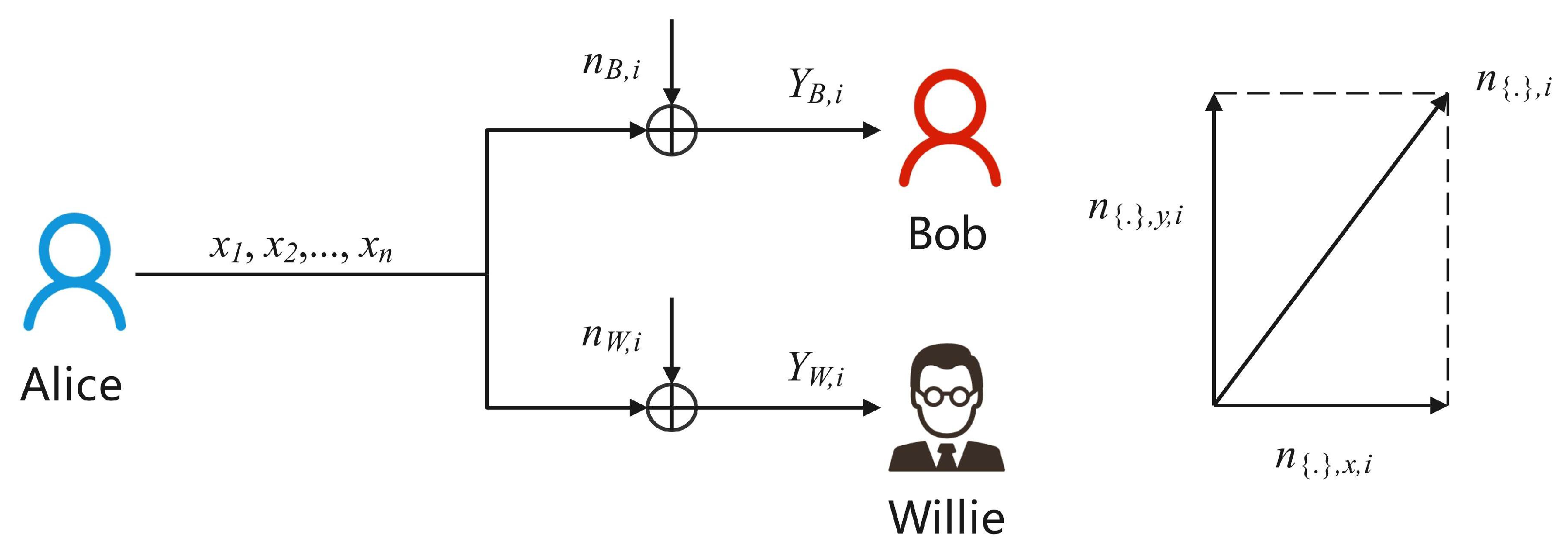
3.1. Communication Scenario
3.2. Codebook Construction
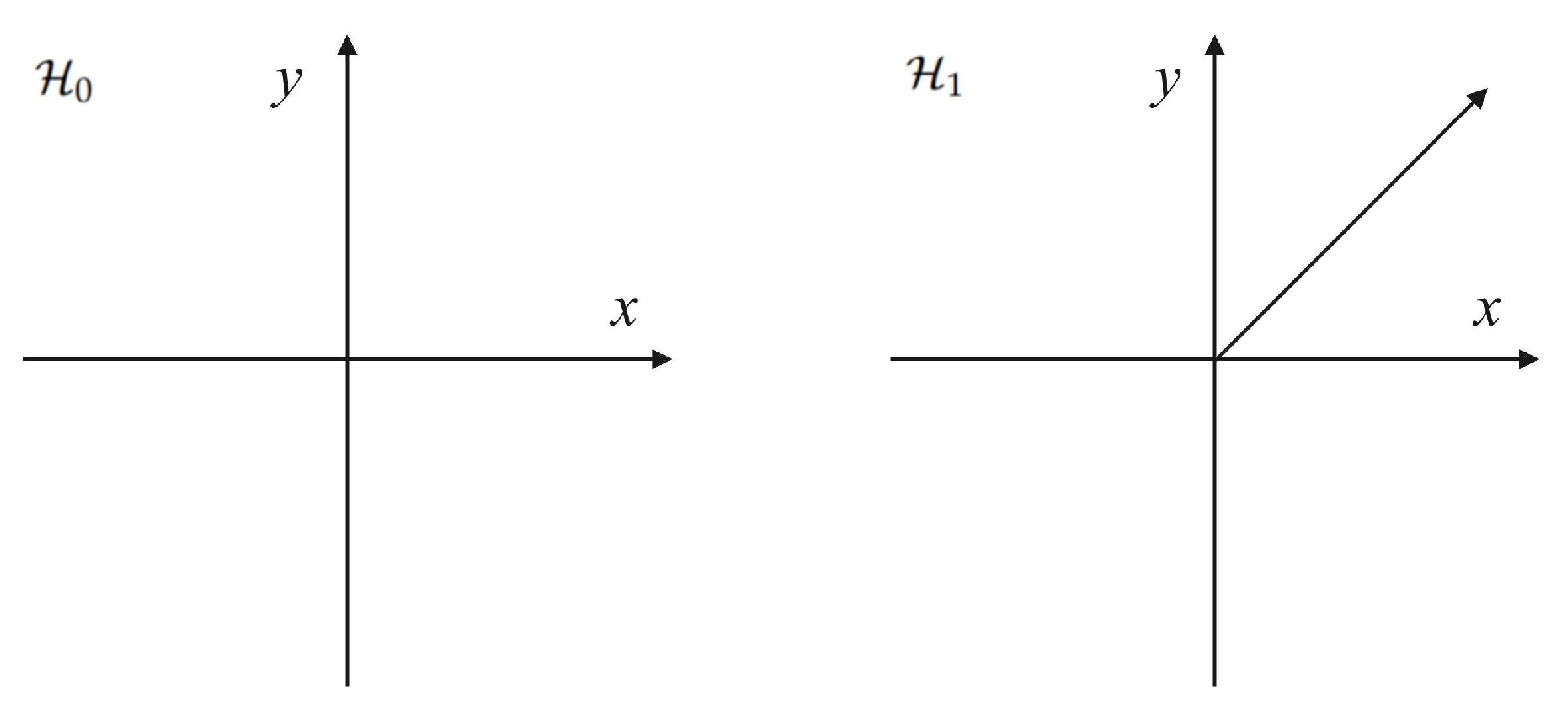
3.3. Hypothesis Test
3.4. Performance Analysis of the Covert Transmission
3.5. Problem Formulation
4. Performance Analysis of the Covert Transmission
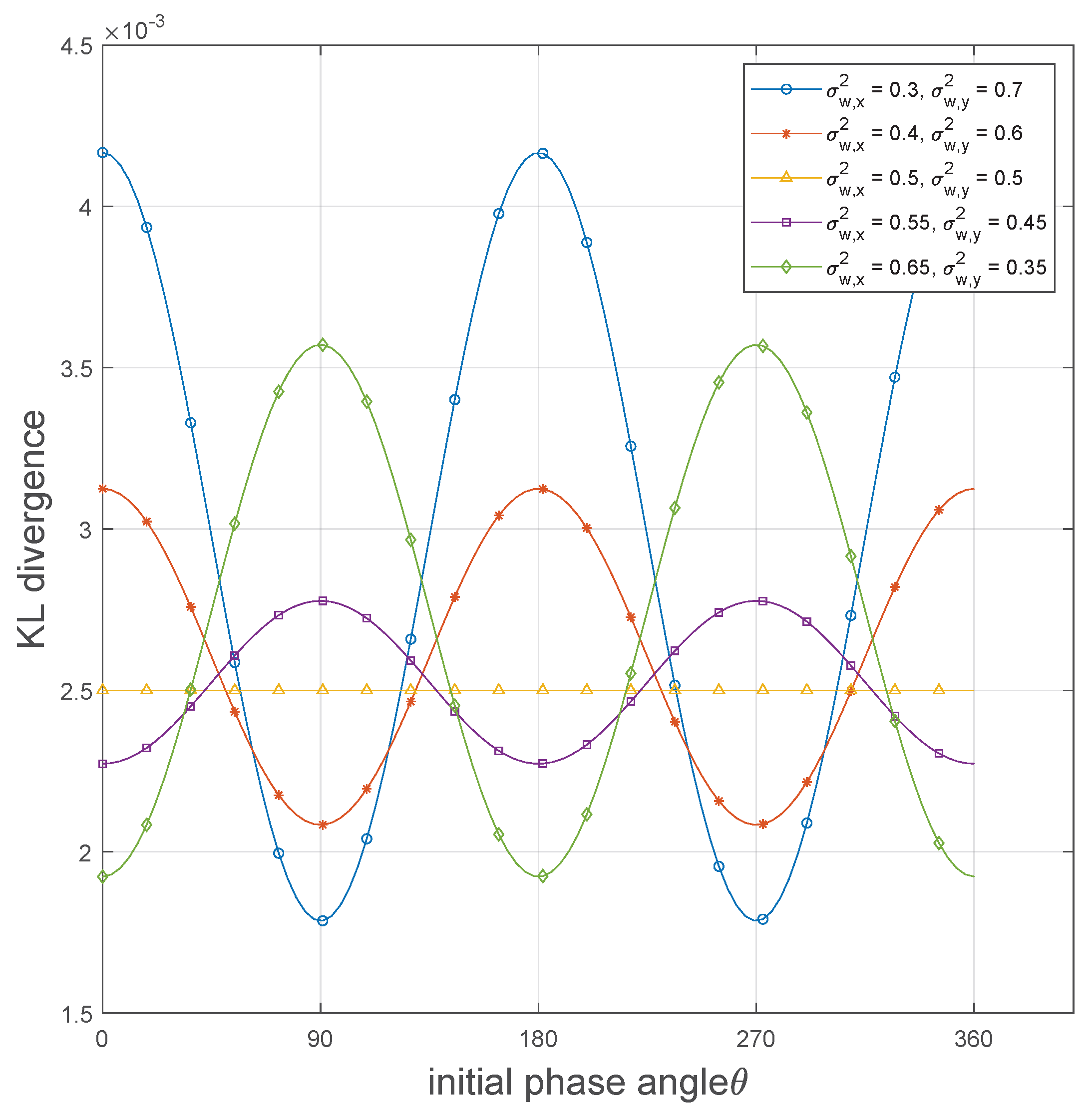
4.1. Analysis of Covertness Performance
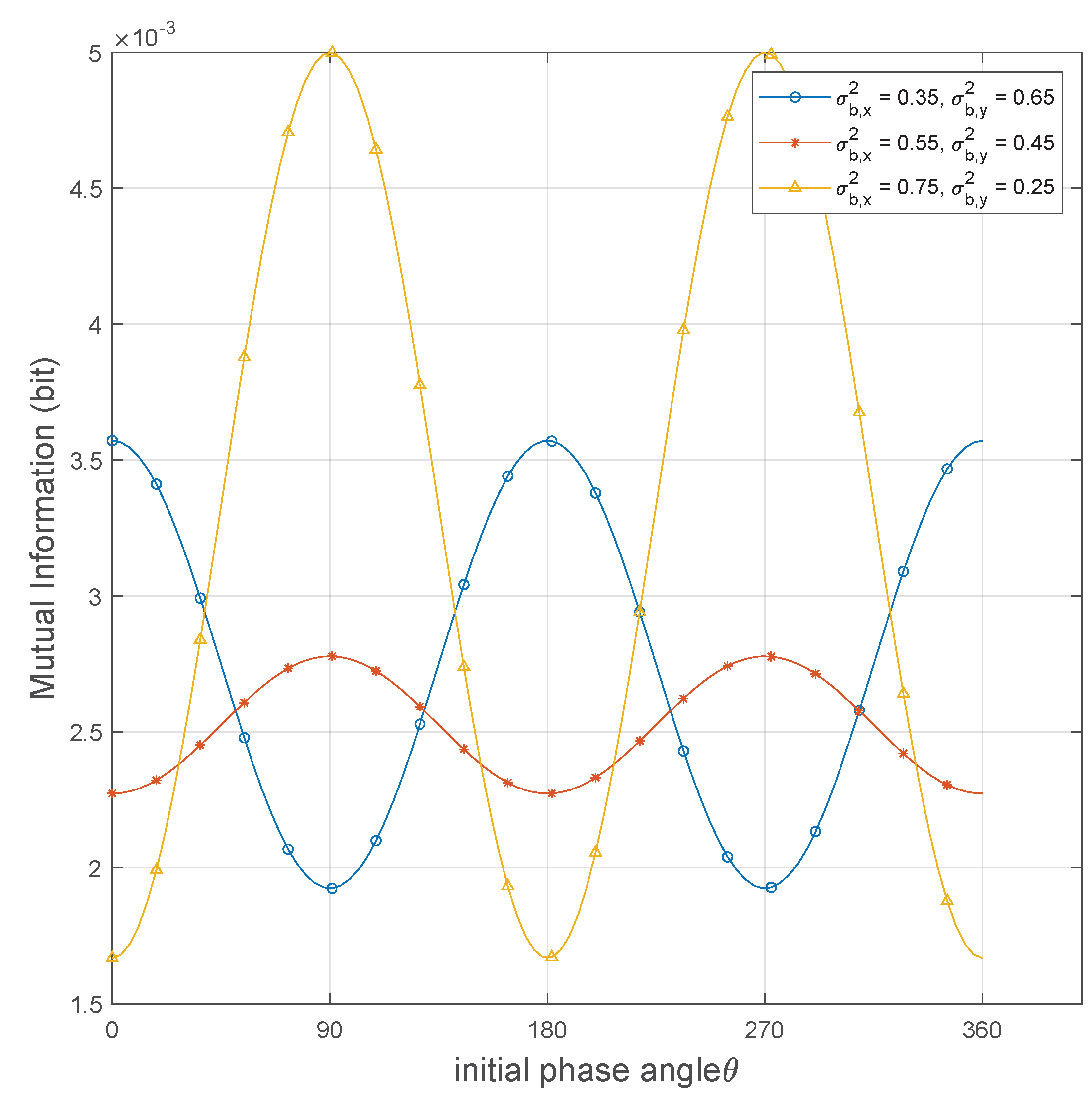
4.2. Analysis of Transmission Performance
5. Design of Amplitude Gain and Phase Angle
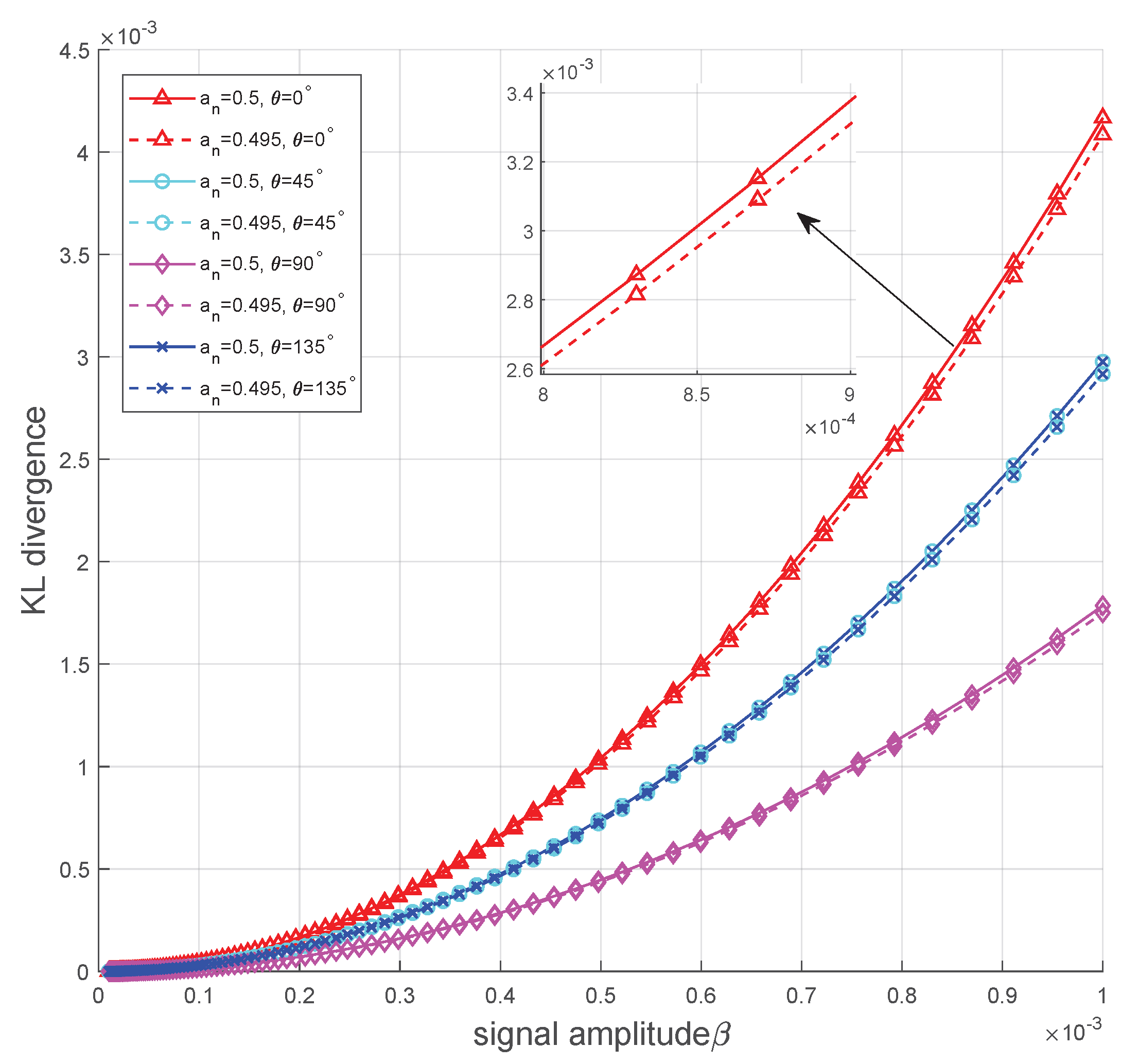
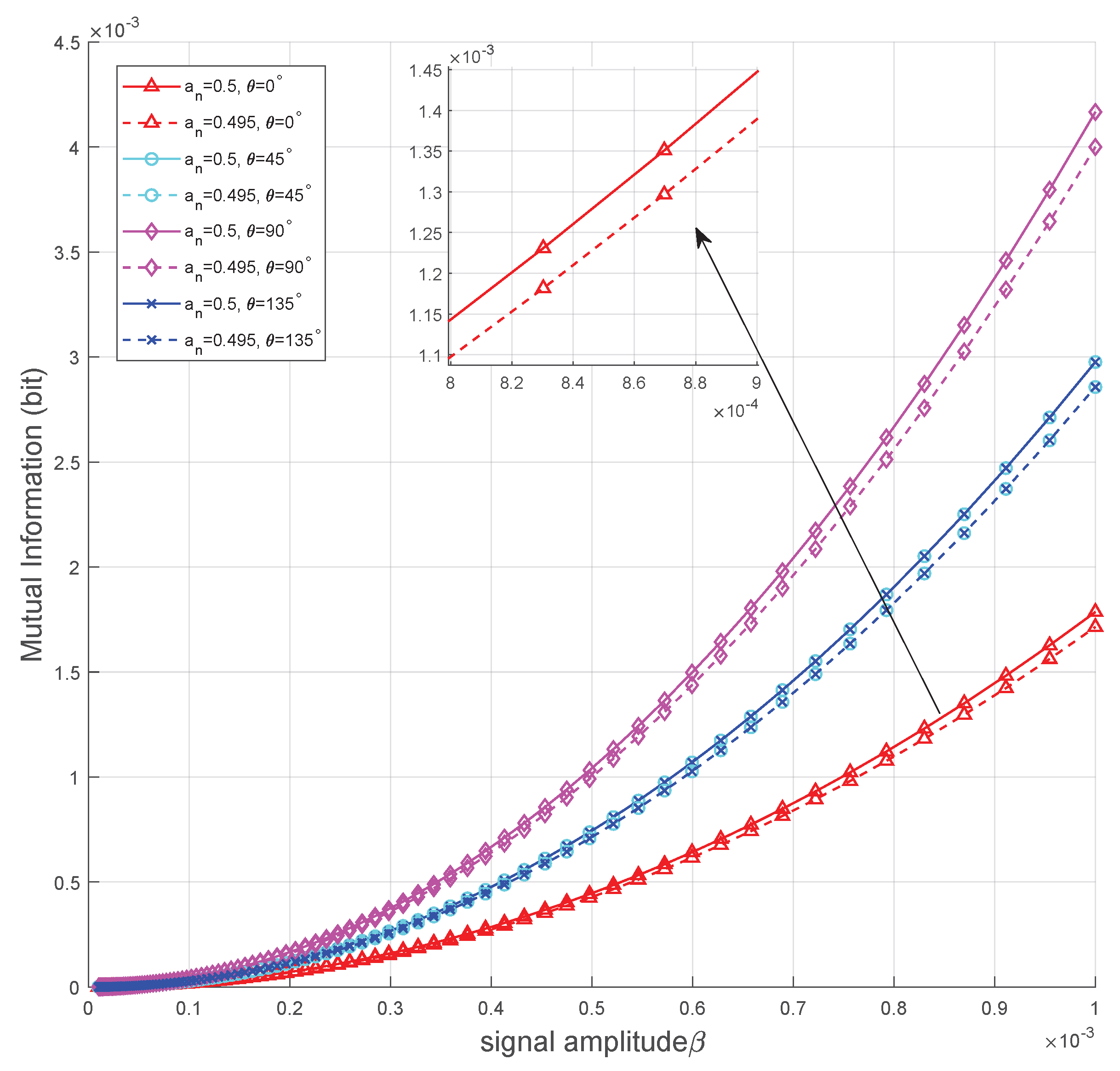
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BPSK | Binary Phase-Shift Keying |
| PLS | Physical-Layer Security |
| NOMA | Non-Orthogonal Multiple Access |
| AWGN | Additive White Gaussian Noise |
| KL | Kullback–Leibler divergence |
| IoT | Internet of Things |
| RRC | root-raised cosine |
References
- Lu, Y.; Xu, L.D. Internet of Things (IoT) Cybersecurity Research: A Review of Current Research Topics. IEEE Internet Things J. 2019, 6, 2103–2115. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Boudreau, G.; Sediq, A.B.; Abou-Zeid, H. A Multi-Dimensional Intelligent Multiple Access Technique for 5G Beyond and 6G Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 1308–1320. [Google Scholar] [CrossRef]
- Heng, Y.; Andrews, J.G.; Mo, J.; Va, V.; Ali, A.; Ng, B.L.; Zhang, J.C. Six Key Challenges for Beam Management in 5.5G and 6G Systems. IEEE Commun. Mag. 2021, 59, 74–79. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Li, Q. Physical Layer Security for Full Duplex Relay System. In Proceedings of the 2023 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Beijing, China, 14–16 June 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of Physical Layer Security in Multiuser Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1550–1573. [Google Scholar] [CrossRef]
- Zhou, Z.; Mu, Y.; Wu, Q.M.J. Coverless image steganography using partial-duplicate image retrieval. Soft Comput. 2019, 23, 4927–4938. [Google Scholar] [CrossRef]
- Ker, A.D. A Capacity Result for Batch Steganography. IEEE Signal Process. Lett. 2007, 14, 525–528. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; An, J.; Xiong, Z.; Xing, C.; Zhao, N.; Niyato, D. Covert Communication Assisted by UAV-IRS. IEEE Trans. Commun. 2023, 71, 357–369. [Google Scholar] [CrossRef]
- Iqbal, A.; Tham, M.L.; Wong, Y.J.; Al-Habashna, A.; Wainer, G.; Zhu, Y.X.; Dagiuklas, T. Empowering Non-Terrestrial Networks With Artificial Intelligence: A Survey. IEEE Access 2023, 11, 100986–101006. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zeng, Y.; Ma, J. Covert Wireless Communication in IoT Network: From AWGN Channel to THz Band. IEEE Internet Things J. 2020, 7, 3378–3388. [Google Scholar] [CrossRef]
- Gao, C.; Yang, B.; Jiang, X.; Inamura, H.; Fukushi, M. Covert Communication in Relay-Assisted IoT Systems. IEEE Internet Things J. 2021, 8, 6313–6323. [Google Scholar] [CrossRef]
- Chen, X.; An, J.; Xiong, Z.; Xing, C.; Zhao, N.; Yu, F.R.; Nallanathan, A. Covert Communications: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2023, 25, 1173–1198. [Google Scholar] [CrossRef]
- Yan, S.; Cong, Y.; Hanly, S.V.; Zhou, X. Gaussian Signalling for Covert Communications. IEEE Trans. Wirel. Commun. 2019, 18, 3542–3553. [Google Scholar] [CrossRef]
- Soderi, S.; Nicola, R.D. CONNECTION: Covert Channel Network Attack through Bit-rate Modulation. In Emerging Information Security and Applications; Springer: Singapore, 2024; pp. 164–183. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, R.; Lin, Z.; Zhang, R.; Cai, Y.; Wu, W.; Wang, J. Improving Age of Information for Covert Communication With Time-Modulated Arrays. IEEE Internet Things J. 2025, 12, 1718–1731. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Guan, X.; Lu, X.; Song, Y.; Chen, D. Covert mmWave Communications with Finite Blocklength Against Spatially Random Wardens. IEEE Internet Things J. 2024, 11, 3402–3416. [Google Scholar] [CrossRef]
- Liu, S.; Khan, M.A.; Bilal, M.; Zuberi, H.H. Low Probability Detection Constrained Underwater Acoustic Communication: A Comprehensive Review. IEEE Commun. Mag. 2025, 63, 21–30. [Google Scholar] [CrossRef]
- Ma, X.; Wang, B.; Tian, W.; Ding, X.; Han, Z. Strategic Game Model for AUV-Assisted Underwater Acoustic Covert Communication in Ocean Internet of Things. IEEE Internet Things J. 2024, 11, 22508–22520. [Google Scholar] [CrossRef]
- Ghazy, A.S.; Kaddoum, G.; Satinder, S. IRS-Aided Secure Reliable Underwater Acoustic Communications. IEEE Trans. Veh. Technol. 2024, 73, 16861–16875. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, T.; Rasheed, W.; Hu, X.; Zhao, C. An Enlarging-the-Capacity Packet Sorting Covert Channel. IEEE Access 2019, 7, 145634–145640. [Google Scholar] [CrossRef]
- Taheri, S.; Mahdavi, M.; Moghim, N. A dynamic timing-storage covert channel in vehicular ad hoc networks. Telecommun. Syst. 2018, 69, 415–429. [Google Scholar] [CrossRef]
- Zander, S.; Armitage, G.; Branch, P. A survey of covert channels and countermeasures in computer network protocols. IEEE Commun. Surv. Tutor. 2007, 9, 44–57. [Google Scholar] [CrossRef]
- Cui, J.; Yan, S.; Hu, J.; Li, N.; Chen, R.; Li, J. How Does Repetition Coding Enable Reliable and Covert Communications? IEEE Wirel. Commun. Lett. 2021, 10, 639–643. [Google Scholar] [CrossRef]
- Topal, O.A.; Kurt, G.K. Covert Communication in Cooperative NOMA Networks. In Proceedings of the 2020 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Ahmadzadeh, S.A.; Agnew, G. Turbo covert channel: An iterative framework for covert communication over data networks. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2031–2039. [Google Scholar] [CrossRef]
- Ji, X.; Zhu, R.; Zhang, Q.; Li, C.; Cao, D. Enhancing Covert Communication in OOK Schemes by Phase Deflection. IEEE Trans. Inf. Forensics Secur. 2024, 19, 9775–9788. [Google Scholar] [CrossRef]
- Bash, B.A.; Goeckel, D.; Towsley, D. Limits of Reliable Communication with Low Probability of Detection on AWGN Channels. IEEE J. Sel. Areas Commun. 2013, 31, 1921–1930. [Google Scholar] [CrossRef]
- Che, P.H.; Bakshi, M.; Jaggi, S. Reliable deniable communication: Hiding messages in noise. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 2945–2949. [Google Scholar] [CrossRef]
- Tahmasbi, M.; Bloch, M.R. First- and Second-Order Asymptotics in Covert Communication. IEEE Trans. Inf. Theory 2019, 65, 2190–2212. [Google Scholar] [CrossRef]
- Bloch, M.R. Covert Communication Over Noisy Channels: A Resolvability Perspective. IEEE Trans. Inf. Theory 2016, 62, 2334–2354. [Google Scholar] [CrossRef]
- Wang, L.; Wornell, G.W.; Zheng, L. Fundamental Limits of Communication With Low Probability of Detection. IEEE Trans. Inf. Theory 2016, 62, 3493–3503. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Koksal, C.E. Fundamental limits of covert communication over MIMO AWGN channel. In Proceedings of the 2017 IEEE Conference on Communications and Network Security (CNS), Las Vegas, NV, USA, 9–11 October 2017; pp. 1–9. [Google Scholar] [CrossRef]
- Bendary, A.; Abdelaziz, A.; Koksal, C.E. Achieving Positive Covert Capacity Over MIMO AWGN Channels. IEEE J. Sel. Areas Inf. Theory 2021, 2, 149–162. [Google Scholar] [CrossRef]
- Arumugam, K.S.K.; Bloch, M.R. Covert Communication Over a K -User Multiple-Access Channel. IEEE Trans. Inf. Theory 2019, 65, 7020–7044. [Google Scholar] [CrossRef]
- Kumar Arumugam, K.S.; Bloch, M.R. Embedding Covert Information in Broadcast Communications. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2787–2801. [Google Scholar] [CrossRef]
- Tan, V.Y.F.; Lee, S.H. Time-Division is Optimal for Covert Communication Over Some Broadcast Channels. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1377–1389. [Google Scholar] [CrossRef]
- Zhang, Q.; Bakshi, M.; Jaggi, S. Covert Communication Over Adversarially Jammed Channels. IEEE Trans. Inf. Theory 2021, 67, 6096–6121. [Google Scholar] [CrossRef]
- Zhang, Q.E.; Bloch, M.R.; Bakshi, M.; Jaggi, S. Undetectable Radios: Covert Communication under Spectral Mask Constraints. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 992–996. [Google Scholar] [CrossRef]
- Hayashi, M.; Vázquez-Castro, Á. Covert Communication With Gaussian Noise: From Random Access Channel to Point-to-Point Channel. IEEE Trans. Commun. 2024, 72, 1516–1531. [Google Scholar] [CrossRef]
- He, B.; Yan, S.; Zhou, X.; Lau, V.K.N. On Covert Communication With Noise Uncertainty. IEEE Commun. Lett. 2017, 21, 941–944. [Google Scholar] [CrossRef]
- Zeng, Y.; Liang, Y.C.; Hoang, A.T.; Peh, E.C.Y. Reliability of Spectrum Sensing Under Noise and Interference Uncertainty. In Proceedings of the 2009 IEEE International Conference on Communications Workshops, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Qiao, S.; Zhu, R.; Ji, X.; Zhao, J.; Ding, H. Optimization of Covert Communication in Multi-Sensor Asymmetric Noise Systems. Sensors 2024, 24, 796. [Google Scholar] [CrossRef]
- Kadampot, I.A.; Tahmasbi, M.; Bloch, M.R. Codes for Covert Communication over Additive White Gaussian Noise Channels. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 977–981. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Ji, X.; Zhu, R. Covert Communication Scheme for OOK in Asymmetric Noise Systems. Sensors 2025, 25, 2948. https://doi.org/10.3390/s25092948
Xu W, Ji X, Zhu R. Covert Communication Scheme for OOK in Asymmetric Noise Systems. Sensors. 2025; 25(9):2948. https://doi.org/10.3390/s25092948
Chicago/Turabian StyleXu, Weicheng, Xiaopeng Ji, and Ruizhi Zhu. 2025. "Covert Communication Scheme for OOK in Asymmetric Noise Systems" Sensors 25, no. 9: 2948. https://doi.org/10.3390/s25092948
APA StyleXu, W., Ji, X., & Zhu, R. (2025). Covert Communication Scheme for OOK in Asymmetric Noise Systems. Sensors, 25(9), 2948. https://doi.org/10.3390/s25092948





