Parameter Calculation and Rotor Structure Optimization Design of Solid Rotor Induction Motors
Abstract
Highlights
- A generalized electromagnetic analytical model for solid rotor motors has been developed, which can consider the effects of rotor structure, saturation and eddy currents.
- Optimized design of slotted and squirrel cage solid rotor induction motors is presented.
- A simple and accurate method for calculating electromagnetic parameters of solid rotor induction motors is provided.
- Technical support for the optimal design of solid rotor induction motors is provided.
Abstract
1. Introduction
- (1)
- A multilayer electromagnetic analytical model considering the saturation effect of solid rotor has been established by combining the equivalent magnetic circuit method, the layered method and the magnetization curve, which is capable of accurately solving the magnetic field distribution and electromagnetic parameters of solid rotor induction motors with different rotor structures.
- (2)
- A multi-objective optimization design of solid rotor induction motors with different rotor structures has been carried out using analytical and finite element methods, and this method improves the design efficiency of the motors.
2. Electromagnetic Field Modeling
2.1. Motor Structure
2.2. Generalized Multilayer Magnetic Field Analytical Model
- (1)
- End coefficients are used to consider the effect of solid rotor end effects.
- (2)
- infinite magnetic permeability of the stator core.
- (3)
- The influence of hysteresis effect of the core is neglected.
- (4)
- The value of the radial magnetic field remains constant through the air gap.
2.3. Generalized Equivalent Circuit Model
3. Optimized Design of Rotor Structures
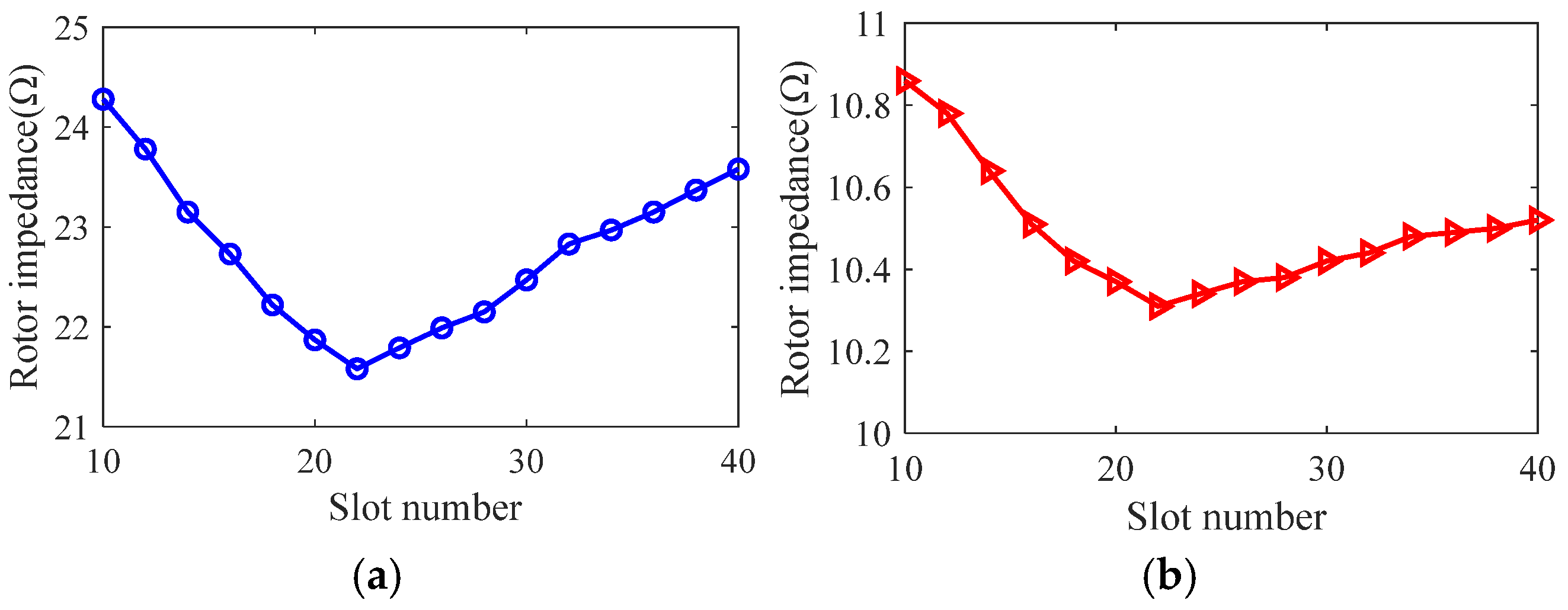
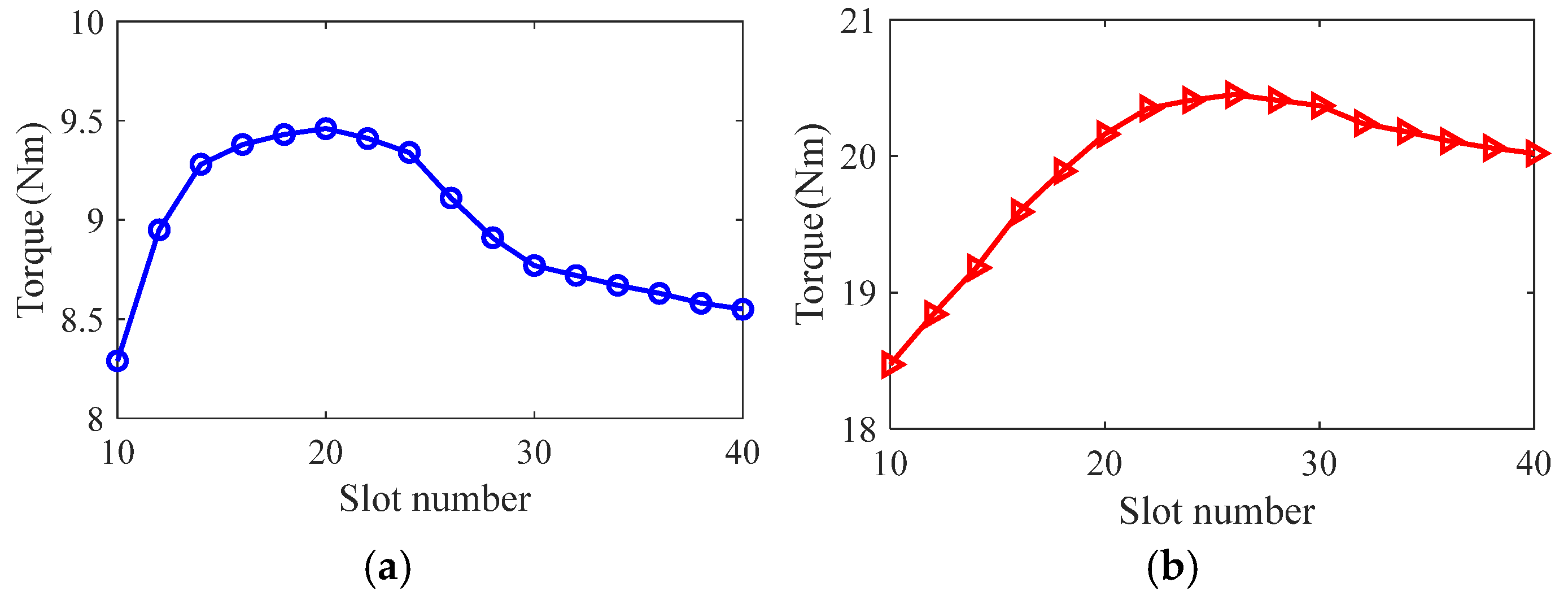
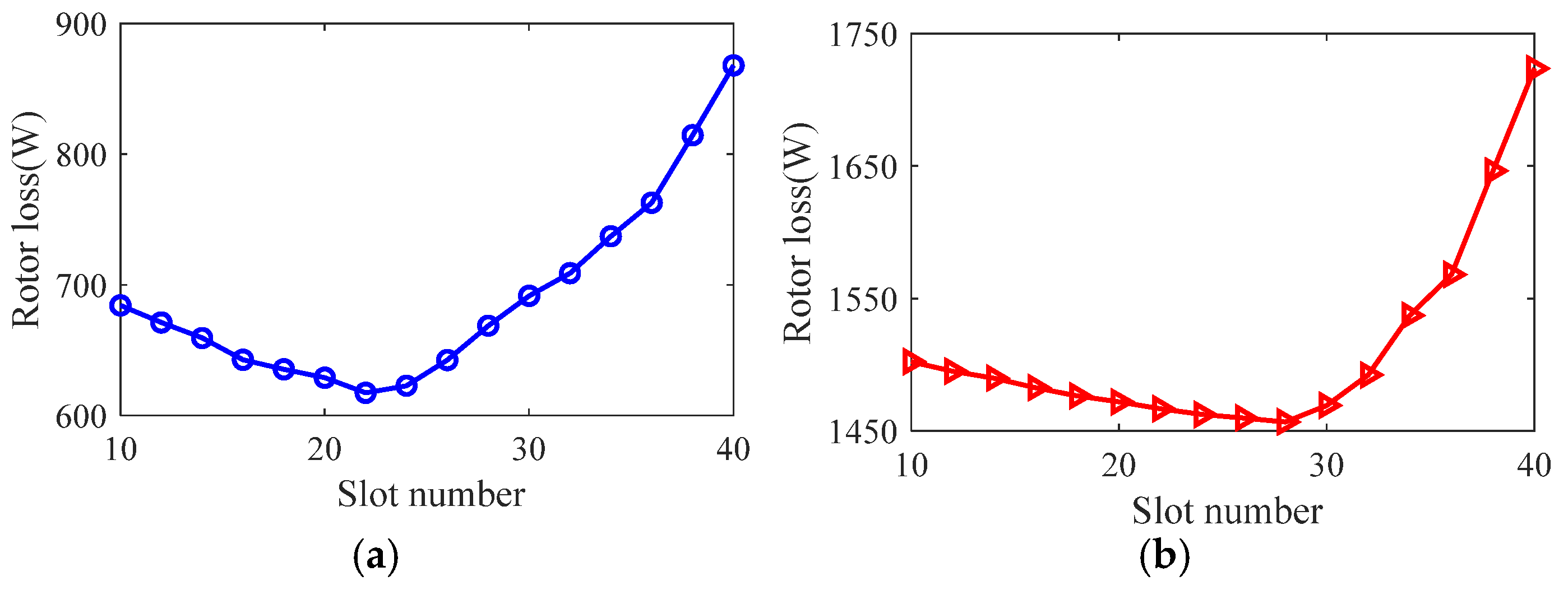
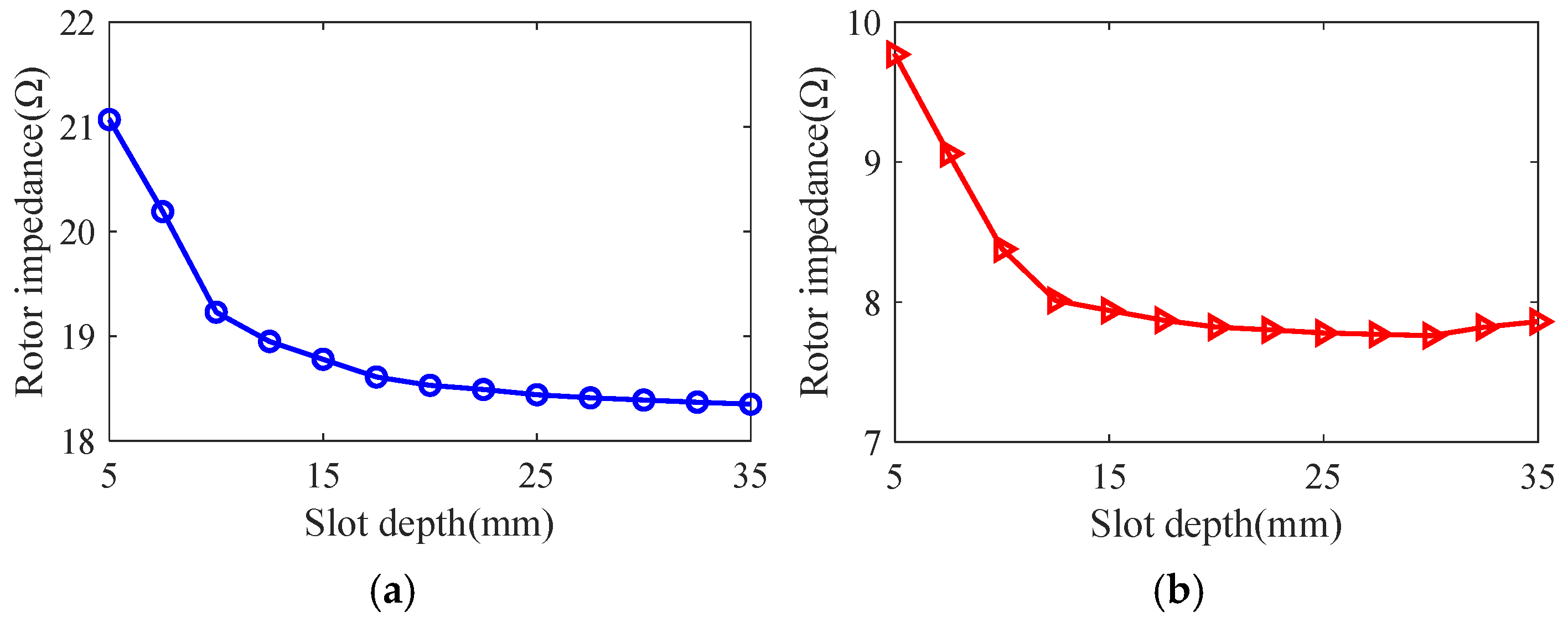
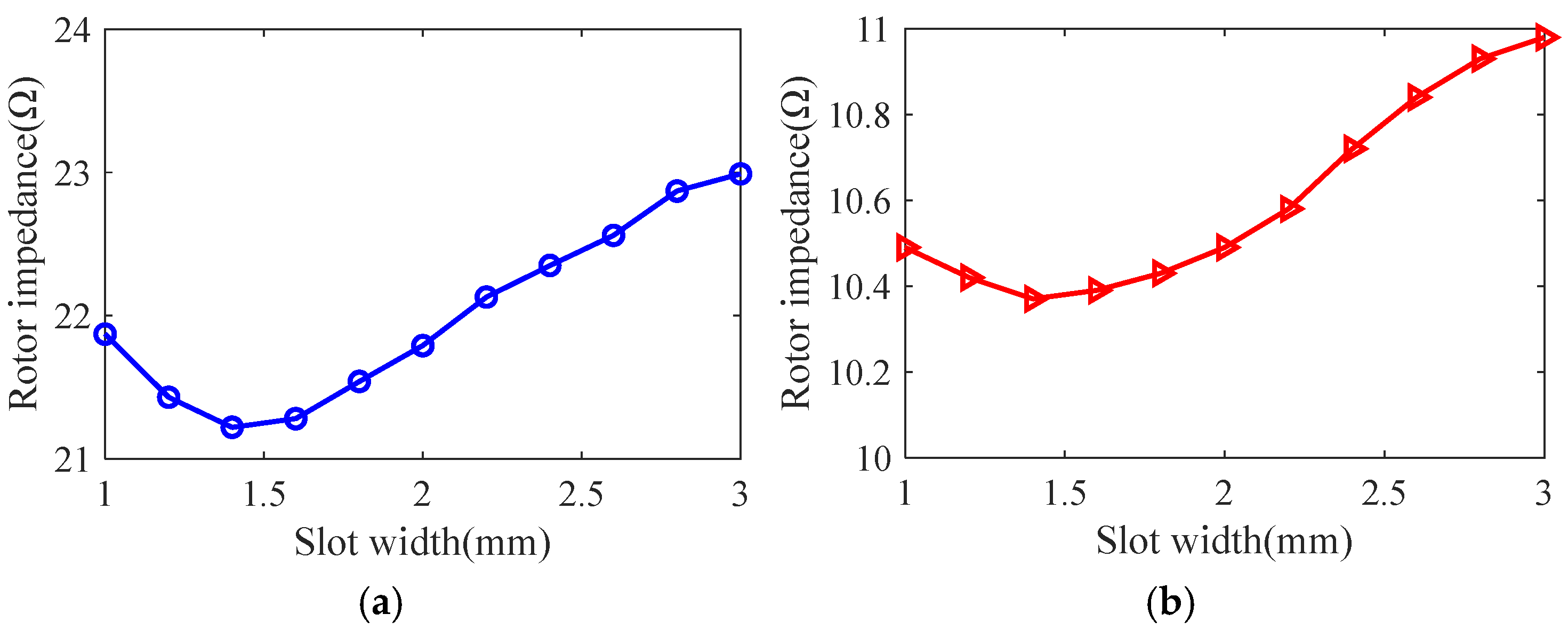
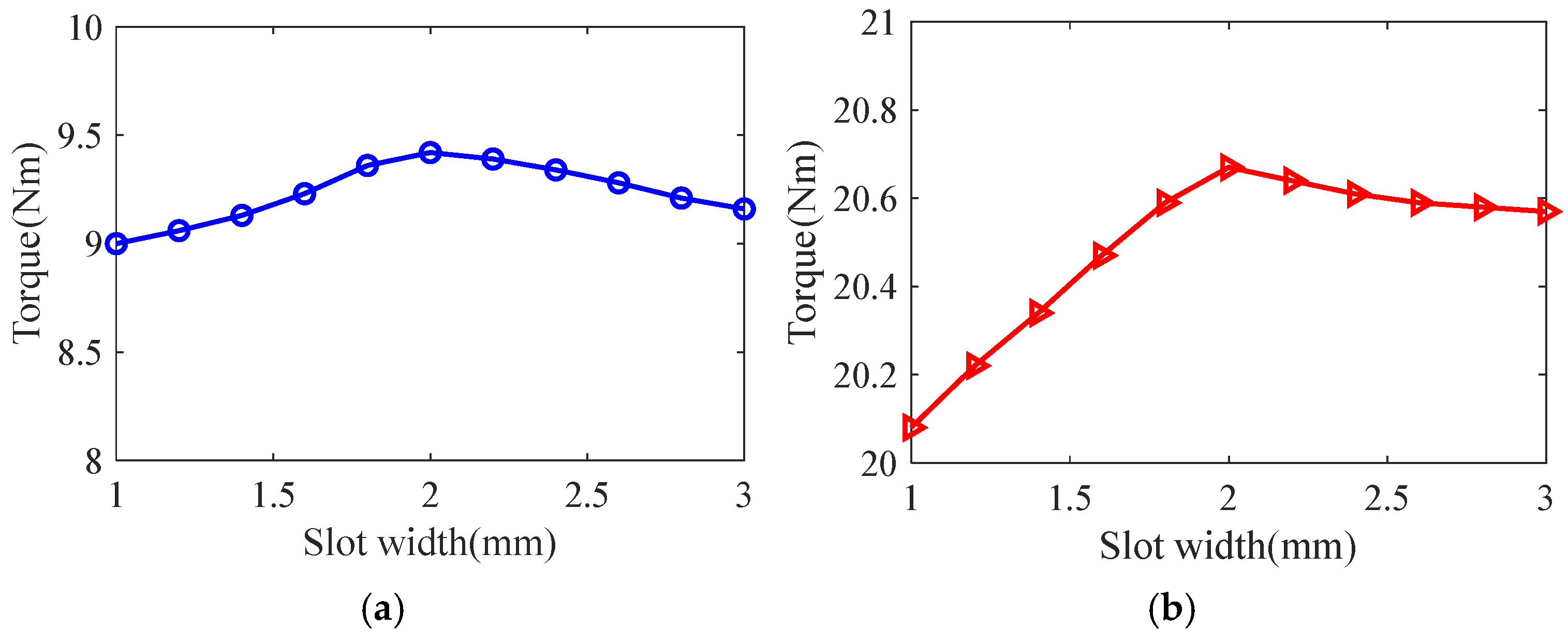
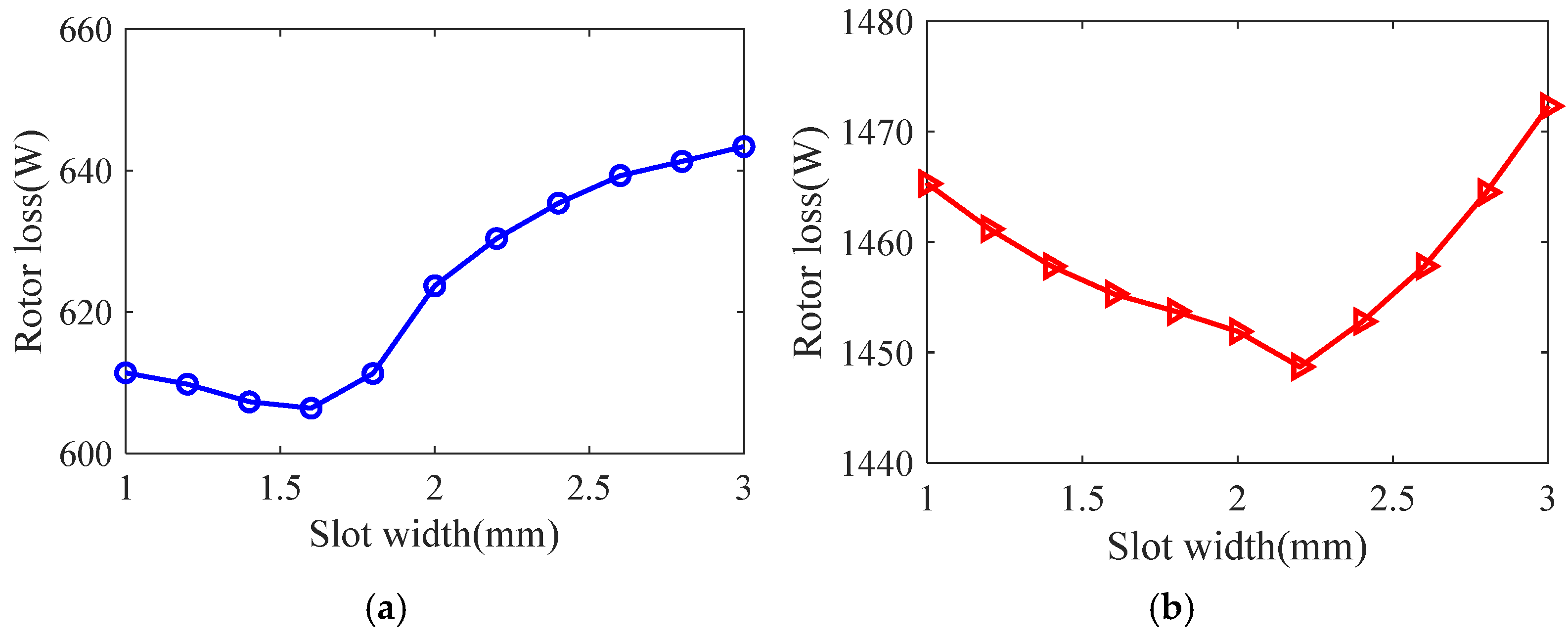
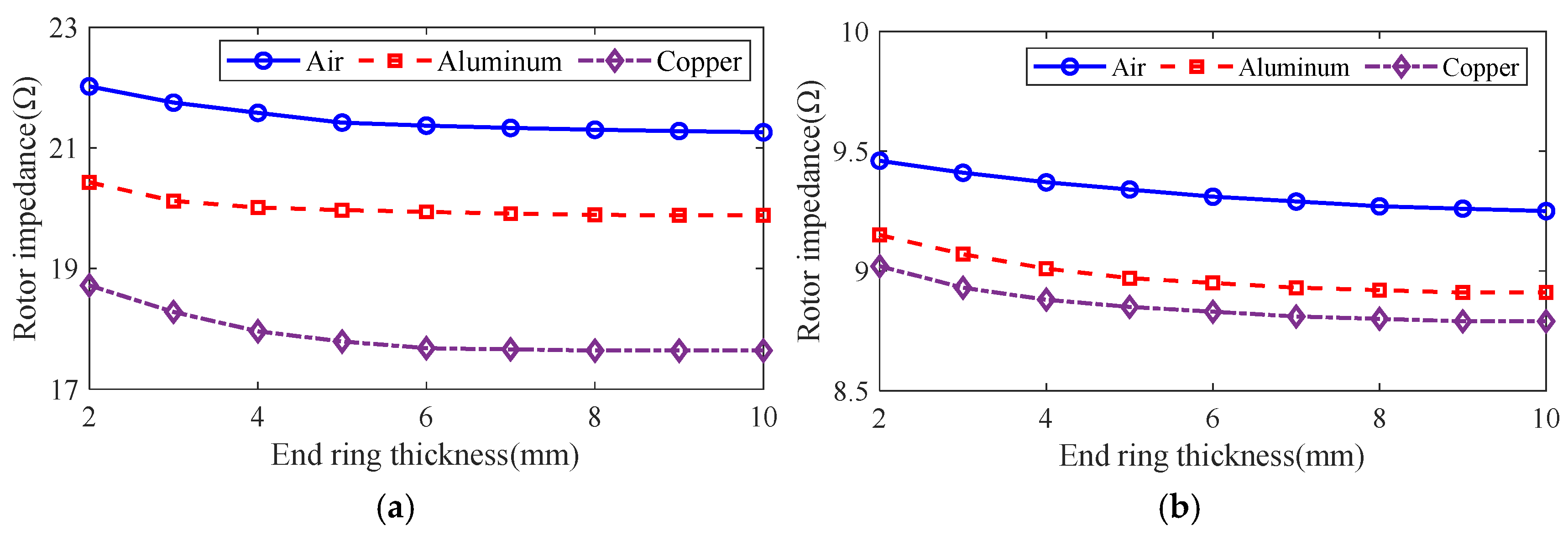
3.1. Effect of Optimization Variables on Motor Performance
3.2. Optimization Goal Analysis
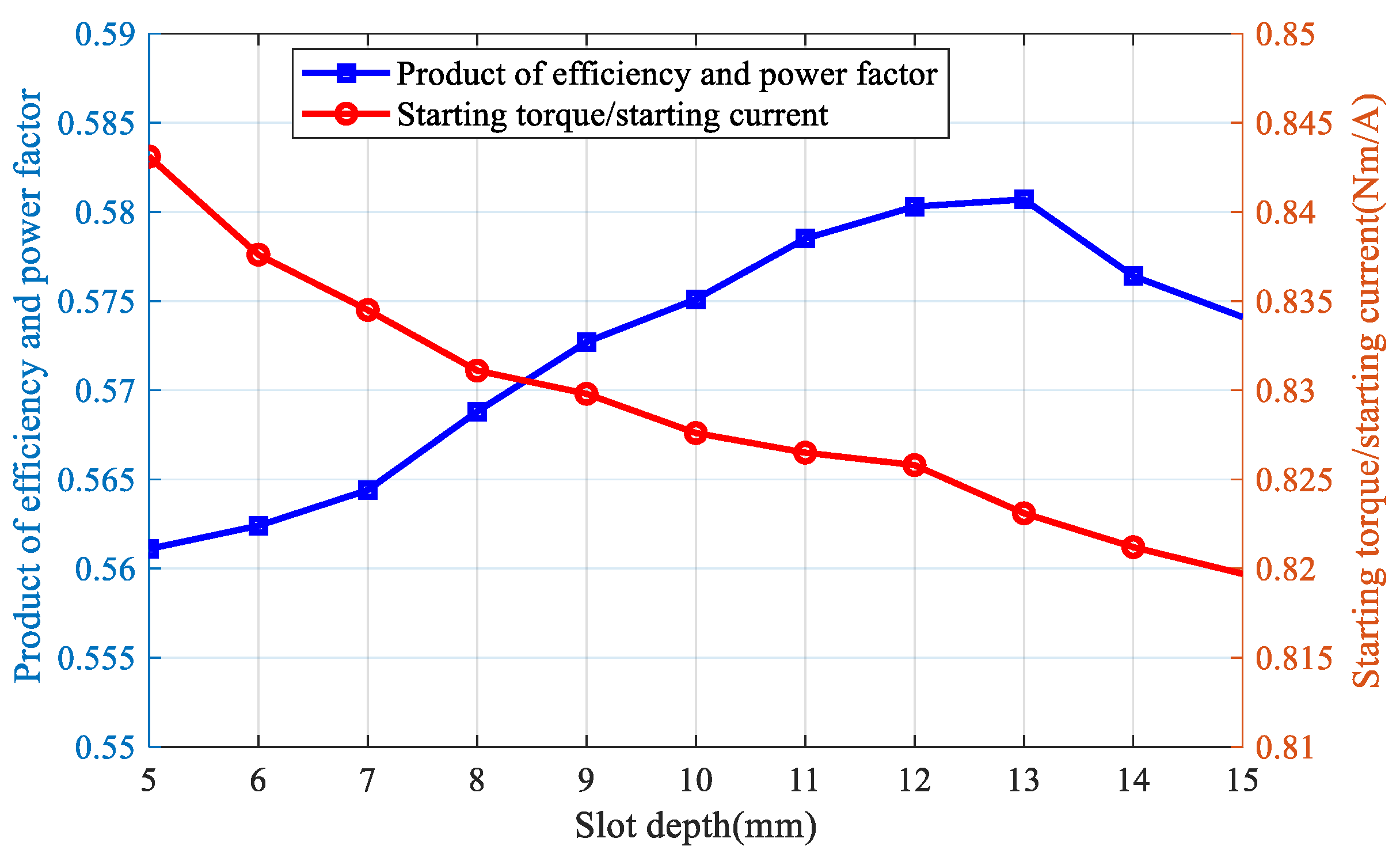
3.3. Optimized Design of Slotted Solid Rotors
- (1)
- To minimize the vibration of the motor, low-order electromagnetic force wave should be avoided. And the tooth harmonics related to the number of slots in the stator and rotor are the main components of the electromagnetic force wave, and the order can be expressed aswhere .
- (2)
- To minimize the additional losses, a close groove fit with fewer grooves should be used.
- (3)
- To limit the asynchronous additional torque generated by the tooth harmonic magnetic potential, the following equation should be satisfied.
- (4)
- To avoid synchronizing additional torque during motor operation, the following equation should be avoided.
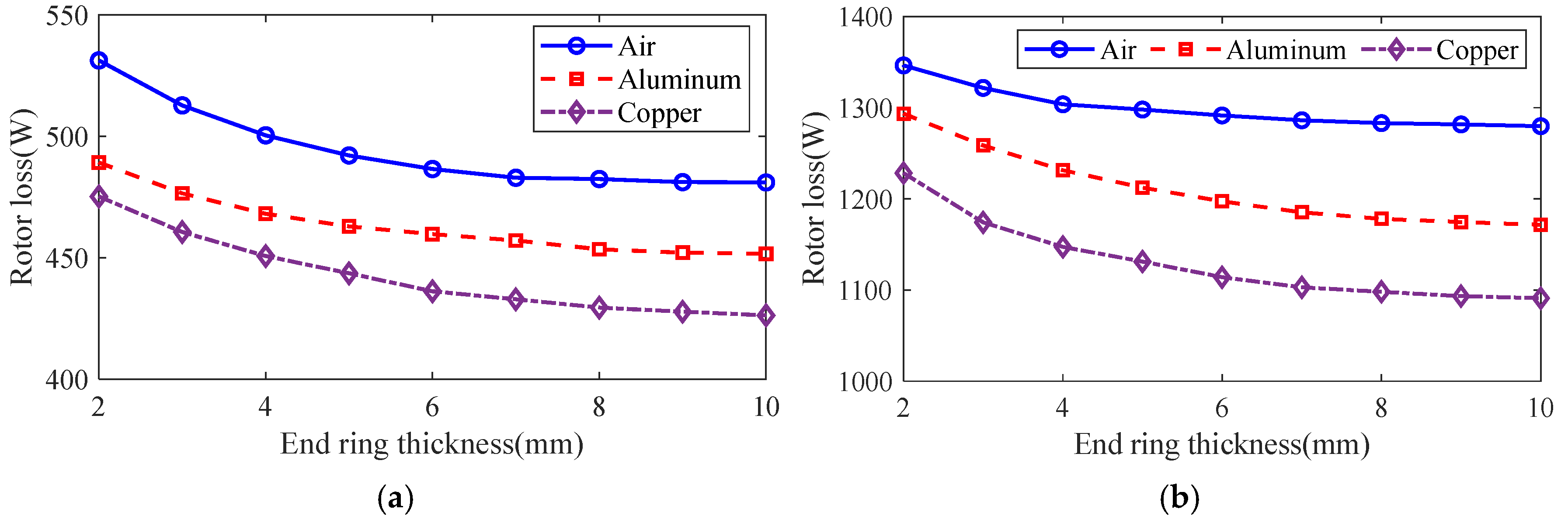
3.4. Optimized Design of Solid Rotor with Squirrel Cage
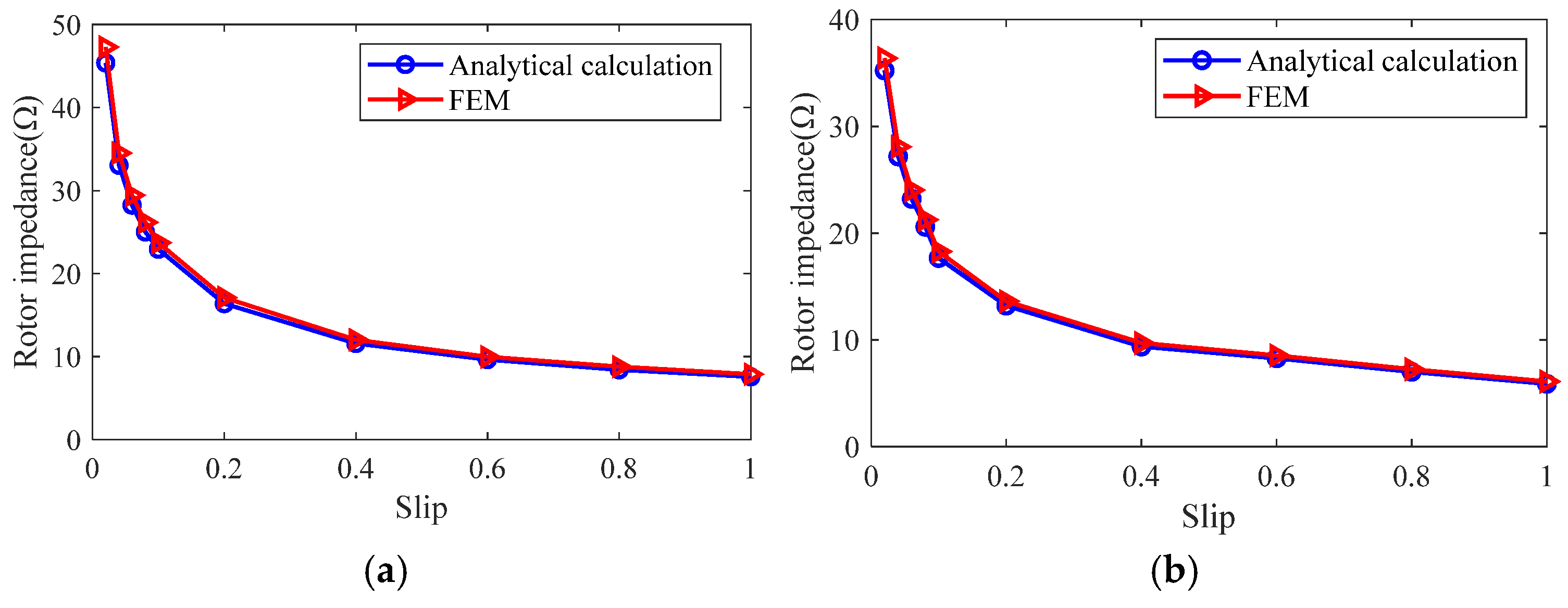
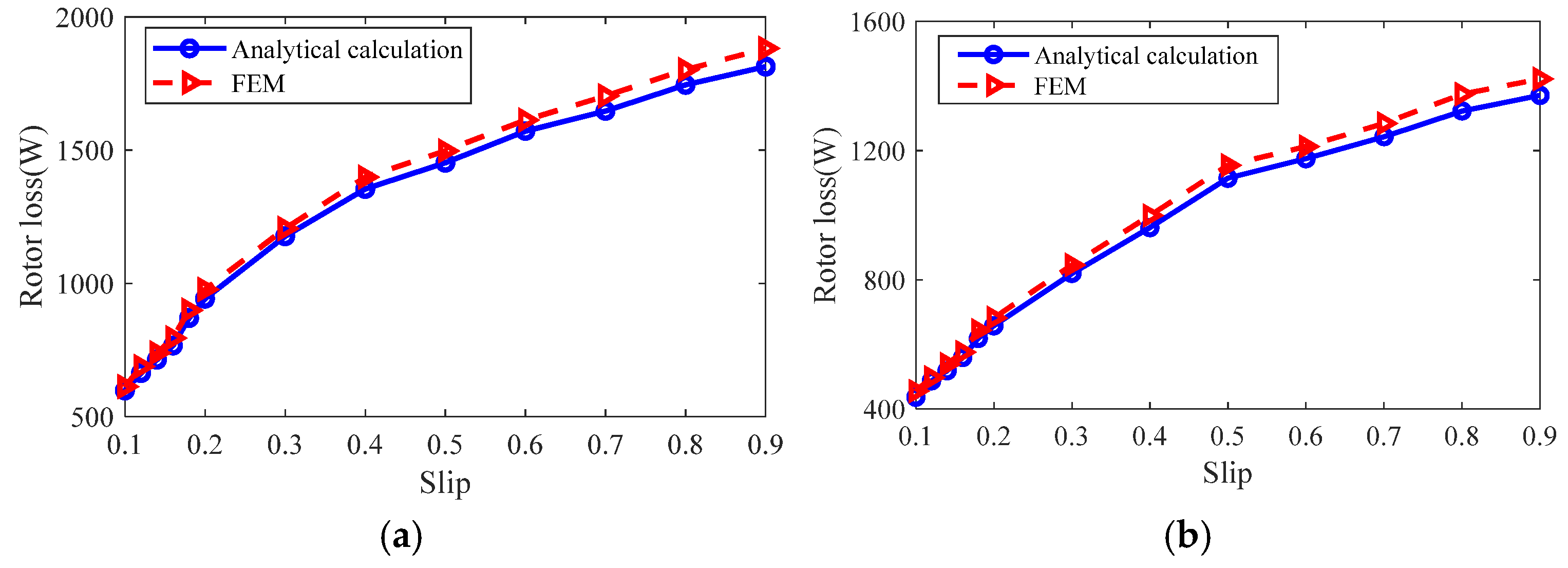
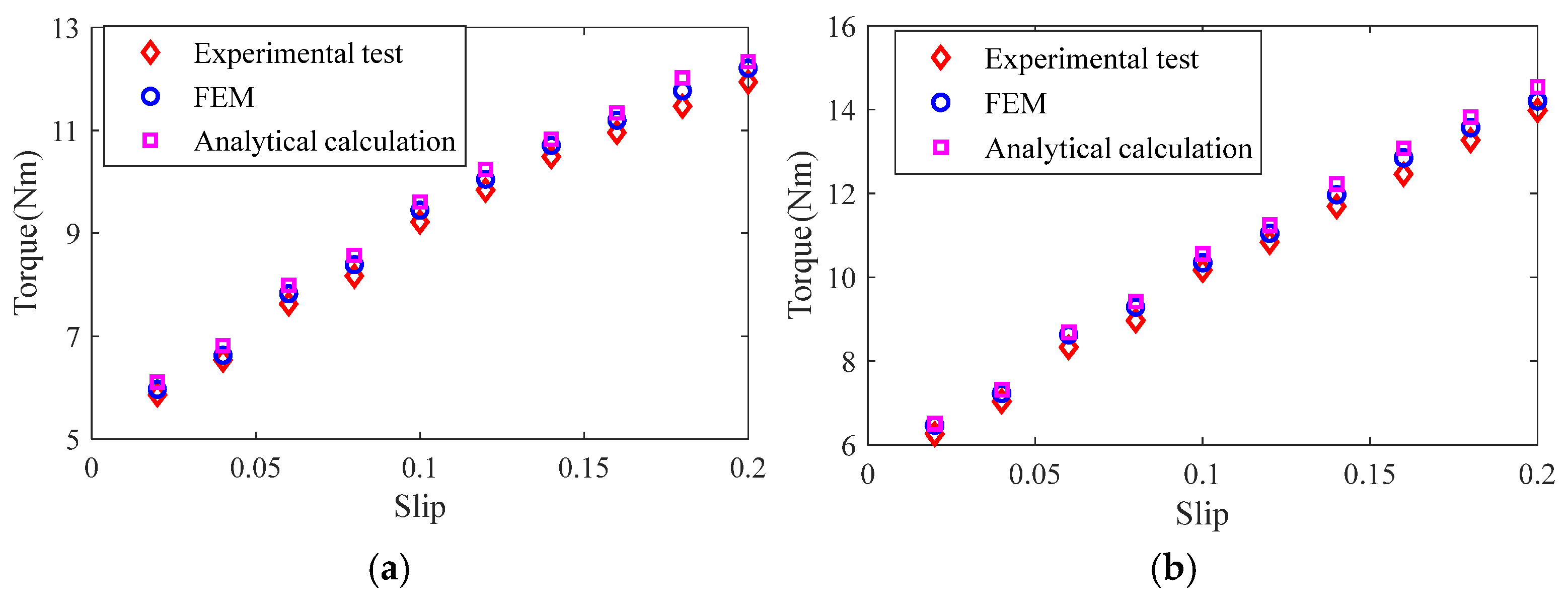
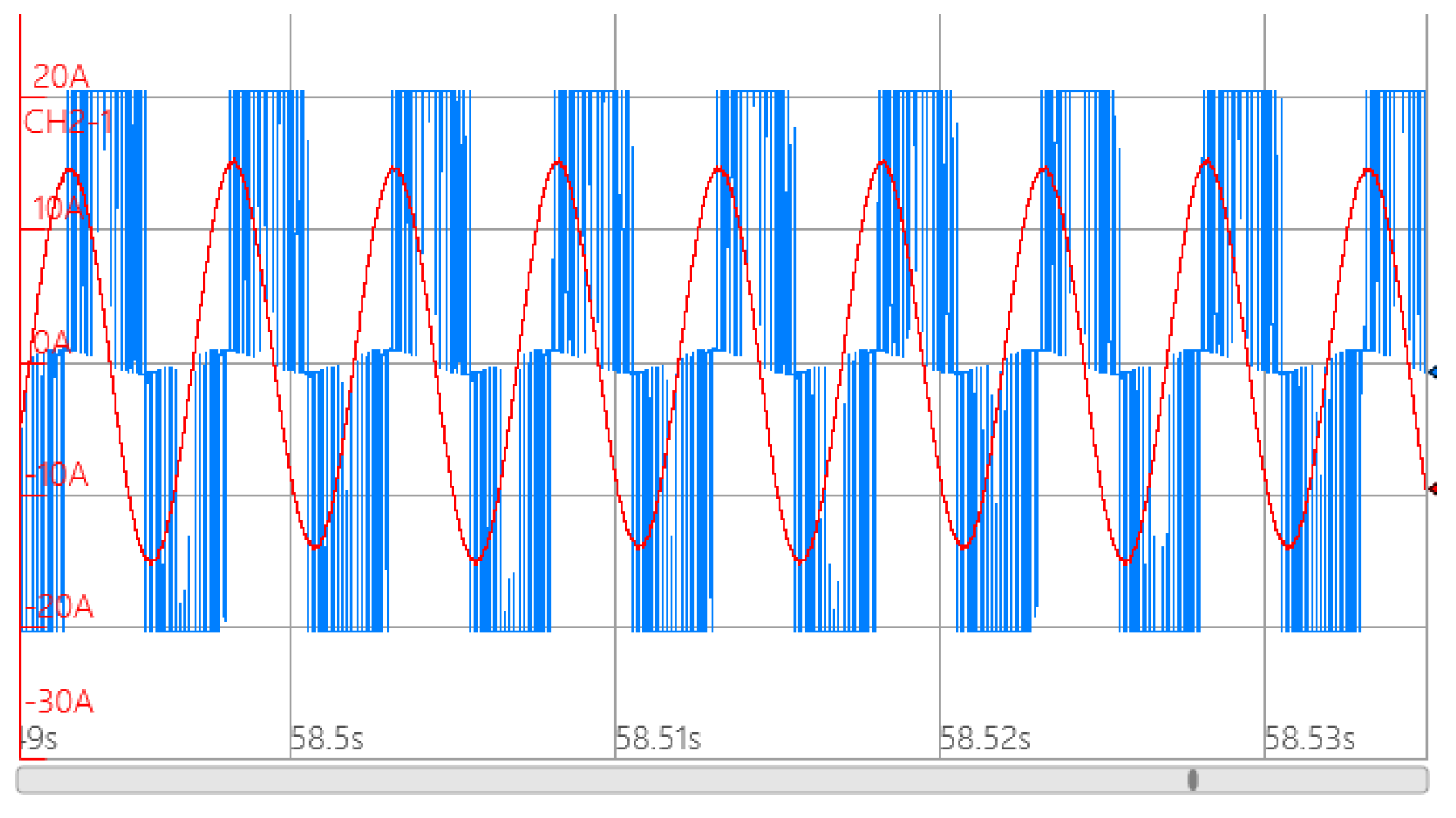
4. Simulation and Experimental Verification
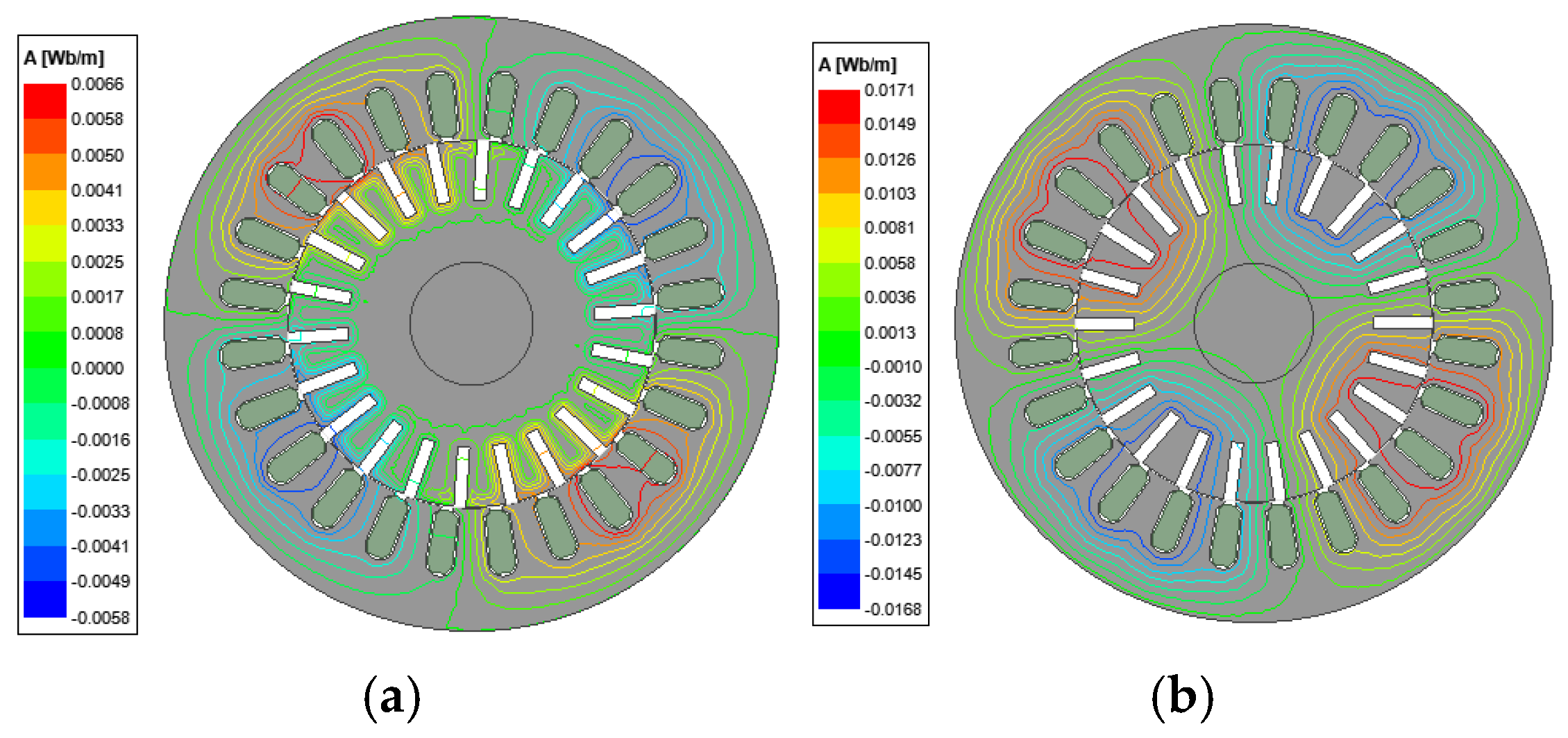
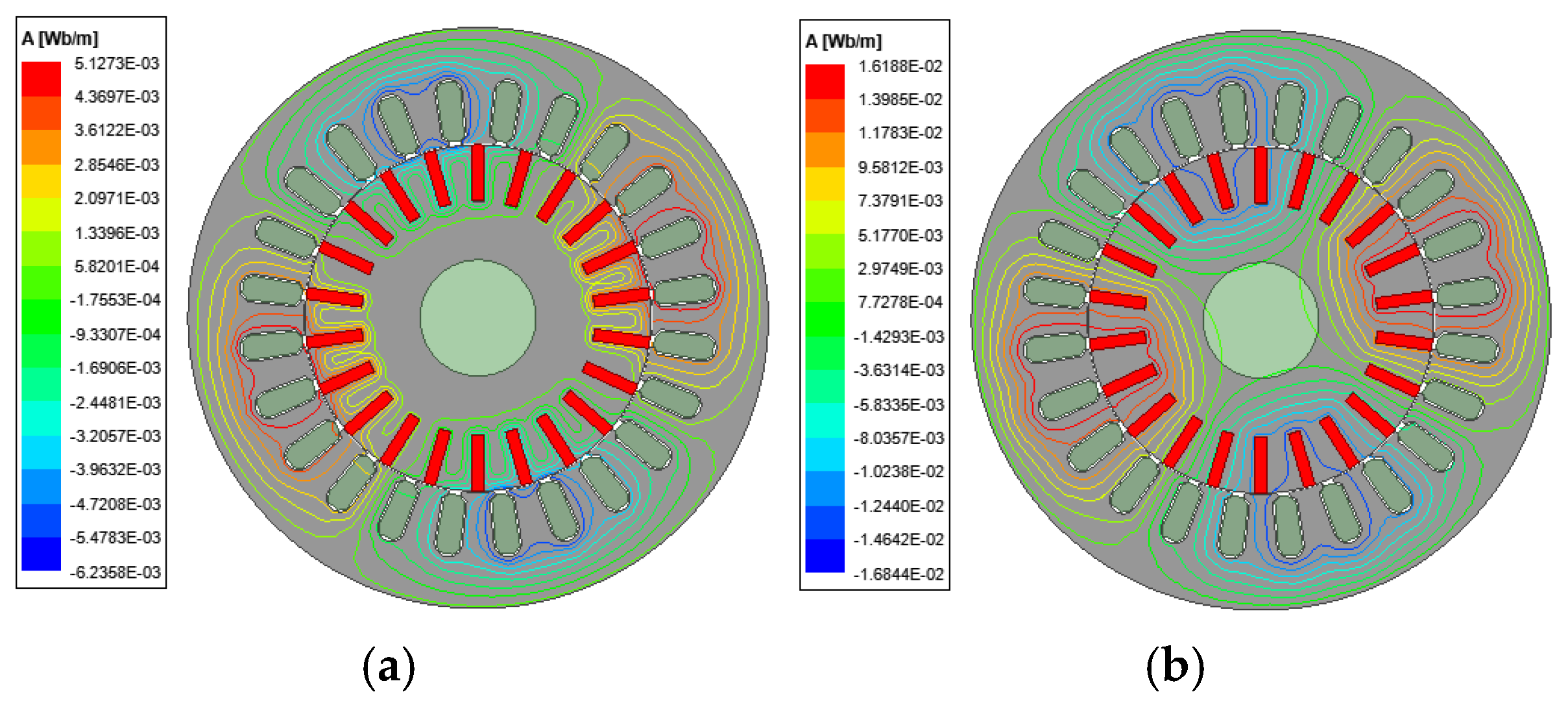
4.1. Finite Element Simulation
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bilek, V.; Barta, J.; Toman, M.; Losak, P.; Bramerdorfer, G. A comprehensive overview of high-speed solid-rotor induction machines: Applications, classification, and multi-physics modeling. Int. J. Electr. Power Energy Syst. 2025, 166, 110520. [Google Scholar] [CrossRef]
- Hong, C.; Huang, W.; Hu, Z. Design and Analysis of a High-Speed Dual Stator Slotted Solid-Rotor Axial-Flux Induction Motor. IEEE Trans. Transp. Electrif. 2019, 5, 71–79. [Google Scholar] [CrossRef]
- Zhao, H.; Chu, C.; Eldeeb, H.H.; Zhan, Y.; Xu, G.; Mohammed, O.A. Optimal Design of High-Speed Solid-Rotor Cage Induction Motors Considering Ferromagnetic Materials Behavior and Manufacturing Process. IEEE Trans. Ind. Appl. 2020, 56, 4345–4355. [Google Scholar] [CrossRef]
- Mellak, C.; Deuringer, J.; Muetze, A. Impact of Aspect Ratios of Solid Rotor, Large Air Gap Induction Motors on Run-Up Time and Energy Input. IEEE Trans. Ind. Appl. 2022, 58, 6045–6056. [Google Scholar] [CrossRef]
- Singh, R.; Kalra, S.; Agrawal, V. Analysis of slit rotor slot of high speed SRIM and comparison with double cage rotor slot. In Proceedings of the 2014 Students Conference on Engineering and Systems (SCES), Allahabad, India, 28–30 May 2014; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Yi, J.; Zhu, Z. Design and analysis of electromagnetic and mechanical structure of ultra-high-speed slotted solid rotor induction motor. Sci. Rep. 2025, 15, 2386. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Deng, Z. Research on slit dimensions of axially slotted solid rotor induction motor. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 1566–1569. [Google Scholar] [CrossRef]
- Yan, B.; Yang, Y.; Wang, X. Design of a Large Capacity Line-Start Permanent Magnet Synchronous Motor Equipped with Hybrid Salient Rotor. IEEE Trans. Ind. Electron. 2020, 68, 6662–6671. [Google Scholar] [CrossRef]
- Sarika, K. Rotor Material Selection for High-Speed Double Cage Solid Rotor Induction Motor. J. Electr. Eng. Technol. 2023, 18, 2885–2894. [Google Scholar]
- Weili, L.; Hongbo, Q.; Xiaochen, Z.; Ran, Y. Influence of Copper Plating on Electromagnetic and Temperature Fields in a High-Speed Permanent-Magnet Generator. IEEE Trans. Magn. 2012, 48, 2247–2253. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, B.; Wang, Y. Incipient winding fault detection and diagnosis for squirrel-cage induction motors equipped on CRH trains. ISA Trans. 2020, 99, 488–495. [Google Scholar] [CrossRef]
- Yan, B.; Li, X.; Sun, Y.; Tan, Y. End Effect Equivalence in the 2-D Finite Element Analysis of a Line-Start Permanent Magnet Synchronous Motor with Hybrid Solid Rotor. Energies 2023, 16, 6766. [Google Scholar] [CrossRef]
- Baghayipour, M.; Aliabad, H.K. Analytical Performance Prediction of a New-Structured Solid-Rotor Line-Start Axial Flux Permanent Magnet Motor. IEEE Trans. Energy Convers. 2022, 37, 2359–2369. [Google Scholar] [CrossRef]
- Boughrara, K.; Dubas, F.; Ibtiouen, R. 2-D Analytical Prediction of Eddy Currents, Circuit Model Parameters, and Steady-State Performances in Solid Rotor Induction Motors. IEEE Trans. Magn. 2014, 50, 7028214. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, S. Analytical Prediction of Operational Impedances in Solid Rotor Induction Machine. In Proceedings of the 2022 4th International Conference on Electrical Engineering and Control Technologies (CEECT), Shanghai, China, 16–18 December 2022; pp. 1166–1170. [Google Scholar] [CrossRef]
- Hong, C.; Huang, W.; Hu, Z. Performance Calculation of a Dual Stator Solid Rotor Axial Flux Induction Motor Using the Multi-Slice and Multi-Layer Method. IEEE Trans. Magn. 2019, 55, 8100709. [Google Scholar] [CrossRef]
- Feng, H.; Cui, X.; Si, J.; Gao, C.; Hu, Y. Equivalent Circuit Model of Novel Solid Rotor Induction Motor with Toroidal Winding Applying Composite Multilayer Theory. Appl. Sci. 2019, 9, 3288. [Google Scholar] [CrossRef]
- Fu, D.; Xu, Y.; Gillon, F.; Gong, J.; Bracikowski, N. Presentation of a Novel Transverse-Flux Permanent Magnet Linear Motor and Its Magnetic Field Analysis Based on Schwarz–Christoffel Mapping Method. IEEE Trans. Magn. 2018, 54, 6000204. [Google Scholar] [CrossRef]
- Oguz, A.H.; Gülbahce, M.O.; Kocabas, D.A. Design and optimization of an axially-slitted high-speed solid rotor induction motor. In Proceedings of the 2015 9th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 26–28 November 2015; pp. 568–573. [Google Scholar] [CrossRef]
- Staszak, J. Solid-Rotor Induction Motor Modeling Based on Circuit Model Utilizing Fractional-Order Derivatives. Energies 2022, 15, 6371. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, J.; Yan, S.; Wang, H. Magnetic field and rotor impedance analysis of solid rotor induction motors using the multilayer analytical method. IET Electr. Power Appl. 2025, 19, e70004. [Google Scholar] [CrossRef]
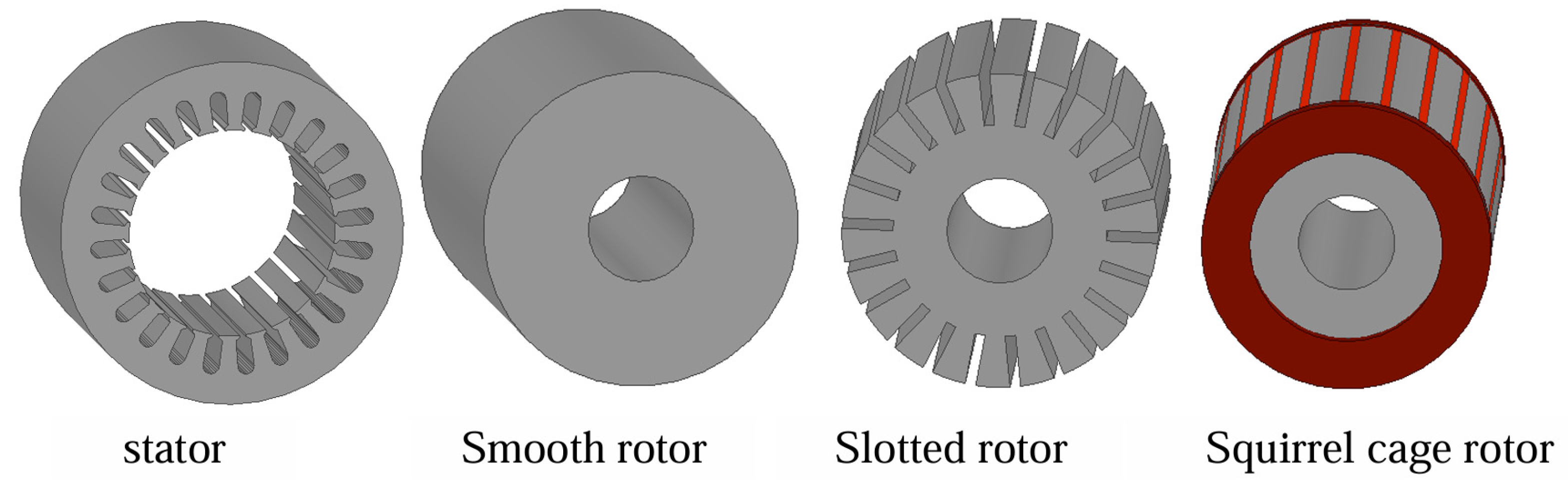
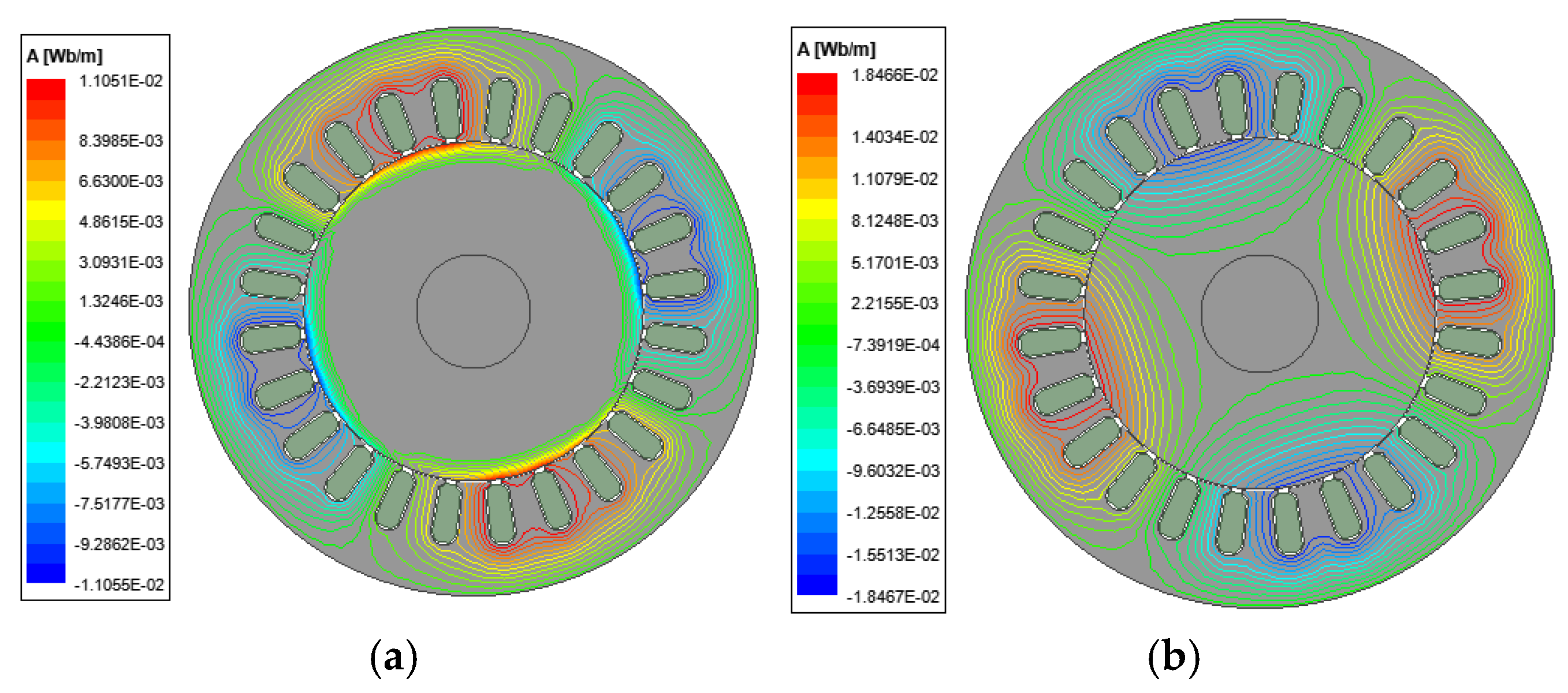
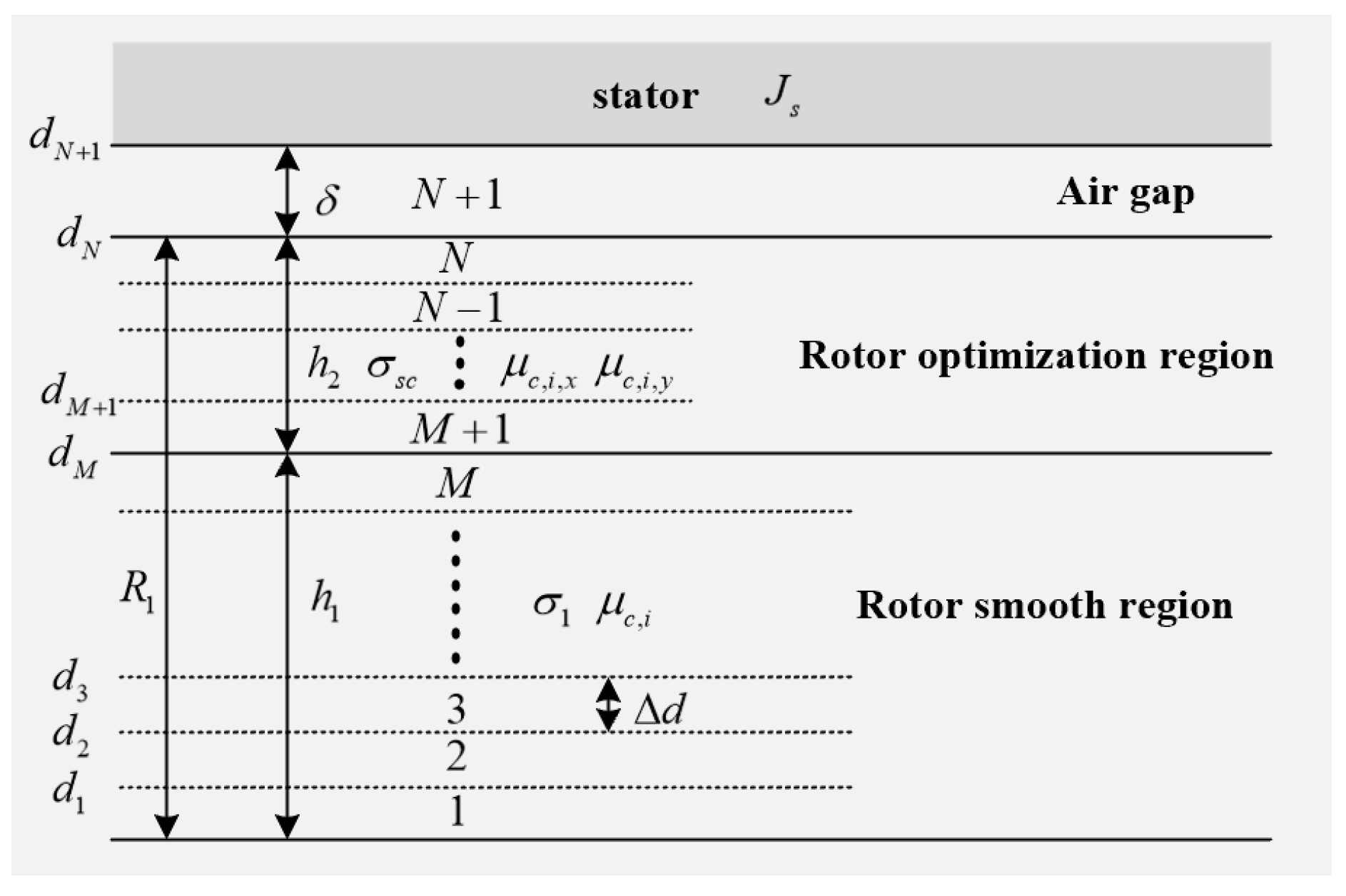
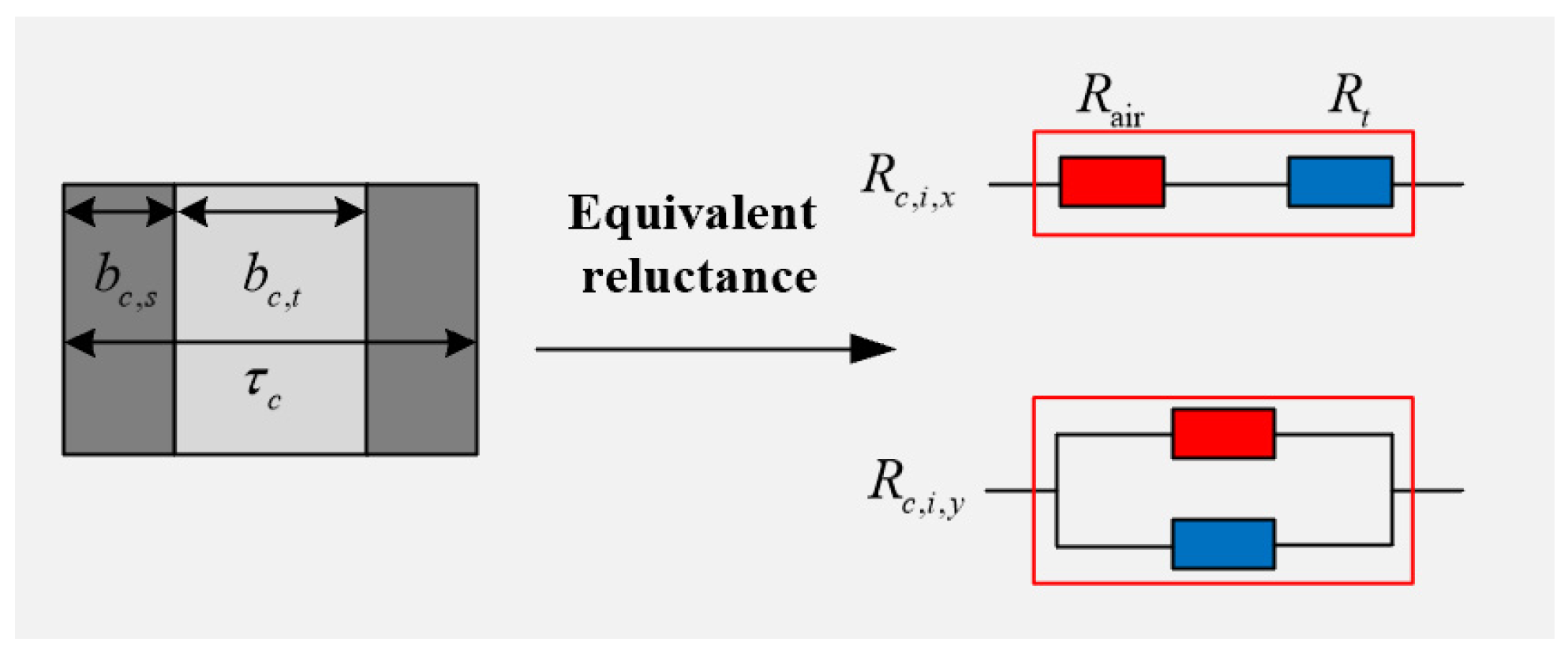









| Parametric | Notation | Value | Unit |
|---|---|---|---|
| phase | m | 3 | |
| rating | P | 3.7 | kW |
| rated frequency | f | 200 | Hz |
| rated speed | n | 5700 | rpm |
| rated voltage | Un | 380 | V |
| Number of stator slots | Qs | 24 | |
| polar logarithm | p | 2 | |
| Winding turns | N1 | 16 | |
| Outer diameter of stator | D1 | 125 | mm |
| Stator inner diameter | D2 | 75 | mm |
| Stator inner diameter | D3 | 74.5 | mm |
| Rotor inner diameter | D4 | 25 | mm |
| Stator-rotor axial length | lef | 100 | mm |
| Slotting Width/mm | |||
|---|---|---|---|
| 0.5 | 0.5791 | 0.8279 | 0.4794 |
| 1 | 0.5801 | 0.8275 | 0.4800 |
| 1.5 | 0.5819 | 0.8265 | 0.4809 |
| 2 | 0.5803 | 0.8258 | 0.4792 |
| 2.5 | 0.5792 | 0.8214 | 0.4758 |
| 3 | 0.5787 | 0.8198 | 0.4744 |
| Motors | Output Power/W | Efficiency | Power Factor | Starting Torque/(Nm) | Starting Torque/A | /(Nm/A) | ||
|---|---|---|---|---|---|---|---|---|
| M2 | 3613.8 | 78.7% | 0.658 | 0.5178 | 22.4 | 25.36 | 0.8833 | 0.4574 |
| M3 | 3753.6 | 81.5% | 0.671 | 0.5469 | 24.1 | 29.27 | 0.8234 | 0.4503 |
| M4 | 3955.7 | 83.4% | 0.691 | 0.5763 | 29.4 | 34.92 | 0.8419 | 0.4852 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhao, J.; Yan, S. Parameter Calculation and Rotor Structure Optimization Design of Solid Rotor Induction Motors. Sensors 2025, 25, 2929. https://doi.org/10.3390/s25092929
Xu H, Zhao J, Yan S. Parameter Calculation and Rotor Structure Optimization Design of Solid Rotor Induction Motors. Sensors. 2025; 25(9):2929. https://doi.org/10.3390/s25092929
Chicago/Turabian StyleXu, Hao, Jinghong Zhao, and Sinian Yan. 2025. "Parameter Calculation and Rotor Structure Optimization Design of Solid Rotor Induction Motors" Sensors 25, no. 9: 2929. https://doi.org/10.3390/s25092929
APA StyleXu, H., Zhao, J., & Yan, S. (2025). Parameter Calculation and Rotor Structure Optimization Design of Solid Rotor Induction Motors. Sensors, 25(9), 2929. https://doi.org/10.3390/s25092929






