A Mobile Wireless Sensor Coverage Optimization Method for Bridge Monitoring
Abstract
1. Introduction
- Two strategies are adopted to improve the HOA and address the strong dependence on initial solutions and the lack of mechanisms to escape local optima in the HOA. First, the Good Point Set theory generates an evenly distributed initial population, enhancing the algorithm’s exploration and stability. Second, a t-distribution perturbation operator with heterogeneous degrees of freedom is introduced to perturb individuals randomly, and the Metropolis criterion is applied to accept poorer solutions with a certain probability, helping the algorithm escape local optima.
- The VFA is introduced and combined with the GPTHOA to form the VF-GPTHOA, improving the algorithm’s convergence speed and accuracy in solving the HMWS deployment optimization problem in the band-like deployment environment of bridges. Once optimization is completed, the GPTHOA determines the optimal paths for sensor nodes to minimize energy consumption.
- The performance of the GPTHOA is tested on the CEC2022 benchmark test functions. In the bridge model (BM), the VF-GPTHOA is applied to optimize the deployment of HMWS nodes. Simulation results demonstrate that the proposed VF-GPTHOA outperforms other algorithms in multiple performance metrics.
2. Related Works
2.1. Virtual Force Algorithm
2.2. Intelligent Optimization Algorithm
3. Models and Definitions
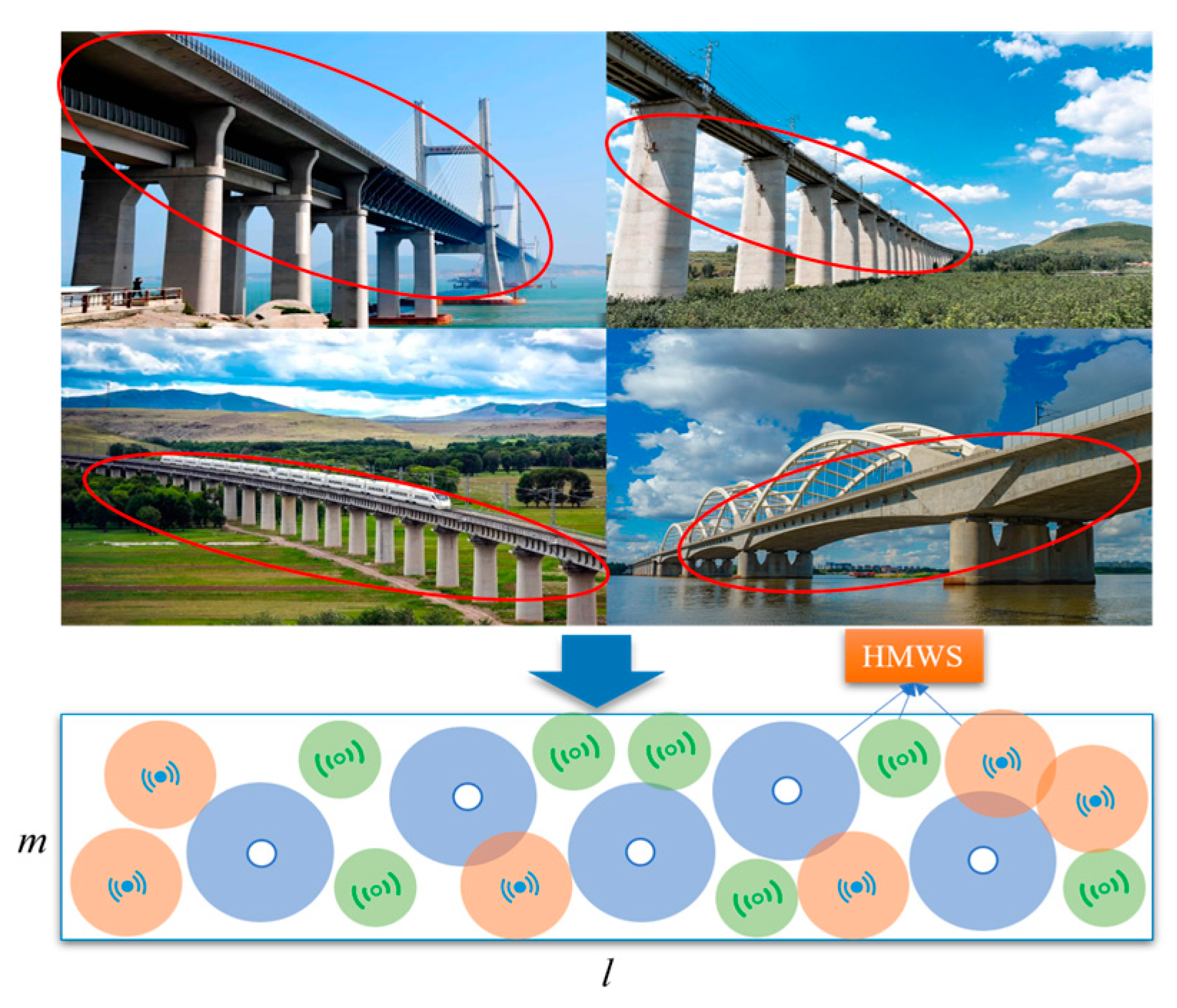
3.1. Bridge Model (BM)
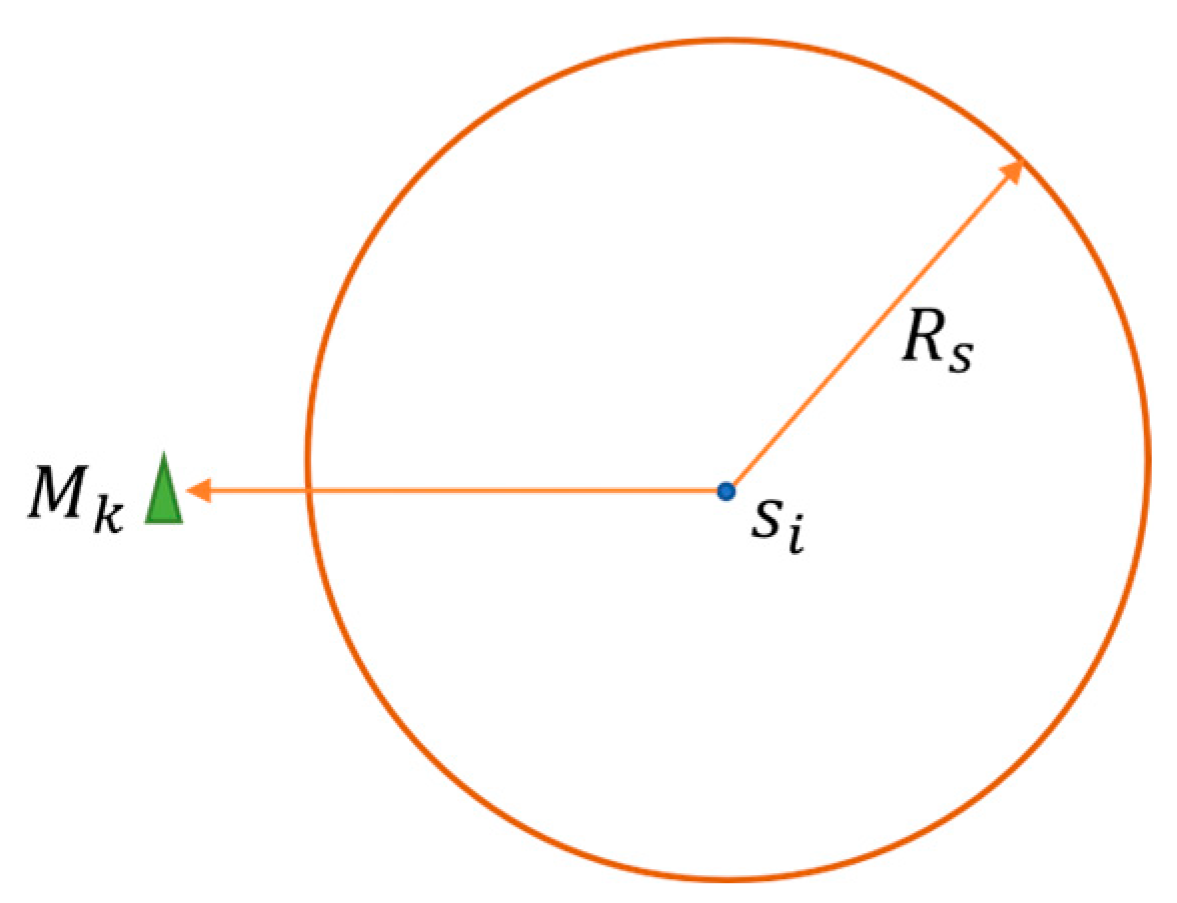
3.2. Coverage Model
3.3. Definitions
3.4. The Theory of Optimal Coverage
4. Hiking Optimization Algorithm (HOA)
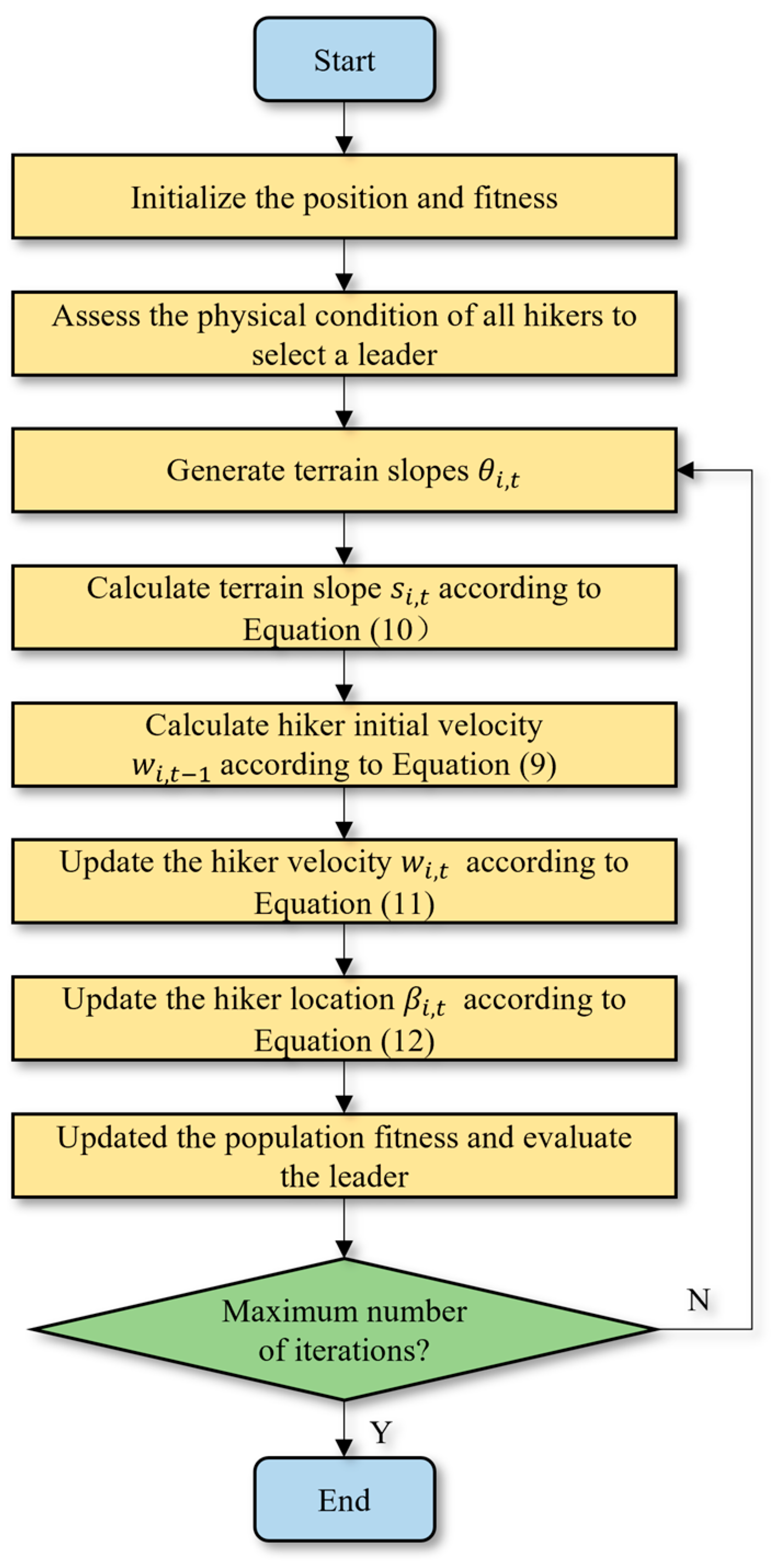
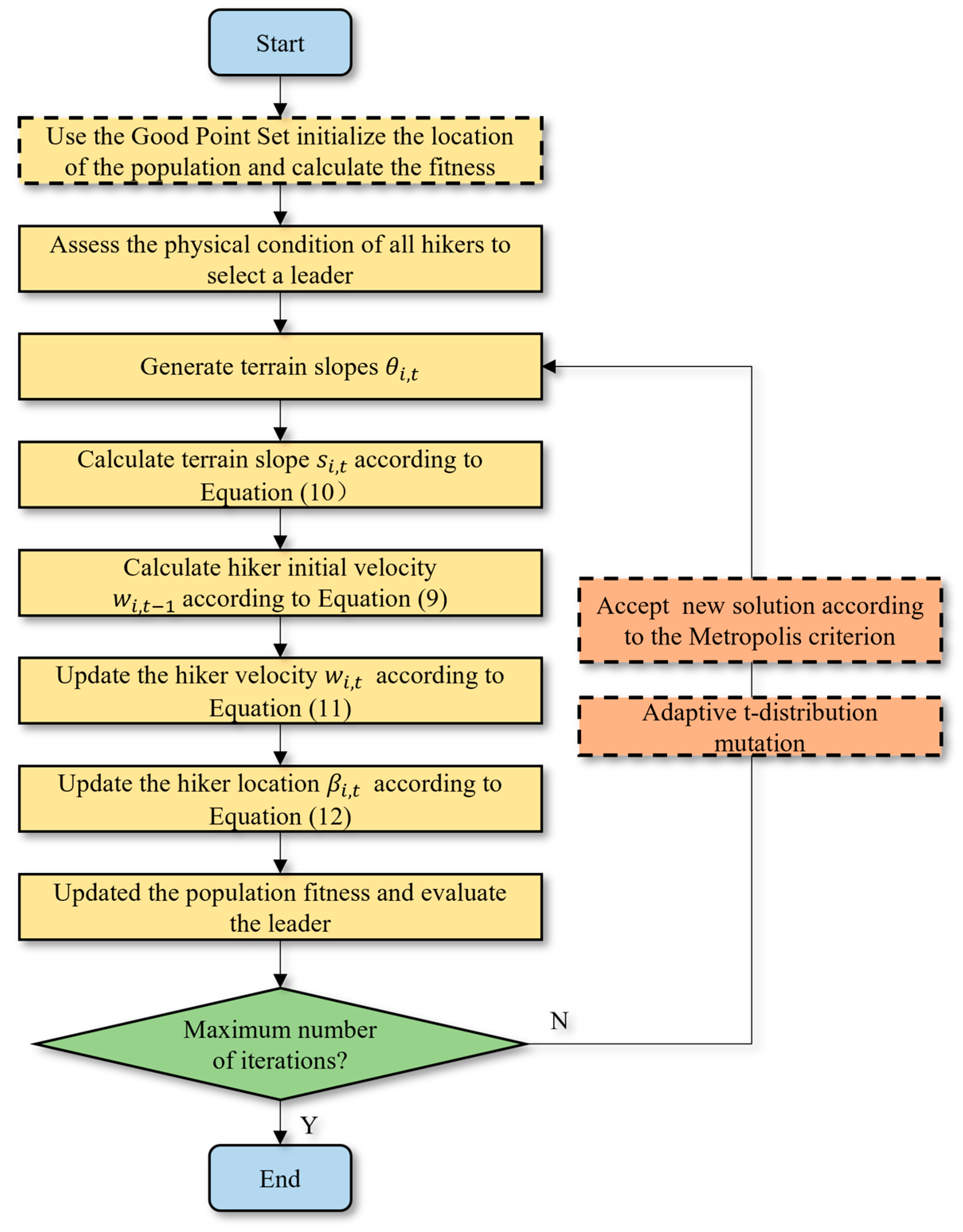
5. HMWS Deployment Optimization Algorithm Based on GPTHOA
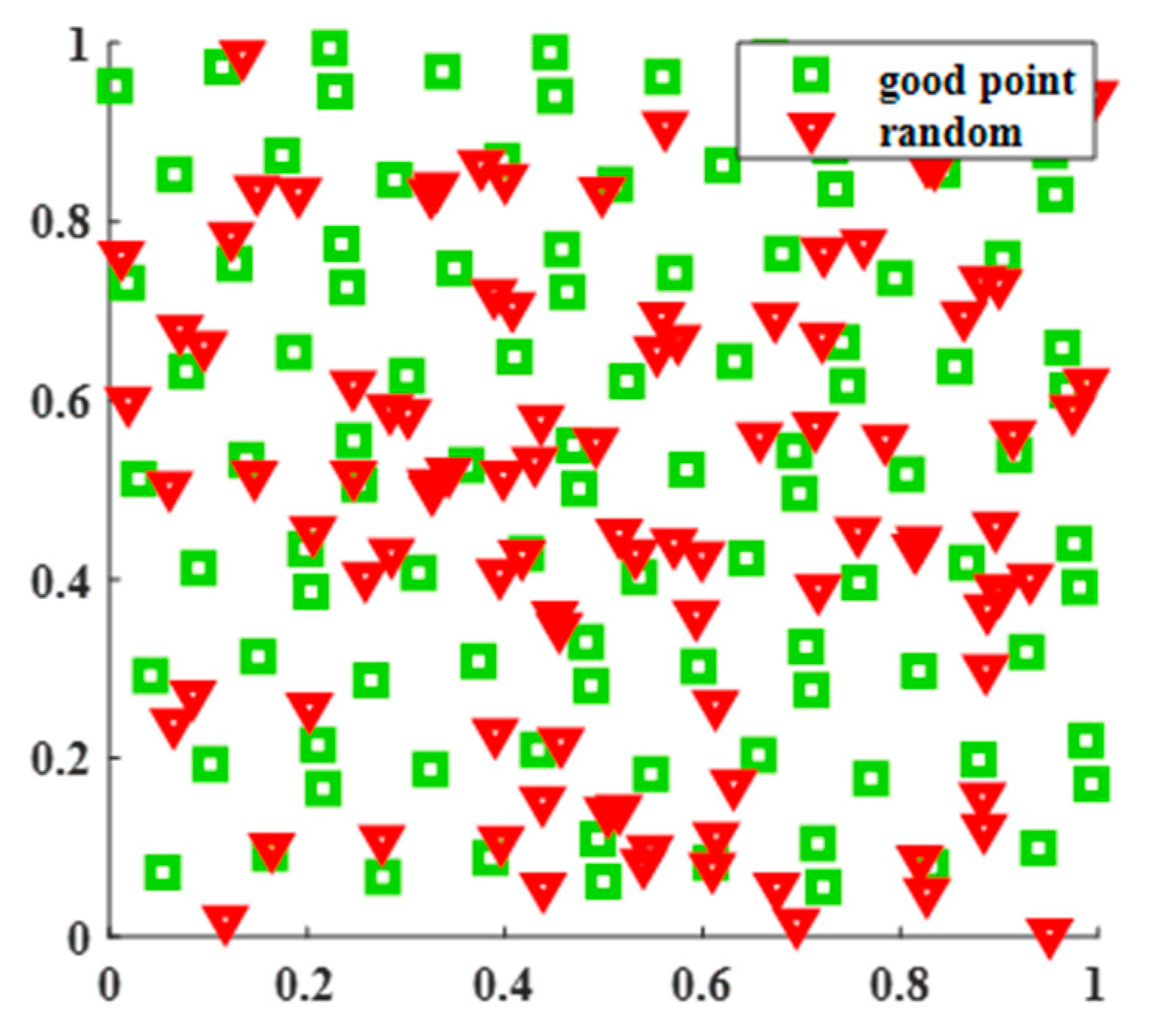
5.1. Initializing the Population by the Good Point Set
- Set is an unit cube in European space, namely, , where .
- Set contains a set of points , where .
- For any given point in , let denote the number of points in that satisfy the system of inequalities in (13).where and point set is considered to have a deviation . If, for any n, , then is considered to be uniformly distributed on with a deviation of .
- Let and the deviation of satisfy , where is a constant that depends only on and (with being an arbitrarily small positive number). In this case, is called a Good Point Set, and is called a good point.
- Let , where is the smallest prime number that satisfies , or let , . In this case, is a good point.
5.2. Heterogeneous-Degree-of-Freedom t-Distributed Perturbation
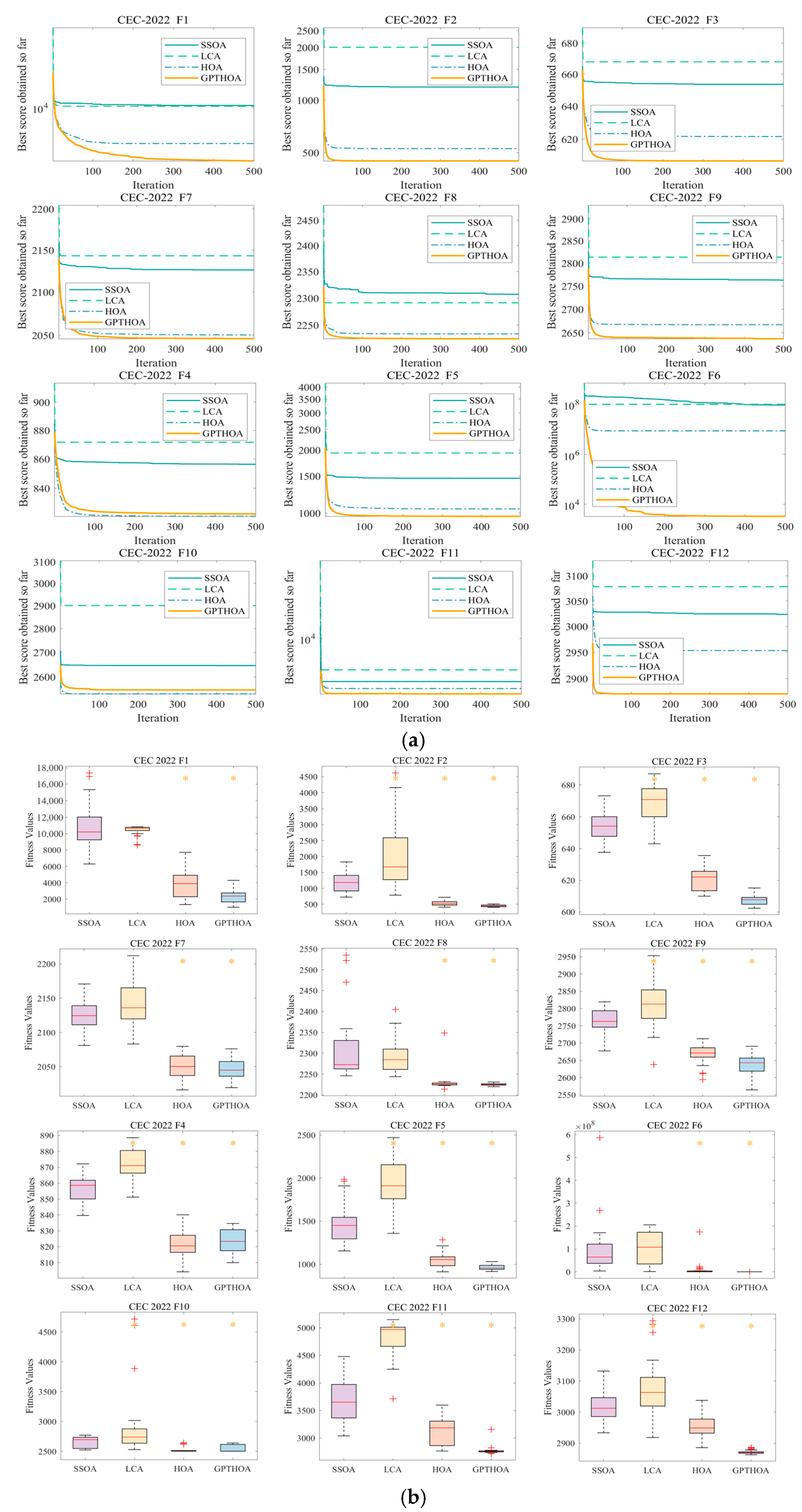
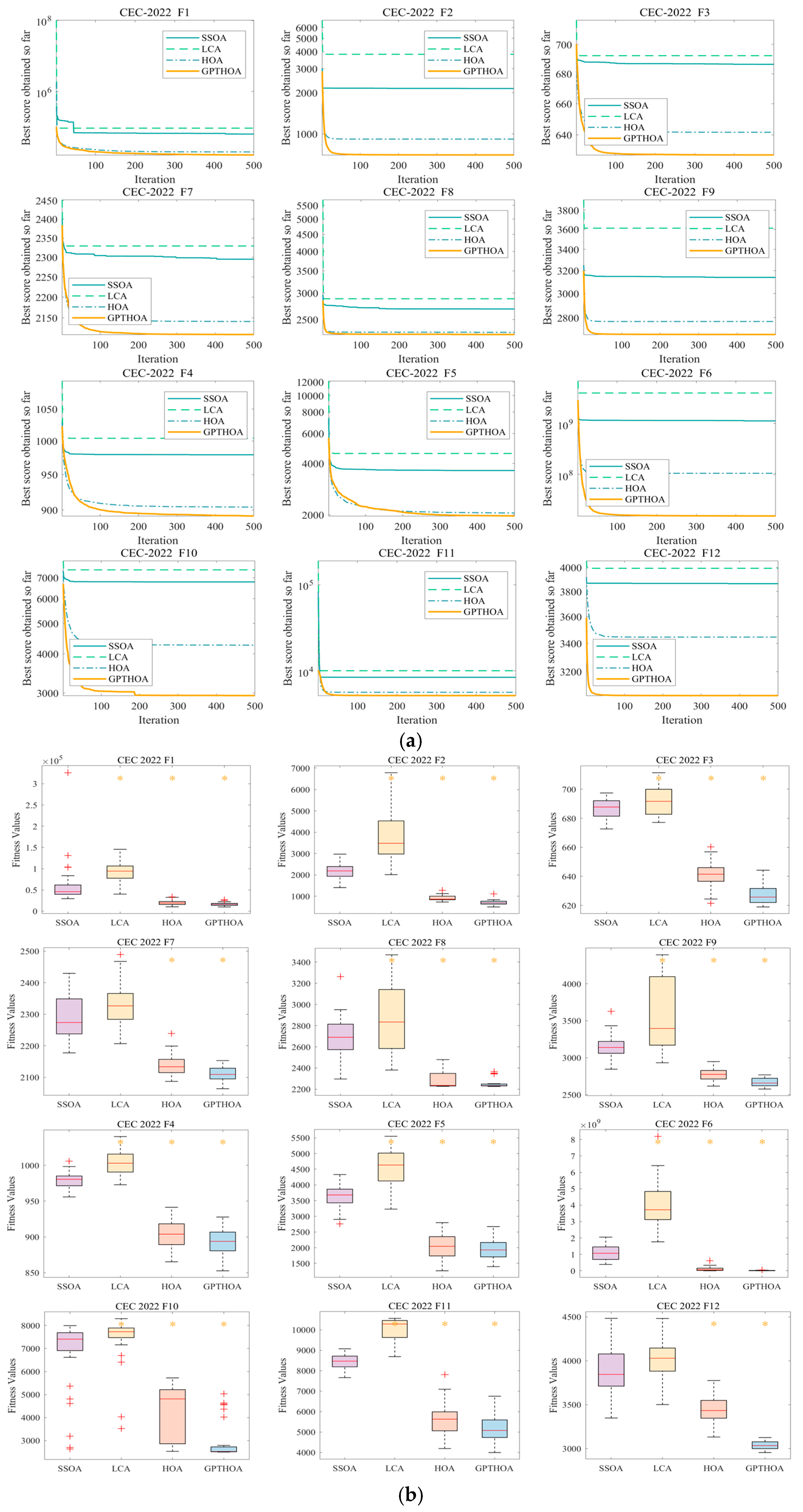
5.3. Performance Test of GPTHOA
5.4. Virtual Force-Guided Coverage Optimization
| Algorithm 1 VF-GPTHOA |
| Require: Sensor node set: ; Perceived distance: ; Total number of hikers: N and Maximum iterations: iter_max. Ensure: Sensor nodes’ location and CR. 1: Initialize the set of deployment scheme using (14). 2: for do //Iterate over all hikers (population individuals) 3: Evaluate a hiker’s fitness using (3). 4: end for 5: Generate initial optimal deployment schemes: //Record the current optimal deployment scheme t (highest fitness) 6: while //Main optimization loop (iteration number control) 7: for do //An independent search is performed for each hiker 8: Extract initial position of hiker i: 9: Determine terrain angle of elevation: 10: Compute the slope using (10). 11: Compute the initial hiking velocity using (11). 12: Determine the actual velocity using (11). 13: Update the hiker’s position using (12). 14: end for 15: Generate new deployment scheme by (15). 16: Decide whether to accept the new deployment scheme by Metropolis criterion. 17: Update the deployment schemes with poor CR by (16) and (17). 18: Update if there is a better solution. //Retain the historical best solution 19: //Iterate counter increment 20: end while 21: return //Return the optimal deployment and its coverage |
6. Simulation Results
6.1. Experiment 1
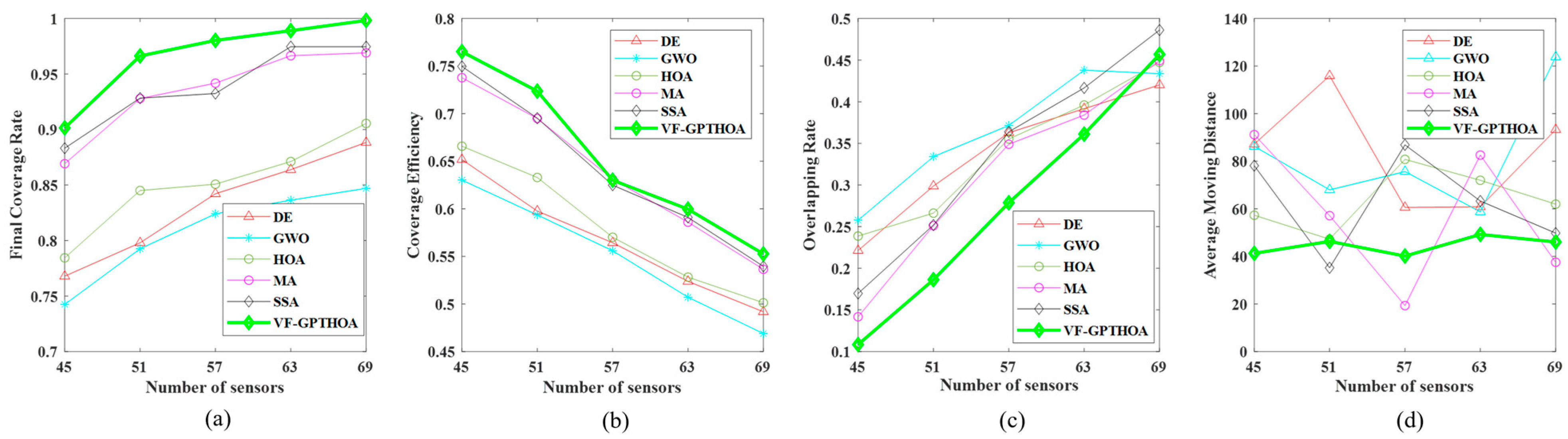
6.2. Experiment 2
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Civera, M.; Sibille, L.; Fragonara, L.Z.; Ceravolo, R. A DBSCAN-based automated operational modal analysis algorithm for bridge monitoring. Measurement 2023, 208, 112451. [Google Scholar] [CrossRef]
- Zheng, S.; Huo, J.; Yang, J.; Cao, F. An energy-efficient multi-hop routing protocol for 3D bridge wireless sensor network based on secretary bird optimization algorithm. IEEE Sens. J. 2024, 24, 38045–38060. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The current development of structural health monitoring for bridges: A review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Martucci, D.; Civera, M.; Surace, C. Bridge monitoring: Application of the extreme function theory for damage detection on the I-40 case study. Eng. Struct. 2023, 279, 115573. [Google Scholar] [CrossRef]
- Yang, J.; Huo, J.; Mu, C. A Novel Clustering Routing Algorithm for Bridge Wireless Sensor Networks Based on Spatial Model and Multi-Criteria Decision Making. IEEE Internet Things J. 2024, 11, 27775–27789. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Li, A.; Zhang, Y. Structural health monitoring system for Sutong Cable-stayed Bridge. Smart Struct. Syst. 2016, 18, 317–334. [Google Scholar] [CrossRef]
- Chae, M.J.; Yoo, H.S.; Kim, J.Y.; Cho, M.Y. Development of a wireless sensor network system for suspension bridge health monitoring. Autom. Constr. 2012, 21, 237–252. [Google Scholar] [CrossRef]
- Linderman, L.E.; Mechitov, K.A.; Spencer, B.F., Jr. TinyOS-based real-time wireless data acquisition framework for structural health monitoring and control. Struct. Control Health Monit. 2013, 20, 1007–1020. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H.; Li, H.N. Wireless Sensor Placement for Bridge Health Monitoring Using a Generalized Genetic Algorithm. Int. J. Struct. Stab. Dyn. 2014, 14, 1440011. [Google Scholar] [CrossRef]
- Temene, N.; Sergiou, C.; Georgiou, C.; Vassiliou, V. A survey on mobility in wireless sensor networks. Ad Hoc Netw. 2022, 125, 102726. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Wang, Y.; Wen, Q. Improved sand cat swarm optimization algorithm for enhancing coverage of wireless sensor networks. Measurement 2024, 233, 114649. [Google Scholar] [CrossRef]
- Zhou, F.; Gao, J.; Fan, X.; An, K. Covering algorithm for different obstacles and moving obstacle in wireless sensor networks. IEEE Internet Things J. 2018, 5, 3305–3315. [Google Scholar] [CrossRef]
- Kiani, V. A greedy virtual force algorithm for target coverage in distributed sensor networks. In Proceedings of the 2020 10th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2020; pp. 317–322. [Google Scholar]
- Wen, Q.; Zhao, X.-Q.; Cui, Y.-P.; Zeng, Y.-P.; Chang, H.; Fu, Y.-J. Coverage enhancement algorithm for WSNs based on vampire bat and improved virtual force. IEEE Sens. J. 2022, 22, 8245–8256. [Google Scholar] [CrossRef]
- Sha, C.; Ren, C.; Malekian, R.; Wu, M.; Huang, H.; Ye, N. A type of virtual force-based energy-hole mitigation strategy for sensor networks. IEEE Sens. J. 2019, 20, 1105–1119. [Google Scholar] [CrossRef]
- Qi, C.; Huang, J.; Liu, X.; Zong, G. A novel mobile-coverage scheme for hybrid sensor networks. IEEE Access 2020, 8, 121678–121692. [Google Scholar] [CrossRef]
- Boufares, N.; Khoufi, I.; Minet, P.; Saidane, L.; Saied, Y.B. Three dimensional mobile wireless sensor networks redeployment based on virtual forces. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 563–568. [Google Scholar]
- Boufares, N.; Minet, P.; Khoufi, I.; Saidane, L. Covering a 3D flat surface with autonomous and mobile wireless sensor nodes. In Proceedings of the International Wireless Communications & Mobile Computing Conference, Valencia, Spain, 26–30 June 2017. [Google Scholar]
- Luo, C.; Cao, Y.; Xin, G.; Wang, B.; Lu, E.; Wang, H. Three-dimensional coverage optimization of underwater nodes under multiconstraints combined with water flow. IEEE Internet Things J. 2021, 9, 2375–2389. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, S.; Singh, J. Nature-inspired algorithms for wireless sensor networks: A comprehensive survey. Comput. Sci. Rev. 2021, 39, 100342. [Google Scholar] [CrossRef]
- Yao, Y.-D.; Wen, Q.; Cui, Y.-P.; Zhao, F.; Zhao, B.-Z.; Zeng, Y.-P. Coverage enhancement strategy in WMSNs based on a novel swarm intelligence algorithm: Army ant search optimizer. IEEE Sens. J. 2022, 22, 21299–21311. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, H. Wireless sensor network deployment of 3D surface based on enhanced grey wolf optimizer. IEEE Access 2020, 8, 57229–57251. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, H.; Hu, Z.; Li, D.; Wang, J.; Liang, W. Node coverage optimization algorithm for wireless sensor networks based on improved grey wolf optimizer. J. Algorithms Comput. Technol. 2019, 13, 1748302619889498. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Rao, S.; Zhou, X.; Hu, J. A novel self-adaptive multi-strategy artificial bee colony algorithm for coverage optimization in wireless sensor networks. Ad Hoc Netw. 2023, 150, 103284. [Google Scholar] [CrossRef]
- Chowdhury, A.; De, D. Energy-efficient coverage optimization in wireless sensor networks based on Voronoi-Glowworm Swarm Optimization-K-means algorithm. Ad Hoc Netw. 2021, 122, 102660. [Google Scholar] [CrossRef]
- Deepa, R.; Venkataraman, R. Enhancing Whale Optimization Algorithm with Levy Flight for coverage optimization in wireless sensor networks. Comput. Electr. Eng. 2021, 94, 107359. [Google Scholar] [CrossRef]
- Syed, M.A.; Syed, R. Weighted Salp Swarm Algorithm and its applications towards optimal sensor deployment. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1285–1295. [Google Scholar] [CrossRef]
- Yao, Y.; Liao, H.; Li, X.; Zhao, F.; Yang, X.; Hu, S. Coverage control algorithm for DSNs based on improved gravitational search. IEEE Sens. J. 2022, 22, 7340–7351. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, S.; Li, Y.; Wen, Q. A node deployment optimization algorithm of WSNs based on improved moth flame search. IEEE Sens. J. 2022, 22, 10018–10030. [Google Scholar] [CrossRef]
- Cao, L.; Yue, Y.; Cai, Y.; Zhang, Y. A novel coverage optimization strategy for heterogeneous wireless sensor networks based on connectivity and reliability. IEEE Access 2021, 9, 18424–18442. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Y.; Xie, D.; Hu, S.; Wang, C.; Li, Y. Coverage enhancement strategy for WSNs based on virtual force-directed ant lion optimization algorithm. IEEE Sens. J. 2021, 21, 19611–19622. [Google Scholar] [CrossRef]
- Meng, Z.; Zhong, Y.; Yang, C. CS-DE: Cooperative strategy based differential evolution with population diversity enhancement. Inf. Sci. 2021, 577, 663–696. [Google Scholar] [CrossRef]
- Yang, J.; Huo, J.; Mu, C. A Spatial Model and Multi-objective Fuzzy Inference-Based Clustering Routing Algorithm for Bridge Monitoring. IEEE Sens. J. 2024, 25, 1669–1681. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, J.; Zhang, S.; Cao, J.; Min, G. Minimizing movement for target coverage and network connectivity in mobile sensor networks. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 1971–1983. [Google Scholar] [CrossRef]
- Ammari, H.M.; Das, S.K. Coverage, connectivity, and fault tolerance measures of wireless sensor networks. In Proceedings of the 8th International Symposium, SSS 2006, Dallas, TX, USA, 17–19 November 2006; pp. 35–49. [Google Scholar]
- Goodchild, M.F. Beyond Tobler’s Hiking Function. Geogr. Anal. 2020, 52, 558–569. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H. An improved NSGA-III integrating a good point set for multi-objective optimal design of power inductors. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 586. [Google Scholar] [CrossRef]
- Amine, K. Multiobjective simulated annealing: Principles and algorithm variants. Adv. Oper. Res. 2019, 2019, 8134674. [Google Scholar] [CrossRef]
- Alzoubi, S.; Abualigah, L.; Sharaf, M.; Daoud, M.S.; Khodadadi, N.; Jia, H. Synergistic Swarm Optimization Algorithm. Comput. Model. Eng. Sci. 2024, 139, 2557–2604. [Google Scholar] [CrossRef]
- Houssein, E.H.; Oliva, D.; Samee, N.A.; Mahmoud, N.F.; Emam, M.M. Liver cancer algorithm: A novel bio-inspired optimizer. Comput. Biol. Med. 2023, 165, 107389. [Google Scholar] [CrossRef]
- Kalita, K.; Ramesh, J.V.N.; Čep, R.; Pandya, S.B.; Jangir, P.; Abualigah, L. Multi-objective liver cancer algorithm: A novel algorithm for solving engineering design problems. Heliyon 2024, 10, e26665. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]





| No. | Functions | ||
|---|---|---|---|
| Unimodal Function | 1 | Shifted and full Rotated Zakharov Function | 300 |
| Basic Functions | 2 | Shifted and full Rotated Rosenbrock’s Function | 400 |
| Basic Functions | 3 | Function | 600 |
| Basic Functions | 4 | Shifted and full Rotated Non-Continuous Rastrigin’s Function | 800 |
| Basic Functions | 5 | Shifted and full Rotated Levy Function | 900 |
| Hybrid Functions | 6 | Hybrid Function 1 (N = 3) | 1800 |
| Hybrid Functions | 7 | Hybrid Function 2 (N = 6) | 2000 |
| Hybrid Functions | 8 | Hybrid Function 3 (N = 5) | 2200 |
| Composition Functions | 9 | Composition Function 1 (N = 5) | 2300 |
| Composition Functions | 10 | Composition Function 2 (N = 4) | 2400 |
| Composition Functions | 11 | Composition Function 3 (N = 5) | 2600 |
| Composition Functions | 12 | Composition Function 4 (N = 6) | 2700 |
| Function | Dim | SSOA | LCA | HOA | GPTHOA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | Worse | Best | Mean | Worse | Best | Mean | Worse | Best | Mean | Worse | ||
| F1 | 10 | 6.29E+03 | 1.07E+04 | 1.74E+04 | 8.59E+03 | 1.04E+04 | 1.08E+04 | 1.34E+03 | 3.75E+03 | 7.71E+03 | 1.01E+03 | 2.32E+03 | 4.29E+03 |
| 20 | 2.63E+04 | 6.11E+04 | 2.53E+05 | 5.17E+04 | 9.06E+04 | 1.34E+05 | 1.08E+04 | 1.96E+04 | 3.06E+04 | 1.02E+04 | 1.67E+04 | 2.33E+04 | |
| F2 | 10 | 7.24E+02 | 1.19E+03 | 1.83E+03 | 7.83E+02 | 2.01E+03 | 4.62E+03 | 4.08E+02 | 5.27E+02 | 7.17E+02 | 4.05E+02 | 4.48E+02 | 5.09E+02 |
| 20 | 1.34E+03 | 2.04E+03 | 3.03E+03 | 2.12E+03 | 3.71E+03 | 5.90E+03 | 6.52E+02 | 9.42E+02 | 1.22E+03 | 5.30E+02 | 6.83E+02 | 8.77E+02 | |
| F3 | 10 | 6.38E+02 | 6.53E+02 | 6.73E+02 | 6.43E+02 | 6.68E+02 | 6.87E+02 | 6.10E+02 | 6.21E+02 | 6.36E+02 | 6.02E+02 | 6.07E+02 | 6.15E+02 |
| 20 | 6.71E+02 | 6.86E+02 | 7.02E+02 | 6.56E+02 | 6.94E+02 | 7.14E+02 | 6.33E+02 | 6.46E+02 | 6.60E+02 | 6.13E+02 | 6.28E+02 | 6.48E+02 | |
| F4 | 10 | 8.40E+02 | 8.56E+02 | 8.72E+02 | 8.51E+02 | 8.72E+02 | 8.89E+02 | 8.04E+02 | 8.21E+02 | 8.40E+02 | 8.10E+02 | 8.23E+02 | 8.35E+02 |
| 20 | 9.55E+02 | 9.80E+02 | 1.00E+03 | 9.85E+02 | 1.01E+03 | 1.04E+03 | 8.69E+02 | 8.95E+02 | 9.32E+02 | 8.52E+02 | 8.87E+02 | 9.11E+02 | |
| F5 | 10 | 1.15E+03 | 1.46E+03 | 1.99E+03 | 1.36E+03 | 1.93E+03 | 2.47E+03 | 9.12E+02 | 1.05E+03 | 1.28E+03 | 9.15E+02 | 9.64E+02 | 1.03E+03 |
| 20 | 2.77E+03 | 3.77E+03 | 4.70E+03 | 3.42E+03 | 4.58E+03 | 5.96E+03 | 1.37E+03 | 2.16E+03 | 3.09E+03 | 1.23E+03 | 1.93E+03 | 2.82E+03 | |
| F6 | 10 | 3.39E+06 | 9.58E+07 | 5.87E+08 | 8.52E+05 | 1.03E+08 | 2.05E+08 | 2.89E+03 | 8.83E+06 | 1.75E+08 | 1.97E+03 | 3.26E+03 | 6.60E+03 |
| 20 | 3.55E+08 | 1.16E+09 | 2.31E+09 | 1.98E+09 | 4.06E+09 | 8.64E+09 | 1.38E+06 | 9.66E+07 | 3.56E+08 | 1.06E+05 | 1.45E+07 | 5.67E+07 | |
| F7 | 10 | 2.08E+03 | 2.13E+03 | 2.17E+03 | 2.08E+03 | 2.14E+03 | 2.21E+03 | 2.02E+03 | 2.05E+03 | 2.08E+03 | 2.02E+03 | 2.05E+03 | 2.08E+03 |
| 20 | 2.15E+03 | 2.26E+03 | 2.41E+03 | 2.21E+03 | 2.35E+03 | 2.54E+03 | 2.07E+03 | 2.13E+03 | 2.26E+03 | 2.08E+03 | 2.12E+03 | 2.18E+03 | |
| F8 | 10 | 2.25E+03 | 2.31E+03 | 2.54E+03 | 2.24E+03 | 2.29E+03 | 2.40E+03 | 2.21E+03 | 2.23E+03 | 2.35E+03 | 2.22E+03 | 2.23E+03 | 2.23E+03 |
| 20 | 2.41E+03 | 2.71E+03 | 3.08E+03 | 2.32E+03 | 2.84E+03 | 4.21E+03 | 2.23E+03 | 2.30E+03 | 2.55E+03 | 2.23E+03 | 2.24E+03 | 2.35E+03 | |
| F9 | 10 | 2.68E+03 | 2.76E+03 | 2.82E+03 | 2.64E+03 | 2.81E+03 | 2.95E+03 | 2.59E+03 | 2.67E+03 | 2.71E+03 | 2.56E+03 | 2.64E+03 | 2.69E+03 |
| 20 | 2.79E+03 | 3.20E+03 | 3.46E+03 | 2.75E+03 | 3.45E+03 | 4.37E+03 | 2.64E+03 | 2.78E+03 | 2.97E+03 | 2.53E+03 | 2.67E+03 | 2.87E+03 | |
| F10 | 10 | 2.52E+03 | 2.65E+03 | 2.77E+03 | 2.53E+03 | 2.90E+03 | 4.71E+03 | 2.50E+03 | 2.53E+03 | 2.64E+03 | 2.50E+03 | 2.55E+03 | 2.64E+03 |
| 20 | 2.90E+03 | 6.58E+03 | 8.16E+03 | 3.35E+03 | 7.31E+03 | 8.27E+03 | 2.52E+03 | 3.69E+03 | 5.47E+03 | 2.50E+03 | 2.86E+03 | 5.33E+03 | |
| F11 | 10 | 3.04E+03 | 3.68E+03 | 4.48E+03 | 3.71E+03 | 4.83E+03 | 5.15E+03 | 2.76E+03 | 3.13E+03 | 3.60E+03 | 2.71E+03 | 2.77E+03 | 3.16E+03 |
| 20 | 6.85E+03 | 8.44E+03 | 9.10E+03 | 8.91E+03 | 1.01E+04 | 1.06E+04 | 4.09E+03 | 5.78E+03 | 7.92E+03 | 4.00E+03 | 5.24E+03 | 6.48E+03 | |
| F12 | 10 | 2.93E+03 | 3.02E+03 | 3.13E+03 | 2.92E+03 | 3.08E+03 | 3.29E+03 | 2.89E+03 | 2.95E+03 | 3.04E+03 | 2.86E+03 | 2.87E+03 | 2.89E+03 |
| 20 | 3.55E+03 | 3.90E+03 | 4.46E+03 | 3.69E+03 | 4.07E+03 | 4.53E+03 | 3.24E+03 | 3.44E+03 | 3.62E+03 | 2.97E+03 | 3.03E+03 | 3.15E+03 | |
| Friedman | 10 | 3.1667 | 3.8333 | 1.8333 | 1.1667 | ||||||||
| 20 | 3.0833 | 3.9166 | 2.0000 | 1.0000 | |||||||||
| VF-GPTHOA | Deployment Optimization |
|---|---|
| Hiker | A set of deployment schemes |
| Leader | Optimal deployment scheme |
| Population size | Number of deployment scheme |
| Hiker’s position | HMWS’ position |
| Best fitness | Maximum CR |
| Parameter | Value | |
|---|---|---|
| BM size | 40 × 200 | |
| Population size N | 100 | |
| Maximum number of iterations iter_max | 1500 | |
| Experiment 1 | Total number of sensors | 60 |
| Sensor type and number | 20 in each of the three categories | |
| 10, 8, and 6 | ||
| Experiment 2 | Total number of sensors | 45, 51, 57, 63, and 69 |
| Sensor type and number | 15, 17, 19, 21, 23 in each of the three categories | |
| 10, 8, and 6 | ||
| Indicator | DE | MA | GWO | SSA | HOA | VF-GPTHOA |
|---|---|---|---|---|---|---|
| CR | 85.29% | 93.17% | 83.86% | 94.68% | 86.33% | 97.07% |
| CE | 0.54 | 0.59 | 0.53 | 0.60 | 0.55 | 0.62 |
| OR | 37.09% | 36.32% | 39.38% | 36.77% | 38.48% | 32.57% |
| AMD/m | 81.3 | 52.1 | 69.8 | 70.4 | 55.6 | 28.9 |
| Indicator | DE | MA | GWO | SSA | HOA | VF-GPTHOA |
|---|---|---|---|---|---|---|
| CR | 0.0076 | 0.0064 | 0.0301 | 0.0091 | 0.0165 | 0.0052 |
| CE | 0.137 | 0.124 | 0.126 | 0.008 | 0.012 | 0.006 |
| OR | 0.0193 | 0.0210 | 0.0323 | 0.0141 | 0.0154 | 0.0115 |
| AMD/m | 18.92 | 23.12 | 32.62 | 24.61 | 25.93 | 16.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, C.; Yang, J.; Huo, J. A Mobile Wireless Sensor Coverage Optimization Method for Bridge Monitoring. Sensors 2025, 25, 2772. https://doi.org/10.3390/s25092772
Mu C, Yang J, Huo J. A Mobile Wireless Sensor Coverage Optimization Method for Bridge Monitoring. Sensors. 2025; 25(9):2772. https://doi.org/10.3390/s25092772
Chicago/Turabian StyleMu, Cong, Jiguang Yang, and Jiuyuan Huo. 2025. "A Mobile Wireless Sensor Coverage Optimization Method for Bridge Monitoring" Sensors 25, no. 9: 2772. https://doi.org/10.3390/s25092772
APA StyleMu, C., Yang, J., & Huo, J. (2025). A Mobile Wireless Sensor Coverage Optimization Method for Bridge Monitoring. Sensors, 25(9), 2772. https://doi.org/10.3390/s25092772





