Unidirectional Orbit Determination for Extended Users Based on Navigation Ka-Band Inter-Satellite Links
Abstract
1. Introduction
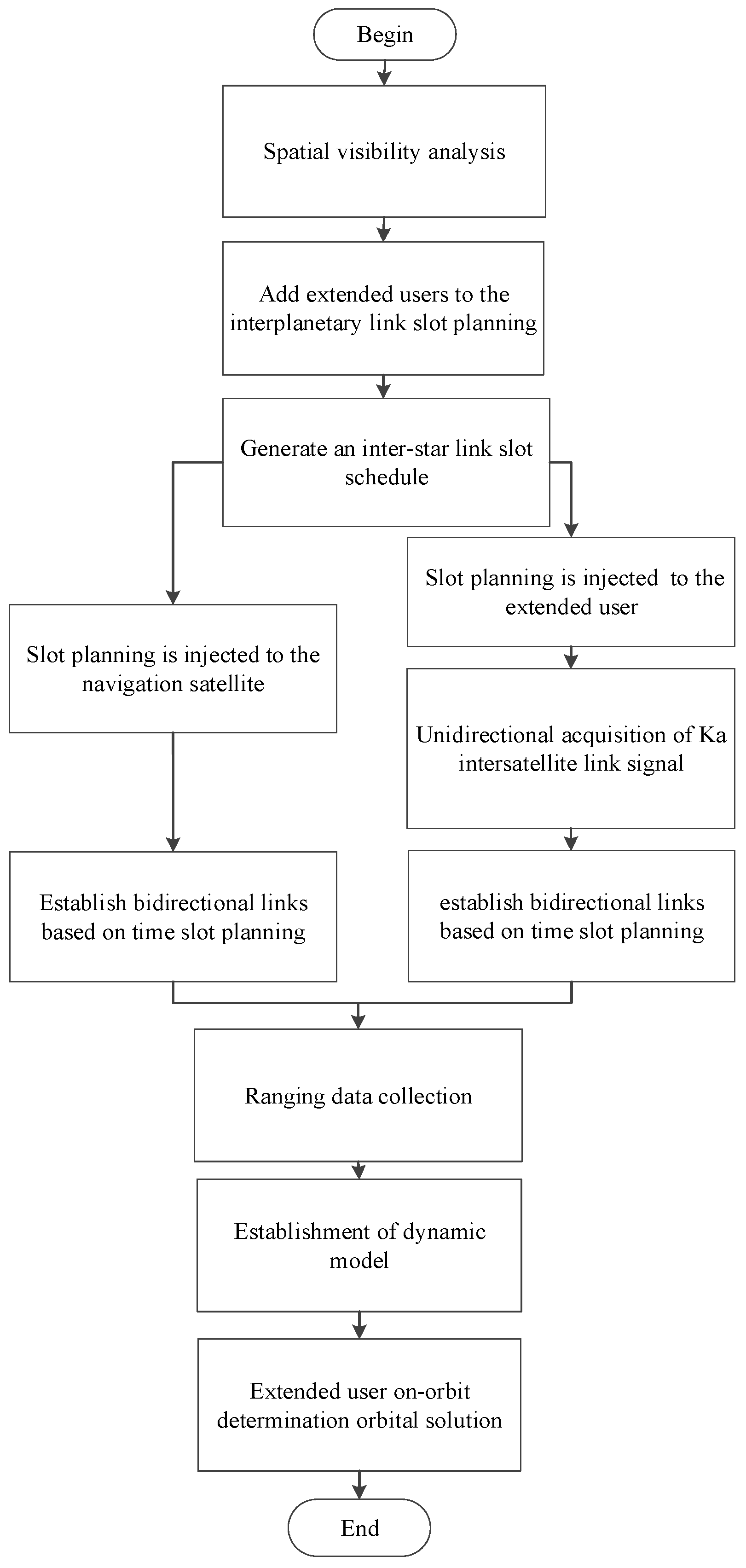
2. The Basic Process of Navigation Inter-Satellite Link Access and Orbit Determination
3. Time–Frequency Compensation and Measurement Model
3.1. Clock Model
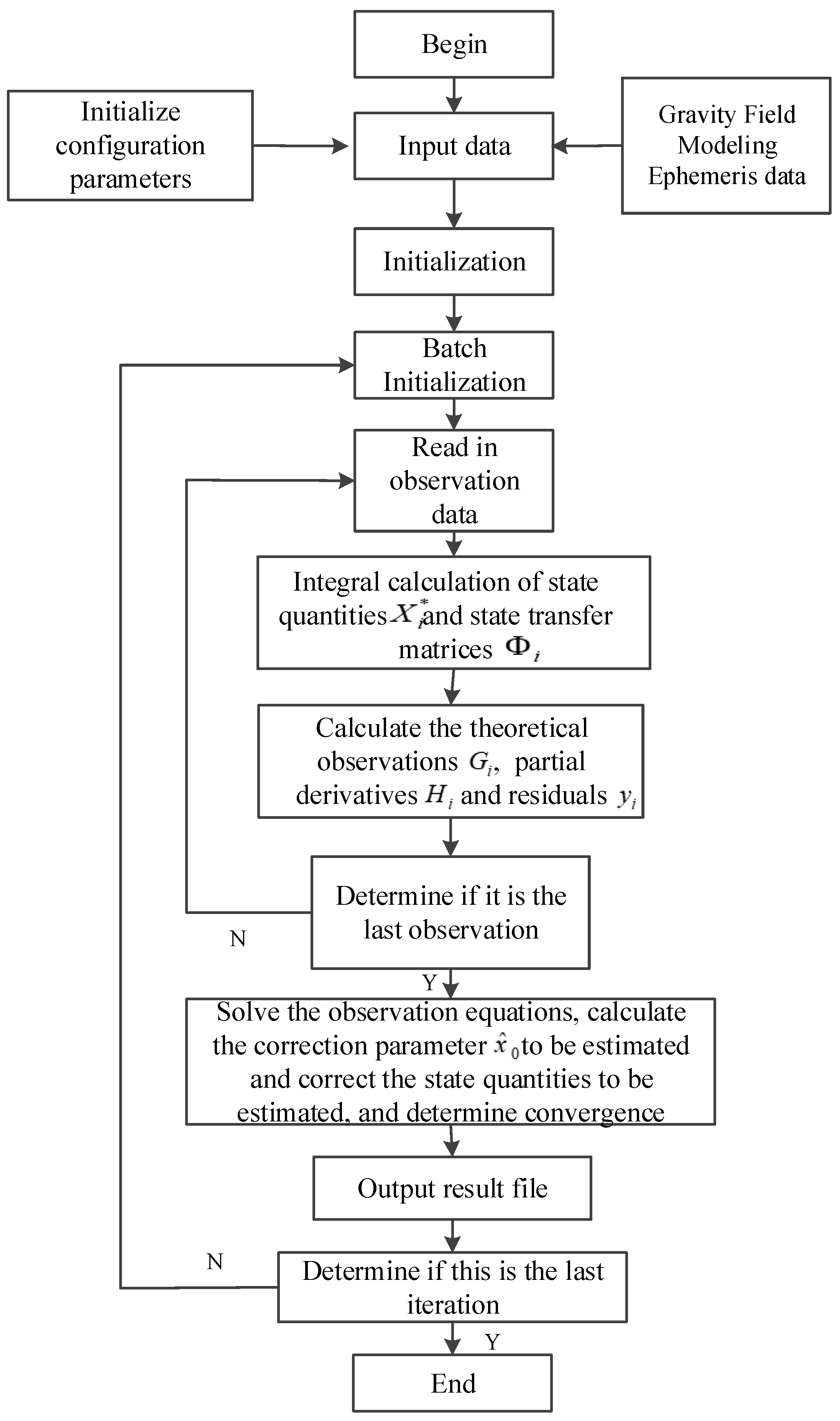
3.2. Unidirectional Orbit-Determination Motion and Observation Equation
4. Orbit-Tracking and -Determination Algorithm Simulation
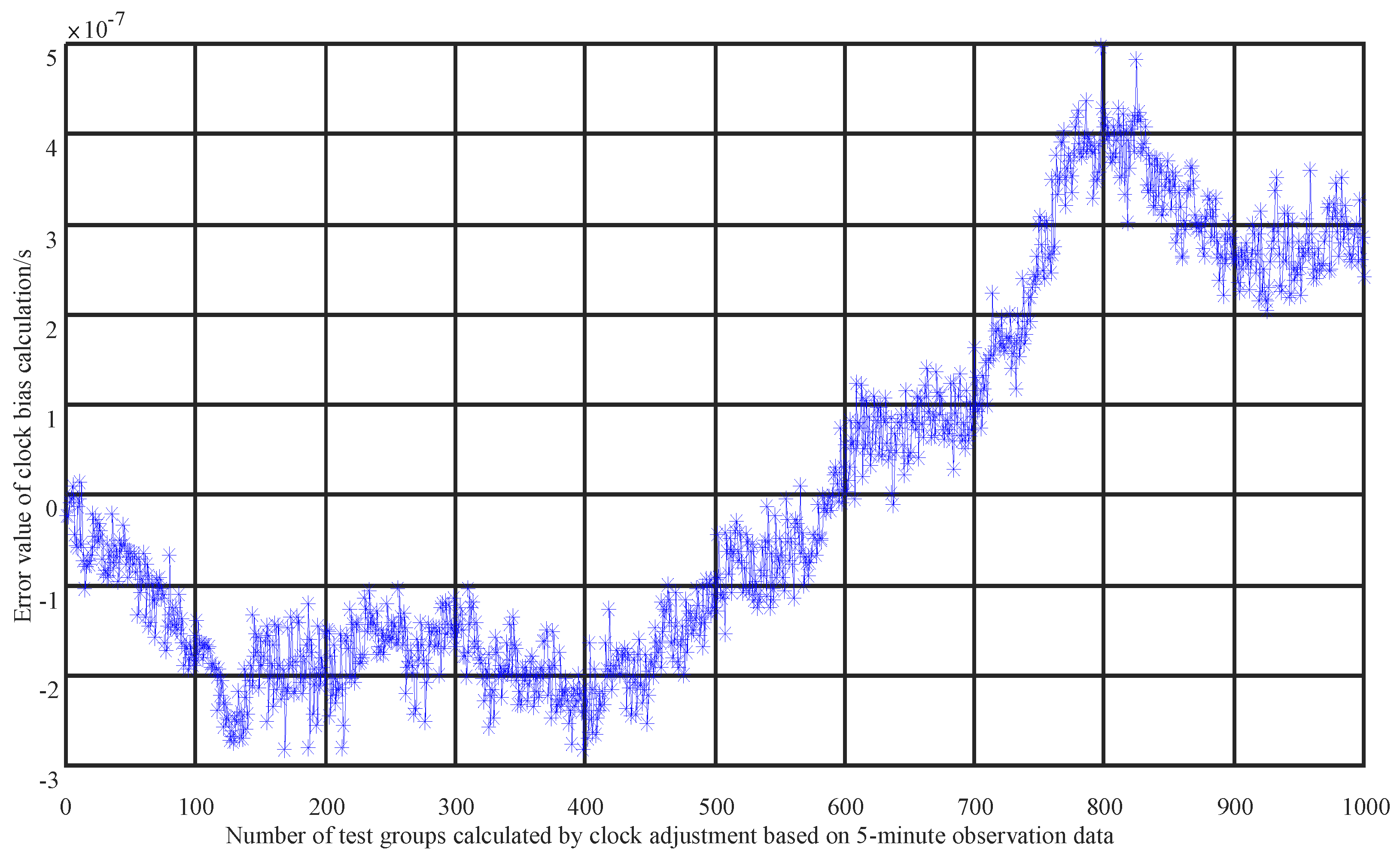
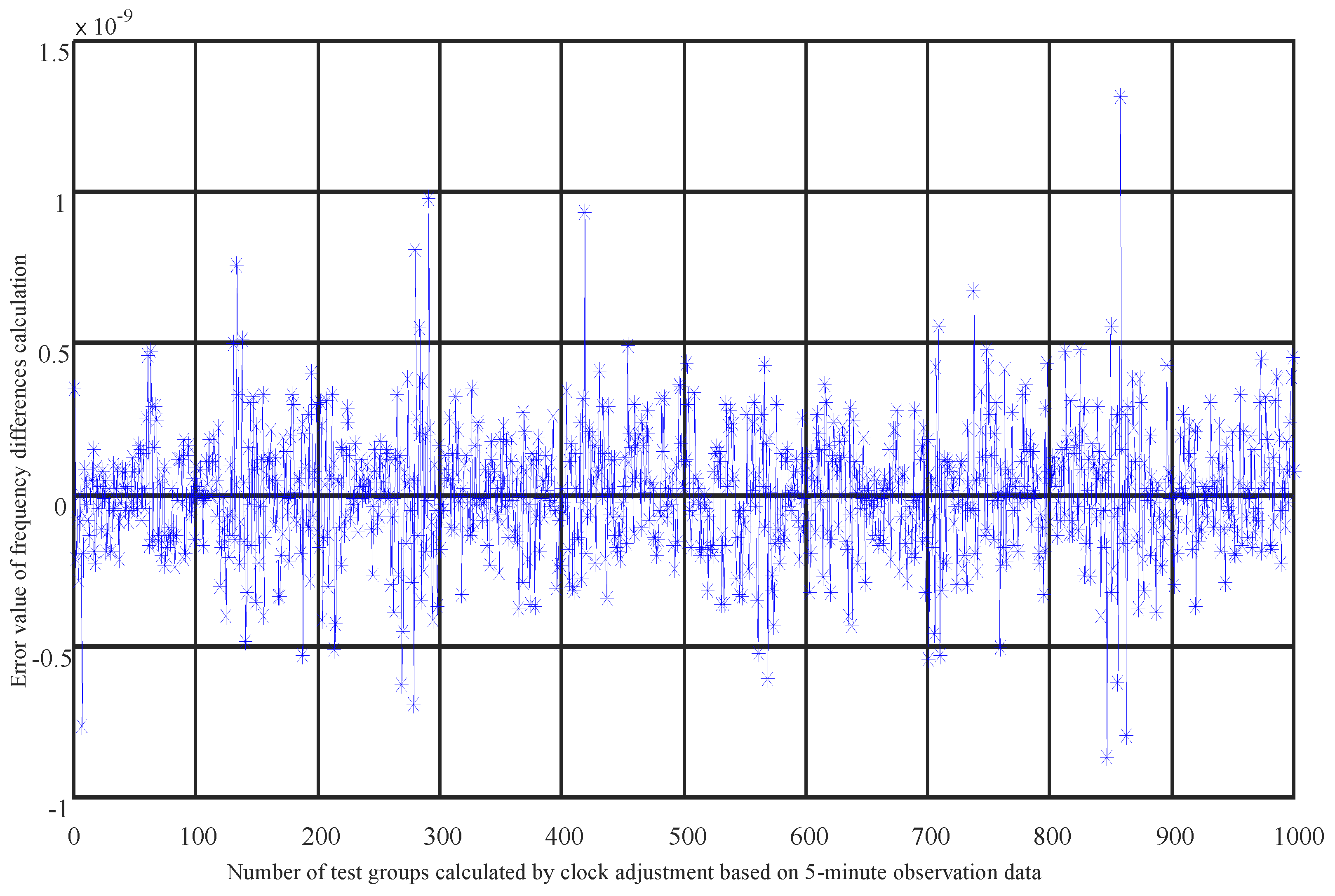
4.1. Accuracy of Clock Difference Calculations
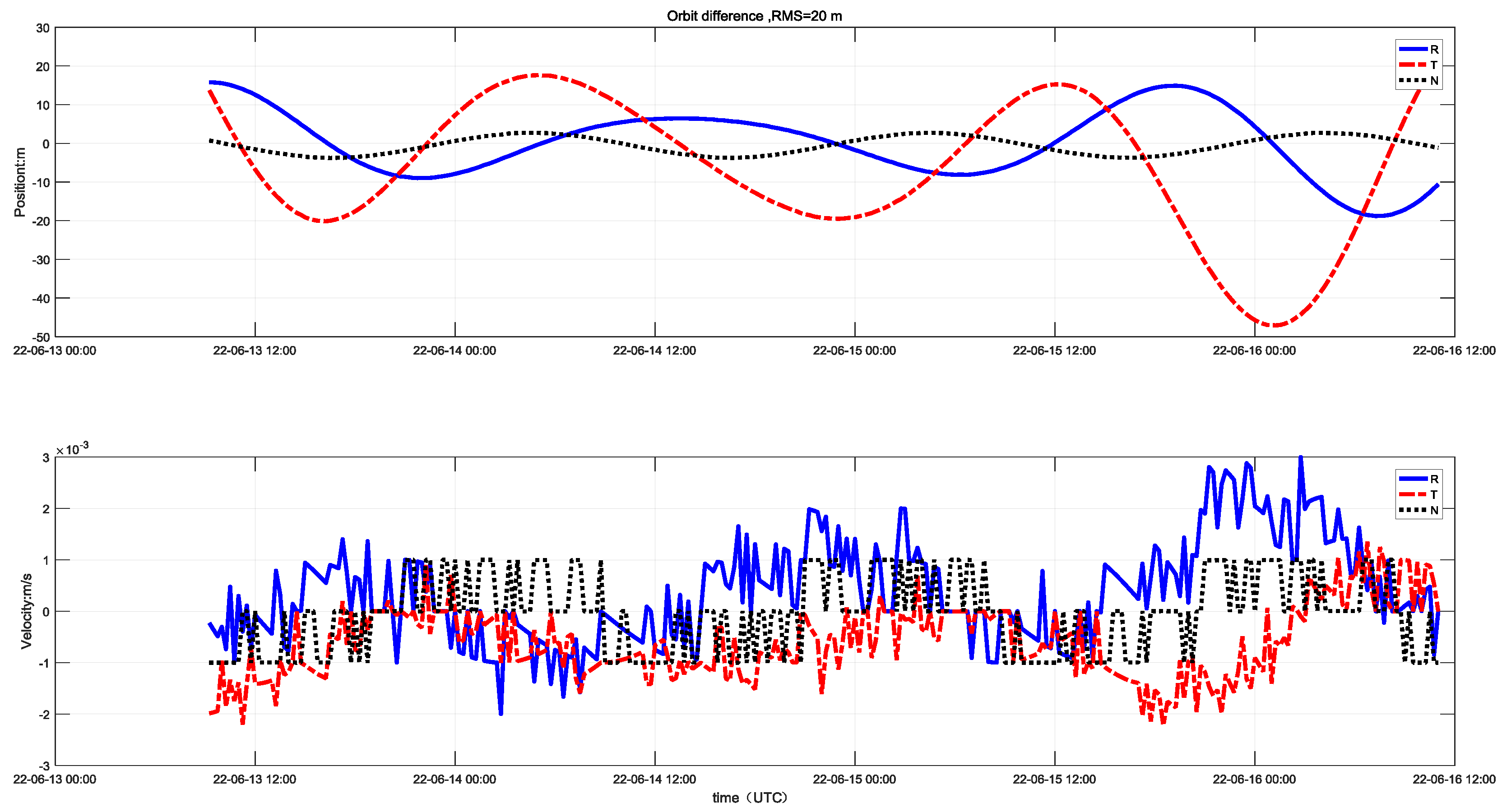
4.2. Simulation Results of Orbit-Determination Precision
4.3. In-Orbit Measurement Results for Orbit Determination
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| TT&C | Tracking, Telemetry and Command |
| GPS | Global Positioning System |
| GEO | GEostationary Orbit |
| IGSO | Inclined GeoSynchronous Orbit |
| MEO | Medium Earth Orbit |
| ECI | Earth-Centered Inertial |
| ms | milliseconds |
| kHz | kilohertz |
| us | microseconds |
| PDOP | Position Dilution of Precision |
| UTC | Universal Time Coordinated |
References
- Kim, J.; Kim, M. Orbit determination of low earth orbiting satellites using space based augmentation systems. J. Spacecr. Rocket. 2018, 55, 1300–1302. [Google Scholar] [CrossRef]
- Fan, S.; Meng, Y.; Gao, W.; Li, J. Summarizing on the Development of Spacecraft Orbit Determination Technology. J. Zhengzhou Inst. Surv. Mapp. 2013, 30, 549–554. [Google Scholar]
- Wang, D.; Xin, J.; Xue, F.; Guo, R. Development and Prospect of GNSS Autonomous Navigation Based on Inter-Satellite Link. J. Astronaut. 2016, 37, 1279–1288. [Google Scholar]
- Luba, O.; Boyd, L.; Gower, A.; Crum, J. GPS III system operations concepts. Aerosp. Electron. Syst. Mag. 2005, 20, 110–118. [Google Scholar] [CrossRef]
- Anderson, M.P.; Langer, J. Crosslink for the next-generation GPS. In Proceedings of the 2003 IEEE Aerospace Conference, New York, NY, USA, 8–15 March 2003. [Google Scholar]
- Wen, X. Research on the Beidou Clock Difference Observation and Strategy of Autonomous Orbit Determination Under the Condition of Inter-Satellite Link. Master’s Thesis, PLA Strategic Support Force Information Engineering University, Zhengzhou, China, 2018. [Google Scholar]
- Song, X.; Mao, Y.; Feng, L.; Jia, X. The Preliminary Result and Analysis for BD Orbit Determination with Inter-satellite Link Data. J. Geod. Geoinf. Sci. 2017, 46, 547–553. [Google Scholar]
- Meng, Y.; Fan, S.; Yang, Q.; Song, X. Analysis of Spacecraft Orbit Determination Method Using GNSS Crosslink. Spacecr. Eng. 2015, 24, 31–37. [Google Scholar]
- Shao, R.; Chang, J.; Lin, X.; Tan, S.; Gong, W.; Lin, B. An autonomous orbit determination algorithm for spacecraftusing extended service of BDS inter-satellite-link. Chin. Space Sci. Technol. 2024, 44, 106–113. [Google Scholar]
- Tian, G.; Cai, W.; Chen, Y.; Li, S.; He, C.; Xu, W. Rapid Chain-building Method for Near-earth High-speed Targets Access to Beidou Inter-satellite Link System. Spacecr. Eng. 2022, 37, 63–70. [Google Scholar]
- Xu, L.; Meng, Y.; Zhang, Z.; Hu, T. Research on Multi-user Random Access Technology of Beidou Inter Satellite Link. In Proceedings of the China Satellite Navigation Conference, Chengdu, China, 23 November 2020. [Google Scholar]
- Xie, J.; Liu, Q.; Bian, L. Development Assumption of National Comprehensive PNT Architecture Based on BeiDou Navigation Satellite System. Space Electron. Technol. 2017, 5, 5–6. [Google Scholar]
- Chen, L.; Zhang, K.; Huang, Y.; Liu, Z.; Ou, G. Performance Analysis of Lunar Spacecraft Navigation based on Inter-Satellite Link Annular Beam Antenna. IEEE Trans. Commun. 2016, 99, 951–956. [Google Scholar] [CrossRef]
- Teng Yun, W.; Wang, Y.; Chen, J.; Feng, X.; Li, X. Inter-satellite link directivity algorithm research and performance validation. J. Instrum. 2014, 2, 96–100. [Google Scholar]
- Chen, J.; Zhou, Y.; Yang, J. Principles of Intersatellite Link Measurement and Communication in Satellite Navigation Systems; National Defense Industry Press: Beijing, China, 2016. [Google Scholar]
- Meng, Y.; Tang, Y. Simulation Analysis of Navigation Constellation Crosslink. J. Astronaut. Metrol. Meas. 2014, 34, 15–24. [Google Scholar]
- Li, Z.; Wu, X.; Rong, M. Basic and Application of STK in System System-of-Systems Operations; Military Science Press: Beijing, China, 2014. [Google Scholar]
- Gong, X.; Yuan, J.; Hu, X.; Wang, B.; Chen, J.; Zhou, S. Accuracy evaluation and improvement strategies of BeiDou broadcast clock error model. Acta Geod. Cartogr. Sin. 2021, 50, 181–188. [Google Scholar]
- Chen, L.; Song, W.; Yi, W.; Shi, C.; Lou, Y.; Guo, H. Research on a method of real-time combination of precise GPS clock corrections. GPS Solut. 2016, 21, 187–195. [Google Scholar] [CrossRef]
- Liu, C.; Wang, L.; Qin, Z. Early analysis of precise orbit and clock offset determination for the satellites of the global BeiDou-3 system. Adv. Space Res. 2019, 63, 1270–1279. [Google Scholar]
- Busca, G.; Wang, Q. Time prediction accuracy for a space clock. Metrologia 2003, 40, S265–S269. [Google Scholar] [CrossRef]
- Han, C.; Cai, Z.; Lin, Y.; Liu, L.; Xiao, S.; Zhu, L.; Wang, X. Time Synchronization and Performance of Bei Dou Satellite Clocks in Orbit. Int. J. Navig. Obs. 2013, 2013, 67–71. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O.; Steigenberger, P. Short-term analysis of GNSS clocks. GPS Solut. 2013, 7, 295–307. [Google Scholar] [CrossRef]
- Li, L.; Li, C.; Huang, W.; Zhou, Y. Orbit determined method of high elliptical orbit satellite based on BDS navigation and inter-satellite link. Chin. J. Space Sci. 2018, 38, 915–924. (In Chinese) [Google Scholar] [CrossRef]
- Qiao, L.; Lim, S.; Rizos, C.; Liu, J. GNSS-Based Orbit Determination for Highly Elliptical Orbit Satellites. Earth 2009, 2, 3. [Google Scholar]
- Vigneron, A.C.; de Ruiter, A.H.; Burlton, B.V.; Soh, W.K. Nonlinear filtering for autonomous navigation of spacecraft in highly elliptical orbit. Acta Astronaut. 2016, 126, 138–149. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits-Models, Methods, and Applications; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Yilmaz, U.C.; Cavdar, I.H. Simplified solution for osculating Keplerian parameter corrections of GEO satellites for intersatellite optical link. Adv. Space Res. 2015, 55, 1878–1884. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, X.; Zhou, S.; Song, X.; Huang, Y.; Mao, Y.; Huang, C.; Chang, Z.; Wu, S. A new autonomous orbit determination algorithm based on inter-satellite ranging measurements. Sci. Sin. Phys. 2015, 45, 079511. [Google Scholar]
- Ruan, R.; Jia, X.; Feng, L.; Zhu, J.; Huyan, Z.; Li, J.; Wei, Z. Orbit determination and time synchronization for BDS-3 satellites with raw inter-satellite link ranging observations. Satell. Navig. 2020, 1, 8. [Google Scholar] [CrossRef]

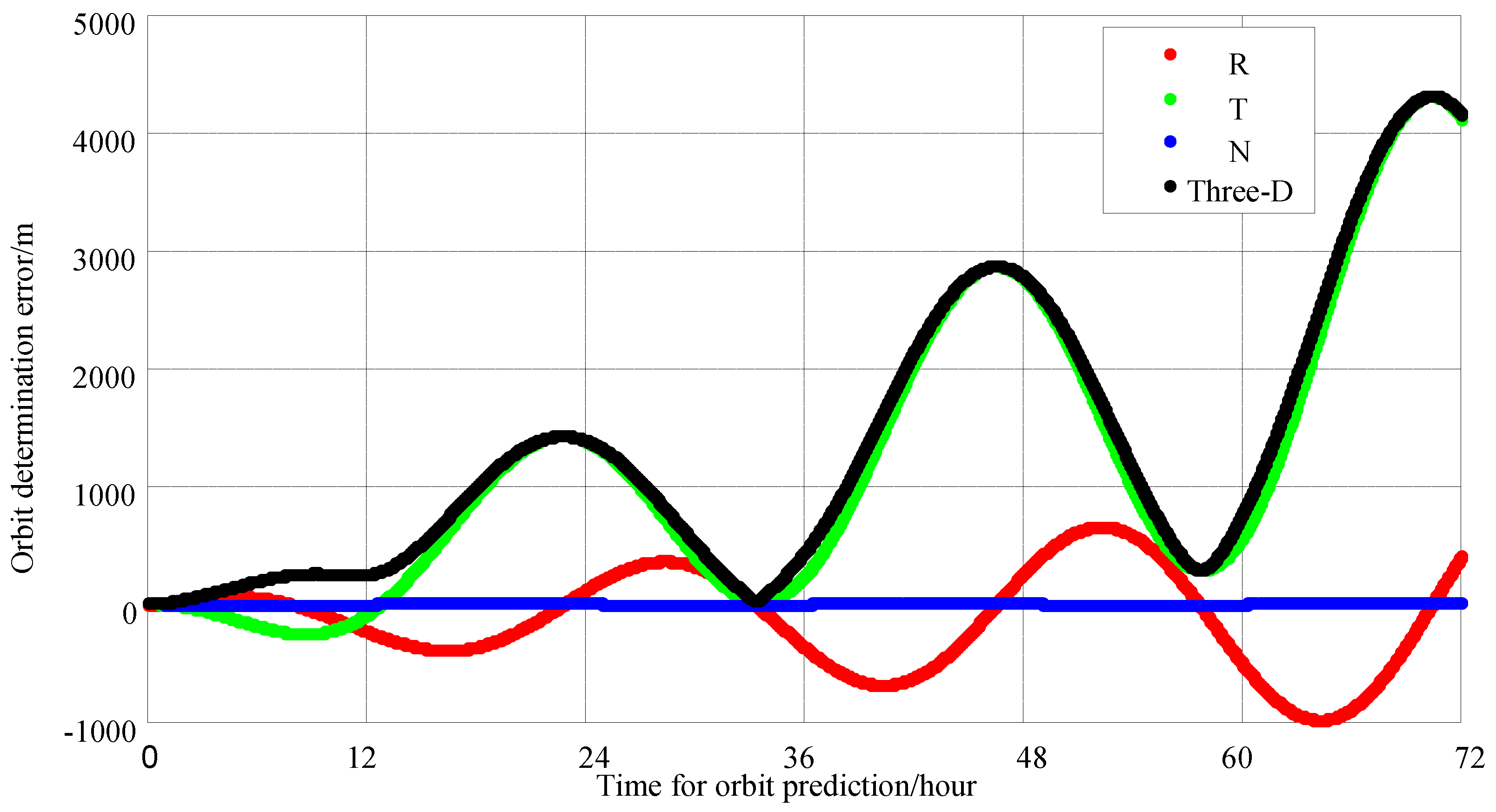
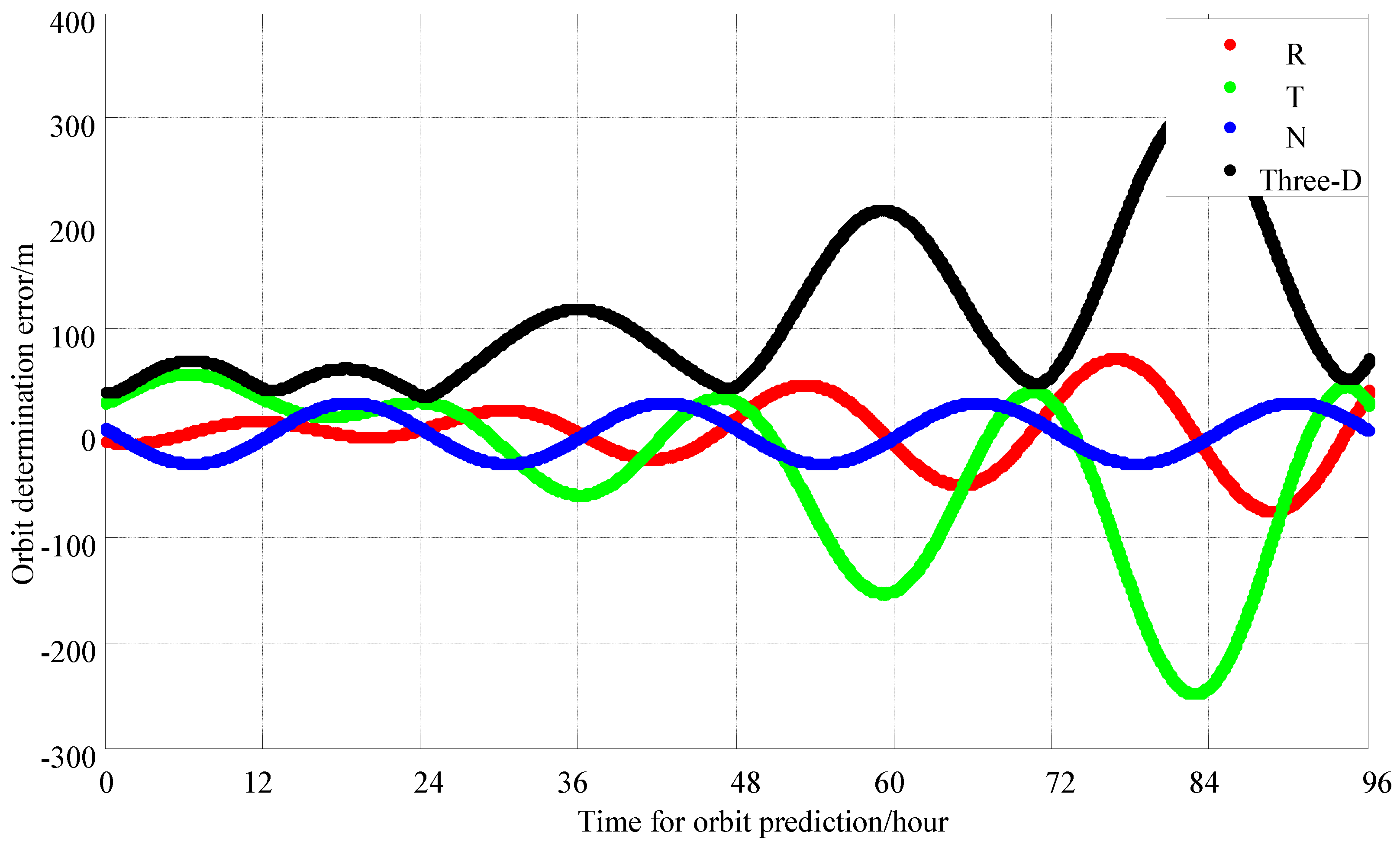
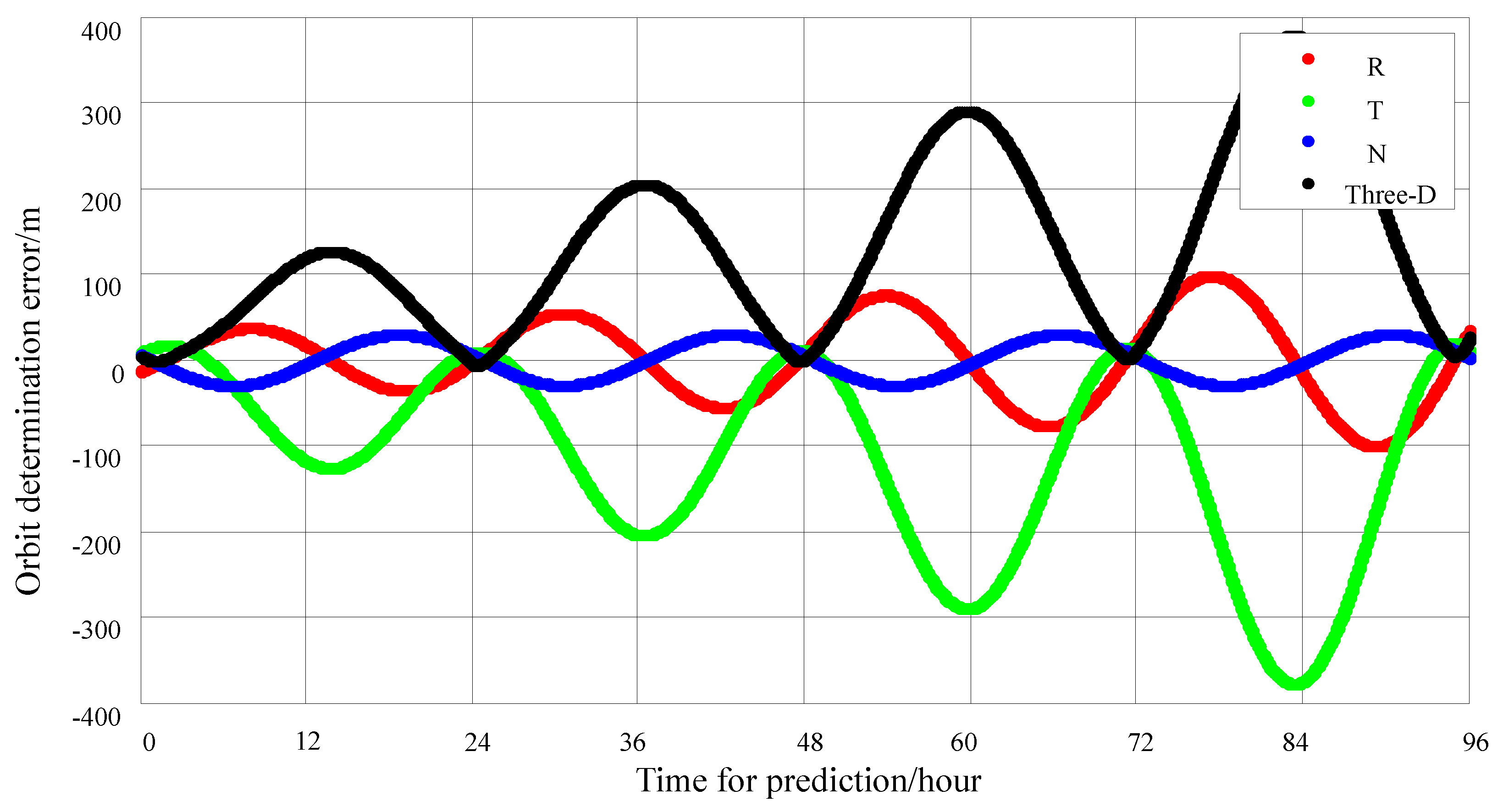

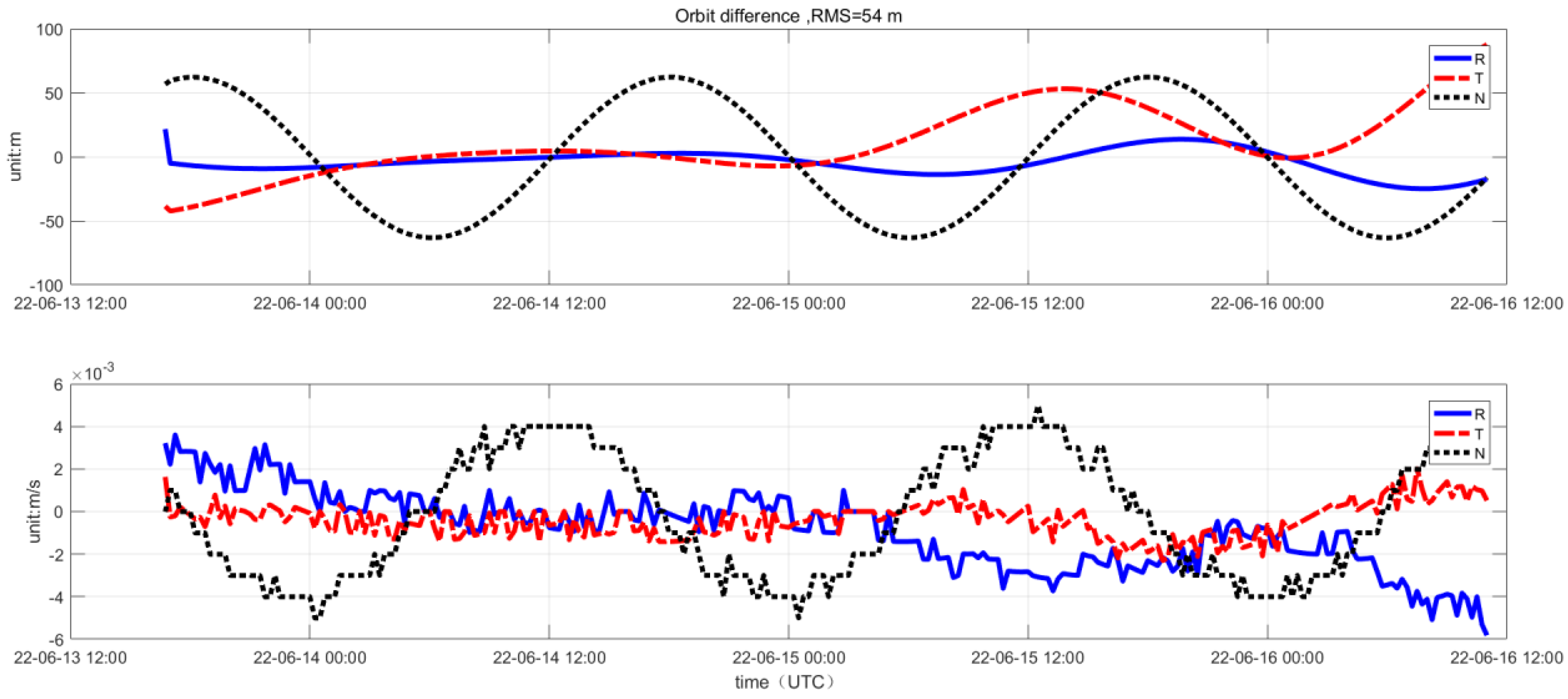
| Scheme | Data Arc Segment | Time Slots per Minute | Time Slots Within 1 h | Observation Period | 24 h Three-Axis Synthetic Error (m) | 72 h Three-Axis Synthetic Error (m) |
|---|---|---|---|---|---|---|
| 1 | 1 h each day | 8 | 480 | 1 day data processing | 1500 m | 5000 m |
| 2 | 1 h each day | 4 | 240 | 2 day data processing | 80 m | 205 m |
| 3 | 1 h each day | 3 | 180 | 2 day data processing | 140 m | 300 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, Y.; Zhang, H.; Yu, Y.; Wang, W.; Liu, B.; Li, H.; Ma, R. Unidirectional Orbit Determination for Extended Users Based on Navigation Ka-Band Inter-Satellite Links. Sensors 2025, 25, 2566. https://doi.org/10.3390/s25082566
Shangguan Y, Zhang H, Yu Y, Wang W, Liu B, Li H, Ma R. Unidirectional Orbit Determination for Extended Users Based on Navigation Ka-Band Inter-Satellite Links. Sensors. 2025; 25(8):2566. https://doi.org/10.3390/s25082566
Chicago/Turabian StyleShangguan, Yong, Hua Zhang, Yong Yu, Wenjin Wang, Bin Liu, Haihan Li, and Rong Ma. 2025. "Unidirectional Orbit Determination for Extended Users Based on Navigation Ka-Band Inter-Satellite Links" Sensors 25, no. 8: 2566. https://doi.org/10.3390/s25082566
APA StyleShangguan, Y., Zhang, H., Yu, Y., Wang, W., Liu, B., Li, H., & Ma, R. (2025). Unidirectional Orbit Determination for Extended Users Based on Navigation Ka-Band Inter-Satellite Links. Sensors, 25(8), 2566. https://doi.org/10.3390/s25082566






