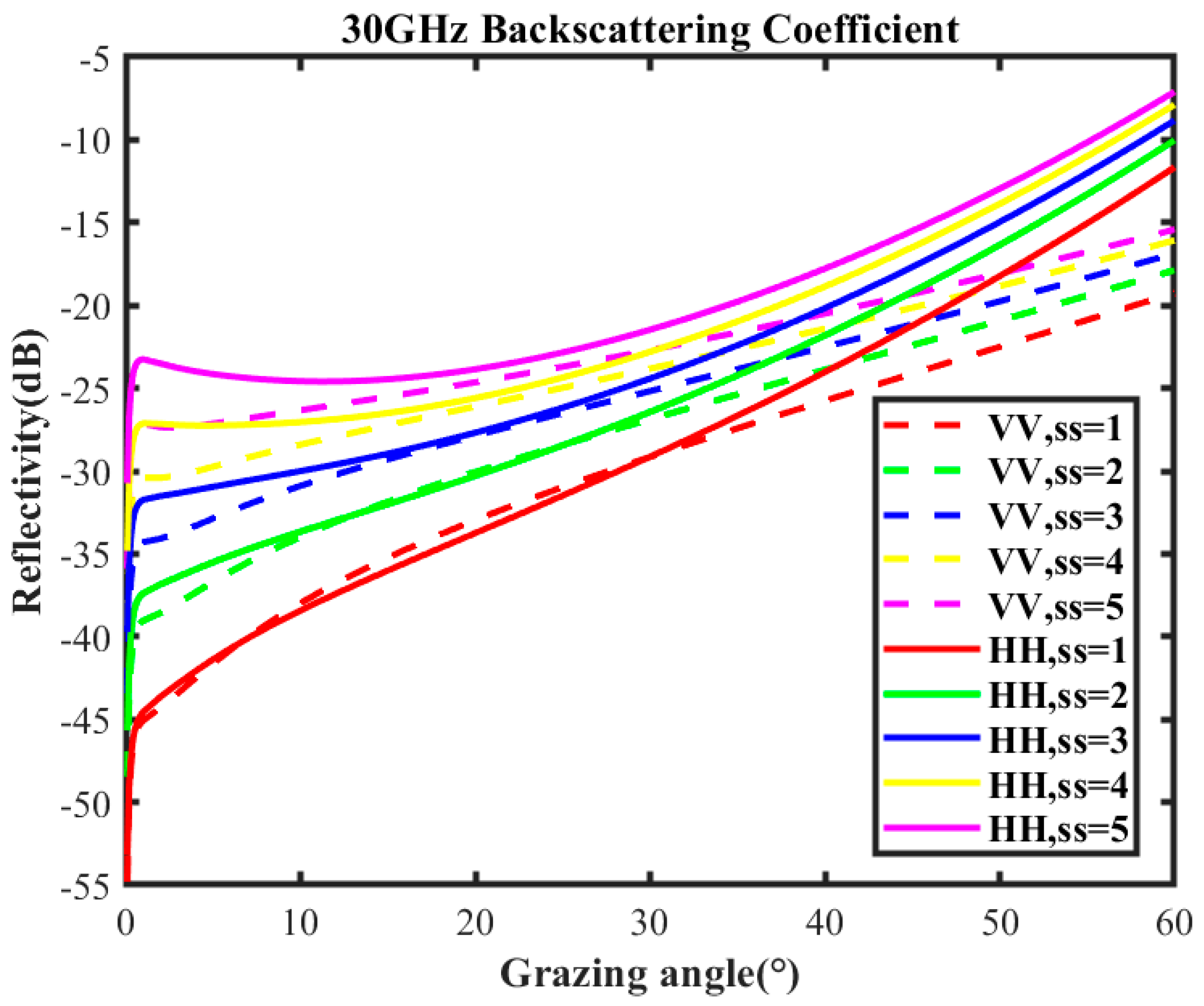
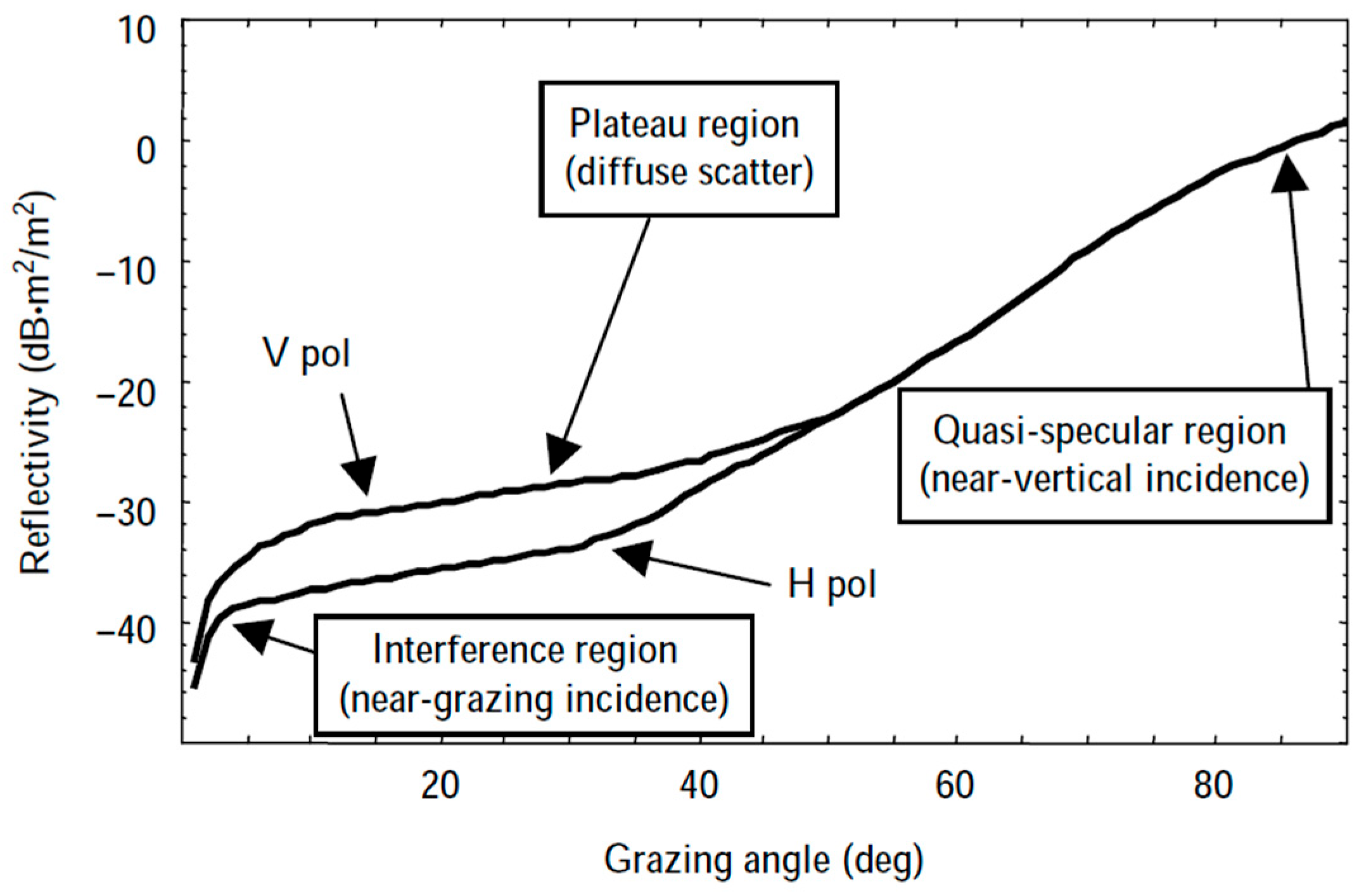
To validate the effectiveness of the proposed method, it is necessary to make use of the selected training samples to test both the constructed surrogate equation and the radar maritime target detection. The surrogate equation is a key prerequisite for training sample selection, and the training samples are a critical factor influencing the target detection performance. The measurement area in this study is Langya Taiwan, located in Qingdao, Shandong Province, China. The backscatter coefficient of sea clutter is measured and provided by specialized research institutes focused on target characteristics. The data acquisition equipment consists of two independent maritime surveillance radars. Both radars operate in a coherent system and transmit linear frequency-modulated (LFM) pulse signals in Ka-band with a carrier frequency of 30 GHz. The only difference between them is their polarization: one utilizes HH polarization, and the other adopts VV polarization. In search mode, the operating bandwidth is 10 MHz, the range resolution is 15 m, and the maximum detection range is 50 km. The search angle covers ±45°, and the radars are capable of staring operation at predefined angles.
4.1. Accuracy Analysis of Sea Clutter Characterization
Based on measured data and the empirical model, sea clutter characteristics are constructed under three scenarios: using PRS, using Kriging, and combining measured data with the empirical model. To evaluate the accuracy of the proposed characterization, a cross-validation method is employed, allowing for the selection of the model with superior predictive performance to determine the optimal training samples.
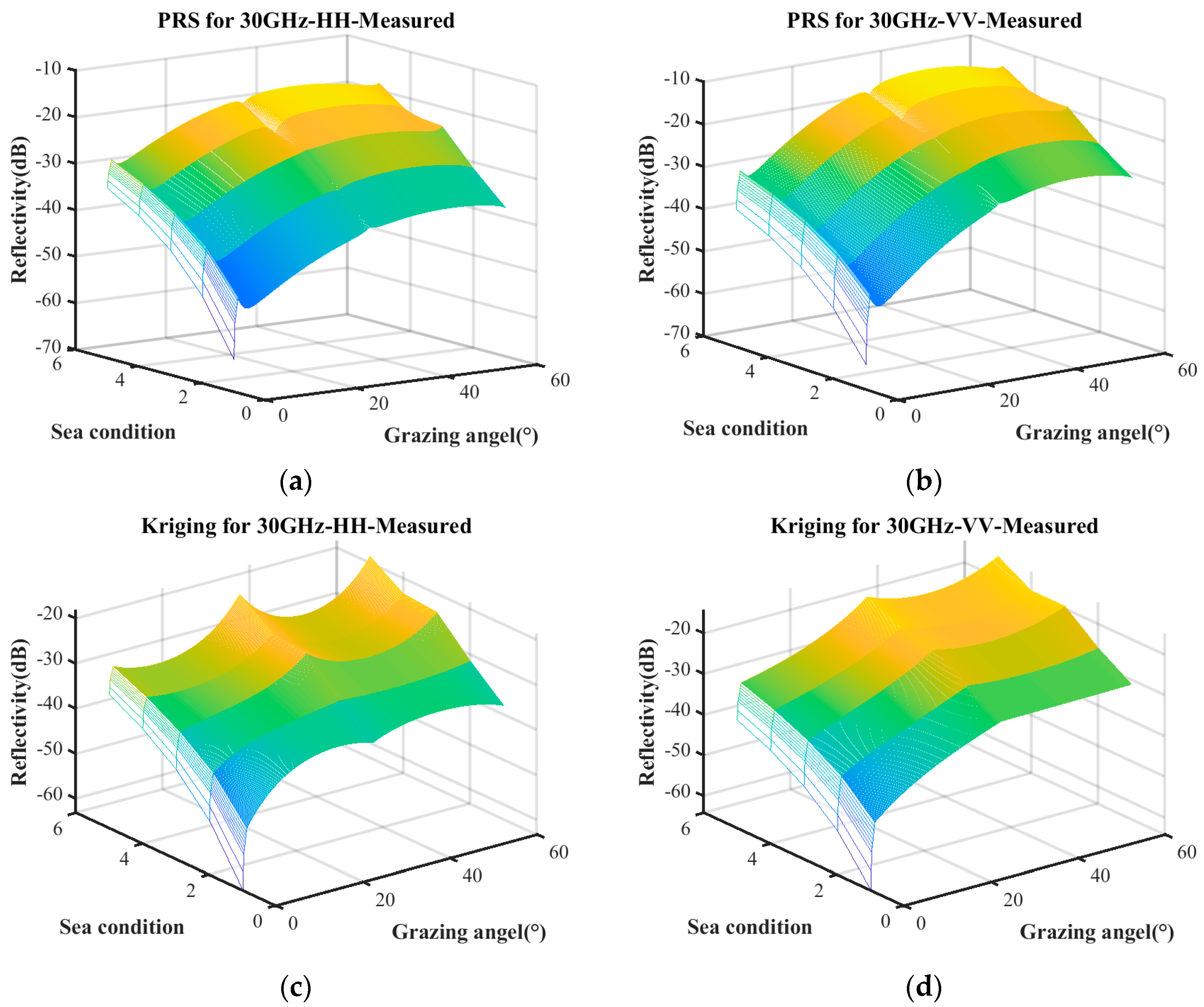
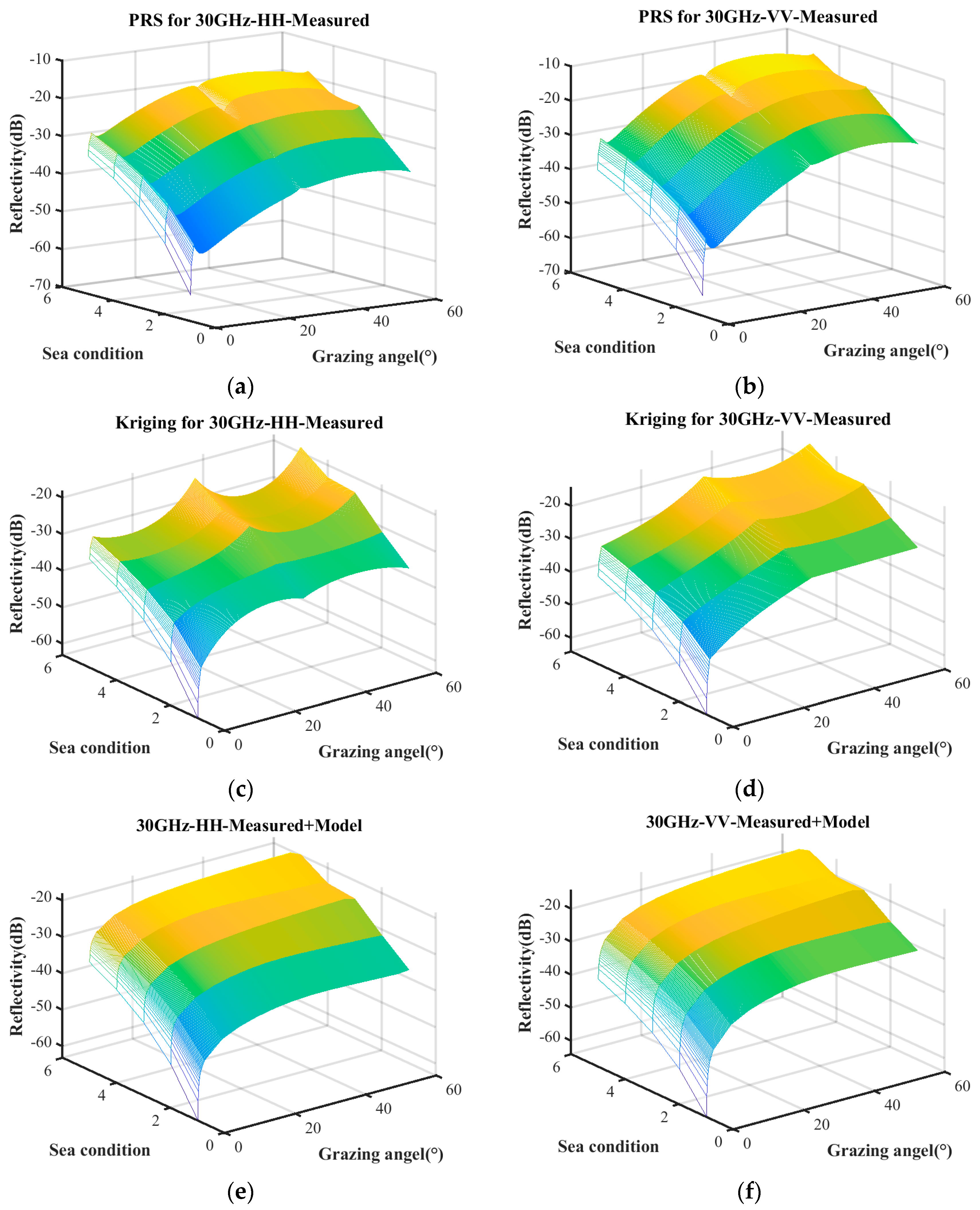
Figure 5 presents the sea clutter characterizations constructed under these three conditions.
Figure 5a–d represent the predictive results obtained solely from measured data using the PRS and Kriging model, whereas
Figure 5e,f refer to the predictions derived from the combination of the empirical model and measured data. The surface plot illustrates the predictive relationship between reflectivity, grazing angle, and sea conditions. Notably, the characterization based on measured data exhibits significant differences compared to the one incorporating both the empirical model and measured data.
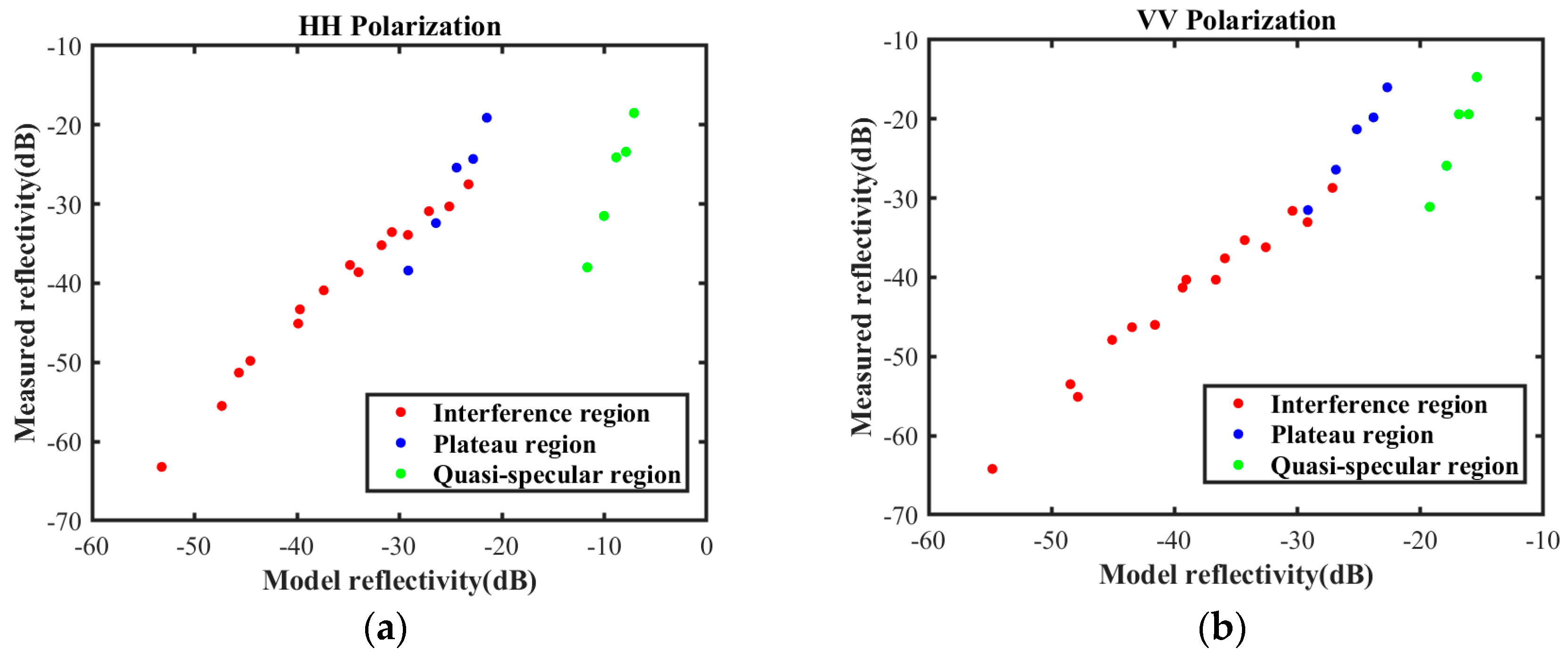
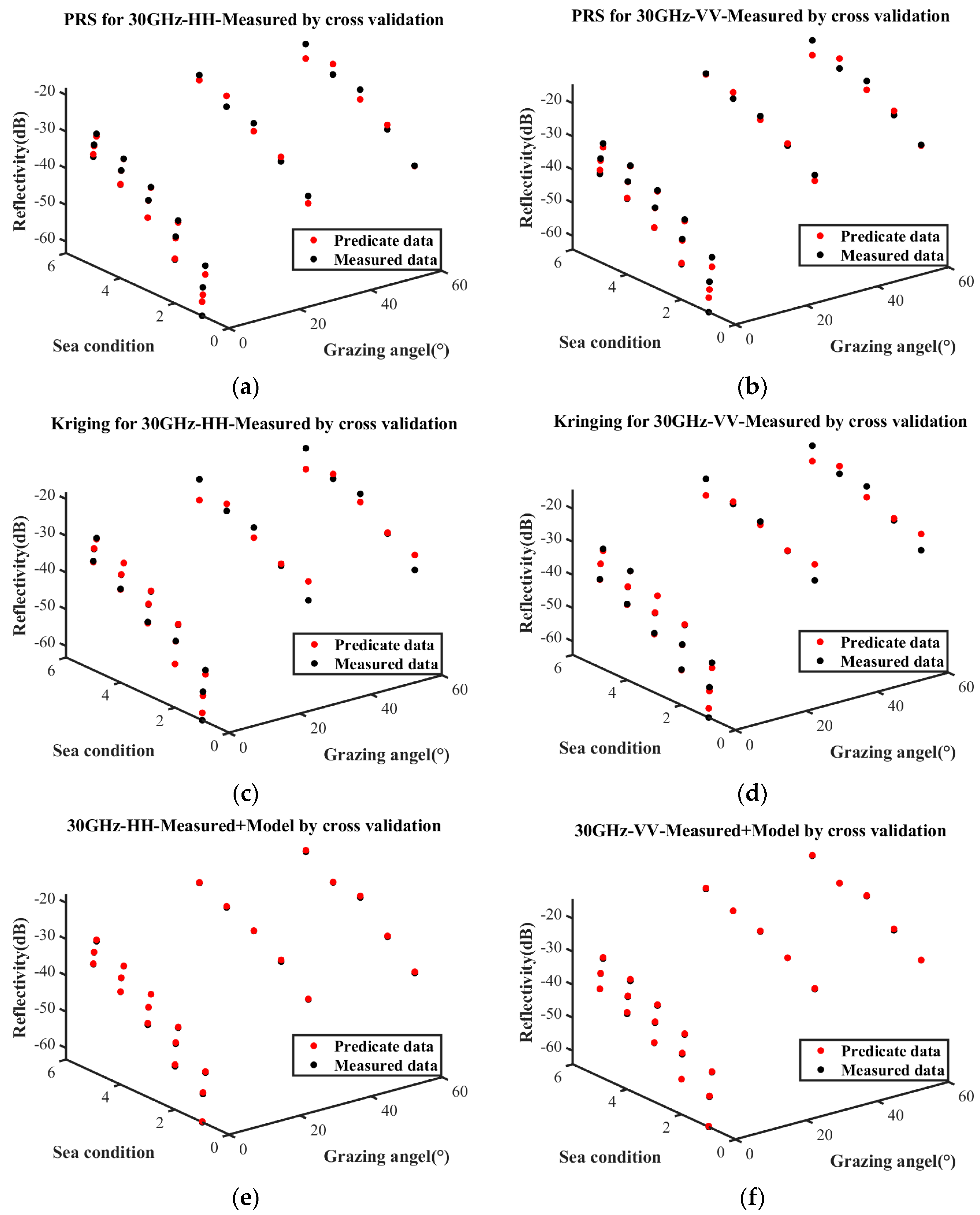
Cross-validation was employed to evaluate the three surrogate equations, and the validation results are presented in
Figure 6. Each point represents the reflectivity under various sea conditions and grazing angles, wherein the red points and black points indicate the predicted values and actual values, respectively. The closer the red points and black points are under the same sea conditions and incidence angles, the more accurate the prediction results.
The metrics used to evaluate the predictive performance are the mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and
. The evaluation metrics of the sea clutter characterization based on the measured data and the combination of the measured data with the empirical model are presented in
Table 4. When relying solely on measured data, the PRS demonstrates better performance than the Kriging model in fitting the distribution of sea clutter characteristics. Compared to the sea clutter characterization based on measured data, the sea clutter characterization based on a combination of the empirical model and measured data has smaller MSE, RMSE, and MAE, and its
is closer to the ideal value of 1. These indices indicate that the equation based on the measured data has poorer fitting accuracy.
By comparing these accuracy metrics, it is evident that the sea clutter characterization based on the combination of measured data and empirical model significantly outperforms that based on only measured data. The former can more accurately describe the characteristics of the observed sea surface, and its training samples would be more suitable for the marine region.
4.2. Target Detection on Different Coverage Training Samples
The position and the quantity of samples are the primary factors in training sample selection. The position is selected based on the fluctuation intensity of the sea clutter, and the quantity of samples is determined by the chosen coverage rate. The number of samples directly determines the volume and the effectiveness of the training samples.
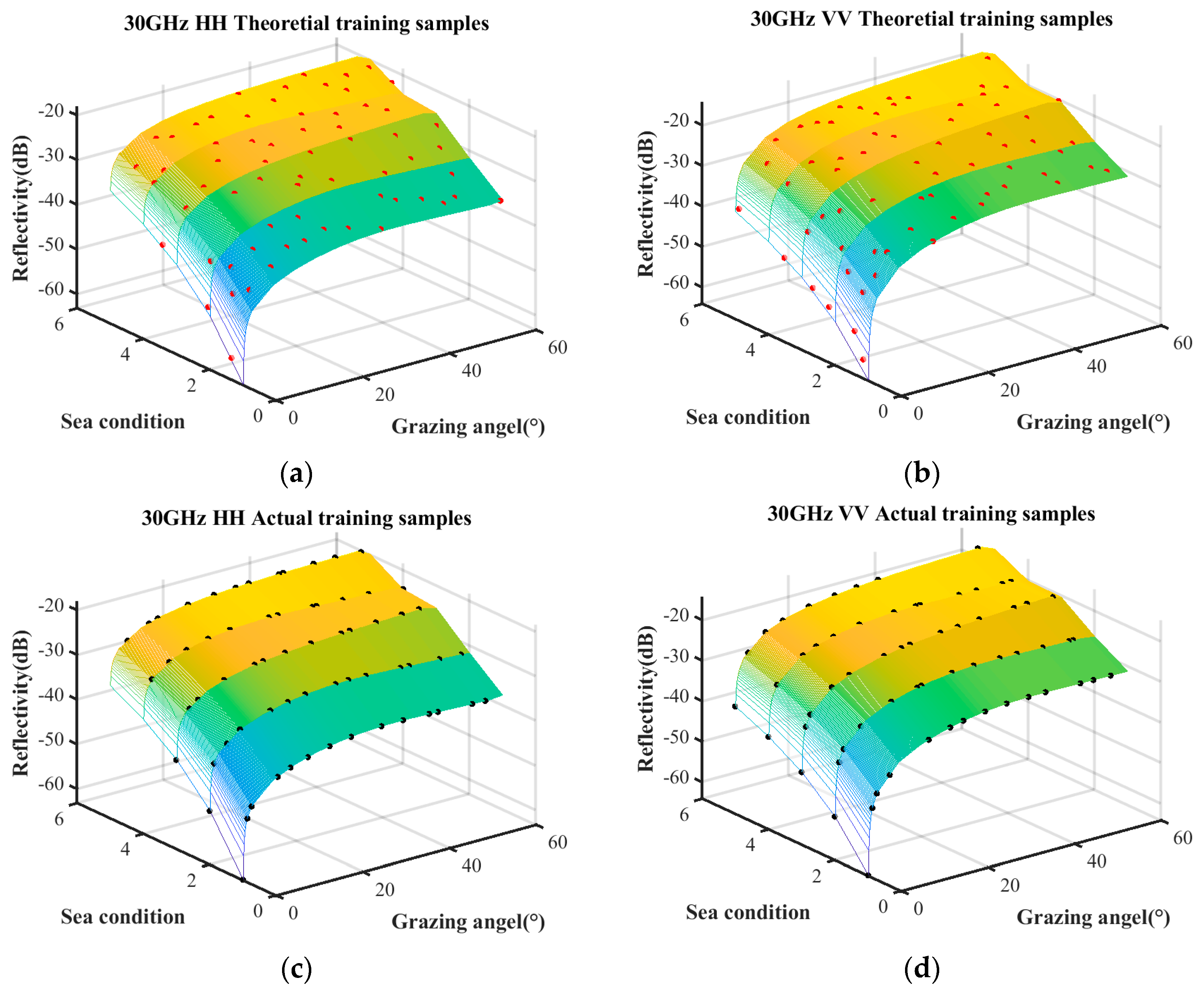
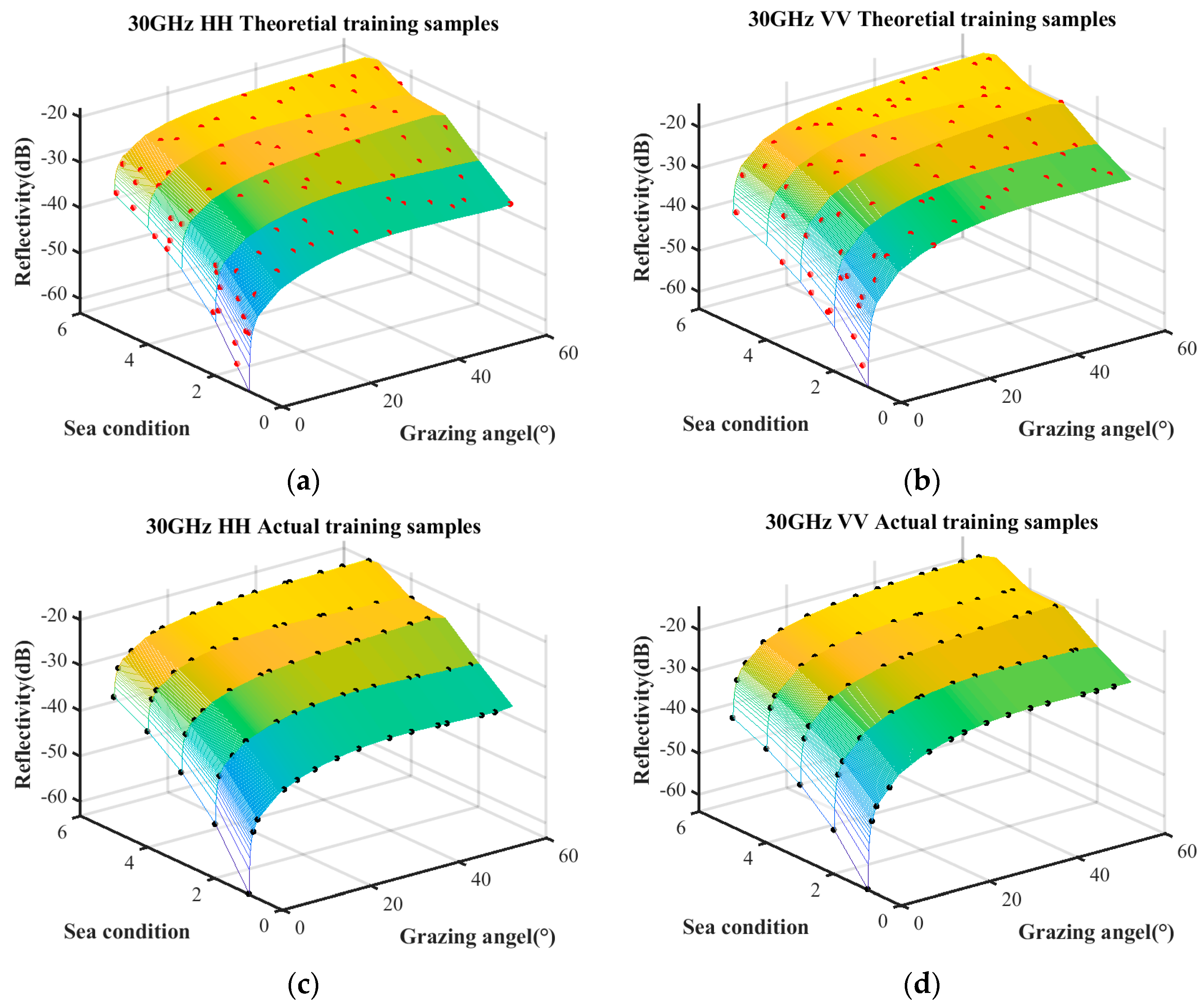
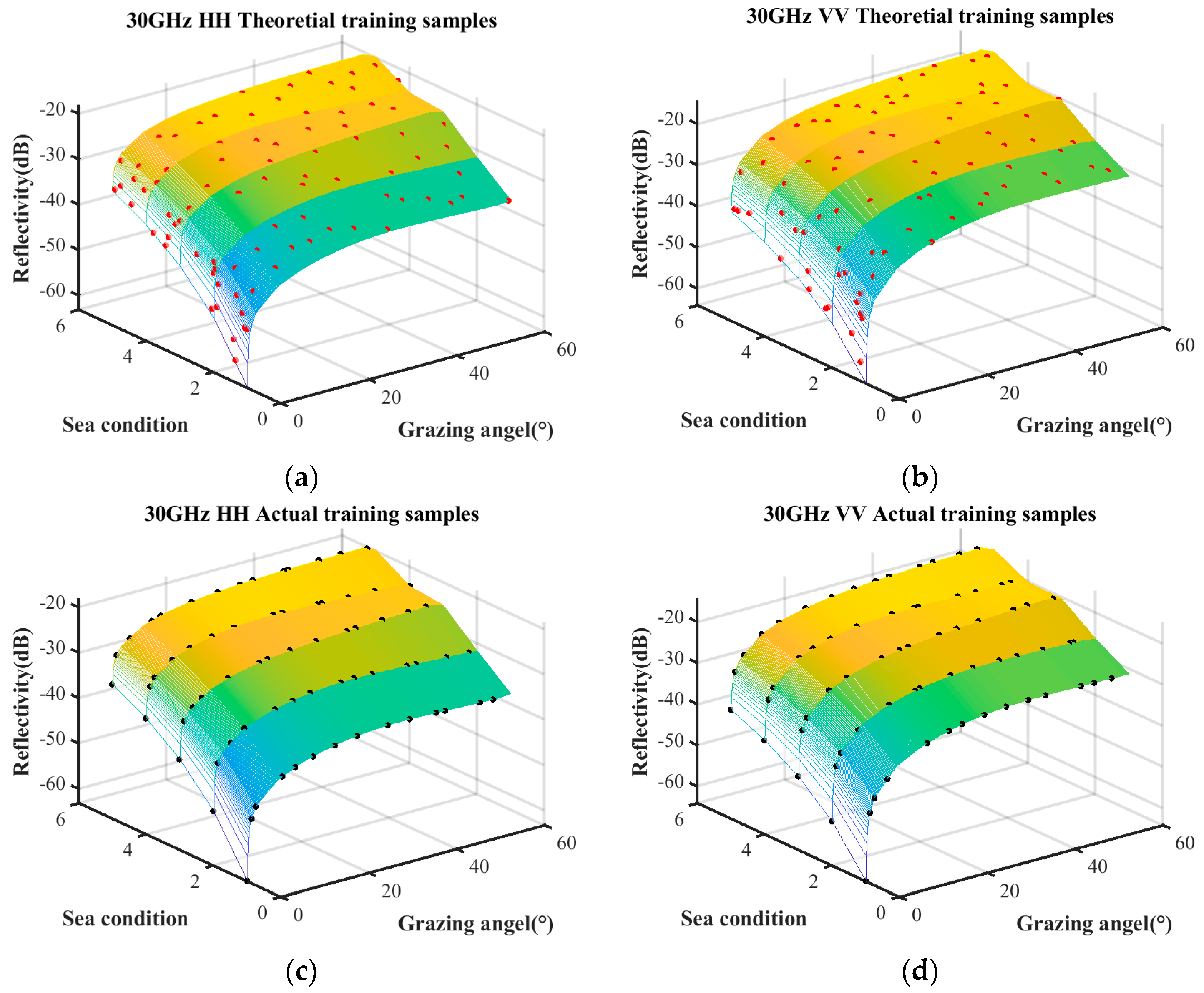
The sample quantities under different coverage rates are discussed first. The trained samples under the condition of a coverage rate of 85%, 90%, and 95% are selected by the surrogate equation based on the combination of measured data and empirical model. The theoretical training samples and the actual training samples are shown in
Figure 7,
Figure 8 and
Figure 9, respectively. The surface represents the predictive relationship between reflectivity, sea condition, and grazing angle, wherein the red points and black points denote theoretical sample points and actual sample points, respectively.
The sample quantities of the theoretical training samples and the actual training samples under the aforementioned three coverage conditions are listed in
Table 5.
With the increase in coverage rate, the theoretical sample quantity increases linearly, while the actual sample approaches saturation when the coverage rate reaches 90%. Additionally, compared to the coverage increase from 90% to 95%, the coverage increase from 85% to 90% obtains a significantly greater number of theoretical samples. Therefore, the coverage rate of 90% minimizes substantial wastage of theoretical samples while ensuring that the actual samples are sufficiently abundant.
After obtaining the training samples, the common time-frequency features are selected for a multi-feature detector to detect maritime targets. These features include common ridge integral (RI), number of connected regions (NR), and maximum connected region size (MS). For each of the three coverage rate training samples, these time-frequency features are combined with a single-class SVM classifier (OneClass-SVM) [
17] to obtain the corresponding feature classifiers. The radial basis function (RBF) is used as the kernel, with the hyperparameter ν set to 0.05, the RBF kernel parameter γ set to
, and other parameters, such as tol (convergence tolerance), set to their default values. To cover a wide range of maritime scenarios as comprehensively as possible, five types of scenarios are selected based on the available measured data, and they are listed in
Table 6: conventional ships under routine sea conditions, small fishing boats and sea surface floats under routine sea conditions, cruise ships under high sea conditions, conventional ships under large incidence angles, and cruise ships under both large incidence angles and high sea conditions.
For each scenario condition, 500 coherent processing interval (CPI) pulse compression data points in the Ka-band are selected to test the classifier performance. Every CPI includes 64 pulse echoes. After performing coherent accumulation on each CPI, a detection threshold set at 9 dB is used to identify suspicious target regions. The corresponding echo information from these regions is then extracted and input into a feature classifier to determine the attributes of the suspicious areas. The detection probability is defined as the ratio of correctly detected targets to the total number of actual targets, while the false alarm probability is defined as the ratio of falsely identified targets to the total number of suspicious locations. The test results are presented in
Table 7. Classifier 1, Classifier 2, and Classifier 3 represent the trainer selected under 85% coverage, 90% coverage, and 95% coverage, respectively.
It can be seen from
Table 7 that the performance of the classifier for conventional ship detection under routine sea condition with the coverage rate of 85% is similar to that with the coverage rate of 90%. The performance of conventional ship detection scenarios under large incidence angles also remains nearly unchanged. However, the classifier with the coverage rate of 85% shows slightly weaker performance in detecting small targets under routine sea conditions, cruise ships under high sea conditions, and cruise ships under both large incidence angles and high sea conditions. Meanwhile, the detection performance with a coverage rate of 90% is equivalent to that with a coverage rate of 95% in all aspects. From the perspective of detection performance, classifiers operating at a coverage rate of 90% are better suited for various application scenarios.
In summary, the performance of the detector with a coverage rate of 85% is somewhat inferior to that obtained with a coverage rate of 90% or higher, particularly in more complex observational scenarios. To enhance the environmental adaptability of the detector while minimizing the excessive waste of theoretical samples, it is recommended to choose a coverage rate of 90% for training samples.
4.3. Target Detection on Different Training Sample Selection Methods
The detection performance is evaluated by comparing feature classifiers constructed using different training sample selection methods, including partition strategies [
18], expert knowledge [
19], K-means clustering [
20], and deep learning methods such as self-organizing maps (SOMs) [
21]. The training sample selection methods and classifier training time are listed in
Table 8. The training datasets for the seven classifiers are constructed based on different sampling strategies. Excluding the time required for experimental data acquisition, the classifier training time is defined as the average duration of 10 repetitions of training the classifier using a large set of routinely collected radar data as input, with MATLAB 2021(a) (requiring the DACE toolbox 2.0 and LibSVM toolbox 2.88) and PyTorch 1.8.0.
Classifier A: The training dataset is generated using the proposed method, selecting 70 training sample positions based on a 90% coverage criterion. From each position, 10 mid-frequency echoes are chosen, resulting in a total of 700 mid-frequency echoes.
Classifier B: This dataset expands upon that of Classifier A by arbitrarily adding 30 additional training sample positions along with their corresponding mid-frequency echoes, introducing redundancy relative to Classifier A.
Classifier C: The training dataset is formed by randomly selecting 70% of the data from a large collection of routinely acquired observational echoes, leading to an exceptionally large sample size.
Classifier D: The dataset consists of 700 mid-frequency echoes, obtained by randomly selecting 140 samples from each of the five predefined test scenarios.
Classifier E: The training dataset is constructed using K-means clustering, where the number of clusters is determined based on the within-cluster sum of squares (SSE). A total of 70 sample positions are selected using the Euclidean distance metric.
Classifier F: The dataset is created by uniformly sampling 50 points from the surrogate equation, which serve as input to the self-organizing map (SOM). Based on this, 70 sample locations are selected to form the training dataset.
Classifier G: This dataset is derived from measured reflection coefficients, where 70 sample positions are identified using SOM to construct the final training set.
Classifier D requires approximately 4 s for model construction, with the time spent on training sample selection being negligible. The primary computational cost lies in feature extraction and classifier training. Classifiers A and B represent the proposed methods. Classifier A builds upon the process of Classifier D by incorporating surrogate equation construction and targeted training sample selection, which adds around 5 s to the overall time. Classifier B further extends Classifier A by introducing a small number of additional training samples.
Classifiers F and G utilize deep learning-based strategies for training sample acquisition. Classifier F performs training based on samples drawn from the surrogate equation of Classifier A, resulting in approximately five additional seconds of training time. Classifier G, in contrast, uses 25 measured data points as input and therefore incurs a relatively lower computational cost.
Classifiers C and E involve clustering procedures that are dependent on the total number of samples. For example, applying K-Means to 1000 frames takes about 2 s, while training a classifier on 700 selected frames requires approximately 7 s.
In summary, the training time for all methods does not exceed 12 s, demonstrating favorable feasibility for practical engineering applications.
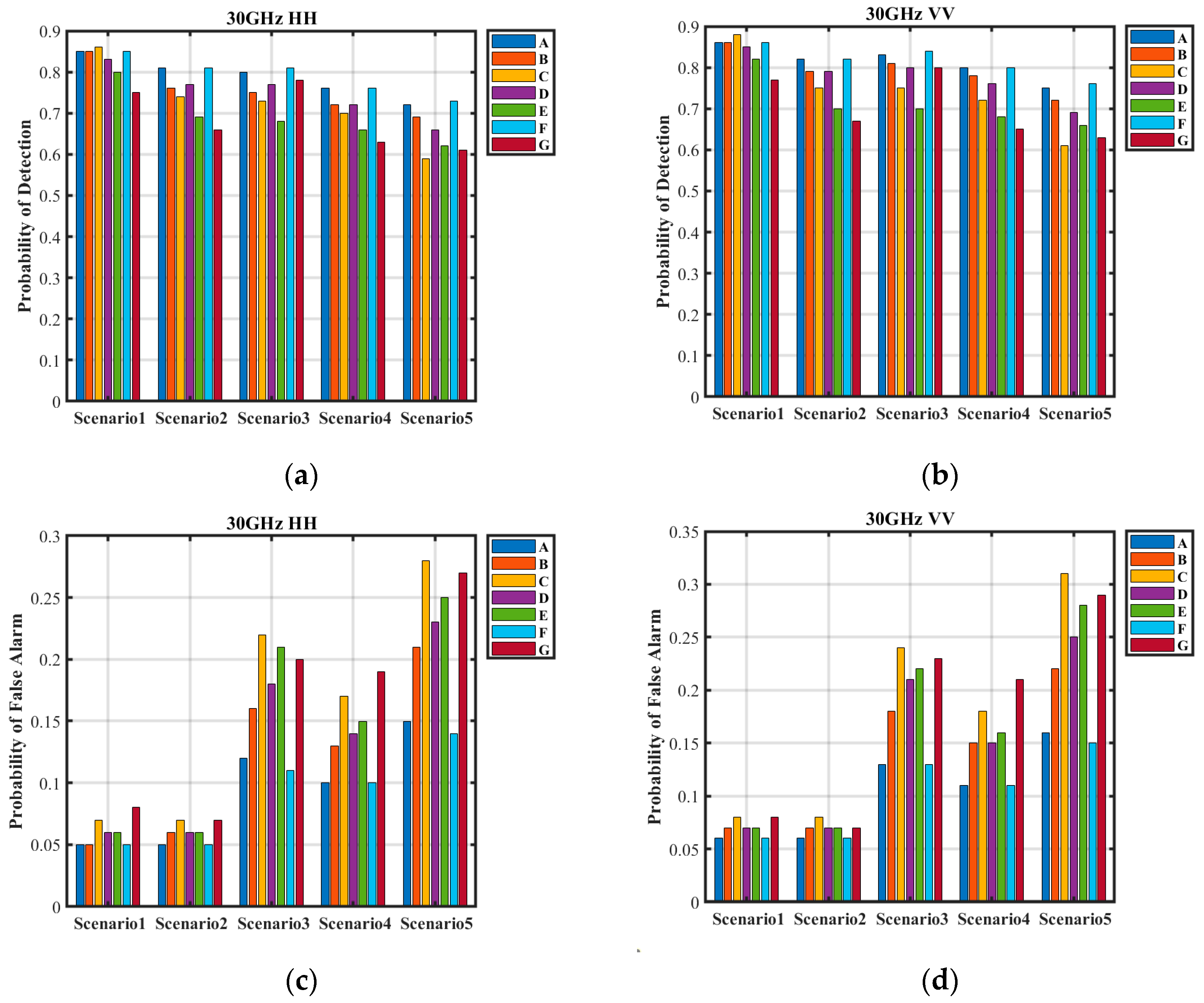
The detection performance of the seven classifiers across five different scenarios is presented in
Figure 10. Among these scenarios, conventional ships operating under routine sea conditions are classified as simple scenarios. In contrast, small targets under routine sea conditions, cruise ships under high sea states, and conventional ships at large incidence angles are categorized as complex scenarios. Finally, cruise ships subject to both large incidence angles and high sea states are considered difficult scenarios.
Table 9 presents the detection probabilities and false alarm rates of the seven classifiers across five scenarios. The proposed method achieves consistently high detection probabilities and low false alarm rates in all cases. In the simple scenario, the detection probability exceeds 0.85, while the false alarm rate remains below 0.06. In the complex scenario, except for the HH polarization condition under large grazing angles (detection probability of 0.76), all detection probabilities exceed 0.8. The false alarm rates are approximately 0.6 for weak targets, 0.13 under high sea state conditions, and 0.11 at large grazing angles. In the difficult scenario, the detection probability is around 0.72, with a false alarm rate of approximately 0.15.
Compared to the proposed method, Classifier B exhibits lower detection probabilities in all scenarios except the simple one, with increased false alarm rates across the board. This decline is attributed to the inclusion of redundant samples, which distort the training sample distribution and reduce the classifier’s ability to accurately distinguish sea clutter characteristics.
Classifier C achieves the highest detection probability in the simple scenario, reaching 0.86 (HH) and 0.88 (VV). However, in the other four scenarios, its detection probabilities are lower than those of the proposed method, and it exhibits the highest false alarm rates across all scenarios. Moreover, its overall detection performance deteriorates further compared to Classifier B. The excessive inclusion of conventional samples may cause the classifier to overlook critical features in complex and difficult scenarios. These results underscore that training sample quality is more crucial than sheer quantity, emphasizing the importance of maintaining a balanced sample distribution.
Both Classifier D and Classifier E demonstrate lower detection probabilities and higher false alarm rates than the proposed method across all scenarios, leading to a notable performance decline. The reliance on expert judgment in sample selection proves less effective than the proposed surrogate equation, particularly in scenarios where negative samples are essential for anomaly detection, as capturing their variations is critical. Similarly, while K-means clustering is generally effective for sample selection, its dependence on the existing data distribution makes it vulnerable to sample imbalance, potentially resulting in skewed training sets.
Classifiers F and G integrate deep learning for sample selection. Classifier F performs worse than Classifier C in the simple scenario but achieves the highest detection probabilities in the remaining four scenarios. By employing large-scale sampling from a surrogate equation as input and using self-organizing maps (SOMs) for sample selection, Classifier F effectively captures sea clutter variations. This results in superior performance compared to traditional methods that separately consider global and local changes. However, due to limitations in acquisition equipment and environmental factors, its overall performance remains comparable to that of Classifier A. In contrast, Classifier G exhibits the lowest detection performance among the seven classifiers. In the difficult scenario, its detection probability drops to 0.61 (HH) and 0.63 (VV), while its false alarm rate increases to 0.27 (HH) and 0.29 (VV). The limited number of input samples for SOM leads to a substantial misrepresentation of sea clutter variations, causing the training samples to deviate significantly from the actual distribution and severely impairing detection performance.
The proposed method selects training samples by integrating observational data with empirical models, without relying on the target data distribution. It demonstrates robust detection performance across diverse scenarios, effectively adapting to the complex and dynamic maritime environment. Furthermore, the method maintains both the interpretability of sample selection and the effectiveness of training samples, ensuring reliable performance in practical applications.