Figure 1.
Experimental device created in SolidWorks software (a) 3D model; (b) 2D sketch; 1—aluminium frame, 2—plastic trough, 3—rubber springs, 4—vibration motor.
Figure 1.
Experimental device created in SolidWorks software (a) 3D model; (b) 2D sketch; 1—aluminium frame, 2—plastic trough, 3—rubber springs, 4—vibration motor.
Figure 2.
(a) VEVOR HY-0.4 asynchronous single-phase motor; (b) centre of gravity of the eccentric weight; (c) mass of the eccentric weight.
Figure 2.
(a) VEVOR HY-0.4 asynchronous single-phase motor; (b) centre of gravity of the eccentric weight; (c) mass of the eccentric weight.
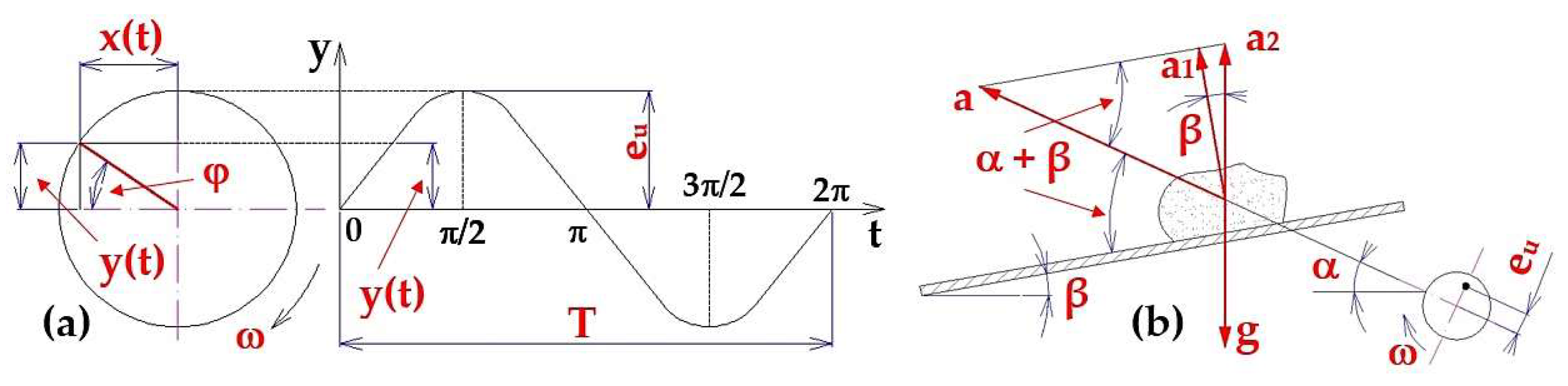
Figure 3.
(a) Time diagram of harmonic motion; (b) acceleration ai [m·s−2] of the material grain.
Figure 3.
(a) Time diagram of harmonic motion; (b) acceleration ai [m·s−2] of the material grain.
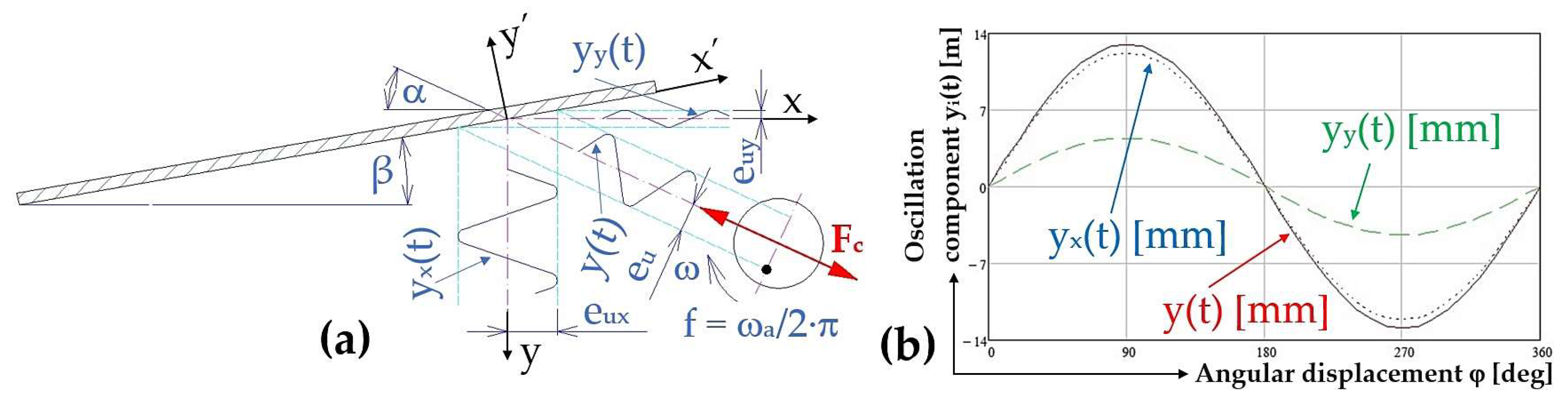
Figure 4.
(a) Components of the trough oscillation in the direction yx(t) [m], and in the direction perpendicular yy(t) [m] to the direction of motion; (b) components of the trough oscillation yi(t) [m] at a throw angle of α = 20 deg and the eccentricity of unbalance of eu = 12.95 mm.
Figure 4.
(a) Components of the trough oscillation in the direction yx(t) [m], and in the direction perpendicular yy(t) [m] to the direction of motion; (b) components of the trough oscillation yi(t) [m] at a throw angle of α = 20 deg and the eccentricity of unbalance of eu = 12.95 mm.
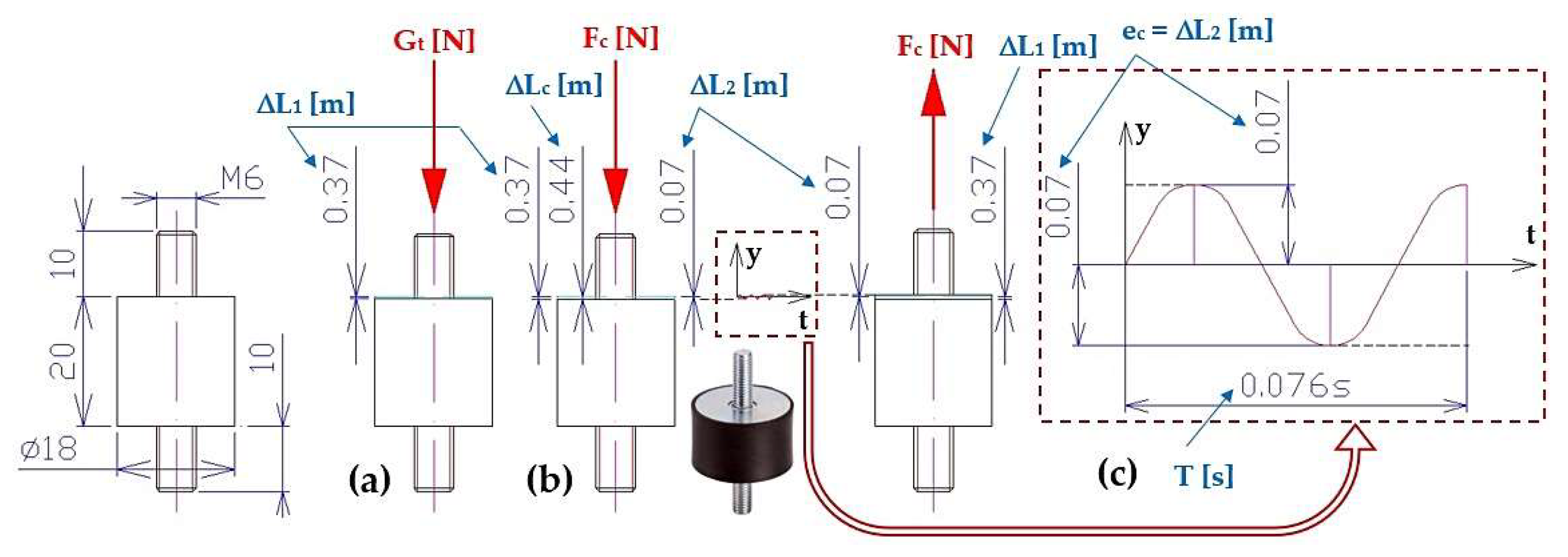
Figure 5.
Elastic deformation of the rubber spring (a) ΔL1 [m] induced by the weight of the system Gs [N], (b) ΔL2 [m] induced by the centrifugal force of the eccentric weights Fc [N]; (c) harmonic motion of the system.
Figure 5.
Elastic deformation of the rubber spring (a) ΔL1 [m] induced by the weight of the system Gs [N], (b) ΔL2 [m] induced by the centrifugal force of the eccentric weights Fc [N]; (c) harmonic motion of the system.
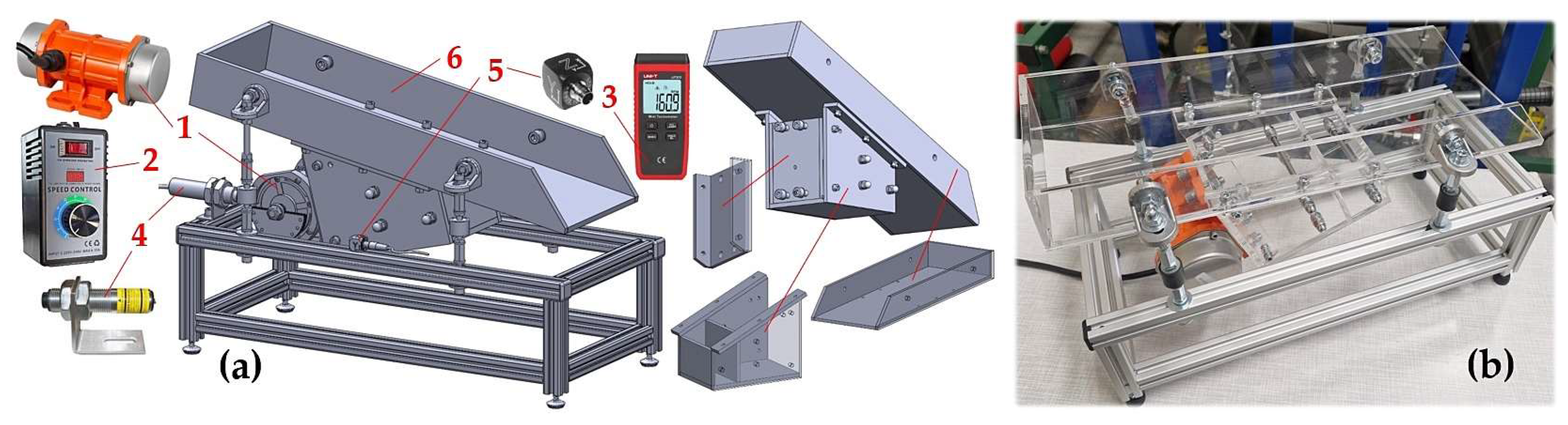
Figure 6.
Vibrating conveyor (a) control and measuring components; (b) realised model with the plastic trough; 1—vibration motor, 2—speed controller, 3—speed sensor, 4—laser sensor, 5—acceleration sensor, 6—plastic trough.
Figure 6.
Vibrating conveyor (a) control and measuring components; (b) realised model with the plastic trough; 1—vibration motor, 2—speed controller, 3—speed sensor, 4—laser sensor, 5—acceleration sensor, 6—plastic trough.
Figure 7.
Measurement chain for detecting and recording vibrations generated by rotating eccentric weights on laboratory equipment.
Figure 7.
Measurement chain for detecting and recording vibrations generated by rotating eccentric weights on laboratory equipment.
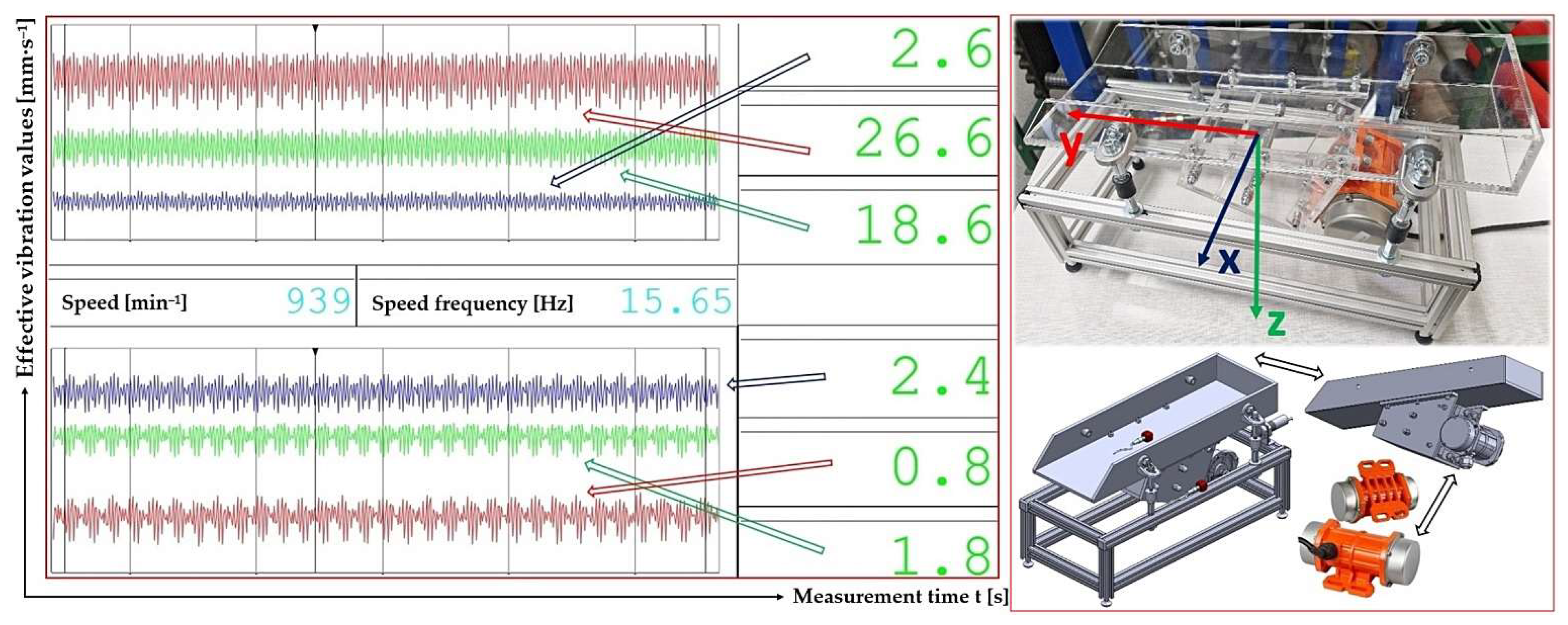
Figure 8.
Records of measured effective vibration velocities by acceleration transducers attached to the trough surface and to the frame of the vibrating conveyor model, in the x(–), y (–), and z-coordinate system (–).
Figure 8.
Records of measured effective vibration velocities by acceleration transducers attached to the trough surface and to the frame of the vibrating conveyor model, in the x(–), y (–), and z-coordinate system (–).
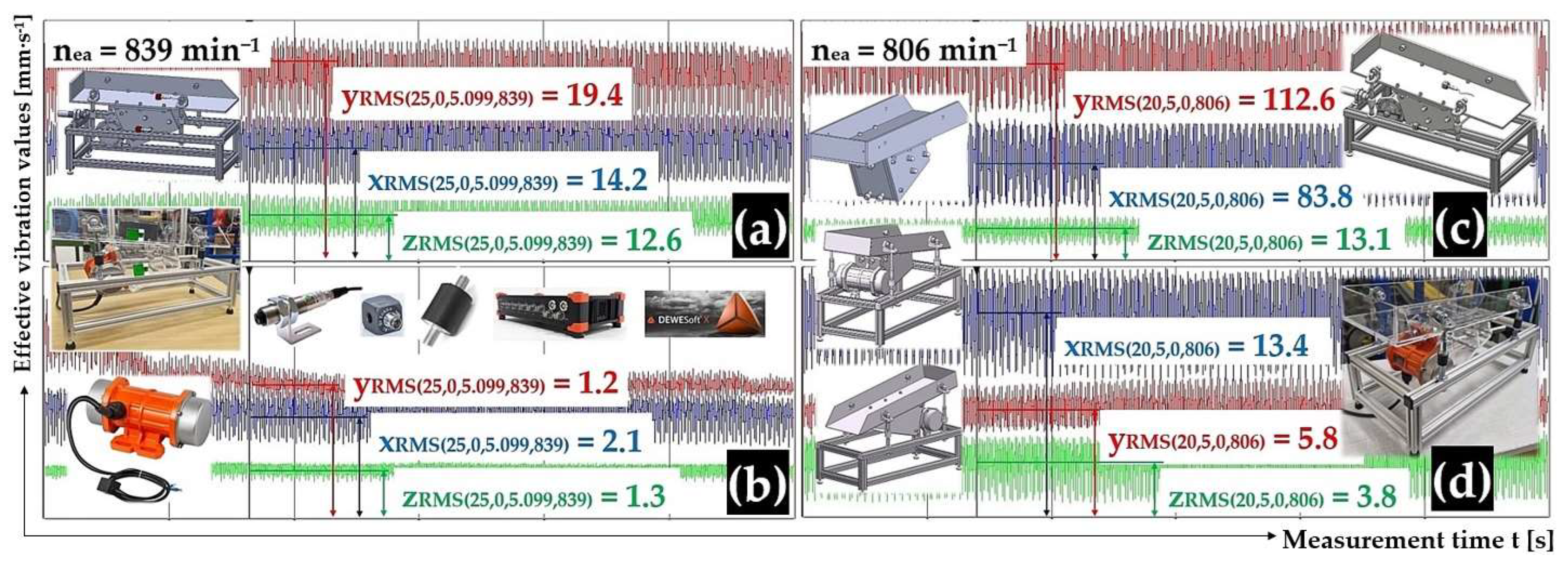
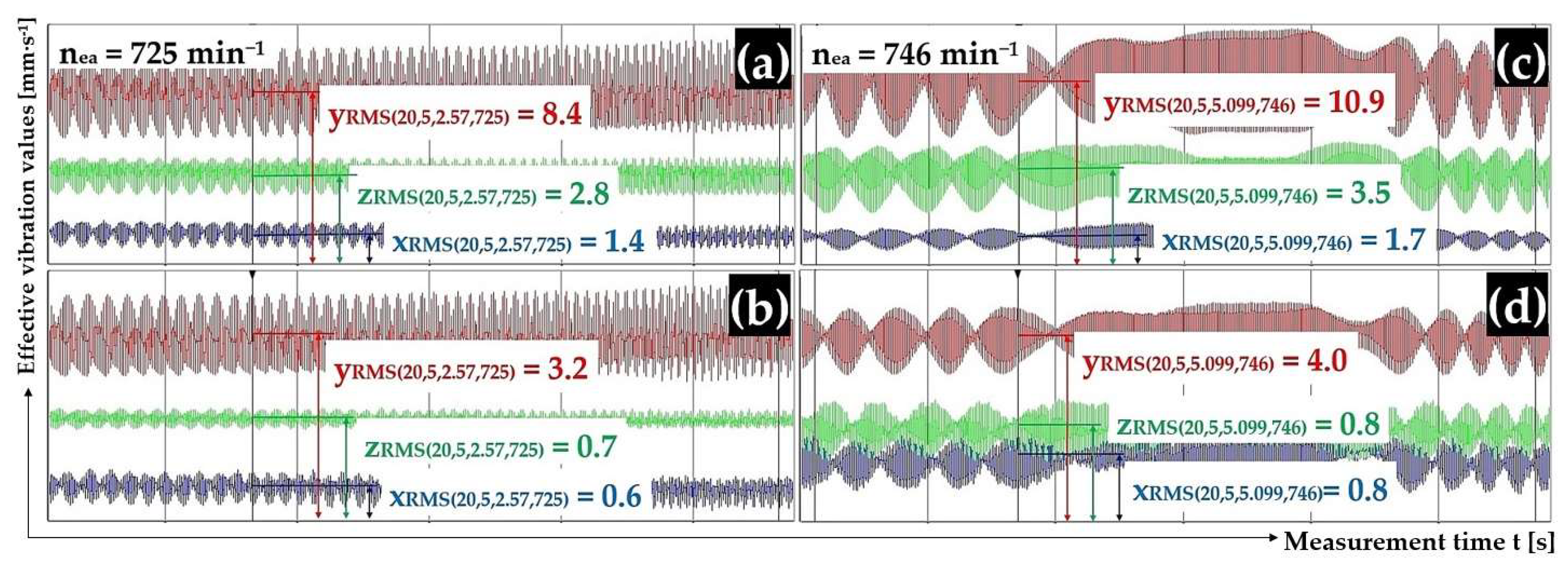
Figure 9.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 9.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
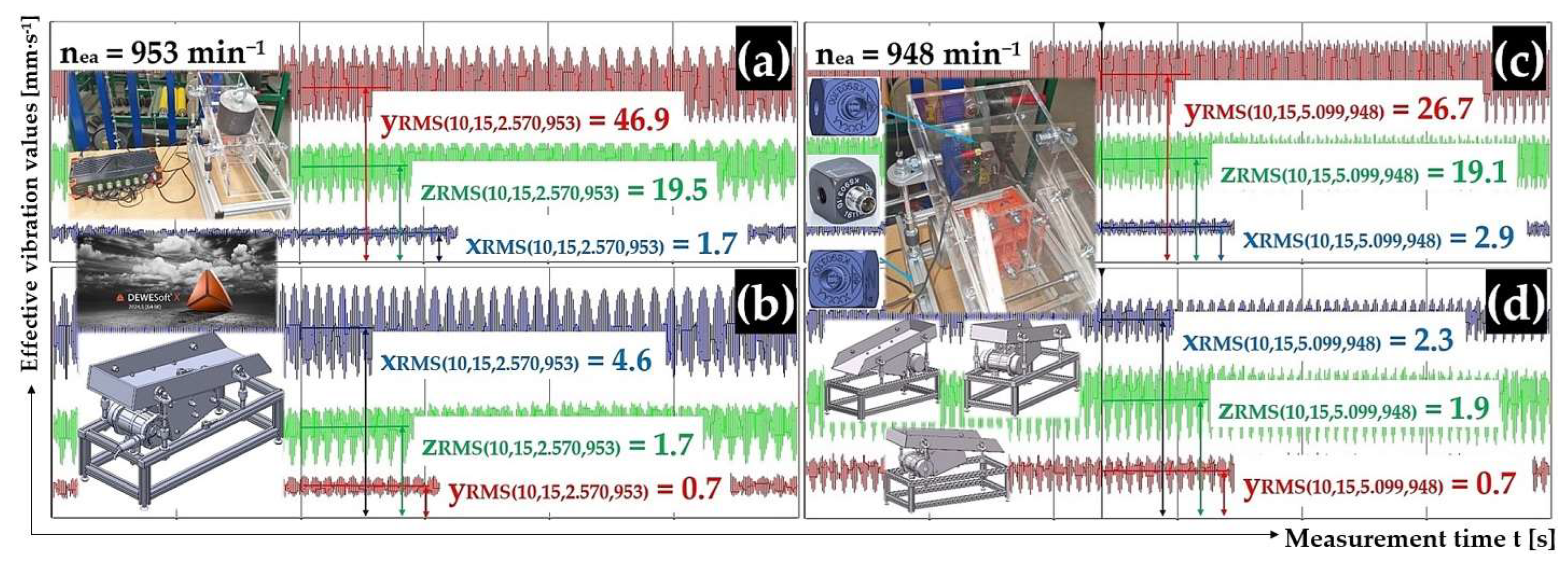
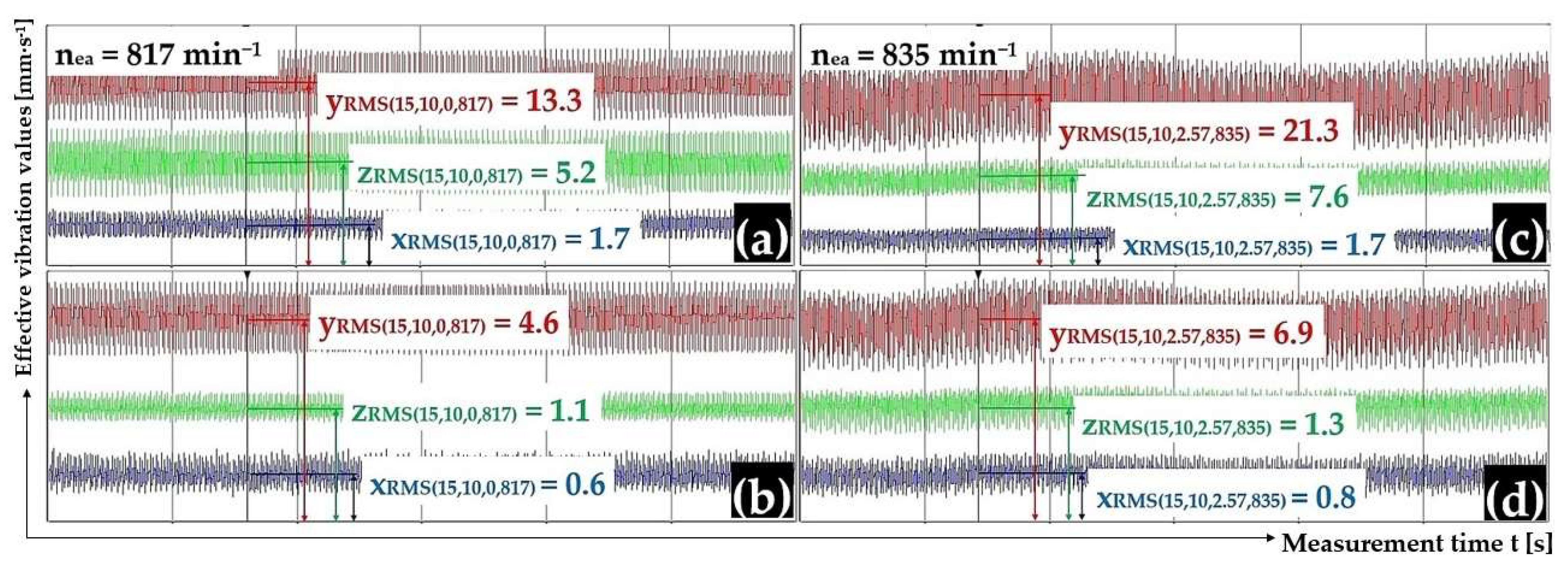
Figure 10.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface and, (b,d) on the frame of the vibrating conveyor model.
Figure 10.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface and, (b,d) on the frame of the vibrating conveyor model.
Figure 11.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 11.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
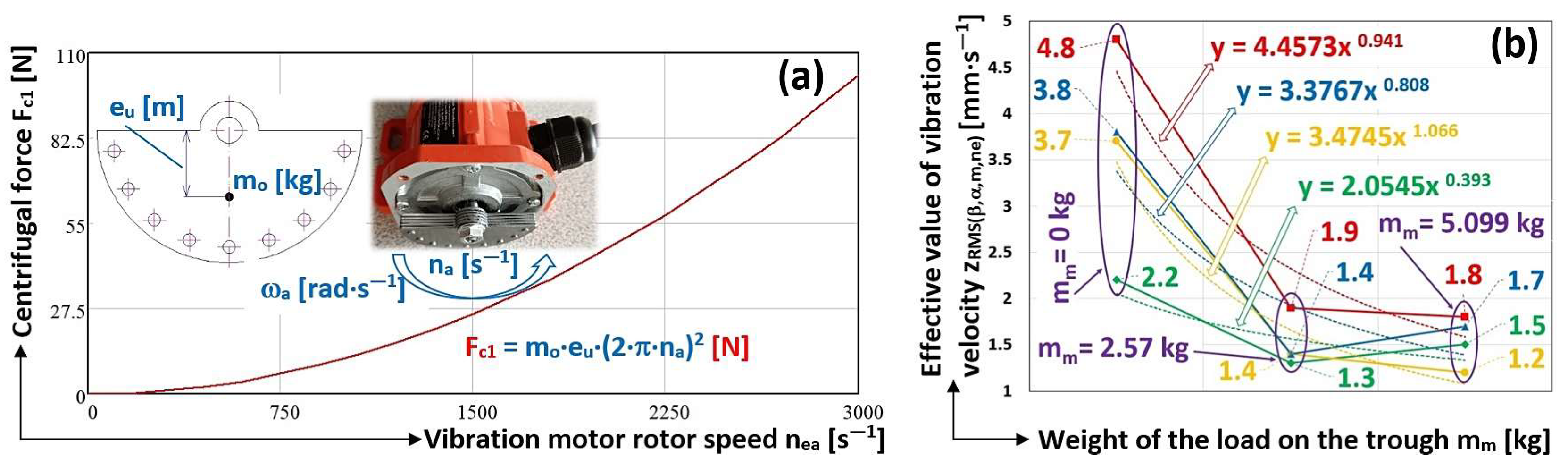
Figure 12.
(a) The magnitude of the centrifugal force induced by the rotating unbalanced mass; (b) the effective values of the vibration velocities in the vertical direction.
Figure 12.
(a) The magnitude of the centrifugal force induced by the rotating unbalanced mass; (b) the effective values of the vibration velocities in the vertical direction.
Figure 13.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 13.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 14.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 14.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] measured (a,c) on the trough surface, (b,d) on the frame of the vibrating conveyor model.
Figure 15.
Effective vibration velocity values zRMS(α,β,m,ne) [mm·s−1] in the vertical direction, monitored on the vibrating conveyor frame.
Figure 15.
Effective vibration velocity values zRMS(α,β,m,ne) [mm·s−1] in the vertical direction, monitored on the vibrating conveyor frame.
Table 1.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 833 min−1.
Table 1.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 833 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | d frame of vibrating conveyor |
| 13.88 | 0 | 25 | 0 | 43.9 1 | 104.4 1 | 11.7 1 | 14.7 2 | 2.8 2 | 1.9 2 |
| 34.3 | 112.2 | 12.3 | 16.0 | 4.4 | 2.5 |
| 38.1 | 108.6 | 11.9 | 15.7 | 3.8 | 2.1 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 116.3 | 325.2 | 35.9 | 46.4 | 11.0 | 6.5 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 38.8 ± 8.0 | 108.4 ± 6.2 | 12.0 ± 0.5 | 15.5 ± 1.2 | 3.7 ± 1.3 | 2.2 ± 0.5 |
Table 2.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 830 min−1.
Table 2.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 830 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.83 | 0 | 25 | 2.57 | 9.8 | 51.4 | 10.4 | 6.1 | 1.4 | 1.2 |
| 8.9 1 | 56.1 1 | 11.9 1 | 6.5 2 | 1.6 2 | 1.4 2 |
| 9.2 | 53.3 | 10.8 | 6.3 | 1.4 | 1.3 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 27.9 | 160.8 | 33.1 | 18.9 | 4.4 | 3.9 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 9.3 ± 0.8 | 53.6 ± 3.9 | 11.0 ± 1.3 | 6.3 ± 0.3 | 1.5 ± 0.2 | 1.3 ± 0.2 |
Table 3.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 839 min−1.
Table 3.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 839 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.98 | 0 | 25 | 5.099 | 13.7 | 24.7 | 15.3 | 2.8 | 1.4 | 1.7 |
| 14.2 1 | 19.4 1 | 12.6 1 | 2.1 2 | 1.2 2 | 1.3 2 |
| 13.9 | 20.6 | 13.4 | 2.6 | 1.4 | 1.5 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 41.8 | 64.7 | 41.3 | 7.5 | 4.0 | 4.5 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 13.9 ± 0.4 | 21.6 ± 4.9 | 13.8 ± 2.4 | 2.5 ± 0.6 | 1.3 ± 0.2 | 1.5 ± 0.3 |
Table 4.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 806 min−1.
Table 4.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 806 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.43 | 5 | 20 | 0 | 78.7 | 125.5 | 12.8 | 15.9 | 6.9 | 3.6 |
| 83.8 1 | 112.6 1 | 13.1 1 | 13.4 2 | 5.8 2 | 3.8 2 |
| 82.2 | 120.1 | 12.9 | 14.5 | 6.2 | 3.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 244.7 | 358.2 | 38.8 | 43.8 | 18.9 | 11.2 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 81.6 ± 4.4 | 119.4 ± 10.6 | 12.9 ± 0.3 | 14.6 ± 2.0 | 6.3 ± 0.9 | 3.7 ± 0.2 |
Table 5.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 862 min−1.
Table 5.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 862 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 14.37 | 5 | 20 | 2.57 | 21.2 | 58.5 | 16.5 | 6.8 | 2.5 | 1.3 |
| 21.1 | 57.6 | 17.1 | 6.7 | 1.8 | 1.4 |
| 21.2 | 58.1 | 16.9 | 6.8 | 2.2 | 1.4 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 63.5 | 174.2 | 50.5 | 20.3 | 6.5 | 4.1 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 21.2 ± 0.1 | 58.1 ± 0.7 | 16.8 ± 0.5 | 6.8 ± 0.1 | 2.2 ± 0.6 | 1.4 ± 0.1 |
Table 6.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 879 min−1.
Table 6.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 879 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 14.65 | 5 | 20 | 5.099 | 7.5 | 27.1 | 14.8 | 3.0 | 1.3 | 1.2 |
| 9.3 | 27.0 | 14.2 | 3.0 | 1.6 | 1.2 |
| 8.6 | 27.1 | 14.3 | 3.1 | 1.4 | 1.2 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 25.4 | 81.2 | 43.3 | 9.1 | 4.3 | 3.6 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 8.5 ± 1.5 | 27.1 ± 0.1 | 14.4 ± 0.6 | 3.0 ± 0.1 | 1.4 ± 0.3 | 1.2 ± 0.0 |
Table 7.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 816 min−1.
Table 7.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 816 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.60 | 10 | 15 | 0 | 3.4 | 88.4 | 20.0 | 17.0 | 2.8 | 3.4 |
| 4.0 | 99.5 | 21.5 | 18.8 | 3.9 | 4.2 |
| 3.9 | 97.1 | 21.3 | 18.2 | 3.2 | 3.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 11.3 | 285.0 | 62.8 | 54.0 | 9.9 | 11.4 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 3.8 ± 0.6 | 95.0 ± 10.2 | 20.9 ± 1.4 | 18.0 ± 1.6 | 3.3 ± 0.9 | 3.8 ± 0.6 |
Table 8.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 961 min−1.
Table 8.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 961 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 16.02 | 10 | 15 | 2.57 | 2.8 | 58.5 | 25.4 | 8.2 | 1.3 | 1.6 |
| 2.4 | 77.3 | 20.5 | 11.0 | 2.0 | 1.3 |
| 2.6 | 77.0 | 23.1 | 9.6 | 1.8 | 1.4 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 7.8 | 212.8 | 69.0 | 28.8 | 5.1 | 4.3 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 2.6 ± 0.3 | 70.9 ± 19.3 | 23.0 ± 3.9 | 9.6 ± 2.2 | 1.7 ± 0.6 | 1.4 ± 0.3 |
Table 9.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 917 min−1.
Table 9.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 917 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 15.28 | 10 | 15 | 5.099 | 2.3 | 27.9 | 17.3 | 3.5 | 0.8 | 1.5 |
| 3.1 | 27.3 | 19.8 | 3.3 | 0.7 | 1.9 |
| 2.9 | 27.6 | 19.2 | 3.5 | 0.8 | 1.7 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 8.3 | 82.8 | 56.3 | 10.3 | 2.3 | 5.1 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 2.8 ± 0.7 | 27.6 ± 0.5 | 18.8 ± 2.3 | 3.4 ± 0.2 | 0.8 ± 0.1 | 1.7 ± 0.3 |
Table 10.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 748 min−1.
Table 10.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 748 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.47 | 15 | 10 | 0 | 6.1 | 122.7 | 23.3 | 23.0 | 4.7 | 5.0 |
| 6.1 | 125.7 | 23.6 | 21.3 | 4.1 | 4.7 |
| 6.1 | 124.2 | 23.5 | 21.1 | 4.3 | 4.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 18.3 | 372.6 | 70.4 | 65.4 | 13.1 | 14.5 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 6.1 ± 0.0 | 124.2 ± 2.3 | 23.5 ± 0.3 | 21.8 ± 1.9 | 4.4 ± 0.5 | 4.8 ± 0.3 |
Table 11.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 853 min−1.
Table 11.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 853 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 15.88 | 15 | 10 | 2.57 | 1.7 1 | 46.9 1 | 19.5 1 | 4.6 2 | 0.7 2 | 1.7 2 |
| 1.8 | 44.6 | 21.2 | 4.2 | 0.8 | 2.0 |
| 1.7 | 46.0 | 19.6 | 4.4 | 0.7 | 1.9 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 5.2 | 137.5 | 60.3 | 13.2 | 2.2 | 5.6 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.7 ± 0.1 | 45.8 ± 1.9 | 20.1 ± 1.7 | 4.4 ± 0.3 | 0.7 ± 0.1 | 1.9 ± 0.3 |
Table 12.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 948 min−1.
Table 12.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 948 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 15.80 | 15 | 10 | 5.099 | 2.9 1 | 26.7 1 | 19.1 1 | 2.3 2 | 0.7 2 | 1.9 2 |
| 2.6 | 26.6 | 18.6 | 2.4 | 0.8 | 1.8 |
| 2.7 | 26.6 | 18.9 | 2.4 | 0.8 | 1.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 8.2 | 79.9 | 56.6 | 7.1 | 2.3 | 5.5 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 2.7 ± 0.3 | 26.6 ± 0.1 | 18.9 ± 0.4 | 2.4 ± 0.1 | 0.8 ± 0.1 | 1.8 ± 0.1 |
Table 13.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 761 min−1.
Table 13.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 761 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.68 | 0 | 25 | 0 | 1.4 | 7.3 | 2.4 | 0.8 | 3.3 | 0.6 |
| 1.1 | 6.8 | 2.2 | 0.7 | 3.0 | 0.6 |
| 1.3 | 7.1 | 2.3 | 0.8 | 3.1 | 0.6 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 3.8 | 21.2 | 6.9 | 2.3 | 9.4 | 1.8 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.3 ± 0.3.0 | 7.1 ± 0.4 | 2.3 ± 0.2 | 0.8 ± 0.1 | 3.1 ± 0.3 | 0.6 ± 0.0 |
Table 14.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 830 min−1.
Table 14.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 830 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.45 | 0 | 25 | 2.57 | 1.1 | 7.7 | 2.6 | 0.8 | 3.6 | 0.7 |
| 1.1 | 7.6 | 2.4 | 0.8 | 3.4 | 0.7 |
| 1.1 | 7.7 | 2.6 | 0.8 | 3.5 | 0.7 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 3.3 | 23.0 | 7.6 | 2.4 | 10.5 | 2.1 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.1 ± 0.0 | 7.7 ± 0.1 | 2.5 ± 0.2 | 0.8 ± 0.0 | 3.5 ± 0.2 | 0.7 ± 0.0 |
Table 15.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 750 min−1.
Table 15.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 750 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.98 | 0 | 25 | 5.099 | 1.2 | 8.7 | 2.5 | 0.8 | 3.8 | 0.8 |
| 1.4 | 9.9 | 2.6 | 0.9 | 4.4 | 0.7 |
| 1.4 | 9.4 | 2.6 | 0.9 | 4.1 | 0.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 4.0 | 28.0 | 7.7 | 2.6 | 12.3 | 2.3 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.3 ± 0.2 | 9.3 ± 1.0 | 2.6 ± 0.1 | 0.9 ± 0.1 | 4.1 ± 0.5 | 0.8 ± 0.1 |
Table 16.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 847 min−1.
Table 16.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 847 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 14.12 | 5 | 20 | 0 | 1.4 | 10.7 | 3.8 | 0.6 | 4.8 | 0.9 |
| 1.6 | 12.7 | 4.0 | 0.7 | 5.3 | 1.1 |
| 1.6 | 12.3 | 3.8 | 0.7 | 5.1 | 1.1 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 4.6 | 35.7 | 11.6 | 2.0 | 15.2 | 3.1 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.5. ± 0.2 | 11.9 ± 1.9 | 3.9 ± 0.2 | 0.7 ± 0.1 | 5.1 ± 0.4 | 1.0 ± 0.2 |
Table 17.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 828 min−1.
Table 17.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 828 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.08 | 5 | 20 | 2.57 | 1.4 1 | 8.4 1 | 2.8 1 | 0.6 2 | 3.2 2 | 0.7 2 |
| 1.7 | 9.3 | 3.0 | 0.7 | 3.6 | 0.8 |
| 1.5 | 9.2 | 3.3 | 0.7 | 3.8 | 0.7 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 4.6 | 26.9 | 9.1 | 2.0 | 10.6 | 2.2 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.5 ± 0.3 | 9.0 ± 0.9 | 3.0 ± 0.4 | 0.7 ± 0.1 | 3.5 ± 0.5 | 0.7 ± 0.1 |
Table 18.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 746 min−1.
Table 18.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 746 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.43 | 5 | 20 | 5.099 | 1.7 | 9.3 | 3.0 | 0.7 | 3.6 | 0.8 |
| 1.7 1 | 10.9 1 | 3.5 1 | 0.8 2 | 4.0 2 | 0.8 2 |
| 1.8 | 9.9 | 3.1 | 0.8 | 3.3 | 0.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 5.2 | 20.1 | 9.6 | 2.3 | 10.9 | 2.4 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.7 ± 0.1 | 10.0 ± 1.3 | 3.2 ± 0.5 | 0.8 ± 0.1 | 3.6 ± 0.6 | 0.8 ± 0.0 |
Table 19.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 817 min−1.
Table 19.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 817 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.62 | 10 | 15 | 0 | 1.7 1 | 13.3 1 | 5.2 1 | 0.6 2 | 4.6 2 | 1.1 2 |
| 1.7 | 12.3 | 4.3 | 0.6 | 4.6 | 0.8 |
| 1.8 | 12.6 | 4.8 | 0.6 | 4.7 | 1.0 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 5.2 | 38.2 | 14.3 | 1.8 | 13.9 | 2.9 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.7 ± 0.1 | 12.7 ± 0.9 | 4.8 ± 0.7 | 0.6 ± 0.0 | 4.6 ± 0.1 | 1.0 ± 0.3 |
Table 20.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 835 min−1.
Table 20.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 835 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 13.92 | 10 | 15 | 2.57 | 1.7 1 | 21.3 1 | 7.6 1 | 0.8 2 | 6.9 2 | 1.3 2 |
| 2.0 | 22.1 | 7.5 | 0.7 | 7.3 | 1.1 |
| 1.8 | 21.6 | 7.5 | 0.8 | 7.1 | 1.3 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 5.5 | 65.0 | 22.6 | 2.3 | 21.3 | 3.7 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.8 ± 0.3 | 21.7 ± 0.7 | 7.5 ± 0.1 | 0.8 ± 0.1 | 7.1 ± 0.3 | 1.2 ± 0.2 |
Table 21.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 779 min−1.
Table 21.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 779 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.98 | 10 | 15 | 5.099 | 1.2 | 25.7 | 9.5 | 0.8 | 8.3 | 1.2 |
| 1.0 | 23.6 | 8.3 | 0.7 | 7.6 | 1.1 |
| 1.0 | 26.5 | 9.5 | 0.9 | 8.5 | 1.2 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 3.2 | 75.8 | 27.3 | 2.4 | 24.4 | 3.5 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 1.1 ± 0.2 | 25.3 ± 2.6 | 9.1 ± 1.2 | 0.8 ± 0.2 | 8.1 ± 0.8 | 1.2 ± 0.1 |
Table 22.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 849 min−1.
Table 22.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 0 kg, nea = 849 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 14.15 | 15 | 10 | 0 | 2.4 | 15.8 | 6.4 | 0.8 | 5.9 | 1.3 |
| 2.0 | 10.6 | 4.3 | 0.7 | 4.4 | 0.8 |
| 1.6 | 9.8 | 3.8 | 0.6 | 3.9 | 0.7 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 6.0 | 36.2 | 14.5 | 2.1 | 14.2 | 2.8 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 2.0 ± 0.6 | 12.1 ± 5.8 | 4.8 ± 2.4 | 0.7 ± 0.2 | 4.7 ± 1.8 | 0.9 ± 0.6 |
Table 23.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 751 min−1.
Table 23.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 2.57 kg, nea = 751 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.52 | 15 | 10 | 2.57 | 2.4 | 15.2 | 5.9 | 0.6 | 5.3 | 0.9 |
| 2.8 | 11.9 | 4.9 | 0.5 | 4.3 | 0.7 |
| 3.2 | 11.5 | 5.1 | 0.6 | 4.2 | 0.8 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 8.4 | 38.6 | 15.9 | 1.7 | 13.8 | 2.4 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 2.8 ± 0.6 | 12.9 ± 3.6 | 5.3 ± 0.9 | 0.6 ± 0.1 | 4.6 ± 1.1 | 0.8 ± 0.2 |
Table 24.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 769 min−1.
Table 24.
Effective vibration rate values iRMS(α,β,m,ne) [mm·s−1] at mm = 5.099 kg, nea = 769 min−1.
| nea | β | α | mm | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) | xRMS(α,β,m,ne) | yRMS(α,β,m,ne) | zRMS(α,β,m,ne) |
|---|
| s−1 | deg | kg | mm·s−1 | mm·s−1 |
| trough of vibrating conveyor | frame of vibrating conveyor |
| 12.82 | 15 | 10 | 5.099 | 3.1 | 23.8 | 9.8 | 0.3 | 8.4 | 1.1 |
| 3.2 | 24.4 | 10.1 | 0.4 | 8.5 | 1.1 |
| 3.0 | 23.6 | 9.6 | 0.4 | 8.2 | 1.2 |
| Σ(iRMS(α,β,m,ne)) [mm·s−1] | 9.3 | 71.8 | 29.5 | 1.1 | 25.1 | 3.4 |
| iRMS(α,β,m,ne)A ± κ5%,3 [mm·s−1] | 3.1 ± 0.2 | 23.9 ± 0.7 | 9.8 ± 0.4 | 0.4 ± 0.1 | 8.4 ± 0.3 | 1.1 ± 0.1 |