Research on Leak Detection and Localization Algorithm for Oil and Gas Pipelines Using Wavelet Denoising Integrated with Long Short-Term Memory (LSTM)–Transformer Models
Abstract
1. Introduction
2. Network Model Optimization
2.1. Data Preprocessing
- (1)
- Represent the leaked data containing noise aswhere s(i) represents the leak data containing noise, f(i) represents the denoised data, e(i) represents the noise data, and n is the total number of data points in the test set.
- (2)
- In the first-level wavelet decomposition, noise data are in A1, and denoised data are in B1. The second-level wavelet decomposition further decomposes the data in B1 into A2 and B2. After the third-level wavelet decomposition, noise data are in A1, A2, A3, and denoised data are in B1, B2, B3. The noise data in A1, A2, and A3 is appropriately reduced or replaced with 0. This paper uses an improved threshold function.where θ is the threshold; di is the wavelet coefficient for threshold selection; ε is a variable that changes with the wavelet coefficient di; N is a constant.
- (3)
- Following the reconstruction, evaluate the low-frequency data signals obtained from wavelet decomposition and the high-frequency data signals quantized by the threshold. If the desired effect is not achieved, proceed with additional wavelet transformations; otherwise, terminate the process.
2.1.1. Flow Data
2.1.2. Backtracking Time Depth
2.1.3. Selection of Time Slices
2.2. LSTM Transformer Composite Architecture Model Based on Wavelet Denoising
- (1)
- The input temporal data Xm are decomposed into temporal sequence segments of different scales, and local temporal sequence features are focused on in the temporal dimension to obtain the temporal sequence matrix . Inject into the multi head attention mechanism of the Transformer model to obtain local feature representation Am.
- (2)
- Calculate the feature weights Sm of different temporal sequences separately to calculate the local self-attention score .In the formula, Wq, Wk, and Wv are weight matrices.
- (3)
- Concatenate the feature vectors output by the Transformer model to form feature vector representations H for pipeline pressure data at different scales.
- (4)
- Inject the feature vector representation H into the LSTM model to further extract temporal features.
- (1)
- Pressure Signals: Full 3-level wavelet decomposition with soft thresholding (β = 0.7).
- (2)
- Flow Signals: 2-level decomposition, hard thresholding (β = 1.2), and 0.8 × amplitude scaling.
- (3)
- Multi-phase Signals: Adaptive decomposition levels determined through Wigner-Ville distribution analysis (Equation (9)).
3. Research on Positioning Algorithms
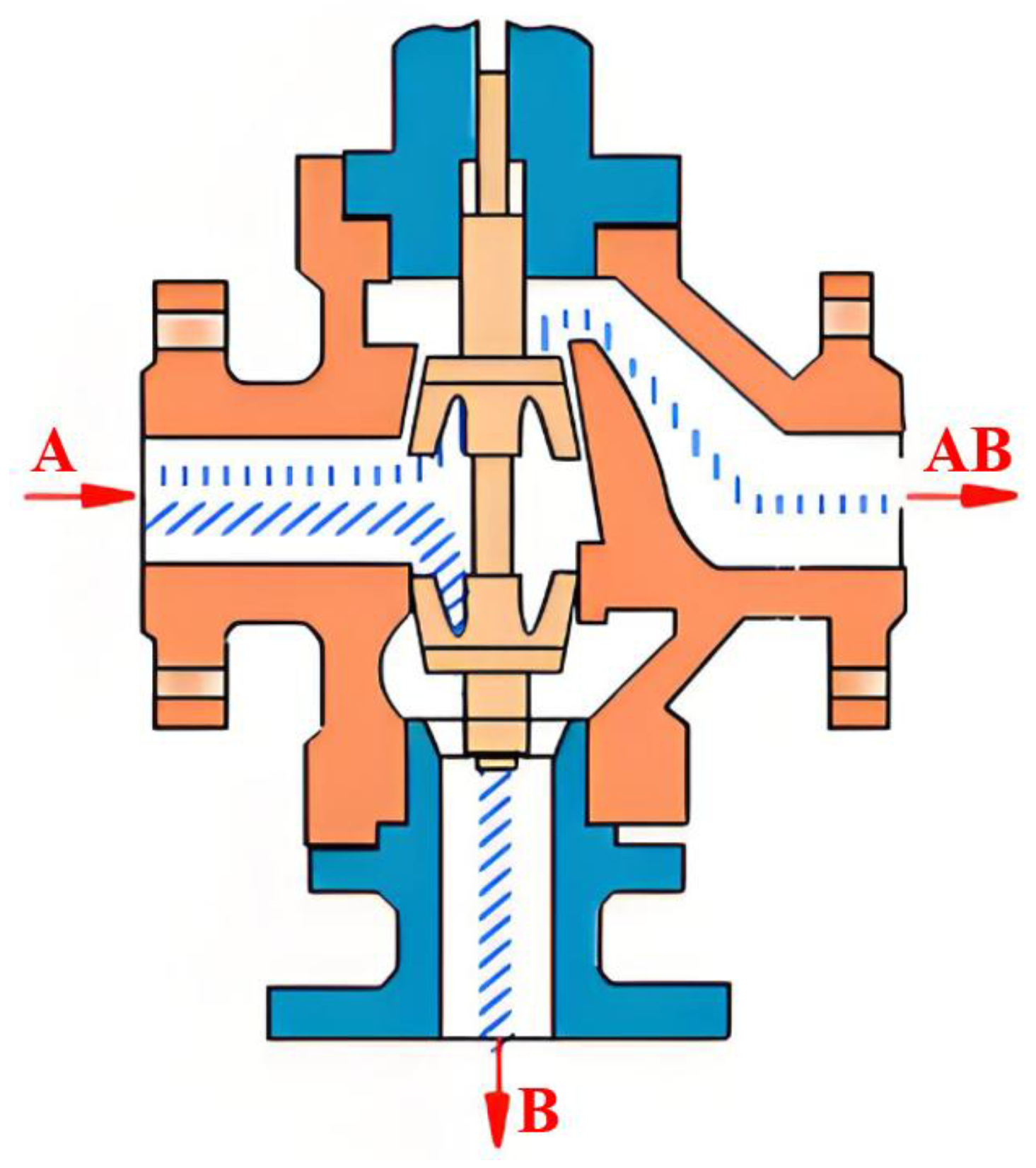
3.1. Leakage Point Localization Algorithm
- (1)
- Read the pressure data from the upstream and downstream stations during the leak period, referred to as datas and datax, respectively.
- (2)
- The sliding mean strategy is adopted to denoise and reduce the dimension of the original datas and datax. Taking the pressure data of the upstream station as an example, that is, datas_denoising[i] = mean(datas_denoising[i × s:(i + 1) × s]), i = 1, 2, …, where a is the window length.where Δt is the time difference in seconds. The point ω1 represents the location where the pressure drop is maximized at the upstream station, while ω2 denotes the location where the pressure drop is maximized at the downstream station. x is the distance from the leak point to the upstream station in meters, v is the pressure propagation speed in meters per second, and L is the distance between the upstream and downstream stations in meters.
- (3)
- To ensure the stability of the algorithm, select s from {1, 2, 3, …, n} and repeat the calculation of a set of leakage point positions Dist. Remove zero elements and elements equal to L from Dist, calculate the range, median, and mean of the remaining elements, and determine the leak location by computing the mean.
3.2. Analysis and Verification of Leakage Point Localization Based on Upstream and Downstream Pressure Fluctuations
- (1)
- Signal Conditioning: Raw pressure data are smoothed via a 0.5 s moving average window and normalized to [−1, 1] range.
- (2)
- Multi-scale Decomposition: db4 wavelet transform extracts frequency components at five resolution levels.
- (3)
- Feature Fusion: Time-frequency characteristics are combined and compressed through PCA.
- (4)
- Model Initialization: LSTM layers are configured with Adam optimizer (lr = 0.001) and Glorot weight initialization.
- (5)
- Hybrid Training: Synthetic data pre-training precedes experimental data fine-tuning with early stopping.
- (6)
- Validation: Predictions are evaluated through 5-fold cross-validation using MAPE, RMSE, and R2 metrics.
4. Experiment and Analysis
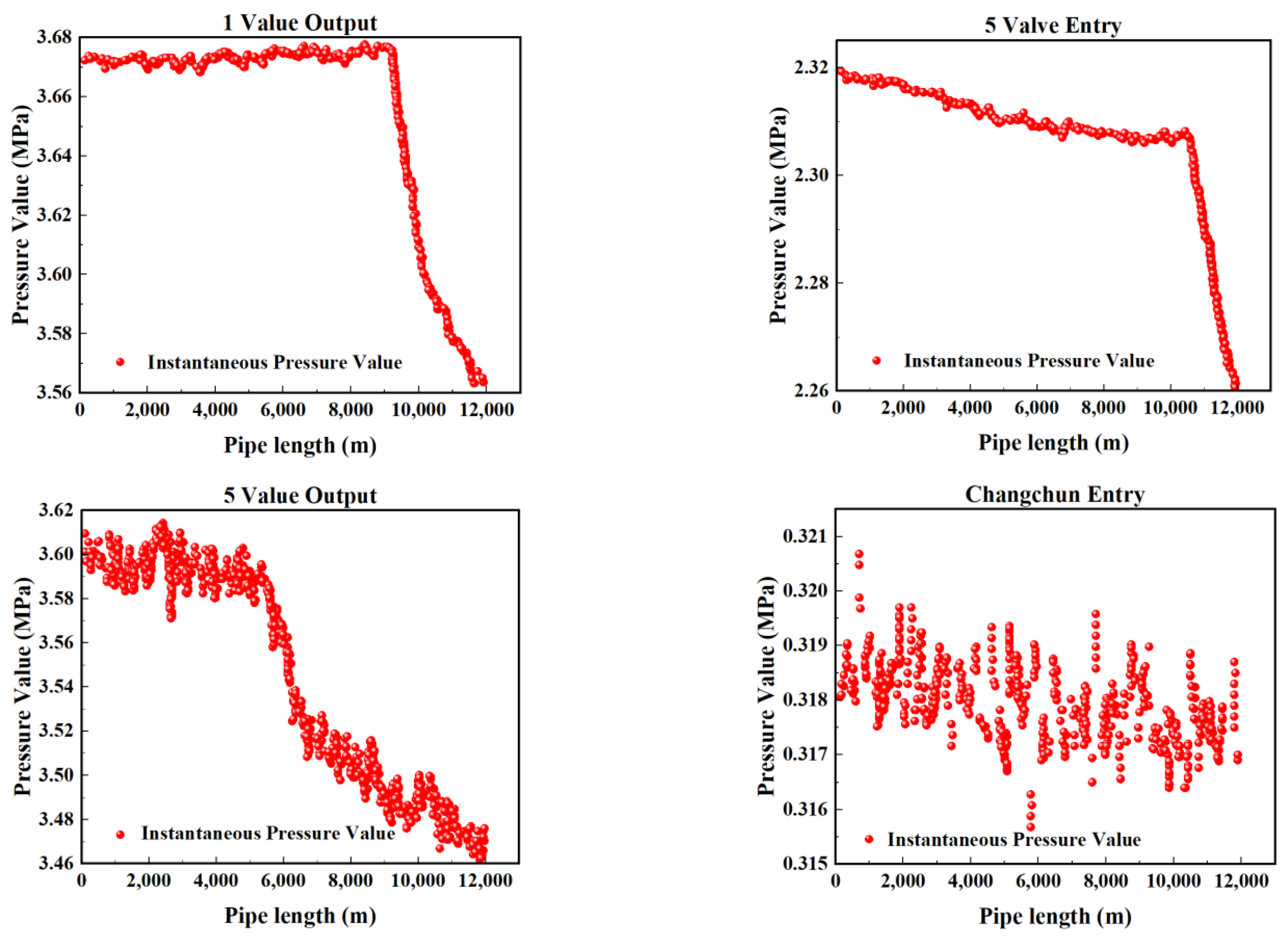
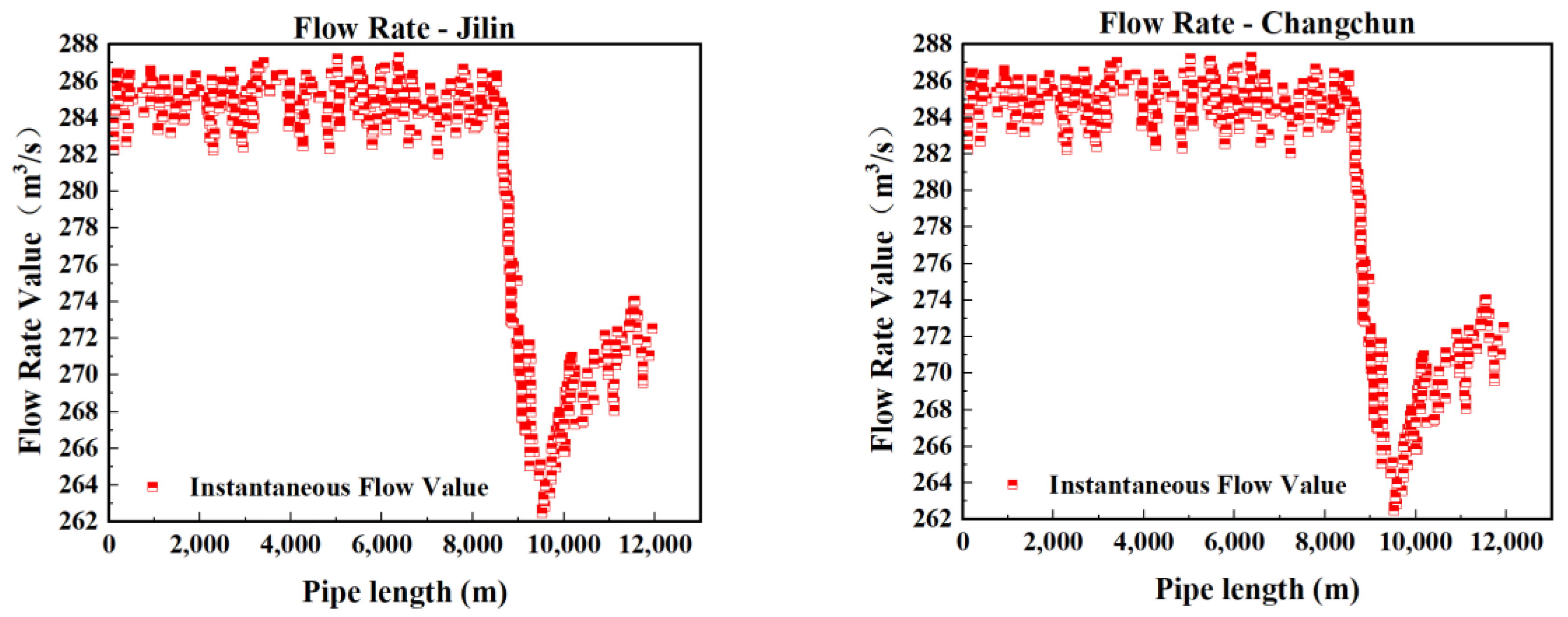
4.1. Experimental Dataset
- (1)
- 15 km intervals along trunk lines;
- (2)
- 500 m spacing near critical valves (Stations #3/#7);
- (3)
- Pump discharge/suction headers (Stations #1/#5/#8);
- (1)
- 14 confirmed leakage incidents (5 artificial, 9 operational);
- (2)
- 326 maintenance-induced pressure transients;
- (3)
- Continuous 28-month normal operation records;
- (1)
- Outlier Removal: 3σ thresholding eliminated 0.17% aberrant values;
- (2)
- Time Alignment: Compensated 50–200 ms transmission delays across nodes;
- (3)
- Normalization: Min–max scaled per sensor’s historical range (0–6.4 MPa);
- (4)
- Wavelet Denoising: db6 wavelet with 5 decomposition levels.
4.2. Experimental Comparison
- (I)
- LSTM Network + Flow Statistical Measures + Upstream and Downstream Valve Openings
- (II)
- LSTM–Transformer Model with Wavelet Denoising (Flow Statistical Measures + Upstream and Downstream Valve Openings)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Jiang, Z.; Li, J.L.; Zhao, Z.D.; Cao, Y.Y. Research on Signal Noise Reduction and Leakage Localization in Urban Water Supply Pipelines Based on Northern Goshawk Optimization. Sensors 2024, 24, 6091–6114. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Na, Y.K.; Kim, E.S.; Kyung, J.E.; Choi, G.H.; Jeong, J. LSTM-Autoencoder Based Detection of Time-Series Noise Signals for Water Supply and Sewer Pipe Leakages. Water 2024, 16, 2631–2653. [Google Scholar] [CrossRef]
- Lin, W.F.; Tian, X.H. Research on Leak Detection of Low-Pressure Gas Pipelines in Buildings Based on Improved Variational Mode Decomposition and Robust Kalman Filtering. Sensors 2024, 24, 4590–4618. [Google Scholar] [CrossRef] [PubMed]
- Ostapkowicz, P.; Bratek, A. Two-Leak Case Diagnosis Based on Static Flow Model for Liquid Transmission Pipelines. Sensors 2023, 23, 7751–7771. [Google Scholar] [CrossRef]
- Niamat, U.; Zahoor, A.; JongMyon, K. Pipeline Leakage Detection Using Acoustic Emission and Machine Learning Algorithms. Sensors 2023, 23, 3226–3245. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Nguyen, T.K.; Ahmad, Z.; Kim, J.M. A Reliable Pipeline Leak Detection Method Using Acoustic Emission with Time Difference of Arrival and Kolmogorov-Smirnov Test. Sensors 2023, 23, 9296–9310. [Google Scholar] [CrossRef]
- Santos, D.N.E.; Reginaldo, S.N.; Longo, N.J.; da Fonseca, R., Jr.; Conte, G.M.; Morales, M.E.R.; Silva, J.M. Advancing oil and gas pipeline monitoring with fast phase fraction sensor. Meas. Sci. Technol. 2024, 35, 125302–125323. [Google Scholar] [CrossRef]
- Orsini, J. Acoustic Monitoring Efficiently Identifies Pipeline Leaks. Opflow 2024, 50, 8–9. [Google Scholar] [CrossRef]
- Pahlavanzadeh, F.; Khaloozadeh, H.; Forouzanfar, M. Online fault detection and localization of multiple oil pipeline leaks using model-based residual generation and friction identification. Int. J. Dyn. Control 2024, 12, 2615–2628. [Google Scholar] [CrossRef]
- Saleem, F.; Ahmad, Z.; Siddique, F.M.; Umar, M.; Kim, M.J. Acoustic Emission-Based Pipeline Leak Detection and Size Identification Using a Customized One-Dimensional DenseNet. Sensors 2025, 25, 1112–1134. [Google Scholar] [CrossRef]
- Tajalli, M.A.S.; Moattari, M.; Naghavi, V.S.; Salehizadeh, R.M. A Novel Hybrid Internal Pipeline Leak Detection and Location System Based on Modified Real-Time Transient Modelling. Modelling 2024, 5, 1135–1157. [Google Scholar] [CrossRef]
- Faysal, A.; Adhreena, M.S.N.A.; Vorathin, E.; Hafizi, Z.M.; Ngui, W.K. Leak diagnosis of pipeline based on empirical mode decomposition and support vector machine. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1078, 012023–012031. [Google Scholar] [CrossRef]
- Faerman, A.V.; Avramchuk, S.V. Comparative Study of Basic Time Domain Time-Delay Estimators for Locating Leaks in Pipelines. Int. J. Networked Distrib. Comput. 2020, 8, 49–57. [Google Scholar] [CrossRef]
- Yu, X.C.; Liang, W.; Zhang, L.B.; Jin, H.; Qiu, J.W. Dual-tree complex wavelet transform and SVD based acoustic noise reduction and its application in leak detection for nature gas pipeline. Mech. Syst. Signal Process. 2016, 72, 266–285. [Google Scholar] [CrossRef]
- Tejedor, J.; Macias, G.J.; Martins, H.F.; Piote, D.; Graells, P.J.; Lopez, M.S.; Corredera, P.; Herraez, G.M.; Lewis, E. A novel fiber optic based surveillance system for prevention of pipeline integrity threats. Sensors 2017, 17, 35–374. [Google Scholar] [CrossRef]
- Rojas, J.; Verde, C. Adaptive estimation of the hydraulic gradient for the location of multiple leaks in pipelines. Control Eng. Pract. 2020, 95, 104226–104236. [Google Scholar] [CrossRef]
- Cai, Y.J.; Santos, R.B.; Givigi, S.N. A pipeline leak classification and location estimation system with convolutional neural networks. IEEE Syst. J. 2020, 14, 3072–3081. [Google Scholar] [CrossRef]
- Kampelopoulos, D.; Papastavrou, G.N.; Kousiopoulos, G.P.; Karagiorgos, N.; Goudos, S.K.; Nikolaidis, S. Machine learning model comparison for leak detection in noisy industrial pipelines. In Proceedings of the International Conference on Modern Circuits and Systems Technologies, Bremen, Germany, 7–9 September 2020; pp. 1–4. [Google Scholar]
- Lukonge, A.B.; Cao, X.W. Leak Detection System for Long-Distance Onshore and Offshore Gas Pipeline Using Acoustic Emission Technology. A Review. Trans. Indian Inst. Met. 2020, 73, 1715–1727. [Google Scholar] [CrossRef]
- Zuo, Z.L.; Ma, L.; Liang, S.; Liang, J.; Zhang, H.; Liu, T. A semi-supervised leakage detection method driven by multivariate time series for natural gas gathering pipeline. Process Saf. Environ. Prot. 2022, 164, 468–478. [Google Scholar] [CrossRef]
- Şahin, E.; Yüce, H. Prediction of Water Leakage in Pipeline Networks Using Graph Convolutional Network Method. Appl. Sci. 2023, 13, 7427–7443. [Google Scholar] [CrossRef]
- Sankarasubramanian, P. An efficient crack detection and leakage monitoring in liquid metal pipelines using a novel BRetN and TCK-LSTM techniques. Multimed. Tools Appl. 2024, 1–29. [Google Scholar] [CrossRef]
- Ullah, N.; Siddique, F.M.; Ullah, S.; Ahmad, Z.; Kim, J.M. Pipeline Leak Detection System for a Smart City: Leveraging Acoustic Emission Sensing and Sequential Deep Learning. Smart Cities 2024, 7, 2318–2338. [Google Scholar] [CrossRef]
- Ahn, B.; Kim, J.; Choi, B. Artificial intelligence-based machine learning considering flow and temperature of the pipeline for leak early detection using acoustic emission. Eng. Fract. Mech. 2019, 210, 381–392. [Google Scholar] [CrossRef]
- Yussuf, W.O.; Adebowale, O.A.; Kingsley, A. Mathematical modelling and simulation of leak detection system in crude oil pipeline. Heliyon 2023, 9, 15412–15426. [Google Scholar]
- Rajasekaran, U.; Kothandaraman, M.; Pua, H.C. Novel EMD with Optimal Mode Selector, MFCC, and 2DCNN for Leak Detection and Localization in Water Pipeline. Appl. Sci. 2023, 13, 12892–12909. [Google Scholar] [CrossRef]
- Siddique, F.M.; Ahmad, Z.; Ullah, N.; Ullah, S.; Kim, M.J. Pipeline Leak Detection: A Comprehensive Deep Learning Model Using CWT Image Analysis and an Optimized DBN-GA-LSSVM Framework. Sensors 2024, 24, 4009. [Google Scholar] [CrossRef]
- Pahlavanzadeh, F.; Khaloozadeh, H.; Forouzanfar, M. Oil pipeline multiple leakage detection and localization based on sensor fusion. Eng. Fail. Anal. 2025, 167, 109038. [Google Scholar] [CrossRef]
- Ali, J.; Masoud, M.; Brian, B.; Mao, D.H.; Bahram, S.; Fariba, M. 3DUNetGSFormer: A deep learning pipeline for complex wetland mapping using generative adversarial networks and Swin transformer. Ecol. Inform. 2022, 72, 101904–101915. [Google Scholar]
- Fatih, K.; Ahmet, Z.; Resul, K.; Sultan, Z. Leakage detection and localization on water transportation pipelines: A multi-label classification approach. Neural Comput. Appl. 2024, 10, 2905–2914. [Google Scholar]
- Zhang, M.; Gao, L.; Zhang, X.; Zhang, S. An infrasound source localisation algorithm for improving location accuracy of gas pipeline leakage detection system. Int. J. Embed. Syst. 2022, 15, 9–18. [Google Scholar] [CrossRef]
- Brahami, M.A.; Abdi, S.M.; Hamdi Cherif, S.; Bendahmane, A. Optimization of a Pipelines Leak Detection Method Based on Inverse Transient Analysis Using a Genetic Algorithm. Arab. J. Sci. Eng. 2022, 48, 1451–1460. [Google Scholar] [CrossRef]
- Farooq, M.S.; Zahoor, A.; Myon, J.K. Pipeline leak diagnosis based on leak-augmented scalograms and deep learning. Eng. Appl. Comput. Fluid Mech. 2023, 1, 2225577–2225593. [Google Scholar]
- Saleem, F.; Ahmad, Z.; Kim, M.J. Real-Time Pipeline Leak Detection: A Hybrid Deep Learning Approach Using Acoustic Emission Signals. Appl. Sci. 2024, 15, 185–204. [Google Scholar] [CrossRef]
- Farzin, P.; Myon, J.K. Leak detection and localization for pipelines using multivariable fuzzy learning backstepping. J. Intell. Fuzzy Syst. 2021, 42, 377–388. [Google Scholar]
- Rohan, P.; Kumara, S. An Efficient Architecture for Modified Lifting-Based Discrete Wavelet Transform. Sens. Imaging 2020, 21, 53–75. [Google Scholar]
- Karimanzira, D. Simultaneous Pipe Leak Detection and Localization Using Attention-Based Deep Learning Autoencoder. Electronics 2023, 12, 46–65. [Google Scholar] [CrossRef]
- Fernando, M.C.F.; Ugli, K.A.M.; Jeongnam, K.; Younho, C.; Kyoung, J. A novel flaw detection approach in carbon steel pipes through ultrasonic guided waves and optimized transformer neural networks. J. Mech. Sci. Technol. 2024, 38, 3253–3263. [Google Scholar]
- Houshang, A.A.; Ali, H.; Reza, H.G. Machine learning approach to transient-based leak detection of pressurized pipelines: Classification vs Regression. J. Civ. Struct. Health Monit. 2022, 12, 611–628. [Google Scholar]
- Vrinda, G. Recent technologies for leak Detection in Pipeline: A review. Water Energy Int. 2021, 64, 29–37. [Google Scholar]



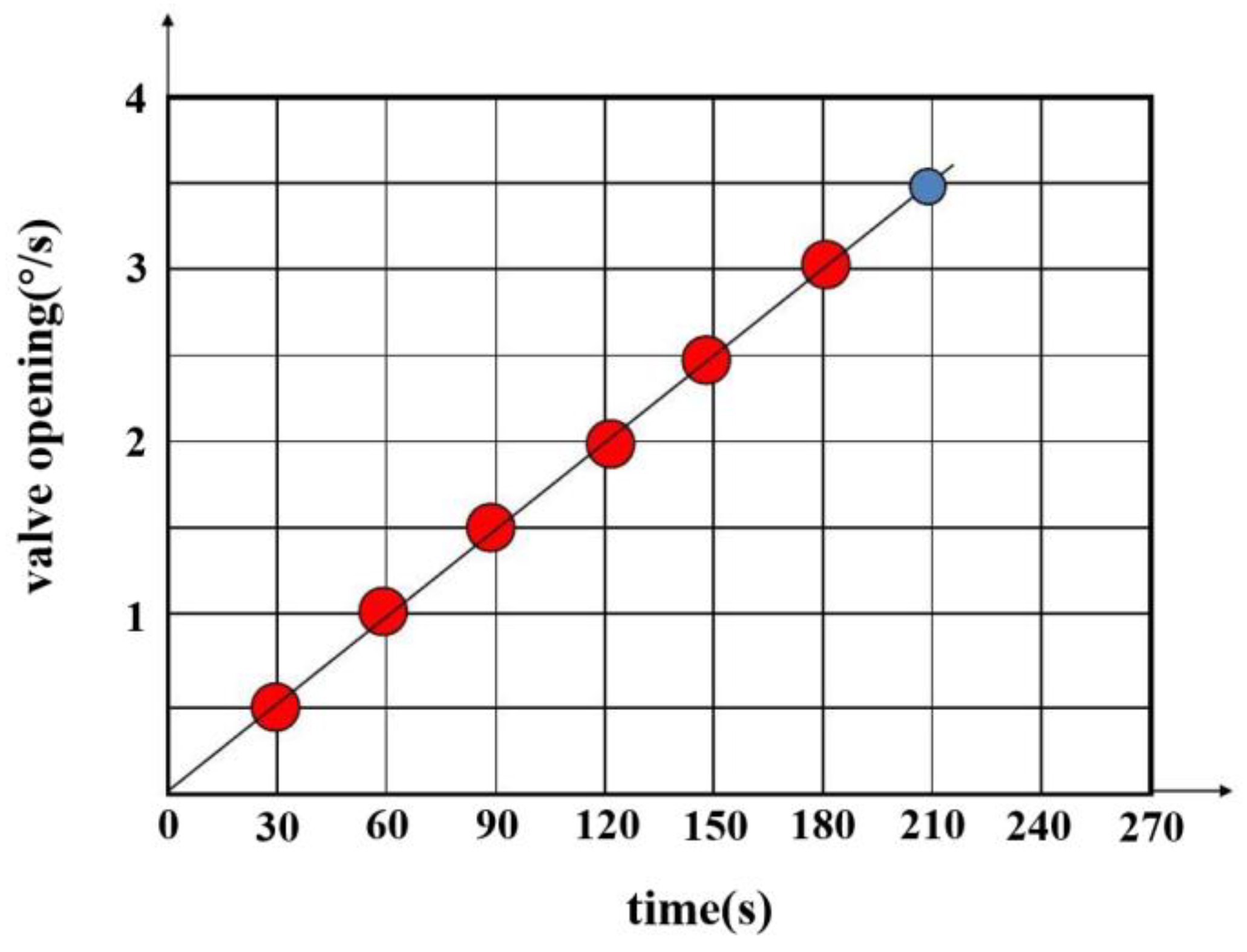
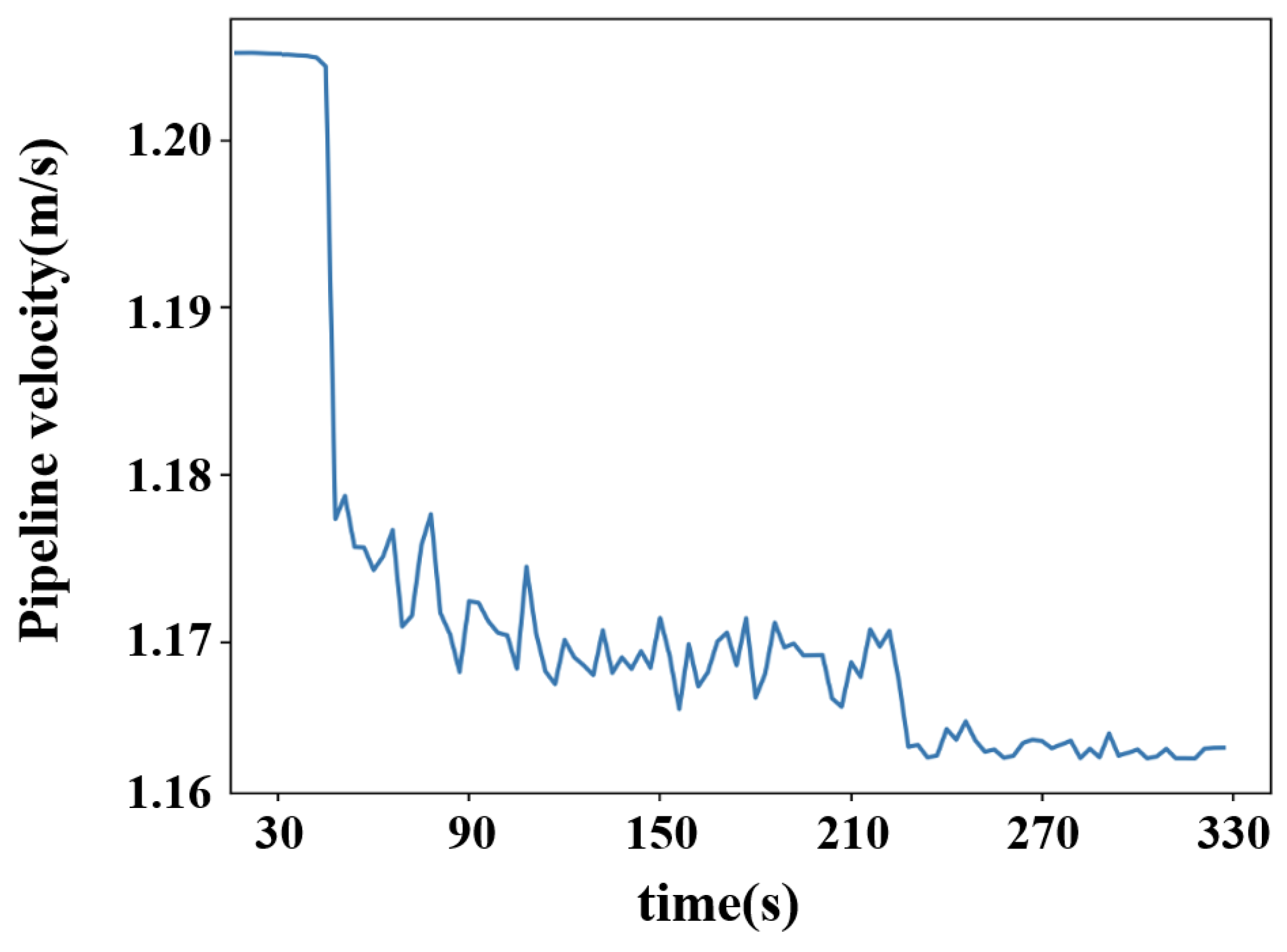
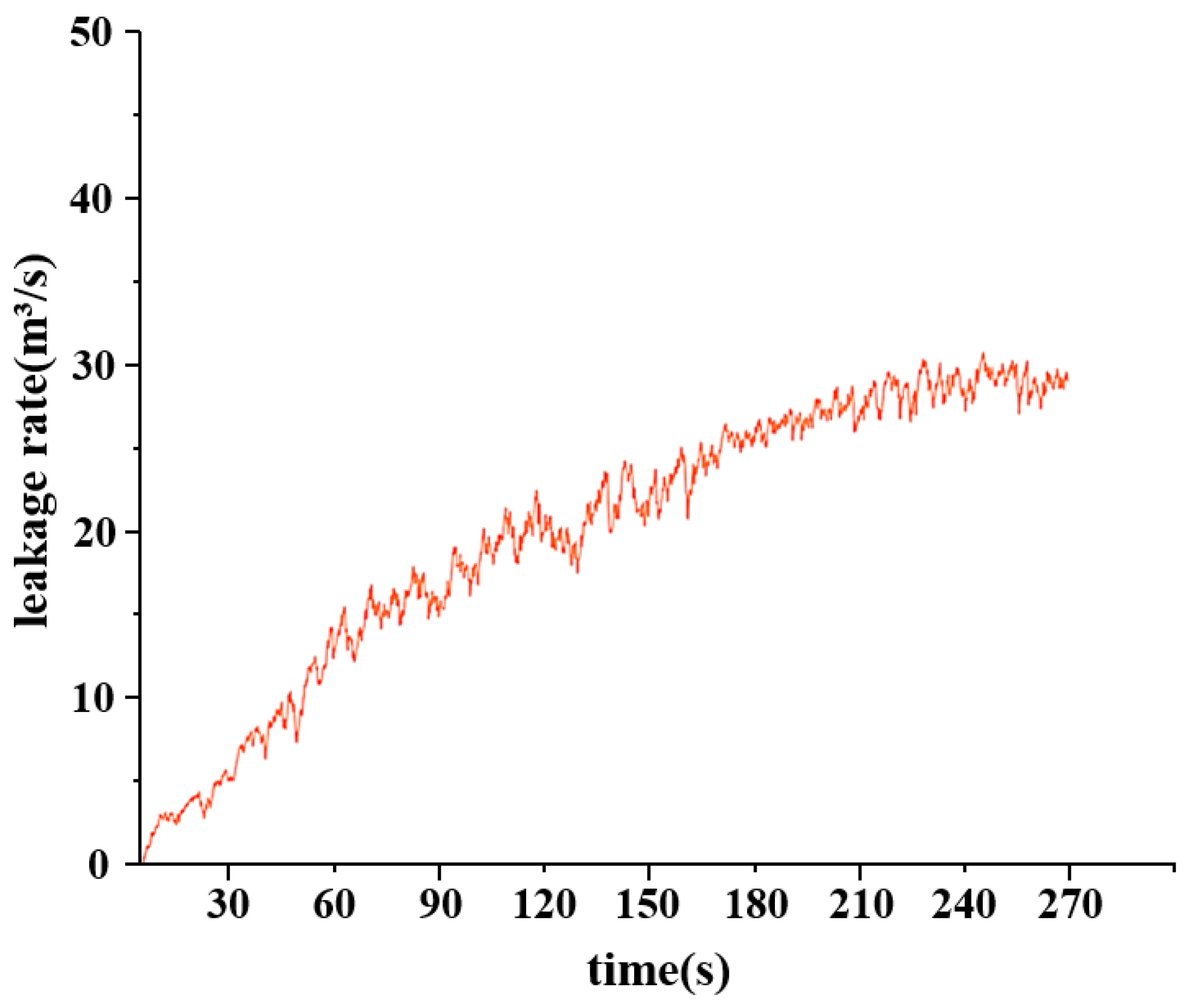


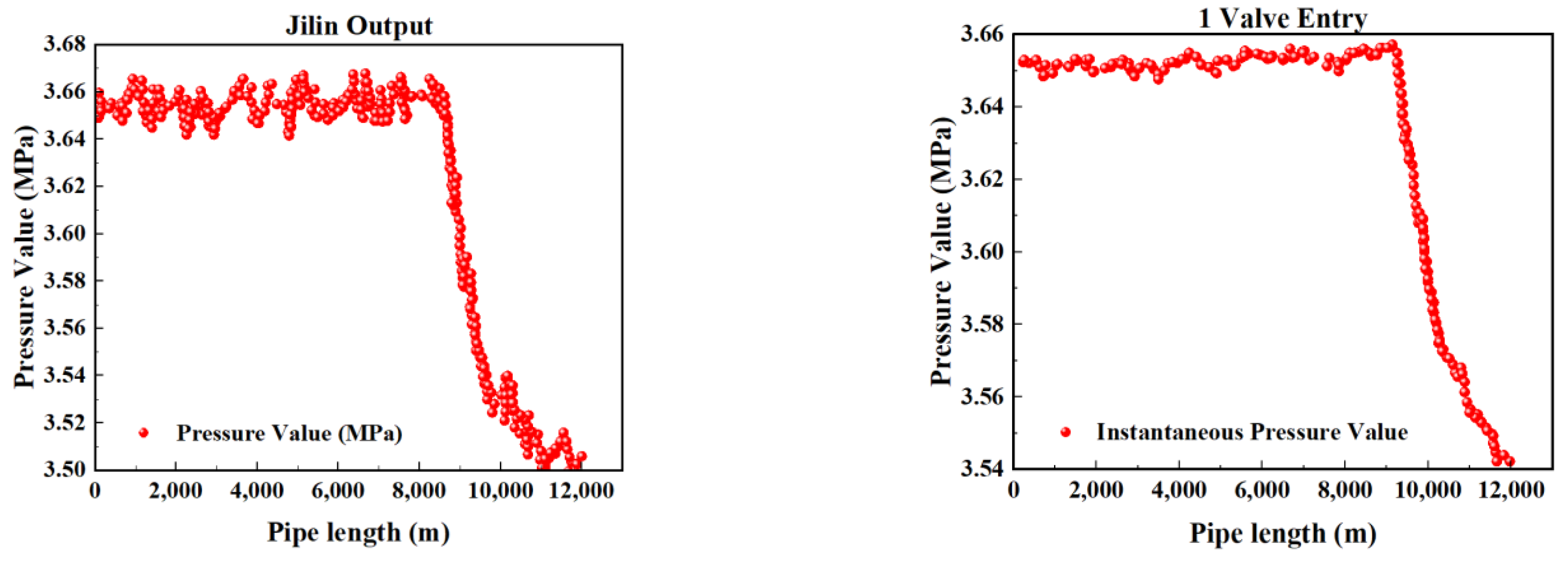

| Time | Research Scholars | Algorithm Model | Disadvantages |
|---|---|---|---|
| 2016 | Xuchao Yu [14] | Double tree complex wavelet transform–singular value decomposition | Difficult to capture leak speed and trends |
| 2017 | Tejedor and Rojas [15,16] | Context Extraction–Multi-Layer Perceptron Fusion | Over-fit, difficult to cope with new data |
| 2020 | Cai and Kampelopoulos [17,18] | Convolutional Neural Networks | Rely on data quality and quantity |
| 2020 | Lukonge [19] | Hilbert–Huang Transform | Insufficient generalization capacity |
| 2022 | Zhonglin Zuo [20] | LSTM–Self Encoder Hybrid Model | Deviation from real features |
| 2023 | Ersin Şahin [21] | Figure Convolutional Neural Network Model | Data overfitting |
| 2024 | Sankarasubramanian [22] | TCK-LSTM Network Model | Large-scale training dataset required |
| 2024 | Niamat Ullah [23] | Bi-LSTM Sequential Deep Learning Model | High dependence on markup data |
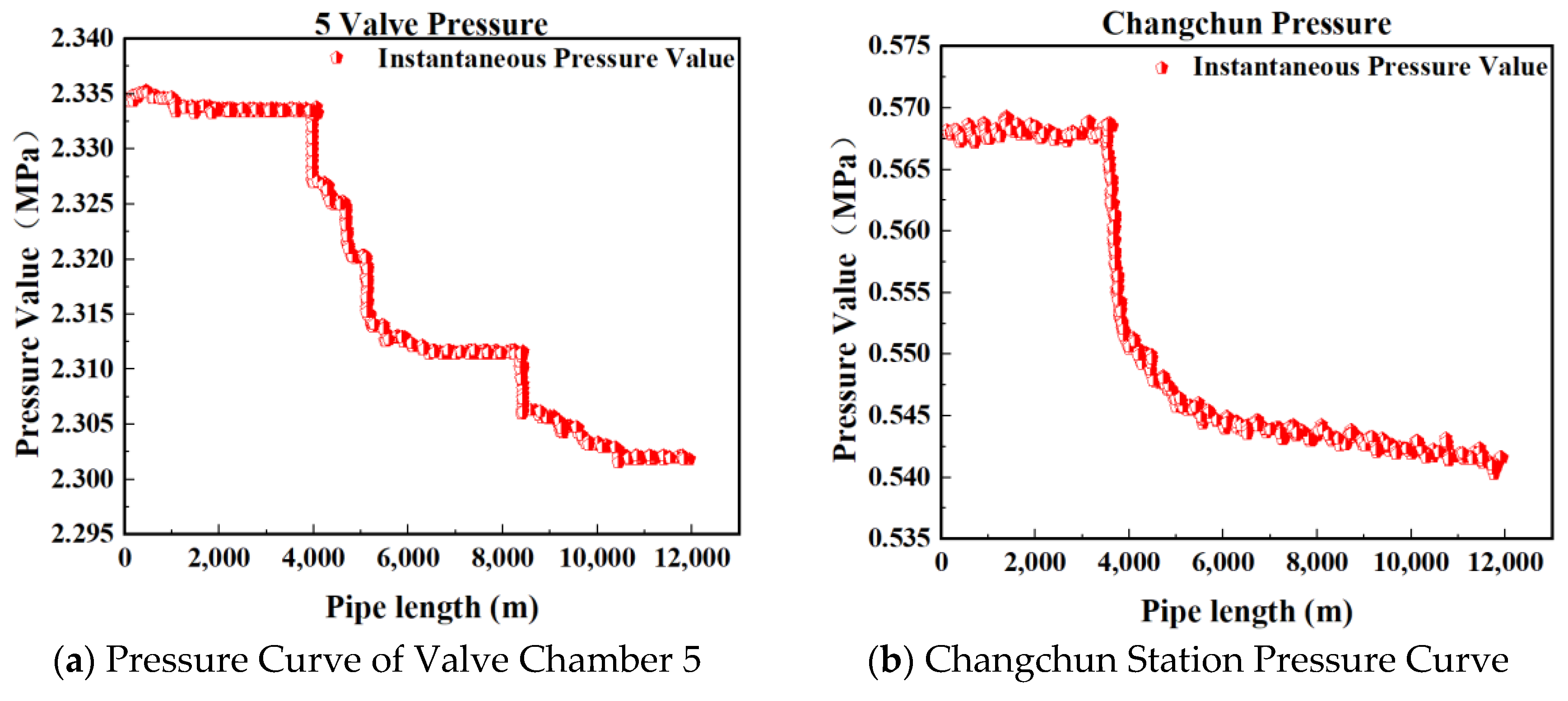
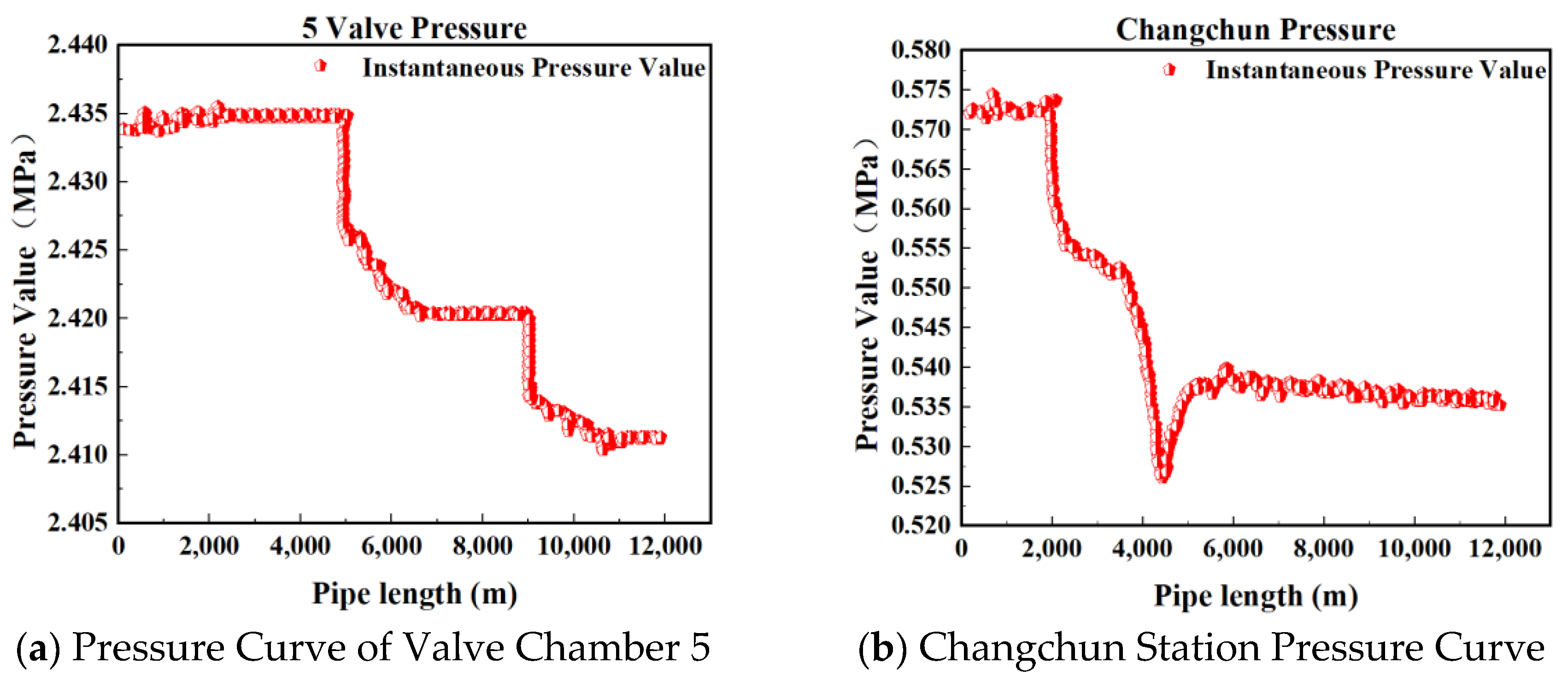
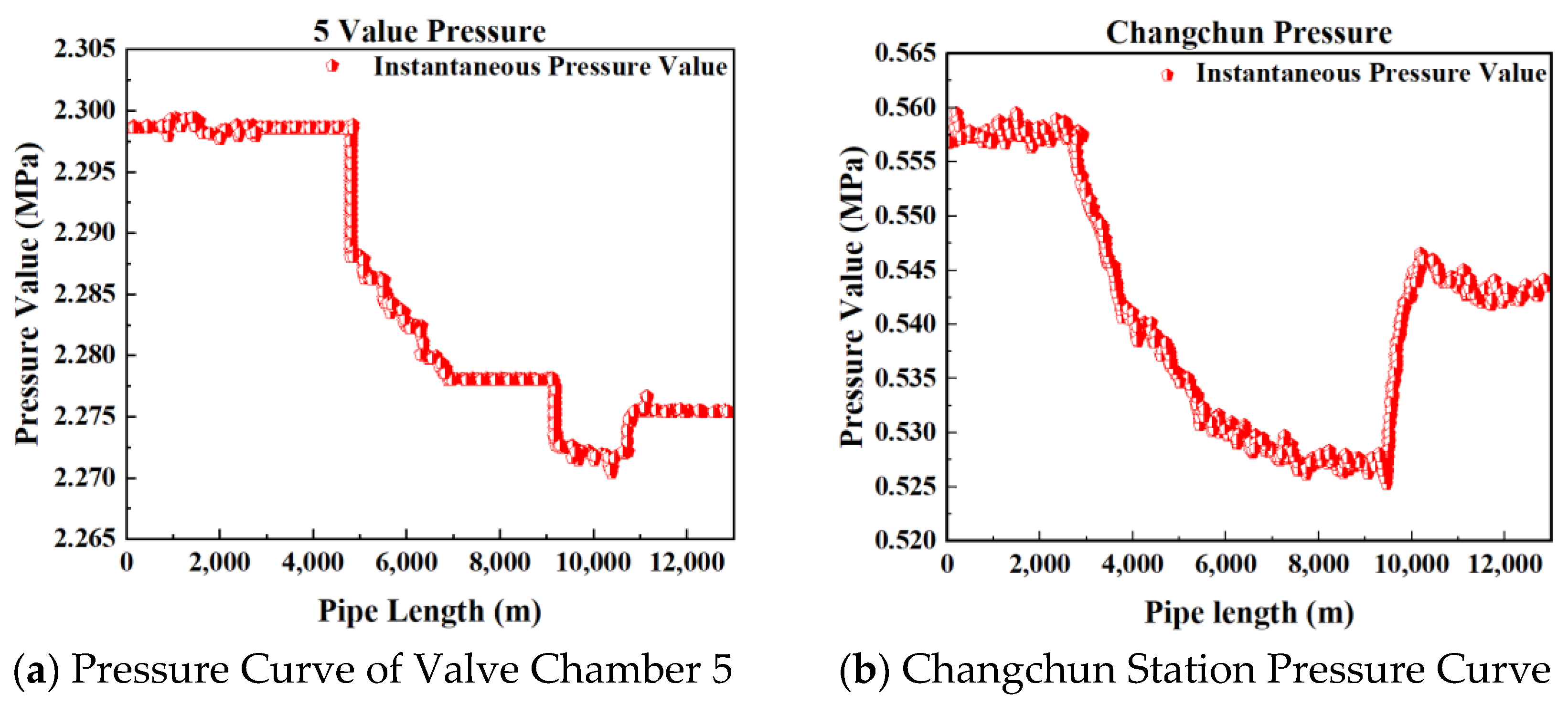
| Dataset | Upstream Pressure Value (MPa) | Downstream Pressure Value (MPa) | Pressure Difference (MPa) | Time Difference (s) |
|---|---|---|---|---|
| Group 1 | 2.43 | 0.55 | 1.88 | 73.80 |
| Group 2 | 2.36 | 0.56 | 1.80 | 103.25 |
| Group 3 | 2.33 | 0.57 | 1.76 | 103.25 |
| Group 4 | 2.29 | 0.55 | 1.74 | 111.20 |
| Time | Upstream Station Testing Point | Downstream Station Testing Point | Leakage Rate | Instantaneous Flow Rate (m3/h) | Leakage Location | Positioning Location |
|---|---|---|---|---|---|---|
| 11:50 | Valve 5 | Changchun Station | 3.00% | 318 | 49.26 | 53.91 |
| 14:15 | Valve 5 | Changchun Station | 1.50% | 320 | 49.26 | 56.63 |
| 14:28 | Valve 5 | Changchun Station | 3.72% | 376 | 49.26 | 48.68 |
| 15:50 | Valve 5 | Changchun Station | 1.60% | 374 | 49.26 | 56.01 |
| Number | Test Set Type | Predicting Leakage | Predict Normal | Total | Accuracy |
|---|---|---|---|---|---|
| Experiment 1 | LSTM Discrete Test Set (Pressure Set) | 2 | 24 | 26 | 92.30% |
| 3 | 271 | 274 | 98.90% | ||
| LSTM Continuous Test Set (Pressure Set) | 755 | 33,085 | 33,840 | 97.80% | |
| Experiment 2 | LSTM Discrete Test Set (Flow Set) | 50 | 3 | 53 | 94.30% |
| 12 | 516 | 528 | 97.70% | ||
| LSTM Continuous Test set (Traffic Set) | 17 | 33,823 | 33,840 | 99.90% | |
| Experiment 3 | LSTM Discrete Test Set (Flow + Pressure Set) | 12 | 1 | 13 | 92.30% |
| 1 | 166 | 167 | 99.99% | ||
| LSTM Continuous Test Set (Flow + Pressure Set) | 4716 | 29,124 | 33,840 | 86.10% | |
| Experiment 4 | Transformer Discrete Test Set (Pressure Set) | 12 | 2 | 14 | 85.70% |
| 0 | 236 | 236 | 99.98% | ||
| Transformer Continuous Test Set (Pressure Set) | 484 | 33,356 | 33,840 | 98.60% | |
| Transformer Continuous Test Set (Flow + Pressure Set) | 8 | 33,832 | 33,840 | 99.90% | |
| Experiment 5 | LSTM Continuous Test Set (Flow Statistics + Upstream and Downstream Valve Opening) | 12 | 64,778 | 64,790 | 99.98% |
| Wavelet Denoising + LSTM Transformer Continuous Test Set (Flow Statistics + Upstream and Downstream Valve Opening) | 2 | 64,788 | 64,790 | 99.995% |
| Data Types | Pressure + the Sum of the First Instantaneous Traffic | Pressure + the Sum of Transient Flow at the End | Pressure + (Difference Between Terminal and First Station) | Pressure + the Sum of Three Valve Motor Currents |
|---|---|---|---|---|
| Total Accuracy Rate | 0.73 | 1.00 | 0.76 | 0.93 |
| Underreporting Rate | 0.78 | 0.00 | 0.78 | 0.11 |
| False Positives | 0.19 | 0.00 | 0.14 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Shang, Z.; Zheng, J.; Zhang, Y.; Weng, G.; Zhao, S.; Bi, C. Research on Leak Detection and Localization Algorithm for Oil and Gas Pipelines Using Wavelet Denoising Integrated with Long Short-Term Memory (LSTM)–Transformer Models. Sensors 2025, 25, 2411. https://doi.org/10.3390/s25082411
Ma Y, Shang Z, Zheng J, Zhang Y, Weng G, Zhao S, Bi C. Research on Leak Detection and Localization Algorithm for Oil and Gas Pipelines Using Wavelet Denoising Integrated with Long Short-Term Memory (LSTM)–Transformer Models. Sensors. 2025; 25(8):2411. https://doi.org/10.3390/s25082411
Chicago/Turabian StyleMa, Yunbin, Zuyue Shang, Jie Zheng, Yichen Zhang, Guangyuan Weng, Shu Zhao, and Cheng Bi. 2025. "Research on Leak Detection and Localization Algorithm for Oil and Gas Pipelines Using Wavelet Denoising Integrated with Long Short-Term Memory (LSTM)–Transformer Models" Sensors 25, no. 8: 2411. https://doi.org/10.3390/s25082411
APA StyleMa, Y., Shang, Z., Zheng, J., Zhang, Y., Weng, G., Zhao, S., & Bi, C. (2025). Research on Leak Detection and Localization Algorithm for Oil and Gas Pipelines Using Wavelet Denoising Integrated with Long Short-Term Memory (LSTM)–Transformer Models. Sensors, 25(8), 2411. https://doi.org/10.3390/s25082411





