A Novel Key Distribution for Mobile Patient Authentication Inspired by the Federated Learning Concept and Based on the Diffie–Hellman Elliptic Curve
Abstract
1. Introduction
1.1. Challenges to Ensuring Authentication and Confidentiality in Healthcare
1.2. Contributions
- Proposing a hierarchical key distribution architecture in the context of an e-healthcare system to enhance the security and privacy of patients based on FL.
- Proposing a novel key distribution protocol based on FL to exchange the local and global model between the root public key generator and sub-public key generator .
- Designing a lightweight key establishing approach between and mobile patient using Diffie–Hellman elliptic curve algorithm.
- Providing patient authentication using a private key and several secure parameters also providing identity preservation using the concept of a local model for each .
- Enhancing the performance for the mobile node in terms of the number of exchange messages [32].
2. Related Work
| Reference | Authentication Technique | Environment |
|---|---|---|
| [38] | Biometric+ECC | Mobile healthcare environments |
| [34] | Shared key | Wireless Medical Sensor Networks |
| [35] | ECC | IoT |
| [37] | Improved mutual authentication | Wireless Body Area Networks |
| [36] | Lightweight anonymous mutual authentication | Wireless Body Area Networks |
| [39] | Federated learning and blockchain | IoT healthcare |
| Our proposal | Federated learning and key distribution | IoT healthcare system |
| Reference | Architecture | Security Goal | Verification Method | Performance Analysis |
|---|---|---|---|---|
| [40] | Cloud of things | Prevent Man-in-the-Middle (MITM) | Scyther | Anonymity, Authentication, Authorization, Accountability, Confidentiality, Integrity, Non-repudiation |
| [41] | IoT-based M-Health system | Signature, Encryption, and Signcryption | Mathematical proof | Computational Cost, Communication Cost |
| [42] | WBANs | Authentication | Mathematical proof | Storage Overhead, Computation Cost, Communication Cost |
| [43] | E-healthcare | Authentication | AVISPA and BAN logic | Storage Cost, Communication Cost, Computation Cost |
| Our proposal | IoT healthcare | Authentication, Confidentiality, and Privacy | AVISPA and BAN logic | Storage Cost, Communication Cost, Computation Cost |
3. Proposed System
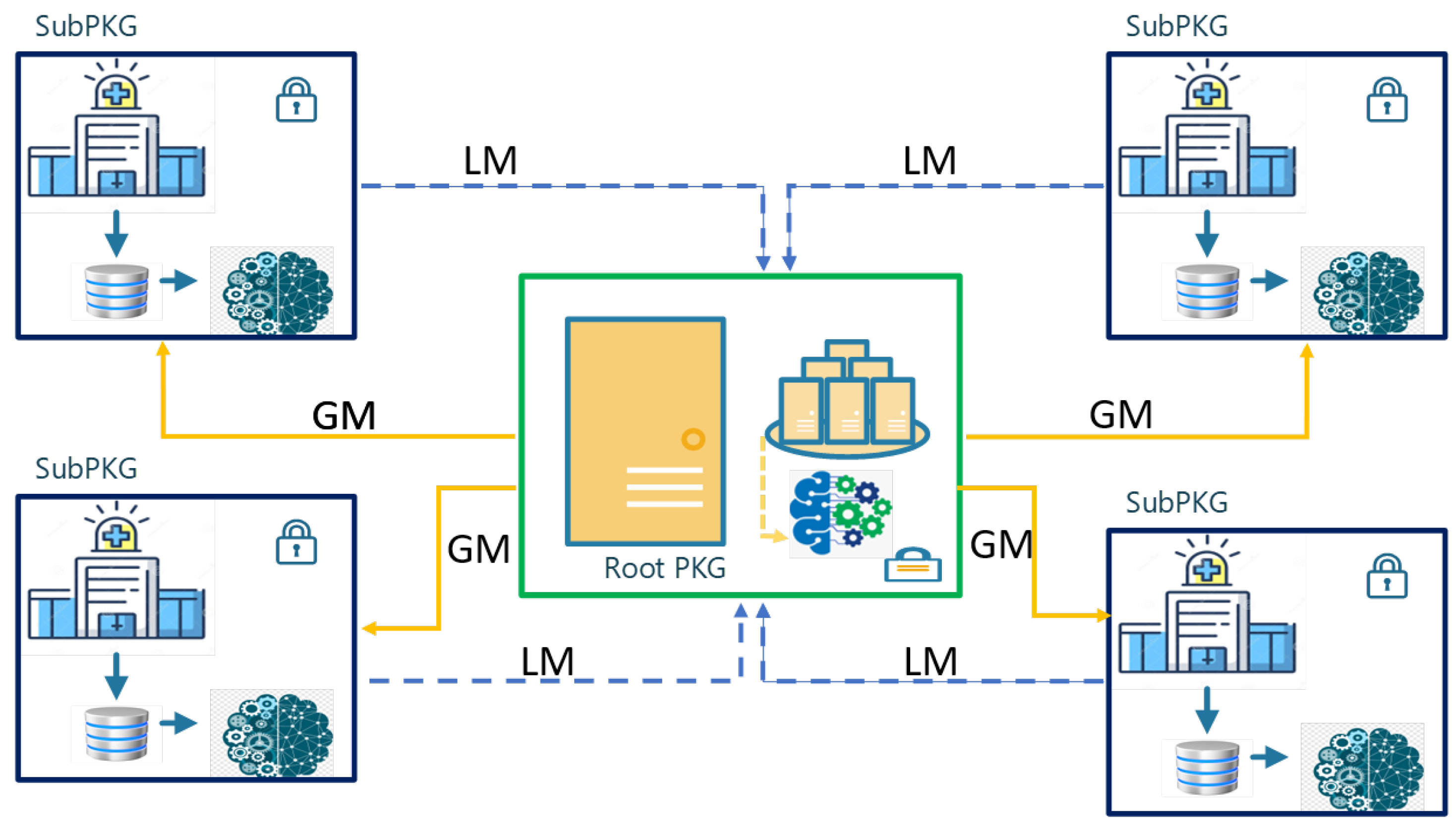
3.1. Architecture Overview
3.2. The Proposed Protocol Overview
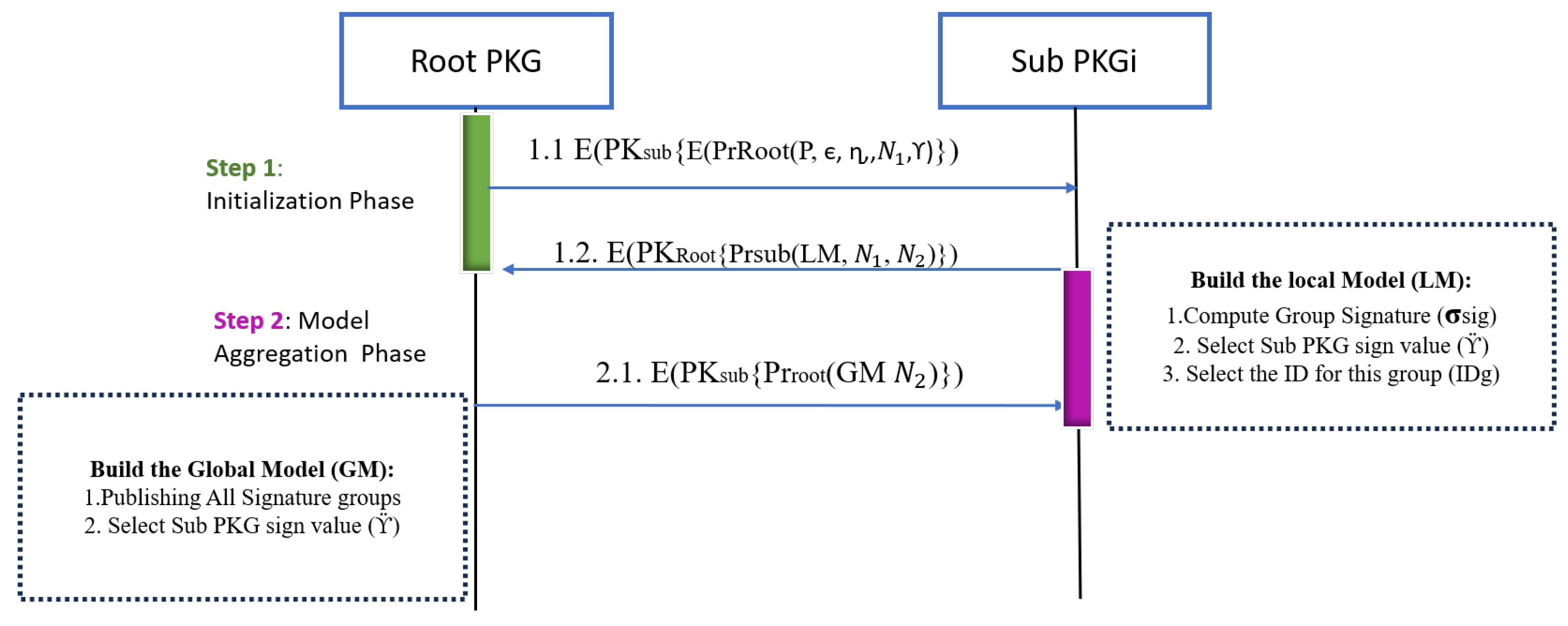
3.2.1. Initialization Phase Between and
- initiates a request to send information about the whole system, which consists of all Sub-PKGs and patients. This information is essential for the Sub-PKGs to construct their local models while considering these parameters.
- Root parameters are elliptic curve ranges for each Sub-PKG (), ranges for group signature (), and root sign value ().
- The parameters are securely handled. Initially, ensuring nonrejection properties, the encrypts these parameters using its private key, to ensure integrity and authentication. Subsequently, it encrypts them once more using the public key provided by the respective Sub-PKG to maintain confidentiality.
- After each receives the parameters from the root and based on the number of patients that it needs to deal with, the determines the group signature , Sub-PKG signing value , and identity for the group . After that, the sends a local model via its private key and encapsulates via the root public key.
- The root aggregates multiple local models from various Sub-PKGs, each equipped with its own set of parameters. This collective information is then used to construct the global model, ensuring a comprehensive consideration of all these individual parameters.
3.2.2. Patient Registration and Key Generation Phase
- The selects generator G based on the range that was created by the , prime number p, and selects a private number to determine the pubic key as .
- The patient selects the private key then determines its public key as and sends the public key to the . Moreover, it determines the shared key as .
- After the receives the patient’s public key it will determine the shared key as .
- Compute a message digest of the data you want to sign, often using a cryptographic hash function like SHA-256.
- The patient computes the digest for the message that equals ; this will be as one block while is unique for each patient.
- Generate a random number k in the range [1, n−1].
- Compute the point (,) = k*G.
- Calculate r = mod n.
- Calculate s = mod n.
- The patient ’s signature () is (r + ,s + ).
3.2.3. Mobile Patient Authentication
- A mobile patient sends a request for to obtain authentication and to be allowed to enter this domain.
- To achieve confidentiality, the mobile patient encrypts its request via ’s public key.
- The request contains the patient signature, patient public key, group identity, hashed secret value, and nonce.
- extracts the assuming that the Sub-PKG has initial values for each that exist in the global model. ) then checks this value by hashing it then compares it with the received digest. After that, it hashes the message using hash algorithm h = H(M).
- find the exact value of (r,s) after subtracting the patient’s secret value from each .
- Calculate the modular inverse of the signature proof .
- Recover the random point used during the signing: R’ = (h ∗ s1) ∗ G + (r ∗ s1) ∗ pubKey.
- Take from R’ its x-coordinate: r’ = R’.x.
- Calculate the signature validation result by comparing whether r’ == r.
4. Security Analysis
4.1. Security Proof Using AVISPA Tool
4.2. BAN Logic
4.3. Security Analysis Against Well-Known Attack
- Brute Force Attack: The attacker cannot reveal the private keys or the symmetric keys in a reasonable time. The EC private key cannot be calculated from the EC public key since it is an Elliptic Curve Discrete Logarithm Problem (ECDLP) [49,50]. The session key SK is generated using the ECDH algorithm which is based on the use of an EC private key for either the patient node or the SubPKG. Breaking ECDH session keys requires solving ECDLP, which is infeasible with classical computers. Consequently, brute force attacks will fail.
- Man-In-The Middle and Eavesdropping Attack: The attacker can intercept the communication between the patient’s node and the to read the data shared between these two entities; however, the attack will fail. In the Patient Authentication Phase, all messages are encrypted either using ECC to encrypt message 5.1 with the public key, or ECDH to encrypt messages 5.2 and 5.3 with the symmetric key SK. To decrypt the messages, the attacker should have the private key which is known only to the and the symmetric key SK which is known only to the patient node and the . Consequently, this attack will fail.
- Replay Attack: The attacker will try to perform a replay attack by resending a valid message to the ; however, the can detect this attack. Replay attacks can be detected using nonce values. In the Patient Authentication Phase, whenever the patient node should be authenticated, a nonce N1 is generated at the node side and passed to the . Another nonce N2 is also generated at the side and passed to the node. By verifying the freshness of these nonce values, both the patient’s node and the can detect the replay attack. A similar approach is used to detect replay attacks in the Patient Registration Phase; when the signature is calculated, a nonce value is generated by the node and passed to the along with the signature. By verifying the freshness of the nonce value, the will make sure that the signature is newly generated; if not, a replay attack is detected due to nonce verification failure.
- Signature Forgery Attack: The attacker tries to impersonate the patient’s node by forging the patient’s node signature; however, this attack will fail. In order to forge a signature, the attacker needs to know the group signature (), the identity of the group (), the root sign (), and the Sub-PKG sign (). These parameters are shared by the in an encrypted message during the Patient Registration Phase. The message is encrypted using a session key SK, which is known only to the patient node and the ; consequently, the attacker will not be able to know the parameters. In addition to these parameters, the attacker should know the patient node’s private key, which is known only to the node.
- Unauthorized Access and Identity Theft: If the attacker gains access to a patient’s signature, they could impersonate a patient and access personal health information. To mitigate this threat, all communication messages between the patient’s node and the are encrypted. Consequently, the attacker will not be able to access the patient’s signature.
5. Experimental Results and Discussion
5.1. Storage Cost
5.2. Computation Cost
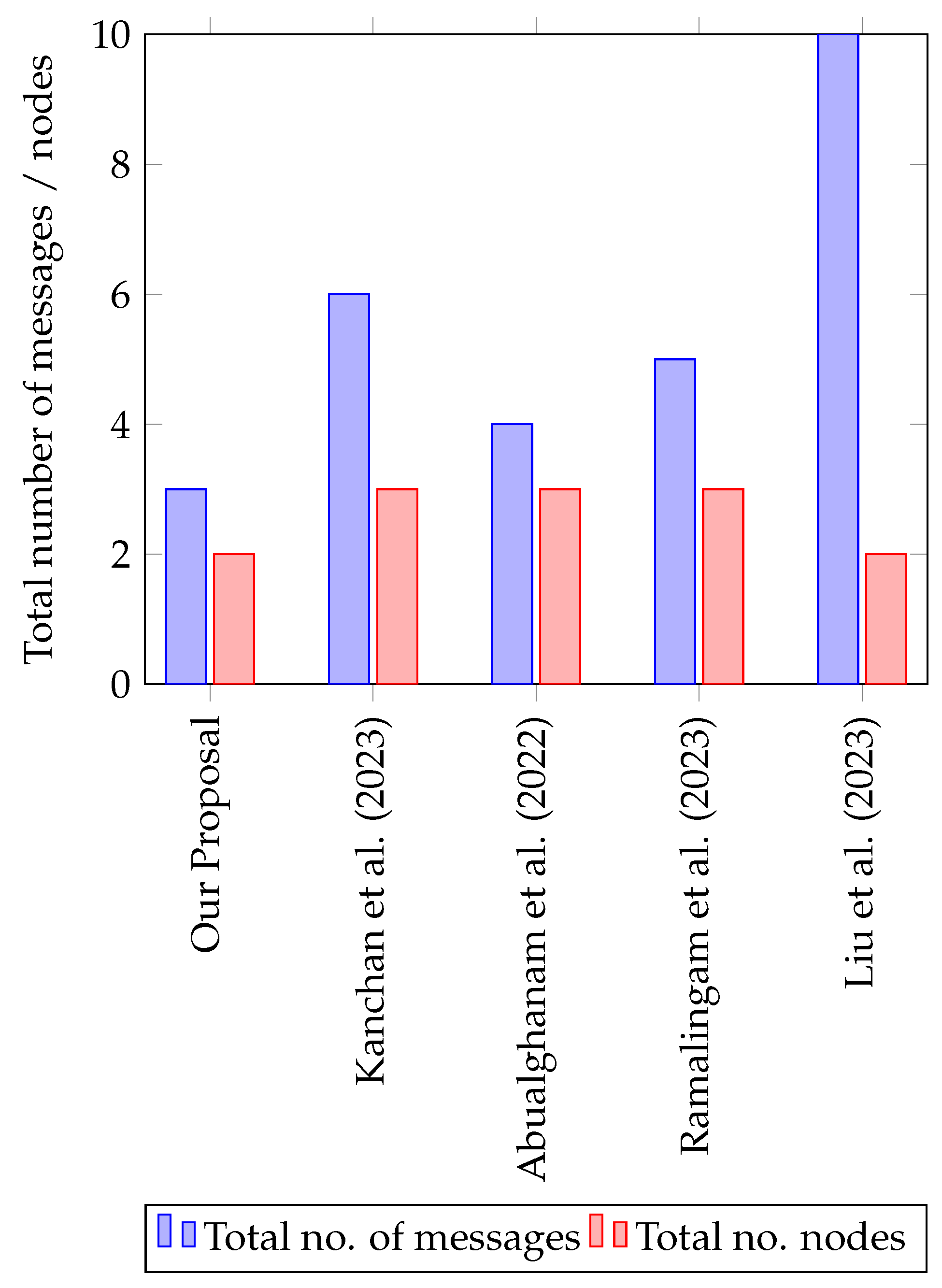
5.3. Communication Cost
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Elliptic Curve Diffie–Hellman
- Elliptic Curves: At the heart of ECDH is the use of elliptic curves over finite fields. An elliptic curve is a mathematical structure defined by Equation (A1).where a and b are constants. The curve is defined over a finite field, which means all calculations are performed modulo a prime number p.
- Key Generation: Each party involved in the key exchange process generates its own elliptic curve key pair. This consists of a private key (a randomly chosen number) and a corresponding public key (calculated by multiplying the base point of the curve by the private key).
- Key Exchange: When two parties want to establish a shared secret key, they exchange their public keys over an insecure communication channel.
- Shared Secret Calculation: Each party uses their private key and the received public key to independently compute a shared secret point on the elliptic curve. The magic of elliptic curve mathematics ensures that these independently calculated shared secrets are equal.
- Shared Secret Derivation: The shared secret point is then used as an input to a key derivation function (KDF) to produce a shared secret key. This shared secret can be used for the symmetric encryption and decryption of data between the two parties.
Appendix A.2. Simulation Code of the Security Proof

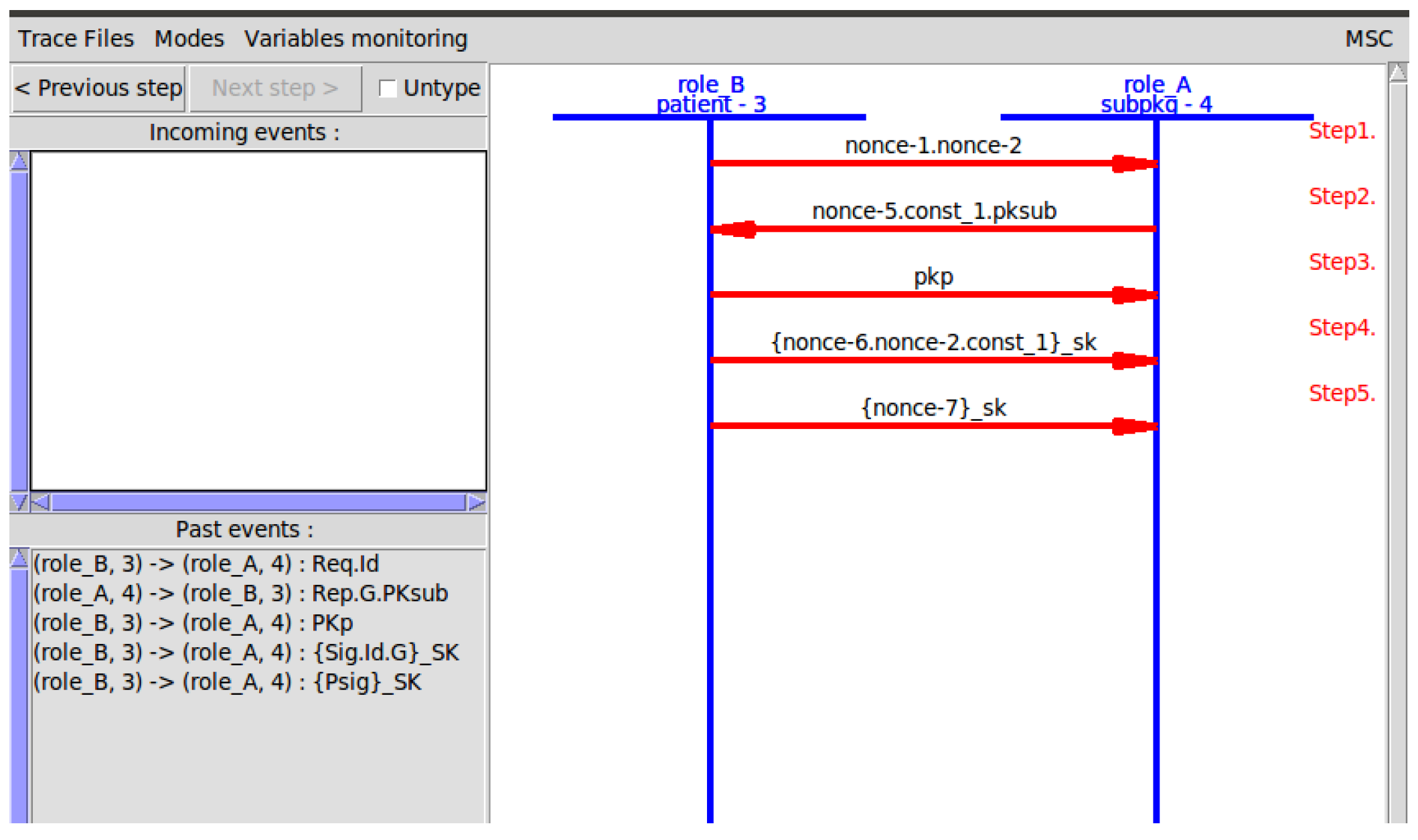




Appendix A.3. BAN Logic
- P∣≡ X: P believes X. This means that P considers X to be true and acts accordingly.
- P ◃ X: P sees X, i.e., when P receive a message contains X, then P sees X.
- P ∣∼ X: P said X.
- P ‖∼: P recently said X.
- P⇒ X: P has jurisdiction over X or P controls X.
- #(X): The formula X is fresh. This means that X has not been sent in a message at any time before the current run of the protocol.
- xk: This means that formula X is encrypted using the key k.
- x : This represents that formula X is encrypted using the inverse key of k, i.e., if k is a public key, then is the private key that corresponds to k.
- PK (k, P): k is a public key for P and there exists a unique key that corresponds to k.
- II(P): P has a private key that is known only to P.
- (X, P): X is signed by P’s private key.
- A B , K is a shared key between only A and B.
- : →: {{P, , , ,} } .
- : →:{{LM, , } } .
- : → {{GM, ,} }.
- A1: means that Root PKG Rooti believes that is the public key of the Sub- Subi.
- A2: means that Root PKG Rooti believes that the Subi has a private key that corresponds to its public key.
- A3: means that Subi believes that is the public key of Rooti.
- A4: means that Subi believes that Rooti has a private key that corresponds to its public key.
- A5: means that Root PKG Rooti believes that Subi controls the generation of message and local model LM.
- A6: means that Subi believes that Rooti controls the generation of message and the parameters P.
- A7: means that Subi believes that part of message is fresh and has not been sent previously.
- A8: means that Root PKG Rooti believes that part of message is fresh and has not been sent previously.
- A9: means that Subi believes that part of message is fresh and has not been sent previously.
- A10: means that Subi believes that Rooti controls the generation of message and the global model GM.
- G1: means that Subi should believe that Rooti has said message . So, Subi authenticates Rooti.
- G2: means that Subi should believe message , which includes the parameters, and consider it true.
- G3: means that Subi should believe that message is fresh and not sent before.
- G4: means that the Root PKG Rooti should believe that Subi has said message , which includes the local model LM. So, Rooti authenticates the Subi.
- G5: means that the Root PKG Rooti should believe that message , which includes the LM is true.
- G6: means that the Root PKG Rooti should believe that message is fresh and not sent before.
- G7: means that Subi should believe that Rooti has said message .
- G8: means that Subi should believe message , which includes the global model GM and consider it true.
- G9: means that Subi should believe that message is fresh and not sent before.
- is Sub-PKGi
- is the public key of
- is the private key of
- is the public key of
- is the private key of
- is the session key between and
- is the public component of
- is the public component of
- is the digital certificate for
- is the digital certificate of
- is the first message in this phase between and
- is the second message in this phase sent from to
- is the third message in this phase sent from to
- is the fourth message in this phase sent from to
- is the fifth message sent from to
- : :
- : :
- : :
- : :
- : :
- A1: means that believes that is a key shared between and
- A2: means that believes that is a key shared between and
- G1: means that should believe that has sent message , which includes N3. So, authenticates .
- G2: means that should believe that has sent message which includes the same nonce N3. So, authenticates .
- :
- : :
- : :
- A1: means that believes that is the public key of .
- A2: means that believes that has a private key that corresponds to its public key.
- A3: means that believes that is the public key of .
- A4: means that believes that has a private key that corresponds to its public key.
- A5: means that believes that part of message is fresh and has not been sent previously.
- A6: means that believes that part of message is fresh and has not been sent previously.
- A7: means that believes that controls the generation of message which includes Psig.
- A8: means that believes that controls the generation of message and the session key SK.
- A9: means that believes that SK is a key shared between and .
- A10: means that believes that SK is a key shared between and .
- G1: means that should believe that has sent message , which includes the patient’s signature Psig.
- G2: means that should believe message .
- G3: means that should believe that message is fresh and has not been sent before.
- G4: means that should believe that has sent message , which includes the session key SK.
- G5: means that should believe message which includes the session key SK.
- G6: means that should believe that message , which includes the session key SK, is fresh and has not been sent before.
- G7: means that should believe that has sent message , which includes the same nonce . So, authenticates .
References
- Razdan, S.; Sharma, S. Internet of medical things (IoMT): Overview, emerging technologies, and case studies. IETE Tech. Rev. 2022, 39, 775–788. [Google Scholar] [CrossRef]
- Mishra, P.; Singh, G. Internet of Medical Things Healthcare for Sustainable Smart Cities: Current Status and Future Prospects. Appl. Sci. 2023, 13, 8869. [Google Scholar] [CrossRef]
- Manickam, P.; Mariappan, S.A.; Murugesan, S.M.; Hansda, S.; Kaushik, A.; Shinde, R.; Thipperudraswamy, S. Artificial intelligence (AI) and internet of medical things (IoMT) assisted biomedical systems for intelligent healthcare. Biosensors 2022, 12, 562. [Google Scholar] [CrossRef]
- Ullah, M.; Hamayun, S.; Wahab, A.; Khan, S.U.; Rehman, M.U.; Haq, Z.U.; Rehman, K.U.; Ullah, A.; Mehreen, A.; Awan, U.A.; et al. Smart Technologies used as Smart Tools in the Management of Cardiovascular Disease and their Future Perspective. Curr. Probl. Cardiol. 2023, 48, 101922. [Google Scholar] [CrossRef]
- Hireche, R.; Mansouri, H.; Pathan, A.S.K. Security and privacy management in Internet of Medical Things (IoMT): A synthesis. J. Cybersecur. Priv. 2022, 2, 640–661. [Google Scholar] [CrossRef]
- Omolara, A.E.; Alabdulatif, A.; Abiodun, O.I.; Alawida, M.; Alabdulatif, A.; Hamdan Alshoura, W. Arshad, H. The internet of things security: A survey encompassing unexplored areas and new insights. Comput. Secur. 2022, 112, 102494. [Google Scholar] [CrossRef]
- Abouelmehdi, K.; Beni-Hessane, A.; Khaloufi, H. Big healthcare data: Preserving security and privacy. J. Big Data 2018, 5, 1–18. [Google Scholar] [CrossRef]
- Borgia, E. The Internet of Things vision: Key features, applications and open issues. Comput. Commun. 2014, 54, 1–31. [Google Scholar] [CrossRef]
- Aminizadeh, S.; Heidari, A.; Toumaj, S.; Darbandi, M.; Navimipour, N.J.; Rezaei, M.; Talebi, S.; Azad, P.; Unal, M. The applications of machine learning techniques in medical data processing based on distributed computing and the Internet of Things. Comput. Methods Programs Biomed. 2023, 241, 107745. [Google Scholar] [CrossRef]
- Hasan, M.K.; Ghazal, T.M.; Saeed, R.A.; Pandey, B.; Gohel, H.; Eshmawi, A.; Abdel-Khalek, S.; Alkhassawneh, H.M. A review on security threats, vulnerabilities, and counter measures of 5G enabled Internet-of-Medical-Things. IET Commun. 2022, 16, 421–432. [Google Scholar] [CrossRef]
- Alhaj, T.A.; Abdulla, S.M.; Iderss, M.A.E.; Ali, A.A.A.; Elhaj, F.A.; Remli, M.A.; Gabralla, L.A. A survey: To govern, protect, and detect security principles on internet of medical things (iomt). IEEE Access 2022, 10, 124777–124791. [Google Scholar]
- Alsaeed, N.; Nadeem, F. Authentication in the Internet of Medical Things: Taxonomy, Review, and Open Issues. Appl. Sci. 2022, 12, 7487. [Google Scholar] [CrossRef]
- Rasool, R.U.; Ahmad, H.F.; Rafique, W.; Qayyum, A.; Qadir, J. Security and privacy of internet of medical things: A contemporary review in the age of surveillance, botnets, and adversarial ML. J. Netw. Comput. Appl. 2022, 201, 103332. [Google Scholar]
- Abualghanam, O.; Qatawneh, M.; Almobaideen, W. A survey of key distribution in the context of internet of things. J. Theor. Appl. Inf. Technol. 2019, 97, 3217–3241. [Google Scholar]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Yang, T.; Andrew, G.; Eichner, H.; Sun, H.; Li, W.; Kong, N.; Ramage, D.; Beaufays, F. Applied federated learning: Improving google keyboard query suggestions. arXiv 2018, arXiv:1812.02903. [Google Scholar]
- Rieke, N.; Hancox, J.; Li, W.; Milletari, F.; Roth, H.R.; Albarqouni, S.; Bakas, S.; Galtier, M.N.; Landman, B.A.; Maier-Hein, K.; et al. The future of digital health with federated learning. NPJ Digit. Med. 2020, 3, 119. [Google Scholar]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar]
- Kanagavelu, R.; Li, Z.; Samsudin, J.; Yang, Y.; Yang, F.; Goh, R.S.M.; Cheah, M.; Wiwatphonthana, P.; Akkarajitsakul, K.; Wang, S. Two-phase multi-party computation enabled privacy-preserving federated learning. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), IEEE, Melbourne, Australia, 11–14 May 2020; pp. 410–419. [Google Scholar]
- Mo, F.; Haddadi, H.; Katevas, K.; Marin, E.; Perino, D.; Kourtellis, N. PPFL: Privacy-preserving federated learning with trusted execution environments. In Proceedings of the 19th Annual International Conference on Mobile Systems, Applications, and Services, Virtual, 24 June–2 July 2021; pp. 94–108. [Google Scholar]
- Hsu, C.Y.; Lu, C.S.; Pei, S.C. Image feature extraction in encrypted domain with privacy-preserving SIFT. IEEE Trans. Image Process. 2012, 21, 4593–4607. [Google Scholar]
- Ji, J.; Wang, H.; Huang, Y.; Wu, J.; Xu, X.; Ding, S.; Zhang, S.; Cao, L.; Ji, R. Privacy-preserving face recognition with learnable privacy budgets in frequency domain. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 475–491. [Google Scholar]
- Chen, C.; Wu, H.; Su, J.; Lyu, L.; Zheng, X.; Wang, L. Differential private knowledge transfer for privacy-preserving cross-domain recommendation. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 1455–1465. [Google Scholar]
- Li, A.; Sun, J.; Zeng, X.; Zhang, M.; Li, H.; Chen, Y. Fedmask: Joint computation and communication-efficient personalized federated learning via heterogeneous masking. In Proceedings of the 19th ACM Conference on Embedded Networked Sensor Systems, Coimbra, Portugal, 15–17 November 2021; pp. 42–55. [Google Scholar]
- Zhang, W.; Yang, D.; Wu, W.; Peng, H.; Zhang, N.; Zhang, H.; Shen, X. Optimizing federated learning in distributed industrial IoT: A multi-agent approach. IEEE J. Sel. Areas Commun. 2021, 39, 3688–3703. [Google Scholar]
- Lim, W.Y.B.; Luong, N.C.; Hoang, D.T.; Jiao, Y.; Liang, Y.C.; Yang, Q.; Niyato, D.; Miao, C. Federated learning in mobile edge networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 2031–2063. [Google Scholar] [CrossRef]
- Fang, C.; Guo, Y.; Hu, Y.; Ma, B.; Feng, L.; Yin, A. Privacy-preserving and communication-efficient federated learning in internet of things. Comput. Secur. 2021, 103, 102199. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Xiong, Z.; Kang, J.; Wang, X.; Niyato, D. Federated learning for 6G communications: Challenges, methods, and future directions. China Commun. 2020, 17, 105–118. [Google Scholar] [CrossRef]
- Al-Issa, Y.; Ottom, M.A.; Tamrawi, A. eHealth cloud security challenges: A survey. J. Healthc. Eng. 2019, 2019, 7516035. [Google Scholar] [CrossRef]
- Usak, M.; Kubiatko, M.; Shabbir, M.S.; Viktorovna Dudnik, O.; Jermsittiparsert, K.; Rajabion, L. Health care service delivery based on the Internet of things: A systematic and comprehensive study. Int. J. Commun. Syst. 2020, 33, e4179. [Google Scholar] [CrossRef]
- Somasundaram, R.; Thirugnanam, M. Review of security challenges in healthcare internet of things. Wirel. Netw. 2021, 27, 5503–5509. [Google Scholar] [CrossRef]
- AbuAlghanam, O.; Qatawneh, M.; Almobaideen, W.; Saadeh, M. A new hierarchical architecture and protocol for key distribution in the context of IoT-based smart cities. J. Inf. Secur. Appl. 2022, 67, 103173. [Google Scholar] [CrossRef]
- Mohammed, I.A. Cloud identity and access management–A model proposal. Int. J. Innov. Eng. Res. Technol. 2019, 6, 1–8. [Google Scholar]
- Jan, S.U.; Ali, S.; Abbasi, I.A.; Mosleh, M.A.; Alsanad, A.; Khattak, H. Secure patient authentication framework in the healthcare system using wireless medical sensor networks. J. Healthc. Eng. 2021, 2021, 9954089. [Google Scholar] [CrossRef]
- Khan, M.A.; Quasim, M.T.; Alghamdi, N.S.; Khan, M.Y. A secure framework for authentication and encryption using improved ECC for IoT-based medical sensor data. IEEE Access 2020, 8, 52018–52027. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, C.; Chen, H.; Yang, F. A lightweight anonymous mutual authentication and key agreement scheme for WBAN. Concurr. Comput. Pract. Exp. 2019, 31, e5295. [Google Scholar] [CrossRef]
- Alzahrani, B.A.; Irshad, A.; Albeshri, A.; Alsubhi, K. A provably secure and lightweight patient-healthcare authentication protocol in wireless body area networks. Wirel. Pers. Commun. 2021, 117, 47–69. [Google Scholar] [CrossRef]
- Mohammedi, M.; Omar, M.; Bouabdallah, A. Secure and lightweight remote patient authentication scheme with biometric inputs for mobile healthcare environments. J. Ambient. Intell. Humaniz. Comput. 2018, 9, 1527–1539. [Google Scholar] [CrossRef]
- Singh, S.; Rathore, S.; Alfarraj, O.; Tolba, A.; Yoon, B. A framework for privacy-preservation of IoT healthcare data using Federated Learning and blockchain technology. Future Gener. Comput. Syst. 2022, 129, 380–388. [Google Scholar] [CrossRef]
- Alkeem, E.A.; Shehada, D.; Yeun, C.Y.; Zemerly, M.J.; Hu, J. New secure healthcare system using cloud of things. Clust. Comput. 2017, 20, 2211–2229. [Google Scholar] [CrossRef]
- Ullah, I.; Amin, N.U.; Khan, M.A.; Khattak, H.; Kumari, S. An efficient and provable secure certificate-based combined signature, encryption and signcryption scheme for internet of things (IoT) in mobile health (M-health) system. J. Med. Syst. 2021, 45, 1–14. [Google Scholar] [CrossRef]
- Tan, H.; Chung, I. Secure authentication and group key distribution scheme for WBANs based on smartphone ECG sensor. IEEE Access 2019, 7, 151459–151474. [Google Scholar] [CrossRef]
- Ali, R.; Pal, A.K. Cryptanalysis and biometric-based enhancement of a remote user authentication scheme for e-healthcare system. Arab. J. Sci. Eng. 2018, 43, 7837–7852. [Google Scholar] [CrossRef]
- Wang, S.; Cao, Z.; Strangio, M.A.; Wang, L. Cryptanalysis and improvement of an elliptic curve Diffie-Hellman key agreement protocol. IEEE Commun. Lett. 2008, 12, 149–151. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R. A logic of authentication. ACM Trans. Comput. Syst. (TOCS) 1990, 8, 18–36. [Google Scholar] [CrossRef]
- Shang, T.; Liu, J. Secure Quantum Network Coding Theory; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yu, S.; Park, K.; Lee, J.; Park, Y.; Park, Y.; Lee, S.; Chung, B. Privacy-preserving lightweight authentication protocol for demand response management in smart grid environment. Appl. Sci. 2020, 10, 1758. [Google Scholar] [CrossRef]
- Sierra, J.M.; Hernández, J.C.; Alcaide, A.; Torres, J. Validating the Use of BAN LOGIC. In Proceedings of the Computational Science and Its Applications–ICCSA 2004: International Conference, Assisi, Italy, 14–17 May 2004; Proceedings, Part I 4. Springer: Berlin/Heidelberg, Germany, 2004; pp. 851–858. [Google Scholar]
- Saadeh, M.; Sleit, A.; Sabri, K.E.; Almobaideen, W. Hierarchical architecture and protocol for mobile object authentication in the context of IoT smart cities. J. Netw. Comput. Appl. 2018, 121, 1–19. [Google Scholar]
- Wesam Almobaideen, M.S. Lightweight Authentication for Mobile Users in the Context of Fog Computing. Int. J. Adv. Comput. Eng. Netw. 2018, 6, 17–22. [Google Scholar]
- Bos, J.W.; Halderman, J.A.; Heninger, N.; Moore, J.; Naehrig, M.; Wustrow, E. Elliptic curve cryptography in practice. In Proceedings of the Financial Cryptography and Data Security: 18th International Conference, FC 2014, Christ Church, Barbados, 3–7 March 2014; Revised Selected Papers 18. Springer: Berlin/Heidelberg, Germany, 2014; pp. 157–175. [Google Scholar]
- Adalier, M.; Teknik, A. Efficient and secure elliptic curve cryptography implementation of curve p-256. In Proceedings of the Workshop on Elliptic Curve Cryptography Standards, NIST, Gaithersburg, MA, USA, 11 June 2015; Volume 66, pp. 2014–2017. [Google Scholar]
- Al-Zubaidie, M.; Zhang, Z.; Zhang, J. Efficient and secure ECDSA algorithm and its applications: A survey. arXiv 2019, arXiv:1902.10313. [Google Scholar]
- Maimuţ, D.; Matei, A.C. Speeding-Up Elliptic Curve Cryptography Algorithms. Mathematics 2022, 10, 3676. [Google Scholar] [CrossRef]
- Kanchan, S.; Jang, J.W.; Yoon, J.Y.; Choi, B.J. Efficient and privacy-preserving group signature for federated learning. Future Gener. Comput. Syst. 2023, 147, 93–106. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.; Han, G.; Cao, J.; Cui, H.; Zheng, D. Secure and efficient smart healthcare system based on federated learning. Int. J. Intell. Syst. 2023, 2023, 8017489. [Google Scholar] [CrossRef]
- Ramalingam, P.; Pabitha, P. Ask-ram-imot: Autonomous shared keys based remote authentication method for internet of medical things applications. Wirel. Pers. Commun. 2023, 131, 273–293. [Google Scholar]
- Jiby, J. Puthiyidam, Shelbi Joseph, B.B. Enhanced authentication security for IoT client nodes through T ECDSA integrated into MQTT broker. J. Supercomput. 2024, 80, 8898–8932. [Google Scholar]
- Jiby, J. Puthiyidam, Shelbi Joseph, B.B. Temporal ECDSA: Atime stamp and signature mask enabled ECDSA algorithm for IoT client node authentication. Comput. Commun. 2024, 216, 307–323. [Google Scholar]
- Yang, X.b.; Liu, Y.; Wu, J.s.; Han, G.; Liu, Y.x.; Xi, X.q. Nomop-ecdsa: A lightweight ecdsa engine for internet of things. Wirel. Pers. Commun. 2021, 121, 171–190. [Google Scholar] [CrossRef]
- Logeshwaran, J.; Shanmugasundaram, N.; Lloret, J. Energy-efficient resource allocation model for device-to-device communication in 5G wireless personal area networks. Int. J. Commun. Syst. 2023, 36, e5524. [Google Scholar] [CrossRef]
- Subramanian, E.; Tamilselvan, L. Elliptic curve Diffie–Hellman cryptosystem in big data cloud security. Clust. Comput. 2020, 23, 3057–3067. [Google Scholar] [CrossRef]
- Kumar, M. A secure and efficient authentication protocol based on elliptic curve diffie-hellman algorithm and zero knowledge property. Int. J. Soft Comput. Eng. 2013, 3, 137–142. [Google Scholar]


| Notations | Description |
|---|---|
| GM | Global model |
| LM | Local model |
| PKG | Public key generator |
| Public key for the | |
| Private key for the | |
| Digital signature for | |
| Digital signature for | |
| ID | Real identity of the patient |
| H | Hash function |
| Elliptic curve range | |
| Ranges for group signature | |
| Root sign value | |
| Sub-PKG sign value |
| Abbreviation | Size (Byte) |
|---|---|
| Digital Signature | 64 |
| Public Key | 64 |
| Private Key | 64 |
| Unique Identifiers | 16 |
| Shared Key | 32 |
| Patient Signature | 64 |
| Root Signature ( | 64 |
| Patient Secret Value ( | 64 |
| Node Type | Storage | Size in (Bytes) |
|---|---|---|
| , , , root parameters , , , n*. | 384 + 64 n | |
| , , , m*SK, , | 320 + 32 m | |
| SK, , , , | 240 |
| Scheme | Number of Shared Keys |
|---|---|
| Our Proposal | 1 |
| [57] | 1 |
| [55] | 2 |
| [32] | 3 |
| [56] | 2 |
| Metric | Description |
|---|---|
| The computing time of the modular multiplication operation. | |
| The computing time of the modular addition operation (negligible). | |
| The computing time of the modular inversion operation. | |
| The computing time of the elliptic curve multiplication operation. | |
| The computing time of the elliptic curve addition operation. |
| Schemes | Signing Cost | Verification Cost | Node Cost | Server Cost |
|---|---|---|---|---|
| Our scheme | TM + TEM + TIN = 41.6 TM | 2TM + 2TEM + TIN + TEA = 71.72 TM | 41.6 TM (once) | 71.72 TM*n |
| [58] | TM + TEM + TIN = 41.6 TM | 2TM + 2TEM + TIN + TEA = 71.72 TM | 41.6 TM*n | 71.72 TM*n |
| [60] | TM + TEM = 30 TM | 2 TEM + TEA = 58.12 TM | (30 TM + 58.12 TM)*n | (30 TM + 58.12 TM)*n |
| [59] | TM + 2TEM = 59 TM | 2TEM + TEA = 58.12 TM | 59 TM*n | 58.12 TM*n |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbuAlghanam, O.; Alazzam, H.; Almobaideen, W.; Saadeh, M.; Saadeh, H. A Novel Key Distribution for Mobile Patient Authentication Inspired by the Federated Learning Concept and Based on the Diffie–Hellman Elliptic Curve. Sensors 2025, 25, 2357. https://doi.org/10.3390/s25082357
AbuAlghanam O, Alazzam H, Almobaideen W, Saadeh M, Saadeh H. A Novel Key Distribution for Mobile Patient Authentication Inspired by the Federated Learning Concept and Based on the Diffie–Hellman Elliptic Curve. Sensors. 2025; 25(8):2357. https://doi.org/10.3390/s25082357
Chicago/Turabian StyleAbuAlghanam, Orieb, Hadeel Alazzam, Wesam Almobaideen, Maha Saadeh, and Heba Saadeh. 2025. "A Novel Key Distribution for Mobile Patient Authentication Inspired by the Federated Learning Concept and Based on the Diffie–Hellman Elliptic Curve" Sensors 25, no. 8: 2357. https://doi.org/10.3390/s25082357
APA StyleAbuAlghanam, O., Alazzam, H., Almobaideen, W., Saadeh, M., & Saadeh, H. (2025). A Novel Key Distribution for Mobile Patient Authentication Inspired by the Federated Learning Concept and Based on the Diffie–Hellman Elliptic Curve. Sensors, 25(8), 2357. https://doi.org/10.3390/s25082357





