An End-to-End General Language Model (GLM)-4-Based Milling Cutter Fault Diagnosis Framework for Intelligent Manufacturing
Abstract
1. Introduction
2. Model Construction
2.1. Framework of Feature-Based GLM-4
2.1.1. Feature Extraction
2.1.2. Semantic Description
2.2. Framework of Data-Based GLM-4
2.2.1. Patching
2.2.2. Token Embedding
2.2.3. Positional Embedding
2.2.4. Transformer Blocks
2.2.5. Classification Head
2.2.6. Training and Inference
3. Experiment and Results
3.1. Case 1: PHM 2010
3.1.1. Dataset Description
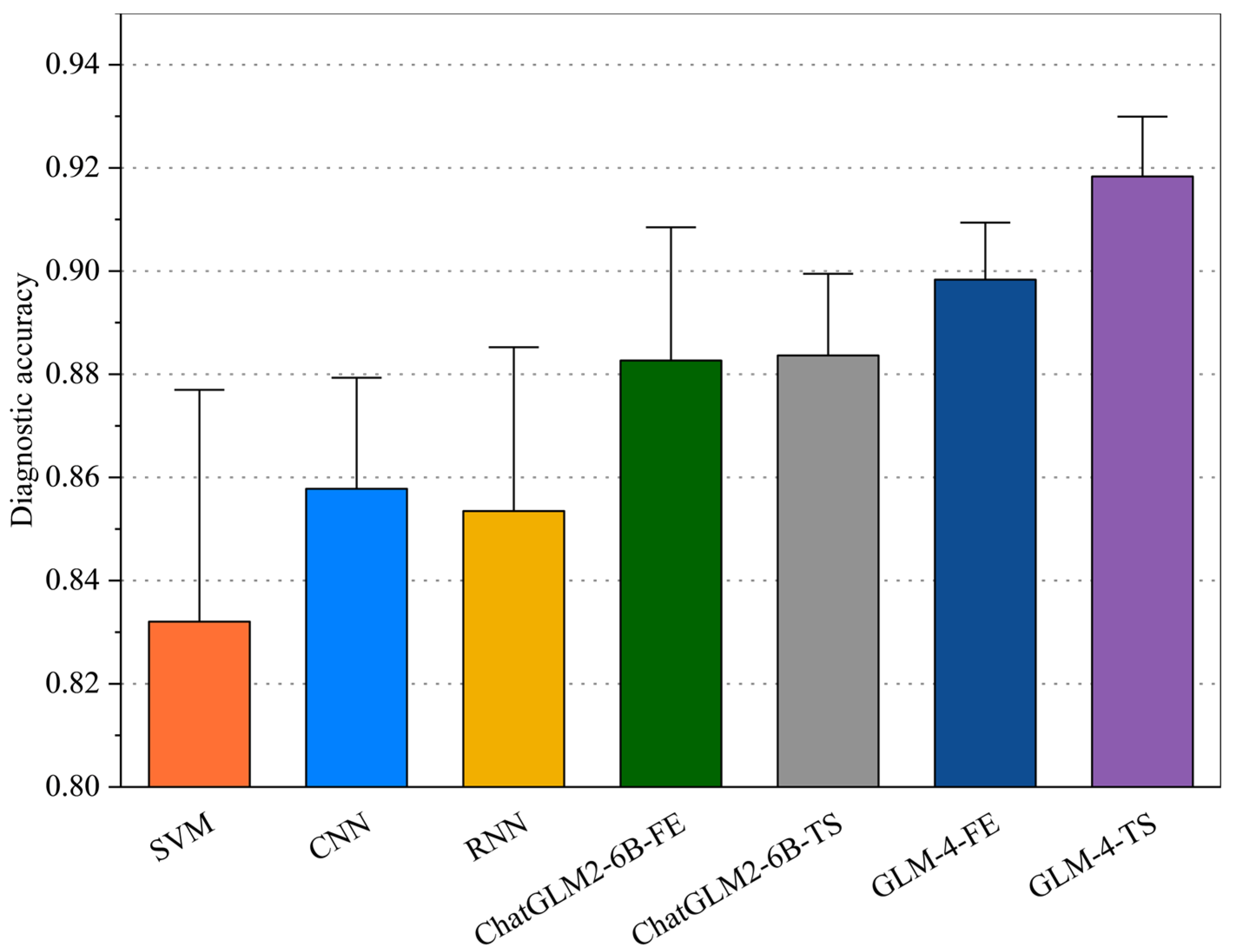
3.1.2. Comprehensive Evaluation
3.2. Case 2: Milling Cutter Experiment
3.2.1. Dataset Description
3.2.2. Comprehensive Evaluation
3.3. Performance Analysis
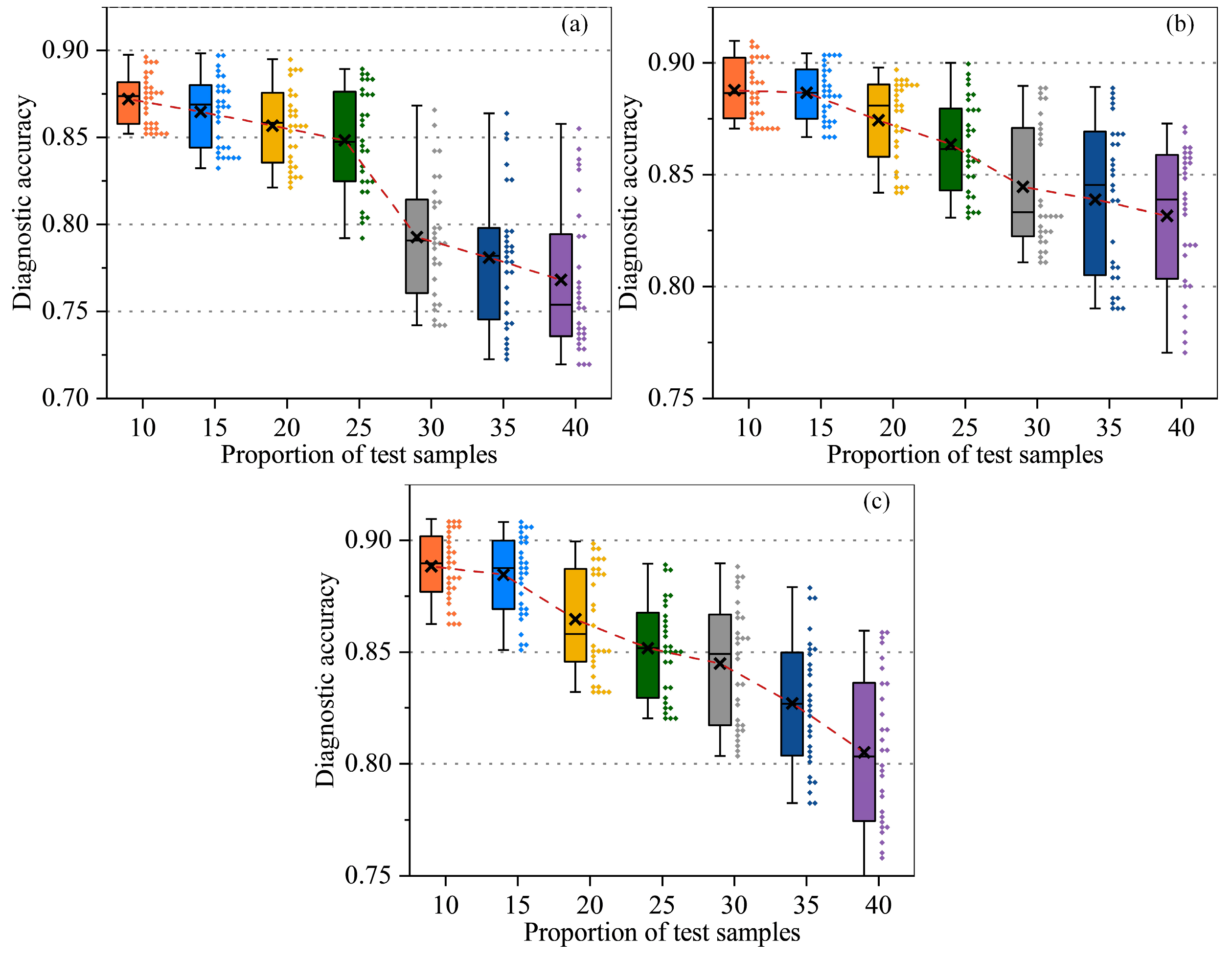
3.3.1. Robustness Analysis
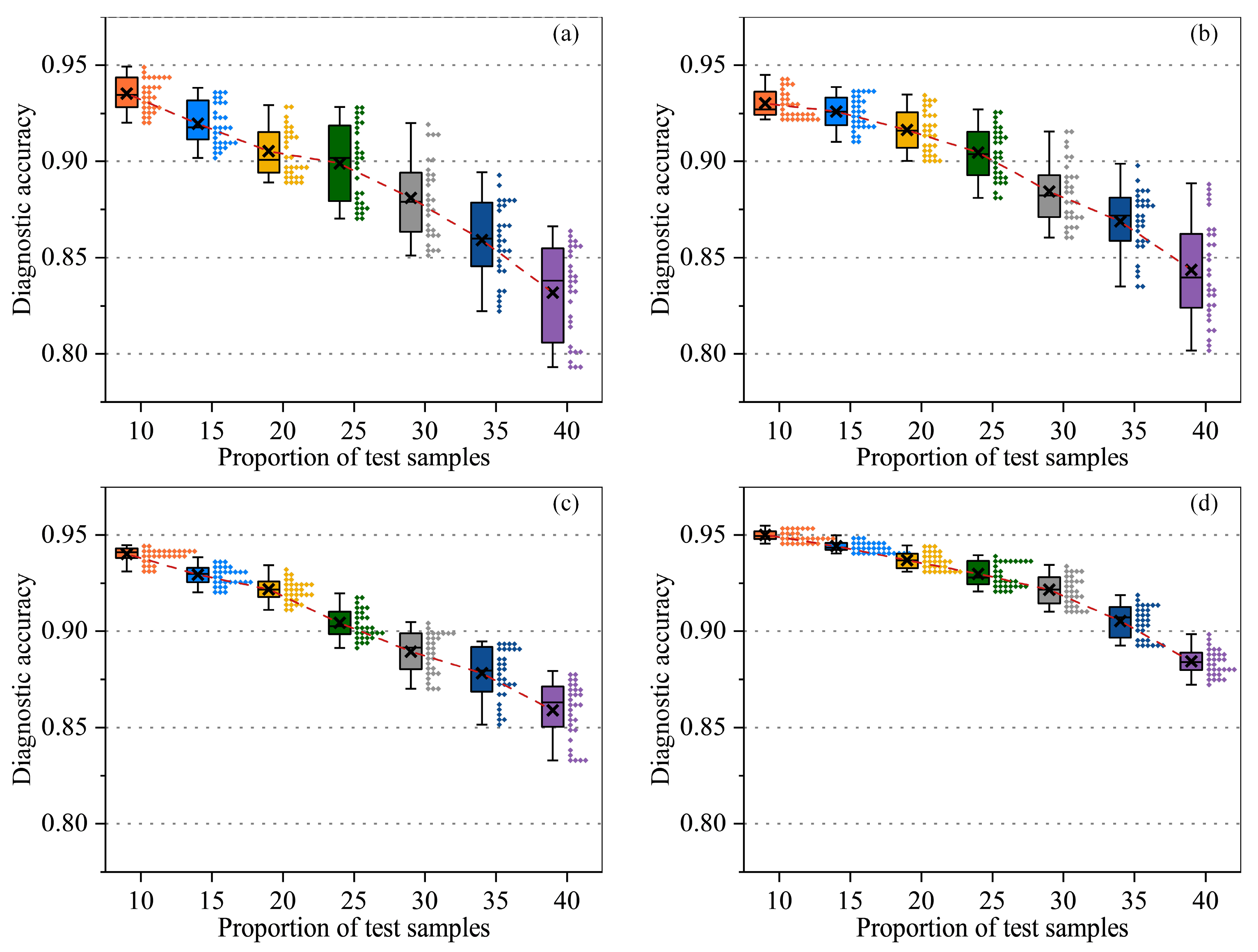
3.3.2. Noise Resistance Analysis
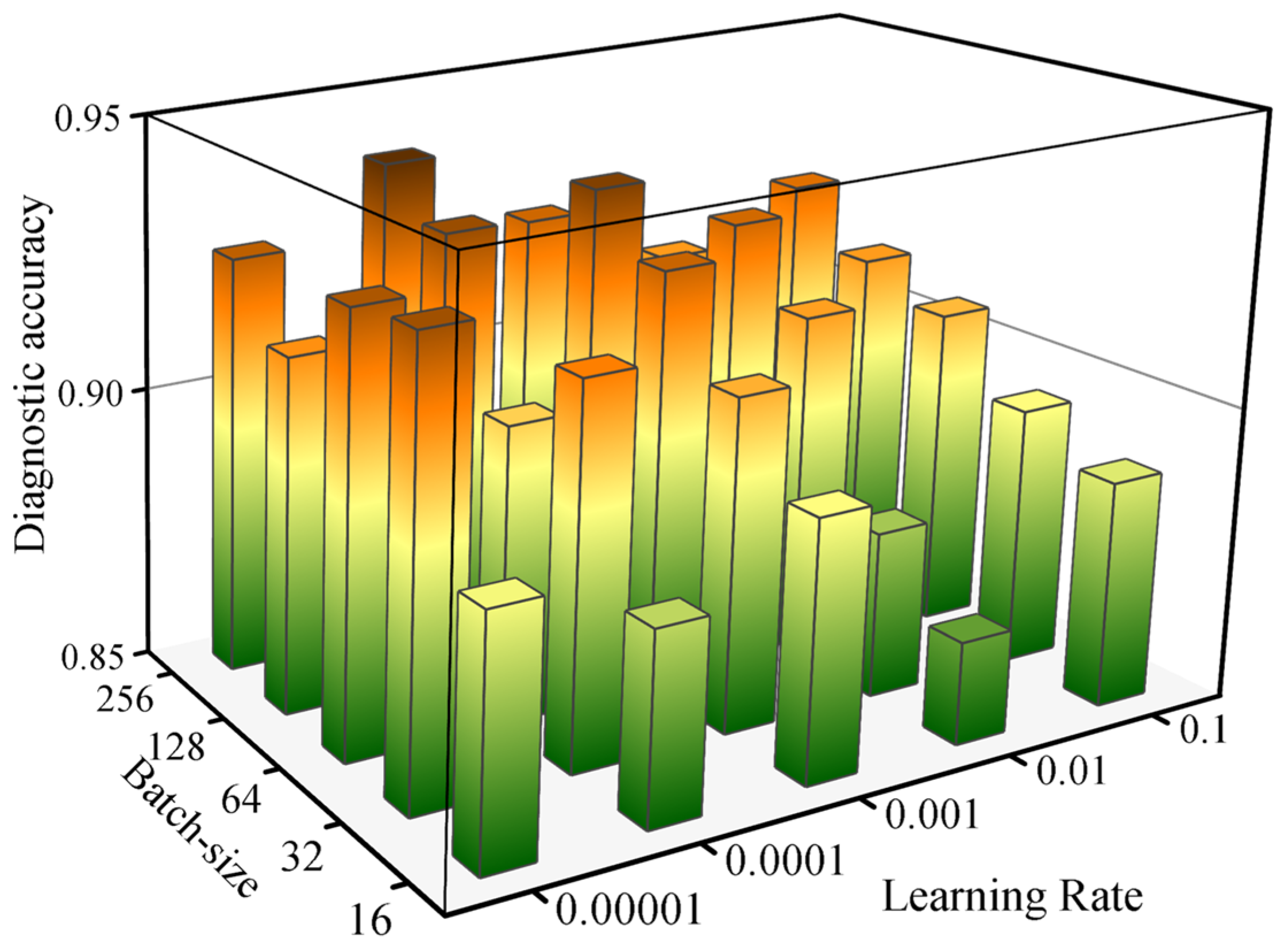
3.3.3. Hyperparameter Analysis
3.3.4. Cross Verification
3.3.5. Training Loss Visualization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| CNC | Computerized Numerical Control |
| CNN | Convolutional Neural Network |
| ChatGLM2 | Chat GLM Version 2 |
| LLM | Large Language Model |
| GLM-4 | General Language Model 4 |
| RNN | Recurrent Neural Network |
| SVM | Support Vector Machine |
| SNR | Signal-to-Noise Ratio |
| LoRA | Low-Rank Adaptation |
| QLoRA | Quantized LoRA |
| PHM | Prognostics Health Management |
References
- He, J.; Sun, Y.; Gao, H.; Guo, L.; Cao, A.; Chen, T. On-Line Milling Tool Wear Monitoring under Practical Machining Conditions. Measurement 2023, 222, 113621. [Google Scholar] [CrossRef]
- Abdeltawab, A.; Xi, Z.; Longjia, Z. Tool Wear Classification Based on Maximal Overlap Discrete Wavelet Transform and Hybrid Deep Learning Model. Int. J. Adv. Manuf. Technol. 2024, 130, 2381–2406. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, X.; Wang, T.; He, Y. Tool Wear Condition Monitoring Method Based on Deep Learning with Force Signals. Sensors 2023, 23, 4595. [Google Scholar] [CrossRef]
- Kale, A.P.; Wahul, R.M.; Patange, A.D.; Soman, R.; Ostachowicz, W. Development of Deep Belief Network for Tool Faults Recognition. Sensors 2023, 23, 1872. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, N.; Yang, Y.; Li, L. An Innovative Deep Reinforcement Learning-Driven Cutting Parameters Adaptive Optimization Method Taking Tool Wear into Account. Measurement 2025, 242, 116075. [Google Scholar] [CrossRef]
- Sun, Y.; Song, H.; Gao, H.; Li, J.; Yin, S. Interpretable Tool Wear Monitoring: Architecture with Large-Scale CNN and Adaptive EMD. J. Manuf. Syst. 2025, 78, 294–307. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J.; Zhong, B.; Ming, W.; Chen, M. Deep Learning-Based Tool Wear Prediction and Its Application for Machining Process Using Multi-Scale Feature Fusion and Channel Attention Mechanism. Measurement 2021, 177, 109254. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Jiang, H.; Wang, R.; Qiu, T.; Wang, X. Intelligent Tool Wear Monitoring and Multi-Step Prediction Based on Deep Learning Model. J. Manuf. Syst. 2022, 62, 286–300. [Google Scholar] [CrossRef]
- Yao, J.; Lu, B.; Zhang, J. Tool Remaining Useful Life Prediction Using Deep Transfer Reinforcement Learning Based on Long Short-Term Memory Networks. Int. J. Adv. Manuf. Technol. 2022, 118, 1077–1086. [Google Scholar] [CrossRef]
- Huang, P.-M.; Lee, C.-H. Estimation of Tool Wear and Surface Roughness Development Using Deep Learning and Sensors Fusion. Sensors 2021, 21, 5338. [Google Scholar] [CrossRef]
- Di, Z.; Yuan, D.; Li, D.; Liang, D.; Zhou, X.; Xin, M.; Cao, F.; Lei, T. Tool Fault Diagnosis Method Based on Multiscale-Efficient Channel Attention Network. J. Mech. Eng. 2024, 60, 82–90. [Google Scholar]
- Liu, X.; Zhang, B.; Li, X.; Liu, S.; Yue, C.; Liang, S.Y. An Approach for Tool Wear Prediction Using Customized DenseNet and GRU Integrated Model Based on Multi-Sensor Feature Fusion. J. Intell. Manuf. 2023, 34, 885–902. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, L.; Dun, Y. Tool Wear Monitoring of TC4 Titanium Alloy Milling Process Based on Multi-Channel Signal and Time-Dependent Properties by Using Deep Learning. J. Manuf. Syst. 2021, 61, 495–508. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Lee, C.-H. Deep Learning Approach for Vibration Signals Applications. Sensors 2021, 21, 3929. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J.; He, Z.; Zi, Y. A Multidimensional Hybrid Intelligent Method for Gear Fault Diagnosis. Expert Syst. Appl. 2010, 37, 1419–1430. [Google Scholar] [CrossRef]
- Ding, Y.; Cao, Y.; Jia, M.; Ding, P.; Zhao, X.; Lee, C.-G. Deep Temporal–Spectral Domain Adaptation for Bearing Fault Diagnosis. Knowl.-Based Syst. 2024, 299, 111999. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, Z.; Ping, S.; Li, W.; Liu, J. TRA-ACGAN: A Motor Bearing Fault Diagnosis Model Based on an Auxiliary Classifier Generative Adversarial Network and Transformer Network. ISA Trans. 2024, 149, 381–393. [Google Scholar] [CrossRef]
- Quan, Y.; Liu, C.; Yuan, Z.; Yan, B. Hybrid Data Augmentation Combining Screening-Based MCGAN and Manual Transformation for Few-Shot Tool Wear State Recognition. IEEE Sens. J. 2024, 24, 12186–12196. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines With Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Jia, S.; Deng, Y.; Lv, J.; Du, S.; Xie, Z. Joint Distribution Adaptation with Diverse Feature Aggregation: A New Transfer Learning Framework for Bearing Diagnosis across Different Machines. Measurement 2022, 187, 110332. [Google Scholar] [CrossRef]
- Tian, M.; Su, X.; Chen, C.; Luo, Y.; Sun, X. Bearing Fault Diagnosis of Wind Turbines Based on Dynamic Multi-Adversarial Adaptive Network. J. Mech. Sci. Technol. 2023, 37, 1637–1651. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Chow, T.W.S.; Li, B. Deep Adversarial Subdomain Adaptation Network for Intelligent Fault Diagnosis. IEEE Trans. Ind. Inf. 2022, 18, 6038–6046. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, H.; Cheng, Y.; Shu, T.; Chen, Y.; Liu, G.; Liang, G.; Zhao, J.; Yan, J.; Li, Y. Survey on Large Language Model-Enhanced Reinforcement Learning: Concept, Taxonomy, and Methods. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Gruver, N.; Finzi, M.; Qiu, S.; Wilson, A.G. Large Language Models Are Zero-Shot Time Series Forecasters. arXiv, 2023; arXiv:2310.07820. [Google Scholar]
- Tao, L.; Liu, H.; Ning, G.; Cao, W.; Huang, B.; Lu, C. LLM-Based Framework for Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2025, 224, 112127. [Google Scholar] [CrossRef]
- Lialin, V.; Deshpande, V.; Yao, X.; Rumshisky, A. Scaling Down to Scale Up: A Guide to Parameter-Efficient Fine-Tuning. arXiv 2024, arXiv:2303.15647. [Google Scholar]
- 2010 PHM Society Conference Data Challenge. Available online: https://phmsociety.org/phm_competition/2010-phm-society-conference-data-challenge/ (accessed on 1 April 2023).





| Feature Domain | Feature Name | Mathematical Expression | Physical Meaning |
|---|---|---|---|
| Time Domain | Mean Value (MV) | The average trend of signal amplitude variation. | |
| Root Mean Square (RMS) | The mean energy of the signal over a given time interval. | ||
| Standard Deviation (SD) | The degree of fluctuation of the signal around the mean. | ||
| Skewness Factor (SF) | Variations in the signal waveform. | ||
| Skewness (Ske) | The degree to which the signal distribution deviates from the mean symmetry line. | ||
| Kurtosis (Kur) | The smoothness of the signal waveform. | ||
| Time Domain | Peak Value (PV) | The maximum instantaneous amplitude of the signal. | |
| Crest Factor (CF) | The extremity of the peak in the signal waveform. | ||
| Impact Factor (IF) | The instantaneous impact characteristics of the signal. | ||
| Frequency Domain | Mean Power Spectrum (MPS) | The variation of signal power with frequency. | |
| Frequency Center (FC) | The static portion of the spectrum. | ||
| Mean Square Frequency (MSF) | The degree of fluctuation of the spectrum near the frequency centroid. | ||
| Time–Frequency Domain | Wavelet Packet Energy (WPE) | The average energy of the signal at different scales. |
| Parameter | Category | Parameter | Category |
|---|---|---|---|
| Model | Roders Tech RFM 760 | Radial cutting depth | 0.125 mm |
| Workpiece material | Nickel-based superalloy 718 | Axial cutting depth | 0.2 mm |
| Cutter/Tool | 3-Tooth ball nose milling cutter | Number of sensors | 3 |
| Spindle speed | 10,400 RPM | Sensing channels | 7 |
| Feed rate | 1555 mm/min | Sampling frequency | 50 HZ |
| Cutting speed | 5000–20,000 rpm | Tool diameter | 6–12 mm |
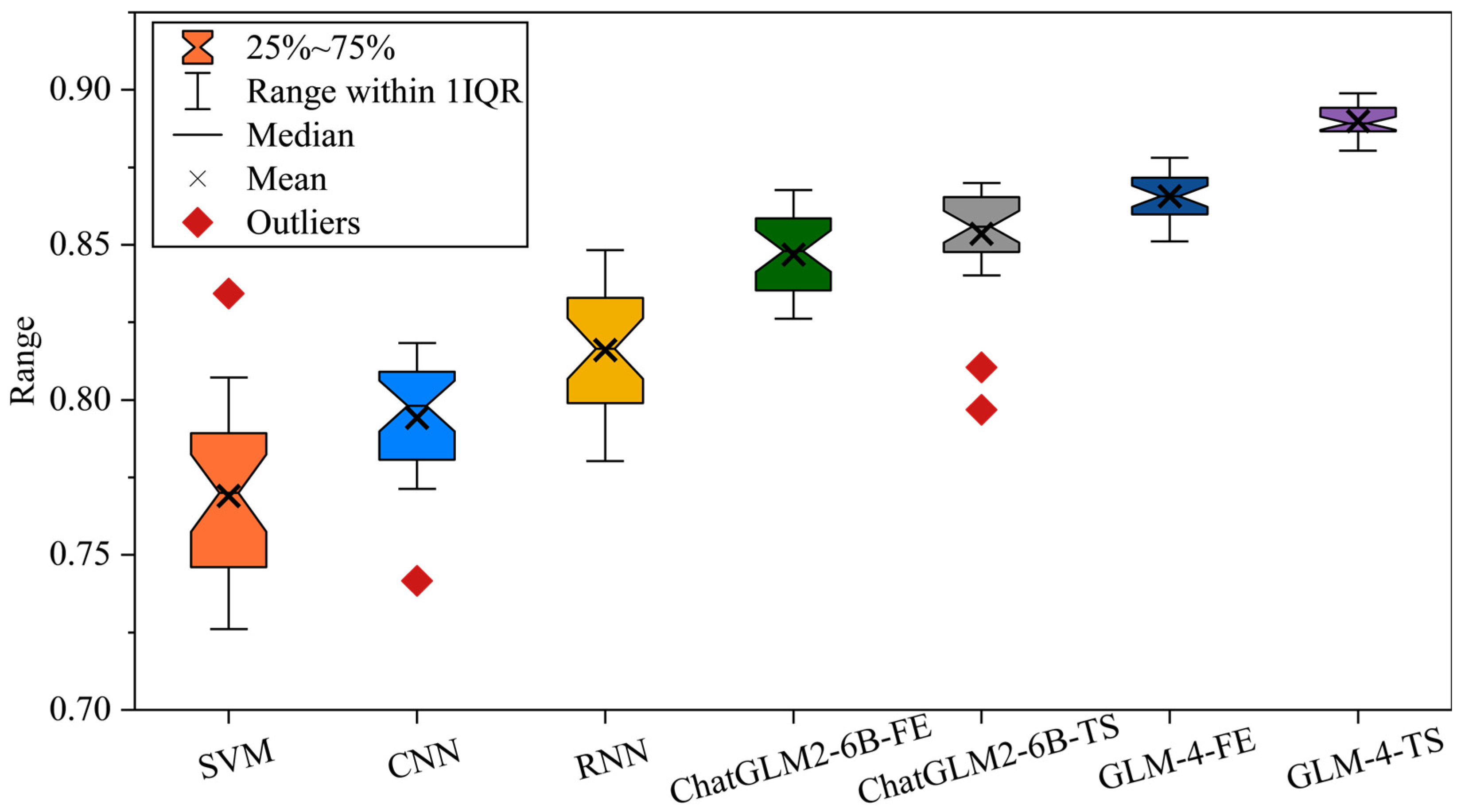
| Model | Diagnostic Accuracy |
|---|---|
| SVM | |
| CNN | |
| RNN | |
| ChatGLM2-6B-FE | |
| ChatGLM2-6B-TS | |
| GLM-4-FE | |
| GLM-4-TS |
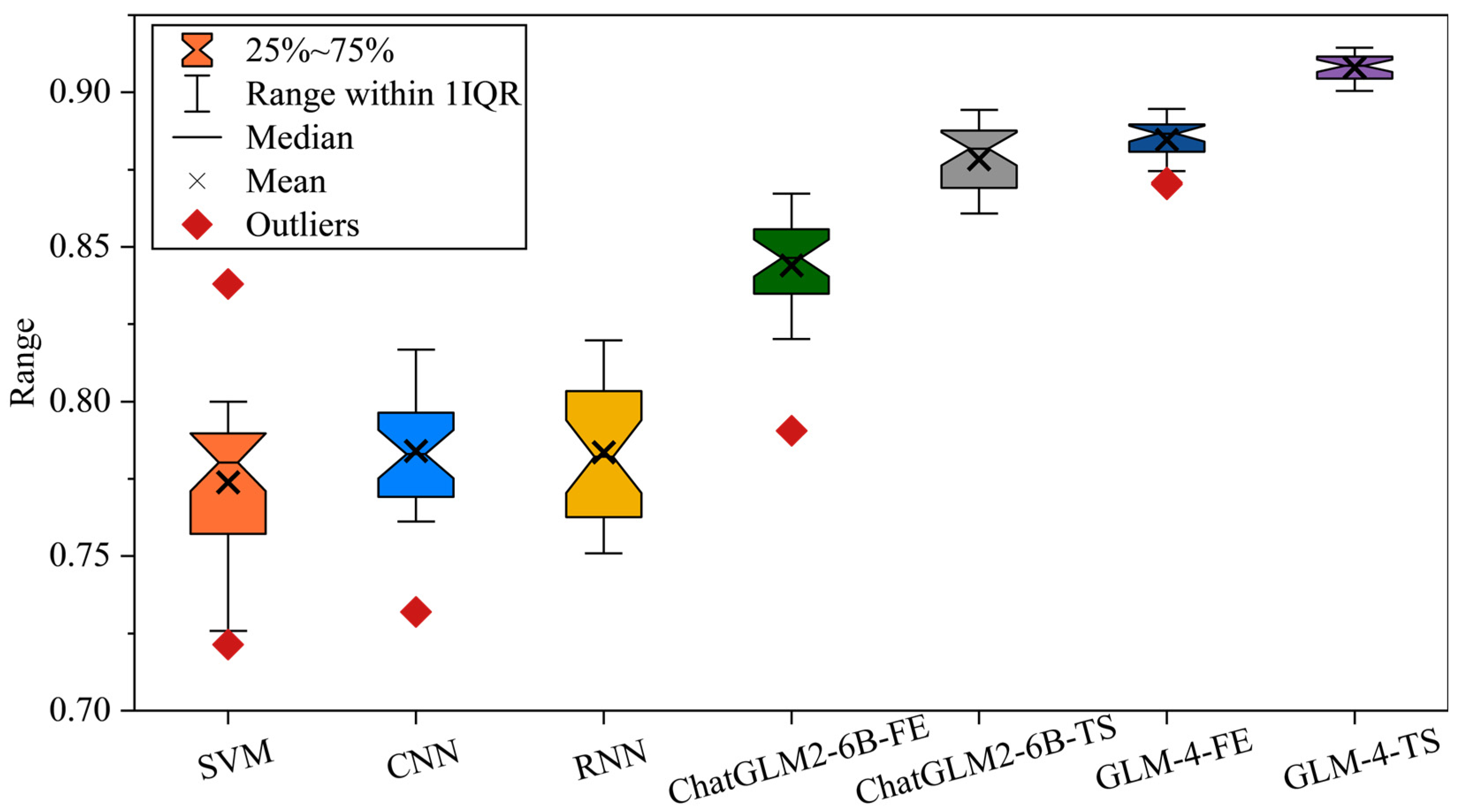
| Model | Diagnostic Accuracy |
|---|---|
| SVM | |
| CNN | |
| RNN | |
| ChatGLM2-6B-FE | |
| ChatGLM2-6B-TS | |
| GLM-4-FE | |
| GLM-4-TS |
| No. | Train | Transfer Dataset | Test Dataset |
|---|---|---|---|
| 1 | Case 1 | 30% Case 2 | 70% Case 2 |
| 2 | Case 2 | 30% Case 1 | 70% Case 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Liu, X.; Lei, Y.; Cao, A.; Xiong, J. An End-to-End General Language Model (GLM)-4-Based Milling Cutter Fault Diagnosis Framework for Intelligent Manufacturing. Sensors 2025, 25, 2295. https://doi.org/10.3390/s25072295
He J, Liu X, Lei Y, Cao A, Xiong J. An End-to-End General Language Model (GLM)-4-Based Milling Cutter Fault Diagnosis Framework for Intelligent Manufacturing. Sensors. 2025; 25(7):2295. https://doi.org/10.3390/s25072295
Chicago/Turabian StyleHe, Jigang, Xuan Liu, Yuncong Lei, Ao Cao, and Jie Xiong. 2025. "An End-to-End General Language Model (GLM)-4-Based Milling Cutter Fault Diagnosis Framework for Intelligent Manufacturing" Sensors 25, no. 7: 2295. https://doi.org/10.3390/s25072295
APA StyleHe, J., Liu, X., Lei, Y., Cao, A., & Xiong, J. (2025). An End-to-End General Language Model (GLM)-4-Based Milling Cutter Fault Diagnosis Framework for Intelligent Manufacturing. Sensors, 25(7), 2295. https://doi.org/10.3390/s25072295





